Global climate mode resonance due to rapidly intensifying El Niño-Southern Oscillation

Abstract

The El Niño-Southern Oscillation (ENSO) influences climate variability globally, encompassing various other modes of variability, and thus represents a key predictable climate signal on seasonal timescales. Yet, its response to greenhouse warming remains uncertain, with models projecting a range of outcomes. Here, we demonstrate that in response to warming, a state-of-the-art high-resolution climate model simulates a rapid transition from a moderate-amplitude irregular regime, as observed in the current climate, to a highly regular oscillation with intensifying amplitude. This behaviour can be attributed to increasing air-sea feedbacks, which approach criticality in the second half of this century, and growing atmospheric noise. As ENSO intensifies in this model, it synchronizes with other prominent climate modes, such as the North Atlantic Oscillation and the Indian Ocean Dipole, thereby imprinting its regular, predictable variability on them. If realized, this global climate mode resonance would have wide-ranging whiplash impacts on regional hydroclimates.

Introduction

Despite the profound influence of the El Niño-Southern Oscillation (ENSO) on the global climate system^1,2, its response to greenhouse warming remains uncertain. Climate models exhibit a wide range of possible future ENSO behaviors^1,3,4,5,6,7, hindering confidence in regional climate projections. The dynamics of ENSO are governed by a delicate balance of positive and negative feedbacks^8,9 that determine both ENSO’s instability¹⁰ and periodicity¹¹. The relative strengths of the individual feedbacks are, in turn, determined by both model parametrizations and the structure of the climate mean state^12,13,14. Previous research, using both simple low-order models¹⁵ and intermediate complexity models¹⁶, has demonstrated how changes in the climate mean state can affect the strength of these feedbacks (such as the zonal advective and thermocline feedbacks) and thereby ENSO characteristics (such as its growth rate, periodicity, and spatial pattern). In addition, recent studies also indicated that the interactions of ENSO with the seasonal cycle^17,18,19 as well as with other more damped empirical modes in the climate system, such as the Indian Ocean Dipole (IOD)²⁰, the Tropical North Atlantic (TNA) mode²¹, or the North Atlantic Oscillation (NAO)²² can shape the dynamics of both ENSO and these other modes^23,24,25.

Over 20 years ago, an ENSO-resolving coupled general circulation model^5,26 exhibited a very intriguing ENSO behavior. It showed a gradual increase in the linear ENSO growth rate in response to greenhouse warming and the crossing of a Hopf bifurcation in the mid-twenty-first century²⁶. This ENSO regime shift towards supercriticality resulted in a rapid intensification in ENSO’s amplitude. Such a drastic transition in qualitative ENSO behavior has not been reported in other complex climate models.

Here we revisit the issue of anthropogenically forced rapid emergence of ENSO supercriticality and its potential repercussions on global climate using an ensemble of state-of-the-art high resolution climate model simulations (AWI-CM3, TCo319 horizonal resolution with ~31 km and 137 vertical layers in the atmosphere and ~4–25 km with 80 vertical layers in the ocean)²⁷, subject to SSP5-8.5 greenhouse gas forcing (see “Methods”). We demonstrate that this model simulates a rapid intensification of ENSO by mid-twenty-first century, a transition to a regular, strongly seasonally-locked oscillation (with periodicities of 2, 3, 4, and 5 years), and an unprecedented resonance with other important modes of climate variability. Using a hierarchy of simplified dynamical ENSO models, with parameters estimated from the complex AWI-CM3 simulations, we study the underlying mechanisms for the qualitative change in ENSO behavior, focusing on coupled air-sea feedbacks and atmospheric noise. While models from the Coupled Model Intercomparison Project Phase 6 (CMIP6) show a wide range of possible future ENSO regularity and amplitude projections, a few models show qualitatively similar behavior to AWI-CM3. If this peculiar ENSO dynamical scenario were to materialize in the future, it could lead to both increased ENSO predictability, due to greater regularity, and, at the same time, to warming-amplified “whiplash impacts”²⁸ on regional climates. These impacts would arise from the compounding effects of (1) more regular ENSO transitions, (2) increased ENSO sea surface temperature (SST) variance, (3) larger ENSO impacts on precipitation and the atmospheric circulation for the same SST anomaly²⁹, and (4) synchronized fluctuations of the other climate modes.

Results

Response of SST and SLP variability to greenhouse warming

As the Earth warms in response to increasing greenhouse gas concentrations, the AWI-CM3 TCo319 model²⁷ simulates a future increase in variability of both SST (Fig. 1e) and sea level pressure (SLP) (Fig. 1f) between the current (Period P1; 2015–2035) and end-of-the-century (Period P2; 2080–2100) climate in many regions of the globe. Further looking at the key regional aspects of these SST and SLP variability changes, we see a striking projected increase in ENSO SST variance as well as in ENSO regularity, i.e., a tendency from an intermittent to a more cyclic ENSO behavior, reminiscent of a Hopf bifurcation³⁰ over this century (Figs. 1a, b, 2a and 3a). Interestingly, the model simulates qualitatively similar changes in the NAO index (Fig. 1c, d), the dominant empirical mode of atmospheric variability over the North Atlantic and Europe, especially in boreal winter (December–January–February: DJF). Both the dominant interannual ENSO timescale, as well as its near-annual combination tones^17,18, are evident in the NAO wavelet power spectrum above a white noise background, and their variance increases with time and rising greenhouse gas concentrations (Fig. 1d). Increasing ENSO influences on the NAO are likely to have important implications for atmospheric impacts and climate predictability over Europe²⁷.

Fig. 1: Oceanic and atmospheric variability in response to greenhouse warming.

a, c Time evolution of the El Niño-Southern Oscillation (ENSO) sea surface temperature (SST) index [K] and the normalized North Atlantic Oscillation (NAO) index [n.u.] for ensemble member 0 (3-month running-mean applied). b, d Ensemble-mean (four members post year 2055) wavelets of the ENSO SST and NAO indices. Black contours enclose regions above 90% confidence level significance tested against a Lorentzian (b) and a white noise (d) spectrum, respectively. e, f Spatial maps of the ensemble-mean standard deviation changes between period 2 (P2, 2080–2100) and period 1 (P1, 2015–2035) of the monthly SST anomaly (SSTA) (e) and December–January–February (DJF) sea level pressure (SLP) anomaly (SLPA) (f). Dots indicate regions where all four ensemble members show disagreement in the sign of changes. Boxes in (e) indicate the cold tongue ENSO region as well as the key regions associated with SST variability of the North Pacific Meridional Mode (NPMM), Indian Ocean Dipole (IOD), Indian Ocean Basin (IOB) mode, and the Tropical North Atlantic (TNA) mode. Boxes in (f) indicate the SLP centers of the NAO.

Fig. 2: El Niño-Southern Oscillation (ENSO) regularity and amplitude changes in observations, Alfred Wegener Institute Climate Model (AWI-CM3), and Coupled Model Intercomparison Project Phase 6 (CMIP6) models.

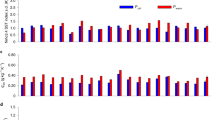
Moving 21-year changes of sample entropy (SampEn) (a) and standard deviation (SD) (b) of the Niño3.4 SST anomaly index in observations (black), the 150-year AWI-CM3 1950 control simulation (CTL1950, blue), and the AWI-CM3 shared socio-economic pathway (SSP)5-8.5 scenario simulation (red). Solid lines and shading indicate the multi-product/multi-member mean and the 1 SD spread of 10,000 inter-realizations using a bootstrap method, respectively. The error bars indicate the mean and 1 SD of values across all overlapping 21-year windows for the observations (1950–2024), CTL1950 (150-yr), and SSP5-8.5 (2050–2100). Violin plots showing the probability density distribution of ENSO regularity change (c) and amplitude change (d) across 49 CMIP6 models. The change is calculated as the difference between 2050–2100 and 1900–2000. Dots represent individual model results, with E3SM-1-1, EC-Earth3, and EC-Earth3-Veg highlighted in distinct colors; the red star marks the AWI-CM3 result (2050–2100 minus CTL1950). In a and c, the y-axis is inverted to emphasize decreasing SampEn, indicating increasing regularity.

Fig. 3: El Niño-Southern Oscillation (ENSO) amplitude, Bjerknes stability, and wind stress structure changes.

a Ensemble-mean moving 21-year seasonally varying (shading) and monthly (blue curve) standard deviation (SD) changes of the ENSO sea surface temperature anomaly (SSTA) index relative to the monthly SD during 2015–2035 (ratio). b Growth rate of the leading eigenmode (ENSO) obtained via Floquet analysis for the Recharge Oscillator (RO) (blue curve) and eXtended Recharge Oscillator (XRO) (magenta curve) models in a moving 21-year window. The seasonal RO growth rate is indicated in shading. c Noise amplitude defined as the seasonally varying SD (shading) and monthly SD (blue curve) of the XRO fit residual. Different ENSO feedbacks (as a function of calendar month) obtained via Bjerknes stability analysis for period 1 (P1) (d, 2015–2035; one ensemble member) and period 2 (P2) (e, 2080–2100; ensemble-mean of four members), as well as their difference (f). The horizontal axes in d–f show the Bjerknes (BJ) index, SSTA growth rate $(R)$, ocean damping rate ($-\varepsilon$), thermocline feedback (TH), zonal advective feedback (ZA), Ekman feedback (EK), thermal damping by the net surface heat flux (TD), dynamic damping by mean horizontal currents (DD), all residuals from nonlinear dynamic heating and unresolved processes (AllRes), as well as the dynamic damping components by mean zonal (DDu) and meridional (DDv) currents and the thermal damping components by shortwave radiation (Q_SW), longwave radiation (Q_LW), latent heat flux (Q_LH), and sensible heat flux (Q_SH). g Latitudinal profiles (averaged of 160°E–150°W) of regressed zonal wind stress anomalies ${\tau }_{x}^{{\prime} }$ onto the monthly ENSO SST index in a moving 21-year window. Dashed curves and shadings indicate the ensemble mean and one SD spread of meridional boundaries defined by the local minima. h, i Basin thermocline adjustment rate ($-\varepsilon$) and Recharge/discharge efficiency ($-{F}_{2}$) in a moving 21-year window. In h and i, red curves denote the meridional width of ENSO zonal wind stress anomalies ${\tau }_{x}^{{\prime} }$ (see “Methods”).

Assessment of model fidelity

Next, using sample entropy (SampEn; see “Methods”) of Niño3.4 SST anomalies as a metric for ENSO regularity together with the Niño3.4 SST anomaly standard deviation (SD), we show that a 1950 control simulation of AWI-CM3 TCo319 exhibits both ENSO regularity (Fig. 2a) and ENSO amplitude (Fig. 2b) similar to the observations and that the increase of both metrics in the AWI-CM3 TCo319 future projections cannot be explained by internal variability. Furthermore, analysis of the CMIP6 model archive demonstrates that while there is a wide range of possible changes in future ENSO regularity (Fig. 2c) and amplitude (Fig. 2d), 55% of CMIP6 models show an increase in ENSO regularity (Fig. 2c) and 82% an increase in ENSO SST anomaly amplitude (Fig. 2d) by the second half of this century under the SSP5-8.5 scenario. In addition, a few models (i.e., E3SM-1-1, EC-Earth3, and EC-Earth3-Veg) show similar increased ENSO regularity and amplitude as AWI-CM3 TCo319 (Fig. 2c, d and Supplementary Fig. 1). We emphasize that we do not expect strong inter-model agreement of ENSO projections across the CMIP6 archive given that considerable biases of climate mean states and ENSO dynamics result in different ENSO regimes across models^8,24.

Physical reasons for the ENSO regime shift

To understand the simulated regime shift in ENSO toward higher variance and increased regularity in AWI-CM3 TCo319, we derive two conceptual ENSO models directly from the simulation output. The first is a version of the recharge oscillator (RO) model¹³ that includes seasonal cycle modulations⁹ and encapsulates the fundamental ENSO dynamics in two coupled ordinary differential equations (ODEs) for SST anomalies in the Niño3.4 region and the zonal-mean equatorial upper-ocean warm water volume. The second is a modified version of the extended recharge oscillator (XRO)²⁴, which also takes into account the seasonally-modulated interactions between ENSO (as described by the RO) and the North Pacific Meridional mode (NPMM), TNA, IOD, and the Indian Ocean Basin (IOB) mode (yielding six coupled ODEs; see “Methods”). We estimate the time-evolving parameters of both conceptual models using multi-linear regression in a moving 21-year window. This allows us to compute the time-dependent linear growth rates and frequencies of ENSO via Floquet eigen analysis³¹ and assess changes in the damping rates and coupling strengths of the interacting modes in response to greenhouse warming.

Both models show that ENSO’s linear growth rate increases considerably later in the twenty-first century, particularly during boreal summer (Fig. 3b). This is consistent with the increase in ENSO variance in boreal winter (Fig. 3a). We emphasize that while ENSO, in an annual mean sense, is still in the stable (subcritical) regime, the presence of atmospheric stochastic noise, can lead to a noise-induced Hopf bifurcation that occurs before criticality (i.e., the point at which its growth rate switches from negative to positive) is reached^32,33. Moreover, the noise amplitude, calculated as the residual from the XRO model projection, increases substantially in boreal spring to summer (Fig. 3c), together with the growth rate, pushing ENSO into the high-variance and highly-regular regime. This is consistent with increased tropical intraseasonal atmospheric variability in the AWI-CM3 TCo319 simulation (Supplementary Fig. 2, ref. ²⁷), which is well known to energize the ENSO mode^2,9,34 and also seen in other climate model simulations³⁵. Comparing the wavelet spectrum of the Niño3.4 index (Fig. 1b) with the linear ENSO frequency for both the RO and XRO (Supplementary Fig. 3), we see close agreement at the dominant interannual frequencies of ~2, 3, 4, and 5 yr⁻¹.

Next, we use the Bjerknes stability analysis (see “Methods”) to determine which feedback changes are responsible for ENSO’s growing instability. Comparing the difference (Fig. 3f) between period 2 (P2: 2080–2100; Fig. 3e) and period 1 (P1: 2015–2035; Fig. 3d) of the individual ENSO feedbacks that make up ENSO’s net growth rate, we find that the increased growth rate primarily results from a reduced damping from thermocline adjustment ($\varepsilon$) and a modest enhancement of the Bjerknes feedback (R). The changes in R can be explained by enhanced Ekman feedback (EK) and reduced dynamic damping (DD), which are slightly offset by a reduced thermocline feedback (TH) and increased thermodynamic damping (TD). The enhanced Ekman feedback is primarily driven by enhanced stratification and an amplified anomalous vertical current response to SST anomalies (Supplementary Fig. 4d, i). The reduced dynamic damping is linked to the weakening of the climatological trade winds and surface currents. For the zonal advective feedback changes, we see a cancellation effect between the mean state and feedback changes, with reduced $d\overline{T}/{dx}$ but strongly enhanced anomalous zonal current response to SST anomalies (Supplementary Fig. 4a, d, h). The reduced thermocline feedback is explained by a weakening of the climatological trade winds and climatological upwelling (Supplementary Fig. 4b, f).

We attribute the reduced damping from thermocline adjustment ($\varepsilon$) to the widening of ENSO wind stress anomalies (Fig. 3g, h and Supplementary Fig. 5a), which leads to increased wind stress curl off the equator, exciting longer Rossby waves. These are less effectively reflected at the western boundary and thus lead to reduced damping from thermocline adjustment (see “ENSO wind stress structure” in “Methods”). Importantly, the projected changes in the ENSO-associated zonal wind stress in the AWI-CM3 TCo319 simulations (Supplementary Fig. 5a) are consistent with the CMIP6 multi-model mean of the response³⁶. The changes of R and ${\varepsilon}$ together lead to the largest growth rate increase in the boreal spring season (Fig. 3f).

The AWI-CM3 model explicitly resolves Tropical Instability Waves (TIWs), which also play a key role in ENSO thermodynamics^4,37, mainly as a negative feedback³⁸. With ocean background currents changing in response to the simulated greenhouse warming, the statistics of TIWs will also change, and their contribution to the ENSO heat budget⁴ will also change. This effect has not been explicitly accounted for in our calculations of the ENSO instability index, but it is captured, among other effects, in the residual term (Fig. 3d–f).

Global climate mode resonance

For climate modes, which are characterized by the variations in SST, such as the TNA mode (Fig. 4b), the IOB (Fig. 4c), the IOD (Fig. 4d), and the NPMM (Fig. 4e), we find a considerable intensification of their amplitude, ranging from 40–75%. All these modes are known to interact with ENSO^18,23,24. To further elucidate the apparent emergent synchronization between ENSO and the other climate modes (i.e., NPMM, TNA, IOD, and IOB) in response to greenhouse warming (Fig. 4), we calculate the power spectrum for each mode for P1 and P2 respectively (Supplementary Fig. 6). We see a clear indication of statistically significant and intensifying spectral peaks for the NPMM, TNA, IOD, and IOB indices at the dominant ENSO frequencies (f_E) as well as at the near-annual ENSO combination tone frequencies (1±f_E) above a Lorentz/Hasselmann background spectrum³⁹, consistent with theoretical expectations^17,18. The emergence of interannual and near-annual ENSO timescales in the spectra of other climate modes provides the first clear evidence that their coupling with ENSO strengthens in response to greenhouse warming in this model. In addition, we see a clear intensification of both the ENSO and ENSO combination mode¹⁷ wind stress variability (Supplementary Fig. 7).

Fig. 4: Amplitude and phase synchronization changes of climate modes.

a–e Ensemble-mean moving 21-year seasonally varying (shading) and monthly (blue curve) standard deviation (SD) changes of each climate mode relative to its monthly SD during 2015–2035 (ratio) for the North Atlantic Oscillation (NAO), Tropical North Atlantic (TNA) mode, Indian Ocean Basin (IOB) mode, Indian Ocean Dipole (IOD), and North Pacific Meridional Mode (NPMM) indices, respectively. f–j Ensemble-mean moving 21-year phase synchronization quantified by the histogram of phase differences (shading) between each climate mode and the Niño3.4 index for NAO, TNA, IOB, IOD, and NPMM, respectively. The blue curves in f–j indicate synchronization strength defined by the SD of the histogram density (PDF) of phase differences. The blue shading in a–j indicates the one SD spread among the four ensemble members.

To better quantify the dynamical linkage between different climate modes, we calculate the phase difference (see “Methods”) between the Niño3.4 index (representing ENSO) and the other indices (Fig. 4f–j). A bounded phase difference indicates stronger phase-coupling between the climate modes under consideration (Supplementary Fig. 8). Here, we focus on 1:1 phase synchronization, meaning that the oscillators maintain a (near-)constant phase difference. Starting around 2060, a strong preference for bounded phase differences emerges between ENSO and each of the other modes (i.e., blue curves in Fig. 4f–j have high values), thus providing further evidence of an intensifying connection between ENSO and the other modes as time progresses. The time-evolving probability distribution of phase differences (red shading in Fig. 4f–j) also documents that the range of phase differences narrows considerably for all modes, supporting the evidence for strengthened phase synchronization with ENSO.

Under present-day conditions, the influence of ENSO on the NAO is detectable but generally weak and indirect. Consequently, current seasonal forecasts for the European climate do not treat ENSO as a primary driver of NAO-related variability or impacts. According to our simulations, however, this could change in the future. The amplitude of the NAO increases by about 20% during the simulation (Fig. 4a), but the overall seasonal amplitude modulation with a peak in February remains relatively stable. The ±π preferred phase difference to ENSO for the NAO is consistent with the well-known out-of-phase relationship between ENSO and the NAO. As greenhouse gas concentrations increase, the preferred phase difference between ENSO and the NAO becomes more robust (Fig. 4f), with dominant peaks between −π and −π/2, consistent with an increasingly negative correlation in boreal winter. Overall, we expect these dynamics to potentially influence the seasonal predictability of the NAO, as illustrated in Supplementary Fig. 9, which shows the projected extended persistence of both ENSO and NAO. It is also illustrated in Fig. 1, which shows that after 2060, 2-year-long La Niña events typically create two subsequent strong NAO events.

Whether the intensification of the NAO linkage to ENSO emerges, simply because the ENSO SST amplitude increases during the simulation, or whether large-scale reorganizations of the extratropical atmospheric circulation facilitate the coupling between the Pacific-North American (PNA) pattern and the NAO in wintertime (DJF) is quantified by a regression analysis for both periods (Fig. 5). For P1, the regression of precipitation and 500 hPa geopotential height (Z500) anomalies onto Niño3.4 SST anomalies and Niño4 precipitation shows no substantial impact in Europe. During P2, for the regressions with both the Niño3.4 SST index in degrees Kelvin (Fig. 5e) and with the normalized Niño3.4 SST index (Fig. 5d), we see increases in the regression coefficient amplitudes and a clear negative NAO pattern emerging. The strongest signal can be found for the normalized Niño3.4 index, which indicates that the amplification of the SST signal itself plays a vital role in strengthening the teleconnection. However, even a 1 K SST change in the Niño3.4 region, the NAO pattern emerges much more strongly in P2 than in P1, indicating a higher sensitivity of the atmospheric response to the same amplitude of warming in the eastern equatorial Pacific. As a result of the increased synchronization between ENSO and the NAO pattern in boreal winter, we also find an enhanced precipitation response over western Europe²⁷ with considerably wetter conditions occurring over the Iberian Peninsula during El Niño events (Fig. 5). Recent studies have suggested that the ENSO–NAO teleconnection may strengthen in response to greenhouse warming, either due to amplified ENSO forcing or increased extratropical sensitivity. Reference⁴⁰ showed that CMIP5 models simulate both enhanced tropical Pacific precipitation variability and a more robust ENSO–NAO correlation in the future, with evidence for stronger stratospheric and tropospheric pathways. Reference⁴¹, using a pacemaker approach with fixed ENSO SST anomalies, attributed the strengthened NAO response to increased extratropical sensitivity linked to a more zonally extended Pacific jet. Our study confirms and extends these results by showing that in a high-resolution coupled model, both mechanisms occur simultaneously: ENSO amplitude increases due to stronger air–sea feedbacks and enhanced atmospheric noise, while normalized regressions reveal that the extratropical circulation becomes more sensitive to ENSO forcing. In addition, we identify a regime shift toward a highly regular, seasonally phase-locked ENSO that entrains other modes like the NAO, suggesting a possible global synchronization of interannual variability under climate change.

Fig. 5: Changes of the El Niño-Southern Oscillation (ENSO) Northern Hemisphere teleconnection during boreal winter.

a Regression of normalized Niño3.4 sea surface temperature anomalies (SSTA) with precipitation anomalies (PrA) (shading, [mm day⁻¹]) and 500 hPa geopotential height anomalies (Z500A) (contours, ±5, ±15, … [m]) during December–January–February (DJF) 2015–2035 (P1); b Regression of Niño3.4 SST anomalies with precipitation anomalies (shading, [mm day⁻¹ K⁻¹]) and Z500 anomalies (contours, ±5, ±15, … [m K⁻¹]) during DJF 2015–2035; c Regression of Niño4 precipitation anomalies with precipitation anomalies (shading, [mm day⁻¹ (mm day⁻¹)⁻¹]) and Z500 anomalies (contours, ±5, ±15, … [m (mm day⁻¹)⁻¹]) during DJF 2015–2035. d–f Same as a–c but for ensemble-mean results during DJF 2080–2100 (P2), respectively. Stippling and dark contours indicate statistical significance at the 95% level using a one-sided Student’s t test.

The increase in ENSO variance and regularity directly leads to increased variance and regularity of the other SST climate modes. In addition, we find that both a reduction of their individual damping rates (Supplementary Fig. 10a–d) and increased ENSO teleconnection strength (Supplementary Fig. 10e–l) also contribute to the global climate mode resonance. The enhanced variance of the NPMM is primarily driven by reduced damping from February to July (Supplementary Fig. 10a), likely associated with SST warming in the subtropical northeastern Pacific and enhanced wind–evaporation–SST (WES) feedback⁴². The reduction in damping rate and the strengthening of ENSO teleconnection are essential for increasing IOD and TNA variance (Supplementary Fig. 10c, d, g, h). Interestingly, the IOB exhibits an enhanced early variance peak in February–March and a secondary peak in May–June by the end of the twenty-first century (Fig. 4c). This change is related to reduced damping in addition to enhanced ENSO teleconnection from November to April (Supplementary Fig. 10b, j).

Discussion

Previous work has shown that the atmosphere is “ringing” with a range of combination tones in response to ENSO forcing, causing an “ENSO frequency cascade”⁴³. Here we show that ENSO not only causes these deterministic signals in the atmosphere, but its intensification can also energize both atmospheric and air-sea coupled climate modes across the globe in response to greenhouse warming. This global climate resonance towards the strengthening ENSO signal is apparent in the raw timeseries (Fig. 1), their amplitudes, spectra, and phase synchronization characteristics (Fig. 4 and Supplementary Fig. 6). ENSO variability increases in the AWI-CM3 simulation because of an intensification of atmospheric noise in boreal summer (Fig. 3c and Supplementary Fig. 2c), reduced damping from thermocline adjustment, and the modest increase of the Bjerknes feedback (Fig. 3f). Its global synchronization towards the extratropics (e.g., with the NAO) is boosted by the growing ENSO amplitude, but also by an overall reorganization of atmospheric teleconnection patterns (Fig. 5), due to a different future atmospheric mean flow. The changes in the mean flow—particularly a stronger, more zonally extended Pacific jet and increased Atlantic baroclinicity—can enhance the propagation, amplification, and momentum deposition of ENSO-forced stationary waves into the North Atlantic sector, thereby strengthening the teleconnection to the NAO.

Increasing ENSO amplitude and teleconnection patterns imply that remote extratropical precipitation responses, such as in Southern California and the Iberian Peninsula (Fig. 5), will also become stronger between alternating El Niño and La Niña events. Even though the recurrence of these events may become more predictable due to the increased regularity/periodicity and amplitude (Fig. 1)⁴⁴, future ENSO teleconnections might generate enhanced whiplash effects on hydroclimate, which requires additional planning and management strategies to minimize the costs of climate damage. While similar increases in ENSO regularity and amplitude can be found in some CMIP6 model projections (Fig. 2), future work needs to assess the detailed dynamics across these models and assess the likelihood of the ENSO regime changes seen in AWI-CM3.

Methods

Earth system model experiments

This study employs the Alfred Wegener Institute Climate Model (AWI-CM3), which couples the OpenIFS (Open Integrated Forecasting System) atmosphere model with the FESOM2 (Finite-volume Sea Ice-Ocean Model) ocean model. The atmospheric component operates at a horizontal resolution of approximately 31 km (TCo319) with 137 vertical pressure levels. It contains the WAM (Wave Model) surface gravity wave model and the hydrology model H-TESSEL (Hydrology in the Tiled ECMWF Scheme for Surface Exchange over Land). The ocean model features a variable horizontal resolution ranging from 5 to 27 km, depending among others on latitude, and includes 80 vertical layers. The reader is referred to a more detailed description of AWI-CM3 and the simulations (except the additional ensemble members)²⁷.

A full transient simulation covering the period from 1950 to 2100, branched off from a 100-year-long spin-up simulation, was conducted using historical forcing from 1950 to 2014 CE, followed by the high-emission shared socio-economic pathway (SSP) 5-8.5 scenario thereafter. To assess the robustness of our results, three additional ensemble simulations spanning the period from 2055 to 2100 were conducted. In line with the micro-perturbation initialization strategy (e.g., ref. ³⁵), a small perturbation was added to the wave model restart files.

A 150-year TCo319 control simulation with fixed 1950 forcing (CTL1950) was also analyzed to characterize internal climate variability and to serve as a baseline comparison. The CTL1950 simulation reproduces the observed SST and precipitation mean state and SST variability reasonably well (Supplementary Fig. 11). The CTL1950 simulation also reproduces the observed characteristics of ENSO, including its seasonal synchronization, spectral characteristics, and teleconnections (Supplementary Fig. 12).

Observational and CMIP6 data

We use four observational SST reconstructions/reanalysis: the Hadley Centre Sea Ice and Sea Surface Temperature dataset v.1.1 (HadISST⁴⁵), the Extended Reconstructed Sea Surface Temperature v.5 (ERSSTv5⁴⁶), the Centennial in situ Observation-Based Estimates of Sea Surface Temperature v.2 (COBE2⁴⁷) for 1871–2024, and the European Centre for Medium-Range Weather Forecasts (ECMWF) Reanalysis 5 (ERA5⁴⁸) for 1940–2024. In addition, ERA5 monthly precipitation and sea level pressure (SLP) fields are used for 1940–2024.

We also analyze simulations from 49 CMIP6 models, including historical runs and SSP5-8.5 projections, providing monthly SST and SLP data (Supplementary Table 1). The simulations are forced by historical anthropogenic and natural forcings up to 2014, followed by future greenhouse-gas forcing under the SSP5-8.5 scenario through 2100, covering the period 1850–2100. All model output was re-gridded to a common 1° × 1° horizontal resolution using bilinear interpolation.

Definitions of climate variability modes

All monthly fields are first quadratically detrended, and then anomalies are computed by subtracting the 21-year running monthly climatology. We then calculate the climate mode indices with the detrended anomalies. The ENSO SST index is represented as SST anomalies averaged over the cold tongue region (180°–90°W, 6°S–6°N). The Niño3.4 SST index is defined as SST anomalies averaged over the Niño3.4 region (170°–120°W, 5°S–5°N). The Niño4 precipitation index is defined as precipitation anomalies averaged over the Niño4 region (160°E–150°W, 5°S–5°N). The North Pacific Meridional Mode (NPMM) index is defined as SST anomalies averaged over 160°–120°W, 10°–25°N⁴⁹. The NPMM SST anomaly index reproduces the original maximum covariance analysis (MCA)-based NPMM index with a correlation of ~0.95⁴⁹. The Tropical North Atlantic (TNA) index is defined as SST anomalies averaged over 55°–15°W, 5°–25°N⁵⁰. The Indian Ocean Basin (IOB) mode index is defined as SST anomalies averaged over 40°–100°E, 20°S–20°N⁵¹. The Indian Ocean Dipole (IOD) mode index is defined as SST anomalies averaged over 50°–70°E, 10°S–10°N minus those averaged over 90°–110°E, 10°S–0°N²⁰. The North Atlantic Oscillation (NAO) index is defined as the principal-component (PC) time series associated with the leading Empirical Orthogonal Function (EOF) of area-weighted SLP anomalies over the North Atlantic sector 90°W–40°E, 20°–80°N⁵².

Spectral analysis: wavelets

Wavelet analysis was used to explore the different climate modes’ time-frequency characteristics and identify dominant periodicities⁵³. A continuous wavelet transform was performed using the Morlet wavelet, which offers an optimal balance between frequency and time localization, making it ideal for capturing oscillatory behavior. The analysis was conducted on normalized Niño3.4 SST and NAO indices, with the resulting wavelet power spectra computed for each ensemble member, followed by calculating the ensemble-mean of the spectra (Fig. 1b, d) to highlight changes in dominant frequencies over time. Statistical significance was assessed using Monte Carlo simulations: Niño3.4 SST was tested against an AR(1) process with a lag(−1 month) autocorrelation coefficient of 0.9, while the NAO index was tested against a white-noise process.

Spectral analysis: power spectral density

The power spectral density (PSD) of the various climate mode indices (the four ensemble members for P2 were concatenated, leading to 84 years of monthly data for P2 but only 21 years of monthly data for P1) was calculated using the Multi-Taper Method (MTM) with 3 tapers and nfft = 256 for P1 and nfft = 1024 for P2⁵⁴. A Lorentzian background spectrum null hypothesis was chosen for the SST modes. The significance level of spectral peaks was therefore determined from the respective PSD percentile at each frequency of PSDs calculated with the same MTM method for 10,000 discrete AR(1) processes with (i) the same lag(−1 month) autocorrelation, (ii) the same variance, and (iii) the same data length as the respective index that is tested against. A white noise null hypothesis was chosen for the NAO atmospheric mode. Here, the significance level of spectral peaks was determined from the respective PSD percentile at each frequency of PSDs calculated with the same MTM method, generated from 10,000 realizations of white noise time series with (i) the same variance and (ii) the same data length as the index that is tested against.

ENSO regularity calculation using sample entropy

We assessed ENSO regularity by calculating the sample entropy (SampEn) of the Niño3.4 SST anomaly index, a nonlinear metric that measures how predictable a time series is⁵⁵. SampEn is an alternative to approximate entropy (ApEn⁵⁶) for quantifying the randomness of a time series; unlike ApEn, it excludes self-matches, thereby reducing bias and improving consistency across different data segments⁵⁷. Compared to an ENSO regularity metric that is defined by the sharpness of the ENSO spectral peak⁵⁸, SampEn is less sensitive to record length, spectral windowing, and other frequency-domain constraints. Lower SampEn values indicate more regular (periodic) behavior, whereas higher values indicate more irregular behavior. Given a time series $\{{x}_{1},{x}_{2},\ldots,{x}_{N}\}$, SampEn estimates the negative natural logarithm of the conditional probability that two sequences of length $m$ that match within tolerance $r$ will also match for $m+1$ points, while excluding self-matches to reduce bias and improve consistency. We used an embedding dimension $m=2$ (the dimensionality of the ENSO RO model) and a tolerance $r=0.2\sigma$, where $\sigma$ is the standard deviation of the time series. The SampEn metric is defined as:

$${{\rm{SampEn}}}\,\left(m,r,N\right)=-{\mathrm{ln}}\left[\frac{{A}^{m}\left(r\right)}{{B}^{m}\left(r\right)}\right]$$

(1)

where ${A}^{m}\left(r\right)$ the probability that two sequences of length m + 1 are similar (matches), ${B}^{m}\left(r\right)$ is the probability that two sequences of length $m$ are similar (candidates). Explicitly,

$${A}^{m}\left(r\right) =\frac{1}{N-m+1}\frac{1}{N-m}\mathop{\sum }\limits_{i=1}^{N-m}\mathop{\sum }\limits_{j=1,\, j \, \ne \, i}^{N-m} \\ \left[{{\rm{number}}}\; {{\rm{of}}}\; {{\rm{times}}}\; {{\rm{that}}} \,{d}\left[{u}_{m+1}\left(j\right),{u}_{m+1}\left(i\right)\right] < r\right]$$

(2)

$${B}^{m}\left(r\right) =\frac{1}{N-m+1}\frac{1}{N-m}\mathop{\sum }\limits_{i=1}^{N-m}\mathop{\sum }\limits_{j=1,\, j \,\ne \, i}^{N-m} \\ \left[{{\rm{number}}}\; {{\rm{of}}}\; {{\rm{times}}}\; {{\rm{that}}}\,{d}\left[{u}_{m}\left(j\right),{u}_{m}\left(i\right)\right] < r\right]$$

(3)

where ${u}_{m}\left(i\right)$ is the subsequence $\{{x}_{i},{x}_{i+1},\ldots,{x}_{i+m-1}\},d\left[{u}_{m}\left(j\right),{u}_{m}\left(i\right)\right]={\max }_{k=1,\ldots,m}|{x}_{i+k-1}-{x}_{j+k-1}|$ is the maximum norm distance. Since the number of matches is always less than or equal to the number of possible vectors, the ratio ${A}^{m}\left(r\right)/{B}^{m}\left(r\right)$ is a conditional probability less than unity, ensuring SampEn is positive. This method provides a single diagnostic value characterizing the regularity of the ENSO time series, facilitating consistent comparison across observations and simulations under different climate scenarios. The observed SampEn effectively captures the decadal variations in ENSO forecast skill, including the modest decrease in predictability after the 2000s (black curve in Fig. 2a, refs. ^59,60,61).

Recharge Oscillator (RO) model formulation and fit

The Recharge-Oscillator (RO) model is a widely recognized framework for diagnosing and understanding ENSO dynamics in observations and climate models^9,13. The RO model captures the oscillatory behavior of El Niño and La Niña events through two coupled equations describing the evolution of ENSO SST anomalies (${T}_{{{\rm{ENSO}}}}$) and equatorial Pacific zonal-mean thermocline depth anomalies ($h$). In its linear form, the model is expressed as:

$$\frac{d}{{dt}}\left(\begin{array}{c}{T}_{{{\rm{ENSO}}}}\\ h\end{array}\right)={{{\bf{L}}}}_{{{\rm{ENSO}}}}\cdot \left(\begin{array}{c}{T}_{{{\rm{ENSO}}}}\\ h\end{array}\right)+\left(\begin{array}{c}{{{\boldsymbol{\xi }}}}_{{{\rm{ENSO}}}}\\ {{{\boldsymbol{\xi }}}}_{{{\rm{h}}}}\end{array}\right)$$

(4)

In Eq. (4), ${{{\bf{L}}}}_{{{\rm{ENSO}}}}=\left(\begin{array}{cc}R & {F}_{1}\\ -{F}_{2} & -\varepsilon \end{array}\right)$, where $R$ represents the SST anomaly growth rate, collectively describing the Bjerknes feedback, $\varepsilon$ denotes ocean damping rate related to the energy leakage at the western boundary and mixing, ${F}_{1}$ represents the effectiveness of the heat content discharge–recharge in controlling SST anomalies, and ${F}_{2}$ represents the discharge–recharge efficiency; ${{{\boldsymbol{\xi }}}}_{{{\rm{ENSO}}}}$ and ${{{\boldsymbol{\xi }}}}_{{{\rm{h}}}}$ are the residual terms encompassing non-resolved nonlinear processes and stochastic noise. The complex eigenvalue of the RO model operator ${{{\bf{L}}}}_{{{\rm{ENSO}}}}$ is the Bjerknes-Wyrtki-Jin (BWJ) index for the ENSO growth rate and periodicity and can be written as:

$${{\rm{BWJ}}}=\frac{R-\varepsilon }{2}+i\sqrt{{F}_{1}{F}_{2}-\frac{{\left(R+\varepsilon \right)}^{2}}{4}}$$

(5)

where the real part of the index is referred to as the ENSO Bjerknes stability (BJ) index in ref. ¹⁰, and the imaginary part as the reciprocal of the Wyrtki periodicity (WF) index in ref. ¹¹.

Due to the strong seasonal dependence of ENSO, we explicitly incorporate seasonality by estimating the parameters as:

$${{\bf{L}}}={{{\bf{L}}}}_{0}+{{{\bf{L}}}}_{1}^{{{\rm{c}}}}\cos \omega t+{{{\bf{L}}}}_{1}^{{{\rm{s}}}}\sin \omega t$$

(6)

where ω = 2π/(12 months), and the subscripts 0 and 1 indicate the mean and annual cycle components, respectively. The parameters of the operators are estimated by multivariate linear regression. We applied the RO model fitting to each ensemble member of the AWI-CM3 simulation using a 21-year moving window.

Extended Recharge Oscillator (XRO) model formulation and fit

To understand the climate mode interactions, we use a modified version of a recently developed extended Recharge Oscillator (XRO), which allows for two-way interactions between ENSO and the other modes²⁴, which consists of a recharge oscillator model for ENSO coupled to seasonally-modulated stochastic-deterministic models for the other climate modes²⁵:

$$\frac{d}{{dt}}\left(\begin{array}{c}\begin{array}{c}{T}_{{{\rm{ENSO}}}}\\ h\end{array}\\ {T}_{{{\rm{NPMM}}}}\\ {T}_{{{\rm{IOB}}}}\\ {T}_{{{\rm{IOD}}}}\\ {T}_{{{\rm{TNA}}}}\end{array}\right)={{\bf{L}}}\cdot \left(\begin{array}{c}\begin{array}{c}{T}_{{{\rm{ENSO}}}}\\ h\end{array}\\ {T}_{{{\rm{NPMM}}}}\\ {T}_{{{\rm{IOB}}}}\\ {T}_{{{\rm{IOD}}}}\\ {T}_{{{\rm{TNA}}}}\end{array}\right)+\left(\begin{array}{c}\begin{array}{c}{{{\boldsymbol{\xi }}}}_{{{\rm{ENSO}}}}\\ {{{\boldsymbol{\xi }}}}_{{{\rm{h}}}}\end{array}\\ {{{\boldsymbol{\xi }}}}_{{{\rm{NPMM}}}}\\ {{{\boldsymbol{\xi }}}}_{{{\rm{IOB}}}}\\ {{{\boldsymbol{\xi }}}}_{{{\rm{IOD}}}}\\ {{{\boldsymbol{\xi }}}}_{{{\rm{TNA}}}}\end{array}\right)$$

(7)

The linear dynamical operator L contains four submatrices, organized as follows:

$${{\bf{L}}}=\left(\begin{array}{cc}{{{\bf{L}}}}_{{{\rm{ENSO}}}} & {{{\bf{C}}}}_{1}\\ {{{\bf{C}}}}_{2} & {{{\bf{L}}}}_{{{\rm{M}}}}\end{array}\right)$$

(8)

where the linear operator submatrix ${{{\bf{L}}}}_{{{\rm{ENSO}}}}$ describes the ENSO internal recharge-discharge dynamics, ${{{\bf{L}}}}_{{{\rm{M}}}}$ represents the internal processes and interactions among the other climate modes; ${{\bf{C}}}$ are coupling submatrices, with ${{{\bf{C}}}}_{2}$ describing the impact of ENSO on other climate modes and ${{{\bf{C}}}}_{1}$ describing the feedback of other modes on ENSO. Similar to the RO model fit, we explicitly incorporate seasonality by estimating the XRO parameters with Eq. (7). The noise parameters are determined from the residuals of the XRO fit. There are a total of 12 noise parameters, i.e., a noise amplitude and decorrelation time scale for each of the 6 state variables in the system. The noise amplitudes ${\sigma }_{{{\boldsymbol{\xi }}}}$ are estimated from the standard deviations of the residuals of the XRO fit. The decorrelation time scales are estimated as ${{{\boldsymbol{r}}}}_{{{\boldsymbol{\xi }}}}=-{\mathrm{ln}}({{{\boldsymbol{a}}}}_{1})/\delta t$, where ${{{\boldsymbol{a}}}}_{1}$ are the lag(−1 month) autocorrelations of the residual of the XRO fit. The range of observed noise time scales ${{{\boldsymbol{r}}}}_{{{\boldsymbol{\xi }}}}^{-1}$ are between 0.25 ~ 0.70 months.

Floquet theory is used to determine the stability of the coupled system with an annual cycle basic state. We determine the Floquet ENSO growth rate and periodicity using the RO model operator (${{{\bf{L}}}}_{{{\rm{ENSO}}}}$) or XRO model operator ${{\bf{L}}}$ via Floquet exponent analysis³¹. The Floquet exponents are determined numerically by integrating $d{{\boldsymbol{Q}}}/{dt}={{\boldsymbol{L}}}\cdot {{\boldsymbol{Q}}}$ over 1 year with a time step of 3.65 days from an initial condition ${{\boldsymbol{Q}}}\left(0\right)={{\boldsymbol{I}}}$ to form a monodromy matrix ${{\boldsymbol{M}}}={{\boldsymbol{Q}}}\left(T\right),T=1\,{{\rm{year}}}$. The Floquet exponents (${\sigma }_{j}$) are calculated from the least damped complex eigenvalues ${\alpha }_{j}$ of ${{\boldsymbol{M}}}$ by using ${\sigma }_{j}=\frac{{\mathrm{ln}}{\alpha }_{j}}{T}$.

Atmospheric noise definitions

To quantify changes in atmospheric noise amplitude, we define atmospheric noise as surface zonal wind variability that is independent of SST-related variability, following ref. ⁶². Specifically, an EOF analysis was applied to monthly tropical SST anomalies to derive the leading modes of variability and their associated PCs. Multivariate linear regression was then performed, regressing the monthly surface zonal wind stress anomalies onto the first 15 leading PCs, which together account for approximately 75% of the variance in tropical SST anomalies. The time series of atmospheric noise was then defined as the residual wind stress, obtained from removing the SST-forced signals. Finally, the amplitude of noise is defined as the standard deviation of the residual wind stress.

Heat budget and Bjerknes stability analysis

To assess possible physical processes that control the changes of ENSO growth rate, we calculate the ocean mixed layer heat budget using a partial flux form^63,64:

$$\begin{array}{c}\frac{\partial {T}^{\prime} }{\partial t}={Q}^{\prime} -\frac{\partial \left(\overline{u}{T}^{{\prime} }\right)}{\partial x}-\frac{\partial \left(\overline{v}{T}^{{\prime} }\right)}{\partial y}-\frac{\partial \left(\overline{w}{T}^{{\prime} }\right)}{\partial z}-{u}^{{\prime} }\frac{\partial \overline{T}}{\partial x}-{v}^{{\prime} }\frac{\partial \overline{T}}{\partial y}-{w}^{{\prime} }\frac{\partial \overline{T}}{\partial z}\\ -\left({u}^{{\prime} }\frac{\partial {T}^{{\prime} }}{\partial x}+{v}^{{\prime} }\frac{\partial {T}^{{\prime} }}{\partial y}+{w}^{{\prime} }\frac{\partial {T}^{{\prime} }}{\partial z}\right)+{Q}_{{Res}},\end{array}$$

(9)

where the overbars denote the climatological monthly-mean seasonal cycle, and the primes denote anomalies; $T$ is the ocean temperature, $u$, $v$, and $w$ the ocean zonal, meridional, and vertical current velocities, $Q$ the net surface heat flux effect on the ocean mixed layer, and ${Q}_{{Res}}$ the unresolved residual. The anomalous heat flux term ${Q}^{\prime}$ is calculated as:

$${Q}^{{\prime} }=\frac{{Q}_{{{\rm{net}}}}^{{\prime} }-{Q}_{{{\rm{bot}}}}^{{\prime} }}{\rho {C}_{p}H}$$

(10)

where $H$ is the ocean mixed layer depth (50 m), $\rho$ is the seawater density (1025 kg m⁻³), ${C}_{p}$ is the specific heat capacity of seawater (3994 J kg⁻¹ K⁻¹), and ${Q}_{{{\rm{net}}}}^{{\prime} }$ represents the net surface heat flux, consisting of four components:

$${Q}_{{{\rm{net}}}}^{{\prime} }={Q}_{{{\rm{SW}}}}^{{\prime} }+{Q}_{{{\rm{LW}}}}^{{\prime} }+{Q}_{{{\rm{LH}}}}^{{\prime} }+{Q}_{{{\rm{SH}}}}^{{\prime} }$$

(11)

representing shortwave radiation, longwave radiation, latent heat flux, and sensible heat flux anomalies, respectively. The shortwave radiation transmitted through the bottom of the mixed layer (${Q}_{{{\rm{bot}}}}^{{\prime} }$) is parameterized following ref. ⁶⁵ as:

$${Q}_{{{\rm{bot}}}}^{{\prime} }={Q}_{{{\rm{SW}}}}^{{\prime} }\left(0.58{e}^{-\frac{H}{0.35}}+0.42{e}^{-\frac{H}{23}}\right)$$

(12)

Taking the volume-average by integrating both hand sides of Eq. (9) from the ocean mixed layer depth to the ocean surface and spatially over the eastern equatorial Pacific box where the SST variability of ENSO is dominant, the heat budget equation can be written as follows:

$$\frac{\partial \langle {T}^{\prime} \rangle }{\partial t}=\underbrace{\left\langle {Q}^{\prime} \right\rangle }_{{{\rm{TD}}}}\underbrace{-\left\langle \frac{\partial \left(\overline{u}{T}^{\prime} \right)}{\partial x}+\frac{\partial \left(\overline{v}{T}^{\prime} \right)}{\partial y}\right\rangle }_{{{\rm{DD}}}}+\underbrace{\frac{\left\langle {\overline{w}}_{{{\rm{bot}}}}{T}_{{{\rm{bot}}}}^{{\prime} }\right\rangle }{H}}_{{{\rm{TH}}}}\underbrace{-\left\langle {u}^{{\prime} }\frac{\partial \overline{T}}{\partial x}\right\rangle }_{{{\rm{ZA}}}}\underbrace{-\left\langle {v}^{{\prime} }\frac{\partial \overline{T}}{\partial y}\right\rangle -\left\langle {w}^{{\prime} }\frac{\partial \overline{T}}{\partial z}\right\rangle }_{{{\rm{EK}}}}\\ \underbrace{-\left\langle {u}^{\prime} \frac{\partial {T}^{{\prime} }}{\partial x}+{v}^{\prime} \frac{\partial {T}^{{\prime} }}{\partial y}+w{\prime} \frac{\partial {T}^{\prime} }{\partial z}\right\rangle }_{{{\rm{NDH}}}}+\underbrace{\left\langle {Q}_{{Res}}\right\rangle }_{{{\rm{Res}}}}$$

(13)

where the angle brackets denote volume/area-average variables over the eastern Pacific box (180°–90°W, 6°S–6°N), ${T}_{{{\rm{bot}}}}^{{\prime} }$ and ${\overline{w}}_{{{\rm{bot}}}}$ the anomalous temperature and climatological vertical velocity at the bottom interface of the ocean mixed layer, respectively. We group the various feedbacks on the right-hand side of Eq. (9) as thermal damping by the net surface heat flux (TD), dynamic damping by mean horizontal currents (DD), thermocline feedback (TH), zonal advective feedback (ZA), meridional advective feedback and vertical advective feedback (combined as Ekman feedback, EK), nonlinear dynamic heating (NDH), and sub-grid scale contributions (SG), respectively. Our definitions of DD and TH represent the advection of anomalous temperature by mean currents via lateral and bottom interfaces, respectively.

Next, we apply the following linear relationship between various oceanic processes with $\left\langle {T}^{{\prime} }\right\rangle$ and h⁹ and replacing $\langle {T}^{{\prime} }\rangle$ with ${T}_{{{\rm{e}}}}$ for simplicity:

$${{\rm{TH}}}={R}_{{{\rm{TH}}}}{T}_{{{\rm{e}}}}+{{F}_{1}}_{{{\rm{TH}}}}h,$$

(14a)

$${{\rm{ZA}}}={R}_{{{\rm{ZA}}}}{T}_{{{\rm{e}}}}+{{F}_{1}}_{{{\rm{ZA}}}}h,$$

(14b)

$${{\rm{EK}}}={R}_{{{\rm{EK}}}}{T}_{{{\rm{e}}}}+{{F}_{1}}_{{{\rm{E}}}K}h,$$

(14c)

$${{\rm{DD}}}={R}_{{{\rm{DD}}}}{T}_{{{\rm{e}}}}+{{F}_{1}}_{{{\rm{DD}}}}h,$$

(14d)

$${{\rm{TD}}}={R}_{{{\rm{TD}}}}{T}_{{{\rm{e}}}},$$

(14e)

$${{\rm{NDH}}}={R}_{{{\rm{NDH}}}}{T}_{{{\rm{e}}}}+{{F}_{1}}_{{{\rm{NDH}}}}h,$$

(14f)

$${{\rm{Res}}}={R}_{{{\rm{Res}}}}{T}_{{{\rm{e}}}}+{{F}_{1}}_{{{\rm{Res}}}}h.$$

(14g)

Substituting these into the ENSO mixed-layer temperature equation, the equation reduces to:

$$\begin{array}{c}\frac{\partial {T}_{{{\rm{e}}}}}{\partial t}=\left({R}_{{{\rm{TH}}}}+{R}_{{{\rm{ZA}}}}+{R}_{{{\rm{EK}}}}+{R}_{{{\rm{DD}}}}+{R}_{{{\rm{TD}}}}+{R}_{{{\rm{NDH}}}}+{R}_{{{\rm{Res}}}}\right){T}_{{{\rm{e}}}}\\+\left({{F}_{1}}_{{{\rm{TH}}}}+{{F}_{1}}_{{{\rm{ZA}}}}+{{F}_{1}}_{{{\rm{EK}}}}+{{F}_{1}}_{{{\rm{DD}}}}+{{F}_{1}}_{{{\rm{NDH}}}}+{{F}_{1}}_{{{\rm{Res}}}}\right)h.\end{array}$$

(15)

From this, the total SST growth rate $R$ and phase-transition rate ${F}_{1}$ are expressed as:

$$R={R}_{{{\rm{TH}}}}+{R}_{{{\rm{ZA}}}}+{R}_{{{\rm{EK}}}}+{R}_{{{\rm{DD}}}}+{R}_{{{\rm{TD}}}}+{R}_{{{\rm{NDH}}}}+{R}_{{{\rm{Res}}}},$$

$${F}_{1}={{F}_{1}}_{{{\rm{TH}}}}+{{F}_{1}}_{{{\rm{ZA}}}}+{{F}_{1}}_{{{\rm{EK}}}}+{{F}_{1}}_{{{\rm{DD}}}}+{{F}_{1}}_{{{\rm{NDH}}}}+{{F}_{1}}_{{{\rm{Res}}}}$$

To estimate these parameters, we account for seasonality explicitly outlined in Eq. (6) using multivariate linear regression. Ensemble mean parameters are calculated by performing regression on concatenated results from all ensemble members. These derived parameters capture the contributions of each process and provide a comprehensive understanding of ENSO feedbacks and their contribution to the ENSO growth rate. The ${R}_{{{\rm{NDH}}}}$ and ${R}_{{{\rm{Res}}}}$ terms are combined as ${R}_{{{\rm{AllRes}}}}$, which consists of tropical instability waves and other unresolved processes.

We have also tested our analysis using different ocean mixed layer depths (30 m, 40 m, and 50 m) and alternative definitions of the eastern Pacific box (e.g., the Niño3.4 region). The results remain quantitatively similar and do not affect our conclusions.

ENSO wind stress structure

The ENSO wind stress structure affects both the growth rate and periodicity of ENSO^9,36. Here, we determine the ENSO wind stress pattern using linear regression of monthly zonal wind stress anomalies $({\tau }_{x}^{{\prime} })$ onto the monthly ENSO SST anomaly index. Following ref. ³⁶, the meridional width of ${\tau }_{x}^{{\prime} }$ is defined as the latitudinal distance between the meridional boundaries, the nearest local minima of ${\tau }_{x}^{{\prime} }$ on either side of the equator, based on the meridional profile averaged over 160°E–150°W (Fig. 2g). The zonal length is defined as the longitudinal distance between the zonal boundaries of ${\tau }_{x}^{{\prime} }$, determined from the zonal profile averaged over 5°S to 5°N across the tropical Pacific. The eastern boundary is identified as the zero-crossing point in the zonal profile; the western boundary is defined as the local minimum within the region from 140°E to 190°E; and zonal centroid location as the midpoint between zonal boundaries (Supplementary Fig. 5b).

Under the assumption that the zonal wind stress anomaly ${\tau }_{x}^{{\prime} }$ has a Gaussian meridional structure, the RO $h$ equation can be reformulated to explicitly incorporate the wind stress structure³⁶:

$$\varepsilon={\varepsilon }_{m}+\frac{\alpha }{2{x}_{c}}$$

(16)

$${F}_{2}\propto \frac{\alpha }{2{x}_{c}}$$

(17)

where ${\varepsilon }_{m}$ is a linear mechanical damping coefficient (2.5 yr)⁻¹, the parameter $\alpha$ characterizes the meridional structure of ${\tau }_{x}^{{\prime} }$, such that the meridional width of ${\tau }_{x}^{{\prime} }$ is proportional to $1/\sqrt{\alpha }$, and ${x}_{c}$ denotes the nondimensional location of the center of wind stress anomalies along the equator measured from the western boundary (with ${x}_{c}\approx 0.35$, Supplementary Fig. 5b). A meridional widening of ${\tau }_{x}^{{\prime} }$ leads to a reduction in $\alpha$, thereby weakening the damping from thermocline adjustment ($\varepsilon$, Fig. 2h) and recharge/discharge efficiency (${F}_{2}$, Fig. 2i). These changes enhance the growth rate and increase the periodicity of ENSO following the RO eigenvalue Eq. (5).

Phase synchronization

Phase synchronization characterizes how interactions between two different processes can lead to synergistic dynamical phase behavior (e.g., the temporal alignment of respective local maxima or minima). A special case of phase-synchronization is frequency-locking³¹, where two systems with normally independent oscillatory behavior develop a joint frequency and locked dynamics. In general, for phase-synchronized systems, the difference between the phases of the interacting processes, or multiples thereof, is statistically distinguishable from a uniform white noise process. In particular, phase synchronization can emerge in nonlinear dynamical systems, which include product terms between two signals.

Practically, phase relationships between two processes, which are represented by their timeseries $x\left(t\right)$ and $y\left(t\right)$ can be calculated using their complex analytical signals^66,67 ${z}_{1}\left(t\right)={A}_{1}\left(t\right){e}^{i{{{\rm{\phi }}}}_{1}\left(t\right)}=x\left(t\right)+i{x}_{H}\left(t\right),$ and ${z}_{2}\left(t\right)={A}_{2}\left(t\right){e}^{i{{{\rm{\phi }}}}_{2}\left(t\right)}=y\left(t\right)+i{y}_{H}\left(t\right)$, where ${x}_{H}\left(t\right),$ ${y}_{H}\left(t\right),$ represent the Hilbert transforms of $x\left(t\right),y(t)$ and ${{{\rm{\phi }}}}_{1}\left({{\rm{t}}}\right),{{{\rm{\phi }}}}_{2}({{\rm{t}}})$ are the respective phases of the signal. The only requirement for the two signals $x\left(t\right),y(t)$ is that they satisfy Bedrosian’s Product Theorem⁶⁸. This can be achieved by appropriate band-pass filtering. To quantify m:n phase synchronization (m, n are integers), we calculate $\delta {{{\rm{\phi }}}}_{\left\{{{\rm{n}}},{{\rm{m}}}\right\}}={{\rm{n}}}{{{\rm{\phi }}}}_{1}\left({{\rm{t}}}\right)-{{\rm{m}}}{{{\rm{\phi }}}}_{2}(t)$. For two un-synchronized (decoherent) processes, we would expect (1) the time evolution of the unwrapped phases $\delta {{{\rm{\phi }}}}_{\left\{{{\rm{n}}},{{\rm{m}}}\right\}}$ to essentially increase, without any long periods of phase “friction”, which can be characterized as consistent plateaus of near constant $\delta {{{\rm{\phi }}}}_{\left\{{{\rm{n}}},{{\rm{m}}}\right\}}$; (2) the probability distribution of $\delta {{{\rm{\phi }}}}_{\left\{{{\rm{n}}},{{\rm{m}}}\right\}}$ (without unwrapping procedure) to be indistinguishable from a uniform distribution between 0–360 degrees^66,69. Respectively, for m:n synchronized signals, (1) we would expect to see long periods of little growth in unwrapped phase differences; (2) the frequency histogram of $\delta {{{\rm{\phi }}}}_{\left\{{{\rm{n}}},{{\rm{m}}}\right\}}$ (without unwrapping procedure) across all angles (0–360°) should deviate statistically (e.g., Kolmogorov-Smirnov test) from a uniform distribution.

We use this approach to calculate the 1:1 difference of unwrapped phases between timeseries characterizing different climate modes simulated by the AWI-CM3 model. All time series were bandpass filtered between 2.5 months and 10 years using a Butterworth filter prior to the analysis to focus on annual to interannual variability and to satisfy Bedrosian’s theorem. We use the standard deviation of the phase difference PDF, $\sigma [{{\rm{PDF}}}(\delta {\Phi }_{1,1})]$, as a measure of the synchronization strength. If there is no synchronization, the phase differences are uniformly distributed, yielding a flat PDF and $\left.\sigma [{{\rm{PDF}}}(\delta {\Phi }_{1,1})]\right)\approx 0$ (Supplementary Fig. 8a, b). In contrast, if there is strong synchronization, the phase differences concentrate around a preferred value (−π/2 for the example shown in Supplementary Fig. 8c, d), producing a sharply peaked PDF, resulting in a larger $\sigma [{{\rm{PDF}}}(\delta {\Phi }_{1,1})]$ (Supplementary Fig. 8c, d).

Statistical significance test

The Fisher z-transformation was used to test statistical significance of the correlation differences as follows:

$$Z=0.5\frac{{\mathrm{ln}}\left(\frac{1+{r}_{1}}{1-{r}_{1}}\right)-{\mathrm{ln}}\left(\frac{1+{r}_{2}}{1-{r}_{2}}\right)}{\sqrt{\frac{1}{{n}_{1}-3}+\frac{1}{{n}_{2}-3}}}$$

(18)

where ${r}_{1}$ and ${r}_{2}$ are the correlation coefficients, ${n}_{1}$ and ${n}_{2}$ are the sample sizes of the first and second group samples. The absolute value |Z| is then compared against a critical value from the t-distribution for a two-tailed test. We rejected the null hypothesis that the two correlations are not significantly different at a 90% confidence level if |Z| exceeds the critical value. The Student’s t test was used to test statistical significance of the regression coefficient.

Given small sample sizes, we apply a bootstrap method to assess whether changes in ENSO regularity are statistically significant. Specifically, the 21-year moving-window values of ENSO regularity are randomly resampled with replacement to generate 10,000 synthetic realizations. From these realizations, we compute the standard deviation of the resulting distribution of mean values.