Introduction

Optical encryption provides a robust mechanism for securing information by leveraging the intrinsic physical properties of light1, such as interference2, diffraction3, and polarization4. This approach has been widely applied across diverse fields, including sensitive information protection5, biometric authentication6, satellite-based quantum communications7, and anti-counterfeiting labeling8. Compared to conventional electronic encryption techniques—such as digital cryptography9—optical encryption offers substantial advantages1,10,11, notably parallel encoding capability, high-speed processing, and immunity to electromagnetic interference, thus providing a highly reliable physical-layer solution for information security.

However, most current optical encryption methods primarily rely on spatial information encoding through modulation and detection devices, including spatial light modulators (SLMs)12, digital micromirror devices (DMDs)13, and charge-coupled device (CCD) cameras. These spatial modulation devices inherently suffer from limited switching speeds and low refresh rates, resulting in relatively low information-flow density and restricted transmission rates. Such limitations significantly hinder the adoption of traditional optical encryption methods in high-speed information transmission scenarios.

To achieve ultrahigh-speed information transmission, recent advances in temporal signal transmission—such as coherent detection14,15, multi-dimensional multiplexing16,17, and high-order modulation formats18—have been widely explored in communication systems. These techniques provide opportunities to dramatically increase the information density of optical encryption, e.g., by extending it from purely spatial to integrated spatiotemporal domains. Nevertheless, directly encrypting temporal signals remains fundamentally challenging because conventional spatial optical encryption schemes fail to adequately prevent unauthorized temporal signal interception. As illustrated in a classic orbital angular momentum (OAM) encryption scheme (Fig. 1a), while spatial encoding stores and encrypts information using spatial modulation patterns, high temporal signal-to-noise (SNR) modulated signals can be directly retrieved by analyzing their light intensity versus time at high spatial SNR locations. Therefore, the core challenge in achieving high-speed optical encryption is to develop an encryption scheme capable of preventing unauthorized interception by eavesdroppers (Eve) in free-space temporal signal transmission, while still allowing legitimate receivers (Bob) to decrypt the transmitted signal without interference.

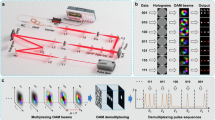
Fig. 1: Schematic diagram of concept and performance of the spatiotemporal noise chaffing scheme.
figure 1

a Monomodal OAM encryption for temporal information transmission: the temporal signal leaks from the circularly distributed intensity pattern, allowing both the eavesdropper (Eve) and the legitimate receiver (Bob) to retrieve the signal. b CVW-multimodal OAM encryption for temporal information transmission: the noise-chaffed signal generated by conjugated mode combinations prevents direct signal detection, while Bob can winnow the information using the correct key. c CVW-multimodal OAM encryption requires precise weight and mode matching for decryption, enhancing security and expanding the key space. d Conventional high-speed optical information transmission faces a trade-off between transmission rate and physical-layer security, whereas the proposed method achieves a balance, reaching a 1.25 Tbps data rate with a 1010-dimensional key space for encryption.

Full size image

Inspired by the concept of “chaffing and winnowing”19 in communication security—where genuine data (“wheat”) is obscured by introducing indistinguishable noise (“chaff”), allowing only authorized recipients to extract the true information—we propose and experimentally demonstrate a novel spatiotemporal noise chaffing system, capable of ultrahigh-speed optical encryption at transmission rates exceeding the terabit-per-second (Tbps) scale. Specifically, as shown in Fig. 1b, our approach leverage the symmetric spatial characteristics of conjugate orbital angular momentum (OAM) modes20 by encoding the temporal information signal and noise separately onto two conjugated OAM states and transmitting them co-axially through free space. Due to their perfect spatial coherence, the signal and noise become indistinguishable to unauthorized interceptors—yielding high spatial SNR but severely degraded temporal SNR for Eve, since temporal signal recovery requires integrating spatial fields at each instant; the conjugate-superposed spatial noise substantially degrades the integrated temporal SNR. Conversely, Bob can recover the signal through mode winnowing at the designated spatial location by applying an inverse OAM mode key, capitalizing on the orthogonality of OAM states. Crucially, we further to enhance encryption security through the introduction of a variable-weight multimodal OAM (VW-multimodal OAM) scheme (Fig. 1c) combined with a multimodal generation neural network (MGNN), substantially expanding the encryption key space. In this scheme, accurate signal recovery by the legitimate receiver requires simultaneous matching of both modal composition and weighting coefficients, effectively mitigating the risk of brute-force attacks.

Through high-speed temporal information transmission experiments, we validate the efficacy and robustness of our proposed method, achieving an unprecedented single-mode data transmission rate of 1.25 Tbps in an 8-channel wavelength-division multiplexing (WDM) coherent system with an encryption key space exceeding 1010 supported by a high-accuracy MGNN that produces holograms with a mean square error as low as 10−9. This record-breaking performance, quantified by the product of transmission rate and key space, surpasses current state-of-the-art optical encryption methods by five orders of magnitude, establishing a new benchmark for ultrafast photonic security technologies (Fig. 1d; see Supplementary Note 1 for comparative details). The proposed technique provides transformative potential for future applications in next-generation high-security optical communications networks, including 6 G and low Earth orbit satellite systems.

Results

Principle of spatiotemporal noise chaffing with CVW-multimodal OAM encryption system

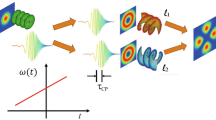
To enable optical encryption for high-speed temporal signals, we introduce a conjugated variable-weight multimodal OAM (CVW-multimodal OAM) encryption system. For illustration and visualization, we propose a vector circle based on the system’s space bandwidth product (SBP)21, where the positions of the vectors are determined by the spatial radii of the different OAM states (see Supplementary Notes 2 and 3). As illustrated in Fig. 2a, a conventional optical encryption system encodes the temporal signal \(S(t)\) onto an OAM mode\(\,{U}_{l}\left(r,\varphi,z\right)\), generating the transmitted electric field \(E\left(r,\varphi,z,t\right)\):

$$E\left(r,\varphi,z,t\right)={U}_{l}\left(r,\varphi,z\right)S\left(t\right).$$
(1)
Fig. 2: Mechanism of noise chaffing CVW-multimodal OAM encryption system.
figure 2

a Encryption and decryption in vector space using monomodal OAM. b Encryption and decryption using conjugated monomodal OAM. c CVW-multimodal OAM with correct decryption. d CVW-multimodal OAM with false decryption.

Full size image

In this conventional scheme, although the legitimate receiver (Bob) can successfully decrypt the transmitted signal using the inverse OAM mode, an eavesdropper (Eve) without the decryption key can still intercept sufficient temporal information—manifested as high-amplitude signals and clear constellation diagrams—by analyzing the ring-like regions with high spatial SNR. In contrast, if a conjugated OAM state \({U}_{-l}\left(r,\varphi,z\right)\) carrying noise \(N(t)\) is chaffed co-axially (Fig. 2b), the electric field becomes symmetrically distributed in the vector space, yielding perfect spatial coherence:

$$E\left(r,\varphi,z,t\right)=S\left(t\right){U}_{l}\left(r,\varphi,z\right)+N\left(t\right){U}_{-l}\left(r,\varphi,z\right).$$
(2)

In this configuration, the combined intensity exhibits a petal-like pattern due to interference. Consequently, random detection by Eve in high-spatial-SNR regions results in a chaffed signal with degraded temporal SNR and a scattered constellation diagram (see Supplementary Note 6). The detected photocurrent for Eve is given by:

$${I}_{{Eve}}\propto \iint {\left|S{\cdot U}_{l}+N\cdot {U}_{-l}\right|}^{2}{rdrd}\varphi \\= \left({S}^{2}+{N}^{2}\right)\iint {\left|{U}_{l}\right|}^{2}{rdrd}\varphi+2{Re}\left(S{N}^{*}\right)\iint \left|{U}_{l}^{2}\right|{rdrd}\varphi .$$
(3)

Consequently, the chaffed conjugated modes cause Eve’s received temporal signal to be heavily degraded, with a diffused constellation diagram that effectively prevents unauthorized information recovery. Conversely, the legitimate receiver (Bob), who possesses the correct decryption key, can winnow the signal precisely at the center of the spatial field. The photocurrent for Bob is:

$${I}_{{Bob}}\propto \iint {\left|S\cdot {U}_{0}+N{\cdot U}_{-2l}\right|}^{2}{rdrd}\varphi \\= {\left|S\right|}^{2}\iint {\left|{U}_{0}\right|}^{2}{rdrd}\varphi+\left[{\left|N\right|}^{2}+2{{Re}}\left(S{N}^{*}\right)\right]\iint {\left|{U}_{-2l}\right|}^{2}{rdrd}\varphi .$$
(4)

Here, the temporal signal \(S(t)\) is concentrated in the fundamental Gaussian mode \({U}_{0}\) at the spatial field center, enabling Bob to reconstruct the pure temporal information, while the noise and mixed components disperse into higher-order modes.

However, encryption based on a monomodal OAM state is inherently vulnerable due to its discrete vector space, making it susceptible to brute-force attacks. Moreover, the petal-like interference intensity pattern of monomodal OAM is strongly correlated with its topological charge, potentially leaking information and posing additional security risks (see Supplementary Note 3). To overcome these limitations, we extend the concept to encode \(S(t)\) and \(N(t)\) onto pairs of conjugated variable-weight multimodal OAM (CVW-multimodal OAM) states rather than monomodal states (Fig. 2c, d). Although the basic encryption and decryption mechanisms remain similar, this approach significantly increases security by expanding the key space. Accurate decryption now requires simultaneous matching of both modal composition and weight coefficients—a requirement that greatly reduces the probability of successful brute-force attacks. Detailed expanded analysis and derivations are provided in Supplementary Note 5. Any incorrect key results in spatial mismatches, dispersing energy away from the central mode and producing a chaotic constellation. This inherent complexity in the key space thus substantially reduces the risk of brute-force attacks and interception, effectively safeguarding the transmitted temporal data.

Ultra-large OAM key space designed by artificial neural network

The key space of the proposed VW-multimodal OAM system is determined by three parameters: the maximum supported OAM order \(L\), the number of OAM states selected for encryption \(M\), and the weight partition precision \(\delta\). The constructed key space \(K\) is given by (detailed analyses are provided in Supplementary Note 8):

$$K=2\cdot \left(\begin{array}{c}L\\ M\end{array}\right)\cdot \left(\begin{array}{c}\frac{1}{\delta }+M-1\\ M-1\end{array}\right).$$
(5)

Figure 3a illustrates the entire process of key space generation. The resultant VW-multimodal OAM field is expressed as:

$$U\left(r,\varphi,z\right)={\sum}_{m}^{M}{c}_{m}{A}_{m}(r,\varphi,z)\exp \left(i{l}_{m}\varphi \right)$$
(6)

where \({c}_{m}\) are the weight coefficients assigned to each of the \(M\) selected OAM modes, and \({A}_{m}(r,\varphi,z)\) denotes the amplitude distribution, which may include both radial and longitudinal field variations. This construction demonstrates an exponentially increasing key space with increasing \(L\) and finer \(\delta\) values. Notably, the parameter \(M\) exhibits a non-monotonic behavior—there exists an optimal \(M\) that maximizes \(K\), beyond which \(K\) decreases as \(M\) approaches \(L\).

Fig. 3: Exponentally expanded key space and design of high-precision holograms.
figure 3

a Parameters defining the key space of CVW-multimodal OAM: the largest order of OAM modes supported by system (L), the number of modes selected for CVW-multimodal OAM (M), and the weight precision (δ). b Key space size for different weight precisions (δ = 0.5,δ = 0.25,δ = 0.125, and δ = 0.1, respectively). c Mean crosstalk value and SNR from 1000 random samplings, showing the effect of increasing δ for different M with a fixed L = 20. d Schematic of a multimodal OAM generation neural network for single hologram broadcasting of CVW-multimodal OAM. e Concept of single hologram generation for CVW-multimodal OAM and comparison of simulation and experimental results for direct mode overlap and MGNN. f Error comparison between different methods (direct overlapping, pattern search optimization, and MGNN) for CVW-multimodal OAM hologram generation.

Full size image

While Eq. (5) predicts the theoretical key space, practical security evaluation requires assessment of the isolation of mode-weight combinations. Isolation is quantified via the mean crosstalk value (CV), calculated over 1000 randomly generated combinations under various \((L,M,\delta )\) configurations. As shown in Fig. 3c, the trends of CV and SNR values for incorrect keys (see calculation methods in Supplementary Note 10) indicate that increasing the number of OAM states and pursuing more precise weight partitioning tend to elevate both CV and SNR. This, in turn, may compromise encryption integrity by reducing the distinguishability between correct and incorrect keys. Based on our analysis of the average CV and SNR values for both correct and incorrect keys, as well as the statistical distribution of tested samples (see Supplementary Fig. 12), we selected the parameters δ = 0.1, M = 10, and L = 20 in this work. These values represent a carefully optimized trade-off between communication performance and security robustness.

To overcome the limitations of conventional approaches—where multiple power-tunable laser sources coupled with SLMs are required for VW-multimodal OAM generation, and direct superposition introduces significant interference errors (Supplementary Note 9)—we propose a compact single-hologram solution leveraging a Multimodal Generation Neural Network (MGNN), as illustrated in Fig. 3d. The MGNN intelligently optimizes the weight coefficients for the selected OAM modes from the system’s supported range (spanning ±\(L\) orders). It compensates for inherent mode interference and intensity non-uniformity through high-dimensional parameter fitting. The output hologram can support VW-multimodal OAM launch with a single beam, eliminating the need for multiple power-tunable sources. Simulation and experimental intensity profiles are provided in Fig. 3e. Compared with conventional pattern search methods22 (given in Supplementary Note 12) for hologram generation, the MGNN significantly reduces the mean square error (MSE)—dropping by four orders of magnitude from 3.25 × 10−5 to 1.76 × 10−9 as shown in Fig. 3f. This dramatic reduction in error results in higher isolation between closely spaced mode-weight combinations, thereby supporting the large key space of the CVW-multimodal OAM encryption system (see Supplementary Fig. 13). The experimentally obtained mode spectra are illustrated in Supplementary Fig. 16 to validate the performance of both PS and MGNN approaches.

Terabit-scale optical encryption for ultrahigh-speed information transmission

Based on the CVW-multimodal OAM encryption system, our approach enables ultrahigh-speed secure information transmission. The experimental validation was performed on an 8-wavelength multiplexed coherent system using a 40 Gbaud 16-QAM temporal signal (See Method Section and Supplementary Note 13). As shown in Fig. 4a, the post-FEC bit error rate (BER) was measured under three conditions—without a decryption key, with the correct key, and with a false key—using both monomodal OAM and CVW-multimodal OAM encryption systems. Under the monomodal OAM encryption scheme, temporal information is significantly leaked, as evidenced by Eve’s ability to intercept the signal through the ring-like spatial intensity distribution. In contrast, the CVW-multimodal OAM system mitigates this vulnerability by superimposing signal and noise, thereby degrading the temporal signal for unauthorized receivers. Eve’s detection yields a chaotic constellation with high BER, while Bob, using the correct decryption key, reconstructs the pure temporal information. Figure 4b displays the spectral analysis for three scenarios within the CVW-multimodal OAM encryption system. The similar spectral amplitudes in the cases “with key” and “without key” indicate that the differences in BER are primarily due to the mixing of signal and noise, confirming the effective decorrelation of temporal information (as further explained in Supplementary Note 7). Moreover, Fig. 4c compares the BER for CVW-multimodal OAM encryption and VW-multimodal OAM encryption with and without noise addition. Although the introduction of noise slightly degrades signal quality, the BER remains below the 20% HD-FEC threshold (2 × 10−2), indicating minimal adverse impact on overall information transmission. Isolation validation experiments further demonstrate that the PF-BER increases by over two orders of magnitude with increasing weight variance and mode Euclidean distance (ED), thereby confirming the robustness and high security of the encryption system (more experimental results are given in Supplementary Fig. 14). By multiplexing all 8 wavelength channels in the C-band (Supplementary Fig. 15), as illustrated in Fig. 4e, the BER for each channel remains below the HD-FEC threshold, achieving a combined data rate of 1.25 Tb/s. The BER distribution visualized in Fig. 4f clearly shows the significant performance difference between the monomodal and CVW-multimodal encryption systems, supporting the efficacy of our approach in securing high-speed optical transmission.

Fig. 4: Terabit-scale optical encryption for ultrahigh-speed information transmission.
figure 4

a Comparison of constellations for Monomodal OAM and CVW-multimodal OAM encryption under three different scenarios: without key, with correct key, and with false key. b Spectrum comparison for three different scenarios in CVW-multimodal OAM, demonstrating the decorrelation of pure and mixed signals. c Bar chart of Bit Error Rate (BER) under different signal waveform peak-to-peak voltages for VW-multimodal OAM and CVW-multimodal OAM, illustrating the minimal impact of noise-path introduction. d Experiment showing the isolation between different CVW-multimodal OAM combinations using PF-BER, revealing that increased weight variance and enlarged mode ED result in higher BER and false information reconstruction. e 8-wavelength multiplexing experiment, presenting ROP and BER for 40 GBaud 16-QAM signals, achieving a combined data rate of 1.25 Tb/s. f BER spatial distribution for Monomodal OAM and CVW-multimodal OAM, demonstrating that Monomodal OAM can successfully reconstruct information without decryption, whereas CVW-multimodal OAM effectively hides the information.

Full size image

Discussion

In this study, we propose and experimentally demonstrate a novel spatiotemporal optical encryption method inspired by the “chaffing and winnowing” paradigm, achieving a record-breaking secure optical transmission rate of 1.25 Tbps with an unprecedented encryption key space exceeding 1010. This breakthrough effectively overcomes the longstanding limitations of low information density inherent in conventional optical encryption methods by seamlessly integrating temporal encoding and spatial encryption. Central to our approach is the exploitation of the symmetric characteristics of conjugated OAM states, which provides a robust physical mechanism for achieving perfect spatial coherence between the temporal signal and noise to support adding effective chaff. Concurrently, the orthogonality of conjugated OAM states facilitates the spatial separation necessary for precise signal winnowing, enabling reliable information reconstruction by the legitimate receiver. In essence, our method embodies the chaffing and winnowing concept in optical encryption. Moreover, we introduce the concept of VW-multimodal OAM to further enhance system security against brute-force attacks. The accompanying MGNN significantly improves the isolation of mode-weight combinations, thereby supporting an expanded key space. Importantly, because our encryption method operates at the physical layer, it is complementary to electronic encryption techniques, such as digital cryptography. The integration of both approaches can create multilayered protection schemes that further strengthen overall information security.

While the encryption key space is fundamentally determined by the system’s SBP, which is closely related to the NA, the use of high-resolution SLM can significantly enhance performance. However, diffraction during free-space transmission imposes limitations on the SBP and thus constrains the overall encryption capacity and communication efficiency (see Supplementary Note 14). Incorporating 4-f relay systems or optical imaging components to mitigate diffraction effects can help maintain spatial coherence and improve system scalability.

Notably, even higher-order modulation formats and advanced multiplexing techniques, e.g., OAM multiplexing, remain available for future implementation, suggesting substantial room for further improvement in transmission speed and capacity. Looking forward, the proposed encryption technique holds significant potential for further miniaturization and integration through advanced photonic platforms, such as metasurfaces23,24,25 and on-chip optical systems26,27. Such advancements could greatly enhance practical applications, paving the way for revolutionary breakthroughs in secure, ultrahigh-speed optical networks. Ultimately, this method presents a compelling paradigm shift in photonic information security, poised to ensure robust data protection and scalable network solutions in the era of 6G28 and beyond.

Methods

Experimental setup

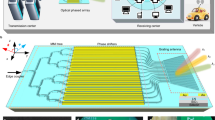
We experimentally demonstrated the CVW-multimodal OAM encryption within an 8-wavelength coherent system, as illustrated in Supplementary Fig. 11. The experimental setup consists of two main components: temporal signal transmission and reception, and spatial light modulation.

Temporal signal transmission and reception

For the temporal signal processing, we employed tunable multi-wavelength external cavity lasers (ECLs) (Keysight N7714A) to generate eight-channel laser sources. One laser was set to 1.552 µm, while the remaining wavelengths ranged from 1.561 µm to 1.533 µm, which were combined using a multi-channel optical coupler. The 1.552 µm laser carried a 40 Gbaud 16-QAM temporal signal, while the other wavelengths were separately modulated with the same format to validate wavelength-division multiplexing (WDM) performance. The temporal signals were generated and launched via an arbitrary waveform generator (AWG) (Keysight M8194A, 120 GSa/s). These signals were output through two individual AWG channels for single-polarization in-phase and quadrature (IQ) modulation and coupled with the lasers using Mach-Zehnder modulators (MZMs) (Sumicem T.MXH 1.5−20PD-ADC-LV). Both signal paths were amplified by erbium-doped fiber amplifiers (EDFAs) (Amonics AEDFA−23-B-FA) and combined using a wavelength-selective switch (WSS) (Finisar Waveshaper 4000S). The signals were further amplified by another EDFA (OVLINK EYDFA-C-HP-BA-30-PM-B) before being split into two paths: (1) Signal Path: Directly transmitted into the CVW-multimodal OAM encryption system for spatial optical encryption; (2) Noise Path: Routed through a 1-m delay line to decorrelate from the signal before entering the encryption system, which has been validated in Supplementary Note 7. After passing through the spatial modulation system, the received light was amplified by an EDFA (OVLINK EDFA-C-BA-GF-26-PM-B), and the individual wavelengths were filtered using optical bandpass filters (OBPFs) (EXFO XTM-50-SCL-U). A variable optical attenuator (VOA) (OVLINK SVOA−1000) was used for power control. A variable local oscillator (LO) was employed to maintain zero-difference detection across different wavelengths, and an integrated coherent receiver (ICR) performed electrical-to-optical (E/O) conversion. The resulting electrical signal was sampled by an oscilloscope (OSC) (Keysight UXR0134A, 256 GSa/s) for subsequent digital signal processing (DSP). For both Tx and Rx, DSP has been written in Supplementary Note 13.

Spatial light modulation

In the spatial modulation stage, the temporal signal and noise entered the system through two separate collimators from different ports. Each path passed through a polarizer to align polarization before reaching spatial light modulators (SLM1 and SLM2) (UPOlabs HDSLM80R), which were preloaded with a conjugated CVW-multimodal OAM phase pair. The optical path lengths were precisely matched to ensure signal-noise overlap. The modulation process was performed as follows: (1) Beam Splitters (BS1 and BS2) (50:50) directed the signal and noise beams toward SLM1 and SLM2, respectively; (2) The modulated beams were then combined at BS3, generating the CVW-multimodal OAM state, carrying the signal-noise mixed temporal information; (3) The combined optical field was experienced 0.4 m free space transmission and then directed to SLM3 (UPOlabs HDSLM80T) for decryption and passed through a lens (\(f=150\,{{\mathrm{mm}}}\)) to perform Fraunhofer far-field transformation. (4) Finally, Beam Splitter BS4 (90:10) separated the optical wave into two paths:

  • Path 1: Coupled into a single-mode fiber (SMF) for further temporal signal processing.

  • Path 2: Captured by a CCD camera to record the spatial field distribution.

The coupled signal from Path 1 was then forwarded for the second stage of temporal processing, completing the full encryption-decryption cycle.

OAM spectrum calculation

For an arbitrary complex amplitude field \(U(r,\varphi,z)\), it can be decomposed into a set of orthogonal OAM basis functions. Given a total of M OAM modes (defined by SBP of system, see Supplementary Note 2), the expansion coefficient \({a}_{m}\left(r,\varphi,z\right)\) corresponding to the m-th OAM mode is given by:

$${a}_{m}\left(r,\varphi,z\right)=\frac{1}{\sqrt{2\pi }}{\int }_{0}^{2\pi }U\left(r,\varphi,z\right)\exp \left(-i{l}_{m}\varphi \right)d\varphi$$
(7)

Here, \({a}_{m}\left(r,\varphi,z\right)\) represents the coefficient of the m-th OAM mode, obtained by projecting the electric field \(U\left(r,\varphi,z\right)\) onto the corresponding OAM basis. The energy of the m-th order harmonic factor can then be calculated as:

$${I}_{m}={\int }_{0}^{\infty }{\left|{a}_{m}\left(r,\varphi,z\right)\right|}^{2}{rdr}$$
(8)

The normalized energy spectrum function can be obtained as:

$${p}_{m}=\frac{{p}_{m}}{{\sum }_{m}^{M}{I}_{m}}$$
(9)

In this expression, \({p}_{m}\) represents the fractional energy contribution of the m-th OAM mode relative to the total energy distributed over the considered set of modes \([{l}_{1},{l}_{2},\ldots,{l}_{m}],m\in M.\)