Introduction

Twisted-layer graphene has emerged as a new platform for realizing non-trivial correlated states1,2,3, with superconducting bi- and multilayer systems attracting particular interest recently4,5,6,7,8. Superconductivity in these two-dimensional (2D) structures can be electrically tuned, enabling the implementation of gate-defined devices. Much research has focused on magic-angle twisted bilayer graphene (MATBG), which has become a versatile platform for superconducting electronics9,10,11,12,13,14. Recently, alternating-twist magic-angle multilayer graphene structures have emerged as a novel family of moiré superconductors8,15,16,17,18; in this configuration, each successive layer is rotated by an angle of  ± θ relative to the previous one, following an alternating sequence. Superconductivity in these multilayer structures is characterized by higher critical currents, critical magnetic fields, and critical temperatures than in MATBG. Moreover, their band structure can be tuned by a transverse electrical field, the so-called displacement field19, providing additional versatility for device operation. As a result, alternating-twist magic-angle multilayer graphene structures are promising candidates for future superconducting electronic devices.

Here, we implement a gate-defined Josephson junction (JJ) in four-layer twisted graphene (MAT4G), see ref. 20 for a similar setup in a trilayer film. Exposing the junction to a perpendicular magnetic field B, we observe a distinct Fraunhofer-like pattern in the junction critical current Icj(B). Our interference pattern differs markedly from the one observed in standard junctions21, a consequence of the extremely weak transverse magnetic screening power of these ultrathin films: i) The periodicity of the pattern is given by the flux ΦW = BW2 with W the junction width, a factor W/2λL larger than the characteristic flux Φλ = 2BWλL in usual junctions, where λL denotes the London penetration depth21. And ii), the maxima in the Fraunhofer-like pattern decay slowly \(\propto 1/\sqrt{B}\), rather than the usual decay ∝ 1/B; recognizing these differences, in the following, we refer to our experimentally observed interference pattern as a Fraunhofer pattern (FP). Interestingly, our FP exhibits pronounced jumps that we attribute to vortices penetrating/leaving the superconducting leads. Our JJ then serves as a sensor allowing for an indirect detection of vortices in gated atomically thin materials. Our observations represent the first experimental evidence for superconducting vortices in magic-angle graphene. Using a JJ allows us to detect vortices without using traditional vortex imaging techniques, which would be extremely challenging in this 2D superconductor22,23,24,25. Until now, most research has focused on the microscopic origin of superconductivity in this correlated material, with a lack of vortex studies26,27,28. Independently of the microscopic origin of superconductivity, which is still under debate, we can quantitatively analyse the observed vortex dynamics thanks to the well-developed phenomenology for these ultrathin materials29,30,31,32,33,34.

Results

Setup and bulk superconductivity

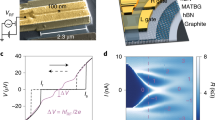
We have engineered a gate-defined JJ of length Lj = 150 nm in a MAT4G film of width W = 1.1 μm along y, length L = 6W along x, and thickness d ≈ 1 nm35, as illustrated in Fig. 1a, b. A graphite bottom gate (BG), a gold top gate (TG), and a gold finger gate (FG) are used to independently control the density nl and the displacement field Dl in the leads and in the junction (denoted as nj and Dj). Given the nanometer scale thickness d of the film d ≪ λL, the device belongs to the class of weak transverse screeners, with the effective screening power given by the Pearl length \(\Lambda=2{\lambda }_{\,{\rm{L}}\,}^{2}/d \, \gg \, {\lambda }_{{{\rm{L}}}}\)36. With the width W ≪ Λ, external magnetic fields H penetrate the entire sample and B ≈ H.

Fig. 1: Device setup and bulk phase diagram.
figure 1

a Schematic cross-section of the thin film JJ device and measurement setup; V is the measured voltage drop and I is the applied current. The top gate (TG), finger gate (FG), and back gate (BG) are indicated. b Schematic top view of the film with width W (along the y-axis) and overall length L (along the x-axis); Lj is the thickness of the JJ along x. The densities in the leads and junction are denoted by nl and nj, the field B and current I directions are indicated. Screening currents js (in green) and vortex currents jv (light blue) circulate in opposite directions. c Phase diagram of the film material, with the voltage V (blue color scale) versus leads' density nl and displacement field Dl, measured in a 4-terminal configuration not crossing the junction at a constant current I = 10 nA. The filling factor ν is plotted on the top axis. The blue dark regions around ∣ν∣ ≈ 2–3 signal superconductivity. Red dots indicate full filling where the junction is tuned into the resistive state. d Differential resistance R measured as a function of I and B with the device tuned to the superconductiong state (green square in (c)). The orange dashed line indicates the fit to extract the edge penetration field Be, with the inset showing a line trace recorded at the white circle B = 72 mT.

Full size image

We first analyse the bulk superconductivity observed in our MAT4G device. Fig. 1c shows the phase diagram of the film in terms of the voltage V (measured at constant probe current I in a 4-terminal configuration not crossing the JJ) as a function of nl and Dl, see Fig. S3B for the same measurement taken across the JJ. Superconductivity is observed between moiré filling factors ∣ν∣ ≈ ±2 and a value slightly beyond ∣ν∣ ≈ ±3, as expected8, see the dark blue domes showing zero voltage. Further characterization of the superconducting domes is discussed in the Supplementary Information.

The dependence of the bulk critical current Icb on the magnetic field B applied normal to the sample plane is shown in Fig. 1d for the device tuned at the green square depicted in Fig. 1c. The critical current Icb is seen as a peak in the differential resistance R = dV/dI which is evaluated numerically from d.c. data (transition between dark blue in Fig. 1d, zero resistance, to a finite one, light blue), where the device switches to the resistive state due to vortex motion. The field dependence of Icb(B) is governed by the edge- and bulk-pinning of vortices34,37,38,39,40. The linear drop in Icb(B) at small fields is characteristic of the Bean-Livingston barrier37 preventing vortices from entering the sample at the film edges y = ± W/234,39,40, as is typical for such films. By linearly fitting Icb versus B, we extract a value for the edge penetration field Be ≈ 100 mT, see orange dashed line in Fig. 1d. Combining this result with the zero-field critical current Icb(0) = 230 nA and using the relation \({\partial }_{B}{I}_{{{\rm{cb}}}}(B)=-d{W}^{2}/2{\mu }_{0}{\lambda }_{{{\rm{L}}}}^{2}\)34, we arrive at an estimate for the London penetration depth λL of order 10 μm, which compares favorably with values of a few μm obtained from other estimates (here, μ0 is the vacuum permeability). For example, we may use the bulk critical current Icb(0) ≈ 230 nA measured in Fig. 1d, obtain the critical current density jcb ≈ 2.1 × 104 A/cm2, and take this value as a lower bound for the depairing current density \({j}_{0}={\Phi }_{0}/3\sqrt{3}\pi {\mu }_{0}{\lambda }_{{{\rm{L}}}}^{2}\xi\) (with Φ0 = h/2e denoting the flux unit). Extracting a value ξ ≈ 40 nm for the coherence length8,16,17 (Fig. S4), we then find an estimate λL < 3.5 μm. Finally, the low value in the saturation of Icb at large fields, see Fig. 1d, is testimony of weak bulk pinning inside the film ∣y∣ < W/234, possibly due to twist-angle variation.

Josephson junction (JJ)

Keeping the leads in one of the superconducting regimes, we form a JJ in our sample by tuning the junction region into a resistive state. The formation of a JJ is confirmed by the observation of a d.c. Josephson critical current Icj < Icb, as shown in Fig. 2a, and the appearance of the Fraunhofer-like interference effect, see Fig. 2b (for details of the device fabrication and gate control see Supplementary Information Figs. S1 and S2 and Methods). The high tunability of our device allows us to define a JJ in several ways by exploring the parameter space of density n and displacement field D in the leads and the junction, see phase diagram in Fig. 1c. The formation of a JJ is achieved by tuning the junction density nj at fixed nl = −4.5 × 1012 cm−2 and Dj = 0 (the displacement field Dl is bound to nj and follows the yellow dashed line within the superconducting dome in Fig. 1c). The differential resistance R then exhibits two steps, i) at low currents Icj when the junction turns resistive, and ii) at high currents Icb when the leads switch to the resistive state, see orange line-trace in Fig. 2a. The two critical currents coalesce when nj enters the superconducting state between the white dashed lines in Fig. 2a, resulting in a uniform superconducting device SSS. Away from this region, we can implement a JJ with a desired critical current Icj—we refer to this weak-link configuration as SJS, with J denoting the resistive junction region, notwithstanding its nature, metallic, semiconducting, or insulating. In all of our measurements, the junction region is tuned to the full-filling peaks (nj = ± 6.2 × 1012 cm−2) as indicated by the red dots in Fig. 1c. This tuning is chosen to produce the most resistive state in the junction region (the junction has been tuned to a magnetically correlated state in ref. 20), see Supplementary Information and Fig. S5 and S6 for further details on junction tuning. Note that our MAT4G device admits the displacement field Dj as an additional tuning knob for changing Icj as compared to junctions defined in MATBG9,10 (Fig. S5F).

Fig. 2: Josephson junction device and Fraunhofer pattern.
figure 2

a Differential resistance R measured as a function of I while sweeping nj and keeping nl fixed. Dj is fixed at zero whereas Dl is swept as shown on the top axis, following the yellow dashed line in Fig. 1c. By sweeping nj, the junction can be tuned from a resistive to a superconducting state, resulting in a SJS or SSS configuration, with the critical currents of the bulk and junction denoted by Icb and Icj. A line trace of the differential resistance R is shown with nj fixed at the dotted orange line. b Differential resistance R measured as a function of I and B for nl = − 3.5 × 1012 cm−2, Dl/ϵ0 = 0.2 V/nm and nj = − 6.3 × 1012 cm−2, Dj/ϵ0 = 0.45 V/nm (blue-red-blue setting in Fig. 1c). The orange and yellow dashed lines show the theoretical predictions for a 2D JJ under weak screening conditions, whereas the dotted yellow line shows the rapid decay ∝ 1/B for a standard JJ. c Differential resistance R measured as a function of I and B with the entire device tuned to the pink triangle shown in the phase diagram Fig. 1c, implying that no junction is formed. This SSS configuration exhibits no interference pattern.

Full size image

Junction in magnetic field

A typical magnetic interference measurement with the device tuned to the junction regime is presented in Fig. 2b. The current I is swept from negative to positive values while measuring the voltage drop across the junction, all at fixed perpendicular applied field B. After each current sweep, B is stepped and a new trace is recorded. The leads are set to the superconducting state (nl = − 3.5 × 1012 cm−2, Dl/ϵ0 = 0.2 V/nm, light blue rhombus in Fig. 1c) and the junction is gated to full filling (nj = − 6.2 × 1012 cm−2, Dj/ϵ0 = 0.45 V/nm, red dot in Fig. 1c); we call this the blue-red-blue setting with a corresponding identifier in the top-right corner of Fig. 2b. Note that a SJS device is characterized by a pair of points in the phase diagram Fig. 1c specifying density n and displacement field D in the junction and the leads. The critical Josephson current Icj(B) is suppressed and modulated as B is varied, resulting in the FP shown in Fig. 2b—the observed pattern is typical for a short junction41 and exhibits the hallmarks of a weak screening device30,31. We observe field-induced oscillations of Icj(B) with the interference period ΔB ≈ 3 mT. The FP are symmetric in current and do not show any skewness. Thanks to the high tunability of our device, we can study these interference patterns throughout the phase space of both junction and leads (see Supplementary Information for further measurements with different nl and Dl).

To further prove that the measured interference pattern is due to the JJ rather than sample inhomogeneity, we carry out the same measurement with the JJ tuned into the superconducting lobe (SSS) as shown in Fig. 2c (with nj = nl ≈ − 4.5 × 1012 cm−2 and Dj/ϵ0 = Dl/ϵ0 ≈ 0.2 V/nm, pink triangle in the phase diagram Fig. 1c). In this measurement, Icj agrees with Icb up to small oscillations in Icj(B) at low fields; their periodicity closely matches the one observed in the pattern of Fig. 2b and we attribute them to a slight mismatch in the tuning between the leads and the junction regions. No interference pattern is observed when the device is fully superconducting, compare Fig. 2b with Fig. 2c.

Fraunhofer interference pattern

Our JJ shows a Fraunhofer-type pattern Icj(B) that is typical for a weak screener with Λ ≫ W30,31,42,43; the field B then penetrates the leads completely and the gauge-invariant phase-difference ΔγB(y) takes the form30,31

$$\Delta {\gamma }_{B}(y)\approx 1.7\frac{{\Phi }_{W}(B)}{{\Phi }_{0}}\sin (\pi y/W)$$
(1)

with the relevant flux determined by the junction width W only, ΦW(B) = BW2, provided that the film leads are longer than the film width, L ≫ W. Furthermore, the usual linear shape21 ΔγB(y) ∝ y/W is replaced by a sine-function, \(\Delta {\gamma }_{B}(y)\propto \sin (\pi y/W)\), a feature that is again due to the deep penetration of the field into the film, see Supplementary Information. This seemingly minor correction has profound consequences for the FP at large B, producing a slow decay of the maxima \(\propto 1/\sqrt{B}\) in the pattern instead of the standard 1/B behavior.

To relate these insights to our experiment, we find Icj(B) by integration over the junction dimensions: assuming a sinusoidal current–phase relation \({j}_{{{\rm{j}}}}(\Delta \gamma )={j}_{{{\rm{cj}}}}\sin (\Delta \gamma+{\gamma }_{0})\) with γ0 a free shift parameter, the integral over W can be evaluated exactly30,31 in terms of the Bessel function J0,

$$\frac{{I}_{{{\rm{cj}}}}(B)}{{I}_{{{\rm{cj}}}}(0)}=\left\vert \right.\,{J}_{0}[1.7{\Phi }_{W}(B)/{\Phi }_{0}]\left\vert \right.,$$
(2)

where the choice γ0 = ± π/2 produces the largest, hence critical, current. The Bessel function J0 then replaces the sinc-function characterizing the FP in the standard context21. The orange line in Fig. 2b is a fit to the data that makes use of the width W = 1.1 μm of the film in the determination of the flux ΦW(B) = BW2. Given that the distance between consecutive zeros of the Bessel function J0(s) is Δs ≈ 3.1, we recover the periodicity ΔB ≈ (Δs/1.7)Φ0/W2 ≈ 3 mT. Note that the zeros in J0(s) become truly equidistant only at large values of the magnetic field. Furthermore, the maxima are well tracked by the slow decay \(\propto 1/\sqrt{B}\), see the dashed yellow line at B < 0. The good agreement between the theoretical prediction and the experimental data holds at fields below ∣B∣ ≈ ± 10 mT, i.e., including the first three minima; thereafter, the fit does not work anymore due to the presence of sharp shifts in the pattern of the size of a fraction of Φ0. We attribute these shifts to vortices that spontaneously penetrate or leave the leads nearby the junction.

Jumps in the Fraunhofer pattern

The measured interference patterns show sudden shifts, i.e., jumps in Icj(B), see Figs. 2b, 3a and b. The measurement protocol for the FP described above produces maps Icj(B) over time scales of hours. The sudden shifts appear in all of our junction tunings, i.e., independent of gate voltages (Fig. S11).

Fig. 3: Vortex penetration.
figure 3

Differential resistance R measured as a function of I and B, for a forward magnetic-field sweep in (a) and a backward sweep in (b). The bottom axes show the corresponding scaled flux ΦW/Φ0 penetrating junction and leads, where ΦW = BW2. The tuning parameters are nl = 4.2 × 1012 cm−2, Dl/ϵ0 = −0.3 V/nm and nj = 6.2 × 1012 cm−2, Dj/ϵ0 = −0.5 V/nm (‘strong-leads’ setting). Sudden shifts of the interference pattern are highlighted with black arrows. Theoretical fits of the measured Fraunhofer patterns (a) and (b) on the basis of the analysis in Ref. 32, with 7 (in (c)) and 4 (in (d)) vortices leaving/penetrating the leads.

Full size image

Pronounced jumps in Icj, see black arrows in Fig. 3a, b, are observed with the leads tuned close to the center of the superconducting dome (with nl = 4.2 × 1012 cm−2, Dl/ϵ0 = − 0.3 V/nm and nj = 6.2 × 1012 cm−2, Dj/ϵ0 = −0.5 V/nm, orange rhombus and red dot in the phase diagram Fig. 1c, we name it the orange-red-orange, or ‘strong-leads’ setting). They are present in both increasing and decreasing sweeps of the magnetic field, are symmetric in I, and are stable on the time scale of hours.

Vortex penetration

With these shifts present in all of our device configurations, we rule out a possible origin related to the experimental setup (Supplementary Information and Fig. S10). We rather attribute these sudden shifts to vortices penetrating and leaving the superconducting leads in the vicinity (closer than 2W) of the junction32. Similar observations have been previously reported32,33,44,45,46,47.

The presence of a vortex (at the position Rv = (xv, yv) and with a flux parallel to B, see Fig. 1b) changes the phase pattern at the junction, Δγ(y) → Δγ(y; Rv) = ΔγB(y) + Δγv(y; Rv), adding a step-like contribution ∣Δγv(y; Rv)∣ < π to the phase difference, see Figs. S14–S16. The phase ∣Δγv(y; Rv)∣ as a function of y (see Supplementary Information for an explicit expression) smoothens and decreases in amplitude with increasing distance xv of the vortex from the junction, see Figs. S14 and S15. Since the vortex currents (jv, blue in Fig. 1b) flow opposite to the screening currents (js, green in Fig. 1b), the presence of a vortex decreases the effect of the B-field and the FP shifts to the right upon vortex entry at positive B > 0 (the shift is to the left for a vortex with opposite circularity entering the lead at B < 0). This is exactly what is seen in the experiment. For example, in Fig. 3c, d, we fit the experimental traces of Fig. 3a, b, by having 7 (in Fig. 3c) and 4 (in Fig. 3d) vortices of ± polarity enter (upon increasing ∣B∣) or leave (upon decreasing ∣B∣) the device leads, see black arrows.

The magnitude of the shift in the FP is primarily determined by the distance xv between the vortex and the junction (see Figs. S14 and S15). When changing the yv coordinate, the largest FP-shifts occur when a vortex is at the center of the film yv = 0, and their magnitude decreases as the vortex approaches the edges yv = ± W/2, see Fig. S16. Additionally, the yv coordinate modifies the minima in the FP—the sharp minima with I = 0 become rounded at intermediate values 0 < yv < W/2, see Fig. S16. In our fit, we place the vortices at the center of the film, i.e., yv = 0, and tune the pattern’s shifts by choosing vortex positions in the range 0.3( → largeshifts) < ∣xv∣/W < 0.8( → smallshifts), see Fig. 1b (detailed parameters are cited in the Supplementary Information). The resolution of the FP minima in the experiment is not sufficient to determine a precise value for the yv coordinate. Note that in Figs. 3a and b, vortices have left the device at B = 0 in both cases. Both the local change in the FP at individual jumps and the accumulated shift at larger magnetic fields are well reproduced by the fit. When the field amplitude ∣B∣ exceeds 10 mT, the patterns become blurred, and the observation of individual jumps is hampered; however, the JJ is still sensitive to the presence of vortices.

Vortex fluctuations

We close our discussion with the analysis of another data set with the leads tuned away from the center of the superconducting dome at a ‘weak-leads’ setting (nl = 4.8 × 1012 cm−2, Dl/ϵ0 = −0.3 V/nm and nj = 6.2 × 1012 cm−2, Dj/ϵ0 = −0.5 V/nm, see the purple rhombus and red dot in the phase diagram Fig. 1c, or ‘weak-leads’ setting). This choice of parameters reduces the superfluid density ρs of the leads26 and at the same time the vortex energy ε0d = πρs, where \({\varepsilon }_{0}=(4\pi /{\mu }_{0}){({\Phi }_{0}/4\pi {\lambda }_{{{\rm{L}}}})}^{2}\) is the vortex line energy. The latter determines the edge barrier Ue for vortex penetration, with Ue smaller than 2ε0d and decreasing with increasing field B, as follows from the analysis in ref. 29, see Fig. S17A in the Supplementary Information. Combining the reduced edge barrier Ue with an increased temperature T, we observe a boost in vortex dynamics, i.e., enhanced vortex fluctuations. Indeed, the FP in Fig. 4a, measured at T = 100 mK, exhibits pronounced bi-stability effects in the voltage–current characteristic, see the grainy white–dark-blue features in Fig. 4a around B ≈ 1.5 mT and B ≈ 2.7 mT. We associate these with vortices penetrating and leaving the leads, thereby shifting the FP back and forth and switching between two different V(I) curves. Furthermore, at these elevated temperatures, the V–I characteristic of the junction is rounded, with the sharp onset of dissipation at Icj replaced by a smooth non-linear rise; we attribute this rounding in V(I) to phase-slips within the Josephson junction48,49. Figure 4b shows both of these effects, phase-slips smoothing the dissipative crossover and sharp steps due to vortex dynamics at B ≡ B* = 2 mT, see black arrows in Fig. 4a. The sharp steps in the V–I curve at B* = 2 mT manifest as white–dark-blue pairs of dots in the differential resistance plot of Fig. 4a.

Fig. 4: Vortex fluctuations.
figure 4

a Differential resistance R measured at T = 100 mK as a function of I and B with parameters nl = 4.8 × 1012 cm−2, Dl/ϵ0 = −0.3 V/nm and nj = 6.2 × 1012 cm−2, Dj/ϵ0 = − 0.5 V/nm (‘weak-leads’ setting). The Fraunhofer pattern is smoothed and white—dark-blue speckles mark the presence of bistabilities in the V—I characteristic. b Voltage—current trace at B* = 2.0 mT, see arrows in Fig. 4a. The V—I characteristic is rounded and exhibits pronounced steps; we associate the rounding with the presence of phase slips in the junction and the steps with vortex fluctuations in the leads. The steps manifest in the speckles visible in Fig. 4a. c Time trace of the voltage V measured at fixed B* = 2.0 mT and current I* = 4 nA, see dotted line in Fig. 4b. We associate the telegraph-type noise with vortex fluctuations in the leads. (d) In green, vortex fluctuations timescale t versus temperature T extracted from the statistical analysis (Fig. S8) of the telegraph-type noise in Fig. 4c. The measured time scales decay in temperature from t ∼ 1.2 s to t ∼ 0.04 s. The expected theoretical decay of t is plotted with the black dashed line. The corresponding barrier \({U}_{{{\rm{e}}}}=T\ln (t/{t}_{0})\approx 2.56\,{{\rm{K}}}\) is shown in orange and is seen to remain constant as expected for an activated process.

Full size image

Next, we fix the field B* = 2 mT and the bias current I* = 4 nA (black dashed line in Fig. 4b), at a point where the presence (absence) of a vortex causes changes in the V(I) characteristic, and measure the voltage as a function of time. A typical time-trace exhibiting telegraph-type voltage-noise is shown in Fig. 4c. The timescale t of these fluctuations is of order seconds and decreases rapidly with temperature, see Fig. 4d, as typical for a thermally activated process (see Supplementary Information, Fig. S8, for the counting statistics of these fluctuations). Below 90 mK, the activation process loses its temperature dependence, which we may attribute to a changeover to a quantum tunneling process of vortices50.

Assuming thermal activation of vortices over the edge barrier governs the voltage fluctuations, we can derive an energy scale for the vortex energy ε0d and hence for the superfluid density ρs = ε0d/π. Given a barrier Ue at temperature T and an attempt time t0, a vortex requires a time \(t \sim {t}_{0}\exp [{U}_{{{\rm{e}}}}/T]\) to overcome the barrier and penetrate into the film leads (we set kB to unity). Knowing the typical dynamical time t of vortex fluctuations, we can derive a quite accurate estimate for \({U}_{{{\rm{e}}}}\approx T\ln (t/{t}_{0})\). Making use of a typical attempt time51,52 t0∼10−11 s, a typical dwell time t∼1 s as observed in our experiment Fig. 4c, and the temperature T = 100 mK, we find a barrier Ue ≈ 2.5 K. The barrier Ue remains constant upon increasing the temperature to T = 115 mK, as supported by the observed decrease in dwell time t. This is illustrated in Fig. 4d, where the black dashed line shows the expected exponential decay of t. From this result, and using the relation Ue ≈ ε0d, see Fig. S17A, we can extract a value ρs ≈ 0.8 K for the superfluid density and a London penetration depth λL∼ 2.8 μm. Furthermore, using the relation TBKT = ε0(TBKT)d/2 and ignoring the reduction in ε0(T) at higher temperatures, we find an upper limit for the Berezinskii-Kosterlitz-Thouless transition temperature TBKT < 1.2 K.

Recently, the superfluid density ρs of twisted-layer graphene has been determined using kinetic inductance measurements, both for a trilayer film26 and for a bilayer system27. Given the differences in the various systems, the comparison of the results in refs. 26,27 with our findings has to remain on a qualitative level, also owing to the fact that our analysis is done away from the superconducting dome center where ρs is well defined. While for the trilayer film a value ρs between 0.1 K and 0.45 K has been reported, a value up to ∼1.2 K has been measured for the bilayer system. Our value ρs ≈ 0.8 K then is well within this range.

Discussion

In conclusion, we have demonstrated the formation of a gate-defined Josephson junction in MAT4G and its application as a vortex sensor. The measured interference patterns agree excellently with the predicted behavior for a weak transverse screener with a Pearl length surpassing the sample dimension, Λ > W. Our data enable us to precisely track the entry and exit of vortices from the device leads and find their location away from the junction. Our observation of vortices in MAT4G using a Josephson junction sensor opens new avenues for exploring vortex motion in this new class of twisted materials.

Methods

Fabrication details

We fabricated a MAT4G stack using the dry pick-up method53. Graphene and hexagonal boron nitride (hBN) flakes were exfoliated on a 285 nm p : Si/SiO2 wafer. A graphene flake of around 90 μm by 20 μm was scratched into four pieces using a tungsten needle with a tip diameter of 2 μm controlled by a micromanipulator. We then picked up each flake using a polydimethylsiloxane/polycarbonate stamp. The top hBN flake, with a thickness of 25 nm, was picked up at 110 °C. Afterwards, the four graphene flakes were picked up at 40 °C while alternatively rotating the stage by  ± 1.8°. To pick up the bottom hBN flake, with a thickness of 62 nm, the flake was contacted by the stack at 40 °C and the temperature of the stage was raised to 95 °C. The stack was then finished by picking up a graphite flake of thickness 23 nm at 100 °C. Afterwards, the stack was deposited on a p : Si/SiO2 chip at 170 °C. The polycarbonate stamp was cleaned using dichloromethane.

To contact the MAT4G, we fabricated edge contacts54 made by electron beam lithography and reactive ion etching. We etched using CHF3/O2 (40/4 sccm, 60W) and evaporated Cr/Au (10/70 nm). The finger gate and the electrode lines were then defined by depositing Cr/Au (10/80 nm). Next, the mesa was defined by etching using CHF3/O2 (40/4 sccm, 60W). Afterwards, a layer of 30 nm of aluminum oxide was deposited by atomic layer deposition. The top gate and its electrode line were then fabricated using electron beam lithography and evaporating Cr/Au (10/80 nm). Optical images after each fabrication step are shown in Figs. S1, A–D.

Measurement setup

We carry out all the measurements in a dilution refrigerator that uses a mixture of 3He and 4He with a base temperature of 55 mK (unless stated otherwise). Our measurements are current-biased, i.e., we apply a current and measure the voltage drop in two (2T), three (3T), and four-terminal (4T) setups, see Figs. S1E–G. In the two and three-terminal configuration, we correct for contact resistances. To generate the bias current, we use a home-built d.c. source in series with a 10 MΩ or 100 MΩ resistor. The voltage is amplified using a d.c. An amplifier built-in-house (see ref. 55) and its output is measured with a Hewlett-Packard 3441A digital multimeter. The bottom, top, and finger gates are connected to d.c. voltage sources also built in-house. When performing radio-frequency measurements, the top gate is connected to a Rhode und Schwarz SMB 100 A signal generator using a bias-tee with R = 10 kΩ and C = 100 nF. For the statistical analysis of vortex fluctuations, the output voltage is further amplified with a gain amplifier, low-pass filtered at 1.1 kHz, and recorded in time using a National Instruments BNC-2110 data acquisition card (DAQ) with a sampling frequency of 20 kHz.