Introduction

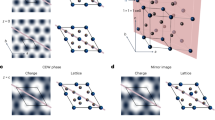
The charge density wave (CDW), a spontaneous translational symmetry breaking in electron liquids, plays a central role in many correlated and topological materials, including high-Tc superconductors1,2,3, kagome metals4,5,6,7,8, axion insulators9,10, and quantum Hall liquids11,12,13,14,15. Historically, the first microscopic mechanism of CDW was described by the Fröhlich model16, where electron-electron scatterings mediated by longitudinal acoustic (LA) phonons are divergent at the Fermi surface nesting vector, QCDW. Consequently, the formation of a CDW accompanied by softening of LA phonons, known as the Kohn anomaly17, and longitudinal lattice distortions as schematically shown in Fig. 1a, b. Recently, it was predicted that topological electrons with anisotropic p-orbital characters can strongly couple to transverse acoustic (TA) phonons, leading to CDW instabilities and TA Kohn anomaly, named the transverse Peierls transition (TPT)13. This new mechanism is shown schematically in Fig. 1c, d. Interestingly, since transverse lattice distortions are two-component vectors, TPTs can lead to unconventional CDWs such as nematic CDWs that break rotational symmetry (Fig. 1e) and chiral CDWs that break inversion and mirror-symmetries (Fig. 1f). The TPT was originally proposed to explain the 3-dimensional quantum Hall effect in the Dirac-semimetal ZrTe513,14,15. However, the TPT induced CDW superlattice peaks in ZrTe5 have not been observed to the best of our knowledge. Recently, x-ray scattering studies18,19,20,21,22 suggest the possible realization of TPT in a topological magnet EuAl4 that is reported to feature the spontaneous chirality flipping20. In this letter, we establish the incommensurate TPT and show experimental signatures of a chiral CDW in EuAl4.

Fig. 1: Longitudinal and transverse Peierls transitions.
figure 1

a Schematic of a classical Peierls transition in 1D. The interaction between a LA phonon and isotropic s-orbital conduction electrons yields a CDW instability. b The LA Kohn anomaly induced by the classical Peierls transition. c Transverse Peierls transition driven by the coupling between conduction electrons with anisotropic orbital characters, such as p-orbitals, and TA phonons. d The TA Kohn anomaly induced by the TPT. Distinct from the LA wave, the TA wave is a vector wave (similar to an electromagnetic wave) and hence can carry finite angular momentum. e, f depict linearly polarized and circularly polarized TA waves, respectively. The linearly polarized lattice distortion breaks (screw) rotational symmetry, Cn, giving rise to a C2 nematic CDW. The circular polarized lattice distortion preserves (screw) rotational symmetry, Cn, and can host a chiral CDW. g Temperature dependence of the incommensurate-CDW superlattice peak at (2, 2, 2-0.183) showing a CDW transition at TCDW = 142 K. Inset shows the crystal structure of EuAl4. Magenta and silver circles represent Eu and Al atoms, respectively.

Full size image

EuAl4 has a tetragonal structure with space and point groups of I4/mmm and 4/mmm (D4h), respectively. At room temperature, EuAl4 is a semi-Dirac topological semimetal20,23,24, which has a linear dispersion along the kz direction and a quadratic dispersion along the kx/ky direction. Below the critical temperature TCDW = 141 K, EuAl4 forms an incommensurate CDW with QCDW = (0, 0, 0.183) in reciprocal lattice units (r.l.u.) along the kz direction18,19,20,21,22. The QCDW connects the semi-Dirac bands20, suggesting a Fermi surface nesting assisted CDW. Figure 1g shows the temperature dependence of the CDW superlattice peak at Q = (2, 2, 2)-QCDW. Below T = 15.4 K, EuAl4 further experiences multiple spin density wave (SDW) transitions including the emergence of chiral SDW and spontaneous chirality flipping20,25,26. In this work, we show experimental observation of incommensurate TPT. Combining x-ray scattering, second harmonic generation, and first principles calculations, our results support chiral CDW in EuAl4.

Results

We first examine the temperature dependent phonon dynamical structure factor, S(Q, ω), of the LA and TA modes in the vicinity of QCDW. Figure 2a-d show S(Q, ω) at two selected temperatures, 300 K and 160 K, and along two momentum cuts, (2, 2, L\(\in\) [1.5, 2.0]) and (0, 0, L\(\in\) [7.5, 8.0]), measured by inelastic x-ray scattering (IXS). The cross-section of IXS is proportional to (\({\sum }_{j}{{{\boldsymbol{Q}}}}\cdot {{{{\boldsymbol{u}}}}}_{j}\)), where Q = kf - ki is the momentum transfer of incident (ki) and scattered (kf) photons, and \({{{{\boldsymbol{u}}}}}_{j}\) is the distortion of atom-j in the unit cell (See Supplementary Materials Section I). The S(Q, ω) spectra along the (2, 2, L\(\in\) [1.5, 2.0]) and (0, 0, L\(\in\) [7.5, 8.0]) directions thus select the TA and LA modes, respectively. By comparing magnified S(Q, ω) maps near QCDW shown in Fig. 2a, b, we observe softening of TA phonons from 300 K to 160 K. This observation is in stark contrast to the LA mode that slightly hardens, as expected in a harmonic approximation on cooling (Fig. 2c, d). Figure 2e summarizes the temperature dependent evolution of extracted TA and LA phonon dispersions. Representative IXS spectra at Q = (2, 2, 1.83) are shown in Fig. 2f, highlighting the softening of TA phonons. Figure 2g shows the extracted TA phonon softening, ΔE (T) = ω0(Q)-ω(Q,T), at T = 300, 160, and 130 K. Here ω0(Q) denotes the sinusoidal bare TA phonon band. The sharp peak of ΔE (T) at QCDW establishes the TA Kohn anomaly and hence strongly supports a TPT. We note that while the transition is driven by TA phonons, to minimize the elastic energy, the lattice deformations in the CDW phase can involve lattice displacements along the c-axis.

Fig. 2: Observation of TA Kohn anomaly.
figure 2

a, b show TA phonon dynamical structure factor, S(Q, ω) along the (2, 2, L\(\in\) [1.5, 2.0]) direction, at T = 300 and 160 K, respectively. Red and cyan diamonds are extracted phonon peak positions at 300 and 160 K, respectively. The dashed curves represent the sinusoidal bare band of the TA phonon. Right panels in (a, b) show magnified view of S(Q, ω) near QCDW (dashed rectangles in the left panels). c, d are the same plots (including color scales) as (a, b) but along the (0, 0, L\(\in\) [7.5, 8.0]) direction to select the LA phonon branch. e Temperature dependence of extracted TA and LA phonon dispersions. The TA phonon modes show a large energy renormalization whereas the LA phonons are slightly hardened. Horizontal and vertical dashed lines in (a−e) corresponding to elastic line and QCDW, respectively. f Temperature dependent IXS spectra at Q = (2,2,1.83). The vertical dashed line represents the elastic line. g TA phonon softening, \(\Delta E(T)\) at 300 K, 160 K and 130 K, relative to the bare band dispersion (dashed sinusoidal curves (a)). The vertical dashed line represents the QCDW. The error bars shown in (a–e) represent 1-standard deviation from least-squares fitting. The error bars shown in (f) represent 1-standard deviation from Poissonian statistics.

Full size image

To uncover the origin of the TA Kohn anomaly, we calculate the electronic band structure and momentum dependent charge susceptibility. Although the Eu f-electrons are far away from the Fermi level20, the large magnetic moment and complex magnetic ground state of EuAl4 have non-trivial effects on the DFT calculated lattice dynamics (See Supplementary Materials Section IV). We therefore performed calculations on SrAl4 with nearly identical electronic structure near the Fermi level (see Supplementary Materials Section IV) and a CDW instability (see Supplementary Materials Section I)27. As shown in Fig. 3a, the heavily hybridized Al p-orbitals form a semi-Dirac point above the EF. A nesting of the semi-Dirac bands produce a charge susceptibility peak at Q ~ (0, 0, 0.12) for SrAl4 as is shown in Fig. 3b. Encouragingly, the calculated phonon spectrum displays a negative energy for the TA (i.e., unstable imaginary mode) and a strong electron-TA phonon coupling. The momentum q, at which the TA mode reaches its minimum shown in Fig. 3c, d, matches well the calculated charge susceptibility and is consistent with the experimentally determined QCDW ~ 0.125 in SrAl4 (see Supplementary Materials Section I). These first-principles calculations together with the experimental observation of the TA Kohn anomaly (Fig. 2) provide compelling evidence of a TPT induced CDW. It is important to emphasize that the CDW in in EuAl4 is not pure in electronic origin16, and the electron-phonon coupling also plays key role27,28,29. Our picture is that while the lattice dynamics is intrinsically unstable as revealed by the DFT calculations and IXS results, a lower free energy is achieved by matching QCDW to the nesting vector to suppress charge fluctuations. This picture is different from strong electron-phonon coupling driven CDW where a complete softening of phonon mode (ωq ~ 0) is realized in an extended momentum space28,29.

Fig. 3: DFT calculation of electron-TA phonon coupling driven TPT.
figure 3

a Electronic band structure of non-magnetic sister compound SrAl4. Light blue, purple, and grey marks represent Al \(3{p}_{x,y}\)-orbitals, Al \(3{p}_{z}\)-orbital, and Sr 5s-orbital, respectively. The Brillouin zone and high symmetry point in momentum space are shown in (b). The “nesting” of the linearly dispersed semi-Dirac bands give rise to a peak in the calculated charge susceptibility, \({\chi }_{0}^{{\prime} {\prime} }\). The susceptibility peak position matches the calculated lattice instability of the TA phonon shown in (c, d). Dashed grey curve and solid black curves are calculated for different electron temperatures. The negative TA phonon at σ = 1 mRy supports electron-TA phonon coupling driven TPT and is consistent with experimental observations.

Full size image

Having the incommensurate TPT established, we then proceed to reveal the possible chiral nature of the CDW by investigating the broken point symmetries using a combination of elastic x-ray scattering and high-sensitivity rotation anisotropy second harmonic generation (RA-SHG). As schematically illustrated in Fig. 4a, b, the achiral nematic CDW breaks the C4 rotational symmetry, whereas the chiral CDW breaks the mirror/inversion symmetries but retains the C4 rotational symmetry (see Supplementary Materials Section I). We start with the elastic x-ray scattering data shown in Fig. 4c, d which closely track the temperature dependence of two 90o-rotated Bragg peaks, (1, 0, 7) and (0, 1, 7), respectively. Across a wide temperature range including TCDW, we observe consistently narrow half-widths-at-half-maximum (HWHM) of both Bragg peaks (HWHM ~ 0.0025 r.l.u) without splitting or broadening. This result puts an upper limit for the rotational symmetry breaking lattice distortions to be on the order of 0.1% of the lattice constant, i.e., <1 pm, smaller than the fundamental atomic position uncertainty ~ 2 pm derived from the Heisenberg uncertainly principle (see Methods). Therefore, our x-ray measurements exclude the rotational symmetry breaking for the CDW phase. Indeed, the C4 rotational symmetry breaking is only observed in the helical SDW phase transition below 13 K (See Supplementary Materials Section I), consistent with a C4-preserving CDW.

Fig. 4: Signature of TPT induced chiral CDW in EuAl4.
figure 4

a, b Two possible lattice distortion patterns that host C2 nematic and C4 chiral CDWs. The colored circles represent distorted atoms with different z-axis coordinates. Since the TA softening selects a specific direction in the C2 nematic CDW, the CDW gap will take a p-wave like gap function where the gap minimums are in the direction that is perpendicular to the nematic direction. The screw C4-preserving chiral CDW induces TA softening along all high symmetry directions and hence yields a s-wave gap function. c, d temperature dependence of the C4-related fundamental Bragg peaks (0, 1, 7) and (1, 0, 7) across TCDW. e RA-SHG patterns at 80 K, 135 K, 155 K, and 220 K. Open circles are measured data, and the blue solid lines are the best fits. Numbers at the corners are scales of the plots, with 1.0 representing 6 counts of the SHG photons per second per microwatt. f Temperature-dependence of fitted coefficients. Open circles are measured data with error bars being one standard deviation. Solid lines are guides to the eyes. Inset: SHG in the oblique incidence geometry overlaid on the crystal structure of EuAl4. g Temperature-dependence of rotation angle \({\phi }_{0}\). Open circles are measured data with error bars being one standard deviation and the grey curve is a guide to the eyes.

Full size image

We then move to the RA-SHG results. Due to the C4 and C2 rotational (screw) symmetry along the c-axis, there should be no SHG signal in the normal incidence geometry, thus we need to perform RA-SHG measurements in the oblique incidence geometry for EuAl4 with the (001) facet (see Methods and Supplementary Materials Section II)30,31. Figure 4e shows the RA-SHG polar plots, i.e., the SHG intensity as a function of the rotating angle ϕ between the light scattering plane and the crystalline a-axis, with both fundamental and SHG polarizations chosen to be parallel to the scattering plane (Pin-Pout), at four selected temperatures: 80 K and 135 K (below TCDW), and 155 K and 220 K (above TCDW). We can see the presence of C4 in RA-SHG for all temperatures and the non-monotonic change in the SHG intensity upon cooling across TCDW. We have identified electric quadrupole as the main SHG radiation source and have ruled out other possibilities (see Supplementary Materials Section II).

To quantify the point symmetry evolution across TCDW, we fit our RA-SHG polar plot at every temperature to extract the isotropic (i.e., a constant), the C2 symmetric (i.e., \(\propto \cos (2\phi )\)), and the C4 symmetric (i.e., \(\propto \cos (4\phi )\)) components, as well as its orientation away from the a-axis (i.e., \({\phi }_{0}\)) (see Supplementary Materials Section II), and show their temperature dependencies in Fig. 4f, g. First, we note that the isotropic and the C4 components are much stronger than those for C2, and furthermore, that the strong isotropic and C4 signals exhibit a similarly dramatic temperature dependence with their intensities peaking around TCDW (Fig. 4f). The weak C2 signal, on the other hand, is nearly temperature independent. We attribute this C2 signal as an experimental systematic background based on its small amplitude and temperature independence across the phase transition. The absence of C4 symmetry breaking is consistent with the elastic x-ray scattering results in Fig. 4c, d. Second, we notice that the RA-SHG rotates away from alignment with the crystal axis as the temperature decreases below TCDW (Fig. 4g). This orientation change, although small, is direct evidence of breaking the in-plane C2 rotational symmetries, the vertical mirror symmetries, and the diagonal mirror symmetries for the CDW phase, as it means an absence of any special in-plane direction to which the RA-SHG pattern locks to below TCDW (see Supplementary Materials Section II for the same results from RA-SHG in other polarization channels)32,33,34,35. These mirror-symmetry breakings are compatible with a CDW that preserves screw-C4 symmetry. Furthermore, this rotation of the RA-SHG pattern shows that the CDW state has handedness, being ferro-rotational or chiral.

Although TPT can host both nematic and chiral CDWs as shown in Fig. 1, the C4 symmetric CDW, as identified in EuAl4, can be energetically favored by considering the form factor of the CDW gap in the electronic structure (See Supplementary Materials IV). As shown in Fig. 4a, b, the C2 nematic CDW gives rise to an anisotropic CDW gap and a TA Kohn anomaly along either (1, 0, 0) or (1, 1, 0) directions, whereas the C4 chiral CDW results in an isotropic CDW gap and the TA Kohn anomalies along both (1, 0, 0) and (1, 1, 0) directions. The isotropic CDW gap fully releases critical TA-phonon dynamics along all in-plane directions, whereas the nematic CDW phase leaves unstable TA-phonons along the nodal direction (Fig. 4a). Since the electron-phonon coupling in Dirac-semimetals can be written as a linear combination of chiral electron-chiral phonon couplings13, the chiral CDW could be pictured as a spontaneous chiral symmetry breaking driven by chiral quasiparticle interactions. Indeed, the soft TA mode shown in Fig. 2 corresponds to a transverse lattice instability along the (1, 1, 0) direction. At the same time, the transverse lattice instability along the (1, 0, 0) direction has also been observed in EuAl421 in agreement with the C4 lattice distortions with broken mirrors. We note that, while our macroscopic x-ray and optical probes cannot distinguish ferro-rotational CDW (point group 4/m) and chiral-CDW (point group 4) with structural twinning, the incommensurability of the CDW naturally favors the chiral CDW.

In summary, we observe incommensurate TPT in the Dirac semimetal EuAl4. We show that both the lattice distortions below TPT and the phonon softening above the TPT preserve the C4 symmetry. Together with the mirror-symmetry breaking below TPT, our results support the assignment of a chiral CDW and highlight the rich landscape of TPT in electron-TA phonon coupled topological materials.

Methods

Sample preparation

High-quality EuAl4 single crystals were grown from a high-temperature aluminum-rich melt26. Eu pieces (Ames Laboratory, Materials Preparation Center 99.99 + %) and Al shot (Alfa Aesar 99.999%) totaling 2.5 g were loaded into one side of a 2 mL alumina Canfield crucible set. The crucible set was sealed under 1/3 atm argon in a fused silica ampoule. The ampoule assembly was placed in a box furnace and heated to 900°C over 6 h (150°C/h) and held for 12 h to melt and homogenize the metals. Crystals were precipitated from the melt during a slow cool to 700°C over 100 h (-2°C/h). To liberate the crystals from the remaining liquid, the hot ampoule was removed from the furnace, inverted into a centrifuge, and spun.

X-ray scattering measurements

The single crystal elastic X-ray diffraction was performed at the 4-ID-D beamline of the Advanced Photon Source (APS), Argonne National Laboratory (ANL), and the integrated in situ and resonant hard X-ray studies (4-ID) beam line of National Synchrotron Light Source II (NSLS-II). The photon energy, which is selected by a cryogenically cooled Si(111) double-crystal monochromator, is 6.977 keV (Eu L3 resonance).

The 4-ID-D, APS

the X-rays higher harmonics were suppressed using a Si mirror and by detuning the Si (111) monochromator. Diffraction was measured using a vertical scattering plane geometry and horizontally polarized (σ) X-rays. The incident intensity was monitored by a N2 filled ion chamber, while diffraction was collected using a Si-drift energy dispersive detector with approximately 200 eV energy resolution. The sample temperature was controlled using a He closed cycle cryostat and oriented such that X-rays scattered from the (001) surface.

The 4-ID, NSLS2

The sample is mounted in a closed-cycle displex cryostat in a vertical scattering geometry. The incident X-rays were horizontally polarized, and the diffraction was measured using a silicon drift detector.

Inelastic X-ray scattering measurements

The experiments were conducted at beam line 30-ID-C (HERIX) at the APS. The highly monochromatic X-ray beam of incident energy Ei = 23.7 keV was focused on the sample with a beam cross section of ~35 × 15 mm2 (horizontal × vertical). The total energy resolution of the monochromatic X-ray beam and analyzer crystals was ΔE ~ 1.3 meV (full width at half maximum). The measurements were performed in transmission geometry. Typical counting times were in the range of 30 – 120 s per point in the energy scans at constant momentum transfer Q.

The cross-section of IXS is proportional to (\({\sum }_{j}{{{\boldsymbol{Q}}}}\cdot {{{{\boldsymbol{u}}}}}_{{{{\boldsymbol{j}}}}}\)), where j runs over all atomic positions in the unit cell, and \({{{{\boldsymbol{u}}}}}_{{{{\boldsymbol{j}}}}}\) is atomic displacement of atom j (see Supplementary Note 1 for more details). This cross-section allows us to selectively probe TA and LA by changing experimental geometries as discussed in the main text.

Second harmonic generation measurements

RA-SHG measurements were conducted using an 800 nm wavelength ultrafast laser source, with a repetition rate of 200 kHz and a pulse width of 70 fs. The fundamental light shines onto the sample in an oblique incidence geometry with an incident angle θ = 11.4°. After passing through an achromatic lens (30 mm focal length), the laser beam is focused onto the sample surface with a full width at half maximum (FWHM) of 30 μm and a fluence of approximately 1.4 mJ/cm2. A half-wave plate and a polarizer are used to select the P- or S-polarized component of the incident fundamental light (P/Sin) and the reflected SHG light (P/Sout), allowing for measurements in four channels: Pin-Pout, Pin-Sout, Sin-Pout and Sin-Sout as a function of the rotation angle of the scattering plane. Here P and S represent photon polarization parallel and perpendicular to the scattering plane, respectively. A set of filters have been used to remove the fundamental 800 nm light before the reflected light being collected by a charge-coupled device. The experiments are conducted in an environment with a pressure less than \(1\times {10}^{-6}\) mbar with a base temperature of 80 K.

Scanning transmission electron microscopy measurements

TEM specimen was prepared by mechanical polishing and ion milling to electron transparency. STEM experiments were performed on a JEOL JEM-ARM200F (NeoARM) aberration-corrected scanning transmission electron microscope (STEM) equipped with a custom-built Gatan double-tilt liquid nitrogen cooling holder. The base temperature of our cooling holder is ~92.5 K and the holder could be stabilized for nearly eight hours per liquid nitrogen filling. Annular dark field images were acquired with 27.4 mrad convergence semiangle and 68−280 mrad collection angle. At 93 K, image series containing 30 fast-scanning, low signal-to-noise ratio atomic resolution images were registered and averaged to produce high quality atomic resolution STEM image.

First principles calculations

Electronic structures

Ab initio calculations were carried out for EuAl4 and SrAl4 (no.139 space group I4/mmm), using the relaxed lattice parameters of the primitive cell. We used DFT within the generalized gradient approximation of Perdew, Burke, and Ernzerhof36. The core–valence interaction was described by means of norm-conserving pseudopotentials. Electron wavefunctions were expanded in a plane waves basis set with a kinetic energy cutoff of 68 Ry to achieve energy accuracy better than 1 meV per atom, and the Brillouin zone was sampled using a 11 × 11 × 11 Γ-centered Monkhorst–Pack mesh. All DFT calculations were performed using the Quantum ESPRESSO package37,38. We adopt a degauss σ = 1mRy of Fermi-Dirac smearing function.

To inspect nesting strength of different momenta on the Fermi surface, we calculated Fermi surface nesting functions39 \({\chi }_{0}^{{\prime} {\prime} }\left({{{\boldsymbol{q}}}}\right)={\sum }_{k}\delta ({\epsilon }_{{{{\boldsymbol{k}}}}}-{\epsilon }_{F})\delta ({\epsilon }_{{{{\boldsymbol{k}}}}{{{\boldsymbol{+}}}}{{{\boldsymbol{q}}}}}-{\epsilon }_{F})\), which are the imaginary part of the static susceptibility functional with the double-delta approximation, and the Dirac-delta function is replaced by a Lorentzian of width 10 meV in the numerical implementation. 16 electronic bands near the Fermi level were interpolated by using maximally localized Wannier functions, to a 100 × 100 × 100 k-grid, to achieve accurate calculation of Fermi surface nesting. The peak at Q = 0.137 (2π/c) provides evidence to connect the lattice instability with Fermi surface nesting.

Phonon band structure and electron-phonon coupling

Lattice-dynamical properties were calculated using density functional perturbation theory (DFPT) and performed using the Quantum ESPRESSO package. The soft TA modes are found to be centered around Q = 0.1(2π/c), in agreement with the nesting effect. Since the imaginary frequencies of these soft modes are small, 0.25 THz, and they only appear after interpolation from a 3 x 3 x 3-grid to the finer grid, an additional DFPT calculation at the exact Q wave vector was performed to confirm the lattice instability40.

Calculations of electron–phonon couplings were performed using the EPW code41. To evaluate phonon self-energy and linewidth, we computed electronic and vibrational states as well as their coupling g-matrix on a 11 × 11 × 11 and 3 × 3 × 3 Brillouin-zone grid, respectively. Based on the Wannier functions, the g-matrix is interpolated to the high-symmetry Γ-Z path, which is used to estimate phonon linewidths from the imaginary parts of phonon self-energies: \({\Pi }_{{{{\boldsymbol{q}}}}\nu }^{{\prime} {\prime} }\left(\omega,T\right)=2\pi {\sum }_{{mn}{{{\boldsymbol{k}}}}}|{g}_{{mn}\nu }({{{\boldsymbol{k}}}},{{{\boldsymbol{q}}}}){|}^{2}[ \, {f}_{T}\left({\varepsilon }_{n{{{\boldsymbol{k}}}}}\right)-{f}_{T}({\varepsilon }_{m{{{\boldsymbol{k}}}}{{+}}{{{\boldsymbol{q}}}}})]\delta ({\varepsilon }_{m{{{\boldsymbol{k}}}}{{+}}{{{\boldsymbol{q}}}}}-{\varepsilon }_{n{{{\boldsymbol{k}}}}}-\omega )\). Note that temperature T was set to be 100 K in the calculation.

Quantum uncertainty of the lattice distortion

The Heisenberg uncertainty principle states that: \(\Delta x\cdot \Delta p\ge \frac{h}{4\pi }\), where h is the Planck constant. \(\Delta p\le \sqrt{2{m}_{{Al}}E}\), where \({m}_{{Al}}\) = 27 u is the atomic mass of Aluminum atom, and \(E \sim 50\) meV is the highest phonon energy. Therefore, the upper limit of \(\Delta x\ge \frac{h}{4\pi \sqrt{2{m}_{{Al}}E}}\) ~ 2 pm.