Flexible Use of Limited Resources for Sequence Working Memory in Macaque Prefrontal Cortex

Abstract

Our brain is remarkably limited in how many items it can hold simultaneously, but it can also represent unbounded novel items through generalization. How the brain rationally uses limited resources in working memory (WM) remains unexplored. We investigated mechanisms of WM resource allocation using calcium imaging and electrophysiological recording in the prefrontal cortex of monkeys performing sequence WM (SWM) tasks. We found that changes in the neural representation of SWM, including geometry, generalizable and separate rank subspaces, reflected WM load. SWM resources, represented by neurons’ signal strength and spatial tuning projected onto each rank subspace, were shared flexibly between ranks. Crucially, the prefrontal cortex dynamically utilized shared tuning neurons to ensure generalization, while engaging disjoint and spatially shifted neurons to minimize interference, thus achieving a trade-off between behavioral and neural costs within capacity. The allocated resources can predict monkeys’ behavior. Thus, the geometry of compositionality underlies the flexible use of limited resources in SWM.

Introduction

Working memory (WM) is severely limited, so you can only keep three to four items simultaneously^1,2. Yet, WM is also remarkably flexible. You can hold anything in it, even from the first time you experience it, e.g., unfamiliar faces or meanings of new sentences in language, through efficient generalization. To understand this duality between limited capacity and generalization in the brain^3,4, we must know the neural representation of WM resources and, most importantly, the cause underlying the resource allocation to support generalization.

Traditional models of visual WM are based on discrete, fixed-resolution representation, which assumes each WM item is stored with either high precision or not at all^5,6. In contrast, continuous resource models (e.g., variable-precision model) treat WM as a limited resource distributed flexibly across trials and items^7,8,9,10,11. This flexibility can account for a range of behavioral findings that prioritize the precision of certain memoranda over others due to differences in their attentional salience or relevance to behavioral goals. For instance, population coding models^12,13 describe that resource limitations are identified by allocating a limited quantity of neural activity between neurons responding to different items, explaining why item precision declines with the number of items held in WM. Many Previous neural imaging and electrophysiological experiments in humans have demonstrated the scaling of blood-oxygen-level-dependent or electroencephalography signals with WM load^{14,15,16,17,18}. At the single-neuron level in animals, neurons in the prefrontal cortex showed reduced activities when adding more objects^15,16,17.

Despite these computational models and the reported neural activities of WM resources, the cause of controlling their allocation and resource flexibility in the variable-precision model has yet to be fully investigated. WM representations are merely imperfect copies of a perceived event but integrate with environmental regularities. Thus, it is often proposed that the structured environment provides us with prior knowledge to help constrain memory representations and control resource allocation^{19,20,21,22,23}. However, stimuli presented in typical WM experiments are usually randomly generated and unrelated to each other; how the brain represents and uses the prior structure to control limited resources in WM remains unclear.

Using sequence WM (SWM) tasks, our team has recently demonstrated the representational geometry of temporal structure in SWM in the macaque prefrontal cortex (PFC) with disentangled low-dimensional ordinal rank subspaces, each storing the item information of a given rank^24,25. More importantly, the geometry of temporal structure provided a neural basis for WM mental programming by recruiting extra-temporal resources²⁶. Based on these studies, we proposed that the decomposed rank subspaces in the SWM may serve as prior knowledge (e.g., as WM slots⁵) to constrain the allocation of WM resources. The representational geometry provided us with the neural substrates for testing those computational models at the single-neuron level. To this end, we analyzed the data from four monkeys performing the SWM task. The task requires monkeys to memorize visuospatial sequences with variable lengths (WM loads: 1, 2, 3, and 4 items) and reproduce them after a short delay. Each sequence consisted of consecutively presented location(s) whose temporal order could potentially be utilized to control the monkeys’ WM resources for generalization. The single-neuron data included in the analysis were collected using two-photon calcium imaging and high-throughput electrophysiology in the lateral PFC.

Results

Paradigm and behavior

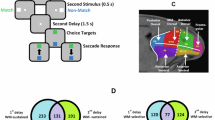
Four macaque monkeys (M1, M2, M3, and M4) were trained to learn a delayed-sequence reproduction task (Fig. 1a, see Methods). On each trial, spatial sequences with a length of 1, 2, 3, or 4 items were visually presented during the sample period, while the monkey had to fixate on the dot at the center of the screen. Each sequence item was drawn (without replacement) from one of the six spatial locations of a ring (or hexagon). Monkeys had to memorize the sequences for a short delay and reproduce the sequences by making sequential saccades or touches to the appropriate locations on the screen^24,27,28. The task with four items was too difficult for the monkeys, so only M1 was tested with length-4 sequences.

Fig. 1: Task paradigm, behavior, and recordings.

a Task structure (see “Behavioral task” subsection of Methods). Tn, the n^th target. The delay (2.5-4 s for M1 and M2; 1.15-1.50 s for M3 and M4) was randomized across trials. b Behavioral performance of each rank in different sequence lengths (from M1, see also Supplementary Fig. 1). Each subpanel shows averaged recall errors relative to target locations, Data and errorbars are presented as mean values and STD across recording sessions (n = 11 sessions). c Averaged correct rates on each rank of different sequence lengths. Error bars represent standard error of the mean (SEM) across recording sessions (n = 11). Line colors indicate ordinal ranks. d The averaged recall variabilities on each rank of different sequence lengths, error bars represent standard error of the mean (SEM) across recording sessions (n = 11). Same format as (c). e Rank error patterns of different sequence lengths (from top to bottom: length-2, -3, and -4). The rank error pattern is shown as a function of ordinal rank, averaged across spatial locations. Error bars represent standard deviation across recording sessions (n = 11). f Illustration of two-photon calcium imaging and high-throughput electrophysiological recording in monkeys’ LPFCs. The blue circles in the example FOV indicate the regions of interest (ROIs) with three example neurons, whose normalized calcium traces are on the lower left. ΔF/F, normalized fluorescence intensity. Red bar, cue on of single trial. The brown circles in the recording grid indicate the recording sites of three example neurons (activities shown in (g)). g Three example neurons exhibiting complex coding for spatial items across different ranks and sequence lengths during the late delay period (0 on time axes denoting onset of the ‘go’ cue). Each subpanel entitled with ${{{\rm{L}}}}_{{{\rm{i}}}}$-${{{\rm{R}}}}_{{{\rm{j}}}}$ represents one length i and rank j combination, with the top part being a spike raster plot and the bottom displaying averaged firing rates (shading: SEMs across trials during the late delay period). Line/dot colors correspond to spatial locations.

Figure 1b shows the distributions of behavioral responses from M1 and how the performance (correct rate) and variability (circular standard deviation, S.D.) of recalled errors of spatial location varied as a function of its ordinal rank and sequence length. Rank had a significant effect on correct rate and precision (the width of the recall error curves), regardless of the sequence length (WM load) (t_{correct rate}(107) = −9.35; t_precision(107) = 12.03; ps <0.001) (Fig. 1c), with the first item remembered significantly more accurately than the following items (planned pairwise comparisons with Bonferroni’s correction, first vs. second item: length-2, p < 0.001, Cohen’s d = 1.69; length-3, p < 0.001, Cohen’s d = 1.88; length-4, p < 0.001, Cohen’s d = 1.53). Thus, there was an apparent primacy effect. Performance was considerably better than the chance for every combination of rank and length (t-test, n = 11, all p < 0.001), except for the performance at rank 4 (accuracy = 0.24, t(11) = 2.90, p = 0.15), where the number of items went almost beyond the monkey’s memory capacity. Furthermore, the amount of information the monkeys had about locations increased from 1 to 3 or 4 items but then saturated, reflecting a limited capacity (mutual information about locations, Supplementary Fig. 1l, see Cowan (K) for a comparision with human capacity in Supplementary Fig. 1m¹⁵).

How does the sequence length affect the fidelity of memory? We compared sequences of different lengths and found that, for every ordinal rank, the accuracy and precision decreased significantly as the number of items increased (t_{correct rate}(107) = −3.62; t_precision(107) = 8.19; both p < 0.001) (Fig. 1c-d). Remarkably, this effect was present even for the first item in a sequence which suggests that as the total number of items in memory increases, the proportion of resources dedicated to each item declines, degrading the fidelity of memory. However, the existence of non-target responses may provide an alternative account for the decreased performance¹³. To enable a fair comparison of the two alternatives, we fitted the data using a mixture model²⁹ and found that the reduction in resources allocated to each item is the primary factor contributing to the performance decline (Supplementary Fig. 1g-k). Furthermore, for ordinal rank 1, the relationship between variability and sequence length seems well described by a power law (compared with linear model: ΔAIC_power = −1.21; p = 0.003, validation test; see Methods for details)^7,11.

While inadequate maintenance primarily accounts for the decline in target location recall precision as sequence length increases, rank interference is more closely associated with the occurrence of transposition errors. When an item was recalled at an incorrect serial position, its recall order was likely to have been swapped with the neighboring orders (Fig. 1e). Such transposition errors significantly increased with increasing order (t(129) = 11.71, p < 0.001). In particular, the error pattern of length-4 sequences was similar to that of length-3 (t(20) = −1.76, p = 0.09), confirming that representations in memory become increasingly variable as their number increases and that the rank-4 item memory is difficult to distinguish from neighboring orders (Fig. 1e) and random noise (Fig. 1b). Similar behavioral performance was also shown in the other three monkeys (Supplementary Fig. 1a-f), except there were individual differences in the WM capacity (Supplementary Fig. 1l). Therefore, such a graded decline in performance for sequences supports the shared resource model of working memory in monkeys, as a simple slot model would predict that each item should be capable of being stored with equal and high-resolution slots^9,10,11,30. Finally, we asked whether the spatial geometries of specific sequences (Supplementary Fig. 2a) have an impact on monkeys’ performance, especially the possible dependency between ranks due to monkeys potentially learning underlying common spatial structures. We found notable differences in accuracy and rank dependency among sequences that shared the same spatial geometry (Supplementary Fig. 2b-c), suggesting that monkeys possibly did not use geometric relations to compress sequences, consistent with our previous behavioral findings in monkeys²⁸.

Neural activity recordings and single-neuron responses

We next investigated how the shared resources between items were represented and flexibly used in SWM in the lateral prefrontal cortex (LPFC). We conducted calcium imaging and electrophysiological recordings in the four monkeys. We injected GCaMP6s virus into the LPFCs of two monkeys (M1 and M2) to enable two-photon calcium imaging across multiple fields of view (FOVs) (Fig. 1f and Supplementary Fig. 3a-c) (M1, 2877 neurons from 16 FOVs; M2, 1139 neurons from 9 FOVs; some neural data (e.g., length-2 and -3 sequences) were published in our previous study²⁴, length-1 and length-4 sequence are reported for the first time in this study). For M3 and M4, we used a 157-channel microdrive electrode system³¹ to record electrophysiological signals of single/multi-units in LPFC (M3, 891 units; M4, 489 units; these data were published in the study²⁵). We focused on neural activity during the late delay period (1 s for M1 and M2, 0.5 s for M3 and M4 before the ‘go’ cue) while the monkeys maintained length-1, -2, or -3 spatial sequences in memory (see Methods).

Neurons exhibited diverse and mixed preferences for sequence length and ordinal rank during the delay period. Some neurons showed attenuated or normalized item preference^15,16 at certain ranks when the memory load increased from 1 to 2 and 3 locations (Fig. 1g, unit 1, Supplementary Fig. 3h-i). For example, when monkeys were asked to remember a single item alone, this type of neuron was strongly selective to item 1. When animals retained length-2 or -3 sequences of items, this neural selectivity to the rank-1 item significantly decreased; at the same time, the selectivity was also reduced at increasing ranks, e.g., a reduction of item-1 selectivity from rank-1 to rank-2 and -3 in the length-3 sequence. However, other than the attenuated neurons described above, a significant proportion of neurons (see proportions of individual monkeys in Supplementary Fig. 3d-g) showed different length × rank mixed selectivity. For example, a neuron showed more robust spatial tuning to item 6 at increasing lengths (Fig. 1g, unit 2), or a neuron tuned to item 3 at only rank-3 in a sequence (Fig. 1g, unit 3). Similar length × rank mixed selectivity neurons were found in all four monkeys with either electrophysiological or calcium imaging signals (see example neurons from two-photon imaging also in Supplementary Fig. 3h-i). Thus, the sequence length and ordinal rank selective activities, potentially representing the SWM resources, seemed conjunctive and deeply entwined at the single neuron level, making it challenging to associate single neural activities with behavioral phenomena of WM resources.

Geometry of SWM by the LPFC neural population

Using the methods developed from our previous studies²⁴, we next identified low-dimensional rank subspaces in the PFC neural states to examine the neural code of WM resources at the population level. We quantified the influence of spatial item and ordinal rank for different sequence loads (length-1, -2, and -3) on neural responses of single neurons during the delay period using linear regression, incorporating spatial item, ordinal rank, and length as variables [6 items × (length 1 + 2 + 3) ranks = 36 combinations] to fit neural signals (calcium or spike responses) of individual neurons (see Methods and Table S1-2 for sample size). Control analyses confirmed that including interaction terms in the regression did not affect the results (Supplementary Fig. 4a-d). We then used the regression coefficients to measure each neuron’s selectivity to each variable.

We obtained vector representations in population states for the 36 location-rank combinations by concatenating the regression coefficients of all neurons from correct trials. We then divided these 36 vectors into six groups (length-1: rank-1; length-2: rank-1 and -2; length-3: rank-1, -2, and -3) and, for each group, performed a principal component analysis (PCA) to obtain the axes that captured the major response variance resulting from item changes (Fig. 2a and Supplementary Figs. 5a-d, 6a,e,i,m). We obtained six two-dimensional subspaces, one for each rank in different lengths. For every length, the subspaces within a sequence (e.g., rank-1 and -2 in length-2; rank-1, -2, and -3 in length-3) were oriented in a near-orthogonal manner in neural state space, as evident from the low decoding accuracy and variance accounted for (VAF, see Methods) ratio between them (Fig. 2b and Supplementary Fig. 5e-h, i-l). Furthermore, for every rank, the subspaces across lengths (e.g., rank-1 in length-1, -2, and -3; rank-2 in length-2 and -3) were nearly overlapped with each other, as evident by the high decoding accuracy and high VAF ratio between them (Fig. 2c and Supplementary Fig. 5e-h, m-p), showing the generalization ability of each rank subspace across sequence lengths. Thus, the geometry of SWM demonstrated a compositional code, as the rank subspaces were disentangled with each other in a sequence and were generalizable across lengths (Fig. 2i, see Supplementary Fig. 5 for individual monkeys).

Fig. 2: Geometrical representation of SWM in PFC neural states.

a The combined responses of all neurons from four monkeys for each length-rank-location combination projected to the corresponding length-rank subspace (e.g., L1-R1 for length-1, rank-1). Responses were obtained through linear regression of averaged late delay activity (1 s for monkeys M1 and M2, 0.5 s for monkeys M3 and M4, before the ‘go’ cue). Locations are color-coded as in Fig. 1g. rPC, rotated principal component. b Cross-rank decoding across sessions and monkeys (n = 66). Each dot indicates a specific monkey-session-length-rank combination. For each length, decoders were trained on one rank and tested on other ranks. c Cross-length decoding, same format as (b). Stars indicated the decoding performance above chance (gray dashed line) (***p < 0.001, two-sided Wilcoxon signed-rank test, n = 66). b, c The boxes show the range from first to third quartiles divided by the median line. The whiskers extend to the most extreme data points within 1.5 times the interquartile range (Tukey method), and circles indicate individual data. d Regression between the behavioral accuracy and ring size (Frobenius norm of projection) across monkey-length-rank combinations (n = 24). e Recall variability (S.D.) as a function of ring size for each monkey-length-rank combination (n = 24), formatted as in (d). f Information regarding the sequence of locations (derived from decoder performance of neural activities, see Methods). Dots indicate monkey means across sessions. Error bars represent SEM across monkeys and sessions (n = 66). g Regression between mutual information of sequence locations derived from neural activities and behaviors (n = 12 length-monkey combinations). h Swap rate as a function of variance account for (VAF) ratios between different rank subspace pairs (n = 24 rank pairs from 4 monkeys). i Schematic representation of SWM geometry as sequence length increases, showing reduced ring size and increased interference between items. d, e, g, h The central line indicates the least squares best fit line, the shaded regions indicate the 95%-confidence interval of the fitted mean. ***p < 0.001, *p < 0.05, n.s. indicates non significant.

Although the compositional code has been shown in our previous studies^24,25,26, we do not know whether the geometry of SWM can explain the monkeys’ behavior regarding item memory precision and recall, as shown in Fig. 1b-e. Indeed, different from mixed single-neuron activities, we discovered that the ring size in each subspace at the collective level, reflecting the encoding strength of item information in memory, could perfectly predict the recalled accuracy (Fig. 2d, two-sided t test, n = 24; β = 0.06 ± 0.01 (SE), t(22) = 4.33, p = 0.0002; 95% CI [β] = [0.03, 0.08]) and precision (Fig. 2e, two-sided t test, n = 24; β = −0.13 ± 0.02 (SE), t(22) = −6.05, p = 4.38e−06; 95% CI [β] = [−0.17, −0.08]) across ranks and lengths. As a control, we also computed rank/length subspaces with more principal components (PC) included (e.g., PC3, 4, and 5) (Supplementary Fig. 6c,g,k,o) and found that, while cumulative explained variance increased with more PCs, the correlations between ring size and task performance remained similar to those in the two-PC case. Interestingly, for rank-1 items across different lengths, the ring size change in the subspace showed a similar trend as the behavioral performance shown in Fig. 1d (Supplementary Fig. 6d,h,l,p). Further control analyses showed that ring size reductions are caused by WM load, not by time-dependent degradation during WM maintenance (Supplementary Fig. 6q-x). Furthermore, the amount of information about sequence locations, derived from decoder performance in neural activities, demonstrated a nonlinear relationship with WM load (Fig. 2f, two-sided Friedman test, χ²(2) = 100.30, p = 1.90e−22, Kendall’s W = 0.758, n = 66; Post-hoc pairwise comparisons with Tukey-Kramer correction: group1 vs. group2, p = 1.84e−13; group2 vs. group3, p = 0.11) and, more importantly, a significantly positive correlation with the information the animal had in behavior (Fig. 2g, two-sided t test, n = 12 length-monkey combinations; β = 1.11 ± 0.37 (SE), t(10) = 3.025, p = 0.012; 95% CI [β] = [0.29, 1.94]). Finally, although SWM relies on separate neural spaces, the rank subspaces are not perfectly orthogonal. The VAF ratios, denoting the interference between rank subspaces, were significantly associated with errors of swapped orders (two-sided t test, n = 24 rank pairs from 4 monkeys; β = 1.15 ± 0.43 (SE), t(22) = 2.66, p = 0.014; 95% CI [β] = [0.25, 2.04]) (Fig. 2h, Supplementary Fig. 6d,h,l,p). Therefore, taken together, the geometry of SWM (see decoding results also in Supplementary Figs. 5 and 6) explained the graded decline in item precision, memory capacity, and errors in monkeys’ behavior, characterizing the WM resources in SWM at the collective level.

Single-neuron basis of WM resources

What is the single-neuron basis of WM resources? How do single neurons flexibly share their neural activities among rank subspaces to reflect WM load and support generalization? To answer these questions, for each neuron, we first projected neural activity constructed on 2-dimensional rank subspaces onto each unit vector along its axis to derive the spatial tunings on each decomposed rank subspace (Fig. 3a). The geometric relationship between a single neuron axis and rank-r subspace was characterized by A_r and φ_r, where A_r measures the signal strength of a single neuron in rank-r subspace, and φ_r specifies the spatial item preference of a single neuron in rank-r subspace.

Fig. 3: Single neural basis of compositionality.

a Illustration of how neural responses in two-dimensional rank subspaces are projected onto each neuron’s single unit vector, thereby deriving a spatial tuning curve. The standard deviation of each rank’s tuning curve denotes the signal strength (A_i), while the preferred location (φ_i) is represented by the phase of the tuning curve. b Illustration of disjoint (top) and overlapping (bottom) neurons. Disjoint neurons aligns primarily with only one single rank subspace, whereas overlapping neurons aligns with both rank subspaces. c The distribution of neuron-to-subspace strength (NSS) indices measures the relationship between each pair of subspaces. Top: in the disjoint neuron dominant scheme, NSS distribution tends to be bimodal. Bottom: in the overlapping neuron dominant scheme, NSS distribution tends to be normal. d Illustration of shared tuning and shifted tuning neurons. φ_diff, differences of preferred locations between different subspaces. e The distribution of φ_diff measures the tuning changes between each pair of subspaces. Top: the shifted neuron dominant scheme with a uniform distribution. Bottom: the shared tuning dominant scheme with a right skew distribution. f NSS and φ_diff distributions pooled across all rank pairs. g Left: percentage of disjoint neurons, error bar represent STD of 100-time samplings (two-sided 1-Proportion z test, n = 4068/ 1596/ 1327/ 832 neurons, z = 10.81/ 5.95/ 9.80/ −0.83, p = 0/ 2.56e−09/ 0/ 0.41). Right: CDFs of φ_diff (K-S test for non-uniformity[dash line], n = 1689/ 679/ 485/ 428, D = 0.08/ 0.08/ 0.09/ 0.11, p = 1.60e−10/ 2.10e−04/ 2.28e−4/ 8.63e−6). h NSS and φ_diff distributions pooled across all length pairs, same format as (f). i Left: percentage of overlapping neurons, error bar represent STD of 100-time samplings (two-sided 1-Proportion z test, n = 4976/1751/1586/1109 neurons, z = 12.50/8.96/3.87/1.65, p = 0/0/1.10e−04/0.10). Right: CDFs of φ_diff (K-S test for non-uniformity[dash line], n = 2929/ 1063/ 870/ 582 neurons, D = 0.41/ 0.37/ 0.39/ 0.30, p = 0/ 1.24e−132/ 9.13e−117/ 2.93e-46). j Summary of the simulation describing how NSS indices and φ_diff affect the relationship between subspaces. See also supplementary Fig. 7. k To maintain generalization between subspaces, an overlapping distribution of NSS indices and a predominant presence of shared tuning neurons are necessary. l Disjoint NSS indices distribution or uniform distributed φ_diff is sufficient to reduce interferences between subspaces.

When a single-neuron axis primarily contributes to one subspace, the neuron is called a ‘disjoint-neuron’. In contrast, if the single neuron contributes significantly to the two subspaces, the neuron is referred to as an ‘overlapping neuron’ (Fig. 3b). The neuron-to-subspace strength (NSS) index measures the relative signal strength of a single neuron with respect to an earlier rank subspace, compared to its strength with a later rank subspace (see Methods). An NSS index close to 1 or −1 indicates that the neuron is disjointly selective to the earlier or later item, while a value close to 0 suggests an overlap between two items^24,26,32. The distribution of NSS indices characterizes the relationship between pairs of subspaces in the neuronal population (Fig. 3c). Next, for neurons contributing to at least two rank subspaces (see Methods for selection criteria), the angle φ_r provided a good summary of the neuron’s spatial preference at each rank. The angular difference (φ_diff) between ranks measured the difference in spatial location preference (Fig. 3d). A φ_diff < 30°suggests the same preferred location at two ranks (referred to as ‘shared tuning’ neuron). In contrast, the larger differences indicate different location preferences across ranks (‘shifted tuning’ neuron) (Fig. 3d). The distribution of φ_diff quantifies tuning changes between rank subspaces in the overlapping neurons (Fig. 3e). The disjoint and shifted tuning neurons represent the exclusive resources encoding one item, the shared tuning neurons denote the shared resources among multiple items in SWM.

We thus defined each neuron’s signal strength (indexed by A_r and NSS) and spatial tuning (indexed by φ_r and their differences between subspaces φ_diff) as the WM resources for each neuron. This measurement is crucial because it suggests that the WM resource of each neuron depends on the geometrical relationship between the neuron activity and its corresponding rank subspace. With this idea, we could then ask how the resources could be flexibly allocated to support generalization and orthogonality. We discovered that, for items within a sequence, neurons tended to be disjoint (|NSS | > 0.4, see Methods) to avoid interference between rank subspaces (left-skew indicates stronger selectivity for the earlier item), and even the small proportion of overlapping neurons (|NSS | <0.4) showed a shift of spatial tuning across the ranks (Fig. 3f). A threshold sensitivity analysis was performed, showing that variations in the threshold had minimal effect on the conclusion (Supplementary Fig. 7i-k). The degree of recruiting disjoint neurons in each monkey was characterized by the ratio of disjoint and overlapping neurons (distribution of NSS) and the degree of shifting location preference was quantified by the cumulative distribution function of φ_diff (see Methods). Three out of four monkeys showed a significantly high degree of recruiting disjoint neurons and a high degree of shifting location tuning (Fig. 3g, except for M4). In contrast, for every rank subspace across different lengths, neurons in the three monkeys largely overlapped and exhibited identical spatial tuning across lengths to ensure generalization (Fig. 3h-i). That is, shared resources (overlapping neurons and shared tunings) were used in the same rank across lengths, and exclusive resources (disjoint neurons and shifted tunings) were recruited for the precision of individual items.

To further probe the relationship between signal strength and spatial tuning contributing to compositionality, we built a model consisting of 1000 artificial neurons (see Methods), where, based on actual data, each neuron’s signal strength (A_r) follows a Weibull distribution or gamma (lognormal) distribution (Supplementary Fig. 7a-d) and item preference (φ_r) follows a uniform distribution. We calculated the cross-rank decoding accuracy based on simulated data to examine the geometrical relationship between subspaces by varying the population’s NSS and φ_diff combinations (Fig. 3j). We found that overlapping neurons (NSSs are close to 0) and shared tunings (φ_diff < 30) are necessary for generalization between subspaces (Fig. 3k). However, disjoint neurons or mixed but spatial tuning random-shifted neurons, as long as one of the conditions is met, can achieve orthogonality between subspaces (Fig. 3l). Although the results of our simulation are consistent with the previous proposals^33,34, it is worth noting that the real neural data from individual monkeys were marked in the simulation space (Fig. 3j and Supplementary Fig. 7e-h), only providing one possible solution for generalization and orthogonality between subspaces, thus suggesting multiple and adaptive neural mechanisms at a single neuron level may coexist within the brain to support compositional code.

Flexible control of single-neuron WM resources

We next asked how resources are dynamically allocated during the sequential processing of spatial items, e.g., from earlier to later items in a sequence. Theoretically, two types of resources could be recruited when adding later items in a sequence: recruiting extra neurons or recycling the used neurons from the earlier items (Fig. 4a). Interestingly, we noticed that the PFC mostly recycled the used neurons in the earlier items (on average, 88% of rank-1 and 95% of rank-2 neurons, see Methods) but gradually recruited substantially few new neurons (e.g., less than 5% of neurons were new for the rank-3 item) to the later items in a sequence (Fig. 4b and Supplementary Fig. 10, also see Discussion). This suggested that recycling the neurons used was the primary strategy for controlling WM resources.

Fig. 4: Dynamics of compositionality in SWM with increased length.

a Illustration of two types of neuronal resource allocation strategies as new items are incorporated into WM. Recruit: extra neurons are recruited. Recycle: neurons initially engaged in earlier items are reused. Recycled neurons include stable (green; encode both earlier and new items) and flexible (blue; switch from earlier to new items) subtypes. b Proportion of recycled neurons and extra neurons for ranks 1-3 in length-3. c An example neuron previously encoding an earlier item was recycled to encode a new item (L3-R3). Shading: SEMs across trials. Line/dot colors correspond to spatial locations. d-g Early condition results (WM not saturated), comparing across lengths (L1-R1 vs. L2-R1) and ranks (L2-R1 vs. L2-R2). d Subspace comparison across lengths, similar to Fig. 3h. e Subspace comparison across ranks. Same format as Fig. 3f. f Correlation between generalization (1-|NSS| across lengths) and orthogonality (|NSS| across ranks) for recycled neurons (n = 363). g Correlation between generalization (180-φ_diff across lengths) and orthogonality (φ_diff across ranks) in stable neurons (n = 253 neurons). h-k Late condition results (near capacity). h-i Comparing across lengths (L2-R2 vs. L3-R2) and ranks (L3-R2 vs. L3-R3). Same format as (d-e). j-k Correlation between generalization and orthogonality for recycled neurons (n = 227) and stable neurons (n = 137). f, g, j, k, The dark line shows the least squares best fit, with the blue region as the 95% confidence interval of the fitted mean, the Spearman correlation coefficient (r) is shown. l-m Saturated condition results, comparing across lengths (L3-R3 vs. L4-R3) and ranks (L4-R3 vs. L4-R4). Same format as (d-e). n Correlation of NSS across monkeys (n = 4 monkeys; both-sided Wilcoxon rank sum test). o Correlation based on φ_diff (n = 4 monkeys; both-sided Wilcoxon rank sum test). p Left: the percentage of overlapping neurons across lengths significantly decreased with increasing items stored in WM (Chi-square test, χ²(2) = 200.87, p = 0; Post hoc pairwise chi-square tests (two-sided) with Bonferroni correction. Early vs. late: χ²(1) = 5.73, p = 0.05; late vs. saturated: χ²(1) = 97.92, p = 0). Right: CDFs of φ_diff shift toward the control level indicated by a dashed line. Group differences were tested using the Kruskal–Wallis test (H(2) = 114.33, all p = 0, two-sided), followed by post hoc pairwise comparisons with Bonferroni correction. q Left: the percentage of disjoint neurons (two sided Chi-square test, χ²(2) = 5.49, p = 0.06, no multiple comparison correction was applied). Right: CDFs of φ_diff shift away from the control level. Same format as (p). Group differences were tested using the two sided Kruskal–Wallis test (H(2) = 1.78, p = 0.41, two-sided). p, q The boxes show the range from first to third quartiles divided by the median line. The whiskers extend to the most extreme data points within 1.5 times the interquartile range (Tukey method), and circles indicate individual data.

Thus, with such a strategy, we predicted that there would be a tradeoff for these recycled neurons between keeping generalization and avoiding interference when the WM load increases^3,4,35. Because the activity of each neuron, on the one hand, was required to be stable to only contribute to the rank subspace of the earlier items to ensure generalization across lengths (e.g., rank-1 neural activities are preserved across length-1, -2, and -3), as indicated by the green area in Fig. 4a and termed as ‘stable neurons’; however, on the other hand, partially neural activities encoding earlier items had to be flexible to allow reuse for encoding later items (Fig. 4a, blue area, termed as ‘flexible neurons’). Figure 4c shows an example ‘flexible neuron’ with such a tradeoff. The neuron showed high neural responses and selectivity (tuned to item-4/5) for the early item (rank-1 in the length-1). However, partial resources (responses and preferred tuning) have to be reallocated for encoding later items (e.g., lower responses and shifted tuning to item-3) (also see other types of example neurons in Supplementary Fig. 10).

We then investigated the neural mechanism, at the population level, of how the PFC adaptively uses limited resources to solve the trade-off between generalization and orthogonality. We expected that when the number of items increased, 1) both generalization and orthogonality would decrease, and 2) as the two properties shared the same neural resources, negative correlations between generalization and orthogonality would be found more substantial for the late items, which could be considered as the signature of resource trade-off. We tested the predictions by investigating the NSS and φ_diff of each item from early to late.

For the earlier items in a sequence where the resource is sufficient, the rank-1 item shared neurons (and spatial tunings) across length-1 and length-2 sequences to ensure generalization (Fig. 4d), and rank-1 and rank-2 items separately recruited disjoint neurons (and shifted tunings) to keep orthogonality (Fig. 4e). Interestingly, even when the resource is sufficient, we found a negative correlation in |NSS| between the ‘stable neurons’ (generalization across lengths) and ‘flexible neurons’ (orthogonality across ranks), showing a competitive relationship (two-sided test with no adjustment for multiple comparision, p = 6.47e−11, n = 363) (Fig. 4f). But, for the ‘stable neurons’, there was no correlation in φ_diff between rank-1 and rank-2 item (two-sided Spearman rank correlation test with no adjustment for multiple comparision, p = 0.65, n = 253 neurons) (Fig. 4g).

However, for the later items, we found that, although the degree of recruiting overlapping neurons slightly decreased, most shared neurons were kept to ensure the generalization across lengths (Fig. 4h). As the resource was scarce, the degree of recruiting disjoint neurons was remarkably decreased. Neurons had to be overlapped between ranks (Fig. 4i). The reduced percentage of disjoint neurons was primarily driven by sequence length rather than by degraded item precision (Supplementary Fig. 9). Importantly, for the neurons contributing to later items, the |NSS| was more negatively correlated between ‘stable’ and ‘flexible’ neurons (p = 0, n = 227) (Fig. 4j). Different from the early item, φ_diff between rank-2 and rank-3 item demonstrated a significantly negative correlation (p = 5.48e−4, n = 137) (Fig. 4k). That is, when the resource was scarce, the later items had to compete for resources including both signal strength (|NSS|) and spatial tuning (φ_diff), showing a more vital stability and flexibility trade-off relationship. The results of correlations in |NSS| and φ_diff were consistently found in all four monkeys (Fig. 4n-o, supplementary Fig. 8).

Neural predictions when SWM goes beyond the capacity

Thus far, we have demonstrated the dynamics of WM resource allocation in SWM at population and single-neuron levels in length-1, -2, and -3 sequences. We therefore predicted that when the number of items exceeded memory capacity in length-4 sequences: 1) the geometry of rank-WMs of unsuccessfully-recalled items would vanish; 2) a decline in memory precision would take place at all ranks due to the resources reallocated; 3) as the resources were used out, the generalization and orthogonality could not be balanced, causing interference with each other. We analyzed the neural activities of the length-4 sequence from M1 when the performance of the rank-4 item was close to the chance level; rank-4 items did interfere with rank-3 (e.g., Fig. 1c-e). We found that the ring structures of the rank-3, and -4 items were nearly undetectable (Supplementary Fig. 10m-n). The ring sizes of ranks were significantly smaller than the corresponding ranks in other sequences with shorter lengths (Supplementary Fig. 10o). Most importantly, at the single-neuron level, neurons across lengths showed low shareability and shifted location tunings (Fig. 4l); neurons across ranks showed a low degree of randomly shifted tuning (Fig. 4m), thus leading to poor compositionality.

Taken together, when multiple items were held in WM, the PFC flexibly adjusted limited resources, including each neuron’s signal strength and spatial tuning, to implement compositionality in SWM. Specifically, the generalization and orthogonality had to be compromised when the memory load gradually increased and reached capacity (Fig. 4p-q).

Anatomical organization of resource allocation in the LPFC

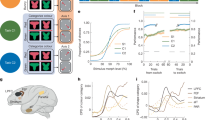
Two-photon imaging (from 0-500 µm, local scales) and electrophysiological recordings (from 1- ~15 mm, mesoscales) allowed us to examine the anatomical organization of the WM resources at different spatial scales. Firstly, to explore the spatial distribution of shared resources (overlapping neurons) across lengths (e.g., rank-1 neurons in length-1, -2, and -3), we calculated a spatial clustering index for overlapping neurons across lengths assessed by their signal strengths in a small cortical distance (6-50 µm) and found no significant anatomical clustering at local scales (Supplementary Fig. 11g-i). We also calculated the correlation matrix of overlapping neurons’ resources (signal strength and preferred item) across subspace pairs (Supplementary Fig. 11c-d). As expected, the shared resources maintained highly similar spatial organizations at both scales to ensure across-length generalization (Fig. 5a-b, see data from other monkeys in Supplementary Fig. 11a-b). We also investigated how the exclusive resources (disjoint neurons) were dynamically and spatially recruited to avoid interference when the number of items gradually increased. We found that, from earlier to later items in a sequence, newly recruited disjoint neurons for each rank tended to migrate toward the medial direction, from ventral to dorsal LPFC, at the large spatial scale (Fig. 5c, e, and f, Supplementary Fig. 11j). However, such migration or other spatial organizations were not found at the imaging FOVs at the smaller spatial scale (Fig. 5d and g, Supplementary Fig. 11k).

Fig. 5: Anatomical organization of the compositional code in the LPFC.

a Characterization of the anatomical organization of neural resources on the mesoscale level. Each subpanel (L_i-R_j) describes contributions of all recorded neurons to rank-j subspace within length-i sequences, each circle represents a neuron (size: normalized signal strength; color: preferred location) on a l mm grid of recording sites. The same site records multiple neurons, resulting in overlap at the center of the circle. The data are from electrophysiological recordings on monkey M3. b Characterization of the anatomical organization of neural resources on a microscale level. Same format as (a), but it shows the two-photon imaging data collected from monkey M1. Normalized rank contributions are overlaid with an average calcium image of the FOV. Representative FOV from one of 25 independent sessions (similar results in 18/25 FOVs). c Anatomical organizations of disjoint neurons across sessions in the mesoscale resolution. Each dot in the heatmap is the estimated probability density of a disjoint neuron weighted by its signal strength and smoothed by a normal function. L: lateral, M: medial, A: anterior, P: posterior. Left to right: contributions to L3-R1, L3-R2 and L3-R3. Data are from M3. d Same as (c) but at microscale. Each circle show an imaging site of disjoint neurons across all FOVs (size: signal strength). Data are from M1. e Mesoscale disjoint neuron distributions along the laterial-medial (L-M, left) and anterior-posterior (A-P, right) axis in M3 (L-M direction: L3-R1 vs. L3-R2: p = 0.01; L3-R2 vs. L3-R3: p = 0.03; L3-R1 vs. L3-R3: p = 1.31e−08; A-P direction: p = 0.44/ 0.04/ 0.21; n = 179/ 29/ 24 neurons). f Same format as (e) for M4 (L-M: p = 0.04/ 1/ 0.02; A-P: p = 8e−03/ 1/ 7.30e−05; n = 28/ 10/ 22 neurons). g Microscale disjoint neuron distributions stacked across FOVs in M1 (X direction: p = 1/0.06/4.89e−04; Y direction: p = 1/ 1/ 1, n = 434/90/72 neurons). e–g Group differences were tested using the two-sided Kruskal–Wallis test, followed by post hoc pairwise comparisons with Bonferroni correction.

Discussion

Using two-photon calcium imaging and electrophysiological recording in the LPFC of four macaque monkeys who performed a length-variable visuospatial sequence WM task, we revealed the allocation mechanism of WM resources at both population and single-neuron levels to support the compositional code of SWM. With limited resources, the PFC recruited shared tuning neurons across different sequence lengths to ensure generalization and used disjoint and shifted tuning neurons to avoid interference between items within a sequence. During the sequential processing of spatial items, WM resources were sequentially and dynamically allocated to achieve the trade-off between generalization and orthogonality. Finally, the geometry of SWM resources reflected WM precision and recall errors in behavior, even when the sequence item exceeds the WM capacity.

Geometry of SWM, resources, and flexible use

Although previous human imaging¹⁴ and single-neuron recordings in animals^15,16 showed that neural activities (e.g., BOLD signals or firing rates) were correlated with the behavioral variability of item precision, these studies have not thoroughly and systematically shown the representation of neural resources and their control principles. In the present study, we demonstrated that the resources at the single neuron level must depend on the representational geometry of WM, e.g., decomposed low-dimensional rank subspaces, where disjoint and shifted tuning (flexible) neurons are utilized to maximize the resource for new item encoding precision and shared tuning (stable) neurons are mainly used for encoding shared representation for generalization. The resource is limited, so the two types of neurons must be balanced and used rationally and efficiently among memory items^36,37. Notably, both types of neurons are not entirely fixed, but partly flexible, allowing them to transform into each other depending on current contexts. For example, in SWM, a single neuron could be disjoint when the resources are sufficient, and the same neuron could gradually become overlapped when resources are scarce. Therefore, the flexible use of limited resources, even at the single-neuron level, strongly supported the variable-precision model^9,10, where WM precision varies continuously and dynamically across items.

Furthermore, previous studies have shown that neural activities (e.g., firing rates or BOLD signals) were analyzed as a resource. Here, we reported that signal strengths and their preferred locations could both function as resources to allocate to sequential items and support the compositionality. That is, neurons could also adjust their preferred locations to serve as resources to help generalization by sharing tuning between ranks in different lengths and avoid interference by shifting tuning between items in a sequence, providing new insights into the definition of WM resources and their underlying control mechanisms.

We argue that the present study did not intend to address the mechanisms of total neural resources. This could be due to the fact that there is an upper bound on the network’s total neural activity at any moment^38,39, and the activity of each neuron is divided by the integrated activity of all neurons (therefore ‘normalized’), mediated by inhibitory interneurons⁴⁰. However, based on our predictions, to achieve compositionality, the PFC, in theory, could use three distinct groups of neurons (for length-3 sequences) to ensure both generalization and orthogonality across lengths and ranks. Interestingly, our neural data showed instead a highly mixed selectivity between ranks in PFC populations. The mixed selectivity in PFC is relatively common, as often reported in many previous studies^41,42,43,44. With the data in the present study, we still do not know why the PFC is parsimonious in recruiting extra neurons instead of reusing mixed-selective neurons⁴⁵. One possibility is that the mixed selectivity offers a significant computational advantage for the mixtures or interactions of task-relevant variables (here, multiple ranks or items in SWM). For example, the multiple rank subspaces can interact with each other through a population structure-enabled gain modulation mechanism⁴⁶ during the gating-in/out processes during the sample and retrieval periods.

Recently, using the same neural dataset, our team has demonstrated the geometry of SWM²⁴, the SWM gate-in process²⁵, and SWM manipulations²⁶. However, all these previous studies assumed that WM resources are static across sequence lengths, which is inconsistent with current behavioral and computational models, such as continuous resource models (or variable-precision models)^9,10. Investigating the changes in neural selectivity (signal strength and item preference) when gradually increasing WM load is key to understanding the underlying mechanisms of the flexible use of limited resources.

In the current task, the identified activities in rank-WM subspaces can also be regarded as prospective sequential actions selected from memory. Future analyses and experiments must explore the dissociation between WM representations and action plans^47,48. For instance, specific rules could be established to differentiate between sequence memories and sequence actions. Additional analyses could be conducted during the action or memory retrieval period. However, in this study, while motor planning may influence the relative ring sizes of ranks in a sequence (e.g., rank-1 > rank-2 > rank-3 in length-3 trials), it is unlikely to impact comparisons of the same rank across different lengths. Therefore, we posit that the underlying mechanisms of resource utilization are consistent regardless of WM and motor planning.

Prior structure as a control of WM resources

In the WM system, our brain must integrate a perceived event with structured prior knowledge to constrain memory representations. Most previous WM experiments only included unrelated sensory stimuli, e.g., spatial locations, shapes, or colors^49,50,51, where WM was represented as a copy of external sensory input. Although we have demonstrated the geometry of SWM in our previous studies^24,25,26, the present study is the first to propose that the PFC took advantage of the geometry as a prior temporal structure to constrain the allocation of resources and further demonstrate the single-neuron level of resources (signal strength and item preference based on WM geometry) and their flexibility and dynamics during the sequential processing of WM on an item-by-item basis. This control of WM resources is essential because it implies that the temporal constraints could broadly apply to various cognitive operations involving a progression through ordinal sets (e.g., language, music, or mathematics), where different stimuli, tasks, and memories are potentially embedded. In a broader sense, the allocation of WM resources, in general, should depend on the neural geometry of WM, which is most likely formed during task learning.

Regarding the rationality of using limited resources, the PFC may use geometry with the compositional code to solve the trade-off between behavioral and neural costs: 1) in behavior, the PFC uses enough exclusive resources to ensure each item’s encoding precision and to avoid interference between items (disentanglement); 2) at the same time, to minimize neural cost, the PFC shares resources on rank representation cross lengths (generalization; note that we have to admit that stronger generalization tests are needed in the future experiments, e.g., to generalize to new WM tasks⁵²). This is in line with the theory of resource rationality³⁶, which proposes that the brain attempts to maximize the number of states the system could possibly represent in a given task while at the same time minimizing a biologically relevant cost. Thus, compositionality, which describes the relational structure between sequential items, could be one of the major causes of controlling resource allocation. In this view, the WM capacity in behavior, a decrease in precision with increased items, could be understood as the outcome of a rational and flexible use of limited resources for compositionality⁵³. We also notice that our current study did not directly test the concept of compositionality, as it requires future tests of component recombination in new tasks.

In a seminal 1956 article, George Miller¹ suggested limitations on our capacity to process information, such as the number of perceptual stimuli that can be held or ranked in short-term memory. In recent years, debates regarding the capacity and fidelity of WM have driven significant advances in our understanding of the nature of their representations. In particular, experiments and computational models have speculated that our brain takes advantage of environmental regularities in long-term memory to control limited memory resources optimally. In agreement with these postulates, the geometry of SWM compositionality and the flexible control that we uncovered in the current study, along with preexisting information theories (efficiency coding and resource rationality) and established neurophysiological principles (population coding and normalization), may provide a fundamental neural mechanism to bridge our understanding of neural circuits and their computational functions in WM capacity.

Methods

Animal model

Four naïve male rhesus monkeys (Macaca mulatta) were used in the study. Monkey M1 (5.0 kg, 4 years old) and monkey M2 (6.1 kg, 4 years old) were used for two-photon calcium imaging. Monkey M3 (9.2 kg, 7 years old) and monkey M4 (10.0 kg, 8 years old) were used for electrophysiological recordings. All experimental protocols of the two-photon imaging study followed the Guide of the Institutional Animal Care and Use Committee (IACUC) of Peking University Laboratory Animal Center and were approved by the Peking University Animal Care and Use Committee (LSC-TangSM-3). All experimental protocols of electrophysiological research followed the Guidelines of the Institute of Neuroscience, Chinese Academy of Science (CEBSIT-2020035R02).

Behavioral task

The monkeys were trained to perform a delayed-sequence reproduction task (Fig. 1a). Each trial began with the appearance of a fixation point in the center of the screen. Monkeys were required to maintain fixation until the “go” signal was presented. For M1 and M2, when they gazed at the fixation point for 500 ms (100 ms for M3 and M4), six circles 1.2° (2° for M3 and M4) in diameter were presented 7° (11° for M3 and M4) away from the fixation point. Together, the six circles composed a symmetrical hexagon. After another 500 ms (480 ms for M3 and M4), one, two, three, or four red targets were presented sequentially. Each target was in one of the six circles. Each target was presented for 200 ms (250 ms for M3 and M4), and the time interval between targets (the inter-stimulus interval, ISI) was 400 ms (300–500 ms for M3 and M4). These targets constituted a specific spatial sequence. After a random delay (2500–4000 ms for M1 and M2, 1150–1500 ms for M3 and M4), the fixation point disappeared (the “go” signal). M1 and M2 were required to saccade to and maintain fixation at the location of each memorized target for 300 ms (the item information of the sequence) in the correct order (the rank information of the sequence) when reproducing the spatial sequence. As feedback, the circle at a fixated location disappeared during fixation (regardless of whether it was the correct location). Unlike M1 and M2, M3 and M4 had to reproduce the sequence by touching the locations on the screen. Whenever the monkey touched an incorrect location, the trial terminated. All four monkeys were rewarded only when they correctly repeated the whole sequence.

M1 and M2 were seated in a primate chair facing a 20-inch LCD monitor during experiments. The reward was 3 drops of juice per trial (~0.5 ml), and a computer-controlled solenoid controlled the reward size. Eye positions were monitored with an infrared oculometer system at a sampling rate of 500 Hz (Eyescan). We used NIMH MonkeyLogic⁵⁴ to control behavior and collect behavioral data. M3 and M4 were seated in a primate chair facing a 21-inch LCD monitor. Eye positions were monitored with an infrared oculometer system at a sampling rate of 500 Hz (Eyelink). We used Matlab psychtoolbox⁵⁵ to control behavior and collect behavioral data.

Sequences

Each location was sampled only once in a single sequence. Theoretically, there should be 6, 30, 120, and 360 unique sequences of length-1, -2, -3, and -4, respectively. However, for M1 and M2, to ensure adequate trial numbers per sequence per session, we did not exhaust all possible combinations for length-3 and -4 sequences. We had to randomly select a subset of length-3 and length-4 sequences for each recording session to ensure enough trials were sampled across our recording sessions. More specifically, a random set of ~80 length-3 and ~30 length-4 sequences, together with the set of 6 length-1 and 30 length-2 sequences, were used in each session. In each trial, one sequence was randomly selected from the sequence set. For M3 and M4, all possible combinations for length-1, -2, and -3 sequences were included. About 340 trials for M1 and M2, ~470 trials for M3, and ~750 trials for M4 were included in each recording session for further data analysis.

Dataset

For M1, length- 1, -2, -3, and -4 trials were randomly intermixed in the experiments. For M2, M3, and M4, only length-1, -2, and -3 sequences were used. Length-1 and -4 sequences of behavioral and neural data from M1 and M2 were included in the analysis for the first time, in contrast to previous studies^24,25. Only recording sessions with enough trial numbers of each length (more than 20) were included in the following analyses. In total, 66 recording sessions (16 for M1, 9 for M2, 29 for M3, 12 for M4) were included. Part of the imaging dataset was also used in our previous study²⁴. In each imaging recording session (M1 and M2), around 157 neurons, on average, were found in the corresponding imaged field of view (FOV). These FOVs were distributed alongside the principal sulcus (PS) (Supplementary Fig. 3a-b). In each electrophysiological recording session (M3 and M4), around 39 neurons, on average, were found in the lateral prefrontal cortex, including its anterior, posterior, ventral, and dorsal sides and FEF²⁴ (Supplementary Fig. 3c-d). The recorded counts of neurons per session for each monkey is described in Table S1-2.

Two-photon imaging and data preprocessing

We performed in vivo two-photon imaging using a Thorlabs two-photon microscope and a Ti:Sapphire laser (Mai Tai eHP, Spectra Physics). A 16 × objective lens (0.8 N.A., Nikon) imaged an area of 512 μm × 512 μm or 800 μm × 800 μm at 30 frames per second. The recording depth ranged from 250 μm to 350 μm below the pia. Each imaging session lasted for 2–3 hours. We aimed to cover most regions in the recording windows alongside the PS (Supplementary Fig. 3a-b).

The image processing pipeline was implemented in Python and JupyterLab. First, two-photon images were temporally down-sampled and spatially smoothed by a Gaussian filter. Then, the images were motion-corrected using a non-rigid algorithm⁵⁶. Source extraction was performed with the CAIMAN package⁵⁷ based on constrained non-negative matrix factorization. A set of scores were calculated for each extracted component. Regions of interest were selected by thresholding these scores or, in ambiguous cases, human inspection. The resulting traces had a frame rate of 7.5 Hz for M1 and 10 Hz for M2. See more details in our previous paper²⁴.

Large-scale electrophysiological recording

We made simultaneous neural recordings over multiple sites across the frontal cortex by implanting the semi-chronic microdrive recording system (Gray Matter Research, USA) in the left hemispheres of M3 and M4²⁵. A 157-channel microdrive (LS-157, tungsten electrodes, AlphaOmega, ~1 MΩ, 1.5 mm inter-electrode spacing) was used in the frontal cortex (Supplementary Fig. 3c). Two days after microdrive implantation, we began to advance the electrodes. All the electrodes were lowered into the surface of the cortices within one week in case dura hyperplasia would block the movement of the electrodes. During the recording sessions, the depths of the electrodes were adjusted appropriately to maximize the amount of the simultaneously recorded units.

We conducted electrophysiological signal recordings at a sampling rate of 40 kHz using a neural recording data acquisition system (OmniPlex, Plexon Inc). Before spike sorting, the raw electrophysiological data underwent high-pass filtering using the IronClust toolbox⁵⁸. The filtering was implemented with a passband range of 300 to 8000 Hz to capture relevant spiking signals while attenuating lower-frequency noise. Single and multi-units were combined for the data analysis, and units with mean firing rates less than 1.2 Hz were excluded.

Behavioral analysis

During the task, M1 and M2 received feedback regarding the accuracy of their responses when the reproduction period concluded. The chance level for each rank was equal to 1/6. The paradigm setting for M3 and M4 differed, as the trial instantly stopped whenever the monkey chose the wrong item. Therefore, for M3 and M4, it was challenging to identify the swap error. Furthermore, the items on each rank did not repeat within a sequence. Therefore, M3 and M4’s theoretical conditional chance levels are 1/6, 1/5, and 1/4 (for length-3 sequences). We first group trials by serial orders (ranks) and sequence lengths to evaluate monkeys’ item error. For each group, we calculated the probabilities of monkeys’ responses relative to targets (Fig. 1b). By calculating the proportion of correct responses to different ranks in different sequence lengths, we could evaluate monkeys’ item errors (Fig. 1c) and the circular variability of monkeys’ recall error distributions on each rank across all lengths (Fig. 1d). To analyze the rank errors of monkeys, considering the specific rank at which an item was presented, we studied how monkeys responded to this item across all locations (Fig. 1e).

Mixture model fitting

A probabilistic model of performance on this task has been proposed⁵ in which there are three possible sources of error on each trial: VonMises variability in memory for the target location, VonMises variability centred on the location of one of the non-target items and a fixed probability of simply guessing at random. This model can be described as follows:

$$P\left(\hat{\theta }\right)=\beta\phi \left(\hat{\theta }-\theta ;\sigma \right)+\frac{\gamma }{2\pi }+\left(1-\gamma -\beta \right){\sum }_{i}^{m}{w}_{i}\phi \left(\hat{\theta }-{\theta }_{i}^{*};\sigma \right)$$

(1)

$${w}_{i}=\frac{{e}^{-\left|r\left({\theta }_{i}^{*}\right)-r\left(\theta \right)\right|}}{{\sum }_{i}^{m}{e}^{-\left|r\left({\theta }_{i}^{*}\right)-r\left(\theta \right)\right|}}$$

(2)

where $\theta$ is the target location(in radians), $\hat{\theta }$ is the response location value, $\gamma$ is the probability of responding at random (guessing), $\phi$ denotes the VonMises distribution with mean of zero and standard deviation $\sigma$, $\beta$ is the probability of misremembering the target location, {${\theta }_{1}^{*}$, ${\theta }_{2}^{*}$,…, ${\theta }_{m}^{*}$} are the location values of the m non-target items and $r\left(\theta \right)$ is the temporal rank of target item, $r\left({\theta }_{i}^{*}\right)$ are the temporal rank of non-target item i. For a given condition in each session, the parameters $\sigma$, $\beta$, and $\gamma$ were trained simultaneously by maximum likelihood estimation with a non-linear optimization procedure⁵⁹, where the loss function for rank-r consisted of the negative log-likelihood of the observed recall errors, L2 penalty on $\sigma$ and L1 penalty on $\beta$, and $\gamma$:

$${{\rm{Loss}}}=-\log \left({{\rm{LLE}}}\right)+\rho \left(\sigma 2\right)+\kappa \left(\beta+\delta \gamma \right)$$

(3)

where $\rho$ and $\kappa$ are the overall factors for balancing the LLE loss and regularization term, $\delta$ is the scaling factor so that less constraints were imposed on $\gamma$.

Mutual information about locations derived from behavior

To determine the amount of information the animal had about a given stimulus, we calculated the information obtained about items in one sequence by observing the monkeys’ behavioral performance. This was quantified using the mutual information: I (item;behavior) = H(item) – H(item|response from behavior), where H(x) = ∑^N_lp(x_l) × log₂p(x_l) represents the uncertainty of the item’s location x_l = [1,2,3,4,5,6], H(item) was determined directly from the likelihood of the location appearing at each possible position in the display (i.e., assuming a flat distribution). For each sequence length $s$, the total mutual information is the summation of the mutual information of all items:

$$I\left(s\right)=\mathop{\sum }_{r=1}^{s}I\left({{{\rm{Item}}}}_{r}\right)$$

(4)

Linear regression

A multi-variable linear regression model was used to determine how various task variables affect the average neural response during the late delay period. The time windows were chosen based on each modality’s delay period and temporal resolution. For imaging (2.5-4 s delay), we used 1000 ms to capture significant activity. For ephys (1.15-1.50 s delay), we used 500 ms to preserve finer details. This approach balances capturing relevant data with maintaining accuracy for each modality. For the sequences of length-1, -2, and -3, we assumed sequence working memory was composed of the locations ([1, 2, 3, 4, 5, 6]) on different ranks across lengths (length-1: rank-1; length-2: rank-1 and -2; length-3: rank-1, -2, and -3), thus including 36 variables. So, any sequence could be represented by a 36-dimensional vector. For example, the sequence [1 2] can be represented by the vector: [0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]^T and the sequence [5 3 1] can be represented by the vector: [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 0 0]^T.

We thus defined these vectors ${{{\bf{X}}}}_{s,r,l}$ as task variables, where $s$ = 1,2,3, $r$ = 1,2,…,$s$ and $l$ = 1,2,…,6. In our model, the averaged neural response of the i^th neuron in one trial during the late delay period (1000 ms before the onset of the “go” signal for M1 and M2, 500 ms before the onset of the “go” signal for M3 and M4) was assumed to be a linear combination of the task variables, such that,

$${{{\bf{y}}}}_{i}={\sum }_{s=1}^{3}{\sum }_{r=1}^{s}{\sum }_{l=1}^{6}{\beta }_{i}\left(s,r,l\right){{{\bf{X}}}}_{s,r,l}+{{{\boldsymbol{\varepsilon }}}}_{i}$$

(5)

${\beta }_{i}\left(s,r,l\right)$ are unknown regression coefficients and ${{{\boldsymbol{\varepsilon }}}}_{i}$ is the trial-by-trial noise. To account for the impact of varying trial numbers across sequence lengths, a weighted approach was incorporated into the loss function of Lassoglm algorithm for regression analysis. Specifically, for each distinct length s, where n_s represents the number of trials in length s, individual trial weights w_s were calculated as follows: ${w}_{s}=\frac{1}{\left({n}_{s}+\bar{n}\right)}$. Here, $\bar{n}$ is the mean trial count of all lengths. The resulting w_s values were then normalized across all trials so that they summed to 1. The optimization aimed to minimize this weighted loss while determining the regression coefficients. For the i^th neuron, its neural responses with the same rank and length were centered to zero. A Lasso regularization term was added to the linear regression model to avoid overfitting, and the regularization amplitude with maximum likelihood was selected. We conducted this analyses using data from all correct trials. See the number of trials for each length in Table S1-2.

Analysis about length-4

In our analysis, we employed different methods across various parts of the study. For the projected geometry presented in Supplementary Fig. 10m, we faced a challenge due to the limited number of sequence-correct trials. To address this, we relaxed the condition to include rank-correct trials. For example, if the target sequence was [1342] and the monkey’s response was [1254], although the trial was incorrect, the correct response on rank 1 allowed us to include this trial in the analysis for length-4 rank-1. To assess whether the location representations of each rank in length-4 sequences exhibit discrimination, we constructed a 6-variable regressor using these trials to identify the corresponding subspace for each rank. We also projected rank-correct trials from length-4 sequences into the length-3 rank subspace, considering that the rank subspaces were derived from pseudo-population analysis. To project trials from each session onto the subspace, we set the neurons from other sessions to zero and performed orthonormalization on the resulting population vectors to obtain the new subspace. Subsequently, we pooled the projected trials from all sessions together and averaged them based on location labels.

We utilized the shape factor(SF) to quantify the degree of geometric distortion in the ring structures as the rank increased. The shape factor provides a numerical measure of how much the observed geometry deviates from a regular polygon, in this case, a hexagon. This metric was chosen because it allows us to objectively compare the geometric integrity of different configurations, particularly as rank increases and the structure potentially becomes more distorted. ${{\rm{SF}}}=\frac{{P}^{2}}{A}$, where $P$ represents the perimeter, A represents the area.

When comparing the ring size for length1-3 in Supplementary Fig. 10n, we assumed that sequence working memory involved locations ([1, 2, 3, 4, 5, 6]) across different ranks and lengths. For instance, length-1 involved rank-1; length-2 involved ranks 1 and 2; length-3 involved ranks 1, 2, and 3, and length-4 involved ranks 1, 2, 3, and 4. This assumption led to the inclusion of 60 variables in the analysis, the number of fully correct sequences was insufficient to support cross-validation. Therefore, we relaxed the condition to include trials where the first three ranks in length-4 were correct. To address the unequal distribution of trial numbers, we applied a weighted approach in the loss function of Lassoglm. When comparing the NSS and φ_diff across L3-R3 and L4-R3 as well as across L4-R3 and L4-R4 in Fig. 4l-m, we relaxed the condition to include trials where the rank-3 and rank-4 were correct in length-4.

Regression rank subspaces

The regression coefficients ${\beta }_{i}\left(s,r,l\right)$ were used to identify the low dimensional subspaces containing the most task-related variance. Specifically, with neurons in total collected from all FOVs for M1 and M2 (recording channels for M3 and M4), N-dimensional vector ${{\boldsymbol{\beta }}}\left(s,r,l\right)={\left[{\beta }_{1}\left(s,r,l\right),\ldots,{\beta }_{n}\left(s,r,l\right)\right]}^{{{\rm{T}}}}$ was used to represent length-rank–item combination $\left(s,r,l\right)$ at the neural population level. To capture the response variance due to item variation at each rank and each length in this neural state space, we divided 36-variable vector ${{\boldsymbol{\beta }}}\left(s,r,l\right)(s={\mathrm{1,2,3}},r=1,\ldots,s,l={\mathrm{1,2}},\ldots,6)$ into six groups along the length-rank index. For each group ${\{{{\boldsymbol{\beta }}}\left(s,r,l\right)\}}_{l=1,\ldots,6}$_, principal component analysis was performed to identify the first n (n = 1,2,3,4,5, main analysis for n = 2) axes that captured the most response variance (see Supplementary Fig. 5a, e, i, m for explained variance). In this way, we can further make the approximation:${{\boldsymbol{\beta }}}\left(s,r,l\right)\approx {{{\boldsymbol{V}}}}_{s,r}{{\boldsymbol{\kappa }}}\left(s,r,l\right),$ where ${{{\boldsymbol{V}}}}_{s,r}=\left[{{{\bf{v}}}}_{s,r}^{1}{{{\bf{v}}}}_{s,r}^{2}\right]$ (of size N×2, with ${{{\bf{v}}}}_{s,r}^{1}$ and ${{{\bf{v}}}}_{s,r}^{2}$ forming an orthonormal basis for length-rank subspace on length s as well as rank r. ${{\boldsymbol{\kappa }}}\left(s,r,l\right)$ (of dimension 2) is the projected value onto this length_s-rank_r (L_s-R_r for short) subspace under the orthonormal basis $\left\{{{{\bf{v}}}}_{s,r}^{1},{{{\bf{v}}}}_{s,r}^{2}\right\}$. In other words, we obtained the collective variable ${{\boldsymbol{\kappa }}}\left(s,r,l\right)$ by projecting the ${{\boldsymbol{\beta }}}\left(s,r,l\right)$ onto L_s-R_r subspace. We quantified Frobenius norm of ${{\boldsymbol{\kappa }}}\left(s,r,l\right)$ as ring size of projected geometry in L_s-R_r subspace.

Variance accounted for (VAF) ratio

To further quantify the alignment of different rank subspaces, we defined the variance-accounted-for (VAF) ratio⁶⁰. For any given spatial location $l$, the signal projected onto L_s-R_r subspace was denoted as ${{{\boldsymbol{g}}}}_{s,r}\left(l\right)={{{\boldsymbol{V}}}}_{s,r}{{\boldsymbol{\kappa }}}\left(s,r,l\right).$ The VAF ratio with respect to subspace a and subspace b was defined as $\frac{{{\rm{Var}}}\left({{{\boldsymbol{V}}}}_{b}{{{\boldsymbol{V}}}}_{b}^{T}{{{\boldsymbol{g}}}}_{a}\right)}{{{\rm{Var}}}\left({{{\boldsymbol{g}}}}_{a}\right)},$ Note that the VAF ratio depends on the order of a and b. The VAF ratio equals 0 if the two subspaces are orthogonal and equals 1 if they completely overlap.

Decoding analysis

To facilitate robust decoding analysis, we used linear decoders implemented in PyTorch. For each trial, to decode a rank-r item, we first projected the calcium activity (or spikes) ${{\rm{x}}}$ of N simultaneously recorded neurons into a low-dimensional space using a linear transformation: ${{{\rm{h}}}}_{r}={{{\boldsymbol{W}}}}_{{{\boldsymbol{r}}}}{{\rm{x}}}+{{{\rm{b}}}}_{r},$ where ${{{\boldsymbol{W}}}}_{{{\boldsymbol{r}}}}$ is an N_h×N matrix and ${{{\rm{b}}}}_{r}$ is an N_r-dimensional bias term. We then computed the dot product of h_r and N_s target vectors. In matrix terms, h_r was multiplied by an N_s×N_h target matrix ${{\boldsymbol{M}}}$, which was of size 6×2 in our case. The outcome was then softmaxed to obtain the scores, ${{{\rm{p}}}}_{r}={{{\rm{softmax}}}}({{\boldsymbol{M}}}{{\rm{h}}}_{r})$. For N_s possible results, the item with the largest score was selected as the decoded item. Note that the target matrix ${{\boldsymbol{M}}}$ was assumed to be rank invariant. That is, the activity patterns in decoding subspaces shared similar spatial layout across ranks. This assumption was based on the finding that activity in regression-based rank subspace can be well approximated by the same geometric structure, see more training details in the subsection “Decoder architecture” in our previous paper²⁴. Specifically, we investigated whether the neural representations of spatial working memory (SWM) items were consistent across different ranks and sequence lengths and balanced trials across lengths for a fair comparision. To assess the generalization performance of the decoders across ranks, each decoder was trained on trials from one rank and tested on other ranks in the same sequence length. Conversely, to evaluate the decoders’ performance across sequence lengths, each decoder was trained on trials from one length and tested on other lengths.

Mutual information about sequence locations derived from neural activity

We adapted previous work⁹ to evaluate how much information the animal had about a given sequence. Unlike the prior approach, which calculated mutual information based on behavioral responses, we also calculated mutual information based on recorded neural activity. Specifically, we trained a decoder to identify sequence of varying lengths and then calculated mutual information from the decoder’s performance. For each sequence length, we used a linear classifier (Support Vector Machine, SVM⁶¹) with fivefold cross-validation to decode sequence identity based on population neural activity in each session. To prevent classifier overfitting due to imbalanced sequence identities for lengths 2 and 3 in M1 and M2, we set a lower bound for each sequence. Once the trial count exceeded this threshold, we performed trial sub-sampling and pooled the processed trials of all sequences together for sequence decoding. By comparing the classifier’s predicted labels with the ground truth, we obtained the classifier’s response distribution in each session. If the observed neural activity contained no information about sequence encoding, the classifier’s performance would approach the chance level. Theoretical chance levels are 1/6 for sequences of length 1, 1/30 for sequences of length 2, and 1/120 for sequences of length 3. However, for M1 and M2, the specific chance level depends on the actual number of sequence types recorded during the session in which they participated: p_s(chance) = 1/ m_s, where m_s is the number of sequences type. The classifier’s use of neural activity to make predictions allows us to measure how much information the classifier’s performance provides about sequence encoding in neural activity: I(s;brain) = H(s) – H(s|prediction from brain) where $H\left(x\right)=-{\sum }_{i}^{N}p\left({x}_{i}\right)\times {\log }_{2}p\left({x}_{i}\right)$ represents the uncertainty of x. The uncertainty of the sequence, H(s), was determined directly from the likelihood of the sequence appearing at each possible sequence in the display (i.e., a flat distribution). We fitted I(s) with the power and linear models, respectively, and chose the Akaike information criterion (AIC) as the model evaluation criterion.

Projecting neural activity in subspaces onto neural axes

To characterize how single neuronal activity reflects cognitive resource in length-rank subspaces, given neuron i, rank r, and length s, we first projected the neural activity in L_s-R_r subspace onto neuron i’s single unit vector (denoted as e_i of size N×1). To quantify how a neuron contributes to this subspace, we defined the signal strength of tuning, the standard deviation of projected activities across spatial items ${A}_{s,r,i}$, such that

$${A}_{s,r,i}={{\rm{Std}}}\left({\left({{{\boldsymbol{e}}}}_{i}\right)}^{T}{{{\boldsymbol{V}}}}_{s,r}{{\boldsymbol{\kappa }}}\left(s,r,l\right)\right)$$

(6)

in which ${A}_{s,r,i}$ measured the standard deviation of the neuron’s tuning curve about spatial items, as illustrated in Fig. 3a.

Threshold of signal strength for spatial location selectivity

To determine if a neuron displayed significant selectivity for the spatial location at different ranks in different lengths, we introduced a quantity called NPR⁶² based on the distribution of square signal strength across the neural population as follows

$${{{\rm{NPR}}}}_{s,r}=\frac{{\left({\sum }_{i=1}^{N}{A}_{{sri}}\right)}^{2}}{N{\sum }_{i=1}^{N}{A}_{{sri}}^{2}}$$

(7)

Given that the ring size is highest in the length-1 rank-1 condition, we calculated NPR_1,1 to measure the percentage of neurons that contribute to the length-1 rank-1 subspace. This value was then used as the threshold to assess selectivity across all length-rank combinations.

NSS and φ _diff for across rank subspace

With the signal strength, we calculated the neuron-to-subspace strength (NSS) index to characterize how a neuron contributes to every pair of subspaces, given neuron i, rank subspaces a and b (a < b):

$${{\rm{NSS}}}=\frac{{A}_{s,a}-{A}_{s,b}}{{A}_{s,a}+{A}_{s,b}}$$

(8)

When the NSS index is close to −1, it means the neuron mainly contributes to subspace b. If the NSS index is close to 1, the neuron mainly contributes to subspace a, if the NSS index is close to 0, the neuron equally contributes to two subspaces. When the absolute value of the NSS index is larger than a certain threshold (which is 0.4 here), the related neuron is defined as a disjoint neuron (Fig. 3b). Otherwise, it is defined as an overlapping neuron (Fig. 3b).

Each overlapping neuron’s spatial item preference could also be an important feature. If most neurons’ spatial preferences are similar between subspaces a and b, then the neural representation could generalize between these two subspaces. Suppose most neurons’ spatial preferences are uncorrelated. In that case, the neural representation is hard to generalize from one subspace to another (see more details in the subsection “Simulation describing how signal strength and preferred tuning affect the generalization across subspaces” below).

Therefore, we introduce ${\varphi }_{{sri}}$ to specify neuron i’s spatial item preference in L_s-R_r subspace,if we project unit vector e_i of the axis of neuron i onto length-s rank-r subspace (${{{\boldsymbol{V}}}}_{s,r}=\left[{{{\bf{v}}}}_{s,r}^{1}{{{\bf{v}}}}_{s,r}^{2}\right]$), the alignment between ${{{\boldsymbol{e}}}}_{i}$ and ${{{\boldsymbol{V}}}}_{s,r}$ can be measured as the scalar projection ${||}{({{\boldsymbol{e}}}_{i})}^{{\bf{T}}}{{{\boldsymbol{V}}}}_{s,r}{||}$, such that

$${\varphi }_{{sri}}=\frac{{arcos}\left({\left({{{\boldsymbol{e}}}}_{i}\right)}^{T}{{{\bf{v}}}}_{s,r}^{1}\right)}{\left|\left|{\left({{{\boldsymbol{e}}}}_{i}\right)}^{T}{{{\boldsymbol{V}}}}_{s,r}\right|\right|}$$

(9)

The phase shift φ_diff is defined as the absolute of distance between ${\varphi }_{{sai}}$ and ${\varphi }_{{sbi}}$, we normalized φ_diff to the range [0,180],${\varphi }_{{\mbox{diff}}}={\varphi }_{{\mbox{diff}}}*\left({\varphi }_{{\mbox{diff}}}\le 180\right)+\left(360-{\varphi }_{{\mbox{diff}}}\right)*\left({\varphi }_{{\mbox{diff}}} > 180\right)$. Then, we compared φ_diff distributions of overlapping neurons between each length-rank subspace pair and used the distributions to measure how spatial preferences are allocated. If φ_diff is smaller than 30° (suggesting the same preferred location in our hexagon items), then the neuron is defined as a shared tuning neuron (Fig. 3d). Otherwise, it is defined as a shifted tuning neuron (Fig. 3d).

Measure how much shift of the preferred location of overlapping neurons between two subspaces

We calculated the Kolmogorov-Smirnov statistic (D) to compare the φ_diff distribution across two rank subspaces with a uniform distribution. The K-S statistic is defined as:

$${{\rm{D}}}={\max }_{x}\left(\left|{\hat{G}}_{1}\left(x\right)-{\hat{G}}_{2}\left(x\right)\right|\right)$$

(10)

where x represents the phase shift φ_diff. ${\hat{G}}_{1}$ is the empirical cumulative distribution function (ECDF) of the φ_diff. ${\hat{G}}_{2}$ is the cumulative distribution function (CDF) of uniform distribution. The K-S statistic quantifies the degree of preferred location shift for overlapping neurons across two rank subspaces. A high ${{\rm{D}}}$ value indicates a stable preferred location across two ranks whereas a lower ${{\rm{D}}}$ value suggests that the preferred location shifts are highly random and flexible.

Determine the most suitable probability distribution for the empirical data

To determine the most suitable probability distribution for the signal strengths of recorded neurons, we employed a model comparison approach. The candidate distributions considered for comparison are gamma, lognormal, exponential, and Weibull distributions. For each candidate distribution, the maximum log-likelihood estimation is computed using the empirical data. The log-likelihood function for each distribution is given by: ${{\mathscr{L}}}\left(A|X\right)={\sum }_{i=1}^{n}\log \left({f}_{A}\left({x}_{i}\right)\right)$, where ${f}_{A}\left({x}_{i}\right)$ represents the probability density function (PDF) of distribution A evaluated at neuron's signal strength x_i. The candidate distribution with the highest maximum log-likelihood score is selected as the optimal model for the dataset. The selected distribution best fits the empirical data based on the likelihood criterion. After selecting the most suitable probability function for signal strength in all monkeys (lognormal distribution for M1, Weibull distribution for M2 and M4, gamma distribution for M3), we need to further determine the parameters of these two distributions. To estimate the parameters that best fit a given dataset, we employed the method of maximum likelihood estimation (MLE). The gamma, Weibull, and lognormal distributions are all characterized by two parameters: shape (α) and scale (β). Assuming that a dataset follows one of these distributions, the objective is to then determine the values of α and β that maximize the likelihood of observing the given data. We implemented the fitting process in MATLAB, using signal strength in specific length and rank as an input; we utilized the built-in functions wblfit, gamfit, and lognfit to perform the optimization procedure and find the optimal values of α and β.

Simulation describing how signal strength and preferred tuning affect the generalization across subspaces

To investigate the effect of signal strength and preferred tuning on generalization across subspaces (i.e., subspace a and subspace b), we simulated the inclusion of N neurons (1000), where the signal strength (A_i, i = 1,2,…,N) concerning subspace a follows a Weibull distribution (Supplementary Fig. 6) [or gamma distribution, gamma (α, β), lognormal distribution, logn (α, β), Table S3]. Although the parameters (α and β) of the Weibull distribution varied in different rank subspaces, for simplification, we assumed that neuron signal strengths in both rank a and rank b follow Weibull (lognormal, gamma) distributions with identical parameters, which were the average of fitted parameters in different rank subspaces.

Furthermore, based on empirical data indicating that the preferred tuning of neurons across all rank subspaces follows a uniform distribution, we simulated the preferred tuning (φ_i, i = 1,2,…,N) of neurons, following uniform distributions U(-π, π) in rank a and rank b. We also included T(500) trials of length 2, in which the stimulus locations in each rank follow discrete uniform distribution U(-π: π/3: π). For each neuron i, based on A_i and φ_i, we can calculate its activity in these trials with a noise that obeys normal distribution with standard deviation equals 0.01. Subsequently, we used a linear classifier (SVM⁶¹) with fivefold cross-validation to decode items(locations) across rank based on population neural activity in each session. Specifically, we conducted cross-rank decoding by controlling two independent variables, cr_x and cr_y. Here, cr_x denotes the correlation index between Weibull (gamma, lognormal) distribution F(α,β;a) and F(α,β;b), while cr_y represents the correlation between uniform distribution U(-π, π;a) and uniform distribution U(-π, π;b). The ranges for cr_x and cr_y are both from −1 to 1, with the dependent variable being the decoding accuracy across subspaces a and b. Finally, we can get a heatmap to visualize the changes in decoding accuracy (Fig. 3j and Supplementary Fig. 7). Based on the simulation, the achievement of orthogonality only requires meeting a high bimodal index in NSS indices (disjoint neurons) or a low K-S statistics in φ_diff (random shifting of preferred tuning), our data is just one solution out of an enormous set of solutions that could all result in orthogonality. Conversely, the achievement of generalization requires meeting the conditions of both a low disjoint index in NSS indices and a high K-S statistics in φ_diff (stable preservation of preferred tuning).

The tradeoff between generalization and orthogonality

As shown in Fig. 3j, both NSS and φ_diff influence generalization and orthogonality between subspaces. Specifically, the closer NSS and φ_diff are to 0, the higher the generalization; conversely, the closer NSS is to 1 and φ_diff to 180, the greater the orthogonality. To investigate the relationship between generalization and orthogonality across different lengths, we decomposed these factors into two dimensions: |NSS| and φ_diff. For NSS, generalization corresponds to 1-|NSS| , and orthogonality corresponds to |NSS|. For φ_diff, generalization corresponds to 180-φ_diff, and orthogonality corresponds to φ_diff. We then used Spearman correlation to assess whether there is a trade-off between generalization and orthogonality based on these dimensions. Early items included the pairs L1-R1 v.s. L2-R1 (across lengths) and L2-R1 v.s. L2-R2 (across rank). Late items included the pairs L2-R2 v.s. L3-R2 (across lengths) and L3-R2 v.s. L3-R3 (across rank). Saturated items included the pairs L3-R3 v.s. L4-R3 (across lengths) and L4-R3 v.s. L4-R4 (across rank).

In Fig. 4b, the calculation of the proportion of disjoint neurons and recycled neurons differs slightly. For L3-R1, the disjoint neurons include those that are free from earlier items (L1-R1 and L2-R1). Specifically, we calculated the NSS between each earlier item and L3-R1, with neurons being selected as disjoint only if they met the criterion of NSS_{earlier items-current item} < −0.4 for all earlier items (i.e., neurons selective only to L3-R1). For L3-R2, the disjoint neurons are those that are free from earlier items (L1-R1, L2-R1, L2-R2, and L3-R1). Similarly, for L3-R3, the disjoint neurons include those free from earlier items (L1-R1, L2-R1, L2-R2, L3-R1, and L3-R2). Each rank corresponds to multiple earlier items, and as the rank increases, the number of earlier items also increases. Consequently, the proportion of disjoint neurons decreases with higher ranks.

Characterizing the functional map

To examine the anatomical organization of WM resources at different spatial scales to support generalization and orthogonality, we calculated the Pearson correlation coefficient of shared resources (overlapping neurons) across subspace pairs. The shared resources included signal strength and preferred stimulus location. We independently calculated the correlation ρ_a,b of these two factors across various subspaces a and b within individual fields of view (FOVs) in M1 and M2, and across recording sites in M3 and M4.

To examine whether the disjoint neurons were dynamically and spatially recruited (specifically, whether there are lateral-medial and anterior-posterior gradients of disjoint neurons in length-3), we first converted the electrode coordinates along the lateral-medial and anterior-posterior axes. Next, we identified disjoint neurons at rank-1, −2 and −3 in length-3. The recording coordinates of these disjoint neurons were then weighted by their normalized signal strengths and smoothed by a kernel function, which can be defined as normal function $f\left(x,{x}_{i}{;h}\right)$.

$$f\left(x,{x}_{i}{;h}\right)=\frac{1}{\sqrt{2\pi}h}{e}^{-\frac{{\left(x-{x}_{i}\right)}^{2}}{2h^{2}}}$$

(11)

For any real values of $x$, the kernel estimator for the pdf is given by

$$\hat{F}\left(x\right)=\frac{1}{{n}}{\sum }_{i=1}^{n}{w}_{i}f\left(x,{x}_{i};h\right)$$

(12)

where ${x}_{i}$ are the spatial coordinates along the lateral-medial axis and anterior-posterior axis for M3 and M4 (x axis and y axis of the FOV for M1 and M2) of disjoint neurons, ${w}_{i}$ are their normalized signal strengths, $n$ is the neuron number, $h$ is the bandwidth. We tested a range of bandwidths to ensure the robustness of our findings. Specifically, we varied $h$ across several values, including 1 mm, 2 mm and 2.5 mm (Table S4). To validate our findings, we performed a control analysis by randomly shuffling the locations of all disjoint neurons 1,000 times. We then calculated the distribution of signal-weighted electrode locations using this shuffled data for comparison. This consistency indicates that our findings are not sensitive to the choice of bandwidth, reinforcing the robustness of the analysis.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.