Introduction

The Mesoproterozoic has traditionally been considered a period of persistently low atmospheric O2 concentrations, estimated at <0.1% to 1% of present atmospheric levels (PAL)1,2,3 (Fig. 1a). Deep oceans were thought to be ferruginous, with oxygenated waters confined to shallow marine settings and euxinic conditions limited to mid-depths along productive continental margins4,5,6,7,8,9,10 (Fig. 1b). However, recent studies have begun to challenge this paradigm, suggesting either that atmospheric O2 levels may have experienced episodic increases or that baseline O2 levels were substantially higher - ranging from 2% and 24% PAL - throughout the Mesoproterozoic11,12,13 (Fig. 1a). Despite these emerging perspectives, the spatial and temporal dynamics of oceanic oxygenation during this interval remain poorly understood. Although local redox proxies have revealed occasional deepening of the redoxcline within Mesoproterozoic basins14, such episodes may reflect localized O2 production by oxygenic photoautotrophs15 rather than global shifts in redox state, especially given pronounced ocean redox heterogeneity and atmospheric-oceanic O2 disequilibrium inferred for this time16. Assessing the extent and timing of global ocean oxygenation beyond the confines of individual basins thus requires a more integrated approach.

Fig. 1: Co-evolution of the Earth system during the Precambrian Eon.
figure 1

a Evolution of atmospheric O2 levels relative to present atmospheric levels (PAL). Historically, the Mesoproterozoic (ca. 1.6–1.0 Ga, green shading) is characterized by low atmospheric O2 levels but exceeding that of the Archean1. However, several intervals of substantially elevated atmospheric O2 have been proposed11,12. Further, a machine learning model based on mafic igneous geochemical data13 (red full line) suggests that there was an oxygenation event around 1.4 Ga. b Evolution of the hydrosphere, showing partial oxygenation of the surface ocean persisted throughout the Mesoproterozoic, while deeper waters remained dominantly anoxic6. c Evolution of the geosphere, including the breakup of the supercontinents (Nuna and Rodinia)17 and the numbers of continental large igneous provinces (LIPs)18. Of note, increased LIP formation occurs at approximately 1.4 Ga. d Secular variations in global seawater δ98Mo reconstructed from euxinic shale and ancient Mn- and Fe-rich sedimentary rocks28,35,36 (including data compiled from the literature by the cited studies). Among them, the large black rectangles represent temporally binned means (± 1 standard deviation, 1 SD). Orange and blue dashed lines represent the average seawater δ98Mo during the Mesoproterozoic7 (1.2‰) and modern81 (2.3‰), respectively. Due to the lack of a δ98Moseawater database for the Mesoproterozoic, it is not possible to compile a complete curve at this time. e Distribution of Precambrian sedimentary manganese and iron ore deposits, compiled by relative reserves, in the context of atmospheric oxygenation82. The Mesoproterozoic witnessed multiple episodes of sedimentary Mn precipitation (~1.45 Ga and ~1.1 Ga) in North China and Western Australia37,38, respectively. GOE Great Oxidation Event; NOE Neoproterozoic Oxidation Event.

Full size image

The interval around ~1.40 Ga is particularly significant because it coincides with the breakup of the supercontinent Nuna (1.45–1.38 Ga)17 and with a surge in large igneous province (LIP) activity on the continents18 (Fig. 1c). Large igneous province activity peaked at ~1.38 Ga, with a smaller, earlier pulse around ~1.42 Ga. These events likely had significant impacts on ocean-atmosphere chemistry, continental weathering rates, nutrient delivery, and ocean redox conditions. Evidence for a transient shift towards more oxygenated deep-ocean conditions between 1.40 and 1.35 Ga has been inferred from greater enrichments of redox-sensitive elements, such as Mo, rhenium (Re), and uranium (U), and their isotopic compositions in black shales such as the Velkerri Formation in North Australia and the Xiamaling Formation in North China19,20,21,22,23. Consistent with previous studies, elevated iodine (I) concentrations and negative cerium (Ce) anomalies in shallow-water carbonates from the 1.45 Ga Tieling Formation24,25,26 – directly underlying the Xiamaling Formation - suggest the potential for a protracted period of elevated O2 levels in the shallow ocean, at least regionally, around 1.4 Ga. Such a prolonged episode of oxygenation is particularly noteworthy, as it marks a major redox perturbation within the otherwise persistently ferruginous conditions that characterized the Mesoproterozoic oceans14. However, the extent of global seafloor oxygenation during this time remains poorly constrained, largely due to the subduction and loss of most ancient deep seafloor records, as well as the inherent limitations of many geochemical proxies in reliably reconstructing global redox conditions.

Molybdenum is a redox-sensitive element, and variations in its isotopic composition (i.e., the ratio δ98/95Mo, expressed as δ98Mo) in sedimentary rocks have been extensively utilized to track fluctuations in water column redox state27,28,29 (Fig. 1d). In modern oceans, the residence time of Mo is approximately 440 kyr30, significantly surpassing the mean global ocean mixing time of 1–2 kyr. Although the Mo reservoir in the widely anoxic Proterozoic oceans would have been significantly smaller, it was still likely well-mixed globally5. Based on well-constrained Mo isotope fractionation and fluxes associated with modern Mo sources and sinks, Mo isotopes are considered a robust proxy for inferring ancient global marine redox conditions27,31,32. The global oceanic δ98Mo value of seawater is primarily governed by the relative burial of Mo under different redox conditions. Strongly euxinic black shales are particularly valuable for capturing this signal, as Mo is removed nearly quantitatively under high aqueous sulfide concentrations ([H2S]aq > 11 μM)33, resulting in minimal isotopic fractionation. In contrast, sediments deposited under all other redox regimes typically exhibit δ98Mo values lower than those of contemporaneous seawater. However, the scarcity of confirmed strongly euxinic shale deposits from the Mesoproterozoic Era has led to significant temporal gaps in the δ98Mo record, limiting our ability to trace global redox evolution during this interval. To address this, we turn to Mn(III/IV) and Fe(III) oxides—hereafter referred to as Mn-oxides and Fe-oxides—which are capable of adsorbing seawater Mo with distinct isotopic fractionations and adsorption efficiencies34,35,36. These metal-rich chemical sediments thus offer a promising alternative archive for reconstructing early Mesoproterozoic seawater δ98Mo and the global extent of ocean oxygenation (Fig. 1d).

In this study, we present Mo isotopic data from two correlative profiles in the northeast of the Yanliao Basin in the North China Craton (NCC), both part of the Tieling Formation at approximately 1.45 Ga. These include (Mn, Fe)-rich sedimentary rocks (economical ore deposit)37,38 (Fig. 1e) and a suite of regionally stratigraphically equivalent siliciclastic rocks interlayered with dolostone, representing deeper subtidal depositional environments. To elucidate redox conditions in the basin water column, we integrate multiple geochemical proxies: redox-sensitive trace element (RSTE) concentrations, total organic carbon (TOC) contents, Fe speciation data, Fe and Mo isotopes in the siliciclastic rocks, and iodine-to-calcium plus magnesium ratios I/(Ca+Mg) in the dolostones. The δ98Mo values from the (Mn, Fe)-rich sedimentary rocks are then incorporated into a Mo isotope mass balance model to quantitatively estimate the extent of global seafloor oxygenation at the time of deposition. Finally, we re-evaluate the duration and spatial extent of global ocean oxygenation during the 1.45–1.35 Ga interval.

Results and Discussion

Geological setting and samples

The 1.45 Ga Tieling Formation39, located along the northeastern margin of the Yanliao Basin in the NCC (Fig. S1a–d), is believed to have been deposited in a marine environment connected to the open ocean to the north40. This interval coincides with the breakup of Nuna, during which the NCC was positioned at low latitudes (~15°N)17. The Tieling Formation is commonly divided into two members. The lower Daizhuangzi (DZZ) Member comprises manganiferous dolostones and shales deposited in an intertidal to deep subtidal environment (approximately 0 to 100 m water depth, respectively). The upper Laohuding (LHD) Member consists of limestones and dolostones deposited in intertidal to shallow subtidal settings (approximately 0 to 20 m water depth)41 (Fig. S1e).

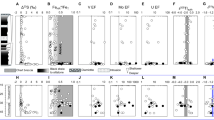
Two stratigraphic profiles in our study area (41.019°N, 120.143°E) span the DZZ Member, and they consist of approximately 90 m of siliciclastic sedimentary rocks interlayered with dolostones (Fig. 2a, and Mn Fe-rich chemical sediments (Fig. 2b). The succession can be sub-divided into four distinct units, listed from base to top: (i) Unit 1, laminated shale; (ii) Unit 2, dolostone; (iii) Unit 3, mostly manganiferous shale, laterally equivalent to coeval (Mn, Fe)-rich sedimentary rocks observed in a stratigraphically equivalent section located 2 km away; and (iv) Unit 4, red mudstone (Fig. 2a, S2). These four units collectively represent deposition in deeper water environments compared to the carbonate-dominated western region of the Yanliao Basin (see detailed description in Supplementary Information). The (Mn, Fe)-rich sedimentary rocks primarily consist of authigenic (Mn, Fe)-oxides, specifically manganite (MnOOH) and hematite (Fe2O3), and diagenetic Ca-rhodochrosite [(Mn, Fe)(Ca)CO3]38 (Figs. 2b, S3). In this study, we collected samples from all four stratigraphic units as well as the (Mn, Fe)-rich sedimentary rocks. Sample details are provided in Supplementary Information.

Fig. 2: Geochemical and isotopic profiles.
figure 2

a Dashed lines on FeHR/FeT profiles represent calibrated thresholds indicative of oxic (<0.22) and anoxic (>0.38) water column conditions9. Black circles in the FeHR/FeT profiles represent an extra supply of hydrothermal iron that affects interpretation of Fe speciation data (see text for detailed explanation). The dashed lines on the Fepy/FeHR profiles represent the lower (0.6) and upper (0.8) thresholds for euxinia9. Dashed lines on I/(Ca + Mg) profiles represent the baseline (~0.5) for Precambrian carbonates24. Shading indicates the approximate position of cycles from ferruginous (white) to oxic (gray) to suboxic (transition color) conditions. b Coeval with Unit 3 Mn-rich shale, other Mn-rich sedimentary rocks can be subdivided into two ore belts of primary Mn-oxide and diagenetic Mn-carbonates, respectively38. Dashed lines on elemental ratio profiles represent the average upper continental crust (UCC)50. The high Mo/Al contents and high Mn-Fe contents exclude the influence of detrital Mo. Oxygenated conditions during deposition of these Mn-rich rocks are verified by uniformly negative δ98Mo and δ56Fe values and a decrease in redox-sensitive trace-element (RSTE) enrichment factors. The error bars for δ98Mo and δ56Fe are smaller than symbol sizes. TOC Total Organic Carbon Content.

Full size image

Basinal redox assessment

Siliciclastic samples from Unit 1 are characterized by elevated FeHR/FeT (>0.38), low Fepy/FeHR ratios (~0), high RSTE (Mo, V, U) concentrations, and high enrichment factors for these elements (RSTEEF; EF = enrichment factors: XEF = (X/Al)sample/(X/Al)PAAS, where X and Al are element-X (ppm) and Al (wt.%) content, respectively, and PAAS = Post-Archean Australian Shale) (Fig. 2a and Supplementary Data 1). Collectively, these data suggest deposition under anoxic and ferruginous bottom water conditions during Unit 1. This interpretation of redox conditions is further supported by iron speciation and isotope data. Units 1, 3 and 4 all exhibit FeOX/FeHR ratios >0.8 (Fig. S4a), indicating that FeHR is primarily associated with Fe-oxides. The δ56Fe values of authigenic Fe-oxides in sediments reflect the extent of Fe(II) oxidation during deposition42,43. In well-oxygenated waters, oxidation of seawater Fe(II) is quantitative, and iron-oxides inherit the δ56Fe values of the Fe(II) source44. In contrast, under suboxic to anoxic conditions, partial Fe(II) oxidation results in isotopic fractionation, enriching Fe-oxides in 56Fe by up to +3‰44,45. Given that seawater has a relatively homogeneous Fe isotope composition of close to 0‰44, the positive δ56FeHR values in Unit 1 samples of between +0.46‰ and +0.78‰ (Fig. 2a; see Methods for details) are best explained by partial oxidation of a deep Fe(II) reservoir under suboxic-anoxic shallow waters at the studied localities. Subsequently, an increase in I/(Ca+Mg) ratios - from ~0 μmol/mol to a peak of ~1.30 μmol/mol in the Unit 2 dolostone - may signal a shift towards more oxygenated bottom waters immediately preceding the deposition of Unit 3 (Fig. 2a; see Supplementary Information for details).

In contrast to Unit 1, siliciclastic samples from Units 3 and 4 have high total Fe and/or Mn concentrations (Fig. 2a). These units also display positive Eu anomalies (Eu/Eu* = 1.1–1.4; Eu/Eu* = EuPAAS/(0.67 × SmPAAS + 0.33 × TbPAAS) (Fig. 2a), consistent with a hydrothermal influence. The metallogenic characteristics of Unit 3, in particular, suggest hydrothermal vent activity in deeper waters, which likely delivered abundant dissolved Fe(II) and Mn(II) below the redox chemocline, resulting in localized metal enrichment38. Under such conditions, extensive Fe precipitation at the redox chemocline may obscure Fe speciation signals, complicating reconstructions of bottom-water redox conditions for Units 3 and 4. Compared to Unit 1, the low RSTEEF and TOC contents in Unit 3 likely indicate the persistence of oxic bottom-water conditions established during the deposition of Unit 2, rather than a return to ferruginous conditions. The input of hydrothermal Fe(II) would also shift the Fe isotopic composition of the local water column towards the hydrothermal endmember (−0.5‰ to 0‰)44. Consistent with this, most of the Unit 3 samples show δ56FeHR values (−0.49‰ to −0.38‰; Fig. 2a) that are similar to those of hydrothermal fluids, supporting the interpretation of quantitative oxidation of hydrothermally derived Fe(II) under oxic conditions - similar to what is observed in contemporaneous Mn-Fe-rich chemical sediments (−0.45‰ to −0.30‰; Fig. 2b). Notably, several Unit 3 samples show even more negative δ56FeHR values (−0.71‰, −0.78‰ and −0.99‰; Fig. 2a), indicating an additional source of isotopically light Fe(II), most likely derived from dissimilatory Fe(III) reduction (DIR) of continentally-sourced minerals, which typically yield δ56Fe values between −2.5‰ and −0.5‰)44.

Further evidence for oxic water-column conditions during the deposition of Unit 3 comes from a pronounced negative δ98Mo excursion, dropping from values as high as +0.80‰ in Unit 1 to as low as −0.43‰ in Unit 3. This isotopic shift, coupled with variable Mn and Fe concentrations (Fig. 2a), is consistent with the preferential adsorption of lighter Mo isotopes onto Mn-oxides and Fe-oxides34. Among these, Mn-oxides have a particularly strong affinity for light Mo isotopes and induce greater isotopic fractionation than Fe-oxides, such as ferrihydrite35,46,47,48. Accordingly, the strong negative correlation observed between Mn/Fe ratios and δ98Mo values across Units 1 to 3 provides compelling evidence for Mn-oxide precipitation and burial during Unit 3 deposition (Fig. S4b). This implies significant water-column oxygenation and the downward penetration of O2 below the sediment-water interface49.

Unit 4 samples show a slight increase in δ56FeHR (−0.13‰ to +0.05‰) and are characterized by RSTEEF and TOC contents similar to those of Unit 3, but with lower Mn/Fe ratios and higher δ98Mo values (Fig. 2a). These geochemical trends suggest that Unit 4 was deposited under somewhat less oxygenated, possibly suboxic, bottom-water conditions. When considered alongside the evidence for shallow water oxygenation from the carbonate-dominated western regions24,25,26, our findings suggest a deepening of the redoxcline and an expansion of water column oxygenation in the basin during deposition of the 1.45 Ga Tieling Formation. This peak in oxygenation appears to be particularly pronounced during the Mn-rich depositional intervals of Unit 3. To assess whether this oxygenation event reflects a more widespread phenomenon rather than a localized feature of a single continental margin, we further utilize Mo isotope data to evaluate the extent and intensity of deep-water oxygenation at a global scale during this time.

Global seawater Mo isotope composition at ~ 1.45 Ga

Ferruginous shales from our siliciclastic section cannot reliably constrain the global seawater Mo isotope signature due to multiple isotope fractionation processes arising from Mo removal from seawater via adsorption onto oxides, organic matter, and sulfides27. In contrast, (Mn,Fe)-rich chemical sedimentary rocks offer a more robust archive for reconstructing ancient seawater δ98Mo. Their formation under oxygenated bottom-water conditions supports the preservation of primary Mn- and Fe-oxides, as previously demonstrated by Yan et al. 38. Nonetheless, this inference depends on a well-constrained understanding of both the magnitude of isotope fractionation and the adsorption efficiencies associated with Mo uptake onto Mn- and Fe-oxide precursors36.

The (Mn,Fe)-rich chemical sedimentary rocks in our study exhibit high Mo/Al ratios (1.2 to 9.0 ppm/wt.%), significantly exceeding the upper continental crust (UCC) average of 0.1850, along with high Mn (20–42 wt.%) and Fe (up to 14 wt.%) concentrations (Fig. 2b). These characteristics indicate that Mo enrichment was mainly derived from the adsorption onto Mn- and Fe-oxides, rather than from detrital input. Generally, (Mn,Fe)-rich chemical sedimentary rocks with either high (>101) or low (<10−1) Mn/Fe ratios display relatively uniform δ98Mo values, primarily influenced by isotopic fractionation during the adsorption of Mo onto Mn- and Fe-oxides, respectively35. In contrast, rocks with intermediate Mn/Fe ratios (10−1 to 101) have δ98Mo values that reflect the relative contributions of Mn- and Fe-oxides, displaying an inverse linear correlation between δ98Mo values and Mn/Fe ratios35. The evolutionary trend between Mn/Fe ratios (15.88 to 1.68) and δ98Mo values (−1.25‰ to −0.35‰) observed in our (Mn, Fe)-rich sedimentary rocks is consistent with this model (Fig. S4c). However, the δ98Mo values of (Mn, Fe)-carbonate rocks deviate from this trend despite sharing similar Mn/Fe ratios with oxide-rich samples (purple rectangle in Fig. S5). This deviation suggests that certain Mn-Fe-rich sedimentary rocks—particularly those with elevated TOC (Fig. 2b) or those significantly altered during diagenesis—are unsuitable for reconstructing seawater δ98Mo.

The reduction of primary Mn- and Fe-oxides during diagenesis can remobilize previously adsorbed Mo, leading to its release into pore waters and subsequent incorporation into diagenetic carbonates38. Non-quantitative Mo scavenging from pore fluids and potential exchange with the overlying water column can result in complex and variable Mo isotope fractionation during carbonate formation51. Organic matter also plays a role: Mo adsorption onto organic carbon occurs via a distinct fractionation pathway from that of Mn- and Fe-oxides, introducing additional complexity36. As a result, TOC-rich (Mn, Fe) carbonates provide unreliable archives for reconstructing the global seawater Mo isotopic composition.

Given these considerations, we restrict our reconstruction of seawater δ98Mo to samples composed of primary Mn- and Fe-oxides (e.g., manganite and hematite) that exhibit low TOC contents and minimal evidence of diagenetic alteration38. Using these well-preserved samples, we calculate Mo isotope fractionation between seawater and oxide phases to estimate contemporaneous global seawater δ98Mo values. The results yield a mean value of +1.72 ± 0.13‰ (1 standard deviation, 1 SD) defined as the seawater δ98Mo signal, with higher seawater values possible if there was any multi-stage Mo isotope fractionation associated with Mn-cycling (see Supplementary Information for details). Our findings, when coupled with previous studies on the Xiamaling Formation in North China - where shales δ98Mo values reach up to +1.70‰ at ~1.37 Ga20,21 - indicate that global seawater δ98Mo around 1.4 Ga was elevated relative to the long-term Mesoproterozoic baseline of +1.20‰7,28,52,53,54 (see Supplementary Information for details).

Estimate of global ocean oxygenation at ~1.45 Ga

Our study utilizes steady-state isotopic mass-balance modeling (see Supplementary Information and Figs. S6, S7 for details) to interpret the high seawater δ98Mo values of at least 1.72‰ at ~1.45 Ga. The models suggest that approximately 80% of the global seafloor area was oxygenated at this time (Fig. 3a). This estimate is comparable to previous reconstructions of widespread oxygenation during the ~1.56 and ~1.36 Ga episodes, as recorded by high seawater δ98Mo value of 2.03‰ in the Gaoyuzhuang Formation, North China29, and by U isotopic and Re mass balance models for the Velkerri Formation, Northern Australia19,23. Notably, our estimate of 80% oxygenated seafloor surpasses previous estimates of <50% oxygenation for mid-Proterozoic seafloor based on Cr and U concentrations in shales5,55.

Fig. 3: Steady-state isotopic mass-balance model and summary of atmosphere and global ocean redox chemistry during the Mesoproterozoic.
figure 3

a Modeling used a seawater δ98Mo value of 1.72‰ from the mean calculated value derived from Mn- and Fe-oxide data in our study (red full line). The mean value ± 1 standard deviation (SD) are provided to account for the results of a sensitivity analysis (blue dotted line). The green full line represents the simulation result using the background value of the Mesoproterozoic seawater Mo isotope (1.2‰). A Mo isotope fractionation of −0.65‰28 was used for the intermediate Mo sink in the isotopic mass-balance model (see Supplementary Information for detailed explanation). Our model yields a higher global-ocean oxygenated area than the background Mesoproterozoic interval (purple, areas of high color intensity denote the core density of the data distribution) as modified from5,55,83, but is comparable to previous assessments of Mesoproterozoic oxygenation episodes at 1.56 and 1.36 Ga (tan interval)19,23,29. The right gray area represents states where the euxinic sinks are dominant, so that the dissolved Mo isotope ratio in the oceans becomes heterogenous. The shaded area in the top right corner represents an unrealistic areal proportion of euxinic and strongly oxic conditions over 100%. A-SO: global oxic seafloor area; A-SE: global euxinic seafloor area. b In the δ98Moseawater compilation panel, the large pink rectangle represents binned means (± 1 SD). The back-calculated δ98Mo values by Mn oxide samples are shown as black hollow circles. Compared with a series of Mesoproterozoic oxygenation episodes, our study reveals a prolonged global oxygenation event at ~1.45–1.35 Ga (blue and gray shadings). Data sources: Cr isotopes from58,84,85; Mo isotopes from this study and7,52; Mn-Fe chemical sediments distribution from37,38,62,63.

Full size image

In the anoxic deep oceans of the Mesoproterozoic Era, the dissolved seawater Mn(II) reservoir may have been at least one order of magnitude greater than today56. Around ~1.45 Ga, this reservoir was probably further augmented by substantial hydrothermal Mn(II) inputs, as evidenced by the widespread deposition of economic Mn ore deposits across multiple basins at that time37,38. The formation and burial of Mn-oxides typically requires at least tens of µM of dissolved O2 concentrations in bottom waters, along with sufficient O2 penetration into sediments49,57. Since Mn-oxides are a major sink for Mo in oxic environments27, the extensive seafloor oxygenation predicted by our model implies that bottom-water O2 concentrations exceeded tens of µM across much of the global deep ocean at ~1.45 Ga. Such widespread deep-ocean oxygenation would have been difficult to achieve through shallow-water oxygenic photosynthesis alone, which likely produced waters with no more than 10 µM O215, especially considering respiratory consumption of O2 by the biological carbon pump in the ocean interior16. Thus, elevated atmospheric O2 levels must also have been present to ensure sufficient O2 delivery into the deep ocean. This interpretation is consistent with emerging geochemical evidence, including predictions of high atmospheric O2 around 1.4 Ga from machine learning analyses of igneous geochemical datasets13, as well as a range of sedimentary redox proxies11,12.

Implications for expansive oxygenation at 1.45–1.35 Ga

Previous studies have identified transient episodes of atmospheric and global oceanic oxygenation between 1.40–1.35 Ga that disrupted long-term redox stasis of the Mesoproterozoic11,19,20,21,22,23. Positive Cr isotope fractionations in Mesoproterozoic carbonates, which can be traced back to as early as ~1.42 Ga58, further support the onset of atmospheric oxygenation during this interval. Our Mo isotope data for ~1.45 Ga offers a crucial snapshot that likely captures the early stages of this expanded oxygenation event. In the broader context of episodic Mesoproterozoic oxygenation, our study identifies a prolonged period (1.45–1.35 Ga) during which anomalously high levels of global ocean–atmosphere O2 levels were common and potentially even continuous. By contrast, other Mesoproterozoic oxygenation events, notably at ~1.56 Ga and 1.1 Ga, are currently thought to be shorter in duration, and in each case their evidence is limited to a single locality32 (Fig. 3b).

The prolonged oxygenation event we identify may have been fueled by enhanced primary productivity linked to greater nutrient delivery - particularly phosphorous - from the weathering of LIPs during the breakup of Nuna59,60,61. Simultaneously, the development of rift basins along continental margins facilitated the burial of Mn-Fe chemical sediments, supported by enhanced hydrothermal activity37,38,62,63 (Fig. 3b). Although LIP-driven weathering and Mn-Fe deposition also characterized the breakup of Rodinia in the Early Neoproterozoic64, the more limited breakup of Nuna may have resulted in a weaker perturbation of the ocean-atmosphere system65,66. This could have constrained the duration and intensity of photosynthetic O2 production, confining it to a geologically short time interval at 1.45–1.35 Ga. Nevertheless, the increased O2 availability during this interval may have been sufficient to tip the surface redox balance toward a more O2-rich atmosphere. This is consistent with the growing prevalence and magnitude of positively fractionated Cr isotope signals during and after ~1.40 Ga32 (Fig. 3b). This stepwise rise in oxygenation implied by our findings underscores the importance of Mesoproterozoic processes as precursors to the more dramatic oxygenation events of the Neoproterozoic.

Methods

Major and trace element analyses

For major element analysis, sample powders were fluxed with Li2B4O7 (1:8) to make homogeneous glass disks at 1250 °C, using a V8C automatic fusion machine (Analymate Company), then analyzed using X-ray fluorescence (Zetium, PANalytical or XRF-1800, Shimadzu) at Yanduzhongshi Geological Analysis Laboratories Ltd. The analytical errors for major elements are estimated to be within 1% based on four replicate analyses of Chinese national standards. For trace element analysis, approximately 50 mg of finely powdered sample was digested with a mixed acid solution containing 1 mL of hydrofluoric acid (HF) and 1 mL nitric acid (HNO3) at 190 °C for over 48 h in sealed Teflon vessels. After digestion, 1–2 mL of perchloric acid (HClO4) was added for further dissolution, then dried down and diluted to 100 g with 2% HNO3 and analyzed for trace elements using an Agilent 7700x inductively coupled plasma mass spectrometer (ICP-MS). Analytical precision, monitored based on replicate measurements of the Chinese reference material GSR-2, was better than 5%.

Organic carbon content (TOC)

For TOC measurements, siliciclastic rocks were leached with excess ~20% hydrochloric acid to remove carbonate phases and washed in distilled water prior to analysis at the State Key Laboratory of Geological Processes and Mineral Resources (GPMR), China University of Geosciences (Wuhan). The dried residue and non-acidified samples were measured using a Jena Multi-EA 4000 carbon-sulfur analyzer. Analytical precision was better than 0.2%, as determined from repeated measurements of the Alpha Resources reference material AR4007 (7.27 wt.% TOC contents).

Iodine-to-calcium+magnesium analyses

For I/(Ca + Mg) analyses of dolomite, sample powders (<200 mesh) were rinsed four times with 18.25 MΩ Milli-Q (MQ) water to remove adsorbed clays and soluble salts. After drying, approximately 5 mg of the cleaned powders were further homogenized in an agate mortar and accurately weighed. The cleaned powders were dissolved in 3% HNO3 for 40 min and then centrifuged to obtain the supernatant. Determination of Ca and Mg contents was performed on matrix solutions prepared in 3% HNO3 and diluted 1:50,000, using a PerkinElmer NexION 300Q inductively coupled plasma mass spectrometer (ICP-MS) at the National Research Center for Geoanalysis, Beijing. JDo-1 (dolostone reference material) was run as a bracketing standard every nine samples to monitor analytical performance; analytical uncertainties were <3% for Mg and <2% for Ca. For I analysis, 1 mL of the supernatant was diluted in a 0.5% MQ water to stabilize iodine24, and analyzed within 48 h using a Thermo Fisher Scientific Neptune Plus multi-collector ICP-MS. The rinse solution for each analysis contained 0.5% HNO3, 0.5% tertiary amine, and 50 µg/g Ca, with a rinse duration of approximately 1 min. Analytical uncertainty for ¹²⁷I, evaluated from repeated measurements of GSR-12 and duplicate samples, was ≤ 6%, and long-term accuracy was verified by repeated analyses of the GSR-12 reference material67.

Iron speciation analyses

Iron speciation analyses were performed on siliciclastic rocks containing >0.5 wt.% total Fe at the State Key Laboratory of Biogeology and Environmental Geology, China University of Geosciences, Wuhan. Sequential extraction procedures were carried out to quantify Fe associated with carbonate (Fecarb), magnetite (Femag), and ferric oxides (Feox), following the method of Poulton & Canfield68. Fecarb was extracted with a sodium acetate solution (pH 4.5) at 50 °C for 48 h; Feox was targeted using a sodium dithionite solution (pH 4.8) for 2 h at room temperature; and Femag was extracted with ammonium oxalate for 6 h at room temperature. Iron concentrations in all extracts were determined by atomic absorption spectrometry, with relative standard deviations (RSDs) of replicate measurements below 5%. Pyrite-associated Fe (Fepy) was determined by gravimetric precipitation of Ag2S following a standard chromous chloride reduction69.

Fe isotope analyses

Fe isotope compositions for siliciclastic rocks and Mn-Fe-rich chemical sediments were undertaken by following those suggested by Hou et al.70 at the Key Laboratory of Mineralization and Resource Assessment of the Ministry of Land and Resources in Beijing. Briefly, samples were dissolved in 3 mL aqua regia, whereas BCR-2 and BIR-1 standards were digested in 2.4 ml HF and 0.6 mL HNO3 at 140 °C for 72 h. All solutions were converted to a 7 M HCl matrix for further purification by anion-exchange resin (Bio-Rad AG MP-1). Purified Fe solutions were evaporated to dryness, refluxed three times in 0.5 mL HNO3 to eliminate chlorides, and finally dissolved in 1% HNO3 at 3 ppm for Thermo Neptune MC-ICP-MS analysis. Whole procedure Fe recoveries were 98%–101%, with blanks less than 0.3% of the total. Mass fractionation was calibrated using standard sample bracketing, and Fe isotope compositions are expressed as per mil deviations relative to the IRMM-014 standard:

$${{{\rm{\delta }}}}^{56}{{\rm{Fe}}}({{\textperthousand }})=1000\times \left[({\scriptstyle{{56}}\atop}\!{{\rm{Fe}}}{/}^{54}{{{\rm{Fe}}}}_{{{\rm{sample}}}})/({\scriptstyle{{56}}\atop}\!{{\rm{Fe}}}{/}^{54}{{{\rm{Fe}}}}_{{{\rm{IRMM}}}-014})-1\right]$$
(1)

Repeated analyses of the in-house standard (CAGS Fe) exhibited consistent offsets relative to the IRMM-014 Fe isotope reference material, with a mean Fe isotope composition of δ56Fe = 0.81 ± 0.08‰ (2 SD, n = 8), in agreement with previously reported values71. Reference materials BCR-2 and BIR-1 were analyzed to monitor instrumental accuracy, yielding δ56Fe values of 0.10 ± 0.07‰ and 0.03 ± 0.08‰, respectively, which were also consistent with published results72.

Whole rock δ56Fe compositions reflect a mixture of detrital and authigenic signals. Here, we use a simple mixing model to calculate δ56Fe values of FeHR: δ56Fe = (FeHR × δ56FeHR + FeU × δ56FeU)/(FeHR + FeU), where δ56Fe is the measured whole rock value, δ56FeHR is the isotopic composition of highly reactive iron, and δ56FeU is the isotopic composition of unreactive iron, which we assume to have crustal values (i.e., 0.1‰)45.

Mo isotope analyses

Chemical procedures for Mo isotope analyses using a 97Mo-100Mo double spike follow those suggested by Li et al.73 at the Guizhou Tongwei Analytical Technology Company Limited in Guizhou. Siliciclastic and Fe-Mn chemical sedimentary rocks were dissolved in ~3 mL of aqua regia at 120 °C for 12 h. Molybdenum separation and purification were achieved using N-benzoyl-N-phenyl hydroxylamine (BPHA) chromatographic resin25. The purified Mo sample solutions were used to determine Mo isotopic composition, using a Thermo-Fisher Scientific Neptune Plus multiple collector inductively coupled plasma mass spectrometer (MC-ICP-MS) at the State Key Laboratory of Isotope Geochemistry, Guangzhou Institute of Geochemistry. The isotopic compositions of Mo were reported as δ98/95Mo (simplified as δ98Mo) relative to the NIST SRM 3134 (= 0.25‰) standard74:

$${{{\rm{\delta }}}}^{98/95}{{\rm{Mo}}}({{\textperthousand }})=\{[({\scriptstyle{{98/95}}\atop}\!{{{\rm{Mo}}}}_{{{\rm{sample}}}})/({\scriptstyle{{98/95}}\atop}\!{{{\rm{Mo}}}}_{{{\rm{NIST}}}3134})-1]\times 1000\}+0.25$$
(2)

The standard solution (NIST 3134) and two reference materials (AGV-2 and IAPSO) were measured repeatedly along with the samples, with δ98Mo values of 0.25 ± 0.05‰ (2 SD, n = 25), –0.08 ± 0.02‰ (2 SD, n = 3) and 2.31 ± 0.01‰ (2 SD, n = 5) respectively, consistent with previously reported values73. The double spike calculation was accomplished using an in-house created Microsoft Virtual Basic program75. The Mo concentration of procedural blanks was 0.32 ± 0.06 ng (2 SD, n = 3), far lower than the total Mo content of samples.

Calculation of seawater Mo isotopic compositions from Mn-Fe oxide data

Calculating seawater δ98Mo by the Mn-Fe oxides follows the suggestion from Goto et al.35. If the Mn-Fe oxides have high Mn content (Mn/Fe ratio > 10), Fe in samples likely does not affect the Mo isotope fractionation. Thus, the determination of the seawater δ98Mo value could be done using a simple calculation with the measured δ98Mo value plus the respective isotopic fractionations35.

$${{{\rm{\delta }}}}^{98}{{{\rm{Mo}}}}_{{{\rm{GSW}}}}={{{\rm{\delta }}}}^{98}{{{\rm{Mo}}}}_{{{\rm{sample}}}}-{\Delta }_{{{\rm{Mn}}}-{{\rm{SW}}}}$$
(3)

where δ98MoGSW represents Mo isotope composition of global seawater (GSW); ΔMn-SW is the isotope fractionation factor generated by the adsorption of dissolved seawater Mo to Mn oxides

When the oxides have Mn/Fe ratios between 1 and 10, both isotope fractionation and efficiency of Mo adsorption onto Mn and Fe oxides should be considered when calculating seawater δ98Mo35.

$${{{\rm{\delta }}}}^{98}{{{\rm{Mo}}}}_{{{\rm{GSW}}}}=\frac{(\;f\times k+1){\delta }^{98}{{{\rm{Mo}}}}_{{{\rm{sample}}}}-f\times k\times {\Delta }_{{{\rm{Mn}}}}-{\Delta }_{{{\rm{Fe}}}}}{f\times k+1}$$
(4)

where f is the Mn/Fe ratio of the oxides (wt%/wt%) and k is a ratio of Mo adsorption efficiency onto Mn oxides to Mo adsorption onto Fe oxides. The specific process of back-calculating δ98MoGSW by Wafangzi Mn-Fe ores and related parameters is shown in Supplementary Information and Supplementary Data 2.

Molybdenum isotope mass balance model

A steady-state isotopic mass-balance model can be used to quantitatively evaluate the Mo isotopic composition of seawater27,28,29. Generally, a fixed riverine and ground water (River + GW) input of Mo is balanced by three major sinks27: (1) Oxygenated environments (O; O2 > 10 μM, representing a threshold value to support the Mn oxides precipitation and burial), and the main pathway for Mo precipitation is through adsorption onto Mn(IV) oxides46,47,76; (2) Strongly sulfidic environments (SE; bottom water [H2S]aq > 11 μM), where Mo will be quantitatively removed from the water column33,77,78,79; and (3) Intermediate environments (M; bottom water redox states range between weakly oxygenated with dissolved oxygen <10 μM, to weakly sulfidic with [H2S]aq < 11 μM), where Mo isotopic fractionation is mainly controlled by authigenic sulfide or organic matter, which most efficiently sequester Mo80. As the adsorption capacity of Fe(III) oxides is far less than sulfide minerals and organic matter, the Fe-oxides in intermediate environments may not be the main host phase that influences Mo isotope fractionation49.

Assuming that the oceanic Mo cycling was steady, the fractions of the fluxes (f) can be expressed as:

$${f}_{{{\rm{River}}}+{{\rm{GW}}}}=1=\sum {f}_{{{\rm{i}}}}({{\rm{i}}}={{\rm{O}}};{{\rm{M}}};{{\rm{SE}}})$$
(5)

Integration of modern parameters (e.g., input flux (F, g·yr−1), output burial rates (R, g·m−2·yr−1), seafloor areas (A, m2), isotope fractionations (Δ); see Supplementary Data 2) yields the following equation:

$${\delta }^{98}{{{\rm{Mo}}}}_{{{\rm{GSW}}}}-[{\delta }^{98}{{{\rm{Mo}}}}_{{{\rm{River}}}+{{\rm{GW}}}}\times {f}_{{{\rm{River}}}+{{\rm{GW}}}}]=\sum {f}_{{{\rm{i}}}}\times {\delta }_{{{\rm{i}}}}$$
(6)

where δ98MoGSW represents the Mo isotope composition of global seawater (GSW); δi = δ98MoGSW + Δi, i = O; M; SE.

The fractional flux under each setting can be described as:

$${f}_{{{\rm{i}}}}={A}_{{{\rm{i}}}}\times {R}_{{{\rm{i}}}}/{F}_{{{\rm{River}}}+{{\rm{GW}}}}$$
(7)

Assuming that the Mo output rates (R, g·m−2·yr−1) of different settings at a given time have the same linear relationship with the corresponding modern values, the Mo output rate in the paleo-oceans can be represented as:

$${R}_{{{\rm{i}}}}={{\rm{\varphi }}}{R}_{{{\rm{i}}}-{{\rm{modern}}}};{{\varphi }} \;{{\rm{is}}}\; {{\rm{a}}}\; {{\rm{constant}}};{{\rm{i}}}={{\rm{O}}};{{\rm{M}}};{{\rm{SE}}}$$
(8)

then

$${A}_{{{\rm{i}}}}={f}_{{{\rm{i}}}}\times {{{\rm{F}}}}_{{{\rm{River}}}+{{\rm{GW}}}}/{R}_{{{\rm{i}}}},i={{\rm{O}}};{{\rm{M}}};{{\rm{SE}}}$$
(9)

Here the variables Ri-modern and FRiver+GW can be readily canceled out when computing the area proportion of each setting:

$${{\rm{A}}}{{\rm{O}}}:{{\rm{A}}}{{\rm{M}}}:{{\rm{A}}}{{\rm{SE}}}=\frac{{{{\rm{f}}}}_{{{\rm{O}}}}}{{{{\rm{R}}}}_{{{\rm{O}}}}}:\frac{{{{\rm{f}}}}_{{{\rm{M}}}}}{{{{\rm{R}}}}_{{{\rm{M}}}}}:\frac{{{{\rm{f}}}}_{{{\rm{SE}}}}}{{{{\rm{R}}}}_{{{\rm{SE}}}}}$$
(10)

The selection of parameters and sensitivity analysis are detailed in Supplementary Information and Supplementary Data 2.