Introduction

Electromagnetic metamaterials are artificial structures with electromagnetic (EM) properties not found in nature. Into the new century, the two-dimensional (2-D) counterpart of metamaterials, which is named as the metasurface, is proposed for its advantages of low profile and easy fabrication. In particular, properties of EM waves, including their amplitude, phase and polarization can be manipulated by these metasurfaces dynamically, with the assistance of reconfigurable components and field programmable gate array (FPGA) circuits.

Recently, by introducing time-domain coding to digital metasurfaces, dynamic manipulations of frequency spectra in free space have become a reality. When it further collaborates with the space-domain coding, some unique functions and physical phenomena such as harmonic beam forming1,2,3,4, frequency conversion5,6,7,8, scattering control9,10,11 and direct information modulation12,13,14,15 are achieved. Such kind of time-varying metasurface is named as time-domain coding metasurfaces (TDCMs), which has great potential in imaging, positioning, sensing, wireless communication and radar detection.

TDCMs can be sorted into two categories according to whether the frequency spectral components of waves after the manipulation are discrete or continuous. The first type generates several discrete harmonics. Active-component loaded TDCMs are reported to modulate the reflection phase between 0 and π alternatively (1-bit), in which multiple harmonics are generated16,17,18. To further realize an arbitrary-order harmonic synthesis, a modulation strategy that modulates the TDCM with a specific phase gradient by multiple (≥2-bit) discrete phase states is employed6,19,20. Later, a metasurface antenna with the self-filtering function is demonstrated to generate a single-tone and sideband-free signal, without continuous or multi-bit temporal modulations21,22,23.

The second type of TDCM generates continuous temporal waveforms, which include much richer frequency spectral information. A programmable TDCM is designed to realize frequency-modulated continuous wave (FMCW) radar signals24. In this prototype, the phase slope of reflected EM waves changes with time to follow a derived expression depending on the required waveform. This is very different from the manipulation of discrete harmonics, whose phase slope is always kept at a fixed value. By abandoning the frequency synthesizing module used in traditional superheterodyne systems, it offers a competitive solution for radar signal modulation with reduced device cost and better system integration. However, due to the several ten MHz bandwidth for most radar systems, such a kind of modulation raises a much higher requirement for the TDCMs. Firstly, ultrahigh-speed modulation signals from the control circuit are demanded, so as to reduce the time slot for each discrete phase state. Secondly, active components used to reconfigure the TDCM are preferred to perform instantaneous and accurate responses so that they can match up with the above ultrahigh-speed signals.

So far, to the authors’ knowledge, almost all TDCMs that can achieve a full 360° phase tuning range are based on varactor diodes. By varying the capacitance of varactors loaded to TDCM cells, their resonant frequencies are reconfigured, leading to a continuous phase change in an analog manner. However, the typical changing speed of the capacitance for a varactor is from several hundred nanoseconds to several microseconds. This feature results in considerable difficulty in providing high-quality frequency modulation with a ten-MHz level bandwidth, which is required in most modern radar systems. Meanwhile, when a varactor diode operates at spectrums above X-band, the available tuning range of capacitance decreases remarkably25. This feature will cause a failure in successfully establishing the 360° full-cycle phase shifting, which is critically important in the frequency modulation procedure of radar signals. Some attempts are also conducted to achieve phase modulation with PIN-diodes15,26,27,28. However, due to their limited phase modulation ability that only covers 2 or 4 discrete phase states, it is not possible for those metasurfaces to generate FMCW signals.

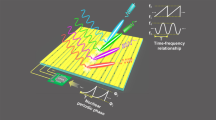
In this work, we report a nanosecond-level TDCM for frequency modulation of wideband FMCW radar signals. The conceptual illustration of the modulation architecture is shown in Fig. 1, in which the TDCM unit is fully digitalized by using an array of PIN diodes. This array is capable of performing a switching time of only several-ten nanoseconds, which enables it to collaborate with a voltage control circuit whose refresh time is smaller than 10 nanoseconds. Theoretical predictions of signal qualities are conducted with respect to the speed of phase tuning, to provide a methodology for the realization of high quality FMCW signals with a high power conversion ratio. To validate target detection capabilities through TDCM modulated radar signals, we also build an FMCW radar prototype with a signal bandwidth of 10 MHz in a succinct architecture. By measuring a flying drone, precise distance and velocity information of targets are obtained in the experiment, which indicates great potential of the TDCM in future cost-effective radar designs. Despite its application in target detection, the proposed signal generation approach is also worth considering for utilization in other scientific and technological fields that employ FMCW signals.

Fig. 1: Concept illustration of frequency-modulated continuous wave signal generation by a full PIN-diode array-based time-domain coding metasurface.
figure 1

By designing a fully digitalized time-domain coding metasurface using an array of PIN diodes, an ultra-high phase tuning speed of several ten megahertz is achieved. In this case, such a time-domain coding metasurface works as a signal generator which generates wideband frequency-modulated continuous wave signals with enough range resolution in radar systems. (fc denotes the frequency of the carrier wave, fb(t) the time-varying frequency shift, and field-programmable gate array).

Full size image

Quality of TDCM modulated FMCW signals

In a frequency modulation with TDCM, each unit is periodically switched in time with time period T. The instantaneous frequency f(t) of the reflected wave can be calculated as24:

$$f(t)={f}_{{{\rm{c}}}}+\frac{1}{2{{\rm{\pi }}}}{\sum }_{m=-\infty }^{+\infty }\frac{d[{\upphi }_{0}(t-mT)]}{dt}$$
(1)

where fc is the frequency of the carrier wave that illuminated onto the TDCM, φ0(t) is the phase response of the reflected waveform in a period of T. When f(t) is a linear FMCW signal, the expression of φ0(t) can be written as:

$${\upphi }_{0}(t)={\Phi }_{0}+\left(\frac{2m{{\rm{\pi }}}}{T}-p{{\rm{\pi }}}\right)t+p{{\rm{\pi }}}{t}^{2},0\le t\le T$$
(2)

in which Ф0 is the initial phase and p is the linear FM slope. In a practical situation, the theoretical reflection phases are quantified into different time slots tq, so that they can be mapped to biasing voltages of corresponding PINs through DAC output pins. In this case, Eq. (1) can be rewritten in a discrete manner as:

$${f}_{d}(t)={f}_{{{\rm{c}}}}+\frac{1}{2{{\rm{\pi }}}}{\sum }_{m=-\infty }^{+\infty }{\sum }_{n=1}^{N-1}\frac{{\upphi }_{0}[t-mT+(n+1){t}_{{{\rm{q}}}}]-{\upphi }_{0}(t-mT+n{t}_{{{\rm{q}}}})}{{t}_{{{\rm{q}}}}}$$
(3)

where N = T/tq. Specifically, when down-converting f(t) from fc to baseband, we can define the baseband response as:

$${f}_{{{\rm{b}}}}(t)=\frac{1}{2{{\rm{\pi }}}}{\sum }_{m=-\infty }^{+\infty }{\sum }_{n=1}^{N-1}\frac{{\upphi }_{0}[t-mT+(n+1){t}_{{{\rm{q}}}}]-{\upphi }_{0}(t-mT+n{t}_{{{\rm{q}}}})}{{t}_{{{\rm{q}}}}}$$
(4)

In order to achieve a quantitative analysis, we assume that the initial phase Ф0 equals zero and linear FM slope p is 500/T2. In this case, the lowest and highest baseband frequencies during the modulation are fL = 0 and fH = 500/T, respectively. Under different quantization frequency fq (fq = 1/tq) quantized by fH, Fig. 2 illustrates their corresponding baseband FMCW time-amplitude diagrams Ab(t) in one period of T.

Fig. 2: Generations of linear frequency-modulated continuous wave signals under different quantization frequencies fq.
figure 2

a fq = fH, b fq = 2fH, c fq = 5fH, d fq = 8fH.

Full size image

We also calculate and plot frequency-power diagrams of baseband FMCW signals under the above cases of fq as shown in Fig. 3. It is noted in Figs. 2a and 3a that, when fq equals fH, a lot of spectrum information is lost especially near fH. The reason is similar to that indicated in the Nyquist sampling theorem and therefore, the minimum value of fq that is capable of properly generating all the spectrum information in the designated FMCW signal is 2fH, which is also verified in Figs. 2b and 3b. However, it is seen in Fig. 3b that, the in-band spectrum (f ≤ fH) is still not properly modulated as a typical FMCW signal29. Meanwhile, a lot of out-of-band (f > fH) harmonics are observed that the power conversion ratio (PCR), which is defined as the power quotient between the in-band FMCW signal scattered from the TDCM and the single-tone EM wave impinging on the TDCM, is only 76.8%. It is known from ref. 6 that, for a single tone signal, 8 (3-bit) phase states are required in a 360o cycling to achieve a PCR better than 95%. Therefore, we further increase fq to 5fH and 8fH, respectively, to examine if the PCR could be higher than 95% for an FMCW signal. As observed in Fig. 3c, d that, the PCR is 97.4% and only 2.3% higher for the fq = 8fH case, while its requirement for the phase tuning speed is almost doubled compared with the fq = 5fH case.

Fig. 3: Baseband frequency-modulated continuous wave frequency-power diagrams under different quantization frequencies fq.
figure 3

a fq = fH, b fq = 2fH, c fq = 5fH, d fq = 8fH.

Full size image

Furthermore, in order to intuitively evaluate the quality of the above TDCM modulated FMCW signals when using them in radar systems, a group of quantitative analysis in Supplementary Note 1 is conducted with respect to the quantization frequency fq. Based on the aforementioned investigations, we can deduce that the choice of fq = 5fH represents a compromise between the signal quality and the speed of phase tuning for the effective generation of FMCW signals using a TDCM.

Generation of Ten-MHz-level FMCW signals based on TDCM

In modern FMCW radar systems, a large spectrum bandwidth is required in most situations, so as to achieve a small range resolution. Based on the above analysis, even for a system whose bandwidth is 10 MHz [corresponding range resolution = 15 m], the quantization frequency fq should be as large as 50 MHz at least, which indicates a maximum allowable quantization time tq = 20 ns.

In the real situation, when the reconfigurable active component in each TDCM unit is switched from one state to another, its corresponding reaction is not instantaneous; there is always a transition time, donated as ttr. It is known from refs. 30,31,32 that, during the transition time of an active component, the physical variables, e.g., capacitance for a varactor diode and resistance for a PIN diode, do not simply increase or decrease over time. As a result, such a kind of transition will cause a nonlinear region between adjacent phase states, which is unwanted in the manipulation. In order to reduce negative effects brought by this phenomenon, ttr is always demanded to be much smaller than tq. However, as mentioned in published article32 and verified in our experiment and simulation, the transition time ttr for most commercial varactor diodes is larger than 50 ns. Such a performance indicates the varactor diode is hard to be deployed in the generation of FMCWs with a bandwidth >4 MHz. Fortunately, the transition time ttr of most PIN diodes is only several nanoseconds, enabling it a good candidate for the fast switching of phase states.

The conceptual illustration of a wideband frequency modulation architecture, composed of a reflective two-dimensional programmable phase-tuning TDCM, is shown in Fig. 1. In such an architecture, in order to achieve the high-speed phase tuning, reflection phase responses of each TDCM unit are digitally controlled by using multiple (=N) PIN diodes connected to different positions. With this measure, this digitalized TDCM unit corresponds to an N-bit phase tuning scheme, in which ‘1’ and ‘0’ present “on” and “off” of the PIN diodes, respectively. The PIN diodes are controlled by an FPGA such that the reflection phase of the unit can be dynamically programmed following a predesigned voltage sequence. With this kind of a setup, when proper PIN diodes and FPGA voltage control circuit are utilized33, a maximum switching speed smaller than 5 ns between adjacent phase states is capable to be achieved in theory.

PIN-diode-controlled ultrahigh-speed phase tuning TDCM

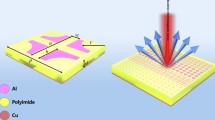
As illustrated in Fig. 4a, a meta-unit of the PIN-diode array based TDCM includes two layers of dielectric substrate and three layers of printed circuits. Two rectangular patches are printed on the upper RF layer with a separation of d and connected face-to-face to the middle ground layer. 16 coding lines are equally distributed along two parallel sides. Each coding line is connected with a PIN diode to control the coding sequence, incorporating with an RC parallel circuit to limit the current of DC signals while allowing RF signals to pass, as well as a capacitor Cg to isolate the DC signals. Biasing lines for the PIN diodes are located in the lower biasing layer through apertures in the ground. They are constructed in an inductive meander structure to provide further isolation between the biasing circuit and the TDCM.

Fig. 4: Structure and performance of the proposed time-domain coding metasurface element.
figure 4

a Structure of the time-domain coding metasurface. b Equivalent circuit of the time-domain coding metasurface. c Reflection amplitude. d Reflection phase.

Full size image

In order to generate a dual-resonance response for the establishment of a reflection tuning range covering a full-360° cycle, the widths of the two rectangular patches are designed to be different from each other. Its equivalent circuit model is given in Fig. 4b, in which L1 and L2 represent the inductances coming from the ground plane which change with the coding of control signals, L3 and L4 represent the inductance of the two patches with vias. Since induced currents are generated when EM waves impinge to these two patches, they also allow the storage of electric energy and behave like capacitors C1 and C2. R1 and R2 are the resistance of the utilized array of PIN diodes in each half, which also change with the coding of control signals. The surface impedance Zs is determined by

$${Z}_{s}=\frac{j\omega {L}_{1}(\,\,j\omega {L}_{3}+\frac{1}{j\omega {C}_{1}}+{R}_{1})}{j\omega {L}_{1}+j\omega {L}_{3}+\frac{1}{j\omega {C}_{1}}+{R}_{1}}+\frac{j\omega {L}_{2}(j\omega {L}_{4}+\frac{1}{j\omega {C}_{2}}+{R}_{2})}{j\omega {L}_{2}+j\omega {L}_{4}+\frac{1}{j\omega {C}_{2}}+{R}_{2}}$$
(5)

The reflection coefficient at normal incidence can be calculated as

$$\varGamma=\frac{{Z}_{{{\rm{s}}}}-{Z}_{0}}{{Z}_{{{\rm{s}}}}+{Z}_{0}}$$
(6)

where Z0 is the characteristic impedance of free space. Based on Eq. (5), amplitude and phase results of Г are plotted in Fig. 4c–d, respectively. In the above two figures, circuit model results are obtained by mapping parameters of L, C to full-wave simulation results, under two coding state of ‘0000000110000000’ and ‘1111111111111111’. In this article, advanced Designed System 2020 is employed for the circuit model calculation and mapping, while HFSS of Ansys Electronics Desktop 2022 is utilized to perform the full-wave simulation. In the magnitude responses, when Zs achieves its maximum, two reflection zeros located at 1/(2π×sqrt((L1 + L3)C1)) and 1/(2π×sqrt((L2 + L4)C2)) are observed. Meanwhile, 0° reflection phase is achieved at these two zero, as long as the surface resistance is larger than the wave impedance. Between these two zeros, there is a reflection pole when Zs achieves its minimum and hence a ± 180° reflection phase. For both coding states, the reflection phase varies from 180° to 0° and then from 0° to −180° with the frequency, indicating a capability to achieve a 360° phase variation at a certain frequency band by introducing more coding states. A good correlation is obtained between simulation and calculation in Fig. 4, validating the predicted circuit model.

During the manipulation procedure, in order to simplify the control here, we choose a coding strategy where the pair of coding lines with the same subscript number, e.g., P1L and P1R, is assigned to the same voltage. With this measure, although 16 PIN diodes are utilized, the TDCM is actually coded in an 8-bit manner. The simulated magnitude and phase responses versus different coding states of the 8 pairs of coding lines are illustrated in Fig. S2a–b of Supplementary Note 2, respectively. As expected, the combination of the two resonances for each coding state varies between those corresponding to the states of ‘0000000110000000’ and ‘1111111111111111’. It is observed that, during the above tuning procedure, when more diodes are coded in the “on” state, which means more corresponding biasing lines are connected to the ground, the two resonances in each combination grow towards a higher frequency spectrum gradually and therefore a larger value of shifted phases. It is also noted that, a phase tuning range larger than 360° is achieved from 4.3 GHz to 4.75 GHz. However, the reflection loss is relatively large (>5 dB) when the operational frequency is smaller than 4.66 GHz. As a result, 4.7 GHz is selected as the working frequency so as to balance the phase tuning range and reflection loss. Additionally, the distribution of reflection phases across coding states is not uniform, which affects the quantization precision required in Eq. (3). To address this, more coding states are introduced with asymmetric voltage assignments, improving phase resolution across the full tuning range. Further details are provided in Supplementary Note 2.

FMCW modulation with PIN-diode array based TDCM

Top and bottom views for the fabricated prototype of the complete TDCM are given in Fig. 5a–b, respectively. The PIN diode of MACOM MADP-000907-14020P, with a minimum switching time of 2 ns and an inherent resistance of 5.2 Ω as indicated in its datasheet33, is utilized in the prototype to achieve a compromise between switching speed and reflection efficiency of the TDCM. It is seen that, biasing lines with the same subscript in different units are connected together in the biasing layer and therefore, only a total of 16 pins are led out. The above pins are connected to a voltage-controlling module given in Fig. 5c, which is specifically designed for this PIN-diode array based metasurfaces and capable of providing 32 high-speed programmable channels of voltage output, each of which can be switched between two voltage states, i.e., +4 V and −4 V. The maximum switching speed of output voltages is 100 MHz achieved by using high-power output current feedback amplifier THS3491IDDA. SSMA connectors and RF cables are utilized for the connection between the TDCM and the controlling module, due to the relatively high switching speed in the control of the biasing voltage. Since the transmission channel is relatively short and wired using RF cables in our system, the delay between different output channels and the error of FPGA-generated signals can almost be considered negligible.

Fig. 5: Structure of the fabricated time-domain coding metasurface.
figure 5

a Front view. b Back view. c Field-programmable gate array board utilized for direct current voltage controlling. d Measurement setup.

Full size image

Firstly, we make experiments to measure reflection coefficients of the prototype under different states of coding lines at 4.7 GHz. The measurement is conducted in a microwave chamber. The configuration of the measurement system is illustrated in Fig. 5d, which is mainly composed of a signal generator, a transmitting horn antenna, a TDCM with 3 × 7 elements, an FPGA voltage controlling module, a receiving antenna, a multiple-channel receiver module, an A/D sampling module, a PC, two voltage sources, a coupler and several sync cables. These sync cables are utilized to synchronize the signal generator, the receiver module and the A/D sampling module with the FPGA.

In the measurement, a 4.7 GHz single-tone signal is generated by the Keysight N5172B signal generator. This signal is transmitted to the transmitting horn antenna through the directly-connected port of the coupler, radiated into free-space and normally illuminates the TDCM placed 1.5 meters away in front of the transmitting horn antenna. The voltage on each biasing line of the TDCM is controlled by the coding sequence generated from the FPGA. After the manipulation, waves reflected by the TDCM are then reradiated back to the free space and received by the receiving horn antenna, which is placed 1 m behind the transmitting one to ensure a good isolation. After that, signals are transmitted to the receiver module, down converted to the baseband and compared with the reference signal obtained from the coupled port of the coupler through the A/D conversion.

A total of 200 coding states are assigned to those 16 coding-lines for a phase tuning range of 360° and a resolution better than 2.0°. For a better observation of measured results, phase and amplitude responses of the total utilized coding states are depicted in Fig. 6a–b, respectively.

Fig. 6: Measured reflection performance of the fabricated time-domain coding metasurface for different coding states.
figure 6

a Coding phase. b Amplitude. c Root mean square phase error.

Full size image

In Fig. 6a, phase responses under three different cases, i.e., simulated coding phase, measured coding phase before adjustment and measured coding phase after adjustment are compared versus their coding-state numbers. It is observed that, due to the loading effect of the meander biasing-line, the measured reflection phases before adjustment are smaller than those in the simulation under the same coding-state number with the same coding sequence. Therefore, an adjustment is conducted by assigning a different coding sequence to the TDCM based on measured results, so as to achieve a numerically closest coding phase with respect to the simulated one under the same coding-state number. For instance, the reflection phase of coding-state No. 51 with the coding sequence ‘1111000011001111’ is 89.5° in the simulation, while it is 57.5° in the measurement with the same coding sequence. By adjusting the coding sequence to ‘1110011111001111’, the measured reflection phase becomes 89.64°, which is very close to the simulated value. In this case, the coding sequence corresponding to the coding-state No. 51 is revised to ‘1110011111001111’ in practical applications. The calculated root-square-mean (RMS) phase error for all 200 coding states ranging from 4.2 GHz to 5 GHz is plotted in Fig. 6c, which remains smaller than 0.11° over a bandwidth of approximately 350 MHz and indicates good accuracy.

It should be noted that the label of the left y-axis in Fig. 6a is defined as “Coding Phase”. This term refers to the absolute phase of each coding state. The reference for the absolute phase of “Coding Phase” is defined by the coding state ‘1111111111111111’ and assigned a value of 180° in our experimental setup. This label is quite different from other labels named as “Reflection Phase” in Fig. 4, which is defined by the phase difference between incident and reflected EM waves. The reference of the “Reflection Phase” is the phase of the incidence at the interface between the metasurface and free space.

In Fig. 6b, measured amplitude responses, which are normalized to the largest received amplitude during the manipulation, under same cases as phase responses are presented. As can be observed, the fluctuation of measured reflectivity is better than 3.0 dB within a full-cycle of 360° phase tuning. The slight difference might be attributed to the deviation of the PIN diode’s resistance in its “on” state. Such a fluctuation can be tolerated by the designed TDCM-aided radar system, since the minimum detectable power level for the receiver is −120 dBm, which provides sufficient margin to accommodate the amplitude fluctuations.

Based on the measurement, a relationship between the coding phase and each individual coding state is established. We can easily obtain the required coding sequence that corresponds to the calculated phase curve to generate target FMCW signals.

Secondly, another experiment is conducted to evaluate the maximum effective phase tuning speed of the PIN-diode based TDCM. In the experiment, a 4.7 GHz single-tone sine-wave is illuminated onto the TDCM. The reflection phase of the TDCM is changed between 0° and 90° coding states with different switching frequencies of 25 MHz, 50 MHz, 75 MHz and 100 MHz, respectively. Signals received from the receiving horn are directly transmitted to the Keysight DSA91304A oscilloscope for observation of time-domain waveforms. Measured results are illustrated in Fig. 7a–d. It is seen in the insets in Fig. 7 that, the phase-shifting point can be clearly observed when the switching frequency is below 75 MHz, while it is imperceptible at 100 MHz. It is also noted that, the difference in reflection amplitude between the 0° and 90° coding states is significant for the first two cases, while it is much smaller than it should be for the third one and almost aliased together for the last one, due to the transition time of the PIN diode is near or even larger than the period of the phase shifting. From the above investigations we can say that, the maximum applicable switching speed between different reflection-phase states for the designed TDCM prototype is around 50 MHz. Such a speed corresponds to a period of 20 ns and is larger than the theoretical minimum switching time of the PIN diode [2 ns in ref. 33].

Fig. 7: Measured time-domain waveforms of signals switched between 0° and 90° coding states under different phase switching frequencies.
figure 7

a 25 MHz, b 50 MHz, c 75 MHz, d 100 MHz.

Full size image

Then, the generation of wideband FMCW signals with the PIN-diode based TDCM is conducted. The setup of this experiment is similar to the one plotted in Fig. 5d. The slight difference is that the coupler is removed and only one receiver channel is included. The received signals from the TDCM are directly stored in the PC for post signal processing after the A/D conversion. In the demonstration, the modulation bandwidth Δf (fH-fL) and waveform period T of the FMCW signal are set to be 10 MHz and 50 μs, respectively.

Figure 8a plots baseband waveforms of generated signals in three periods of T in the case of fq = 50 MHz. Its corresponding time-frequency curve is extracted in Fig. 8b, by taking derivatives of the measured φ0(t) with respect to time. The inaccuracy of modulated phases leads to a decreased efficiency of frequency modulation and therefore some unwanted harmonics are presented in the form of burrs in Fig. 8b. However, even in this situation, the calculated linearity δ of such a generated FMCW signal is below 0.76%, which is sufficiently high for a practical radar system34,35,36,37.

Fig. 8: Measured result of modulated linear frequency-modulated continuous wave signal generated by the time-domain coding metasurface.
figure 8

a Baseband waveforms in three periods. b Baseband time-frequency curve in three periods, c Baseband waveforms in one period.

Full size image

Finally, to further physically evaluate the detection capability of modulated FMCW signals, a succinct radar system is built to perform experiments of drone detections with this TDCM. Theoretical performances of such a signal for target detection, including resolutions and precisions with respect to distance and velocity, are listed in Table S1 of Supplementary Note 3. The photograph of the radar system is given in Fig. 9a, which is mounted on the roof of our office building. The setup is slightly different from the one depicted in Fig. 5d that a signal probe is installed between the transmitting and receiving horns to act as a reference for signal processing of FMCW signals. A DJI Matrice 600 is sent into the air and equipped with a corner reflector to enhance the intensity of the echo.

Fig. 9: Drone detection experiment based on the time-domain coding metasurface generated frequency-modulated continuous wave signal.
figure 9

a Setup of the radar system. b The target of a drone equipped with a corner reflector. c Top view of the entire experiment scenario.

Full size image

In the experiment, the average power of the signal emitted from the transmitting horn antenna is 5 watts. It is first illuminated onto the TDCM, modulated in the time-domain and scattered into the detection area. Afterwards, reflected waves coming from the target are radiated back to the receiving horn antenna. Finally, received signals are demodulated into digital signals and compared with signals from the reference probe for further processing. The FMCW constructed with a bilateral sweep triangular waveform is utilized in our system to avoid the coupling between range and Doppler frequency. The baseband sampling rate is 45 MHz. A two-dimensional FFT is utilized in signal processing, in which a 4096-point FFT is conducted for the range estimation, while an 8192-point FFT is conducted for the speed estimation. By exploiting 2-D-FFT, the Range-Velocity map (RV-map) can be obtained from the raw radar echoes in cooperation with the clutter suppression algorithm.

The flying trajectory carried out in the test is always right in front of the horn antennas. The drone starts at A1 located about 50 meters away and ends at A2 which is over 130 meters away. Two tests are carried out, in which the speed of drone is kept at 6 m/s and 12 m/s by using the cruise control function, respectively.

Detected ranges and velocities are extracted based on the maximum response in the RV-map, and measured results corresponding to the distance around 100 m, 115 and 130 m are given in Fig. 10. These results (98.9 m, 5.85 m/s), (114.7 m, 5.89 m/s), (131.6 m, 5.80 m/s), (98.8 m, 11.99 m/s), (115.4 m, 12.05 m/s), (131.8 m, 11.89 m/s) are basically consistent with the preset settings, which showcases the TDCM-based radar’s ability of precisely measuring both the range and velocity of a single target. The differences are mainly attributed to the resolution and accuracy of the system, as well as the influence brought by gusts of wind. Figures of beat frequency spectrum corresponding to all the 6 cases are also included in Fig. 10. The maximum side-lobe levels (MSLs) are all smaller than −13 dB. Given that our experiment is conducted in a scenario featuring a single target against a clear background airspace, the demonstrated performance is sufficient to meet the requirements for target detection.

Fig. 10: Range-velocity map and beat frequency spectrum of the target measured by the metasurface-based radar under different cases.
figure 10

a (R = 100 m, V = 6 m/s), b (R = 115 m, V = 6 m/s), c (R = 130 m, V = 6 m/s), d (R = 100 m, V = 12 m/s), e (R = 115 m, V = 12 m/s), f (R = 130 m, V = 12 m/s).

Full size image

Discussion

In this work, we report a PIN-diode based metasurface that is capable to achieve nanosecond-level time-domain coding and FMCW radar signals. We also implement such radar signals to successfully demonstrate drone detection in a radar system. The achievable maximum modulation speed of our metasurface is as fast as 50 MHz. With this enhancement, the modulation bandwidth for the FMCW signal generated by a metasurface can reach up to 10 MHz, corresponding to a range resolution of 15 meters. In contrast, the largest modulation bandwidth reported in published varactor-based articles is only 1 MHz, resulting in a range resolution of 150 meters, which is insufficient for practical detection. Since the minimum switching speed of the utilized PIN-diode (MADP-000907-14020P) is only 2 nanoseconds, with proper improvements to the metasurface, the phase manipulation speed could be further enhanced beyond the current level of 20 ns. Faster manipulation speed will bring larger bandwidth and smaller frequency modulation nonlinearity for the generated signals, which are both highly beneficial for improving the performance of metasurface-aided radar systems. It should also be pointed out that, this approach may also be of interest in various sensing applications that utilize FMCW signals, such as vital signs monitoring in the biomedical field, studying atmospheric fluctuations in meteorology, and investigating mineral distributions in geological surveys. Moreover, the proposed metasurface can contribute to wireless communications as well, where the ultrahigh-speed coding will greatly increase the capacity and speed. The proposed approach is also capable of being easily extended to higher operational bands.

Methods

Details on the metasurface

The used dielectric substrate is F4B with a relative dielectric constant of 2.65 and a loss tangent of 0.0014. The period of the unit cell is a = 27 mm and other parameters shown in Fig. 4a are: b = 13.8 mm, c = 9.9 mm, d = 1.1 mm, e = 8.9 mm, f = 2.78 mm, g = 1.39 mm, h = 1.25 mm, i = 2.5 mm. The utilized PIN diode is MACOM MADP-000907-14020p.

In the equivalent circuit, parameters that do not change with the coding of control signals are: C1 = 0.672 pF, C2 = 0.627 pF, L3 = 1.182 nH, L4 = 0.888 nH. In contrast, parameters that change with the coding of control signals are: L1 = 1.058 nH, L2 = 1.075 nH, R1 = 1.578 ohm, R2 = 1.198 ohm for the coding state of ‘0000000110000000’ and L1 = 0.52 nH, L2 = 0.67 nH, R1 = 0.1 ohm, R2 = 0.07 ohm for the coding state of ‘1111111111111111’.

High-speed voltage control module

To control the state of the coding units of programmable metasurfaces, we designed a high-speed voltage control module as shown in Fig. 5c, which is characterized by the following features:

128 channels of continuous voltage output with a tunable range between −16 V and +16 V and a maximum switching frequency of 50 KHz.

32 channels of discrete voltage output at merely −6 V and +6 V and a switching frequency larger than 100 MHz.

Multiple interfaces for synchronization with external systems.

Evaluation of detection range

For FMCW radar systems, there is no theoretical minimum detection distance in principle. However, in practical radar detections, the ranging results within the first range bin tend to be relatively inaccurate due to transmitter leakage (Tx leakage), near-range aliasing and ADC sampling limitations. To address this, we define Rmin as the practical minimum detection range, Rrb as the range bin, NR-FFT as the point of FFT (Fast Fourier Transform) applied to the range dimension and B as the modulation frequency band. The formula is given by:

$${R}_{\min }={R}_{{{\rm{rb}}}}=\frac{T\cdot {f}_{{{\rm{s}}}}\cdot c}{2\cdot B\cdot {N}_{{{\rm{R}}}-{{\rm{FFT}}}}}$$
(7)

where T is the modulation period, fs is the sampling rate, c is the speed of light. By substituting the values of the respective parameters, the calculated Rmin is 8.24 meters in our system.

The maximum distance considered from the power aspect can be derived from the radar equation as:

$${R}_{\max 1}={\left(\frac{{P}_{{{\rm{TDCM}}}}{G}_{{{\rm{TDCM}}}}{G}_{{{\rm{r}}}}{\lambda }^{2}{\sigma }_{{{\rm{t}}}}{N}_{{{\rm{SP}}}}}{{(4\pi )}^{3}k{T}_{{{\rm{s}}}}{B}_{{{\rm{n}}}}{L}_{{{\rm{s}}}}\cdot SN{R}_{\min }}\right)}^{1/4}$$
(8)

where GTDCM is the scattering gain of the TDCM, Gr is the antenna gain for the receiver, λ is the radar’s operating wavelength, σt is the radar cross-section (RCS) of the target, k is Boltzmann’s constant, Ts is the system’s noise temperature, Ls is the total system losses, NSP is the signal processing gain, which is rising from frequency-domain accumulation via an 8192-point Doppler FFT, Bn is the effective noise bandwidth of the receiver. PTDCM represents the peak scattering power of the TDCM and is expressed as

$${P}_{{{\rm{TDCM}}}}=\eta \times {\sigma }_{{{\rm{TDCM}}}}\times \frac{{P}_{{{\rm{t}}}}{G}_{{{\rm{t}}}}}{4\pi {R}^{2}}$$
(9)

where η is the reflection efficiency of TDCM, σTDCM is the RCS of the TDCM, Pt is the transmit power, Gt is the antenna gains for the transmitter, R is the distance between the TDCM and the transmitter’s antenna. SNRmin is the minimum signal-to-noise ratio, defined as

$$SN{R}_{\min }=\frac{{P}_{\min }}{k\cdot {T}_{{{\rm{s}}}}\cdot {B}_{{{\rm{n}}}}\cdot {L}_{{{\rm{s}}}}}$$
(10)

where Pmin is the receiver’s minimum detectable power. Based on detailed values [as listed in Table S2 of Supplementary Note 4] of the above parameters, the calculated maximum detection distance Rmax is approximately 19166.89 meters.

When the maximum distance is considered from the signal aspect, the maximum unambiguous range can be calculated by the following formula:

$${R}_{\max 2}=\frac{cT}{2}$$
(11)

where c is the speed of light, T is the modulation period. The calculated Rmax2 in our system is 7500 meters, which is smaller than Rmax1 and can therefore be recognized as the maximum detection distance.