Ultrafast Coulomb blockade in an atomic-scale quantum dot

Abstract

Controlling electron dynamics at optical clock rates is a fundamental challenge in lightwave-driven nanoelectronics and quantum technology. Here, we demonstrate ultrafast charge-state manipulation of individual selenium vacancies in monolayer and bilayer tungsten diselenide using picosecond terahertz source pulses, focused onto the junction of a scanning tunneling microscope. Using pump–probe time-domain sampling of the defect charge population, we capture atomic-scale snapshots of the transient Coulomb blockade, a hallmark of charge transport via quantized defect states. We leverage the Franck–Condon blockade, which restricts accessible vibronic transitions and promotes unidirectional charge transport, to effectively mitigate back tunneling to the tip electrode. Our master equation approach models the non-reciprocal tunneling process due to vibrations and angular momentum multiplicities, accurately reproducing the time-dependent tunneling current across different coupling regimes. Capturing and controlling ultrafast charge dynamics in low-dimensional materials at the atomic scale opens frontiers in lightwave-driven nanoscale science and technology.

Introduction

Artificial atom qubits, such as quantum dots (QDs) and color centers, have attracted significant interest in light of their applications in quantum sensing, communication, and photonic quantum computing^1,2,3. In particular, the inherently strong confinement for solid-state atomic-scale defects imposes a large characteristic energy scale that leads to exceptionally long coherence times, and operability beyond cryogenic environments⁴. Spin-selective optical decay pathways enable high-fidelity spin initialization and optical readout⁵. While optical access is advantageous for addressing individual QDs at THz to PHz frequencies⁶, electrical interfaces offer crucial benefits for scalable on-chip integration. The primary engineering challenge lies in developing suitable leads for atomic interfaces. Although extreme ultraviolet lithography is making progress towards atomic contacts, scanning probe hydrogen resist lithography^7,8 has already demonstrated proof-of-concept devices. Promising candidates for well-defined atomic interfaces are two-dimensional (2D) materials that are chemically versatile, tunable via external fields, and they can host atomic-scale QDs⁹. Several spin-bearing, optically active defect emitters have been identified in transition metal dichalcogenides (TMDs)^10,11 and hexagonal boron nitride^12,13, including substitutional defects and vacancies. However, achieving device-scale electron transport through single defects in 2D materials has so far remained elusive.

The tunneling contact in scanning probe microscopy offers a means of studying quantized electron transport through single defects and exploring the Coulomb blockade regime at the atomic scale. Steady-state Coulomb blockade of adatoms, molecules, and defects has previously been observed in scanning tunneling microscopy (STM)^14,15,16. Dangling bonds of an H-terminated Si surface have been demonstrated to exhibit quantized transport^8,17 and Coulomb blockade⁸. Similarly, chalcogen vacancy defects in TMDs introduce discrete defect states deep in the band gap of the host material, with narrow defect resonances followed by vibronic sidebands^18,19. These defect states can be probed individually via scanning tunneling spectroscopy (STS), revealing the influence of spin-orbit coupling¹⁸ and layer-dependent binding energy^16,20. To operate and control single-electron dynamics in these atomic QDs at their natural time scale, ultrafast probes are required. Recent technological advancements in ultrafast probes now bring this vision within reach, making it possible to capture “movies” with simultaneous picosecond temporal resolution, millielectronvolt energy resolution, and picometer spatial precision^21,22. Ultrafast STM has resolved charge carrier dynamics in semiconductors^23,24, coherent lattice dynamics of bulk crystals^25,26, single molecules²⁷, and atomic defects^28,29. However, the direct observation of ultrafast single-electron dynamics at the atomic scale has remained an open challenge.

Here, we address this challenge by demonstrating ultrafast Coulomb blockade at an atomic defect in a 2D semiconductor by lightwave-driven STM (LW-STM). By applying tailored single-cycle THz pulses to the STM tip, we achieve a controlled population of atomic defect orbitals and trace their subsequent depletion in the time domain. The temporal evolution of the Coulomb blockade quantifies the charge-state lifetime of selenium vacancies (Vac_Se) in WSe₂/graphene heterostructures. By controlling the coupling strength of the tunnel junction via dc bias and tip–sample distance, along with a theoretical model utilizing the master equation, we identify the Franck–Condon blockade as a key mechanism to prevent back tunneling to the source electrode. This study represents the direct observation of ultrafast electron dynamics at the atomic scale with LW-STM, opening new avenues for advancing our microscopic understanding and control of ultrafast electron transport at atomic length scales.

Results and discussion

Coulomb blockade at a single Selenium vacancy

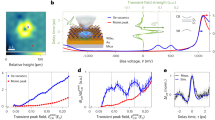
The STM geometry enables the resonant exchange of electrons (e⁻) in the single-atom Vac_Se QD between tip (source electrode) and sample (drain) through sequential tunneling processes (Fig. 1a, b). A finite tunneling current occurs if the e⁻ exchange proceeds in series, i.e., from the source (tip) to the QD to the drain (substrate), or vice versa. Thereby, the coupling strength to the source and drain can be precisely controlled via the tip–sample distance and TMD layer thickness, respectively. In standard STM/STS, static lead potentials enable measuring energy-selective, stochastic tunneling processes and average QD populations. Ultrafast pump-probe schemes in LW-STM allow us to access also the charge dynamics of the atomic QD. In the near-field of the tunneling junction, strong-field THz source pulses act as ultrafast bias transients that add to any static dc bias, as illustrated schematically in the equivalent circuit diagram in Fig. 1c. We preserve state-selectivity of the tunneling process by tailoring the amplitude and carrier-envelope phase of the THz transient to a single-cycle, unipolar pulse resonant with an electronic defect state^27,30,31.

Fig. 1: A selenium vacancy (Vac_Se) in few-layer WSe₂ as a single atom quantum dot.

a Illustration of the experiment: Vac_Se in two monolayer (2 ML) WSe₂ on quasi free standing epitaxial graphene (QFEG) and conductive SiC studied with lightwave-driven STM. Free-space propagating THz pulses induce transient voltage bursts at the STM tip that enable electron tunneling into localized defect states of Vac_Se. b Energy diagram illustrating electron tunneling from the tip to the Vac_Se in a double-barrier model, where the Fermi level (E_F) is pinned by the QFEG substrate. The electron transfer depends on the different coupling strengths Γ, which are based on energy (voltage) differences, the tip-sample spacing z and the WSe₂ layer thickness d that determines the coupling of Vac_Se to the tip (T) and the substrate (S), respectively. The charge occupation at Vac_Se exponentially relaxes to its equilibrium state. c Schematic representation of sequential electron tunneling depicted as an equivalent circuit. The time-dependent tip voltage bias (V_t) is the sum of: (i) constant V_dc, and (ii) single THz voltage pulse with peak amplitude ${V}_{{{{\rm{THz}}}}}^{{{{\rm{pk}}}}}$, or (iii) pump and probe THz pulses with individual amplitude and time delay Δt.

The key observable in LW-STM is the rectified charge Q_LW transferred between tip and substrate per lightwave (THz) transient. Similar to the current in conventional STM, Q_LW can be efficiently increased by reducing the tip-sample distance z. In a QD geometry, a rectified charge requires two consecutive tunneling events from one lead to another via the discrete QD state. Here, two regimes can be distinguished: Q_LW≤ 1e/pulse and Q_LW > 1 e/pulse. In the latter regime, multiple e⁻ tunnel per source pulse, which is only possible if the state that facilitates tunneling is short-lived, indicating strong QD–substrate coupling, Γ_S, where the charge-state lifetime (τ₀) is much shorter than the source pulse duration (τ_LW), ${\tau }_{0}={\Gamma }_{{{{\rm{S}}}}}^{-1}\ll {\tau }_{{{{\rm{LW}}}}}$. The coupling of the tip electrode can be tuned continuously from the weak-injection regime, (${\Gamma }_{{{{\rm{T}}}}}^{-1}\gg {\tau }_{{{{\rm{LW}}}}}$) to the strong-injection regime. In van der Waals materials, and in particular for localized in-gap states (orbitals), the weak coupling between layers and across 2D heterostructures results in long-lived excitations. As a result, the regime of Q_LW > 1 e/pulse is not always accessible, because the large Coulomb energy associated with double charging of the QD inhibits multiple electron transfers within the short pulse duration. However, by using two time-delayed THz pulses, it becomes possible to probe e⁻–e⁻ correlations, such as the Coulomb blockade in the time domain.

Previous studies could show that the average charge-state lifetime τ₀ can be estimated via the maximum tunneling rate at saturated current through a localized state^15,32. Specifically, when the tip–sample coupling Γ_T greatly exceeds the substrate coupling Γ_S, the relationship ${\Gamma }_{{{{\rm{tot}}}}}^{-1}={\Gamma }_{{{{\rm{S}}}}}^{-1}+{\Gamma }_{{{{\rm{T}}}}}^{-1}\approx {\tau }_{0}$ holds, which can be achieved by approaching the tip. Additional WSe₂ layers effectively decouple Vac_Se and substrate, allowing control over τ₀ across several orders of magnitude. In a previous study, we reported average charge-state lifetimes of single Vac_Se in the top layer of 1–4 ML WSe₂, ranging from 1 ps to several ns¹⁶. Owing to the spatial distribution of the defect orbital, top and bottom Vac_Se in the same layer exhibit similar coupling strength to the substrate and thus comparable charge-state lifetime¹⁶. This study lays the basis for investigating ultrafast charge dynamics in the time domain using LW-STM. As a starting point, we consider a neutral Vac_Se in 1 ML and 2 ML WSe₂ characterized by the LUMO and LUMO+1 states (Fig. 2a), residing in the unoccupied spectrum of the WSe₂ band gap. STM topography and orbital images reveal the three-fold symmetric orbital shape of the defect state (Fig. 2b)¹⁸.

Fig. 2: Vac_Se defect states accessed via ultrafast LW-STS and LW-STM.

a dI/dV spectra of Vac_Se in 1 ML (yellow) and 2 ML (turquoise) referenced to pristine WSe₂ (gray). b STM topography and constant-height dI/dV orbital mapping of a top Vac_Se in 2 ML WSe₂. The height set point z₀ corresponds to V_dc = 1.2 V and I_dc = 100 pA (Methods). c LW-STS of Vac_Se in 1 ML (yellow) and 2 ML (blue), each referenced to pristine WSe₂ (gray). The tip–sample distance is z₀ − 4 Å for 1 ML and z₀ − 3 Å for 2 ML. d LW-STM orbital images of Vac_Se in 1 ML (upper panels) and 2 ML (lower panels) at THz peak voltage indicated with (i)–(iv) in (c). All lightwave measurements are performed at V_dc = 0 V. Integration time per data point is 2 s for LW-STS and 20 ms for LW-STM, corresponding to 20 M and 0.2 M THz pulses at 10 MHz repetition rate.

Quenching of lightwave-driven orbital imaging

To maximize the time resolution of THz pulses, the majority of LW-STM/STS experiments have so far been performed in a configuration where V_dc ≪ V_THz and at or close to V_dc = 0 V to minimize dc background currents. Figure 2c shows the rectified charge per THz waveform (transient) in units e/tr as a function of peak THz voltage, which, in first order, reproduces the I(V) characteristic of the tunnel junction²⁸. The onset of the two rising edges in the ${Q}_{{{{\rm{LW}}}}}({V}_{{{{\rm{THz}}}}}^{{{{\rm{pk}}}}})$ curve (black arrows) aligns with the expected spectral locations of the lowest unoccupied molecular/defect orbital (LUMO) and LUMO+1. Additionally, the LW-STM map of the LUMO [Fig. 2d (i)] closely resembles the dc STM measurement. However, the situation is strikingly different for LW-STS of Vac_Se on 2 ML WSe₂ (Fig. 2c turquoise). In this case, we are unable to resolve the defect states through LW-STM [Fig. 2d (iii) and (iv)], even though their STS spectrum matches closely the spectrum of Vac_Se on 1 ML WSe₂. Instead of observing an enhancement in the LW-driven rectification at the defect position, which would typically arise from additional tunneling channels, we see a reduction of LW-driven tunneling at the defect center. This observation suggests that the Vac_Se on 2 ML WSe₂ enters a different lifetime regime, affecting the ultrafast tunneling process. The sub-nm point-like reduction of LW rectification to the conduction band in configurations (ii) and (iv) differs from the defect orbital and appears as a consequence of local band bending due to the charged Vac_Se^33,34.

We attribute the loss of in-gap defect state contrast in 2 ML to an enhanced charge-state lifetime, related to the electronic decoupling of Vac_Se via the additional WSe₂ layer¹⁶. The average charge-state lifetime of different Vac_Se/2 ML obtained from dc current saturation measurements ranges from ${\tau }_{0}^{{{{\rm{2\,ML}}}}}=50 \;{{\rm{to}}}\; 86 \, {{\rm{ps}}}$ (Fig. S1), significantly longer than the sub-1 ps source voltage duration. Consequently, multiple tunneling events per pulse are highly unlikely. Subsequently to the injection by the source pulse, the e⁻ can relax through two possible pathways: (i) forward tunneling to the substrate, contributing to a measurable current, or (ii) backward tunneling to the tip. Due to the small duty cycle in LW-STM, intermediate to strong charge injection from the tip is required to facilitate tunneling within the short duration of the THz peak field. Hence, back tunneling is the more probable pathway if the charge-state lifetime exceeds a few picoseconds, quenching charge rectification. As a result, a transiently charged Vac_Se in 2 ML is more likely to relax by discharging via the STM tip (back tunneling) instead of the substrate (forward tunneling), resulting in zero net charge rectification. In contrast, the smaller lifetime of Vac_Se in 1 ML (${\tau }_{0}^{{{{\rm{1\,ML}}}}} < 3$ ps) enables notable charge rectification from tip to substrate during the transient THz pulse, which explains the orbital contrast observed in the LW-STM images for Vac_Se in 1 ML WSe₂. For THz peak voltages reaching the conduction band, femtosecond carrier relaxation and strong delocalization of continuum states enable sub-cycle charge rectification during the THz gate, irrespective of the layer thickness, yielding an unperturbed onset of conduction band states (gray curves in Fig. 2c).

Back tunneling suppression via Franck–Condon blockade

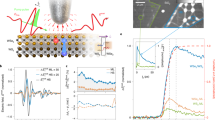
Next, we study the effect of the dc bias on THz charge rectification for a Vac_Se in 2 ML (Fig. 3a). To ensure comparability across different Vac_Se, we define a relative voltage offset from the LUMO ΔV_z  = V_dc − V_LUMO(z) to account for local shifts of the relative LUMO position with tip height, lateral tip position, and sample heterogeneity (Methods). The first two factors arise from the well-known voltage drop across a double-barrier tunneling junction³⁵. In contrast to Fig. 2d (iii), where we set V_dc = 0 V, we start to observe orbital contrast in LW-STM as V_dc nears the LUMO resonance, as seen in Fig. 3b. This effect becomes more pronounced as ΔV_z approaches zero. We attribute the reestablished LW-STM contrast to a suppression of back tunneling. This suppression can be explained by the so-called Franck–Condon blockade³⁶, which is more significant than the (slowly-varying) bias-dependent change of the tunneling barrier. Note that the orbital shape of Vac_Se in Fig. 3b appears saturated, unlike in the monolayer case in Fig. 2d (i). Due to the required ΔV ≈ 0 V, dc electrons block the THz electrons at some tip positions. The same orbital shape as for the 1 ML case can be recovered for specific V_dc and tip heights, as shown in Fig. 4b. When V_dc exceeds the onset of the Vac_Se resonance (ΔV_z > 0 V), significant dc currents occur, eventually leading to the saturation of I_dc and causing charge fluctuations that substantially increase the noise in the THz current (Fig. 3c).

Fig. 3: Suppression of back tunneling via the Franck–Condon blockade.

a Schematic illustration of reduced back tunneling rate at elevated V_dc. b LW-STM orbital images of Vac_Se/2 ML showing a strong nonlinear increase of net rectified charge and orbital sensitivity as ΔV = V_LUMO − V_dc → 0 V. Measurement obtained at ${V}_{{{{\rm{THz}}}}}^{{{{\rm{pk}}}}}=0.49$ V, V_LUMO = 0.7 V, and z = z₀ −3 Å. c dI/dV (green shaded curve) and I(V) spectrum (black, upper panel) and rectified charge (black, lower panel) as a function of V_dc measured with ${V}_{{{{\rm{THz}}}}}^{{{{\rm{pk}}}}}=0.32$ V and z = z₀ − 3 Å. The simulation (red curve) assumes a single vibrational mode ℏΩ = 8 meV, a Huang-Rhys factor of 2.2, and experiment values for THz waveform, LDOS and z (Methods). The data for (b) and (c) were obtained on ${{{{\rm{Vac}}}}}_{{{{\rm{Se}}}}}^{2.2}$ and ${{{{\rm{Vac}}}}}_{{{{\rm{Se}}}}}^{2.4}$ respectively (Fig. S1). Black crosses in panel b indicate an equivalent position of the point spectrum. Integration time per data point is 100 ms for LW-STS and 15 ms for LW-STM, corresponding to 4.1 M and 0.6 M THz pulses at 41 MHz repetition rate. d Transitions between vibronic states of the charged and neutral Vac_Se LUMO in the Franck–Condon picture at high V_dc(ΔV → 0 V) are limited to ground state transitions. e At reduced V_dc transitions to higher vibronic modes of the neutral state become available, enhancing the effect of back tunneling.

Fig. 4: Influence of strong and weak tip interaction on charge rectification.

a Schematic illustration of the electronic coupling strength of Vac_Se to the STM tip at different tip height. b LW-STM orbital images with ${V}_{{{{\rm{THz}}}}}^{{{{\rm{pk}}}}}=0.49$ V and at V_dc = 0.7 V ($\Delta {V}_{{z}_{0}}=0.0$ V). Images left to right at increasing tip—sample distance show a transition from the saturated (Δz = −3.5 Å) to the unsaturated (Δz = −1 Å) orbital shape. Reduced charge rectification at the center of Vac_Se at Δz = −3.5 Å is related to strong back tunneling, i.e., efficient charge depletion by the tip. The dotted line marks the position for cross sections in Fig. S5b. c Q_LW point spectrum (black curve) as a function of tip--sample distance measured on the orbital lobe of Vac_Se. The maximum at −2.5 Å emphasizes the interplay of forward and backward tunneling, modeled by a simulation (red) that assumes a single vibrational mode with an energy of 8 meV and a Huang-Rhys factor of 2.2 (Methods). The data for b and d were obtained on ${{{{\rm{Vac}}}}}_{{{{\rm{Se}}}}}^{2.2}$ and ${{{{\rm{Vac}}}}}_{{{{\rm{Se}}}}}^{2.4}$ respectively (Fig. S1). Black crosses in b mark the equivalent position of the point spectrum in (c). Integration time per data point is 100 ms for z-spectroscopy and 15 ms for LW-STM, corresponding to 4.1 M and 0.6 M THz pulses at 41 MHz repetition rate.

In the Franck–Condon blockade regime, changes in the phonon population of a defect can introduce an asymmetry between forward and backward tunneling. In Fig. 3d, e, the principle of the Franck–Condon blockade is schematically illustrated. Within the Franck–Condon approximation, each charge-state of the defect is represented by a harmonic potential with a single vibrational mode of characteristic energy ℏΩ. Due to fast vibrational cooling in 2D semiconductors³⁷ (curved black arrow), charge-state transitions primarily occur from the vibrational ground state (dark red), centered around the relaxed nuclei positions. The displacement of the potential energy surface between different charge states increases with the electron-phonon coupling strength. As a result, electron transfer (vertical blue arrows) is generally accompanied by vibrational excitation. However, when the dc bias is set close (within the order of the vibrational energy) to the LUMO orbital energy (Fig. 3d), the overlap with energetically accessible low-lying vibrational states of the neutral defect is greatly reduced³⁸. In contrast, when the dc bias is much lower (Fig. 3e), all vibrationally excited states remain accessible. Consequently, back tunneling can be significantly suppressed by raising the electrochemical potential of the tip.

We model the transient charging and discharging of the atomic defect by a time-dependent Markov process, described by the so-called Master equation, as detailed in the Methods section. This model treats the defect by three electronic states (one ground state and two charged states, LUMO and LUMO+1), as well as a single vibrational mode (ℏΩ ≈ 8 meV) with multiple quanta, and a Huang-Rhys factor of S ≈ 2.2 for a Vac_Se in 2 ML WSe₂. These parameters are extracted from experimental STS spectra and the average charge-state lifetime τ₀ from STM approach curves (Fig. S6a, b). The transition matrix is expressed as the sum of the transition rates due to sample, tip, and phonon relaxation. To calculate the rectified charge, we model the actual waveform of the THz transient (Fig. S6c). The simulations, shown in Fig. 3c (red), qualitatively and quantitatively reproduce the steep increase of the THz current as a function of dc bias within tens of meV of the defect resonance. Importantly, the strong suppression of back tunneling at elevated bias is attributed to a reduction in the energetically allowed vibronic transitions into the neutral state. The Franck–Condon blockade acts as an effective backflow valve, favoring unidirectional charge transport when charge-state lifetimes exceed the pulse duration, which is crucial for achieving charge rectification in LW-STM.

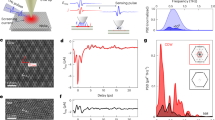
Optimal tip distance between weak and strong coupling

The coupling of the atomic QD to the tip contact not only sensitively depends on the tip bias, but also on the tip–sample distance (Fig. 4a). Figure 4b shows a series of LW-STM images illustrating the evolution of the orbital contrast at different tip heights at V_dc = 0.7 V, corresponding to ΔV = 0 at z₀. In contrast to Fig. 2c the orbital images are saturated as a consequence of a transient population that produces a convolution of defect orbital and a local variation in Franck–Condon blockade. The black curve in Fig. 4c presents a Q_LW approach curve obtained on a Vac_Se orbital lobe. Both spatial (Fig. 4b) and height (Fig. 4c) dependence reveal an initial increase, followed by a decrease of the LW signal as the tip approaches the defect. Initially, reducing the tip height compensates for the short duty cycle in LW-STM and enhances the signal. However, at very close distances, stronger back tunneling suppresses the rectified current, resulting in a maximum rectification near z − z₀ = − 2.5 Å. Two factors contribute to this effect: Due to the voltage drop across the WSe₂ layers, smaller tip heights (or closer lateral tip position) shift the LUMO resonance to higher voltages, thereby reducing ΔV and thus enhancing back tunneling, as previously discussed. Additionally, the increasing tunneling rate Γ_T(z) becomes much larger than the defect–graphene tunneling rate, Γ_S. This promotes back tunneling, dominating over the Franck–Condon blockade. Our simulations (Fig. 4c, red) reproduce the shape and magnitude of the experimental Q_LW(z) curve, accounting for both the z-dependent voltage drop and the increase in Γ_T(z). While quenching of excited states via electron transfer to the tip was previously reported for photo-excited molecules^39,40, here we directly map this process with ultrafast time resolution.

Time-domain detection of the ultrafast Coulomb blockade

Finding optimal parameters for ΔV and z enables time-domain mapping of the transient Coulomb blockade close to its average charge-state lifetime. Here, we use a sequence of two time-delayed THz transients in combination with V_dc, such that V_dc+${V}_{{{{\rm{THz}}}}}^{{{{\rm{pk}}}}}$ accesses the localized in-gap defect state, but remains below the onset of the conduction band (Fig. 5a, d). In Fig. 5b, e, we show the transient Coulomb blockade at Vac_Se in 1 and 2 ML WSe₂. In these measurements, Q_LW(Δt) describes the rectified charge by the probe transient only (kHz amplitude modulation), while the pump transients interact at full repetition rate (41 MHz). Near the overlap Δt = 0 ps, the signal is dominated by interference between the THz waveforms, such that we restrict our analysis to time delays Δt > 1.5 ps. For time delays much longer than the average charge-state lifetime τ₀, the transient signal recovers to the equilibrium value ${Q}_{{{{\rm{THz}}}}}^{{{{\rm{eq}}}}}$, corresponding to unperturbed rectification by the probe transient. For orbital images acquired at different time delays, we plot the relative change of rectified charge $\Delta {Q}_{{{{\rm{THz}}}}}={Q}_{{{{\rm{THz}}}}}-{Q}_{{{{\rm{THz}}}}}^{{{{\rm{eq}}}}}$, obtained by subtraction of a reference map at a large delay (Δt ≫ τ₀). The differential images clearly reveal the orbital structure of Vac_Se with negative amplitude, providing a direct and dynamic visualization of a Coulomb blockade at the atomic scale.

Fig. 5: Ultrafast Coulomb blockade detection using THz pump – THz probe time-domain sampling.

a STM topography and STS spectrum of Vac_Se in 1 ML WSe₂. The gray spectrum references pristine WSe₂. The illustration shows the concept of pump-probe measurements, where a THz pump pulse (red) charges the system while a time-delayed THz probe pulse (blue) measures the transient charge occupation. b The rectified charge of the THz probe pulse as a function of THz–THz delay. The black line is an exponential fit to the relaxation of the charge state. Orbital images at selected delays, illustrating the change of rectified charge ΔQ_LW with respect to an equilibrium reference at 10 ps. c Dependence of the charge-state lifetime extracted via exponential fitting in panel b as a function of ΔV = V_LUMO − V_dc. The horizontal line (gray) marks the intrinsic charge-state lifetime from dc measurements. Error bars correspond to the fit uncertainty, and lifetime values below 0.5 ps are shorter than the time resolution of the experiment. d–f Same analysis for Vac_Se in 2 ML. Due to significant THz reflections, apparent as dips in Q_LW(Δt), the extraction of a charge-state lifetime from the pump-probe measurement in panel (e) must be matched with a simulation as detailed in the Methods. The data was obtained on different Vac_Se characterized in Fig. S1: a–c at ${{{{\rm{Vac}}}}}_{{{{\rm{Se}}}}}^{1.2}$, d–e at ${{{{\rm{Vac}}}}}_{{{{\rm{Se}}}}}^{2.3}$, and f at ${{{{\rm{Vac}}}}}_{{{{\rm{Se}}}}}^{2.4}$. Integration time per data point is 100 ms for LW-STS and 30 ms (1 ML) or 15 ms (2 ML) for LW-STM, corresponding to 4.1 M and 1.2 M or 0.6 M THz pulses at 41 MHz repetition rate.

We model the lightwave-driven pump-probe (LW-PP) point spectrum by a single exponential fit (dashed black line) that allows to extract the relaxation dynamics of the Vac_Se QD. This effective charge-state lifetime τ_eff combines the interplay of intrinsic charge relaxation to the substrate and ultrafast back tunneling to the tip. To disentangle these contributions, we record LW-PP spectra at increasing V_dc. We determine τ_eff via exponential fitting of the spectra at time delays between 1.5 ps and 12 ps, ensuring robust convergence of fit parameters. The error bar includes disturbances related to THz trailing oscillations at high V_dc. τ_eff strongly increases as ΔV → 0 and peaks near ΔV = 0 V, where it reaches the intrinsic charge-state lifetime τ₀ (Fig. 5c). At ΔV ~ 0 V, back tunneling is strongly suppressed and the intrinsic relaxation channel to the substrate becomes the dominant mechanism for charge relaxation. Notably, the effective charge-state lifetime is rapidly quenched for negative ΔV. This highlights the critical role of the Franck–Condon blockade for this experiment. At ΔV < − 50 mV the time resolution and transient signal amplitude become insufficient to resolve the Coulomb blockade. Our master equation model enables simulations of charge rectification at various time delays using a model of our experimental waveform (Methods). Exponential fitting of simulated LW-PP spectra with similar boundary conditions as in the experiment clearly reveals the trend of increasing effective charge-state lifetime near ΔV = 0 V (Fig. 5c). The onset of quasi-static charging at dc biases above the LUMO resonance, as shown in Fig. 3c, precludes ultrafast measurements due to dominant stochastic tunneling.

We performed the same series of measurements at a Vac_Se in 2 ML WSe₂ with an intrinsic charge-state lifetime τ₀ = 86 ps. As the charge-state lifetime exceeds the time window of trailing reflections from windows in our beam path, which can amount up to 30% field amplitude (Fig. S2), Q_LW(Δt) deviates from a simple exponential decay, instead displaying dips indicative of interference with these reflections. Since ΔV values close to 0 V are necessary to suppress back tunneling effectively, the impact of trailing reflections on the measurements can only be minimized, though not entirely eliminated. At elevated V_dc close to the onset of the defect state, the amplitude of THz pulse reflections is sufficiently high to interact with the Vac_Se states, causing additional excitations and experimental replica at various time delays. Nevertheless, an ultrafast Coulomb blockade lasting over few-10 ps is clearly revealed by the LW-PP spectrum and ultrafast orbital images in Fig. 5e. For simple and robust extraction of an effective charge-state lifetime, we determine the equilibrium signal at Δt > 250 ps and fit a single exponential model only to the unperturbed data from 1.5 to 15 ps. Simulated LW-PP spectra on the basis of the Franck–Condon blockade and the full transient waveform with multiple reflections quantitatively model the experiment, including the effect of THz pulse reflections (Methods, Fig. S2). Limiting the fit interval to Δt < 15 ps causes large fit errors for τ_eff ≳ 20 ps, however, it ensures robustness of the fit in experiment and simulation. Again, the sharp decrease of τ_eff with more negative ΔV emphasizes the increasing relevance of back tunneling for Vac_Se in 2 ML with extended τ₀. As ΔV strongly depends on the lateral and vertical position of the tip, distinct ΔV regimes can coexist within a single LW-STM image. In the defect periphery, where ΔV > 0, large dc currents permanently charge the defect, effectively quenching Q_LW. At the circular transition region, where ΔV ≈ 0, charge fluctuations dominate, leading to significant noise in Q_LW (Fig. S5c).

The lack of a WSe₂ moiré structure in our sample reduces mechanical strain and facilitates fast delocalization of phononic excitations. At time scales <5 ps, signatures of coherent motion of the WSe₂ layer interfere with THz field-induced modulations and remain indistinguishable in the experiment. In consequence, we do not resolve a coherent motion of the WSe₂ layer or energy modulation of the defect state driven by inelastic excitations of the Vac_Se states as reported by Roelcke et al.²⁸, which would also modulate the Franck–Condon blockade significantly. In contrast to fast charge relaxation on a metallic substrate, finite charge-state lifetimes and the Coulomb blockade in our samples impose a stochastically uncorrelated perturbation to any coherent signal since the charge relaxation is not phase locked. Furthermore, the decoherence of lattice excitations is amplified by charge transfers from pulse replicas that become relevant at elevated V_dc.

In conclusion, using THz pump–THz probe time-domain sampling, we capture real-space snapshots of the transient Coulomb blockade. By fine-tuning the transient THz waveform, dc bias offset, and tip height, we selectively populate specific defect orbitals of single selenium vacancies in monolayer and bilayer WSe₂ and track the charge transfer into the substrate. A rate equation model accurately describes the time-dependent tunneling process across the different coupling regimes, applicable to other materials and quantum systems. Our experiments overcome challenges posed by back tunneling, revealing a Coulomb blockade that persists for two orders of magnitude longer than the duration of THz voltage pulses. Quenching of the LW-STM signal due to population depletion by the tip electrode is mitigated by breaking the symmetry between charge transfer from and to the tip via the Franck–Condon blockade, acting as a charge backflow valve. The Franck–Condon blockade drastically reduces the charge-transfer rate from the defect state to the tip by limiting the number of available vibrational transitions. Precise control of the transient bias and coupling strength between the STM tip and the defect state enables net charge rectification, essential for LW-STM measurements. This work complements recent advances in observing defect resonances²⁹, coherent lattice dynamics²⁸, charge density waves⁴¹, and bidirectional subcycle tunneling currents⁴² with LW-STM, establishing a pathway for probing ultrafast charge dynamics in low-dimensional materials and localized quantum states. We envision that tunneling asymmetries induced by vibrational transitions, spin and orbital momentum multiplicities will enable lightwave-driven charge control in complex materials, pushing the frontiers of ultrafast nanoscale electronics.

Methods

Sample preparation

Our WSe₂ samples are grown via metal organic chemical vapor deposition on few-layer epitaxial graphene supported by a conductive silicon carbide (c-SiC) substrate. The plasma frequency of c-SiC is sufficient to effectively suppress THz reflections from the bottom surface. Intercalation of the graphene layers with hydrogen prior to WSe₂ growth terminates the dangling silicon bonds, providing a homogeneous electrostatic background. Further details of the sample growth procedure were previously reported along references^16,43. Key advantages of epitaxially grown samples on quasi-free-standing graphene (QFEG) are the electronic homogeneity (no moiré), a Fermi energy pinned in the center of the large WSe₂ band gap, and weak hybridization with the substrate¹⁶. The strong out-of-plane confinement facilitates electron-phonon coupling, well-defined defect states, and high contrast of the defect states inside the band gap, enabling LW-STM at nonzero V_dc.

High-temperature annealing in UHV is required to clean samples after ambient exposure. We generate isolated Vac_Se in the top WSe₂ layer via light sputtering with Ar ions, approximately 2 s at 0.12 kV acceleration bias, 0.16 kV discharge voltage, and a sub-μA sputter-current¹⁶. Multiple Vac_Se in 1–2 ML WSe₂ were investigated for this study, emphasizing the robustness and repeatability of the technique. Fig. S1 lists STM topography, dI/dV spectra, and current saturation curves of the relevant Vac_Se.

STM height set point and average charge-state lifetime

For a reproducible definition of the tip height z₀, the STM feedback loop was opened on pristine WSe₂ at a set point current of 100 pA with applied bias voltage of 1.5 V (1 ML) or 1.2 V (2 ML), corresponding to an energy 200 meV above the conduction band onset. We estimate an absolute tip–sample distance at z₀ of (7 ± 2) Å. The average charge-state lifetime (τ₀) of Vac_Se states scales with the decoupling layers of the sample and is determined via the current saturation in STM approach curves^15,16,32. For simplicity, we consider only the first unoccupied defect state (LUMO) of Vac_Se for the determination of τ₀. Reduced localization due to a lower binding energy slightly reduces the average charge-state lifetime of the LUMO+1 defect state¹⁶. For different Vac_Se, τ₀ slightly vary due to differences in their dielectric environment, however, the energy spectra and orbital shape remain comparable within a few-10 meV shifts (Fig. S1).

Voltage drop and definition of ΔV

In our double barrier tunneling junction geometry, the effective voltage from the tip to the Vac_Se defect states depends on the WSe₂ dielectric screening and the absolute height set point z₀. The relative voltage ΔV = V_dc − V_LUMO(z) is important to compare LW-STM data across different Vac_Se, where the onset of the LUMO, V_LUMO(z), varies on the order of tens of meV due to inhomogeneity of the sample and as a function of z. While for ΔV < 0 the dc current is negligible, ΔV > 0 V generates a notable dc current and thus increases the Vac_Se population statically in the experiment. In orbital imaging, we define ΔV at a single point on the orbital lobe of Vac_Se, avoiding complications of lateral dependence. We determine V_LUMO(z) directly from a dI/dV measurement at z or via extrapolation of V_LUMO(z₀) on the basis of measurements performed in ref. ¹⁶, Fig. 2. Owing to the high sensitivity towards thermal drifts on the sub-Å scale, we estimate an accuracy δ_ΔV≈ 10 mV.

LW-STM setup and near-field waveform detection

Our LW-STM system is a commercial low-temperature STM from CreaTec Fischer & Co. GmbH with free-space optical access to the STM junction via large numerical aperture parabolic mirrors focused on the tip apex. THz pulses are generated via tilted pulse front optical rectification in lithium niobate pumped by a multi-MHz Yb:fiber laser with pump pulse energies of a few μJ. The system achieves peak THz voltages at the STM tip up to 0.5, 1, and 2 V at 41, 20, and 10 MHz repetition rates, respectively. We use frustrated internal reflection in a PTFE prism as well as a double or single mirror sequence to adapt the phase and polarity of single-cycle THz pulses at the STM tip⁴⁴. Pump and probe pulses are generated independently and are recombined in collinear geometry via a c-cut sapphire window. Purging of the optics setup with dry air reduces ambient absorption before pulses are coupled into the vacuum chamber. Operating conditions of the scanning probe microscope are 5 K base temperature and 10⁻¹⁰ mbar pressure.

To discriminate lightwave-driven currents, we mechanically modulate the THz path at an intermediate focus using frequencies between 800 and 1000 Hz that are compatible with the 10⁹ transimpedance amplifier of the STM and show weak mechanical and electric noise. I_LW is then extracted via lock-in demodulation and calibrated with respect to the absolute current. We convert current to rectified charge per transient (e/tr) on the basis of the laser repetition rate and the 50% duty cycle of the modulation. In pump-probe measurements, only the probe pulse is modulated, while pump pulses enter the junction at full repetition rate. We find that high DC currents prevent sensitive measurements of Q_LW because of large noise floors.

The THz peak voltage is calibrated against V_dc using a recently developed approach based on the strongly nonlinear onset of the WSe₂ conduction band³¹ measured in a clean pristine region of the sample (Fig. S2a–c). On the basis of this amplitude calibration, we determine the relative time origin (Δt = 0) and temporal resolution of the experiment (380 fs) by cross correlation of equal THz fields where only the sum field rectifies charges (Fig. S2d). In a second step, we measure the transient near-field waveform at the STM tip using THz cross correlation (THz-CC)^29,31. Here, we set relative amplitudes such that a strong THz gate pulse rectifies electrons to the conduction band in a linear section of the dI/dV curve, while a time-delayed weak THz pulse modulates the THz peak voltage. This approach allows waveform characterization without requiring complex retrieval algorithms^31,45 (Fig. S2e, f). Waveform sampling at extended delays reveals THz reflections at approximately 40, 60, 80, 100, and 120 ps due to sapphire windows of the vacuum chamber, cryostat, and the beam combiner, which are unavoidable in our setup (Fig. S2g). Thickness variation of sapphire windows and the beam combiner effectively reduces the amplitude of major THz reflection to below 30% of the main pulse, causing reflections at 40 and 80 ps to show distorted waveforms due to interference effects.

Theoretical model

The dynamics observed in the tunnel junction can be well represented by a time-dependent Markov process, which is described by the so called Master equation $\dot{N}=M\cdot N$, where N is a vector containing the occupation probabilities of all considered states of the system and M is the transition matrix. Here, we considered three distinct electronic states: The electronic ground state at energy E₀ = 0 eV, where the defect is charge neutral (Q₀ = 0 e), as well as two negatively charged states (Q_1,2 = −e), with an additional electron in either the LUMO (E₁) or the LUMO+1 (E₂). In addition, we model each electronic state with a single vibronic mode with 6 (14) vibrational excitation levels plus the vibrational ground state, yielding a total of 21 (45) different vibronic states for 2 ML (1 ML) WSe₂. The different number of required vibrational levels is due to different Huang-Rhys factors between 1 ML and 2 ML WSe₂ (see below).

Transition between these states can occur due to inelastic charge transfer between defect and tip or sample, or via vibrational relaxation within one electronic state. Accordingly, the transition matrix can be written as the sum of the transition rates due to sample, tip and phonon relaxation:

$$M={M}^{{{{\rm{s}}}}}+{M}^{{{{\rm{t}}}}}+{M}^{{{{\rm{ph}}}}}$$

(1)

The transitions related to a change of charge state are given by

$${M}_{f{\lambda }^{{\prime} }i\lambda }^{{{{\rm{s}}}}}={T}_{f{\lambda }^{{\prime} }i\lambda }({z}_{s},0)\cdot {V}_{{\lambda }^{{\prime} }\lambda }\cdot {\Upsilon }_{fi}$$

(2)

$${M}_{f{\lambda }^{{\prime} }i\lambda }^{{{{\rm{t}}}}}={T}_{f{\lambda }^{{\prime} }i\lambda }({z}_{t},V)\cdot {V}_{{\lambda }^{{\prime} }\lambda }\cdot {\Upsilon }_{fi}\cdot {\Lambda }_{fi},$$

(3)

with indices i and f representing the initial and final electronic state, λ and ${\lambda }^{{\prime} }$ the initial and final vibrational state, ${V}_{{\lambda }^{{\prime} }\lambda }$ the Franck–Condon factors, and ${T}_{f{\lambda }^{{\prime} }i\lambda }$ the tunneling matrix element, respectively. ϒ_fi captures the effect of various multiplicities of the involved states, and Λ_fi represents their relative coupling strength to the tip.

The tunneling matrix element ${T}_{f{\lambda }^{{\prime} }i\lambda }(z,V)$ describes the tunneling probability of an electron between the tip or sample and the defect state, depending on bias voltage V and distance z between the defect and lead:

$${T}_{f{\lambda }^{{\prime} }i\lambda }(z,V)=\left\{\begin{array}{ll} \int_{-\infty }^{V}{{{\rm{d}}}}E\,g(E-\Delta {E}_{f{\lambda }^{{\prime} }i\lambda })\,{e}^{-2\kappa z}\quad &,{{{\rm{if}}}}{Q}_{f}-{Q}_{i}=-e\\ \int_{V}^{\infty }{{{\rm{d}}}}E\,g(E+\Delta {E}_{f{\lambda }^{{\prime} }i\lambda })\,{e}^{-2\kappa z}\quad \;\;\; &,{{{\rm{if}}}}{Q}_{f}-{Q}_{i}=+ e\\ 0\, \qquad \qquad\qquad\qquad\quad\qquad\quad &,\; {{{\rm{otherwise}}}} \;\;\quad \end{array}\right.$$

(4)

with $\Delta {E}_{f{\lambda }^{{\prime} }i\lambda }$ being the energy difference between the initial and final vibronic state and decay rate $\kappa=\sqrt{2{m}_{e}(\phi -E+eV/2)}/\hslash$. The transition threshold is broadened by a Gaussian line shape g(E) and normalized to integrate to the quantum of conductance G₀ = 2e/ℏ for z = 0.

For the Franck–Condon factors ${V}_{{\lambda }^{{\prime} }\lambda }$, we assume only a rigid shift in normal mode coordinates and negligible Duschinsky rotation⁴⁶:

$${V}_{{\lambda }^{{\prime} }\lambda }=\frac{\min ({\lambda }^{{\prime} },\lambda )!}{\max ({\lambda }^{{\prime} },\lambda )!}\,{S}^{| {\lambda }^{{\prime} }-\lambda | }\,{e}^{-S}\,{\left[{L}_{\min ({\lambda }^{{\prime} },\lambda )}^{| {\lambda }^{{\prime} }-\lambda | }(S)\right]}^{2},$$

(5)

with Huang-Rhys factor S and Laguerre polynomials ${L}_{n}^{\alpha }$.

The effect of the various multiplicities on the transition rates is captured by the factor ϒ_fi. Since we are only considering transitions for which either the final or initial state is a singlet, we can write ϒ_fi = m_f, with m_f being the multiplicity of the final state.

The last term Λ_fi for the tip-mediated transitions captures the relative coupling of LUMO and LUMO+1 to the tip, which can vary with lateral tip position. The additional factor Λ_fi is normalized to 1 for the tip–LUMO coupling and has typical values between 0.5 and 1.0 for the tip–LUMO+1 coupling, chosen to match the experimental dI/dV spectra.

For the charge-neutral phonon relaxations, the transition matrix is written as a decay to the vibrational ground state with lifetime τ_ph:

$${M}_{f{\lambda }^{{\prime} }i\lambda }^{{{{\rm{ph}}}}}=\left\{\begin{array}{ll}1/{\tau }_{{{{\rm{ph}}}}}\quad &{{{\rm{,\; if}}}}f=i,{\lambda }^{{\prime} }=0{{{\rm{and}}}}\lambda > 0\\ 0 \qquad\quad &,{{{\rm{otherwise.}}}} \qquad\qquad\;\;\end{array}\right.$$

(6)

Lastly, the diagonal entries of the total transition matrix are set to M_ll = −∑_k≠lM_kl.

For static bias voltages, the master equation is solved for $\dot{N}=0$ to obtain the bias and z dependent equilibrium occupation N_eq. The dc current is then given by the net charge transfer between defect and sample ${I}_{{{{\rm{dc}}}}}={\sum }_{k}{\left({W}^{s}N\right)}_{k}$, with ${W}_{f{\lambda }^{{\prime} }i\lambda }^{s}={M}_{f{\lambda }^{{\prime} }i\lambda }^{s}\cdot ({Q}_{f}-{Q}_{i})$. In order to evaluate the evolution of the system under a transient bias voltage, the master equation is solved in discrete time steps ${N}_{i+1}-{N}_{i}=M\left(V({t}_{i})\right)\Delta t\cdot {N}_{i}$, starting from the equilibrium occupation at V_dc.

Implementation of simulation

The simulations are based on the master equation and require experimental parameters that can be obtained from static measurements of the Vac_Se (Fig. S1). We extracted the energies of localized defect states E₁ and E₂ via the zero-phonon lines and the tip coupling factor L_f,i from the experimental dI/dV spectrum at the set point z₀. The average charge-state lifetime τ₀, and the tunneling barrier κ were obtained via a rate equation fit to the I(z) approach curve¹⁶.

The vibronic broadening of the defect state resonances was approximated by a single vibrational mode with ℏΩ = 8 meV and a Huang-Rhys factor of S = 2.2 (2 ML) for both charge states. We find that a Gaussian lineshape with 3 meV bandwidth provides a good match with the experimental dI/dV (Fig. S6b), while being consistent with literature on Vac_S in WS₂, observing a dominant phonon mode of 12 meV and a Huang-Rhys factor of 1.2¹⁸. Considering an average 40% softening of the phonon modes in WSe₂ as compared to WS₂⁴⁷, we choose a phonon mode of ℏΩ = 8 meV, and fit the Huang-Rhys factor to the STS spectrum. For the simulations on 1 ML WSe₂ we cannot directly fit the vibronic satellite peaks of the LUMO resonance. Instead, we rescale the Huang-Rhys factor from 2 ML WSe₂ by a factor of about two, as previously found for C_S in 1 ML and 2 ML WS₂¹⁹. Therefore, we choose S = 5 for Vac_Se in 1 ML WSe₂, while we assume the phonon mode energy to remain constant, ℏΩ = 8 meV¹⁹.

Although lifetime broadening of a state with tens of picoseconds of lifetime would lead to a Lorentzian lineshape with a few tens of μeV broadening, we justify the choice of Gaussian lineshapes by the presence of additional low-energy vibrational modes with a high Huang-Rhys factor (S ≫ 1), e.g., well-known interlayer phonons for multi-layer TMDs⁴⁸. These low-energy phonons impose an additional Franck–Condon blockade that explains the difference between simulation and experiment at bias voltages overlapping with the LUMO resonance (ΔV > 0 V). In particular, the breakdown of simulations at ΔV ≈ 10 mV in Fig. 3c emphasizes the limitation of the 1-phonon mode treatment. A thorough 2-mode treatment would require significantly more computational resources without major benefits to our model.

The effective strength of the Franck–Condon blockade also depends on the phonon lifetime τ_ph. We distinguish three regimes in the evolution of charge-state transitions between tip and defect: (I) A voltage gate for charging, (II) vibronic relaxation, and (III) charge relaxation, sketched in Fig. S3. The THz peak voltage ${V}_{{{{\rm{THz}}}}}^{{{{\rm{pk}}}}}$ of few-100 mV enables transitions from the neutral ground state to high vibronic modes of the charged state. Vibronic relaxation in a 2D semiconductor with strong electron-phonon coupling typically occurs faster than the THz gate timescale. Additionally, due to local resolution of LW-STM, combined with the fast lateral diffusion of phonon modes, the atomic-scale QD remains unaffected by the lifetime of acoustic phonons. As a result, we expect relaxation of the charged Vac_Se to the vibrational ground state within few-100 fs, as seen for thermalization and cooling of photoexcited charge carriers³⁷. We conservatively assume τ_ph = 1 ps for the simulations. After the source pulse and at small ΔV ≲ 0 V, charge-state transitions from low vibrational modes of the charged state have only a few vibrational modes in the neutral state available, creating an asymmetry between forward and backward tunneling that reduces the impact of back tunneling. In addition, our simulation considers the LUMO and LUMO+1 multiplicity as a quartet (J = 3/2) and a sextet (J = 5/2) state, respectively¹⁸, further enhancing this asymmetry (Fig. S5).

The voltage drop in 2 ML WSe₂ is approximated by a plate capacitor model, ${V}_{{{{\rm{eff}}}}}={V}_{{{{\rm{dc}}}}}\frac{z}{z+d/{\epsilon }_{r}}$, with a gap composed of vacuum and WSe₂ using a dielectric constant ϵ_r = 6.5 and d = 6.5 Å for WSe₂ layer spacing⁴⁹ (Fig. S6e). Due to the complex tip shape and iso-potential surfaces that are not parallel to the substrate plane, the voltage drop does not only depends on the tip height z but also on the lateral position of the tip. An accurate description of the effective bias potential can be obtained by integrating the wavefunction with the spatial dependence of the electric potential within the junction⁵⁰. In most simulations shown in this work, this effect is not crucial to reproduce the experimental data. However, for the Q_LW(z) measurements, this simple plate capacitor model is not sufficient to model the experiment quantitatively, see Extended Fig. S6g (red line). Because the Franck–Condon blockade depends strongly on the effective applied V_dc, it is very sensitive to changes in the voltage drop and therefore needs a more sophisticated model for the voltage drop. For this reason, we introduced a slightly modified junction model for the Q_LW(z) measurements. The tip position for tunneling is assumed to be at height z₀, whereas the effective plane of the plate capacitor is at a larger distance from the sample z_{V D} > z₀ (Fig. S6e–g). For the 1 ML WSe₂ the simple plate capacitor model is used with an d/ϵ_r = 0.1 Å.

To match the simulations of the Vac_Se in 1 ML WSe₂ in Fig. 5 quantitatively, we assume a 0.4 Å uncertainty on the experimental z₀ that may arise from small lateral variations in the tip position between the I(z) spectroscopy and THz pump-probe measurements.

The simulation includes a model of the extended transient waveform to reproduce the experimental time-domain signal. Since pump and probe are indistinguishable in the experiment and equally interact with the Vac_Se state, the Coulomb blockade causes a transient signal that is symmetric at Δt = 0 ps. This significantly impacts measurements at Δt > 15 ps, where transient signals from the main pulse and reflections overlap, causing a non-trivial curvature. Thus, we restrict the data interval for exponential fitting between 1.5 and 15 ps. As another consequence of reflections, extended coherent signals are quenched due to destructive interference from multiple excitations.