Introduction

Achieving global carbon neutrality and addressing the escalating challenges of climate change demand transformative advancements in sustainable energy systems1. Nuclear energy has emerged as a cornerstone of this transition, offering a highly efficient and low-emission alternative to fossil fuels. However, the long-term viability of nuclear energy depends heavily on the availability of uranium, its primary fuel source2,3. Currently, uranium is predominantly sourced from terrestrial uranium ores (U3O8), but these reserves are finite and projected to be depleted within the next century. This limitation poses a significant challenge to meeting the growing demand for nuclear energy, especially as more countries adopt nuclear power to achieve decarbonization goals4,5. In this context, seawater uranium extraction represents a revolutionary technology, since the ocean contains approximately 4.5 billion tons of dissolved uranium, which is about 1000 times the known terrestrial uranium reserves6. Unlike terrestrial reserves, seawater uranium is constantly replenished through geological processes, representing an essentially inexhaustible resource7. However, the ultra-low concentration of uranium (~ 3.3 ppb) and the presence of competing ions such as sodium and magnesium significantly hinder economically viable extraction, making this a grand scientific and technological challenge8,9.

Over the past few decades, various methods have been developed to extract uranium from seawater, including ion exchange, adsorption, chemical precipitation, biological capture, photocatalysis, and electrochemistry10. COF-based photocatalytic and electrochemical approaches have demonstrated excellent uranium uptake in recent reports, achieving high adsorption efficiency through the synergistic combination of catalytic H2O2 generation and uranyl chelation or precipitation11,12. These methods, however, require external energy input and more elaborate material synthesis, which may limit their broader practical application and scalability13. In contrast, amidoxime-based adsorbents, particularly polyamidoxime (PAO) hydrogels, exhibit remarkable selectivity and strong affinity for uranyl ions (UO22+)14. They can be synthesized directly from nitrile-containing precursors via oximation reactions, offering cost-effective, scalable, and versatile production routes15. PAO hydrogels, with abundant amidoxime groups and excellent hydrophilicity, have been extensively studied for uranium extraction. Nevertheless, their three-dimensional crosslinked networks trap large amounts of water through hydrogen bonding16, significantly reducing water mobility and uranyl ion diffusion, thereby limiting access to active binding sites and reducing overall adsorption performance.

To address these limitations, various strategies have been explored, including hydrogel-based adsorbents in the form of ultra-thin films17 (~100 µm) or superfine fibers18 (~250 nm). These designs increase the contact area between the adsorbent and seawater, enhancing uranyl ion diffusion and improving the utilization of functional groups. However, such materials often suffer from poor mechanical properties, are prone to damage, and present challenges in recovery, making them unsuitable for practical deployment in real marine environments. An alternative promising approach involves constructing uranyl ion transport channels within hydrogel materials. Techniques such as ice templating19, pore-forming agents20, and bacterial fermentation21 have been employed to enhance pore structures. While these methods have achieved some improvements in adsorption performance, the resulting adsorbents typically suffer from small pore sizes, uneven pore distribution, and limited pore connectivity, which constrain further performance enhancements. Therefore, the development of innovative materials with advanced pore architectures is essential to significantly improve adsorption capacity and operational efficiency.

Leaf veins efficiently transport water and nutrients through interconnected hierarchical networks, while natural honeycombs exemplify bulk porous structures with thin-walled, hexagonally arranged channels (Fig. 1a). Inspired by these optimized biological systems, we have developed a bulk adsorbent featuring a honeycomb-like hierarchical porous architecture for efficient and scalable uranium extraction from seawater (Supplementary Fig. 1). Its thickness (10 mm) is a hundred times greater than that of conventional ultrathin films (100 μm)17,21. This structural design significantly enhances mechanical stability, thereby facilitating deployment and recovery in marine environments. By integrating mass transfer analysis with COMSOL simulations, we demonstrate that this material features a multi-level interconnected channel network. This network comprises hexagonal longitudinal (5 mm), transverse (100 μm), and intrinsic (2 μm) channels, which enable two synergistic pathways: (1) laminar flow through macrochannels (Reynolds number Re = 922.50) and (2) diffusion-enhanced transport within microchannels (effective diffusivity Deff = 6.96 × 10−9 vs. 1.74 × 10−9 m2/s). Together, these pathways maximize uranium capture and functional group accessibility. In natural seawater, HTC-PAO achieved a uranium adsorption capacity of 14.69 mg/g after 35 days under conditions without an external energy field, with capacities 2.40 and 1.42 times those of intrinsic micropore polyamidoxime (IM-PAO) and large-pore polyamidoxime (LP-PAO), respectively. By providing a scalable and efficient solution, this study marks a significant step forward in the sustainable utilization of seawater uranium resources, offering new opportunities for securing the future of nuclear energy.

Fig. 1: Schematic illustration and morphological characterization of nature-inspired honeycomb-like hierarchical porous channel adsorbents.
figure 1

a The establishment process of the natural-inspired honeycomb-like hierarchical porous channel network model. b SEM images of HTC-PAO.

Full size image

Results

Material preparation and morphology analysis

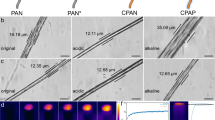
PAO was synthesized via the oximation reaction of PAN. To systematically investigate the impact of the internal channel structures of adsorbents on adsorption performance, three adsorbents with different internal channel structures were prepared. The PAO was directly crosslinked with glutaraldehyde and freeze-dried to obtain IM-PAO. LP-PAO was prepared by mixing PAO with glutaraldehyde, pouring the mixture into silicone molds with honeycomb columns (Supplementary Fig. 2a), and freeze-drying it. HTC-PAO was prepared by pouring the mixture into a brass-framed mold (Supplementary Fig. 2b, c). A directional temperature gradient was then applied to induce inward ice crystal growth toward the center, after which the sample was freeze-dried (Supplementary Fig. 3). The resulting HTC-PAO was approximately five times thicker than a coin (Supplementary Fig. 4). The material was characterized using scanning electron microscopy (SEM). The result confirmed that IM-PAO retained only the intrinsic microporous structure of PAO (Supplementary Fig. 5a). LP-PAO exhibited large honeycomb-like hexagonal longitudinal pores while maintaining the intrinsic microporous structure of PAO (Supplementary Fig. 5b, c). In contrast, HTC-PAO exhibited an interconnected triple-channel architecture, comprising hexagonal longitudinal (5 mm), transverse circular (100 μm), and intrinsic polyamidoxime (2.5 μm) channels (Fig. 1b). The wall thickness between adjacent hexagonal macroscopic channels is approximately 500 μm.

Analysis of mass transfer mechanisms

As shown in Fig. 2a, adsorption kinetics is governed by a multistep uranyl ion transport process, involving convection transfer resistance at the external surface (\({R}_{{\rm{surf}}}\)), the diffusion transfer resistance within the porous adsorbents (\({R}_{{\rm{diff}}}\)), and the apparent reaction resistance at the sorption interface (\({R}_{{\rm{react}}}\))22,23. Under continuous seawater flow, uranyl ions rapidly reach the adsorbent surface and coordinate with amidoxime groups, resulting in low \({R}_{{\rm{surf}}}\) and \({R}_{{\rm{react}}}\). Intraparticle diffusion through tortuous pores is inherently slow, making \({R}_{{\rm{diff}}}\) the dominant factor governing adsorption performance. Structural parameters such as external surface area (\({A}_{{\rm{ext}}}\)), diffusion depth (δ), tortuosity coefficient (τ), and sorption surface area (\({A}_{{\rm{sorb}}}\)) can be tuned to reduce all contributions to total resistance (\({R}_{{\rm{total}}}\)) and thus enhance overall adsorption. Supplementary Fig. 6 presents a digital photograph of HTC-PAO. Compared to conventional circular holes, hexagonal holes offer superior tessellation, effectively reducing and homogenizing wall thickness. On an equal mass basis, the honeycomb channel affords 1.55 times the external surface area (\({A}_{{\rm{ext}}}\)) of the triangular circular-hole design and 2.39 times that of the rectangular arrangement (detailed calculation methods are provided in the Supplementary Text 1). In addition, it exhibits a smaller maximum diffusion depth (\({\delta }_{\max }\)) compared with both configurations (Fig. 2b). As a result, the honeycomb-like polyamidoxime adsorbent exhibits lower surface resistance (\({R}_{{\rm{surf}}}\)) and diffusion resistance (\({R}_{{\rm{diff}}}\)), enhancing overall mass transfer. Moreover, the geometric properties of the hexagonal holes alleviate stress concentration24, making this configuration promising for multidisciplinary applications.

Fig. 2: Mass transfer mechanisms of adsorbents with different channel structures.
figure 2

a Schematic diagram of uranyl ion transport during adsorption. b External surface area and maximum diffusion depth of honeycomb and circular holes. c Morphological evolution from primary to hierarchical pore structures of sorbents with enhanced mass transfer.

Full size image

As shown in Fig. 2c, IM-PAO retains only the intrinsic microporous structure without forming additional channels. This structure is characterized by a small external surface area (\({A}_{{\rm{ext}}}\)), long diffusion depth (δ), high tortuosity coefficient (τ), and limited sorption surface area (\({A}_{{\rm{sorb}}}\)), resulting in high \({R}_{{\rm{surf}}}\), \({R}_{{\rm{diff}}}\), and \({R}_{{\rm{react}}}\). In contrast, LP-PAO features a large honeycomb pore structure while maintaining the intrinsic microporous framework. This configuration increases \({A}_{{\rm{ext}}}\) and reduces δ, thereby lowering \({R}_{{\rm{surf}}}\) and \({R}_{{\rm{diff}}}\). However, its τ remains relatively high, and \({A}_{{\rm{sorb}}}\) remines limited. HTC-PAO, on the other hand, possesses a hierarchical pore structure that not only further reduces δ compared with LP-PAO but also decreases τ, leading to an even lower \({R}_{{\rm{diff}}}\). The presence of interwall transverse pores significantly increases \({A}_{{\rm{sorb}}}\), leading to lower \({R}_{{\rm{react}}}\) than both IM-PAO and LP-PAO. Consequently, HTC-PAO exhibits significantly lower total mass transfer resistance (\({R}_{{\rm{total}}}\)) compared to IM-PAO and LP-PAO. The mass transfer characteristics and adsorption performance of adsorbents with different internal channel structures were further investigated through experiments and simulations.

Material characterization and adsorption performance in simulated seawater

Fourier Transform Infrared (FTIR) spectroscopy was used to analyze PAN, PAO, IM-PAO, LP-PAO, and HTC-PAO (Supplementary Fig. 7). The FTIR spectrum of PAN exhibited a characteristic C ≡ N stretching vibration at 2240 cm−1. In contrast, PAO, IM-PAO, LP-PAO, and HTC-PAO displayed two distinct absorption peaks at 934 cm−1 (N─O) and 1598 cm−1 (C = N), with the C ≡ N band absent, confirming the successful conversion of the nitrile group in PAN to the amidoxime functional group. The amidoxime group in PAO was further confirmed by high-resolution N1s XPS, which showed two characteristic peaks of C = N and N─H in IM-PAO, LP-PAO, and HTC-PAO (Supplementary Fig. 8). Four deconvoluted peaks were detected in the high-resolution C1s spectra of IM-PAO, LP-PAO, and HTC-PAO, corresponding to C─C, C = N, C = O, and O─C = O bonds (Supplementary Fig. 9). These results provided further confirmation of the successful conversion of the C ≡ N group to the C = N group.

Mercury intrusion porosimetry (MIP) measurements showed that the pore volume of HTC-PAO was approximately 1.5 times that of IM-PAO and LP-PAO (Fig. 3a). Analysis of the mercury intrusion-extrusion curves revealed that for IM-PAO (Supplementary Fig. 10a) and LP-PAO (Supplementary Fig. 10b), the curves overlapped, indicating that mercury could not exit once it entered the material. In contrast, the extrusion curve of HTC-PAO (Supplementary Fig. 10c) was lower than its intrusion curve, demonstrating partial mercury release. This result suggests that HTC-PAO exhibits superior mass transfer performance and improved internal pore connectivity. As shown in Supplementary Fig. 11, the specific surface area of HTC-PAO (1.93 m2 g−1) was 1.95 and 1.25 times that of IM-PAO and LP-PAO, respectively, providing more available adsorption sites. Correspondingly, HTC-PAO exhibited markedly higher uranium adsorption capacity (1.80 times and 1.27 times that of IM-PAO and LP-PAO, respectively), confirming that the enlarged pore volume and surface area play a critical role in the observed adsorption enhancement. The seawater transport capacity of IM-PAO, LP-PAO, and HTC-PAO was tested by bringing their surfaces into contact with a Rhodamine B solution (Fig. 3b). Due to the introduction of the interconnected triple-channel architecture, the seawater transport speed in HTC-PAO was 7.8 mm/s, which is 2.04 and 1.3 times faster than IM-PAO and LP-PAO, respectively. The experimental results are consistent with the theoretical analysis of the mass transfer process. For details on the specific experimental process, please refer to the methods. Water contact angle measurements confirmed that HTC-PAO exhibited superior hydrophilicity, improving the compatibility between the adsorbent surface and water molecules in the solution (Supplementary Fig. 12). This enhanced interaction with uranyl ions in the aqueous solution, thereby promoting the adsorption process. Additionally, compared to thin-film adsorption materials (Supplementary Fig. 13), hexagonal large-channel bulk adsorption materials exhibit superior mechanical properties (Fig. 3c).

Fig. 3: Characterization of materials and adsorption properties in simulated seawater.
figure 3

a Mercury intrusion porosimetry analysis for IM-PAO, LP-PAO, and HTC-PAO. b Seawater transport ability of IM-PAO, LP-PAO, and HTC-PAO. c Mechanical properties of HTC-PAO. d The uranium adsorption capacity of IM-PAO, LP-PAO, and HTC-PAO as a function of pH. e Uranium adsorption kinetics of HTC-PAO in simulated seawater. f XPS spectra before and after uranium adsorption of HTC-PAO. g High-resolution XPS spectra of U 4f for HTC-PAO. h Uranium adsorption kinetics and the fitting curves for IM-PAO, LP-PAO, and HTC-PAO, based on the Pseudo first-order and Pseudo second-order models. i Equilibrium adsorption characteristics of HTC-PAO: Freundlich and Langmuir isotherm models with fitting curves.

Full size image

To evaluate the uranium adsorption capacity of IM-PAO, LP-PAO, and HTC-PAO, three adsorbents were immersed in uranium-simulated seawater at a concentration of 8 ppm. The adsorption performance was found to be pH-dependent, as pH affected both the surface charge of the adsorbent and the speciation of uranium. As illustrated in Fig. 3d, the uranium adsorption capacity of IM-PAO, LP-PAO, and HTC-PAO exhibited a pH-dependent variation. The adsorption capacity initially increased and then decreased as the pH was raised from 3 to 9, with the peak uranium uptake occurring at pH 6. Under acidic conditions (pH < 4.0), uranyl ions (UO22+) predominantly exist in a positively charged state. In this environment, the adsorbent surface also carries a positive charge, leading to strong electrostatic repulsion between the adsorbent and uranyl ions. This repulsion prevents effective interactions between the adsorbent’s functional groups and uranyl ions, resulting in low uranium adsorption efficiency. As pH increases, the adsorbent surface becomes less positive, reducing electrostatic repulsion and facilitating stronger interactions with uranyl ions, which enhances adsorption. However, at pH levels above 6.0, uranyl ions form negatively charged carbonate complexes, such as UO2(CO3)22−, UO2(CO3)34−, and UO2(CO3)46−. These complexes repel the negatively charged adsorbent surface, decreasing electrostatic attraction and reducing uranium adsorption capacity at higher pH values. Notably, HTC-PAO demonstrated superior uranium adsorption capacity compared to IM-PAO and LP-PAO across all pH ranges, underscoring the critical role of its hierarchical porous structure in improving sorption performance.

To clarify the adsorption mechanism, the kinetics of uranium adsorption by IM-PAO, LP-PAO, and HTC-PAO in simulated seawater were investigated. The adsorption performance of HTC-PAO for uranium (VI) was evaluated by immersing the adsorbent in aqueous solutions with uranium concentrations of 4, 8, and 16 ppm at pH 6 for a duration of 48 h. The residual uranium concentration was quantified using UV–visible absorption spectroscopy, with arsenazo (III) employed as the colorimetric reagent. After 48 h of contact, the saturated uranium adsorption capacities of HTC-PAO were determined to be 391.2, 782.4, and 1100.24 mg/g for the 4, 8, and 16 ppm solutions, respectively (Fig. 3e). Additionally, the adsorption performances of IM-PAO and LP-PAO were also evaluated (Supplementary Fig. 14). The uranium adsorption kinetics for IM-PAO, LP-PAO, and HTC-PAO, measured at various time intervals, are summarized in Supplementary Table 1. The saturated adsorption capacities of IM-PAO and LP-PAO were much lower than the HTC-PAO under the same conditions. The observed kinetic differences highlighted the advantages of using adsorbents with hierarchical porous structures, as these materials promote efficient filling of internal channels and rapid ion diffusion, thereby facilitating the adsorption process.

The chemical composition of uranium-loaded HTC-PAO was investigated via X-ray photoelectron spectroscopy (XPS) to verify the adsorption process (Fig. 3f). For comparative analysis, the chemical compositions of IM-PAO and LP-PAO were also examined (Supplementary Fig. 15). EDS analysis revealed a uniform distribution of uranium in HTC-PAO, along with the presence of additional elements including carbon (C), nitrogen (N), and oxygen (O), as illustrated in Supplementary Fig. 16. Figure 3g displayed the characteristic doublet peaks of U 4f5/2 (392.36 eV) and U 4f7/2 (381.65 eV) in the XPS spectrum of uranium-loaded HTC-PAO, thereby confirming the adsorption of uranium on the HTC-PAO surface relative to the unadsorbed state. Likewise, IM-PAO and LP-PAO exhibited corresponding characteristic peaks, providing further evidence of uranium adsorption on their surfaces post-adsorption (Supplementary Fig. 17). Supplementary Fig. 18 presented digital images of HTC-PAO before and after uranium adsorption, showing a distinct color change from pale yellow to orange-red upon uranium uptake.

The adsorption kinetics of IM-PAO, LP-PAO, and HTC-PAO were analyzed using both pseudo-first-order and pseudo-second-order models (Fig. 3h and Supplementary Fig. 19). For all three adsorbents, the pseudo-second-order model yielded higher R2 values than the pseudo-first-order model (closer to 1), indicating a better fit. This suggests that the adsorption process is governed primarily by chemisorption rather than physisorption, essentially involving coordination between PAO functional groups and uranyl ions. The kinetic fitting parameters are summarized in Supplementary Table 2. In an 8 ppm uranium solution, the equilibrium adsorption capacities (qe) of IM-PAO, LP-PAO, and HTC-PAO were 433.97, 612.07, and 779.28 mg/g, respectively. Notably, HTC-PAO achieved an adsorption capacity 1.80 times greater than IM-PAO and 1.27 times higher than LP-PAO, highlighting the superior uranium uptake enabled by its hierarchical porous structure. Uranium concentrations in simulated seawater were varied within the range of 4 to 150 ppm, and the adsorption isotherms for IM-PAO, LP-PAO, and HTC-PAO were systematically analyzed. The uranium adsorption data were well fitted by the Langmuir isotherm model, indicating that the adsorption process is primarily monolayer chemisorption, which is consistent with the adsorption kinetics analysis. The theoretical maximum adsorption capacity (qm) of HTC-PAO was calculated to be 1343.6 mg/g (Fig. 3i and Supplementary Table 3), significantly higher than that of IM-PAO (712.16 mg/g) and LP-PAO (1024.38 mg/g) (Supplementary Fig. 20). These results demonstrate that HTC-PAO possesses markedly enhanced uranium adsorption performance in simulated seawater, underscoring its strong potential for practical application in marine uranium extraction.

Mathematical modeling and transient analysis of adsorption kinetics

To elucidate the effects of honeycomb channels and hierarchical porous architecture on mass transfer and uranyl adsorption, COMSOL Multiphysics was employed to simulate the uranium adsorption from seawater. Simulation models of IM-PAO, LP-PAO, and HTC-PAO were constructed under dynamic flow conditions, with seawater entering from the top and exiting from the bottom (Supplementary Fig. 21). The detailed boundary conditions are provided in the Supplementary Text 2, and the model parameters are listed in Supplementary Tables 4–6. A coupled dual-physics model was developed, comprising two modules: (1) the laminar flow module, which describes seawater flow and thereby characterizes the transport of uranyl ions to the adsorbent surface; and (2) the transport of dilute species module, which simulates diffusion of uranyl ions within both seawater and the porous adsorbent, incorporating an adsorption term to represent coordination with functional groups at the adsorption sites. Detailed material parameters are provided in Supplementary Table 7. By coupling these two modules, the intrinsic relationships among flow velocity, concentration distribution, and adsorption capacity were quantitatively analyzed.

The computational domain was meshed using two schemes: hexahedral meshes for the adsorbent and free tetrahedral meshes for the surrounding seawater. The hexahedral meshes ensured high mesh quality and numerical stability, improving computational efficiency while maintaining accuracy. In contrast, the tetrahedral meshes provided greater geometric adaptability and supported local refinement, enabling accurate resolution of concentration gradients. Additional local mesh refinement in the central adsorption region further optimized the balance between simulation accuracy and computational cost. To ensure the accuracy of the results, a mesh convergence study was conducted by comparing the results from the coarse (128,304 elements), medium (693,073 elements), and fine (890,922 elements) meshes. Key output parameters, including the velocity field, concentration profile, and adsorption capacity, showed less than 1% variation between the medium and fine meshes, indicating good convergence (Supplementary Table 8). As a result, the chosen mesh with approximately 693,000 elements was selected adequate for ensuring reliable simulation results.

As shown in Fig. 4a, the honeycomb channels in LP-PAO and HTC-PAO effectively reduced flow bypass and increased internal flow velocity, thereby enhancing uranyl diffusion into the adsorbent. This is supported by the concentration contour plots in Fig. 4b. Compared with IM-PAO, LP-PAO exhibited a 15.56% increase in diffusion depth. Meanwhile, HTC-PAO achieved a 99.48% increase in diffusion depth compared to LP-PAO. These results demonstrate that the hierarchical porous design significantly improves mass transfer efficiency. Furthermore, the simulation-predicted uranium adsorption capacities show good agreement with experimental data, as illustrated in Fig. 4c. The maximum deviation for IM-PAO, LP-PAO, and HTC-PAO was less than 17%, and the average error remained below 7% (Supplementary Table 9), confirming the accuracy and robustness of the simulation model. Using the simulation model, the time-dependent values of \({R}_{{\rm{surf}}}\), \({R}_{{\rm{diff}}}\), and \({R}_{{\rm{react}}}\) were determined based on the simulated uranyl adsorption kinetics and the spatial concentration distributions within the adsorbent matrix (Fig. 4d–f). Among the three resistance components, \({R}_{{\rm{diff}}}\) accounted for the majority of the overall mass transfer resistance, highlighting the critical role of internal diffusion in limiting adsorption performance. Notably, HTC-PAO exhibited a significantly lower \({R}_{{\rm{diff}}}\) than IM-PAO and LP-PAO, supporting the proposed mechanism that its hierarchical triple-channel architecture enhances mass transfer efficiency by reducing both the effective diffusion depth (δ) and tortuosity factor (τ). In addition, HTC-PAO also shows a markedly reduced \({R}_{{\rm{react}}}\) attributed to its larger specific surface area, which is consistent with the mass transfer analysis. In contrast, the \({R}_{{\rm{surf}}}\) of HTC-PAO, IM-PAO, and LP-PAO are comparable, suggesting that under the influence of the flow field, uranyl ions can easily reach the surface of the adsorbent, and the impact of the difference in material morphology is weakened.

Fig. 4: COMSOL simulation of adsorption processes in different adsorbents.
figure 4

a Cloud maps of the flow velocity field of IM-PAO, LP-PAO, and HTC-PAO. b Comparison of adsorption concentration cloud maps of IM-PAO, LP-PAO, and HTC-PAO. c Comparison chart of simulation results and experimental data. d–f Mass transfer resistance analysis of uranyl ions during the adsorption of IM-PAO, LP-PAO, and HTC-PAO. The total transfer resistance consists of three parts: the convection transfer resistance at the external surface (\({R}_{{\rm{surf}}}\)), the diffusion transfer resistance within the porous adsorbents (\({R}_{{\rm{diff}}}\)), and the apparent reaction resistance at the sorption interface (\({R}_{{\rm{react}}}\)).

Full size image

Reusability, selectivity, and adsorption performance in natural seawater

Reusability is a crucial parameter for assessing the economic viability and long-term stability of adsorbent materials. To evaluate the regeneration potential of HTC-PAO, its uranium adsorption capacity was determined after multiple adsorption-desorption cycles. Uranium-loaded HTC-PAO was regenerated by immersion in an elution solution consisting of 1 M Na2CO3 and 0.1 M H2O2 for 1 h. Cyclic testing revealed consistent performance characteristics, with the adsorbent sustaining a uranium adsorption capacity of 671.55 mg/g and achieving a desorption rate of 91.3% over five operational cycles (Supplementary Fig. 22 and Supplementary Table 10). The sustained reusability of HTC-PAO demonstrates its capacity for long-term uranium extraction without significant performance degradation, thereby reducing operational costs. The mechanism of the desorption process is as follows: uranium desorption is achieved through complexation chemistry, where concentrated carbonate solutions produce [UO2(CO3)3]4− complexes. The elution efficiency is enhanced when hydrogen peroxide is incorporated into the carbonate system, resulting in the formation of [UO2(O2)(CO3)2]4− species with superior stability. The addition of hydrogen peroxide enhances the formation of this complex, which is thermodynamically more stable than the uranyl tris-carbonato complex, with stability four orders of magnitude greater. This increased stability facilitates the release of uranyl ions from the adsorbent surface, allowing efficient desorption. The gradual attenuation of the uranium adsorption capacity during the reusability tests of HTC-PAO is attributed to two main factors. First, some of the binding sites on the adsorbent become occupied by tightly bound uranyl ions, which are difficult to elute due to the strong coordination between the uranyl ions and the amidoxime groups. These tightly bound ions are not easily displaced by the elution solution. Second, the elution process itself may cause partial damage to the binding sites, reducing their ability to effectively capture uranyl ions in subsequent cycles. Over time, this degradation of active sites leads to a decrease in the adsorbent’s overall capacity.

For the selectivity assessment, the competitive adsorption behavior of HTC-PAO was investigated within a simulated seawater matrix, incorporating coexisting ions25 such as U, V, Mn, Co, Ni, Cu, Pb, Zn, and Cr (Supplementary Table 11). Notably, vanadium, exhibiting comparable charge and ionic radius to uranium, competed for adsorption sites on the surface of HTC-PAO. Despite this competition, uranium demonstrated the highest selective adsorption capacity among the ions tested (Fig. 5a). These results emphasized the exceptional selectivity of HTC-PAO for uranium, thereby positioning it as a promising candidate for the targeted and efficient extraction of uranium from complex, naturally occurring seawater matrices. To simulate natural seawater conditions, a recirculating marine water system was constructed for evaluating HTC-PAO’s uranium recovery efficiency, with the system configuration presented in Supplementary Fig. 2326. In this experimental setup, 10 mg of HTC-PAO was placed between two layers of sponge in the seawater test tube, and the flow rate of the seawater was adjusted to ensure consistent and uniform flow during the adsorption process. This configuration allows for more precise monitoring and facilitates the effective collection of the adsorbent after the uranium extraction test. It also prevents material displacement, allowing continuous circulation of natural seawater through the system. After 35 days of continuous adsorption, the adsorption capacity of HTC-PAO reached 14.69 mg/g, which was 2.40 times and 1.42 times that of IM-PAO and LP-PAO (Fig. 5b). Adsorption kinetics analysis (Fig. 5c) showed that HTC-PAO not only had superior uranium adsorption capacity, but also significantly faster adsorption rate compared with IM-PAO and LP-PAO. HTC-PAO reached the equilibrium adsorption level of IM-PAO after 6 days and achieved LP-PAO’s equilibrium level by day 12. Therefore, the hierarchical porous channels of HTC-PAO promotes the rapid diffusion of uranyl ions, significantly speeds up the adsorption process, and maximizes the adsorption capacity of the polyamide oxime hydrogel adsorbent. Without external energy input, HTC-PAO exhibits a remarkably high uranium adsorption capacity among known macroscale polyamidoxime adsorbents in natural seawater (Fig. 5d and Supplementary Table 12).

Fig. 5: Material selectivity and adsorption properties in natural seawater.
figure 5

a The adsorption selectivity of IM-PAO, LP-PAO, and HTC-PAO was studied by simulated seawater system. b The uranium adsorption capabilities of IM-PAO, LP-PAO, and HTC-PAO within the context of natural seawater. c Kinetics of Uranium Adsorption by IM-PAO, LP-PAO, and HTC-PAO in Natural Seawater. d Report on the adsorption capacity of existing amidoxime adsorbents for uranium in natural seawater1,15,20,21,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47.

Full size image

Discussion

Guided by nature-inspired design principles, we developed a honeycomb-like bulk adsorbent with hierarchical porous channels for enhanced uranium extraction from seawater, utilizing a combination of template methods and directed freeze-thaw technology. Its macroscopic structure is 100 times thicker than that of ultra-thin hydrogels, which provides superior mechanical strength and enables efficient deployment and retrieval in marine environments. By integrating mass transfer mechanism analysis with experimental testing, we examined the impact of internal channel architecture on adsorption performance. The interconnected triple-channel network, composed of hexagonal longitudinal channels, transverse circular channels, and intrinsic polyamidoxime channels, significantly improves mass transfer, reduces diffusion resistance, and enhances functional site utilization, leading to exceptional uranium adsorption efficiency. Finite element analysis using COMSOL Multiphysics simulations further elucidates the role of internal channel of adsorbents in governing adsorption kinetics, aligning with experimental results. As a result, HTC-PAO achieves a uranium adsorption capacity of 14.69 mg/g over 35 days, confirming its strong uranium uptake capability among macroscale polyamidoxime-based hydrogel adsorbents operating without additional energy input. Additionally, HTC-PAO demonstrates excellent ion selectivity, reusability, and cost efficiency, positioning it as a promising candidate for scalable and sustainable uranium harvesting. These findings underscore the significant potential of HTC-PAO in advancing the utilization of seawater uranium resources, contributing to the future of sustainable nuclear energy.

Methods

Synthesis of PAO

PAO was synthesized according to existing literature. First, 5.6 × g of NH2OH⋅HCl was completely dissolved in 100 mL of DMF. To achieve a neutral pH in the solution, 4.12 grams of sodium carbonate (Na2CO3) and 1.6 grams of sodium hydroxide (NaOH) were meticulously incorporated, followed by an hour-long stirring at a controlled temperature of 45 °C. Then, the mixture was combined with 4 × g of PAN and stirred at 65 °C for 24 h. Afterward, 30 mL of DMF solution containing 2.8 × g of NH2OH⋅HCl, 0.8 × g of Na2CO3, and 2.06 × g of NaOH was added. The resulting mixture was reacted at 65 °C for another 24 h. After the reaction reached completion, the liquid phase was separated using high-speed centrifugation (1.08 × 104 × g, 25 min) to obtain the supernatant. The supernatant was dropped into anhydrous ethanol using a dropper with a rubber tip and mechanically stirred for 24 h to completely remove the residual dimethylformamide. The mixture was filtered and then vacuum dried at 40 °C to obtain PAO powder.

Preparation of HTC-PAO

To commence, introduce 1.2 × g of PAO powder into 12 mL of a 0.3 M NaOH solution and ensure thorough mixing; subsequently, incorporate 400 μL of glutaraldehyde solution and blend meticulously until homogeneity was achieved. Next, pour the mixture into a silicone mold and place a brass frame around the edges of the mold. Then, place it in the freezer for 12 h. Remove the material from the mold and freeze-dry it for 24 h to obtain a large block of HTC-PAO honeycomb material. For the control sample LP-PAO, the preparation steps were the same as for HTC-PAO, except that after the mixture is poured into the silicone mold, it was placed directly in the refrigerator to freeze, then removed from the mold and dried by freeze-drying. For the control sample IM-PAO, the same steps as for HTC-PAO were followed, but the mixture was directly poured into the silicone box for freezing, and then demolded and dried. To ensure smooth demolding, the following precautions were taken: (1) demolding was performed only after the freeze-drying process was fully completed, as the fully dried sample possesses sufficient mechanical strength to withstand stress; (2) the sample was carefully and slowly separated from the mold starting from the peripheral edges, applying a uniform force parallel to the channel direction. Before conducting uranium adsorption experiments, HTC-PAO was treated with alkali by soaking it in a 20 mM NaOH solution at 60 °C for about 30 min.

Characterization

The diverse array of functional groups present within the polymers was characterized through the application of Fourier transform infrared spectroscopy (FT-IR, PerkinElmer Frontier). Elemental analysis was conducted utilizing X-ray photoelectron spectroscopy (XPS, Thermo Escalab 250Xi), a sophisticated technique renowned for its precision and depth of insight. Morphological analysis was conducted using a tungsten filament scanning electron microscope (Axia ChemiSEM). Structural characterization of HTC-PAO, LP-PAO, and IM-PAO was performed via mercury intrusion porosimetry (AutoPore V 9620) to evaluate their pore size distributions. The hydrophilic properties of the material were assessed utilizing a sophisticated contact angle apparatus (Dataphysics OCA50). Uranium concentrations were quantified employing a UV–visible spectrophotometer (UV1800PC) alongside inductively coupled plasma mass spectrometry (ICP-MS; PerkinElmer NexION 300X).

Seawater transportation test

3 mL of Rhodamine B dye solution was mixed uniformly with 120 mL of seawater to prepare the stained seawater, which was then poured into a Petri dish. Adsorbents IM-PAO, LP-PAO, and HTC-PAO, each with a thickness of 10 mm, were fixed at the bottom exterior of another Petri dish, with the honeycomb channels oriented perpendicular to the ground. A spirit level was used to ensure that all three adsorbents were aligned on the same horizontal plane. The Petri dish containing the stained seawater was placed on a lift stage and leveled. The lift stage was slowly raised until the seawater surface just contacted the three adsorbents. After 1 s of contact, the stained seawater was withdrawn. Once the staining had stabilized, the adsorbents were vertically sectioned, and the average penetration distance of the stained seawater was measured using a vernier caliper.

Uranium adsorption in simulated seawater

Simulated seawater was prepared using deionized water, 128.161 × g of NaCl, and 964.85 mg of NaHCO3, resulting in 5000 mL of solution. The measured ionic concentrations showed 438.607 mM for NaCl and 2.297 mM for NaHCO3 in the solution. For preparation of 8 ppm uranium-containing simulated seawater, 40 mL of concentrated uranyl nitrate solution (1000 ppm) was incorporated into the mixture. The pH was adjusted using NaOH (1 M) and HCl (1 M) solutions. The pH-dependent adsorption performance was investigated between pH 3.0 and 9.0, utilizing 5 mg of pretreated adsorbent in 5000 mL of 8 ppm uranium-spiked simulated seawater for each experimental condition. Shake at a temperature of 25 °C and at a rotational speed of 140 rpm. The uranium extraction performance was evaluated through a 48-h experimental duration using uranyl-containing simulated seawater. To evaluate the uranium adsorption capacity of HTC-PAO, alkali-treated HTC-PAO was immersed in 5000 mL of simulated seawater containing an uranium concentration of 8 ppm and a pH level of 6. Subsequently, experiments were conducted to assess uranium adsorption. The amount of uranium adsorbed was calculated using Eq. (1)26:

$${q}_{{\rm{t}}}=\frac{\left({C}_{0}-{C}_{{\rm{t}}}\right)\times V}{m}$$
(1)

In the equation,\({C}_{0}\) (mg/L) and \({C}_{{\rm{t}}}\) (mg/L) denote the initial uranium concentration prior to adsorption and the instantaneous uranium concentration at time t, respectively. V (L) represents the volume of simulated seawater containing uranium, m indicates the dry weight of the adsorbent, and \({q}_{{\rm{t}}}\) (mg/g) signifies the amount of uranium adsorbed at time t.

Adsorption kinetics

Simulated seawater solutions with varying concentrations of uranium (4, 8, 16, 32, 64, and 128 ppm) at a pH level of 6 were meticulously prepared to investigate the adsorption kinetics of the HTC-PAO adsorbent. In summary, a precise quantity of 5 mg of alkali-treated HTC-PAO was introduced into 5000 mL of simulated seawater. The experiment was conducted under controlled conditions at a rotation speed of 140 rpm and a temperature maintained at 25 °C. Uranium concentration was measured at four-hour intervals. The acquired data were subsequently subjected to fitting procedures utilizing both the pseudo-first-order (Eq. (2)) and pseudo-second-order (Eq. (3)) models27:

$${\mathrm{ln}}\left({q}_{{\rm{e}}}-{q}_{{\rm{t}}}\right)={ln}{q}_{{\rm{e}}}-{k}_{1}t$$
(2)
$$\frac{{t}}{{{q}}_{{t}}}=\frac{1}{{k}_{2}{q}_{{\rm{e}}}^{2}}+\frac{t}{{q}_{{\rm{e}}}}$$
(3)

In the equations, t represents the contact time (min), while \({k}_{1}\) and \({k}_{2}\) denote the rate constants. The variable \({q}_{{\rm{e}}}\)(mg/L) indicates the total amount of uranium adsorbed by the adsorbent, whereas \({q}_{{\rm{t}}}\) (mg/L) signifies the amount of uranium adsorbed at time t. Additionally, t (min) refers to the duration of contact between the adsorbent and the solution.

The equilibrium isotherm data were analyzed and fitted to the Langmuir model (as delineated in Eq. (4)) and the Freundlich model (illustrated in Eq. (5)):

$$\frac{{C}_{{\rm{e}}}}{{q}_{{\rm{e}}}}=\frac{{C}_{{\rm{e}}}}{{q}_{{\rm{m}}}}+\frac{1}{{k}_{3}{q}_{{\rm{m}}}}$$
(4)

In the equations, \({C}_{{\rm{e}}}\) represents the equilibrium concentration (mg/L), while \({q}_{{\rm{m}}}\) denotes the maximum adsorption capacity (mg/g). Additionally, \({k}_{3}\) signifies the equilibrium constant associated with the binding strength (L/mg). The value of \({q}_{{\rm{e}}}\) can be ascertained through the following relationship:

$${\mathrm{lg}}{q}_{{\rm{e}}}={\mathrm{lg}}{k}_{4}+\frac{1}{n}{\mathrm{lg}}{C}_{{\rm{e}}}$$
(5)

In the equation, \({k}_{4}\) is an approximate indicator of the adsorption capacity, and \(\frac{1}{n}\) is a function representing the adsorption intensity during the adsorption process.

Development of adsorbent models

The adsorbent models were constructed using the commercial finite element software COMSOL Multiphysics (version 6.2). The IM-PAO model was based on a simple cubic structure to resemble the experimental sample (Supplementary Fig. 21a), while the LP-PAO and HTC-PAO models were constructed based on regular hexagonal pore arrays (Supplementary Fig. 21b, c). To avoid issues such as excessively dense grids, prolonged computation time, and poor convergence caused by structural complexity, this study simplified the intrinsic micropores and lateral pores of the adsorbents into a homogeneous continuous medium. Macroscopic parameters, including permeability, porosity, and effective diffusion coefficient were employed to characterize the differences in diffusion behavior of uranium-containing seawater through adsorbents with different structures. Due to the absence of oriented secondary channels within the LP-PAO material, isotropic parameters were adopted for it. Its permeability, porosity, and effective diffusion coefficient are the same as those of IM-PAO. In contrast, as the HTC-PAO material contains internally oriented secondary channels, different parameters were assigned along the X, Y, and Z directions to fully reflect the anisotropy induced by these oriented channels. The specific parameter settings are provided in Supplementary Tables 4–7.

Numerical simulation

The simulation adsorption model consists of the Navier–Stokes equations and the convective-diffusion-reaction equations. The Navier–Stokes equations are used to simulate the fluid movement process both outside and inside the adsorbent, while the convective-diffusion-reaction equations are used to simulate the diffusion and transport process of uranyl ions in seawater and within the adsorbent, as shown in Eqs. (6)–(9).

$${\rho }_{{\rm{f}}}\left(u\cdot \nabla \right)u=\nabla \cdot \left[-{pI}+K\right]$$
(6)
$$\frac{1}{{\varepsilon }_{{\rm{p}}}}{\rho }_{{\rm{f}}}\left(u\cdot \nabla \right)u\frac{1}{{\varepsilon }_{{\rm{p}}}}=\nabla \cdot \left[-{pI}+K\right]-\left(\mu {\kappa }^{-1}\right)u$$
(7)
$${\rho }_{f}\nabla \cdot u=0$$
(8)
$$\frac{\partial \left({\varepsilon }_{{\rm{p}}}{c}_{{\rm{i}}}\right)}{\partial t}+\frac{\partial \left[(1-{\varepsilon }_{{\rm{p}}}){\rho }_{{\rm{s}}}\cdot {c}_{{\rm{P}},{\rm{i}}}\right]}{\partial t}+\nabla \cdot {J}_{{\rm{i}}}+u\cdot \nabla {c}_{{\rm{i}}}={R}_{{\rm{i}}}+{S}_{{\rm{i}}}$$
(9)

In the equation, \({\rho }_{{\rm{f}}}\) represents the fluid density, u is the fluid velocity, p is the fluid pressure, I is the unit tensor, K denotes the viscous stress tensor, \({\varepsilon }_{{\rm{p}}}\) is the porosity, κ is the permeability, \({c}_{{\rm{i}}}\) is the concentration of uranyl ions in the solution, \({\rho }_{{\rm{s}}}\) is the solid phase density of the adsorbent, \({c}_{{\rm{P}},{\rm{i}}}\) is the concentration of uranyl ions on the adsorbent, \({J}_{{\rm{i}}}\) is the diffusion flux, \({R}_{{\rm{i}}}\) is the adsorption rate, and \({S}_{{\rm{i}}}\) is the source term of the substance.

The calculation of the viscous stress tensor K is presented in Eqs. (10) and (11)28, which are respectively used to calculate the flow field outside and inside the adsorbent:

$$K=\mu \left[\nabla u+{\left(\nabla u\right)}^{T}\right]$$
(10)
$$K=\mu \frac{1}{{\varepsilon }_{{\rm{p}}}}\left[\nabla u+{\left(\nabla u\right)}^{T}\right]-\frac{2}{3}\mu \frac{1}{{\varepsilon }_{{\rm{p}}}}\left(\nabla \cdot u\right)I$$
(11)

The calculation Eq. (12) of permeability κ is as follows:

$$\kappa=\frac{{d}_{{\rm{p}}}^{2}}{180}\frac{{\varepsilon }_{{\rm{p}}}^{3}}{{\left(1-{\varepsilon }_{{\rm{p}}}\right)}^{2}}$$
(12)

In the equation, \({d}_{{\rm{p}}}\) represents the particle size and \({\varepsilon }_{{\rm{p}}}\) represents the porosity.

The calculation Eq. (13) of the diffusion flux \({J}_{{\rm{i}}}\) is as follows:

$${J}_{{\rm{i}}}=-\left({D}_{{\rm{D}},{\rm{i}}}+\frac{{\varepsilon }_{{\rm{p}}}}{{\varepsilon }_{{\rm{p}}}^{-1/3}}{D}_{{\rm{e}},{\rm{i}}}\right)\nabla {c}_{{\rm{i}}}$$
(13)

In the equation, \({D}_{{\rm{D}},{\rm{i}}}\) represents the dispersion coefficient, and \({D}_{{\rm{e}},{\rm{i}}}\) represents the diffusion coefficient.

The calculation Eq. (14) for the adsorption rate \({R}_{{\rm{i}}}\) is as follows:

$$\frac{\partial \left[(1-{\varepsilon }_{{\rm{p}}}){\rho }_{{\rm{s}}}{c}_{{\rm{P}},{\rm{i}}}\right]}{\partial t}=(1-{\varepsilon }_{{\rm{p}}}){\rho }_{{\rm{s}}}\cdot \frac{\partial {c}_{{\rm{P}},{\rm{i}}}}{\partial {c}_{{\rm{i}}}}\cdot \frac{\partial {c}_{{\rm{i}}}}{\partial t}-{c}_{{\rm{P}},{\rm{i}}}{\rho }_{{\rm{s}}}\frac{{\partial \varepsilon }_{{\rm{p}}}}{\partial t}={R}_{{\rm{i}}}$$
(14)

The calculation Eq. (15) for the concentration of uranyl ions on the adsorbent \({c}_{{\rm{i}}}\) is as follows:

$${c}_{{\rm{P}},{\rm{i}}}=\frac{{k}_{3}{c}_{{\rm{P}},\max }{c}_{{\rm{i}}}}{1+{k}_{3}{c}_{{\rm{i}}}}$$
(15)

In the equation, \({k}_{3}\) represents the Langmuir constant during the adsorption process, \({c}_{{\rm{P}},\max }\) represents the maximum adsorption capacity of the adsorbent for uranyl ions.

Mass transfer resistance

Mass transfer resistance refers to the obstacle encountered when a substance is transferred from the fluid to the adsorbent interior during the adsorption process. This resistance will affect the adsorption rate and efficiency. For mass transfer process, mass transfer resistance includes surface resistance (\({R}_{{\rm{surf}}}\)), diffusion resistance (\({R}_{{\rm{sorb}}}\)) and reaction resistance (\({R}_{{\rm{react}}}\)), surface resistance (\({R}_{{\rm{surf}}}\)) is calculated by Eq. (16), diffusion resistance (\({R}_{{\rm{sorb}}}\)) is calculated by Eq. (17), reaction resistance (\({R}_{{\rm{react}}}\)) is calculated by Eq. (18):

$${R}_{{\rm{surf}}}=\frac{1}{{K}_{{\rm{s}}} \cdot A}=\frac{{C}_{{\rm{amb}}}-{C}_{{\rm{surf}}}}{\dot{m}/A}$$
(16)
$${R}_{{\rm{sorb}}}=\frac{\tau \cdot {\delta }_{{\rm{sorb}}}}{\varepsilon \cdot {D}_{{\rm{p}}} \cdot A}=\frac{{C}_{{\rm{surf}}}-{C}_{{\rm{sorb}}}}{\dot{m}/A}$$
(17)
$${R}_{{\rm{react}}}=\frac{1}{{K}_{{\rm{r}}} \cdot A}=\frac{{C}_{{\rm{sorb}}}-{C}_{{\rm{sorb}},{\rm{eq}}}}{\dot{m}/A}$$
(18)

In the equations, \({K}_{{\rm{s}}}\) represents the external mass transfer coefficient, A represents the adsorbent surface area, the τ represents the tortuosity, ε represents the porosity, \({\delta }_{{\rm{sorb}}}\) represents the diffusion depth, \({D}_{{\rm{p}}}\) represents the diffusion coefficient, \({K}_{{\rm{r}}}\) represents the reaction rate constant, \({C}_{{\rm{amb}}}\) is the concentration of uranyl ions in the environment, \({C}_{{\rm{surf}}}\) is the concentration of uranyl ions on the surface of the adsorbent, \({C}_{{\rm{sorb}}}\) is the concentration of uranyl ions inside the adsorbent, and \({C}_{{\rm{sorb}},{\rm{eq}}}\) is the concentration of uranyl ions inside the adsorbent after adsorption equilibrium is reached.

Material reusability

Uranium was eluted from the used adsorbent using an elution solution containing 1 M Na2CO3 and 0.1 M H2O2 at room temperature for 1 h. After the elution process, the material was immersed in pristine water for a duration of 30 min. Subsequently, it underwent an alkali treatment before being introduced into simulated seawater to conduct uranium adsorption experiments. The elution efficiency was calculated using Eq. (19)29:

$${EE}=\frac{{C}_{{\rm{el}}}\times {V}_{{\rm{el}}}}{({C}_{{\rm{i}}}-{C}_{{\rm{f}}})\times {V}_{{\rm{u}}}}\times 100\%$$
(19)

In the equation, EE (%) represents the elution efficiency, \({C}_{{\rm{el}}}\) (mg/L) is the uranium concentration in the elution solution, \({V}_{{\rm{el}}}\) (L) is the volume of the elution solution, \({C}_{{\rm{i}}}\) and \({C}_{{\rm{f}}}\) are the initial and final uranium concentrations, respectively, and \({V}_{{\rm{u}}}\)(L) is the volume of the uranium-spiked simulated seawater.

Adsorption selectivity

The adsorption selectivity of the adsorbent for uranium was evaluated through ion selectivity experiments to assess its extraction ability in the presence of interfering ions. Simulated seawater was prepared using natural seawater as the base and adding various metal salts (such as U, V, Mn, Cr, Ni, Co, Pb, Mo, Cu). The concentration of all metal ions was 100 times higher than their normal concentration in natural seawater (Supplementary Table 11). A 5000 mL solution containing 5 mg of adsorbent was used for the experiments. Uranium extraction was carried out at 25 °C with stirring at 140 rpm for 48 h. The adsorption capacity was used to evaluate the uranium adsorption selectivity of IM-PAO, LP-PAO, and HTC-PAO, as well as their selectivity for other competing ions.

Extraction of uranium from natural seawater

Natural seawater (uranium concentration approximately 3.3 ppb; 200 L) was collected from the western coast of Haikou City, Hainan Province, China. The suitability of the prepared adsorbent in real environmental conditions was evaluated using this seawater. The seawater was introduced into a circulating water system, with the adsorbent (10 mg) positioned within a sea test tube of the system. The experiment was conducted over 35 days, with samples taken every 7 days. The variations in uranium concentration within seawater were assessed utilizing Inductively Coupled Plasma Mass Spectrometry (ICP-MS). After 35 days of immersion, the adsorbents maintained their structural integrity, with no disintegration observed under visual inspection (Supplementary Fig. 18).