Introduction

Magnetic resonance imaging (MRI) is indispensable for medical diagnostics because it is non-destructive and non-invasive. However, its low sensitivity can be a significant issue. Dynamic nuclear polarization (DNP) increases the sensitivity by enhancing the nuclear spin polarization via polarization transfer from highly polarized electron spins1,2,3,4,5,6,7. Conventional DNP using thermal equilibrium electron spin polarization has a theoretical maximum enhancement factor of 660 for 1H and 2600 for 13C. This is attributed to the difference between the gyromagnetic ratios of electron spins and nuclear spins. Although enhancement factor exceeding 10,000 times is practically achieved, attaining this high enhancement requires the generation of high electron spin polarization in thermal equilibrium under extreme conditions such as high magnetic fields ( ~ 6.7 T) and cryogenic temperatures ( ~ 1.4 K)8,9,10,11,12,13.

Triplet-DNP via photoexcited triplet electrons can enable nuclear hyperpolarization at much higher temperatures because high electron-spin polarization between triplet sublevels is independent of temperature. This is because of spin-selective intersystem crossing (ISC) (Fig. 1a)14,15,16,17,18,19,20,21. Polarization is transferred from the electron spins to nuclear spins via microwaves resonant with the electron spins and by controlling the microwave intensity to match the Larmor frequency of the electron spins in the rotating frame with that of nuclear spins in the laboratory frame. The magnetic field region where triplet electron spin resonance (ESR) occurs is broadened by dipole interactions between electron spins [zero-field splitting (ZFS) interactions], and variations in the molecular orientation relative to the magnetic field. Hence, only a fraction of spin packets satisfies the resonance condition. Wenckebach et al. introduced an integrated solid effect (ISE) sequence using microwave irradiation while the magnetic field was swept to make more spin packets available for polarization transfer. Because the sweep range was limited to approximately 10 mT, ESR spectra had to be sharpened by orienting matrix single-crystals doped with triplet polarizing agents very precisely in the magnetic field22,23,24,25. This method enabled 10% or higher nuclear spin polarization, but had several major challenges for practical applications. For example, it is not practical for medical professionals to precisely adjust crystal orientation in relation to magnetic fields as part of their routine work. Also, centimeter-scale single-crystal growth is problematic in terms of cost and scale-up. Finally, since the matrix is mainly composed of hydrophobic aromatic molecules chosen for their long proton spin-lattice relaxation times T1H, it is difficult to introduce a high-concentration MRI probe like pyruvate due to poor miscibility.

Fig. 1: Design strategies of polarizing agents for enhanced triplet dynamic nuclear polarization.
figure 1

a Schematic of triplet dynamic nuclear polarization. Following the photoexcitation of polarizing agents, spin-selective intersystem crossing generates spin-polarized triplet electrons. Subsequently, the triplet-electron spin polarization is transferred to nuclear spins via an integrated solid effect (ISE). b ISE sequence and electron spin resonance (ESR) simulation using the EasySpin toolbox in MATLAB R2024a54. The zero-field splitting (ZFS) parameters (D and E) and triplet sublevel populations (px, py, pz) used for the simulation are as follows: (C60: D = −342 MHz, E = 20 MHz, px = 0.5, py = 0.5, pz = 0, Pentacene: D = 1500 MHz, E = −50 MHz, px = 0.6, py = 0.3, pz = 0.1). c Decay of visualized ESR signals with T1e = 2 µs (black line) and T1e = 30 µs (red line). d Chemical structures of polarizing agents indene-C60 mono-adducts (ICMA), indene-C60 bis-adducts e-1, trans-1, trans-2, trans-3, and trans-4.

Full size image

To solve these problems, we previously proposed a chemical approach, molecular design of polarizing agent, instead of the physical approach, single-crystal orientation control26. ESR spectral widths of triplets become narrower by reducing the ZFS parameters D and E, which reflect electron spin delocalization and rhombicity, respectively. By modifying the commonly used polarizing agent pentacene with a thienyl group and extending the π-conjugated system, the D value was reduced from 1360.1 MHz to 1311.5 MHz. Further reduction would require other molecules with increased π conjugation.

Fullerenes are promising as polarizing agents because of their large delocalized electronic structure relative to pentacene, which results in weaker dipole interactions between triplet electron spins and narrower ( ~ 10 mT) ESR spectral linewidths27,28,29,30,31. While fullerene derivatives have been employed in a different liquid-state DNP context32,33, they have not been reported as polarizing agents of triplet-DNP because of their short (less than a few μs) triplet electron spin-lattice relaxation times (T1e), even at 100 K. In the ISE sequence, the magnetic field sweep rate must be slower than the effective precession frequency to satisfy the adiabatic condition. Hence, the sweep is typically several tens of microseconds (Fig. 1b) and it is difficult to use C60 fullerene as polarizing agent due to its short T1e. The short T1e of fullerenes is in contrast to the general trend that weaker spin-spin interactions have a longer T1e. This is attributed to the high fullerene symmetry that causes thermally activated molecular vibrations to induce pseudo-rotations, thereby changing the molecular ZFS axis relative to the magnetic field and inducing spin relaxation34,35,36,37.

In this work, we investigate the dependence of the T1e on the number and position of substituents in various fullerene derivatives (Fig. 1c) to suppress pseudo-rotation. Indene-C60 monoadducts (ICMA) and indene-C60 bis-adducts (ICBA) are used because of good dispersibility in o-terphenyl commonly used as a triplet-DNP amorphous matrix (Fig. 1d)38. ICBA is obtained as a mixture of many regioisomers; methods for isolating each regioisomer via liquid chromatography has been established for organic solar cells. Trans-2,3,4 had three regioisomers (a), (b), and (c), depending on the direction of CH2 groups on the two indene substituents. In (a), they pointed in the same direction; in (b), they pointed away from each other; and in (c), they faced each other. Equatorial regioisomers e-1 and e-2 had CH2 groups facing each other and pointing in the same direction, respectively39. Our evaluation of ICMA and ICBA regioisomers [trans-1, trans-2a, b, c, trans-3a, b, c, and trans-4a, b, c, e-1,2 in Fig. 1d] reveals that the di-substituted ICBAs have longer T1e values relative to the monoadduct ICMA; trans-3a had an especially long (80 µs) T1e. Substituents reduced the C60 Ih point group symmetry and broke the degeneracy of highest-occupied molecular orbitals (HOMOs) (hu) and lowest-unoccupied molecular orbitals (LUMOs) (t1u), which could suppress pseudo-rotations. Theoretical calculations suggest that the triplet excited states (T1) of equatorial, trans-3, and trans-4 regioisomers have single-well potential energy surfaces that suppress pseudo-rotations. In particular, trans-3 had the highest minimum-energy crossing point with the T2 state. Symmetry considerations combined with theoretical calculations also indicate that the ICBA regioisomers have nearly 100% polarizations attributed to ISC anisotropy. ICBA trans-3a demonstrates superior performance in triplet-DNP relative to conventional pentacene-based polarizing agents. The 14.2% 1H polarization is the highest value reported for amorphous materials and well-above the 10% practical requirement. These results thus demonstrate the potential of substituted fullerenes as triplet spin-polarization sources, which have been mainly developed for organic photovoltaics40.

Results and discussion

Each polarizing agent was mixed with o-terphenyl (OTP), dispersed in molten OTP at 333 K, and rapidly cooled with liquid nitrogen. Because the OTP glass undergoes crystallization at room temperature, all measurements were conducted at 140 K to maintain the glass state. The polarizing agent concentrations were 0.05 mol%, which yielded strong ESR intensities without aggregation, as determined by an intensity dependence on concentration for ICBA trans-3a (Fig. S1). ESR spectra and signal decays for each sample were acquired at the X-band (0.29–0.34 T) following irradiation with 1.5 mJ, 527 nm, 100 Hz laser pulses (Fig. 2). ESR spectra were simulated with Matlab, with parameters summarized in Table 1. The ZFS principal interaction axes were the same as those for C60, with all D < 0 and E > 0 (Fig. S16)30,41,42. ICBA isomers were first separated by high-performance liquid chromatography (HPLC) with 5PBB column, then purified with Buckyprep column. ICBA isomers were identified with 4–6 ppm 1H-NMR spectra, as reported previously (Fig. S2)39.

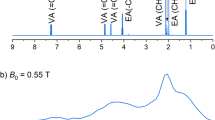
Fig. 2: Time-resolved electron spin resonance (ESR) spectra.
figure 2

Time-resolve ESR spectra of indene-C60 monoadducts and indene-C60 bis-adduct regioisomers in o-terphenyl at 140 K. Signals were detected 0.5–5 µs after the laser pulse, with the 30 ns time resolution. The ESR spectra were simulated using MATLAB R2024a and are shown as red lines. Source data are provided as a Source Data file.

Full size image
Table 1 D and E values, the relative population ratios px, py, and pz in the zero-field spin state, and average decay time T1e,ave for substituted fullerenes
Full size table

Suppression of fullerene pseudo-rotation by substituent modifications

ESR spectra of AEAEAE patterns (A: absorption, E: emission) specific to the y-directional polarization of the triplet sublevel were obtained for ICMA and all ICBA isomers. In general, for C60 and its derivatives, there was approximately 70% y-polarization for D < 0 at the zero-field spin state. Simulations for ICBA indicated that all regioisomers exhibited close to 100% spin polarizations, except for trans-130,43. Polarization derived from differences in ISC rates between the S1 state and each triplet sublevel, attributed to spin-orbit coupling (SOC) anisotropy. Theoretical calculations of SOC between the S1 state and energetically proximate triplet states indicated uniaxial ISC selectivity for all the regioisomers (Table S3). This should be explained by symmetry considerations. For example, two π orbitals of the equatorial isomer shown in Fig. 3 are associated with the ISC transition between S1 and T3, which are the initial and final states, respectively, of the transition. In general, the SOC vector is well approximated as the sum of the contributions from each atomic center, each of which is generated by transitions between atomic orbitals with different magnetic quantum numbers. In the case of 2p orbitals, the direction of the generated SOC vector is simply depicted as the rotation axis of two 2p orbitals. The SOC vectors of the two atoms symmetrically positioned with respect to the mirror plane either enhance or cancel each other out depending on the component. In this example of the equatorial isomer, the in-plane components, X and Y, are canceled out and only the out-of-plane component, Z, remains and results in uniaxial ISC (see Fig. S17 for more details). The linewidths of all isomers, except e-1,2, were within 10 mT, which was significantly sharper than that ( ~ 50 mT) for pentacene and its derivatives. This enabled most of the polarized triplet spins in the ICBA isomers to be available for triplet-DNP in the ISE sequence.

Fig. 3: An example of the relationship of the molecular symmetry and the direction of SOC.
figure 3

By the ISC transition between S1 and T3 states of the equatorial isomer, the in-plane components, X and Y, of the SOC are canceled and only the out-of-plane components, Z, remains. Source data are provided as a Source Data file.

Full size image

ESR signal decays for each regioisomer were acquired to analyze the pseudo-rotation suppression effects of fullerene substituents (Fig. 4). The decays were measured at the absorption peak at the low-field side of each ESR spectrum. Fitting was conducted with a double-exponential function, and the weighted average decay time with the coefficients of each time constant was defined as T1e,ave (Fig. S3, Table S1). The T1e,ave of unsubstituted C60 was as short as 2.2 μs (Fig. S4), and that of mono-substituted ICMA was only 4.1 μs. Di-substituted ICBA isomers had significantly longer T1e,ave. In particular, ICBA trans-3a exhibited a significantly long T1e,ave of 87.3 μs, which was several times those of other isomers.

Fig. 4: Electron spin resonance (ESR) signal decays.
figure 4

ESR decay at the peak top of each ESR spectrum under 527 nm pulsed irradiation in o-terphenyl glass for 0.05 mol% concentrations at 140 K. Source data are provided as a Source Data file.

Full size image

In general, polarized triplet electron spin relaxation was affected by spin-spin interactions. These interactions were weaker for lower |D| values, resulting in longer spin-lattice relaxation times. However, the trans-3a |D| value was not significantly less than those for other isomers. Therefore, its T1e,ave could be attributed to pseudo-rotation suppression via symmetry lowering by the substituents. This effect was most pronounced in trans-3a, resulting in a significantly longer T1e,ave relative to that (2.2 μs) for unmodified fullerene and the several microsecond values for pentacene26. The T1e,ave varied slightly with substituent orientations. While the trans-2b T1e,ave appeared longer relative to those of trans-2a and trans-2c, all of these isomers exhibited very weak ESR signals with poor signal-to-noise ratios, suggesting significant spin relaxation processes. It was difficult to fully understand substituent orientation effects, but they may be associated with different packing structures in the OTP matrix and thus different molecular mobilities.

Theoretical analysis of pseudo-rotation suppression

Potential energy surface landscapes were analyzed for ICBA regioisomers to elucidate molecular mechanisms for different spin-lattice relaxation times T1e for the various substitution orientations. The mono- and di-substituted ICBA isomers were modeled with C60H2 and C60H4 to focus on the substitution topologies and to simplify the analysis. For the substituted systems, there could be triplet states energetically close to T1 because the HOMOs and LUMOs of unsubstituted C60 in the Ih point group symmetry are quintuply and triply degenerate, respectively. Figure 5 shows potential energy surface cross-sections along linear coordinates between the characteristic geometries, such as the energetically lowest point within the highest symmetry. There were no constraints for the symmetries and minimum energy crossing points for T1/T2 states near the T1 energy minimum. The highest symmetries for C60H2, equatorial, trans-1, trans-2, trans-3, and trans-4 were C2v, Cs, D2h, C2, C2, and Cs, respectively.

Fig. 5: Calculation of the potential energy surface.
figure 5

Potential energy surfaces along the linear coordinate between the energetically lowest point within the highest symmetry and characteristic geometries. Calculations were performed with the ORCA 5.0.4 program package and minimum energy crossing points between T1 and T2 states were obtained by using minimum-energy conical intersection calculations at the same level. The top three figures (C60H2, trans-1 and trans-2) have energetically lowest points without constraints, while the three bottom figures (Equatorial e-1, trans-3 and trans-4) have minimum energy crossing points for T1/T2 states near the T1 energy minima. Red and blue curves represent T1 and T2 energy surfaces, respectively. Dotted gray lines represent the barrier heights between the energy minima. The structures of trans-3 and trans-4 at the minimum energy crossing points retained almost the same symmetry as the most stable structure of T1 (C2 and Cs, respectively), but are denoted as C1 in the figures. Source data are provided as a Source Data file.

Full size image

The potential energy curve shapes in Fig. 5 consist of two groups. The energy minima structures of C60H2, trans-1, and trans-2 did not retain the highest symmetries and relaxed to lower symmetries. Their barrier heights between the energy minima were 339 cm−1, 378 cm−1, and 354 cm−1, respectively, indicating that transverses between the different minima could occur, and which could cause pseudo-rotations (i.e., change in the principal axes). In contrast, the energy minimum structures of equatorial, trans-3, and trans-4 retained the highest symmetries, and pseudo-rotations were suppressed. The closest minimum energy crossing points with T2 were at 2475 cm-1, 2099 cm-1, and 1337 cm−1, respectively, and transitions to the T2 state could be thermally activated. This should explain the T1e temperature dependence for trans-3a (Fig. S5, Table S2). Structural fluctuations were not necessary to cause fluctuations of the polarized axis, which was the source of short T1e times. Trans-1 had a double well shape for the T1 potential energy curve and a longer T1e time than trans-4, which lacked the double well. Even if the symmetry was reduced during pseudo-rotation, as long as rotation and mirror-plane symmetry operations remained active, the principal axis parallel to the rotational axis and perpendicular to the mirror plane should have exhibited minimal fluctuations. In summary, the theoretical analysis predicted suppression of pseudo-rotations, especially for equatorial, trans-3, and trans-4, in good agreement with experimental results.

Triplet-DNP experiments

Triplet-DNP measurements demonstrated the ICBA potential as polarizing agents to produce high nuclear polarization, even without molecular orientation control. Polarizing agents had 0.05 mol% concentrations via the melt-quench method, as in for ESR measurements. Triplet-DNP was performed with the ISE sequence of microwave irradiation (17.6 GHz, 50 W) and magnetic field sweeps (10 mT) under 1.5 mJ, 527 nm pulsed laser irradiation at 100 K. The microwave pulse width was set to 25 µs. The repetition frequency was 500 Hz, which is long enough for the photoexcited triplet electrons to completely deactivate to the ground state (Fig. S6). We measured the repetition frequency dependence from 300 Hz to 700 Hz but there are no significant differences among these repetition frequencies (Fig. S8). The OTP model matrix exhibited a long ( ~ 80 s) 1H spin-lattice relaxation time T1H in the glassy state at 100 K (Fig. S7a). We compared performances of ICBA trans-3a, trans-4a, and e-1 polarizing agents, based on enhancement of the OTP 1H-NMR signal at optimized magnetic fields (Figs. S9, 10). The 1H-NMR enhancement with ICBA trans-3a was approximately twice that with ICBA trans-4a and e-1 because ICBA trans-3a had a longer T1e,ave than that of trans-4a, and a sharper ESR spectra than that of e-1 (Fig. S11). Figure 6a compares build-up curves of 1H signal in OTP with the polarizing agents; pentacene, 6,13-di(thiophen-2-yl)pentacene (DTP), and ICBA trans-3a. The 1H in OTP was polarized using pentacene (0.05 mol%) and DTP (0.07 mol%) at 100 K. Since Pentacene and DTP have poor photostability and are susceptible to degradation under the high laser power optimized for ICBA, triplet-DNP experiments were conducted under low-power laser irradiation condition (1.4 mJ/pulse) and compared the build-up behaviors based on the 1H NMR intensity normalized by 1H numbers. The build-up curves were fit with the equation I = A[1−exp( − t/Tb)], where Tb is the build-up time constant. The performances of the polarizing agents were compared with the initial gradients [dI(t)/dt | t=0] of the 1H-NMR build-up curves. The value of dI(t)/dt | t=0 for ICBA trans-3a was 1.83 × 10−15 s−1, which was 21 times larger than that of pentacene (8.53 × 10−17 s−1) and larger than 3.6 times that of DTP (5.10 × 10−16 s−1). The initial gradient is determined by the product of the polarization transfer efficiency and the electron polarization. As the gradient is also related to the generation efficiency of the photoexcited triplet electrons, strict comparisons of polarization transfer were difficult, but it was concluded that ICBA trans-3a had the best polarization performance under the current experimental condition.

Fig. 6: 1H polarization build-up curves and achieved maximum polarization.
figure 6

a Build-up curves of 1H NMR intensity for o-terphenyl (OTP) doped with pentacene (blue triangles), 6,13-di(thiophen-2-yl)pentacene (DTP) (green squares), and ICBA trans-3a (red circles). Build-up time constants were obtained by fitting the curves (solid lines) with I = A[1−exp( − t/Tb)]. b Build-up curve of 1H NMR intensity of partially deuterated OTP (OTP:[D14]OTP = 10:90 wt%), doped with 0.05 mol% of ICBA trans-3a. Source data are provided as a Source Data file.

Full size image

The final 1H polarization was calculated using a partially deuterated matrix because the triplet-DNP efficiency improved with longer matrix T1H because of increased 1H polarization accumulation. A mixture of OTP and fully deuterated [D14]OTP (OTP: [D14]OTP = 10:90 wt%) with the T1H of 188 s at 100 K was used as the matrix (Fig. S7b). The laser intensity was increased to 13 mJ/pulse. The thermal NMR signal of tetraphenylmethane crystalline powder at room temperature was used as a reference for polarization calculations (Fig. S14). For the partially deuterated OTP, 0.05 mol% was the optimum ICBA trans-3a concentration because higher concentrations resulted in shorter T1H. This limited the triplet-DNP efficiency (Fig. S12, 13). A 14.2% 1H polarization and a 22,000-fold NMR enhancement factor for the partially deuterated OTP matrix were obtained after 420 s of triplet DNP with ICBA trans-3a. This exceeded the previously reported values of 7.8% polarization and the 14,000-fold enhancement for the pentacene derivative DTP (Fig. 6b)26. The average polarization of the ICBA trans-3a triplet electron spins in random orientation was computed to be 21% (Fig. S18)44,45. Therefore, the 14.2% proton polarization achieved in this experiment indicates that polarization accumulated to a value close to that of the polarizing agent.

We identified fullerene derivatives as ideal polarizing agents via photoexcited triplet electron spin polarization. Short spin-lattice relaxation times of fullerenes were avoided via suppression of pseudo-rotation by reducing molecular symmetries with two substituents at specific sites. The substituted fullerenes extended spin-lattice relaxation times and increased polarization via anisotropic spin-orbit coupling, while maintaining small |D| values and sharp ESR spectra. Theoretical calculations revealed the mechanism whereby pseudo-rotation was energetically suppressed for specific ICBA isomers, opening up a path for designing ideal polarizing agents. While polarizing agents with narrow ESR line widths and long T1e have been established in the radical-based DNP field, we have developed clear design guidelines for achieving this in triplets with strong ZFS interactions. The triplet-DNP with ICBA trans-3a exhibited a 14.2% final 1H polarization, thus demonstrating a higher polarization above the 10% practical threshold for disoriented amorphous systems. The 1H polarization could be further improved with a deuterated polarizing agent to increase the overall concentrations of polarization agents. Furthermore, we expect that exploring fullerene derivatives with further reduced symmetry, through molecular design such as using C70 derivatives or varying their substituents, will lead to longer T1e and higher triplet-DNP efficiency. This study demonstrated that triplet-DNP is not restricted by the requirement of precise orientation control in single crystals, which has been fundamental issue for triplet-DNP. While a proof-of-principle was demonstrated with the OTP model matrix, it is important in future work to identify a biocompatible matrix to hyperpolarize MRI probes such as pyruvate. Lasers with wavelengths in the visible region can selectively excite fullerene derivatives, while pyruvate is not excited and radicals are not generated. Fullerene derivatives exhibit excellent dispersibility in various matrices, and it is expected that they can also be dispersed in biocompatible matrices containing high concentrations of pyruvate. The development of such a matrix is currently underway in our group. Molecular design guidelines for triplet polarizing agents offer ways for practical applications of optical DNP.

Methods

All reagents and solvents were used without further purification unless otherwise noted. Fullerene C60, ICMA, and ICBA isomer mixtures were purchased from Sigma-Aldrich. Each ICBA isomer was separated using 5PBB and Buckyprep columns (Kyoto, Japan). OTP and [D14]OTP were purified by zone melting. For ESR and triplet-DNP measurements, each polarizing agent was mixed with OTP by grinding. The resulting powder was placed in an ampoule that was sealed under vacuum and heated to 333 K. The resulting melt was rapidly cooled with liquid nitrogen. The obtained glassy solids were removed from the ampoule and ground with a mortar. The ICBA isomers were dissolved in 10 mL of toluene, filtered, and then injected into an HPLC. Isomers were first separated with a 5PBB column at 8 mL/min; pure toluene was switched to a 7:3 toluene:hexane mixture. Separated isomers were further purified with a Buckyprep column at 10 mL/min using toluene as the solvent.

General characterization

1H NMR (400 MHz) spectra were acquired on JEOL JNM-ECZ400 (Tokyo, Japan) and Bruker Ascend NMR 400 MHz spectrometers (Germany). Zone-melt refining was performed with a MiniZone II Zone Refiner (TX. USA). Transient absorption measurements were conducted with a UNISOKU TSP-2000 system (Osaka, Japan). ICBA was separated with a Shimadzu HPLC consisting of a CTO-20A column oven, a CBM-20A Bus module, and SPD-20A UV-vis detection (Kyoto, Japan). COSMOSIL 5PBB (particle size, 5 nm) and COSMOSIL Buckyprep columns with a guard column were used in the HPLC separations.

Time-resolved ESR

Time-resolved ESR measurements were performed at room temperature, as described previously26,46. Samples were photoexcited with a 527 nm pulsed laser (Tolar-527, Beamtech Optronics) in a dielectric resonator inside an electromagnet (MC160-60G-0.8 T, Takano Original Magnet). Laser pulse widths were 200 ns at a 100 Hz repetition rate and 0.3 W power. ESR spectra of photoexcited triplets were obtained after photoexcitation from the sum of signal intensities over a period of 5 µs. The cavity had a resonance frequency 9 GHz with a Q-value of approximately 2750. Microwaves (1 mW) were generated with a SG24000H (DS Instruments), amplified by a power amplifier (ALN0905-12-3010, WENTEQ Microwave Corp), and converted to DC with a diode detector (DHM185AB, Herotek). ESR signals were amplified and noise was reduced with two amplifiers (SA-230F5, NF ELECTRONIC INSTRUMENTS, 5305 differential amplifiers, NF ELECTRONIC INSTRUMENTS). The signals were detected with an oscilloscope (DSOX3024T, Keysight), and spectra were analyzed in MATLAB version R2024a (The Mathworks, Inc.).

Calculation of T 1e,ave

The weighted average spin-lattice relaxation time (T1e,ave) of the triplet electron spins was calculated with weights derived from coefficients of lifetime components of each term in the decay curve fit given by A exp(-t/τA) + B exp(-t/τB).\({T}_{1{{{\rm{e}}}},{{{\rm{ave}}}}}=\frac{A{\tau }_{A}+B{\tau }_{B}}{A+B}\)

Triplet-DNP experiment

The triplet-DNP experimental apparatus was described previously26,46. It consisted of an electromagnet (MC160-60G-0.8 T, Takano Original Magnet), a microwave resonator, a coil for magnetic field sweeps, and a pulsed laser (Tolar-527, Beamtech Optronics). The sequence control and NMR signal detection were performed with an OPENCORE NMR spectrometer47. The powder samples were inserted in glass capillaries (FPT-220, FUJISTON, 2.2 mm diameter, 1.4 mm inner diameter) and sealed under vacuum.

The laser repetition frequency was 500 Hz, with an output power of 8.4 W, and a 200 ns pulse length. Continuous microwaves were generated with a SG24000H (DS Instruments) and converted to pulsed waves with a pin diode (S1517D, L3HARRIS). The pulses were amplified to 50 W with a power amplifier (AMP4081P-CTL, EXODUS ADVANCED COMMUNICATIONS) and sent to the resonator via coaxial cable. The magnetic field was swept by applying an amplified triangular wave to a copper wire installed in the resonator. The triangular wave was generated from a function generator (WF1974, NF ELECTRONIC INSTRUMENTS), amplified by a factor of ten ( ± 50 V) with an operational amplifier (137-PA05, Apex Microtechnology), and applied to the copper wire. The cavity resonance frequency was 17.6 GHz with a Q-value of approximately 1350.

NMR signals were acquired with an OPENCORE NMR spectrometer. A solenoid coil was used as the NMR probe and mounted on top of the resonator. For NMR detection, the sample was raised to the probe coil with a stepper motor within one second after triplet-DNP. A magic echo sequence was used because protons in solid samples were difficult to detect with ordinary single-pulse.

Calculation of the enhancement factor

The enhancement factor (ε) of each sample after the triplet-DNP sequence at 100 K and 0.629 T was calculated by comparing the integrated 1H-NMR intensities of the hyperpolarized nuclei with the 1H NMR intensity of tetraphenylmethane at thermal equilibrium at 300 K and 0.629 T (Fig. S14). To compare enhancement factors at the same temperature, the thermal signal of tetraphenylmethane was multiplied by a temperature factor of 300/100 and converted into NMR intensities at 100 K:

$${{{\rm{\varepsilon }}}}=\frac{{N}_{{ref}}}{{N}_{{DNP}}}\frac{{T}_{{DNP}}}{{T}_{{ref}}}\frac{{g}_{{ref}}}{{g}_{{DNP}}}\frac{{E}_{{DNP}}}{{E}_{{ref}}}$$
(1)

where N represents the number of 1H spins, T is the temperature, and g and E are the receiver gain and the recorded signal voltage, respectively. The 1H spin polarization (P) was calculated from:

$$P={{\varepsilon }}\tanh \frac{\gamma {{\hslash }}B}{2{kT}}$$
(2)

where γ, ℏ, B, k, T are the gyromagnetic ratio, the reduced Planck’s constant, the magnetic field, Boltzmann’s constant, and the temperature, respectively.

Computational details

All calculations were performed with the ORCA 5.0.4 program package48. Geometry optimizations were performed using time-dependent density functional theory with the Tamm-Dancoff approximation49. We used the LC-BLYP functional50 with the range separation parameter µ=0.15 and def2-SVP basis sets51,52. The minimum energy crossing points between T1 and T2 states were obtained by using minimum-energy conical intersection calculations at the same level.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.