Introduction

The rapid development of flexible electronics1, energy devices2, soft robots3, and human–machine interfaces4 has stimulated strong demand for hydrogels with enhanced mechanical properties. However, conventional hydrogels, characterized by loose crosslinking networks, low solid content, and the absence of multilevel architectures, remain fragile and are prone to premature failure under load. These limitations significantly restrict their practical applications. To address this challenge, diverse structural design strategies have been proposed to enhance hydrogel mechanics, such as double-network architectures5,6,7,8, phase separation9,10,11,12, and nanocrystalline domains13,14,15. These approaches typically introduce sacrificial dissipation mechanisms, including hydrogen bonding, electrostatic and coordination interactions, interfacial sliding, and crystalline dissociation. However, achieving hydrogels with both high fracture strength and toughness remains major challenge.

Inspired by the hierarchical architectures of natural tough materials, such as fish scales16 and shells17, the construction of multiscale structures has recently been recognized as an effective approach for enhancing the mechanical properties of hydrogels18. Structural units at different length scales provide complementary reinforcement mechanisms. At the molecular scale, representative mechanisms include reversible hydrogen bonding6,8, electrostatic interactions19,20, and coordination interactions21,22, which serve as dynamic sacrificial bonds for polymer chains, dissipating energy through reversible breakage and reformation and thereby significantly enhancing toughness. At the nano- and microscale, higher-order structures, such as microcrystalline or microfibrillar23,24,25, phase-separated architectures26,27,28, mineralized networks29,30, and lamellar bilayers31,32,33,34 dissipate energy through pathways including crystallite dissociation, fibril pull-out, interfacial sliding, phase deformation, sacrificial fracture of inorganic clusters, and layer sliding or delamination. These mechanisms supplement the rapid yet limited energy dissipation provided by molecular-scale dynamic bonds, together giving rise to a hierarchical multiscale toughening system35. At the macroscopic scale, oriented architectures can effectively redistribute stress and promote crack pinning and deflection, thereby significantly enhancing fracture toughness and fatigue thresholds23. Similarly, structures including gradient structures36 and lamellar structures37 reinforce hydrogels by enabling efficient stress transfer and dispersion. Multiscale architectures thus not only provide energy dissipation at individual levels but also enable synergistic interactions across scales, ensuring efficient load transfer and uniform stress distribution. For instance, freeze-casting-assisted salting-out can generate ordered microcrystals and microfibers that assemble into an oriented porous network, leading to denser fiber packing and extended load-transfer lengths, and ultimately yielding increased mechanical performance23. These advances have laid the groundwork for further constructing reinforcement strategies combining with hot-pressing38, pre-stretching39, alternating mineralization40, etc. Taken together, multiscale design thus provides distinct advantages for hydrogel design, providing a promising strategy to achieve the integration of strength, toughness, and crack resistance through hierarchical energy-dissipation networks18.

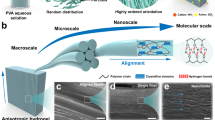
Here, we propose a strategy to construct a configuration of sandwich mineralized hydrogels (SM-PVA) via a freeze-assisted bidirectional migration process. Unlike the existing energy dissipation structures of traditional hydrogels (Supplementary Fig. 1), the hierarchical energy dissipation structure (dense–porous–dense sandwich structure surrounding a physical mineralized crosslinking center) could allow stress to transfer through the multiple layers and the mineralized centers, ensuring that the hydrogels have increased mechanical strength (33.51 MPa), high strain capacity (1026.55%), and increased tear resistance (286.39 kJ m−2). The SM-PVA hydrogel shows comparable mechanical performance in the parallel and perpendicular directions to the freezing direction in the plane. The structure formation, evolution and energy dissipation mechanism of the hydrogel was further revealed. In addition, these hydrogels can be recycled multiple times and continue to exhibit stable performance. More importantly, various cations and anions can bidirectionally migrate using this strategy to enhance the properties of the hydrogels, exhibiting universality and broadening the application range.

Results

Formation of the sandwich mineralized structure

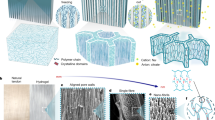
The key to our strategy lies in the interaction between the composite polyvinyl alcohol (PVA) with metal cations and induction solution (Fig. 1a–e). Specifically, Ca2+ was selected as the metal cation in PVA, while Na3C6H5O7 and Na2CO3 were mixed into the induction solution. Ca2+ was used to coordinate with the hydroxyl groups in PVA25,41,42, forming a stable PVA/CaCl2 matrix. When pre-freezing PVA/CaCl2 was immersed in the induction solution, the bidirectional diffusion of ions was driven by the chemical potential. On the one hand, Ca2+ tends to migrate to the both sides of the hydrogel, at which time the Ca2+ drive the movement of the PVA molecular chains, leading to more self-entanglement via the disturbance of ion diffusion28. On the other hand, C6H5O73− and CO32− from the induction solution tends to migrate into the hydrogel, and CaCO3 will precipitate. The CaCO3 grains nucleated and grew in situ between the PVA chains and eventually became mineralized crosslinking centers that wrapped the polymer network (Fig. 1d and Supplementary Fig. 2), and the free C6H5O73− further promoted the strong self-aggregation of the PVA chains through the Hofmeister effect43. Under the interactions between ions and molecules, a highly entangled and relatively fixed structure had formed on both sides of the hydrogel with relatively dense structures on each side, while a porous layer with an oriented nanofibrous structure was constructed in the middle of the hydrogel (Supplementary Figs. 3 and 4a–c). Due to the change in diffusion concentration, a thin transition layer would be gradually formed between the two layers (Supplementary Fig. 4d). The sandwich-like mineralized structure (Fig. 1c), featuring the in-phase interface of the dense–porous–dense layers, the heterogeneous interface between CaCO3 and PVA fibers, and highly entangled molecular chains, plays a crucial role in hierarchical energy transfer and dissipation, resulting in the SM-PVA hydrogel exhibiting excellent strength, toughness, and tear resistance.

Fig. 1: Preparation and hierarchical structure of the high-strength, high toughness, antifracture sandwich mineralized hydrogel.
figure 1

a Schematic illustration of the formation of sandwich-like mineralized hydrogel induced by bidirectional ion migration. b Three-dimensional diagram of the sandwich mineralized hydrogel. c Scanning electron microscopy (SEM) image of the SM-PVA hydrogel. d SEM image of mineralized center in the dense layer (ⅰ) and porous layer (iii) of the SM-PVA. Energy-dispersive spectroscopy (EDS) map of calcium in dense layer (ii) and porous layer (iv). e Schematic of the aggregated polymer chains, including the nanocrystal domains and chain entanglements. f The thickness of the dense layer and porous layer changes with induction solution treatment duration. Data are presented as mean values ± SD (n = 3). g Correlation between the thickness of various areas in SM-PVA hydrogels prepared with different freezing thickness. Data are presented as mean values ± SD (n = 3). h Interactions between calcium ions and other ion and molecules. Each column in (h) represents a single simulation value.

Full size image

We investigated the evolution of the sandwich structure and found that the proportion of the dense layer increased steadily in the early stages. Once the complex hierarchical structure matured, the growth in thickness gradually slowed (Fig. 1f). Specifically, the dense layer accounted for 22.84% of the total thickness at 3 h and increased to 67.76% after 24 h. This evolution is further influenced by the dense layer and concentration gradient, which limits its continued growth (Fig. 1g and Supplementary Fig. 5). The thickness of the dense layer does not linearly correlate with the overall membrane thickness. With an increase in SM-PVA hydrogel thickness from 0.58 to 2.89 mm, the dense layer thickness increased marginally from 0.36 to 1.07 mm. As shown in Supplementary Fig. 6, the thickness of the dense layer increase with both Ca2+ concentration and the anion concentration of the inducing solution, and are further modulated by the anionic composition ratio, reaching a maximum thickness of 0.76 mm at 25% carbonate content. In addition, owing to the interaction of Ca2+ and the PVA molecules, which affects nucleation of the initial PVA chain, the entanglement and dehydration caused by the disturbance of the molecular chain in the subsequent bidirectional ion diffusion process continues to affect nucleation43 (Supplementary Fig. 7). Thus, the crystallinity of the SM-PVA hydrogel decreased to 17.8% compared with that of PVA without bidirectional migration (26.6%) (Supplementary Fig. 7b).

The mineralization process was further validated using molecular dynamics (MD) simulations. The results show that the relatively high binding energies of Ca2+ with C6H5O73− and CO32− promote their preferential binding during the initial stages of ion migration. The binding affinities follow the order C6H5O73− > CO32− > H2O > Cl−, as shown in Fig. 1h, Supplementary Figs. 8; 9 and Supplementary Table 1. Combining the Ksp-based solubility equilibrium theory and the calculated binding energy, calcium ions would transform into the calcium carbonate (Supplementary Fig. 10). Micron-sized CaCO3 aggregates form clustered domains within the SM-PVA hydrogel, acting as fiber clamps by absorbing the stress transferred between the fibers (Supplementary Fig. 2). Additionally, the low degree of mineralization of the hydrogel prevents the formation of a continuous three-dimensional framework composed of CaCO3, thereby preventing network embrittlement16.

A more uniform and stable structure is crucial. By characterizing the hydrogel structures formed via directional freezing-ion migration (SM-PVA), nondirectional freezing-ion migration (SM-PVA ND), nonfrozen ion migration (SM-PVA NF) and directional freezing-mineralization (FM-PVA), we found that directional freezing yielded a more uniform sandwich-like architecture with well-aligned microchannels oriented along the ice growth direction (Supplementary Fig. 11a–c). In contrast, SM-PVA ND showed a less uniform sandwich structure with disordered porous layers. This stems from the directional exclusion of PVA chains and Ca2+ ions during ice growth, forming a homogeneous, oriented pre-concentrated network that supports stable ion diffusion and layered structure formation. In contrast, no sandwich-like structure was observed in SM-PVA NF and FM-PVA hydrogels (Supplementary Fig. 11d, e), suggesting that freezing or mineralization alone is not sufficient to induce the multiple layers formation.

Enhancement of mechanical properties

The sandwich mineralized structure can synergistically enhance the mechanical properties of the hydrogel. A stepwise analysis of each processing step revealed that both directional freezing and ion migration play key roles in achieving the enhanced mechanical performance of the hydrogel (Supplementary Figs. 12–14). For comparison, we prepared three other hydrogels under the same experimental conditions: (i) a PVA hydrogel prepared via one freeze-thaw process (FT-PVA D), (ii) a hydrogel prepared with mineralization process (M-PVA), and (ⅲ) a PVA hydrogel with hierarchical and anisotropic structures prepared via freeze-salting out (FS-PVA). Benefiting from the multiple reinforcing mechanisms derived from its sandwich-mineralized architecture, SM-PVA exhibited high mechanical performance, achieving an ultimate stress of 25.79 MPa, a toughness of 120.98 MJ m−3, an ultimate strain of 807.49%, and a modulus of 13.3 MPa (Fig. 2a–c). Specifically, the compact layers and crystalline domains enhance strength through dense chain packing and strain-induced crystallization, while the porous fibrillar layers, interfacial regions, and CaCO3 clusters contribute to stress redistribution and sacrificial energy dissipation, thereby improving toughness and crack resistance. These synergistic mechanisms endow SM-PVA with significantly higher strength and toughness compared with FT-PVA D, M-PVA, and FS-PVA. Notably, relative to FT-PVA D, which lacks crystallinity and exhibits a loose and homogeneous structure, the strength of SM-PVA was 1611 times higher (25.79 vs. 0.016 MPa), while the toughness was enhanced by a factor of 3102 (120.98 vs. 0.039 MJ m−3). In addition, SM-PVA demonstrated a fracture energy of 201.14 kJ m−2, surpassing FT-PVA D (0.32 kJ m−2), M-PVA (0.81 kJ m−2), and FS-PVA (36.73 kJ m−2) by factors of 628, 30, and 5, respectively (Fig. 2c and Supplementary Fig. 15a). The strength, toughness, and fracture energy could be further improved to 33.51 MPa, 177.39 MJ m−3, and 286.39 kJ m−2, respectively, by increasing the PVA content to 15 wt% (Supplementary Fig. 15b).

Fig. 2: Mechanical properties of the SM-PVA hydrogel.
figure 2

a Photographs of SM-PVA hydrogel under tensile loading, showing excellent stretchability. Stress–strain curves (b) and comparisons (c) of the strengths, moduli, toughnesses and fracture energies of the FT-PVA D, M-PVA, FS-PVA and SM-PVA hydrogels. Data in (c) are presented as mean values ± SD (n = 3). d Images of SM-PVA hydrogels with and without notches for lifting a 19.8 kg bucket. e Cyclic loading–unloading curves at different strain levels. f Total energy, dissipated energy, and energy dissipation ratio of SM-PVA at corresponding strain levels (from e). Each column represents a single measurement. g Crack growth rate (dc/dN) per loading cycle under increasing energy release rates, controlled by the corresponding maximum strain. Stress‒strain curves (h) and comparisons (i) of the strengths, moduli, toughnesses and fracture energies of the SM-PVA∥, SM-PVA⊥. Data in (i) are presented as mean values ± SD (n = 3). j Ashby diagrams of ultimate tensile strength versus fracture energy of the SM-PVA hydrogels and other reported tough hydrogels. k Ashby diagrams of elongation at break versus fracture energy of the SM-PVA hydrogels and other reported tough materials.

Full size image

Additionally, the notched SM-PVA sample exhibited a high crack insensitivity during tensile testing. The initial crack propagated in the tensile direction, gradually passivated and transformed into a C type crack, during which there was no observable extraction or fracture at the notch (Supplementary Fig. 16). Impressively, a hydrogel strip with a width of 7 mm and two 2 mm wide notches successfully lifted a bucket approximately 30000 times (~19.8 kg) heavier than itself (Fig. 2d; Supplementary Movies 1 and 2). The energy dissipation capacity of SM-PVA was also prominent. SM-PVA continuously consumed energy under a continuously increasing strain from 100 to 600%, the energy dissipation improved from 3.75 to 23.37 MJ m−3, and the dissipation efficiency was greater than 85% at a strain of 600% (Supplementary Fig. 17). When the SM-PVA hydrogel was test using individual samples at each strain level, at 800% strain, the dissipated energy and dissipation ratio increased significantly to 110.11 MJ m−3 and 91.65%, respectively (Fig. 2e, f). It exceeded the dissipation performance of many tough hydrogels and even outperformed natural spider silk, positioning SM-PVA as one of the top-performing materials (Supplementary Table 2).

We determined quantified the fatigue threshold (Γ0) of SM-PVA using the single-notch method. Pronounced mechanical hysteresis was observed in all tested samples, indicating substantial energy dissipation during cyclic deformation (Supplementary Fig. 18). As shown in Fig. 2g, SM-PVA exhibits excellent fatigue resistance, achieving a fatigue threshold of 11.2 kJ m−2. Following 1000 loading cycles at 175% strain, the notched SM-PVA hydrogel exhibited minimal crack growth, accompanied by an energy release rate of 11.78 kJ m−2 (Supplementary Fig. 19). This high fatigue resistance is attributed to the synergistic toughening of the layered architecture, mineralized domains, and crystalline regions, which effectively impede crack propagation, resembling natural materials like fish scales.

Moreover, we further compared the mechanical properties of the directionally frozen hydrogels along both the parallel (SM-PVA∥) and perpendicular (SM-PVA⊥) directions, as shown in Fig. 2h, i. Notably, the strength, fracture energy and toughness of SM-PVA⊥ were 26.03 MPa, 225.09 kJ m−2 and 95.11 MJ m−3, which are similar to those of SM-PVA∥, exhibiting the similar performances in the perpendicular and parallel directions in the plane (Fig. 2b, c). The comparable in-plane mechanical performance of SM-PVA can be attributed to the synergy between its macroscopic sandwich-like architecture and microscopic energy-dissipating mechanisms. The isotropic dense layers, occupying the majority of the cross-sectional area, suppress the anisotropy arising from the porous layers. Meanwhile, the toughening mechanisms—including CaCO3 cluster fracture, crystalline domain dissociation, and interfacial delamination—dissipate energy similarly in both orientations, thereby contributing to comparable in-plane mechanical performance. Therefore, despite structural differences in the orientation of the porous layers between SM-PVA∥ and SM-PVA⊥, the in-plane mechanical properties remain nearly identical. This strategy offers a potential analytical solution for fabricating hydrogels with similar in-plane mechanical properties via conventional ice-templating methods (Supplementary Table 3).

In summary, SM-PVA hydrogels have ultrahigh strength, toughness and tear resistance, surpassing most reported tough hydrogels (Fig. 2j; Supplementary Fig. 20 and Supplementary Table 4). These hydrogels can maintain high strength and toughness when notched with a fracture energy 19–300 times greater than that of the advanced DN hydrogel, which exceeds those of the vast majority of reported tough hydrogel materials, most tough anhydrous polymers, wood, bone and some metal alloys, such as Cu alloys (<241 kJ m−2) and Zn alloys (<100 kJ m−2) (Fig. 2k and Supplementary Table 5).

Strengthening and crack-resistance mechanisms

To elucidate the strengthening and crack-resistance mechanisms of SM-PVA in relation to its multiscale structures, the deformation process was divided into distinct regimes—from the linear elastic stage to softening, strain-hardening, and final fracture—within which we interpreted the corresponding structural responses and energy dissipation mechanisms.

Within the elastic regime, the stress–strain curve exhibits an almost ideal linear response (R2 ≈ 0.99). The SAXS/WAXS patterns show no noticeable anisotropy (Fig. 3a and Supplementary Fig. 21a–c) and a nearly constant domain spacing (L). However, the crystalline domain size (D) slightly decreases from 6.19 to 5.96 nm (Fig. 3b–d), which is attributed to the disorientation of imperfect crystallites, leading to smaller coherent segments. Cyclic loading–unloading tests demonstrate that the material fully recovers within 600 s (Fig. 3e and Supplementary Fig. 22a). This structural rearrangement of crystalline defects is reversible, with no permanent damage occurring during the loading and unloading process. Industrial CT further shows intact CaCO3 clusters at 20% strain (Fig. 3f), excluding their contribution to dissipation in the elastic regime. Energy dissipation is thus mainly governed by molecular chain rearrangement and reversible hydrogen bond rupture/reformation.

Fig. 3: Strengthening and crack-resistance mechanisms of SM-PVA hydrogels.
figure 3

a Stress–strain curve of SM-PVA divided into four regimes: linear elastic (Ⅰ, 0–10% strain), nonlinear softening (Ⅱ, 10–80% strain), strain-hardening (Ⅲ, 80–720% strain), and fracture (Ⅳ, >720% strain). Representative 2D SAXS patterns at selected strains are also shown. SAXS profiles (b) and WAXS profiles (c) of SM-PVA at 0, 10, 80, 200, and 500% strain (intensity in arbitrary units, arb. units). d Evolution of inter-crystalline spacing (L) and crystalline domain size (D) with increasing strain. Each column represents a single measurement. e Evolution of recovery ratio over time. The recovery ratio is defined as the ratio of the second cycle energy dissipation ratio to the first one. f Industrial CT images of SM-PVA at 0, 20, 80, and 800% strain. g Finite element simulation showing the stress distribution across the cross-section of SM-PVA under tensile loading. h FEM-simulated stress distribution in a notched SM-PVA model. i FEM-simulated stress distribution in a porous hydrogel without the sandwich mineralized structure.

Full size image

In the nonlinear softening regime, stress growth slows while structural damage becomes evident. SAXS/WAXS reveals strain-induced fibril alignment and a further decrease in crystalline domain size from 5.96 to 5.84 nm (Fig. 3d), indicating that the crystalline domains are not entirely rigid and can unfold under deformation, thereby continuously contributing to toughening44. CT imaging detects blurred CaCO3 clusters at 80% strain (Fig. 3f), suggesting partial collapse, where particle fracture and interfacial debonding absorb external mechanical work and thereby provide additional toughening mechanisms. Cyclic testing at the same strain level shows only 87.50% recovery after 7200 s, confirming that irreversible damage has occurred (Supplementary Fig. 22b). In this stage, energy dissipation mainly arises from chain slippage, crystalline dissociation, and partial failure of CaCO3 clusters.

During the strain-hardening regime, the slope of the stress–strain curve gradually increases, reflecting enhanced load-bearing capacity. SAXS/WAXS patterns show pronounced orientation-induced scattering, consistent with progressive molecular alignment (Fig. 3a and Supplementary Fig. 21a–c). In this process, the highly oriented nanofibrils within the porous middle layer provide additional toughening mechanisms. The sandwich structure facilitates further alignment of the oriented fibrous network during deformation, while fibril pull-out, bridging, and frictional sliding across crack flanks dissipate substantial energy and help stabilize crack propagation. Moreover, molecular chains and fibers partially spanning the interfaces are forced to deform or rupture, thereby contributing further to energy dissipation (Supplementary Fig. 23a–d). The crystalline domain size continuously decreases to 5.79 nm at 500% strain (Fig. 3d), which contributes to sustained toughening. This process is accompanied by variations in domain spacing—an initial increase from 13.08 nm at 80% strain to 14.36 nm at 200% strain, reflecting domain separation under macroscopic strain45 (Supplementary Fig. 21d), followed by a sharp decrease to 8.21 nm at 500% strain. At this stage, new crystalline domains are generated through more ordered chain packing44, thereby contributing to the reinforcement. CT analysis confirms progressive CaCO3 fracture (Fig. 3f), which absorbs external work and further enhances dissipation. Consistently, the recovery ratio of hysteresis energy decreases to 77.83% after 7200 s (Supplementary Fig. 22c), reflecting the accumulation of irreversible structural responses.

In the fracture regime, catastrophic failure occurs, with stress growth slowing and then rapidly dropping. Owing to their higher chain density and stiffness (Supplementary Fig. 23e, f), the compact layers dominate load-bearing during stretching, thereby effectively enhancing the strength, as confirmed by finite element simulations (Fig. 3g). SEM imaging (Supplementary Fig. 11a) and crack propagation observations (Supplementary Fig. 24) further reveal that the porous layer, featuring a continuous aligned network, can redistribute stress and delay rupture, typically fracturing after the compact layers. Once the compact layers fail, crack propagation mainly proceeds along the compact–porous–compact interfaces, where extensive interfacial damage becomes a key dissipation pathway. Ultimately, large-scale chain scission, fiber pull-out, and interfacial debonding of the sandwich structure dominate the energy dissipation in this stage.

The crack insensitivity of SM-PVA was further elucidated by finite element simulations (Fig. 3h). During tensile loading, CaCO3 clusters facilitated stress redistribution across the dense–porous–dense layered structure, acting as barriers at the crack tip to deflect stress and suppress crack growth. In contrast, hydrogels lacking the sandwich mineralized structure exhibited sharp crack tips and rapid crack propagation (Fig. 3i). Consistently, Supplementary Fig. 24 shows that failure of the dense region was followed by progressive interfacial delamination, leading to extraction of the highly oriented porous layer. This suggests that, once initiated, cracks preferentially propagate along the interface, thereby retarding catastrophic failure. As strain increased, the porous layers formed by interlocked fibers became increasingly aligned, promoting fibril pull-out, bridging, and stress redistribution, which helped delay crack initiation and propagation23 (Supplementary Fig. 23a–c). In addition, sacrificial components, such as PVA microcrystals and CaCO3 aggregates acted as microscale energy traps dissipating stress via localized deformation, microcrystal fracture, and interfacial debonding (Supplementary Fig. 23g, h). Collectively, these mechanisms significantly enhance the fracture toughness of SM-PVA. Cyclic loading tests further confirmed the material’s crack resistance: after 1000 cycles at 175% strain, notched samples exhibited negligible crack extension (Supplementary Fig. 19).

Tunability

The mechanical properties of SM-PVA hydrogels are regulated by their ion migration behavior. The strength and toughness of the hydrogels first increased and then decreased with increasing Ca2+ concentration in the PVA solution, peaking at 10 wt% (Supplementary Fig. 25a). The higher concentration of Ca2+ diffusion enhances long chain entanglement and results in the formation of more in situ CaCO3 aggregates, but an excessive amount of Ca2+ may hinder molecular chain crystallization46 and cause uneven shrinkage on the gel surface due to increased diffusion interference (Supplementary Fig. 26), ultimately resulting in a decrease in strength. At 30 wt% Ca2+, the strength and toughness decreased to 12.45 MPa and 44.03 MJ m−3, respectively. Additionally, the presence of compound anions in the induction solution strongly influences the mechanical properties of the hydrogel. At compound ion concentrations in range of 0.25–2 M, the strength and toughness varied from 0.08 MPa and 0.117 MJ m−3 to 25.7 MPa and 120.9 MJ m−3, respectively, and were positively correlated with the ion concentration (Supplementary Fig. 25b). In addition, the water content decreases from 85.08 to 29.03 wt%, aligning closely with values documented for salting-out toughened hydrogels (Supplementary Fig. 25b)39,47,48.

Interestingly, different ratios of C6H5O73− and CO32− also significantly affected the regulation process (Supplementary Fig. 25c). CO32− improved the hydrogel by forming an in situ mineralized center and reinforced phase, whereas C6H5O73− promoted the strong aggregation of molecular chains by modulating the PVA molecular chain and its surrounding water environment and enhanced and stabilized the hydrogel via densification of the gel network39. At a total concentration of 2M, the mechanical strength of the SM-PVA hydrogels first increased but then decreased with increasing percent CO32−, and the optimal ratio for enhancement was 3:1.

In addition, the mechanical performance is related to the size of the SM-PVA. On one hand, the internal multilevel structures and molecular chain interactions of the hydrogel gradually developed and matured over time, leading to an increase in the dense layer thickness, which resulted in a gradual improvement in the mechanical properties of the hydrogel (Supplementary Fig. 25d, e). On the other hand, the thickness of the hydrogel also influences mechanical performance. As the hydrogel thickness increases from 0.58 to 1.45 mm, the tensile strength and toughness reduced from 22.42 MPa and 111.20 MJ m−3 to 15.32 MPa and 56.63 MJ m−3, but the fracture resistance remains relatively stable (Supplementary Fig. 25f).

These results show that SM-PVA hydrogels have excellent mechanical tunability, easily adjusted through parameter modifications for different applications. For instance, soft robotics may require highly tough hydrogels, wearable sensors require moderate modulus and flexibility, and implantable devices benefit from dynamically tunable stiffness. Optimizing mechanical properties through parameter control offers a versatile platform for developing functional hydrogels for demanding environments.

Generality, applicability and recyclability

Various mechanically enhanced hydrogels were prepared in different ion systems. They all exhibited a sandwich multilevel structure and in situ mineralization (Supplementary Fig. 27). The mechanical properties of this series of hydrogels were tested, and the results are shown in Fig. 4a, b. Compared with those of the hydrogel without bidirectional ion migration (12.62 MPa, 50.26 MJ m−3, and 36.73 kJ m−2), the strength, toughness and fracture of the SM-PVA/SrCO3 (24.96 MPa, 115.50 MJ m−3, and 91.10 kJ m−2), BaCO3 (21.59 MPa, 89.79 MJ m−3, and 116.20 kJ m−2), MgCO3 (21.45 MPa, 99.95 MJ m−3, and 158.20 kJ m−2), and CaSO4 (24.53 MPa, 118.50 MJ m−3, and 289.61 kJ m−2) hydrogels were all enhanced (compared with FS-PVA/SO42−, 14.34 MPa, 72.80 MJ m−3, 54.80 kJ m−2), indicating the universality of this method. It can be envisaged that for different application scenarios, we can also conveniently regulate hydrogel performance by selecting an appropriate ion type.

Fig. 4: Generality of the strategy, applicability and recyclability of the SM-PVA hydrogels.
figure 4

The generality of the freeze-assisted bidirectional ion migration strategy to enhance hydrogels with different combinations of mineral cations (a) and anions (b). Data are presented as mean values ± SD (n = 3). c–f Damping performance of SM-PVA hydrogel fibers. Time-resolved impact force oscillation and photographs of freely falling objects buffered by cotton yarn (c, d) and the hydrogel fibers (e, f). In the hydrogel experimental group, a segment of SM-PVA was incorporated as a shock absorber in the middle of the cotton thread. g Identification of different ankle bending extents using the SM-PVA/CNTs–OH hydrogel sensor. h Cyclic stability of the SM-PVA/CNTs–OH hydrogel sensor under stretching during 4000 s. i Recycling process of the SM-PVA hydrogel. j Hydrogel recyclability and stress–strain recovery over second and third cycles.

Full size image

Building upon combined high strength and toughness, we demonstrated the potential applications of this method in engineering scenarios. We monitored the change in force oscillation caused by freely falling 500 g weights over time (Fig. 4c–f). By successfully utilizing fine SM-PVA fibers with a cross-section of 0.8 × 1.2 mm, the maximum impact was reduced from 57.88 to only 19.50 N (Fig. 4c, d). This led to efficient kinetic energy absorption while maintaining structural integrity and preventing the cotton fibers from breaking, whereas partial fiber fracture occurred in the cotton without the hydrogel (Supplementary Movies 3; 4 and Fig. 4d, f). During the first maximum stress period, the composite line with the SM-PVA hydrogels absorbed 1.76 kJ of energy within 78 ms. This demonstrates the excellent potential of this hydrogel as a shock absorber, safety component, and load-bearing structural material. Furthermore, we further demonstrated the potential of SM-PVA hydrogel in flexible sensing by compositing with hydroxyl-functionalized multi-walled carbon nanotubes (CNTs–OH) (Fig. 4g, h and Supplementary Fig. 28). The addition of CNT will weaken the mechanical robustness of the hydrogel to a certain extent. The SM-PVA/CNTs–OH sensor exhibited stable sensing performance under small strains and customizable motion detection capability. No obvious signal attenuation or baseline drift was observed during 4000 s of loading–unloading cycles, highlighting its potential for flexible electronic sensing applications (Fig. 4h). Additionally, the gel demonstrated excellent cyclic performance and recyclability, with no decline observed over three cycles, and the strength remained above 25 MPa (Fig. 4i, j).

Discussion

In summary, we report a general strategy for the simple construction of sandwich-type hierarchically structured tough hydrogels. The coordination ions are introduced into the gel precursor, and as the ions diffused and precipitated during the bidirectional ion migration process, the composite sandwich mineralization structure is easily formed. The structure of dense-porous-dense multiple layers with mineralized cluster center by ion regulation greatly improves the strength (33.51 MPa) and fracture energy (286.39 kJ m−2) of the hydrogels, and exhibits a similar performances in both the parallel and perpendicular directions in the plane. Our experimental findings provide insight into the mechanisms of deformation and energy dissipation in these gels. Moreover, the strategy of constructing a gel with a multilevel composite structure through ion regulation to produce enhanced gels is universal and adjustable and can be a reference for recyclable strong hydrogels.

Methods

Preparation of the SM-PVA hydrogels

First, 10 wt% PVA aqueous solutions were prepared by dissolving PVA and anhydrous CaCl2 (with mass percentages of 5%, 10%, 20%, and 30 wt% relative to that of PVA) in pure water (RO) with magnetic stirring and heating in a water bath at 90 °C. When the PVA concentration was increased to 15 wt%, the CaCl2 content was set to 0.25 wt% relative to that of PVA. Subsequently, 50 g of each PVA/CaCl2 solution was poured into a custom directional freezing mold that consists of a long steel plate at the bottom that contacts the cooling source and a solution-directional freezing chamber surrounded by the upper end of the steel plate, silicone strips, and a polytetrafluoroethylene (PTFE) plate. The directional temperature field was constructed through the steel plate to promote directional prefreezing of the PVA/CaCl2 solution. The exposed part of the lower steel plate of the mold was immersed in a −80 °C ethanol bath. Once the solution was fully frozen, it was removed and soaked in reinforcing solution containing Na3C6H5O7 (0–2 M) and Na2CO3 (0–2 M) for 3–24 h. This material was labeled SM-PVA. The hydrogel prepared via the same procedure but using nondirectional freezing was designated as SM-PVA ND.

To verify that a variety of different mineralizing anions and cations could be used, 10 wt% PVA solutions containing 0.09 mol kg−1 magnesium chloride, barium chloride, or strontium chloride (equivalent to 10 wt% CaCl2 relative to the mass of PVA) were prepared. Then, each solution was subjected to directional freezing in the mold at −80 °C. The mixture was then soaked for 24 h in induction solution containing 1.5 M Na3C6H5O7 and 0.5 M Na2CO3. These samples were labeled SM-PVA/MgCO3, SM-PVA/BaCO3 and SM-PVA/SrCO3. The hydrogel prepared via the same procedure, using calcium chloride as the cation source and an induction solution containing 1.5 M Na3C6H5O7 and 0.5 M Na2SO4, is designated as SM-PVA/CaSO4.

Preparation of other hydrogels

A 10 wt% PVA aqueous solution devoid of ions was prepared with magnetic stirring and heating in a water bath at 90 °C. The solution was subjected to nondirectional freezing in the mold at −80 °C, followed by natural melting at room temperature. This material was labeled FT-PVA ND. To prepare the FT-PVA D hydrogel, the freezing step in the FT-PVA ND fabrication process was replaced with directional freezing at –80 °C, followed by natural thawing at room temperature. When 10 wt% CaCl2 (relative to the mass of PVA) was added to the PVA solution prior to directional freezing, the resulting hydrogel was designated as FT-PVA/Ca2+ D. Further salting-out of FT-PVA/Ca2+ D was achieved by immersing the frozen sample in 1.5 mol L−1 sodium citrate for 24 h, yielding FS-PVA/Ca2+.

Separately, a 10 wt% PVA solution containing 10 wt% CaCl2 (relative to the mass of PVA) was cast into PTFE molds and treated with 0.5 M sodium carbonate for 24 h to form M-PVA. When the same solution was subjected to directional freezing prior to carbonate treatment, the resulting hydrogel was named FM-PVA. Immersion of the same solution in a mixed solution of 1.5 mol L−1 sodium citrate and 0.5 mol L−1 sodium carbonate for 24 h yielded SM-PVA NF.

For PVA solutions without added ions, directional freezing of a 10 wt% PVA solution at −80 °C followed by salting-out under the same conditions as SM-PVA gave FS-PVA or FS-PVA/SO42−, depending on the anion used.

Preparation of SM-PVA strain sensors and SM-PVA dampers

SM-PVA was cut into fibers with cross-sections of 0.8 × 1.2 mm as the buffering functional module. Both ends were connected to cotton threads via clamps, with the effective length of the SM-PVA fibers being 43 mm. The cotton threads at both ends were connected to a sensor and a 500 g weight; a complete cotton thread without SM-PVA served as the control, wherein the sensor and 500 g weight were directly connected.

To prepare the SM-PVA strain sensor, 2 wt% hydroxyl-functionalized multi-walled carbon nanotubes (MWCNTs–OH) were added to the PVA/CaCl2 solution, followed by the standard SM-PVA fabrication process to obtain SM-PVA/CNTs–OH hydrogels. The hydrogels were further fully swollen in deionized water to reduce their stiffness. The resulting hydrogels were cut into the required shapes for use as strain sensors. During testing, one end of the sensor was fixed while the other end was either loaded with a weight or attached to a specific area on a robotic device to evaluate its sensing capability. The resistance changes during deformation were recorded using a UT61E+ digital multimeter connected to a data logging software.

Mechanical tests

For tensile testing, the hydrogels were cut into dumbbell-shaped specimens with a gauge length of approximately 15 mm and a width of 5 mm. The thickness of each sample was measured using a digital caliper. All the mechanical tests were conducted using an Instron 68TM-10 universal testing machine. Unless otherwise stated, all tensile tests were performed at a loading rate of 60 mm min−1. The area under the stress‒displacement curve was integrated to determine the toughness of the hydrogel. Additionally, cyclic tensile testing was conducted with a gauge length of 10 mm, and a stress‒strain curve was obtained at a loading and unloading rate of 100 mm min−1. Cyclic tests to evaluate self-recovery involved stretching the hydrogel to a predefined deformation, unloading, and then conducting a second loading–unloading cycle after the prescribed interval.

For pure shear tests, the fracture behavior and tear resistance of the hydrogels were evaluated using an Instron 68TM-10 universal testing machine. A pair of rectangular hydrogels measuring 20 mm in width and 40 mm in height were prepared, and their thicknesses were measured with calipers. An 8 mm notch was made on the long edge of one of the samples, whereas the other sample was unmodified. An initial gripping distance of 10 mm was maintained for each sample. For the notched sample, a strain rate of 10% s−1 was applied until the critical strain (εc) corresponding to unstable crack propagation was reached at the maximum stress. The unnotched sample was then tested until the strain (ε) reached the critical strain (εc). The fracture energy was calculated by multiplying the area under the stress–strain curve of the unnotched sample by the initial gripping distance (H) as in ref. 6.

$$\varGamma=H{\int }_{0}^{{\varepsilon }_{{{\rm{c}}}}}\sigma {{\rm{d}}}\varepsilon$$
(1)

A single-notch approach was employed to evaluate the fatigue resistance of the hydrogels21,39,49. To prevent crack propagation induced by dehydration, all specimens were coated with silicone oil prior to testing. Cyclic tensile tests were conducted on both notched and unnotched samples of identical dimensions under the same experimental conditions. The strain energy density of the unnotched sample during the Nth loading cycle with a maximum stretch of λmax was calculated as:

$$W\left({\lambda }_{\max },\,N\right)={\int }_{1}^{{\lambda }_{\max }}\sigma {{\rm{d}}}\varepsilon$$
(2)

Notched specimens, with initial crack lengths (c0) less than 1/5 of the original gauge length, were subjected to approximately 1000 cycles to stabilize the crack tip prior to measurement. The subsequent crack growth per cycle (dc/dN) was monitored optically after N loading cycles under the maximum stretch λmax. The corresponding energy release rate G during the Nth cycle was determined by:

$$G\left({\lambda }_{\max },\,N\right)=2k\left({\lambda }_{\max }\right){{\cdot }}c\left(N\right){{\cdot }}W\left({\lambda }_{\max },\,N\right)$$
(3)

where k is a stretch-dependent geometric factor approximated by:

$$k=\frac{3}{\sqrt{{\lambda }_{\max }}}$$
(4)

By varying the applied λmax, the relationship between dc/dN and G was established. The fatigue threshold Γ0 was subsequently determined by extrapolating the dc/dN–G curve to its intersection with the G-axis.

Material characterizations

The morphology of the graded hydrogels was first examined using a field emission scanning electron microscope (SEM, Thermo Fisher Apreo 2C). The samples were rinsed with deionized water, freeze-dried, and cryofractured in liquid nitrogen to expose the internal cross-sections, which were then sputter-coated with gold for imaging. Elemental analysis of the mineralized domains was conducted via energy-dispersive spectroscopy (EDS, OXFORD ULTIM Max65). To further visualize the internal structure of the sandwich-like architecture, a 3D profile measuring system (Keyence VR-5200) was used to capture cross-sectional topography. Based on the clear optical contrast, the midpoint of the sharp transition zone is defined as the interfacial boundary. X-ray computed tomography scans were performed using a NanoVoxel 2000 system (Sanying Precision Instruments) at 100 kV and 400 μA with a resolution of 4 μm, 1440 projections, and an exposure time of 0.7 s. The source-to-detector and source-to-sample distances were 608.77 and 49.26 mm, respectively. Surface morphology was also characterized by atomic force microscopy in tapping mode. To assess molecular structure, Fourier-transform infrared spectroscopy (Thermo Fisher Nicolet iS10) was conducted on 1-mm-thick dried hydrogel films over the wavenumber range of 400–4000 cm−1. X-ray diffraction (Rigaku Ultima IV) was used to evaluate the relative crystallinity of the SM-PVA and FS-PVA hydrogels in the 2θ range of 5°–60°, scanned at 2° min−1 under 40 kV and 40 mA with a Cu-Kα radiation source. Small-angle and wide-angle X-ray scattering (SAXS/WAXS) tests were conducted on a NanoStar U SAXS/WAXS system (Bruker, Germany) with a Cu-Kα source (λ = 0.154 nm, 50 kV, 0.6 mA). SAXS measurements were performed at a sample-to-detector distance of 1047.5 mm (q = 0.007–0.23 Å−1), and WAXS at 60.5 mm (q = 0.21–2.45 Å−1), both with 300 s exposure. The calcium ion content was quantified using atomic absorption spectroscopy (AAS, Agilent 240FS) after complete acid digestion of the polymer matrix. The citrate ion content was determined by high-performance liquid chromatography (HPLC, Thermo Fisher UltiMate 3000) following ultrasonic-assisted extraction in deionized water.

Water content and crystallinity measurement

The water content of the HA-PVA hydrogels was determined by comparing their weights before and after freeze-drying. Excess surface water on the hydrogel was gently removed, and the sample was immediately frozen using liquid nitrogen, followed by freeze-drying. The initial weight before drying (mw) and the dry weight after freeze-drying (md) were measured using an analytical balance. The water content (fw) was calculated using the following equation:

$${f}_{{{\rm{w}}}}=\left({m}_{{{\rm{w}}}}-{m}_{{{\rm{d}}}}\right)/{m}_{{{\rm{w}}}} \, {{\rm{\cdot }}}100\%$$
(5)

The crystallinity of each sample was measured via DSC. A glutaraldehyde solution was prepared by mixing 5 ml of a 50% (v/v) glutaraldehyde solution, 500 μl of 37 wt% hydrochloric acid, and 50 ml of RO water to induce excessive chemical crosslinking, which fixes the amorphous PVA polymer chains and minimizes further crystallization during subsequent drying26. Dried hydrogel samples were obtained after freeze-drying. The samples were placed in standard aluminum pans and heated from 50 to 260 °C at a rate of 20 °C min−1 under a nitrogen atmosphere with a flow rate of 30 ml min−1. The heat flow curve shows a narrow peak in the range of approximately 200–250 °C, which corresponds to the melting of the crystalline domains. Integrating the endothermic peak area between 200 and 250 °C provides the melting enthalpy of the crystalline domains per unit mass of the dry sample (Hcrystalline). Therefore, the crystallinity (X) of the hydrogels is represented as:

$$X={H}_{{{\rm{crystalline}}}}/H$$
(6)

where H (138.6 J g−1) is the enthalpy of fusion of 100 wt% crystalline PVA measured at the equilibrium melting point.

MD simulations

The partial charges of the CO32−, C6H5O73− and PVA molecules were calculated using Gaussian 16 code, and the 6–311 g (d, p) basis functions were applied. The OPLSS-AA force field and MKTOP were used to parametrize all the atoms, such as the bond parameters, angle parameters and dihedral angles.

The coordination structures of the Ca2+ ions in the electrolyte were simulated by MD simulations. Five PVA molecules, 4 CaCl2 molecules, 220 Na3C6H5O7 molecules, 110 Na2CO3 molecules and 22322 H2O molecules were randomly inserted into a cube box with a side length of 10.0 nm.

The MD simulations were performed in the GROMACS 2021 software package. The steepest descent method was applied to minimize the initial energy for each system with a force tolerance of 1 kJ mol−1 nm−1 and a maximum step size of 0.002 ps before the MD calculations. In all three directions, periodic boundary conditions were imposed. The Leapfrog algorithm was used to integrate the Newtonian equation of motion. The MD simulations were processed in an NPT ensemble, and the simulation time was 20 ns. In the NPT simulations, the pressure was maintained at 1 bar by the Berendsen barostat in an isotropic manner to constrain the bond lengths of the hydrogen atoms. Particle mesh Ewald (PME) with fourth-order interpolation was used to evaluate the electrostatic interactions with a grid spacing of 1.0 Å, whereas a cutoff of 1.0 Å was employed to calculate the short-range van der Waals interactions.

Finite element simulation

Finite element simulations were conducted using the commercial software Abaqus. The model employed a linear elastic constitutive law based on Hooke’s law, assuming no plastic deformation. The elastic modulus E was calculated as:

$$E=\frac{F{L}_{0}}{A{{\boldsymbol{\nabla }}}{{\bf{L}}}}$$
(7)

where F is the applied force, L0 is the original length, A is the cross-sectional area, and ∇L is the elongation or compression length.

Poisson’s ratio ν is defined as the ratio of transverse strain to axial strain during uniaxial deformation:

$$v=\frac{{\varepsilon }_{{{\rm{l}}}}}{\varepsilon }$$
(8)

where εl and ε are the transverse and axial strains, respectively.

The porous material was modeled using the Yeoh hyperelastic model. This model is based on the strain energy density function W, which is expressed in a simplified form using the principal invariants of the deformation tensor. For isotropic and incompressible materials (constant volume), the strain energy density typically depends only on the first principal invariant I1:

$$W={\sum }_{i=1}^{{{\rm{N}}}}{{{\rm{C}}}}_{{{\rm{i}}}0}{\left({I}_{1}-3\right)}^{{{\rm{i}}}}$$
(9)

where

$${I}_{1}={\lambda }_{1}^{2}+{\lambda }_{2}^{2}+{\lambda }_{3}^{2}$$
(10)

Here, \({\lambda }_{{{\rm{i}}}}^{2}\) representing the principal stretches, and Ci0 are material constants obtained by fitting experimental data.

Symmetric boundary conditions were applied to the porous material, with the bottom surface fixed and a uniform tensile displacement applied at the top surface.