Introduction

Active matter is a fascinating realm of nonequilibrium systems, characterized by individual motile components that harness stored or environmental energy to generate non-conservative forces which drive the emergence of complex, coordinated motions across space and time1,2,3,4,5,6,7,8,9,10. Ubiquitous in active matter are traveling patterns and propagating waves, manifesting in diverse phenomena such as liquid-liquid phase separation11,12, metabolic synchronization waves in yeast13, and the intriguing dynamics of magnetic colloidal chiral fluids14. The recent discovery of autonomous waves in bacterial biofilms adds another layer to this complexity15,16. These biofilms exhibit not only oscillatory translations and rotations15, but also local fluctuations in cell density, culminating in synchronized spiral waves anchored by stationary cores16. Despite the unveiling of these captivating phenomena, our capacity to control the propagation of these active waves remains a formidable challenge17,18. This difficulty underscores the limitations in our understanding of how macroscopic properties in active matter systems arise from the intricate interplay of their constituent parts, despite extensive theoretical exploration1,19,20,21,22,23,24. Given the significance of mastering active traveling waves for the future control and engineering of active matter, there is a pressing need to develop delicate tools capable of manipulating these emergent waves17,18. Such advancements would not only enhance our control over these systems but also deepen our comprehension of the underlying principles governing their behavior.

Living liquid crystals (LLCs) represent a unique class of active matter, consisting of swimming bacteria embedded within passive lyotropic liquid crystals (LCs)25,26,27. These LCs are in the nematic phase, characterized by their alignment along a non-polar direction, represented by the director \(\hat{{{\bf{n}}}}\equiv -\hat{{{\bf{n}}}}\) 28,29. It has been shown that patterned LC directors, especially those with topological defects, can attract bacteria, leading to the formation of vortices around these defects30,31. Moreover, bacteria tend to concentrate and form polar jets within alternating bend and splay director fields32. When active LLC droplets are suspended in a passive thermotropic LC environment, their locomotion trajectories can be effectively controlled33. This controllability offers a promising platform for addressing the challenge of managing active traveling waves. In this work, we aim to leverage patterned LLCs to gain insights into the mechanisms behind the formation of traveling waves, and we will endeavor to achieve precise control and management of these dynamic waves.

We initially observed active traveling waves in patterned LLCs propagating in opposite directions, Fig. 1. It is shown that bacteria are condensed within the splay bands, forming undulations as their density surpasses a critical threshold. Subsequently, these undulated waves travel along the path defined by the pattern. The term “travel” here carries a dual significance: the bacteria propagate within the waves, following the prescribed direction, and the undulating waves themselves also migrate in the same direction. Furthermore, the passive background LCs are distorted to develop a phase lag to the bacterial wave, resulting in a passive traveling wave running after the bacterial wave. Thus, a traveling pattern of double traveling waves is formed. Both experiments and theoretical modeling are employed to comprehend the dynamics of these active-passive wave duets. Our analysis indicates that the breaking of parity and time-reversal (PT) symmetry within the traveling waves is actuated by the symmetry breaking of the interaction between the undulating waves and the director reorientation induced by these waves. We have also created multiple rings of traveling waves, both in the same and opposite chirality. Furthermore, programmable traveling waves can be manipulated in arbitrary letter shapes. Thus, these advancements pave the way for the design of intelligent living materials and micromachines, marking a significant step forward in active matter research.

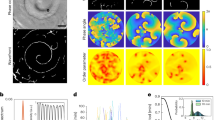
Fig. 1: Formation of double traveling waves.
figure 1

a Director field of the pattern with two splay distortions. b Micrograph of the pattern under polarizing optical microscope (POM). P polarizer, A analyzer. c Two straight bacterial streams (red and blue) at t = 0 s. White arrows indicate opposite stream directions. d Time sequence of two traveling bacterial waves 1 and 2. ① and ② mark two regions in waves 1 and 2. e Temporal evolution of θ along x direction. Source data are provided as a Source Data file. f Bacterial waves and LC waves at different moments. Red and blue lines represent bacterial waves and LC waves, respectively. Circled numbers with corresponding color mark wave crests and troughs in different waves. Black arrows represent the traveling direction. Active-passive waves travel in the same direction with a phase lag. The bottom red vertical arrow indicates the h in (j). g Trajectory of the tracked dead bacterium before the wave propagates. The black line represents the bacterial stream. White straight arrow indicates the traveling direction and curved arrow represents rotation direction. h Trajectory of the tracked dead bacterium at the traveling wave stage. Colored lines are trajectories of the tracker. i Temporal evolution of average speed of the traveling waves. Source data are provided as a Source Data file. j Space-time graph of the traveling wave. h(x, t) represents the height profile of the wave (y coordinate). The definition of h and the correspondence of the x-axis are indicated in (f). k Power spectrum of the bacterial wave by FFT. ω and k refer to normalized frequency and wavenumber, respectively. l Simulated flow field around the wave. Black arrows indicate flow field velocity. The green line and arrow indicate the bacterial wave and traveling direction, respectively. Color bar: normalized vorticity \(\Omega\). m Simulated active force indicated by black arrows. Scale bars: 100 μm.

Full size image

Results

Emergence of bacterial and LC traveling waves

The LLC25 is composed of an aqueous dispersion of bacteria bacillus subtilis in chromonic nematic disodium cromoglycate (DSCG), see Supplementary Fig. 1 and methods. The LLC is confined by two photopatterned plates with a gap of 10 μm30,34. If a pattern is designed as \(\hat{{{\bf{n}}}}=({n}_{x},{n}_{y},{n}_{z})=(|\cos \psi |,\sin \psi,0)\), where \(\psi=\frac{\pi y}{L}\) and \(L=100\,{{\rm{\mu }}}{{\rm{m}}}\), Fig. 1a, b and Supplementary Fig. 2, the swimming bacteria are condensed in the splay distortions forming two unipolar streams32.

At t = 0 s, swimming bacteria form two streams in opposite directions (Fig. 1c and Supplementary Movie 1). Two active traveling waves of bacteria in opposite directions are developed with time evolution, Fig. 1d, e and Supplementary Fig. 3. As the bacterial concentration crosses a critical threshold \({c}_{{{\rm{critical}}}}\approx 1.2\times {10}^{15}{{{\rm{m}}}}^{-3}\), Supplementary Fig. 3a, b, the bacterial streams experience a bending instability and develop transversal undulations, Supplementary Movie 1. The critical concentration can be calculated theoretically by the equation \(c=\frac{{Kh}}{\alpha l{U}_{0}{L}^{2}}\), where K is an average Frank elastic constant of the LC, h is the cell thickness, \(\alpha\) is a constant, l is the length of a bacterium, \({U}_{0}\) is the hydrodynamic force dipole of the strength and L is the bacterial coherence length (period of the bacteria waves in experiment)25. In our experiment, we take \(K=10-12{{\mathrm{pN}}},h=10\; {{\rm{\mu }}}{{\rm{m}}},\,\alpha \sim 1,l=5\; {{\rm{\mu }}} {{\rm{m}}},\,{U}_{0} \sim 1{{\mathrm{pN}}} \; {{\rm{\mu }}}{{\rm{m}}},L=100 \; {{\rm{\mu }}}{{\rm{m}}}\), and then we can get the critical concentration \(c \sim 2\times {10}^{15}{{\rm{m}}}^{-3}\), which is the same order as experimental results \({c}_{{{\rm{critical}}}}\approx 1.2\times {10}^{15}{{{\rm{m}}}}^{-3}\). Undulation happens as the bacterial activity is high enough, and the activity is affected by the bacterial concentration. The fluctuation of bacterial stream increases, which disrupts the balance between bacterial orientation and LC director and thus undulation forms. The amplitude of the undulating waves increases at the early stage and finally reaches a relatively steady value, while the wavelength remains constant, Supplementary Fig. 3c, d. The temporal evolution of the undulating wave is quantified by the alignment parameter \(q=\left\langle \cos (2\theta )\right\rangle\), Supplementary Fig. 3e, where θ represents the angle between the local bacterial stream and the x-axis. At t = 0 s, the bacterial stream is well aligned along the x-axis, producing \(q \sim 1\), Supplementary Fig. 3e. As the bending undulation evolves, the local bacterial orientations increasingly point along the y-axis, leading to a decreasing q, Supplementary Fig. 3e.

Remarkably, the undulating waves themselves migrate along the \(\pm\)x direction, respectively with the bacterial propagation. Figure 1d shows that regions ① and ② in two neighboring waves come across and then separate, indicating that the two waves are traveling. The distribution of θ along the x-axis with time evolution provides another evidence of traveling waves of bacterial streams, Fig. 1e. Meanwhile, the local LC director fields are perturbed to form a similar undulating wave by the bacterial stream, following the bacterial traveling waves, Fig. 1f and Supplementary Movie 2. Compared to the average speed of swimming bacteria \({v}_{b}\approx 12 \; {{\rm{\mu }}}{{\rm{m}}}/{{\rm{s}}}\), Fig. 1d, the speed of the active traveling waves is much slower with \({v}_{{wave}}\approx 0.9 \; {{\rm{\mu }}}{{\rm{m}}}/{{\rm{s}}}\), Fig. 1i. Although the LC waves propagate in the same direction of bacterial waves, there is a phase lag between the active and passive traveling waves. As shown in Fig. 1f, at t = 90 s, 120 s and 150 s, blue regions ① and ② (LC wave) always run after red regions ① and ② (bacterial wave). The interaction between the distorted director and undulating bacteria waves is the key to understand the mechanism behind the traveling waves of both bacteria and LCs.

The transition between polar jet and traveling wave of bacterial stream can be visualized by tracking a dead bacterium, Fig. 1g, h and Supplementary Movie 3. At the initial stage of the polar jet, the dead bacterium circulates locally without translation, Fig. 1g, which represents the flow field around the bacterial stream. As the bacterial wave starts to travel, the tracer bacterium keeps circulating around the moving peak of the traveling wave, Fig. 1h, indicating that the local flow field is traveling in the same direction as the bacterial stream. We plot the temporal evolution of the wave speed at two stages (Fig. 1i), clearly showing the transition from polar jet to traveling wave state. The spatiotemporal mapping of the active traveling waves along the +x-axis is shown in Fig. 1j. Color represents the height profile of the waves, and the maximum corresponds to the peak of the waves, Fig. 1j, indicating that the waves travel from -x to +x. By applying the fast Fourier transform (FFT) to the profile data of the traveling wave, we get the power spectrum of the wave (Fig. 1k), which reflects the dispersion relation of the wave. The non-zero dispersion in the second and fourth quadrants with odd parity demonstrates the unidirectional wave traveling along the +x-axis. Both Fig. 1j, k prove that waves are unidirectional.

To gain insight into the flow field and active force, continuum simulation is conducted, Fig. 1l–m. The numerical simulation shows that there is a forward flow field with the propagating wave, and the flow field matches the active force (Fig. 1l–m and Supplementary Movie 4). The distribution of the flow field is consistent with our experiment results shown in Fig. 1h. Based on this understanding, active waves that travel in the same direction can also be rectified by using the pattern designed as \(\hat{{{\bf{n}}}}=\left({n}_{x},{n}_{y},{n}_{z}\right)=(-\cos \psi,\sin \psi,0)\), \(\psi=\frac{\pi y}{L}\) and \(L=100\,{{\rm{\mu }}}{{\rm{m}}}\) (Supplementary Fig. 4 and Supplementary Movie 5). All active-passive traveling waves propagate in one direction.

Mechanism of active traveling waves

To unravel the physical underpinning of active traveling waves, we model the active units as a point particle with constant self-propelled velocity \({v}_{0}\) adhering to the Stokes drag law as a consequence of balanced hydrodynamic forces35. The self-propelled direction of the particle is defined as P, and the nematic directors are denoted as \(\hat{{{\bf{n}}}}=(\left|\cos \psi \right|,\sin \psi,0)\), where \(\psi=\frac{\pi y}{L}\) and \(L=100\,{{\rm{\mu }}}{{\rm{m}}}\), see Supplementary information. Figure 2a shows the traveling bacteria waves in two splay bands with opposite directions. Moving wave crests indicate the propagating waves (Fig. 2a and Supplementary Movie 6). The diagonal maximum bands distribution in the simulated space-time graph and quadrants distribution in the simulated power spectrum indicate the unidirectional waves, which are in agreement with experimental results in Figs. 1 and 2b, c.

Fig. 2: Simulation results and mechanism of active traveling wave.
figure 2

a Simulated time sequence of two traveling undulating bacterial streams. Black arrows indicate traveling directions. b Simulated space-time graph of active traveling wave along the +x-axis. c Corresponding simulated power spectrum of the traveling wave. ω and k refer to normalized frequency and wavenumber, respectively. d Mechanism of active traveling wave. The solid black line is the bacterial wave in the splay region. Red and blue dashed lines represent rough direction of director and bacteria, respectively. Curved arrows represent different torques at two regions ① and ②, which cause different viscosities and thus a rectified net driving force for the wave propagating. The dashed black line is the traveling bacterial wave at the next moment. e Mechanism of standing bacterial wave in uniform director field compared to that in (d). f Spatial distribution of the angle \(\beta\) (color bar) between bacteria and LC director in splay director field. The solid black line is the center line of the bacterial wave in the splay region. Brown arrows represent the orientation of bacteria with angle \(\theta\). Black short bars are the director field with angle \(\psi\). g Spatial distribution of the angle \(\beta\) (color bar) in a uniform director field. h Spatial distribution of the torque in the splay region. Brown and black arrows represent the bacteria's orientation and the force induced by the torque, respectively. i Spatial distribution of the torque and force in a uniform director field.

Full size image

The breaking of PT symmetry of the traveling waves is rooted in the broken symmetry of the interaction between the bacterial wave and the LC director, which is caused by the broken symmetry in the designed pattern, Fig. 2d. As shown in the first half period of Fig. 2d, the background director field is roughly represented by the red dash lines while the bacterial stream causes the reorientation of the local director field. Due to the constant bacterial stream, the director is persistently out of equilibrium due to the surface anchoring29,33,36. The core of this interaction is a torque that the bacterial stream exerts on the LC director. To quantify this, we introduce the angle \(\beta=\psi -\theta\), where θ represents the angle between the local bacterial stream and the x-axis, and \(\psi\) is the nematic angle anchored on the substrates, Fig. 2f, g. This aligning torque is mathematically captured in our agent-based model for bacteria (see Supplementary Text) by the reorientation dynamics: \({\partial }_{t}\theta={\gamma }_{B}\sin \left(2(\psi -\theta )\right)+{D}_{r}\xi ({{\rm{t}}})\). Here, the key term \({\gamma }_{B}\sin \left(2(\psi -\theta )\right)\) creates the torque that aligns the bacterium with the local nematic director (\(\psi\)) of the LC. This is the primary mechanism for the feedback from LC to bacteria. The bacterial flows trigger a polar viscous response in the LC. The bacterial stream imposes a counterclockwise (CCW) torque on the designed director at region ① and a clockwise (CW) torque on the director at region ②, Fig. 2d, f. The difference in designed directors between region ① and region ② produces different out-of-equilibrium director reorientation and thus different viscosities \({\eta }_{+}\ne {\eta }_{-}\). The difference \({\eta }_{+}\ne {\eta }_{-}\) produces a rectified net driving force that can be estimated as \({F}_{{{\rm{net}}}}\propto ({\eta }_{+}-{\eta }_{-}){v}_{b}\), where \({v}_{b}\) is the speed of bacteria. Such a symmetry breaking of the driving force can be visualized numerically by mapping the spatial distribution of force, \({{\bf{F}}}=\nabla \times \left(0,\,0,{T}_{Z}\right)\), where \({T}_{z}\propto \sin (2\beta )\) is the torque exerted from bacteria to LC, Fig. 2h, i. As indicated in Fig. 2f, h, the distribution of \(\beta\) and torque are not symmetric around the wave in the splay region and the induced force point rightwards, driving the wave to move rightwards. Thus, in the director field with broken symmetry, the active force caused by the swimming bacteria will push the flow field forward and thus the wave propagation.

As a comparison, the undulating waves of bacterial streams in a uniform director field are also demonstrated, in which the waves are not propagating, Supplementary Fig. 5 and Supplementary Movie 7. As shown in Fig. 2e, the bacterial stream imposes the same CCW and CW torques at regions ① and ②, which produces \({F}_{{{\rm{net}}}}=0\), indicating there is no symmetry broken in the interaction between the bacterial stream and LC directors. There is no force along the x-axis and thus no traveling wave, Fig. 2g, i.

Mechanism of double traveling waves

In order to gain insight into active-passive traveling waves, we use tensor Q to describe the orientation of LC and P to describe the orientation of bacteria, see Supplementary information. At the early stage after bacterial undulating wave forms, the orientation of LC is distorted by the movement of bacteria and the generated undulating instability is in the same phase of bacteria waves, Fig. 3a. Because of the symmetry breaking in the self-propelled polar movement of bacteria, there is a phase difference between the active bacteria wave and passive LC wave, where bacteria wave is ahead of LC wave, Fig. 3a. As a consequence of the phase difference, bacteria wave and LC wave interact with each other: bacteria rotate the LC molecule through the director-flow coupling by generating active flow, thus pushing the LC wave forward. Correspondingly, due to the anchoring of LC to bacteria, the LC wave can attract the bacterial wave and drag bacteria backward. The interaction between these two waves leads to a steady phase difference in a balanced state, thus stable double traveling waves. The effect of the bacteria on LC can be described by the equation

$$\left({\partial }_{t}+{{\bf{v}}}\cdot {{\boldsymbol{\nabla }}}\right){{\bf{Q}}}-{{\bf{S}}}-\Gamma {{\bf{H}}}{{\boldsymbol{+}}}{{{\boldsymbol{F}}}}_{{{\rm{anch}}}}=0,$$
(1)

where \({{\bf{v}}}\cdot {{\boldsymbol{\nabla }}}{{\bf{Q}}}\) describes advection (Adv) of the nematic field by the flow and here \({{\bf{v}}}\) is the fluid velocity. The tensor \({{\bf{S}}}=\left(\xi {{\bf{A}}}+{{{\mathbf{\Omega }}}}\right)\left({{\bf{Q}}}+\frac{{{\bf{I}}}}{{2}}\right)+\left({{\bf{Q}}}+\frac{{{\bf{I}}}}{{2}}\right)\left(\xi {{\bf{A}}}-{{{\mathbf{\Omega }}}}\right)-\xi \left({2}{{\bf{Q}}}+{{\bf{I}}}\right){{\rm{Tr}}}\left({{\bf{QW}}}\right)\) describes alignment with the fluid flow, including flow alignment (FL, \(\left(\xi {{\bf{A}}}+{{\mathbf{\Omega }}}\right)\left({{\bf{Q}}}+\frac{{{\bf{I}}}}{{2}}\right)+\left({{\bf{Q}}}+\frac{{{\bf{I}}}}{{2}}\right)\left(\xi {{\bf{A}}}-{{\mathbf{\Omega }}}\right)\)) and corotation with the local vorticity (CR, \(\xi \left({2}{{\bf{Q}}}+{{\bf{I}}}\right){{\rm{Tr}}}\left({{\bf{QW}}}\right)\)), (see Supplementary text and Supplementary Table 1). \(\Gamma {{\bf{H}}}\) and \({{{\boldsymbol{F}}}}_{{{\rm{anch}}}}\) contributions are from the free energy and external anchoring, respectively. To identify the key factor in the interaction, we analyze the contribution of different factors to the evolution of \({{\bf{Q}}}\) at the steadily traveling state, Fig. 3b. We find that elasticity and anchoring are in the same phase of \({{\bf{Q}}}\), so do not contribute to the phase change or translational motion of the director. The spatial profiles of FL, CR and Adv are ahead of \({{\bf{Q}}}\) (LC), thus continuously increasing the phase \({{\bf{Q}}}\), driving the director field to move forward. Since FL, CR and Adv all originate from the activity, and the phase of their total contribution is closer to that of P (bacteria), we can conclude that the LC wave is effectively attracted by the bacterial wave. In turn, the bacterial wave is attracted by the LC wave as well because of the anchoring of the LC on the bacteria. Thus, the interaction and phase difference cause the passive LC wave to travel and active-passive waves finally reach a stable traveling state. Note that the phase difference is affected by the bacteria's velocity and the anchoring strength of the LC on the bacteria. As shown in Fig. 3c, d, the simulation results of double traveling waves are in agreement with experimental results. Simulations show that active bacterial wave and passive LC wave are propagating in the same direction with a steady phase difference.

Fig. 3: Mechanism of double traveling waves.
figure 3

a Schematic of double traveling waves. At first, undulation in the bacterial stream causes wave deformation in LC. As the bacterial wave (green) travels forward, there is a phase lag between the LC wave (red) and the bacterial wave. These two waves attract each other and the LC wave travels as well. Finally, active-passive waves reach a stable traveling state with a steady phase difference. b Different effects exerted by bacteria on LC contributing to the traveling of LC wave. Along the x-axis, the acting effects show different phases of the LC wave. Green and orange solid lines represent bacteria (\({{{\rm{P}}}}_{{{\rm{xx}}}}\)) and LC (\({{{\rm{Q}}}}_{{{\rm{xx}}}}\)) waves, respectively. Dashed lines are contributing effects. FL means flow alignment. CR means corotation with the local vorticity. Adv represents advection. Total means the total effect. c Simulated double traveling waves between crossed polarizers. Red and blue lines represent bacterial waves and LC waves, respectively. Circled numbers with corresponding color mark wave crests and troughs in different waves. Black arrows indicate traveling directions. d Traveling bacterial wave and LC wave without polarizers. Red arrows indicate the bacterial wave and black bars are LC directors. The color bar means the order parameter of Q. The circled numbers and arrows show the traveling wave peaks.

Full size image

Control of traveling waves of different chirality

With the understanding of the mechanism, we can create swirling traveling waves with distinct chirality. For instance, a circular ring of splay band designed as \(\hat{{{\bf{n}}}}=\left({n}_{x},{n}_{y},{n}_{z}\right)=(\cos \psi,\sin \psi,0)\), where \(\psi=\arctan \frac{y}{x}+\frac{\pi \sqrt{{x}^{2}+{y}^{2}}}{L}\) and \(L=100\,{{\rm{\mu }}}{{\rm{m}}}\) is created by covering the center part during the photopatterning procedure, Supplementary Figs. 2 and 6. Double swirling traveling waves in counterclockwise (CCW) direction are formed with time evolution, Supplementary Fig. 6 and Supplementary Movie 8.

Furthermore, if a pattern with the director field is designed as \(\psi=\arctan \frac{y}{x}+{\left(-1\right)}^{[\frac{\sqrt{{x}^{2}+{y}^{2}}}{L}]}\times \frac{\pi \sqrt{{x}^{2}+{y}^{2}}}{L}\), where \(L=100\,{{\rm{\mu }}}{{\rm{m}}}\), Fig. 4a, b, two polar streams of opposite chirality are formed, Fig. 4c, d and Supplementary Movie 9. Since the bacteria mainly come from outside, undulations form in the outer circle first, and the bacterial stream in the inner circle undulates later. When both of the circulating streams begin to undulate, two active waves propagate in opposite directions (Fig. 4e, f). Simulation well captures the swirling traveling waves in opposite chirality, Fig. 4g and Supplementary Movie 9.

Fig. 4: Swirling traveling waves in multiple rings of designed chirality.
figure 4

a Director field of the pattern with circular splay regions in opposite chirality. b Micrograph of the pattern in (a) under POM. P polarizer, A analyzer. c Map of bacterial velocities by particle image velocimetry (PIV). d The number of petals (crests) changes with the diameter of streams. Error bars represent the standard deviation (SD) from five independent measurements. Source data are provided as a Source Data file. e Time sequences of undulating streams in (a). Colored lines represent different streams. Circled numbers in the waves indicate that the waves are traveling. White arrows indicate propagating directions. f Distribution of θ along polar angle \(\varphi\) at two moments in (e). Source data are provided as a Source Data file. g Simulation result of the swirling traveling waves in opposite chirality. h Director field of the pattern with circular splay regions in the same chirality. i Micrograph of the pattern in (h) under POM. j PIV mapping of bacterial velocities. k Time sequence of traveling waves in (h). l Simulation of the swirling traveling waves in the same chirality. Scale bars: 100 μm.

Full size image

Likewise, swirling traveling waves in the same chirality can also be realized by using the director field \(\psi=\arctan \frac{y}{x}+\frac{\pi \sqrt{{x}^{2}+{y}^{2}}}{L}\) with \(L=50\,{{\rm{\mu }}}{{\rm{m}}}\), Fig. 4h, i. Bacterial streams form unidirectional traveling waves in the same direction (Fig. 4j, k, Supplementary Fig. 7, and Supplementary Movie 10). The experimental results are consistent with the simulation (Fig. 4l). Note that in both traveling waves with the same and opposite chirality, there are more petals (crests) in the wave for the circle with a larger radius (Fig. 4d).

Programmable traveling waves

Through a programmable photopatterning system, patterns can be programmed to generate desired traveling waves in arbitrary shapes37. In our experiment, we use patterns with shapes like letters “U”, “S”, “T”, and “C” (Fig. 5a, b). Hence, bacterial stream can form traveling waves following the letter shapes (Fig. 5c, d and Supplementary Movie 11). Note that in letter “T”, two different propagating bacterial streams from opposite sides of the pattern can merge into a stronger undulating stream, which then travels in a single direction. Thus, programmable traveling waves are enabled by manipulating the designed patterns.

Fig. 5: Traveling waves in arbitrary letter shapes.
figure 5

a Director fields of “U”, “S”, “T”, and “C”. b Micrographs of the patterns under POM. P polarizer, A analyzer. c Colored trajectories in “U”, “S”, “T”, and “C”. d PIV mapping of bacterial velocities. Scale bars: 100 μm.

Full size image

Discussion

In active matter systems, when the activity level surpasses a critical threshold, it can induce bending instability within the long-range nematic order of active nematics38,39. This instability manifests as undulating waves, a phenomenon that is particularly fascinating due to its roots in the coupling between activity-driven flows and orientational order14,19,32,38,39,40,41,42,43,44,45,46. The interplay between these factors presents an intriguing area of study, as it underpins the emergence of complex dynamic behaviors in active fluids. In previous literatures, the active traveling waves in active fluids are usually induced at the boundaries or the liquid-liquid interface11,14,47.

In this work, the orientational order of LCs and the interactions between the active units—namely, the bacteria—and the out-of-equilibrium reorientation of LC molecules introduce new dynamic effects. The nonequilibrium interaction within the system is responsible for triggering active traveling waves within the bacterial streams in the background LCs. The active traveling waves can further actuate the LCs to travel, leading to the formation of a unique traveling pattern of active-passive traveling waves with a steady phase difference. The traveling waves observed in this work are fundamentally distinct from the phenomenon described in the Taylor swimming sheet model48. In the Taylor swimming sheet, a wave of deformation travels in one direction, while the sheet itself moves in the opposite direction. In contrast, the waves and the bacterial streams in our study move in the same direction, highlighting a unique characteristic of the active matter system under investigation.

In conclusion, our research has led to the discovery of double traveling waves within living liquid crystals (LLCs) that are patterned by predesigned splay bands. We observe the concentration of bacteria within the bands, which, upon reaching a critical density, form undulations. These undulations in both bacterial streams and LC fluid subsequently propagate along the predefined trajectories. Both experimental and theoretical approaches are employed to decipher the behavior of the double traveling waves. Our findings reveal that the breaking of PT symmetry in the traveling waves stems from the nonequilibrium interactions between the undulating waves and the LC directors, which in turn initiates wave propagation. Leveraging this insight, we successfully demonstrated the creation of multiple concentric rings of traveling waves, moving in both the same and opposite chirality. Furthermore, we achieve the formation of traveling waves in a programmable manner, showcasing the potential for precise control over this dynamic system. Overall, this work opens opportunities to create smart living materials and micromachines.

Methods

Bacteria dispersion preparation

The LLC solution is prepared by mixing 14 wt% disodium cromoglycate (DSCG, Fig. S1) and 86 wt% terrific broth (TB) as a nematic host. TB solution serves as a growing and motility medium for B. subtilis. The bacteria grow in a sealed tube with 10 ml of TB at 37 °C inside the shaking incubator at a speed of 150 rpm for 10–12 h. Then, 0.4 ml of the liquid medium with bacteria is centrifuged at 3074 × g for 2 min, and then the medium is extracted, upon which 0.1 ml of 14 wt% solution of DSCG in TB is added to the bacteria and carefully mixed with a mixer device. The dispersion of B. subtilis in DSCG is injected into the cell at 40 °C on the hot stage and sealed with epoxy glue. The sample is observed under a microscope (from Soptop).

Sample preparation

Glass substrates are washed in an ultrasonic bath with detergent for 10 min. Then they are rinsed with deionized (DI) water and isopropyl alcohol (IPA) and dried in the oven at 85 °C for 15 min. The glass is put in an ultraviolet (UV) ozone chamber for 10 min. An SD1 solution containing 0.2 wt% photosensitive material azo dye SD1 (Fig. S1) in N, N-dimethylformamide (DMF) solvent is spin-coated on the glass substrates at 3000 rpm for 30 s. Then the glass substrates are annealed at 90 °C for 45 min to evaporate the solvent. The glass substrates are illuminated by a maskless photopatterning setup to get the predesigned pattern with photosensitive azo dye oriented perpendicular to the linearly polarized light. To protect the azo dye layer from water and anchor the LC molecules, the substrates are spin-coated with an RM257 solution at 3000 rpm for 30 s. The RM257 solution is prepared by mixing 10 wt% RM257 (Fig. S1) and 0.1 wt% photoinitiator Irgacure 651 in toluene. A UV lamp with an intensity of 1.4 mW/cm2 and wavelength of 365 nm is used to polymerize the sample for 5 min (partially fabricated by direct projection UV photolithography by Tuotuo Technology TTT-07-UV Litho-BIO S). Two substrates with mirror-symmetric patterns are assembled together, gapped by 10-μm diameter glass spheres in glue.

The maskless photopatterning setup mentioned above is based on a projector display (Fig. S2). The optical elements used in this setup are purchased from JCOPTIX, China. The pattern in Fig. 1 with \(\hat{{{\bf{n}}}}=({n}_{x},{n}_{y},{n}_{z})=(|\cos \psi |,\sin \psi,0)\), where \(\psi=\frac{\pi y}{L}\) and \(L=100\,{{\rm{\mu }}}{{\rm{m}}}\), is generated by rectangular segments shown in Fig. S2c. The polarizer rotates at a speed of R1 = 18°/5 s in the clockwise sense. The segments are displayed on the y-axis at a speed of R2 = 10 μm/5 s. Hence, the pattern with a period of 100 μm is produced.

For a pattern designed as \(\hat{{{\bf{n}}}}=({n}_{x},{n}_{y},{n}_{z})=(\cos \psi,\sin \psi,0)\) with a covered center part, where \(\psi=\arctan \frac{y}{x}+\frac{\pi \sqrt{{x}^{2}+{y}^{2}}}{L}\) and \(L=100\,{{\rm{\mu }}}{{\rm{m}}}\) in Fig. S6, the segment in the designed shape starts at the position at t = 0 s and the rotary polarizer starts along the x-axis, Fig. S2b. The polarizer and segment rotate at the same speed of R1 = R2 = 10°/5 s in a clockwise direction. After 180 degrees of rotation, the designed pattern is created.

Data acquisition and analysis

We use an advanced upright polarized light microscope from Soptop with a 20× magnification objective. Optical microscopy images are captured by a 9 MP USB3.0 C-mount microscope camera from Soptop (resolution 4096 × 2160 pixels). The video sequences are recorded at 10 and 20 Hz rate. The sequences of images are analyzed by ImageJ2-Fiji. The velocity map is done by particle image velocimetry (PIV) MATLAB package. By enhancing the contrast of the image, we can get the number of bacteria by using analyzing particles in ImageJ-Fiji. We then divided the number of bacteria in a stripe by the stripe volume V = HWh to calculate the concentration, where H = 263.7 μm is the height of the stripe, W = 701.6 μm is the width of the image along the x-axis and h = 10 μm is the cell thickness. Polar angle φ and the angle θ between bacteria and flow direction are calculated by tracking the bacteria trajectories and recording the position data of bacteria at the given moment. With two neighboring positions \(\left({x}_{1},{y}_{1}\right)\) and \(\left({x}_{2},{y}_{2}\right)\), θ at the first position can be calculated by \(\theta={\tan }^{-1}\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}\). Then θ along the x-axis can be calculated. The velocity of the traveling wave is measured by tracking several peaks of the wave at different moments and calculating the average. To plot the space-time graph, we extract the x and y (height profile h) coordinates of the bacteria wave at different moments and plot the map using the software Tecplot360. We carry a fast Fourier transform (FFT) on the h(x, t) data and square the absolute value of this FFT to get a power spectrum in frequency ω, and wavenumber k.