A deep learning-based multiscale integration of spatial omics with tumor morphology

Abstract

Spatial Transcriptomics (spTx) offers unprecedented insights into the spatial arrangement of the tumor microenvironment, tumor initiation/progression and identification of new therapeutic target candidates. However, spTx remains unlikely to be routinely used in the near future. Hematoxylin and eosin (H&E) stained histological slides, on the other hand, are routinely generated for a large fraction of cancer patients. Here, we present a deep learning-based approach for multiscale integration of spTx with tumor morphology (MISO). We train MISO to predict spTx from H&E and validate it on a dataset of 72 10X Genomics Visium samples. We further validate our approach on 348 samples from five indications from the MOSAIC consortium and show that MISO significantly outperforms competing methods in extensive benchmarks. We demonstrate that MISO enables near single-cell-resolution, spatially-resolved gene expression prediction.

Introduction

Classical transcriptomics methods like microarray and bulk RNA sequencing have been crucial in cancer research¹, aiding in understanding tumorigenesis^2,3,4, tumor heterogeneity⁵, and developing treatments. However, these techniques merge information from diverse cell types and structures within a tissue sample, masking signals from rare cell populations and the spatial dynamics around tumors. The functionality of a cell type is influenced by signals from neighboring cells^6,7, highlighting the importance of spatial context in immune cell response and tumor microenvironment arrangement for understanding tumorigenesis⁸, progression⁹, and patient prognosis¹⁰.

Advanced technologies such as 10X Genomics Visium and 10X Xenium offer higher resolution spatial transcriptomics, but are costly and not widely used in clinical settings. In contrast, haematoxylin and eosin (H&E)-stained slides remain a diagnostic standard in cancer care. Recent advancements in Artificial Intelligence (AI) have shown that high-resolution H&E images can predict molecular features like mutations¹¹, molecular phenotypes^12,13, bulk transcriptomic expression¹⁴ and patient outcomes¹⁵.

The increased availability of spTx datasets has fueled the development of models that predict spatially resolved transcriptomic features directly from H&E slides. Current spTx technologies like Visium measure gene expression in “spots” (55 µm in diameter for Visium V2). On H&E whole-slide images (WSI), small patches called tiles (typically of size 112 µm x 112 µm) are generally used as inputs to models, and can easily be matched with spots. Methods predicting spatial gene expression from tiles hold the promise to generate rich virtual spatial gene expression directly from H&E slides at minimal additional cost. Prior methods have attempted to predict gene expression at the tile level, without encoding the local spatial arrangements between tiles^16,17. More recent methods attempt to capture the spatial organization of WSI by leveraging neighborhood information^18,19,20,21.

However, current approaches rely on either small or low-resolution datasets of spatial transcriptomics data^17,22,23,24 limiting their robustness on external validation cohorts. Jaume et al. recently introduced HEST-1k²⁵, a large dataset of 1229 samples, to address this limitation, but HEST-1k remains heterogeneous in terms of data acquisition technology, resolution, species (most samples coming from mice), and therapeutic domain.

Additionally, SpTx technologies like Visium do not reach spatial single-cell resolution, instead measuring gene expression in mini-bulk at the level of spots. Recently, several technologies of single-cell-level spatial transcriptomics have been developed, such as 10X Genomics Xenium²⁶ or NanoString’s CosMx²⁷, but they remain expensive, and restricted in the number of transcripts that can be measured simultaneously. Previous attempts have been made to bridge the gap between these two levels of resolution, such as BayeSpace²⁸, XFuse²⁹ or iStar³⁰. Yet, they still carry some limitations as they are trained on small datasets, and their evaluation relies on in-sample performance. For instance, iStar’s design requires Visium-level-resolution sequencing data matched to an H&E slide (or to a consecutive slice) to be able to infer a super-resolved gene expression, strongly limiting its applicability in real-world settings where only H&E images are available.

Here, we introduce MISO (Multiscale Integration of Spatial Omics), a unified deep learning framework to integrate spatial knowledge at multiple scales. MISO relies on a local self-attention mechanism to model the spatial organization of the tissue, allowing to infer close to single-cell resolution gene expression on datasets where only H&E slides are available (Fig. 1). We designed a loss function specifically to tackle the patient-to-patient variability that is common in spTx³¹. Relying on a robust statistical framework, we derived theoretical upper bounds to the performance of models predicting spatial gene expression, introducing a rigorous selection framework for the genes on which spTx prediction methods should be trained. We trained models not only to predict gene expression at the level of spots, but also to learn a finer-grained resolution of spatial omics data, effectively approaching the resolution of spatial single-cell sequencing. Once trained, MISO only requires H&E images to predict spTx on new samples (out-of-domain prediction), while most alternative super-resolution approaches also require Visium data to perform the same kind of inference (in-domain prediction). We trained and validated MISO on a dataset (PETACC8-Visium) of 72 Visium samples from 72 patients with colorectal cancer, to our knowledge the largest curated dataset in this disease. We extensively benchmarked MISO against competing methods across different organs and diseases in the HEST-1k dataset. Finally, we investigated how training the model on a larger pancancer dataset of 348 samples from the MOSAIC initiative improved the model’s performance and its ability to generalize.

Fig. 1: Overview of the pipeline.

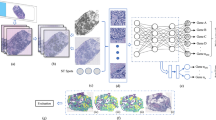
a Workflow of the study (1) Models with the local attention MIL architecture were trained to predict the spatial expression of genes in a cohort of 48 samples with 10X Visium sequencing. (2) Those models were used as “teachers” in a distillation setting: they were used to generate pseudo-labels in the same cohort, and a lighter architecture was trained to predict these pseudo-labels with weak supervision, allowing to generate predictions with a finer-grained resolution. These high resolution predictions were validated against cell type annotation and 10X Xenium sequencing. Scale bars: 2 mm. b Architecture of the model.

Results

MISO can robustly predict spatial gene expression from histology images

We propose MISO, a deep learning-based model to predict spTx from histology. MISO is a transformer that takes as input a whole H&E slide represented by a set of local tiles centered on the locations of Visium spots. For each slide, tile images centered on the location of Visium spots were selected. Tile features were extracted using H0-mini, a Vision Transformer model showing superior robustness in the latest benchmarks³². The set of tiles in the whole slide is then processed by a local attention multiple instance learning (LAMIL) architecture³³ to predict gene expression values at each Visium spot.

To evaluate the impact of the local attention mechanism, we implemented two alternative approaches. First, we considered a baseline MLP similar to HE2RNA¹⁴ and STNet¹⁶ that does not use any spatial context. Second, we trained a transformer-based approach that models spatial interactions through self-attention (see Methods). This approach does not discriminate between short and long-range interactions, and its quadratic complexity imposes a strong limit on the size of the transformer model that can be used.

The Local Attention Multiple Instance Learning (LAMIL) architecture overcomes these limitations by restricting the computation of cross-attention scores to neighboring tiles only. This significantly reduces the computational burden compared to generic transformers, while keeping relevant information, as we expect gene expression in one spot to be influenced by neighboring spots due to cell-cell interactions. A key hyperparameter of this method is the number k of neighbors used in the self-attention computation, higher values covering larger areas while increasing the computational cost. We set k = 36, which offered a tradeoff between GPU memory usage and performances (see Methods).

Importantly, there is no general consensus regarding the processing and modeling of spTx data. In previous works, pre-processing methods varied from simply using raw data to log-CPM normalization³⁴, SCTransform³⁵ or min-max scaling^36,37. However, those methods fail to address inter-patient variability, thus classical regression models trained with Mean Squared Error (MSE) may be confounded by this patient effect. Here, we propose a different approach by training our models with a loss based on cosine similarity to maximize, for each gene and each sample, the correlation between predictions and raw counts. This means that each sample from the training set had to be processed at once in the same batch. Early experiments performed with the baseline architecture (Supp. Fig. 1) showed that models trained with this loss function were indeed more accurate.

All spTx gene expression methods start by selecting which genes to train on. Some rely on selecting the N most variable genes^19,38, others focus on the most expressed ones^16,36,37. However, the lack of consensus on gene pre-selection impedes comparisons between methods. Here, we derived a theoretical upper bound on the performance that can be achieved by a model predicting spatial gene expression, that we denote ${R}_{max }$ (see the Methods section). ${R}_{max }$ is an estimate of the Pearson correlation that would be achieved by a perfect oracle having access to all deterministic variation factors when predicting spTx gene expression. We then selected lists of genes with the cleanest signal to train on by decreasing values of ${R}_{max }$. We validated our approach by showing that performances tend to decrease when including genes with smaller ${R}_{max }$ (Supp. Fig. 2 and Supp. Table 1), and that the best correlations achieved were linearly related to the value of ${R}_{max }$ (Supp. Fig. 3). Our enrichment analysis revealed that genes with the highest ${R}_{max }$ were significantly associated with known cancer-hallmark pathways such as resistance to apoptosis, epithelial–mesenchymal transition (EMT), MYC-driven proliferation, angiogenesis, immune evasion, and altered metabolism (Supp. Figs. 4 and 5). This suggests that MISO is likely to be effective at capturing genes involved in oncogenesis, because these genes tend to be more highly expressed and associated with more pronounced morphological changes. As a result, MISO may be especially valuable for identifying biologically and clinically relevant patterns directly from histopathology.

To evaluate and compare performances between methods, we computed the Pearson and Spearman correlation per gene and per slide, giving a total of N_samples x N_genes metrics. Unless specified otherwise, the reported values are the average correlations across genes and samples.

MISO outperforms competing methods in in-domain and out-of-domain settings

We benchmarked MISO and the two alternative approaches (MLP and transformer), based on H0-mini features, against HisToGene³⁸ and Hist2ST¹⁹, which do not rely on feature extraction with a pretrained encoder, as well as iStar, relying on HIPT features³⁹. For this task, we trained all methods on a dataset of 48 samples of colorectal cancer patients, sequenced with 10X Visium technology, from the PETACC8-Visium cohort (see Methods). All models were trained on 25 random train/test splits of the data, with 80% of the samples used to train the model and 20% to validate it. To evaluate performances, we computed average Spearman and Pearson correlation per gene/slide pair on the test set. HisToGene and Hist2ST, which do not rely on pretrained feature extraction, were significantly longer to train. In particular, on our data, both models could not be trained on a Tesla T4 GPU with 15 G of memory and had to be trained on CPU (10 min per epoch on 32 cores with 124 G of RAM, compared with 1 min for MISO on GPU) and performed worse than methods  exploiting precomputed features (Fig. 2a). MISO significantly outperformed other methods. Impressively, MISO’s performances were on par with our transformer-based approach that uses more spatial information (at the cost of higher computational cost) (p = 0.15, aggregated p-value over train/test splits, see Methods). Models were further evaluated on a held-out test set of 24 samples from the same cohort (Fig. 2b). MISO remained the best-performing approach, with average Pearson and Spearman of 0.447 and 0.457 respectively. The comparison with every other method was statistically significant (against the second best-performing method—the MLP baseline, p = 1.5 × 10^-17, one-tailed t-test). Recently, Wang et al.⁴⁰ realized a comprehensive benchmark of methods aiming to predict spatial gene expression from histology slides, using the HER2ST²³ dataset. This dataset consists of 36 samples from 8 patients with HER2-positive breast cancer, sequenced with microarray technology. The benchmark relied on the prediction of the expression of 785 genes. To further compare our approach to various competing methods, we trained MISO on the same task, with 4-fold cross-validation, using the same split as in Wang et al.’s benchmark. We report the average Pearson correlation per gene and slide. MISO outperformed all other methods (Fig. 2h), not only for the prediction of all 785 genes (R(MISO) = 0.223, std = 0.076, compared with the best competing method, R(EGNv2) = 0.168, std = 0.064, p = 7.7 × 10^-51, one-tailed t-test), but also specifically to predict the sets of 30 Highly Variable Genes (HVGs) (R(MISO) = 0.304, std = 0.104, R(EGNv2) = 0.236, std = 0.094, p = 0.0058, one-tailed t-test) and 40 Spatially Variable genes (SVGs) (R(MISO) = 0.370, std = 0.073, R(EGNv2) = 0.284, std = 0.072, p = 5.2 × 10^-6, one-tailed t-test).

Fig. 2: Gene expression prediction at spot level.

a Boxplot of the performances (Spearman correlation per split, averaged across genes and slides) obtained for the prediction of the 100 genes with highest ${R}_{max }$, in n = 25 random train/test splits of the 48 training samples (box: interquartile range (IQR); horizontal line: median; whiskers: 1.5 times IQR); p(MISO vs transformer) = 0.15, p(MISO vs MLP) = 0.008, p(MISO vs iStar) = 1.7 × 10^-45. b Spearman correlation per gene for the same 100 genes, averaged across slides in external validation on the 24 test samples of the PETACC8-Visium cohort; p(MISO vs transformer) = 2.9 × 10^-39, p(MISO vs MLP) = 1.5 × 10^-17, p(MISO vs iStar) = 8.6 × 10^-32. c Example slide from the test set, with Visium capture area outlined in red. Scale bar: 2 mm. d, e Raw counts of genes COL1A2 and KRT8 respectively, measured with Visium technology. f, g Predictions (rescaled between 0 and 1) of MISO for the expression of COL1A2 and KRT8 resp. h Violin plot of the cross-validation performance per gene (averaged across slides) of MISO and competing methods, as reported in Wang et al., for all genes (n = 785), highly variable genes (HVGs, n = 30) and spatially variable genes (SVGs, n = 40) (box: IQR, white dot: median, whiskers: 1.5 times IQR); p(MISO vs EGNv2, all genes) = 7.7 × 10^-51, p(MISO vs EGNv2, HVGs) = 0.006, p(MISO vs EGNv2, SVGs) = 5.2 × 10^-6. P-values were obtained from a one-sided t-test, as described in the method section. In a., further aggregation of p-values over repeated train/test splits was done by computing the median p-value and multiplying by 2 (n.s. non significant, *p-value < 0.05, **p-value < 0.01, ***p-value < 0.001, ****p-value < 0.0001). Source data are provided as a Source Data file.

Next, to evaluate the robustness of MISO to out-of-domain (OOD) transfer, we applied the model trained on PETACC8-Visium to a subset of the HEST-1k dataset²⁵. This dataset is rather heterogeneous in terms of biological conditions and data acquisition procedure. We selected samples from human subjects sequenced with Visium technology, with at least 37 spots remaining after quality check (see Methods). We further excluded samples for which less than half of the 100 genes were sequenced, leading to a total of 293 samples. MISO reached an average Pearson and Spearman of 0.240 and 0.250 respectively (Table 1). Unsurprisingly, it performed well in colorectal cancer samples (N = 19, Pearson = 0.373, Spearman = 0.411) but also in breast, lung and endometrial cancer, as well as in non-cancer skin and eye samples. When further restricting the dataset to samples acquired at a resolution of 0.5 MPP (N = 156) to match the training conditions, MISO reached higher performances (Pearson = 0.320 and Spearman = 0.337).

Table 1 Performances of MISO in external validation on Visium samples from human subjects in HEST-1k

Increasing training-set size and diversity improves generalization capabilities of MISO

To investigate the potential of larger cohorts with more diversity, we trained MISO on 348 samples from the MOSAIC initiative (Supp. Table 2, see Methods). This dataset contained samples from breast, ovarian and bladder cancer, NSCLC and mesothelioma. When applied to the 293 HEST-1k Visium samples from human subjects (Table 1), the MOSAIC-trained model (Pearson = 0.269, Spearman = 0.264) outperformed the one trained on PETACC8-Visium and the difference grew when selecting samples scanned at 0.5 MPP (Pearson = 0.359, Spearman = 0.374). As expected, performances were particularly improved in breast and lung cancer.

We further applied this model to the HER2ST dataset, used this time as an external validation (Supp. Fig. 6). The MOSAIC-trained MISO performed on par with EGNv2, and outperformed all other competing methods trained in cross-validation, with an average correlation of 0.171 on the set of 734 genes present in MOSAIC, 0.236 on the 26 Highly Variable Genes and 0.247 on the 36 Spatially Variable Genes. This is remarkable, as MISO was trained in an out-of-domain fashion while all other methods in the benchmark were trained on this specific dataset.

Local attention and model distillation enable highly efficient and accurate predictions at near single-cell resolution directly from H&E

We extended MISO to robustly infer super-resolved expression maps from histology slides alone, as opposed to methods requiring spTx data in inference. Following previous work^14,30, we leveraged weakly supervised learning to increase the spatial resolution of available sequencing, by further dividing tiles into 256 patches of size 7 μm x 7 μm (see Methods). MISO is able to perform this task from H&E alone, greatly increasing its applicability to real-world settings.

The resolution augmentation is computationally expensive, as a slide is represented by a tensor of size N_spots x 256 × 768, 256 being the number of patches per tile and 768 the number of features extracted by H0-mini. In particular, it becomes impractical to use the cosine similarity-based loss that requires to process each slide at once. To circumvent this, we employed a knowledge distillation approach⁴¹ (see Methods). Spot-level predictions of the previously trained supervised model (“teacher” model) were used as pseudo-labels to train a lighter architecture (“student” model).

To evaluate qualitatively this super-resolution approach and better understand how the model’s predictions are related with morphological information, we exploited an in-house dataset of tiles from TCGA-COAD samples for which nuclei were contoured and classified by pathologists (see Methods). We measured the association between these nuclei annotations and our higher-resolved expression maps. A patch was considered positive for a given nucleus type if it overlapped with its segmentation mask. Focusing on the most frequently annotated cell types, we investigated their association with the model’s predictions. As expected, EPCAM (Epithelial cell adhesion molecule) expression was highest in patches positive for tumor epithelial cells (p-value < 10^-10, one-tailed t-test). CD74 expression was slightly higher in lymphocytes than in other cell types (p-value < 10^-10, one-tailed t-test), consistently with its expected presence in B cells. COL1A1, marker of type I collagen, was more expressed in patches positive for fibroblasts (p-value < 10^-10, one-tailed t-test). Finally, the expression of IGKC (Immunoglobulin kappa constant) was significantly associated with the presence of plasma cells (p-value < 10^-10, one-tailed t-test) (Fig. 3). Additionally, potentially due to leakage, MISO predictions were also influenced by the surroundings of each cell: for instance, EPCAM predicted expression in non-epithelial cells was highly correlated with the density of healthy or cancer epithelial cells on the same tile (Spearman correlation = 0.57, p-value < 10^-10, one-tailed t-test), and similarly, the predicted expression of IGKC in any cell type was highly correlated with the local density of plasma cells (Spearman correlation = 0.70, p-value < 10^-10, one-tailed t-test). This highlights a potential limitation in the resolution that can be achieved, as the model captures signal not only from a given cell of interest, but also from its neighborhood.

Fig. 3: Relation between model’s predictions and cell types.

a Boxplot of the predicted expression of marker genes over patches positive for various cell types in TCGA-COAD annotated tiles (a patch was considered positive for a given nucleus type if it overlapped with its segmentation mask); the number of patches positive for each type is n(cancer cells) = 11,396, n(fibroblasts) = 3910, n(lymphocytes) = 2392, n(plasma cells) = 1283, n(neutrophils) = 1829, n(other) = 6849 (Cancer: cancer cell, Plasma: plasma cell, box: interquartile range (IQR); horizontal line: median; whiskers: 1.5 times IQR; circles: outliers) b. Example of a tile annotated with cancer epithelial cells, with the predicted expression of EPCAM, normalized between 0 and 1. c Example of a tile annotated with fibroblasts, with the predicted expression of COL1A1, normalized between 0 and 1. Source data are provided as a Source Data file. Scale bars: 100 μm.

We further evaluated our approach quantitatively on Xenium samples that provide a ground truth at single-cell resolution. We used two samples: one of colorectal cancer and one of breast cancer (Fig. 4). 480 genes were sequenced in each sample. We restricted this set to the genes among the 5000 with the highest ${R}_{max }$ in FFCD data, resulting in 175 genes for the colon sample and 117 for the breast sample. We then trained our models to predict the expression of these genes.

Fig. 4: Validation of the super-resolved expression maps.

a H&E sample of colorectal cancer. b. Ground truth expression of IGKC obtained with the 10X Xenium technology. For comparison with the model’s predictions, transcripts were summed on patches of size 7 µm x 7 µm. Brighter shades indicate higher expression c. Prediction of the expression of IGKC by the MISO super-resolution approach. d, e Same as b. and c., for the expression of EPCAM. f, g Ground truth and predicted expression of EPCAM, zoomed in in the area indicated by the blue squares in d. and e. h. H&E sample of breast carcinoma. i Ground truth expression of EPCAM obtained with the 10X Xenium technology. j Prediction of the expression of EPCAM by the MISO super-resolution approach. Scale bars in (a−g). 2 mm.

We benchmarked our method on this task against the iStar algorithm³⁰, that we retrained in the same configuration as MISO, on the same genes. One notable difference between the two approaches is the resolution level, as iStar operates with slightly larger patches of size 8μm x 8μm for a resolution of 0.5 micron per pixel (MPP). When comparing both approaches, we used interpolation to downsample MISO predictions to the same resolution. To validate the predictions generated by our models to the ground truth, we first aligned the Xenium sample to the associated H&E image. Then, we divided the WSI into small patches and summed the detected transcripts over each one.

On the colon adenocarcinoma sample, with 7 µm x 7 µm patches, the model achieved an average Spearman correlation of 0.211, and a Pearson correlation of 0.197 (Table 2). In particular, Spearman correlations above 0.50 were achieved for 9 genes (Table S3). When comparing against iStar, MISO performances were significantly superior (p = 4.3 × 10^-9, one-tailed t-test, Table 2).

Table 2 Performance of the super-resolution approaches based on MISO and iStar, on two public Xenium samples from colorectal cancer (CRC) and breast carcinoma

For the Breast Carcinoma sample, the highest resolution level of the associated H&E image was 0.36 MPP. We applied our models (trained at 0.5 MPP) at this resolution, meaning that the smallest patches we considered were of size 5 µm x 5 µm (5.8 µm x 5.8 µm for iStar). We measured an average Spearman and Pearson correlation of respectively 0.162 and 0.160 (Table 2). The expression of EPCAM and KRT8 were well predicted, with a Spearman correlation of 0.518 and 0.511 resp., and the model achieved Spearman correlations above 0.4 for five additional genes (Supp. Table 3). With 10 µm x 10 µm patches, average Spearman and Pearson correlation were respectively 0.246 and 0.247 (Table 2), and Spearman correlation above 0.5 was achieved for eleven genes (Supp. Table 3). MISO performances were on par with those obtained with iStar at the finest resolution level (p = 0.26, one-tailed t-test) and superior when downsampled by a factor 2 (p = 0.013, one-tailed t-test) (Table 2 and Supp. Fig. 7).

Training on larger cohorts from the same cancer type improves super-resolution

We retrained our models on MOSAIC data, that includes breast cancer samples. Performance on the breast cancer sample improved, although statistical significance was not reached (Table 2). Spearman correlations above 0.5 were in particular reached for EPCAM (0.562), SCD (0.531) and KRT8 (0.529) (Supp. Table 3). With 10 µm x 10 µm patches, average Spearman and Pearson correlation were respectively 0.262 and 0.261 (p = 0.23 for the comparison against the model trained on FFCD, one-tailed t-test) (Table 2 and Supp. Fig. 7), and Spearman correlation above 0.5 was achieved for fifteen genes (Supp. Table 3).

Overall, these results validate the relevance of our approach to extract high-resolution predictions in a fully out-of-domain setting, using only H&E-stained slides.

MISO identifies spatial prognostic patterns of gene expression

To explore MISO’s potential in identifying prognostic biomarkers, we investigated the relationship between predicted gene expression and histological patterns associated with clinical outcomes in breast cancer. We first developed a deep learning model to predict overall survival (OS) from histology slides, which allowed us to identify high-risk and low-risk regions within each tumor (see Methods, section Differential Rank analysis). We then used MISO to predict the expression of 117 spatially variable and biologically relevant genes in these same regions to determine which genes were spatially associated with prognosis.

We initially validated this approach on 15 breast cancer samples from the MOSAIC cohort, where we could compare MISO’s predictions to ground truth Visium spatial transcriptomics data. For each slide, we calculated a Differential Rank (DR)-score for every gene, which measures the difference in its expression between the 25 highest-risk and 25 lowest-risk tiles (see Methods, section Differential Rank analysis). A positive DR-score indicates higher expression in poor-prognosis regions, while a negative score indicates higher expression in good-prognosis regions. The DR-scores derived from MISO’s predictions showed strong agreement with those calculated from the Visium data (Spearman correlation = 0.62, p < 5.2 × 10^-13, two-tailed t-test), confirming MISO’s ability to identify prognostically relevant spatial expression patterns.

In this validation set, we found that genes associated with immunoglobulins (IGKC, IGLC1, IGHA1, IGHG1 and IGFBP7), along with several mesenchymal and collagen-related genes (MYL9, ACTA2, SPARC, COL1A1, COL1A2, COL3A2 and COL6A3), were consistently enriched in low-risk areas. The association of immunoglobulins with favorable prognosis in breast cancer is documented^42,43. The role of MYL9, ACTA2, SPARC and collagens, expressed primarily in mesenchymal cells, is not as clear but their expression in low-risk areas might be related to the fact that the survival model tends to focus on the tumor core to identify high-risk patterns and fibrotic tissue might appear in low-risk areas as a negative pattern. Conversely, genes linked to mitochondrial function (COX6A1), glycolysis (ENO1), cell cycle (MYBL2), and metabolism (NME2) were significantly associated with high-risk regions, consistent with established roles in breast cancer progression^44,45,46,47.

Next, we applied this method to the entire TCGA-BRCA cohort to leverage a larger dataset (Fig. 5). The analysis revealed similar patterns: immunoglobulin-related genes (IGKC, IGHA1) and mesenchymal markers (ACTA2, MYL9) were enriched in low-risk areas. In high-risk regions, we identified genes involved in cell cycle (CCNB1, MKI67, MYBL2), mitochondrial function (COX7C, BIRC5), and metabolism (NME2).

Fig. 5: Spatial biomarkers.

a Example slide from a TCGA patient with basal breast cancer and poor predicted prognosis. Scale bar: 2 mm. b Local survival scores output by the model trained to predict overall survival. Shades of blue indicate areas associated with a lower risk by the model, while red indicates areas associated with a high risk. c Predicted expression of IGKC, MKI67 and SCUBE2 on the same slide, normalized between 0 and 1. d Bar plot showing the DR scores of 8 example genes in good prognosis patients with different molecular subtypes from TCGA-BRCA; n(luminal A) = 143, n(luminal B) = 60, n(HER2) = 20, n(basal) = 46. Boxes represent the average value over slides, while error bars indicate the 95% confidence interval obtained by bootstrapping 10,000 times over samples. e Same as d, with intermediate prognosis patients; n(luminal A) = 284, n(luminal B) = 120, n(HER2) = 40, n(basal) = 92. f Same as d. and e., with poor prognosis patients; n(luminal A) = 143, n(luminal B) = 61, n(HER2) = 20, n(basal) = 47. Source data are provided as a Source Data file.

Delving deeper, we stratified patients by molecular subtype (Luminal A, Luminal B, HER2-enriched, and Basal-like) and prognostic risk group (Supp. Fig. 8). Proliferation markers like MKI67, MYBL2, and CCNB1 were consistently overexpressed in high-risk tiles across all subtypes, with the strongest association observed in Basal-like and HER2-enriched patients predicted to have poor outcomes. For instance, MKI67 had an average DR score of 0.39 [0.28; 0.49], in Basal-like patients with poor predicted outcomes, and 0.38 [0.20; 0.56] in HER2-enriched patients with poor predicted outcomes. Interestingly, the prognostic significance of immune-related gene IGKC expression varied by subtype and prognosis. In Luminal A and B patients, high IGKC expression was consistently found in low-risk areas, irrespective of the prognosis (Supp. Fig. 10). However, in Basal-like patients with a good prognosis, IGKC expression (average DR score = 0.10 [-0.05; 0.24]) was often co-located with the proliferation marker MKI67 within high-risk tumor regions, suggesting an active anti-tumor immune response. In contrast, for Basal-like patients with a poor prognosis, IGKC expression was concentrated outside the tumor (average DR score = -0.13 [-0.25; -0.04]), indicating a pattern of immune exclusion that is consistent with worse clinical outcomes (Fig. 5c, Supp. Fig. 9-10).

Together, these findings demonstrate that MISO can serve as a powerful tool to uncover spatial gene expression patterns with significant prognostic value, even in large cohorts where only H&E-stained slides are available.

Discussion

We introduced MISO, a multiscale deep learning approach to explore relations between tissue morphology and local changes in gene expression. The development of our model leveraged a new dataset of 48 training samples and 24 test samples in colorectal cancer and 348 samples from the MOSAIC initiative, all coming from distinct patients.

We proposed a statistical framework to model the noise in spTx data, and show that one of the main limiting factors for the performance of predictive models was the quality of the labels obtained from Visium, as it is prone to shot noise due to the finite sequencing depth.

Under those constraints, MISO was able to predict the spatial expression of a large set of genes. Remarkably, even when it was evaluated out-of-domain, MISO significantly outperformed competing methods applied in-domain.

Through distillation technique, MISO was able to further refine the spatial resolution of the sequencing, effectively approaching the scale of spatial single-cell RNAseq, as validated qualitatively and quantitatively against 10X Xenium sequencing data. Compared to previous works that investigated super-resolution of spatial transcriptomic, our approach benefitted from a rich training dataset, allowing for its direct application on new cohorts where only H&E-stained histology slides are available. We emphasize the importance of this point, as many of the super-resolution approaches developed in the past rely on training the method de novo on a sample for which Visium sequencing is available.

Finally, we used MISO to investigate spatial gene expression patterns that can be linked with patient outcomes in different molecular subtypes of breast cancer, highlighting the presence of immunoglobulin-related transcripts in low‑risk regions and proliferation biomarkers in high‑risk regions.

The promising performance of our approach should encourage future works to explore the potential of spatially-resolved omics data on large datasets. By leveraging the highly-resolved data on already existing large H&E datasets (e.g. TCGA), one could explore scientific avenues unlocked by the availability of spatial transcriptomics. Such examples could include finding context-specific drug-target matches, identifying small and localized immune niches⁴⁸, or investigating cell-cell communication⁴⁹ or cellular organization impact on clinicopathological and molecular features as recently demonstrated by Su et al. in colorectal cancer patients⁵⁰.

Methods

The research reported here complies with all relevant ethical regulations.

PETACC8-Visium is part of a cohort collected for a clinical trial registered under NCT00265811. The study details are available at https://clinicaltrials.gov/study/NCT00265811. The use of this data was approved by the Comité de Protection des Personnes (CPP) Ile-de-France IV. All participants included in the current study provided written informed consent for participation in the clinical trial, as well as a biological consent specifically authorizing the use of their samples for translational research purposes.

MOSAIC is a non-interventional clinical trial registered under NCT06625203. Study details are available at https://clinicaltrials.gov/study/NCT06625203. Patient consent was obtained in compliance with local regulations: written consents were obtained for patients from GR, Charité, Erlangen, CHUV and Pittsburg where required based on ethical committees requirements. For some patients, Owkin obtained a waiver of consent. The study protocol was approved by the Institutional Ethics Committee of each contributing institution: Ethikkommission der Charité – Universitätsmedizin Berlin; Commission cantonale d'éthique de la recherche sur l'être humain CER-VD; Ethikkommission der Medizinischen Fakultät der Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU); Comité de Protection des Personnes (CPP) Sud-Est I; Institutional Review Board of the University of Pittsburgh.

Data

PETACC8-Visium

The cohort used to train the model contained 48 slides of distinct Colon Adenocarcinoma patients with 10X Genomics Visium V1 spatial transcriptomics from a subset of the PETACC-8 cohort⁵¹. Spatial transcriptomics was obtained from Formalin-Fixed Paraffin-Embedded (FFPE) samples and the captured area covered 6.5 mm × 6.5 mm. Both Haematoxylin, Eosin & Saffron (HES)-stained slides’ images and Visium capture area images were available. On average, samples contained around 4000 spots, and the expressions of up to 15,000 genes were measured in each spot. HES slides were scanned at a resolution of 0.5 micron per pixel. Among those 48 patients, 23 were males and 25 were females (administrative gender). Age ranged from 26 to 74, with a median of 60 years old. 11 patients were MMR deficient and 37 were MMR proficient. All patients were stage III according to the American Joint Commission on Cancer (AJCC) staging system. 24 new samples were made available after model development and were used as an external validation cohort.

HER2ST

This dataset consists of 36 samples from 8 patients with HER2-positive breast cancer, sequenced with microarray technology.

HEST-1k

This dataset comprises 1229 paired spatial transcriptomics and Haematoxylin & Eosin (H&E)-stained slides’ images retrieved from 153 publicly available cohorts and covering 26 different organs and 2 species (Homo Sapiens and Mus Musculus). 367 samples out of the 1229 are cancer samples from 25 different subtypes. H&E slides were scanned at various magnifications including 10x (1.15 to 0.8 MPP), 20x (0.8 to 0.4 MPP) and 40x (0.4 to 0.1 MPP). Spatial transcriptomic data were acquired according to different transcriptomic technologies (ST, Visium, Visium HD and Xenium). In this work, we used a subset of HEST-1k with 338 human samples acquired with Visium technology. Further quality checks reduced it to 293 samples (all resolutions) including 156 samples scanned at a resolution allowing to readily extract images at a resolution 0.5 micron per pixel, with a tolerance of up to 20% (meaning 0.4 to 0.6 MPP).

On average, Visium samples contained around 1700 spots, and the expressions of up to 29,000 genes were measured in each spot.

MOSAIC

MOSAIC, a non-interventional clinical trial, is an ongoing initiative led by Owkin and 5 hospitals aiming to generate the world’s largest spatial atlas in cancer. It collects and generates six data modalities (extensive clinical data, H&E slides, 10X Visium spatial transcriptomics, single-nuclei transcriptomics and bulk RNAseq, and whole-exome sequencing). The technology used is Visium V2 Cytassist, applied to FFPE samples, and the captured area covers 6.5 mm × 6.5 mm. Here, we leveraged 348 samples (328 patients) from the breast cancer (n = 15 samples), bladder cancer (n = 120), ovarian cancer (n = 104), NSCLC (n = 62) and mesothelioma (n = 47) cohorts. 164 patients were female and 162 were male patients (administrative gender—information missing for two patients). Age at diagnosis ranged from 22 to 87, with a median of 66 years old. The samples are originating from the 5 founding hospitals in the MOSAIC consortium: Lausanne University Hospital—CHUV (117 samples), Charité—Universitätsmedizin Berlin (94 samples), Universitätsklinikum Erlangen (74 samples), University of Pittsburgh (24 samples) and Institut Gustave Roussy (39 samples) (detailed breakdown in Supp.Table 2). The detailed methods associated with the MOSAIC data were introduced in recent work⁵². The exploratory analyses conducted here are part of the objectives specified in the study protocol.

TCGA

This study exploits publicly available data from the TCGA colon adenocarcinoma (TCGA-COAD) and breast cancer (TCGA-BRCA) cohorts. We selected samples from primary tumors only, for which a paraffin-embedded (FFPE) histology slide was available. In TCGA-COAD, 38 slides were annotated (see Annotation of nuclei). In TCGA-BRCA, we retained 1076 slides from patients for which clinical data were available and contained information on overall survival and the molecular subtype.

Administrative gender, assigned based on legal documents, was collected in PETACC8-Visium and MOSAIC. Both cohorts had a balanced gender distribution. Sex and gender were not further considered in the present work as the balanced distribution ensures that the models trained on this data were not biased towards the learning of gender-specific patterns.

Modeling noise in spatial transcriptomic data

Spatial transcriptomic data is in general sparse and noisy. Hence, most previous works select genes based on their expression level (highly expressed genes) or on their spatial variation (highly variable genes).

Here, to model intrinsic performance-limiting factors, we derived an estimate of the Pearson correlation that would be achieved by a perfect oracle having access to all deterministic variation factors. As outlined in previous work⁵³, counts in spatial transcriptomic data should follow a Poisson law

$${X}_{{ig}} \sim {Poisson}\left({\,\lambda }_{{ig}}\right),$$

(1)

$$P\left({X}_{{ig}}=k\right)=\frac{{{\,\lambda }_{{ig}}}^{k}}{k!}{e}^{-{\,\lambda }_{{ig}}}$$

(2)

where ${X}_{{ig}}$ is the measured count for gene $g$ in spot $i$, while ${\,\lambda }_{{ig}}$ is an unobserved latent variable that can depend both on underlying biology (for instance, the cell composition in a spot) and on technical effects such as inter-spot contamination⁵⁴. Since all spots are different, the distribution of counts for a given gene on a slide should behave as a mixture-of-Poisson. This is often modeled as a negative binomial distribution^55,56,57, which is a special case of mixture-of-Poisson.

Since measured gene expression is not the biological ground truth, but rather a random variable with statistical fluctuations, we want to evaluate how much signal is contained in the data. A way to measure this is to compute the Pearson correlation between the unobserved latent variable ${\,\lambda }_{{ig}}$ that contains the real signal, and the measured counts ${X}_{{ig}}$.

We denote this value by ${R}_{max }$, as it is the correlation that would be reached by a perfect oracle having access to ${\lambda }_{.g}$. By definition,

$${R}_{max }=\frac{E\left[\left({\lambda }_{.g}-\,E\left[{\lambda }_{.g}\right]\right)\left({X}_{.g}-E\left[{X}_{.g}\right]\right)\right]}{{\sigma }_{\lambda g}{\sigma }_{{Xg}}},$$

(3)

where ${\sigma }_{\lambda g}$ and ${\sigma }_{{Xg}}$ denote the standard deviation of ${\,\lambda }_{.g}$ and ${{X}}_{.g}$ respectively. The expectancy of ${\lambda }_{.g}$ can simply be estimated through

$$E\left[{\lambda }_{.g}\right]={\mu }_{g}={\sum }_{i}\frac{{\lambda }_{{ig}}}{N}$$

(4)

and its variance through

$${\sigma }_{\lambda g}^{2}=E\left[{\left({\lambda }_{.g}\,-\,E\left[{\lambda }_{.g}\right]\right)}^{2}\right]={\sum }_{i}\frac{{\left({\lambda }_{{ig}}-{\mu }_{g}\right)}^{2}}{N}={\sum }_{i}\frac{{\lambda }_{{ig}}^{2}-{\mu }_{g}^{2}}{N}$$

(5)

The expected value of ${X}_{.g}$ is simply the average over values ${\lambda }_{{ig}}$ of the expected values of $N$ Poisson variables, i.e.

$$E\left[{X}_{.g}\right]={\sum }_{i}\frac{E\left[{X}_{{ig}}\right]}{N}={\sum }_{i}\frac{{\lambda }_{{ig}}}{N}={\mu }_{g}$$

(6)

while its variance can be expressed as

$${\sigma }_{{Xg}}^{2}=E\left[{\left({X}_{.g}-E\left[{X}_{.g}\right]\right)}^{2}\right]$$

(7)

$$=E\left[{X}_{.g}^{2}\right]-{E\left[{X}_{.g}\right]}^{2}$$

(8)

$$={\sum }_{i}\frac{{\lambda }_{{ig}}\left({\lambda }_{{ig}}\,+\,1\right)}{N}-{\mu }_{g}^{2}$$

(9)

$$={\sigma }_{\lambda g}^{2}+{\mu }_{g},$$

(10)

where we made use of the fact that

$$E\left[{X}_{.g}^{2}\right]={\sum }_{i}\frac{E\left[{X}_{{ig}}^{2}\right]}{N}={\sum }_{i}\frac{{\lambda }_{{ig}}\left({\lambda }_{{ig}}\,+\,1\right)}{N}$$

(11)

Finally, we can estimate the correlation between ${\lambda }_{.g}$ and ${X}_{.g}$,

$${R}_{max }=\frac{1}{N}{\sum }_{i}\frac{{\left({\lambda }_{{ig}}-{\mu }_{g}\right)}^{2}}{{\sigma }_{\lambda g}{\sigma }_{{Xg}}}$$

(12)

$$=\frac{1}{N}{\sum }_{i}\frac{{\lambda }_{{ig}}^{2}-{\mu }_{g}^{2}}{{\sigma }_{\lambda g}{\sigma }_{{Xg}}}$$

(13)

$$=\frac{{\sigma }_{\lambda g}}{{\sigma }_{{Xg}}}$$

(14)

We do not have directly access to ${\sigma }_{\lambda g}$ but, following Eq. (5), we can substitute it with $\sqrt{{\sigma }_{{Xg}}^{2}-{\mu }_{g}}$, giving the final formula

$${R}_{max }=\sqrt{1-\frac{{\mu }_{g}}{{\sigma }_{{Xg}}^{2}}.}$$

(15)

Interestingly, for a pure Poisson distribution (i.e. ${\lambda }_{{ig}}$ is constant over the spots), the mean $\mu$ and variance ${\sigma }^{2}$ are equal, hence the formula is exactly zero. In this case, there is no spatial variation of gene expression to assess: the only variations observed are due to statistical noise. Formula (8) is a way to measure how much the distribution of counts over the slide deviates from a pure Poisson distribution.

${R}_{max }$ is in fact highly correlated with the average expression and spatial variability, measured by Moran’s index. For instance, in the PETACC-8-Visium training cohort (Supp. Fig. 11 and 12), the three lists of 100 genes with respectively highest average expression, highest average Moran’s index and highest average ${R}_{max }$ share no less than 86 common genes. The fraction of shared genes increases with the size of the gene lists and reaches for instance 90% with 1000 genes (900 common genes) and 95% with 5000 genes (4733 common genes).

Preprocessing of spatial transcriptomic data

The pre-processing of the spatial-transcriptome profiles were done using 10X Genomics Space Ranger software. Raw sequenced reads were aligned on a probe reference. Then we use our in-house matter detector to remove spots for which the histology image displayed a lack of matter.

For counts normalization, Bhuva et al.⁵⁸ showed that library size is associated with tissue structure and that usual corrections like CPM or SCTransform could result in loss of information. As such we chose to use raw counts and employ a cosine loss function to correct for sample variations.

Preprocessing of histology slides

Histology slides are high dimensionality data, with up to 100 000 × 100 000 pixels for a single whole-slide image. For deep learning applications, it has thus become standard to divide the whole-slide image into hundreds to thousands of subparts referred to as tiles. In our work, we applied the same approach by extracting square images of size 224 × 224 pixels (~112 × 112 μm) centered on each of the ~5000 spots. Given that, in the 10x Genomics Visium technology, each spot measures 55 μm and that two spots are 100 μm apart, this enables a dense covering of the slide while capturing the image information associated with each sequenced spot. In addition to the Space Ranger matter detection, we also used an in-house deep learning matter detection model, trained internally on a dataset of manually annotated whole-slide images. This enabled a finer selection of tiles that contain matter and removed artifacts (such as blurry areas or bubbles).

For each tile, a 768-dimension feature descriptive vector is extracted using H0-mini, a pre-trained vision transformer model of 86 million parameters obtained through the self-supervised distillation of H-Optimus-0 foundation model^32,59 on a total of 43 million histology tiles from TCGA. By design, a vision transformer separates an input image into several patches, here 256 patches of 14 × 14 pixels each, that are encoded through patch-level representations (or tokens). In addition, a class token is also trained to capture the global semantics of the input image. Through two distinct objectives, the distillation process aims at aligning output class and patch tokens of a student model (H0-mini) with those of a teacher model kept frozen (H-Optimus-0). Due to the inherent contrastive nature of the distillation and the diversity of histology tiles derived from TCGA, H0-mini shows superior robustness to variations in staining conditions and scanner devices compared to state-of-the-art foundation models. In practice, H0-mini output class tokens are used for the tile-level prediction task, while patch tokens are used for the weakly supervised approach as they provide a more fine-grained representation of the input slides. Since the slides from the validation cohort were scanned at a lower resolution, tile images of size 112 × 112 pixels were resized to 224 × 224 before feature extraction.

Models for spatial transcriptomic prediction

The baseline architecture consists essentially of an MLP, that processes in parallel every spot, to predict gene expression. We considered a baseline with 2 layers and respectively 2048 and 1024 hidden units per layer.

Self-attention in transformer networks is defined by a scaled dot-product attention. In our case, the feature vector representing a tile ${x}_{i}$ is passed through three linear layers to generate three vectors named key (${K}_{i}$), query (${Q}_{i}$) and value (${V}_{i}$). The self-attention weight between two tiles $i$ and $j$ is defined as

$${w}_{{ij}}={Softmax}\left(\frac{{Q}_{i}{{K}_{j}}^{T}}{\sqrt{d}}\right),$$

(16)

where $d$ is the dimension of the key and query vectors. The output representation of the self-attention module is defined as

$${h}_{i}={W}^{T}\left({\sum }_{j}{w}_{{ij}}{V}_{j}\right),$$

(17)

where $W$ is a projection matrix. The full transformer block is defined by

$${{x}_{i}}^{(1)}={LN}\left({x}_{i}\right),$$

(18)

$${{x}_{i}}^{(2)}={{x}_{i}}^{(1)}+{SelfAttention}\left({x}^{(1)}\right),$$

(19)

$${{x}_{i}}^{(3)}={LN}\left({{x}_{i}}^{(2)}\right),$$

(20)

$${z}_{i}={FF}\left({{x}_{i}}^{(3)}\right),$$

(21)

where ${LN}$ denotes a Layer Norm operator⁶⁰ and ${FF}$ a feedforward neural network (a single linear layer in our case).

Self-attention computation is computationally heavy when performed for all pairs of tiles, as in the standard transformer architecture. As a consequence, on the task considered here, the size of the transformer that could be trained was limited to a first feature embedding layer with 512 hidden units, followed by one transformer block with internal dimension 256.

Local Attention Multiple Instance Learning was introduced in previous work by Reisenbüchler et al.³³. It consists of a transformer-like architecture, in which self-attention is not computed for every pair of instances, but only for neighboring instances. This means that, in the previous equations, ${w}_{{ij}}$ is zero except if tile $j$ is one of the k nearest neighbors of tile $i$, based on euclidean distance in the space of tile coordinates.

Here, we considered an architecture with a first feature embedding layer with 2048 hidden units, followed by one transformer block with internal dimension 1024 and 64 attention heads. Another densely connected layer was used to map the output of the transformer block to 2048, and a last linear layer with dimension equal to the number of genes was applied for gene expression prediction. The number of neighbors used in attention computation was optimized by cross-validation.

We varied the number k of neighbors (Supp. Fig. 13) used in self-attention computation from the list (0, 6, 18, 36, 60, 90 and 126), corresponding to a growing hexagon around the spot. With k = 0, MISO (average Spearman correlation = 0.347, std = 0.048, average Pearson correlation = 0.330, std = 0.043) and the baseline architecture (average Spearman = 0.346, st = 0.045, average Pearson = 0.329, std = 0.042) obtained consistent performances. The performance of MISO increased first quickly with the number of neighbors, up to a plateau between k = 18 (average Spearman = 0.365, std = 0.052, average Pearson = 0.348, std = 0.046) and k = 91 (average Spearman = 0.368, std = 0.045, average Pearson = 0.349, std = 0.048), demonstrating the relevance of neighborhood interaction for the determination of local gene expression (comparison between the best architecture and the baseline: p = 0.016). For further experiments, we used 36 neighbors that offered a compromise between performance (average Spearman = 0.369, std = 0.052, average Pearson = 0.349, std = 0.048) and GPU memory usage (6767MiB, against 10,693MiB with k = 61 and 14,867MiB with k = 91).

The super-resolution approach follows the idea of a two-step prediction. For each pair of sequenced spot and tile image, we divided the 224 × 224 pixel image into 256 adjacent patches, of size 14 × 14 pixels (~7 × 7 μm). We then modified the baseline architecture by making the MLP prediction at the patch level and added an aggregation mechanism (average pooling) during training. Then, the loss function was calculated on those aggregated predictions.

Loss function

Raw spatial transcriptomic data present strong inter-sample variations, as the sequencing depth for a given gene may vary a lot across slides. Contrary to bulk and single-cell transcriptomic, so far, no consensus method has emerged yet to normalize this kind of data. As a consequence, training a model to reproduce raw counts by minimizing Mean Squared Error (MSE) might not be optimal, as the scale will be different from one sample to another. To overcome this issue while making minimal assumptions about the data, we chose instead to train the model directly to predict the relative expression of a given gene across spots from the same sample. We defined a loss function based on cosine similarity, that is invariant under any rescaling of the labels and predictions. During training, all spots from a given slide were processed in the same batch, the cosine similarity between predictions and labels was computed separately for each slide of the batch, and averaged over slide. To maximize cosine similarity by gradient descent, the loss function was defined as

$$L=1-{cosine}({labels},{preds})$$

(22)

Experiments with the baseline architecture (MLP) demonstrated superior performance of our cosine similarity-based loss compared to MSE (Average Spearman correlation of 0.346 and 0.293 respectively, p-value < 10^-4, Fig. S1).

Distillation and super-resolution

When performing weakly supervised learning for super-resolution, the number of instances in a given slide was multiplied by 256 (the number of patches in a tile image), making it computationally challenging to go through the same training procedure. We overcame this by using a distillation technique. For a given list of genes, the LAMIL architecture (the teacher model) was first trained with cosine similarity-based loss, then the predictions of this architecture were used as labels for training the weakly supervised model (the student model) with MSE. The intuition was that the predictions of a model trained with cosine similarity-based loss would be rid of technical variation across samples. The metrics of the weakly supervised model were still computed against the raw Visium counts. The comparison of spot-level performances showed the superiority of this approach against a naïve one in which raw counts were directly predicted by the weakly supervised model using MSE.

We found that knowledge transfer significantly improved the performance of our weakly supervised model with respect to de novo training, from a spearman correlation of 0.369 to 0.427 in external validation to predict the expression of the 100 genes with highest R_max (Table 3).

Table 3 Spot-level performances of the weakly supervised models trained with or without knowledge distillation, on the PETACC8-Visium test set of 24 samples

To compare iStar and MISO at a super-resolved level, MISO predictions were downsampled with linear interpolation to match the resolution of iStar.

HisToGene

HisToGene is a transformer-based context-aware method enabling the prediction of a spot’s transcriptomics profile from its corresponding histological tile. The context-window used by the method encompasses the entire histological slide, and uses as an input both the tile and the position of the spot in the slide. In addition to enabling spot-level predictions, HisToGene also allows for super-resolved predictions by sampling overlapping tiles (the predicted transcript for a sub-tile is then the average of the transcript of all the tiles overlapping this sub-tile). The super-resolution factor is dependent on the overlap factor, enabling a high increase in resolution at the cost of a quadratically growing computational cost. We were able to use HisToGene as a spot-level method with our datasets, but not as a super-resolution method due to this important computational cost. Indeed, the method was benchmarked on the HER2 + ²³ and the CSCC²⁴ dataset, in which slides only have ~300 spots, compared to the ~5000 spots in our Visium10x data.

Hist2ST

Hist2ST is similar to HisToGene, with the main difference being the way the spatial context is taken into account to make spot-level predictions. HisToGene relies on a single transformer while Hist2ST uses a convmixer⁶¹, a transformer and a graph neural network, enabling a better modelisation of the spatial context of a spot. This resulted in increased performances for Hist2ST compared to HisToGene. In the original implementations, both methods focus on top variable genes, with the counts being log-scaled normalized. We slightly modified them to predict raw counts instead to ensure fair comparison with MISO. Likewise, we adapted some of the hyper-parameters to account for the larger amount of training data (number of epochs, most notably). While Hist2ST does not offer super-resolution capabilities, we found it to suffer nonetheless from the same computational drawback as HisToGene: as the context-window is the whole slide, it does not scale easily to ~5000 spots data (requiring over 100 Go of RAM and therefore making it costly to train on GPUs).

iStar

As the iStar method was designed to make predictions on either the training slide or a consecutive one only, a small adaptation of the method was needed to evaluate it in the same setting as MISO. The iStar model is trained to predict rescaled count values (using min-max scaling on a per-gene basis, computed over the training sample). During inference, the predicted counts are rescaled back to their correct original range. In our external inference scenario, we perform the min-max scaling using all the samples from the training set and use these min-max values to scale back the predictions at inference, without guarantees that this range is correct due to the significant inter-patient variability. This strategy prevents us from leaking inference-time information into the validation. All the other parameters (for data preprocessing and training) are the same as in the original implementation. Furthermore, the performances reported are averages from models trained on the same 25 random train/test splits of the data used for MISO.

Annotation of nuclei

11,640 cells, across 126 tiles from 38 slides of the TCGA-COAD cohort were internally annotated. This annotation process was done by 7 pathologists hired for the task with several redundancies to maximize agreements between experts. Each tile has a size of 448 × 448 pixels and was annotated at the highest resolution level available (0.25 µm per pixel). The annotated tiles were selected in order to maximize distinct cell type populations, as well as the presence of low-abundance populations such as eosinophils and neutrophils. The annotation process was the following: pathologists point the approximate center of each cell and register their identified cell type. Afterwards, the interactive nuclei segmentation framework NuClick⁶² is used to infer segmentation around each individual point. Cell types annotated were: Apoptotic Body (n = 1119), Cancer Cell (n = 4592), Cell with unknown type (n = 449), Endothelial Cell (n = 116), Eosinophil (n = 341), Epithelial Cell (non-cancerous) (n = 73), Fibroblast (n = 1328), Lymphocyte (n = 949), Macrophage (n = 257), Mitotic Figures (n = 80), Neutrophil (n = 809), Red Blood Cell (n = 1008), Plasma cells (n = 497) and Smooth Muscle Cell (n = 22).

Differential rank analysis

The survival model trained to predict OS on the TCGA-BRCA was based on the Chowder architecture^15,63. We used the 25 tiles with highest score and the 25 tiles with lowest score for the final prediction. The model was trained in 5-fold cross-validation, with 10 epochs per run, and reached an average cross-validated concordance index of 0.67. Once the model was trained, it was used to compute tile-level risk scores on 15 breast cancer slides from the MOSAIC cohort and on the TCGA-BRCA cohort.

To explore the potential of MISO to identify prognostic biomarkers, we used the model previously trained to predict the list of the 100 genes with the highest ${R}_{max }$ in the PETACC8-Visium cohort, and enriched it with a model trained to predict the expression of 17 additional genes known to be prognostic in breast cancer⁶⁴: AURKA, BAG1, BCL2, BIRC5, CCNB1, CD68, CTSV, ERBB2, ESR1, GRB7, GSTM1, MKI67, MMP11, MYBL2, PGR, SCUBE2 and TFRC.

First, we applied both the survival model and MISO to the 15 breast cancer samples from MOSAIC, where MISO predictions could be compared to ground truth values obtained from Visium sequencing. To build patient-level scores indicating the association between the expression of a given gene and patient prognosis, we first transformed gene expressions – both Visium ground truths and MISO predictions – into their ranks across spots, to take into account the fact that genes have varying baseline expression levels, with values ranging from 0 to the number of spots. These values were rescaled between 0 and 1 by dividing them by the number of spots for each slide. Then, we computed the average rank-transformed expression in the 25 tiles with highest risk score and in the 25 tiles with lowest risk score. Finally, for each gene and each slide, we computed the difference between the two values, denoted as Differential Rank (DR)-score, ranging from -1 to 1. Negative values indicate genes more highly expressed in areas associated with a good prognosis, and positive values those more highly expressed in areas predictive of poor outcomes.

To investigate genes consistently enriched in areas associated with a high or low risk by the survival model, we considered the 20 genes with highest or lowest DR-score, using either the Visium sequencing or the predictions from MISO and retained genes identified by both methods. The 13 common low-risk genes were genes related IGKC, IGLC1, IGHA1, IGHG1, IGFBP7, MYL9, ACTA2, GSTM1, SPARC, COL1A1, COL1A2, COL3A2 and COL6A3, while the 7 common high-risk genes were COX6A1, ENO1, KRT8, MYBL2, S100A1, S100A14, and NME2.

Training and evaluation of the models

In PETACC8-Visium, models were trained with 25 repeated random splits of the training set of 48 samples, where 80% of the data was used for training and 20% for testing. In MOSAIC, models were trained with a single five-fold cross-validation. For each test fold, the metrics we report are the Pearson and Spearman correlations for each gene/slide pair, averaged over genes and over samples within the test set.

When running inference on external data (the 24-sample test set of PETACC8-Visium, HEST-1k and HER2ST), all models trained in cross-validation were applied to the test cohort, and their predictions were averaged.

For the training on HER2ST, in order to perform a fair comparison with the benchmark realized by Wang et al.⁴⁰, models were trained with four-fold cross-validation, using the exact same train, validation and test folds. Since our pipeline does not make use of an internal validation set for early stopping, the validation samples were discarded. For each gene, we computed the Pearson correlation per gene and per slide, averaged over all patients and folds.

Statistics and p-values

To compare the correlations achieved by two models on the same gene and sample, we used a one-tailed t-test on Fisher z-transformed correlation coefficients⁶⁵ (Hinkel et al., 1988). Aggregation of p-values over repeated train/test splits was done by computing the median p-value and multiplying by 2.

Similarly, to compare the average (over samples) correlations achieved by two models on the same gene in HER2ST, as well as the correlations per gene on each Xenium sample, we used a one-tailed t-test on Fisher z-transformed correlation coefficients.

When reported, 95% confidence intervals were obtained by bootstrapping samples 10,000 times with replacement.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.