Introduction

Quantum network and quantum repeater are among the most promising ways to extend the size of a quantum system, which can enable important applications such as distributed quantum computing1,2,3,4, long distance quantum communication5,6,7,8,9 and network-enhanced quantum metrology10,11,12. In a quantum network or quantum repeater protocol, one of the core tasks is distributing heralded quantum entanglement between distant nodes. So far, heralded entanglement between two quantum network nodes has been demonstrated experimentally over either short (lab size) or long (metropolitan size) distances4,13,14,15,16,17,18,19,20,21,22. Currently quantum network has been realized with various physical systems. Among all these physical platforms, trapped atomic ion is a promising candidate. High local gate fidelity (better than 99.9%23,24, critical to entanglement swapping and entanglement distillation), long coherence time ( ~1 h25), and record-high rate ( ~200 Hz13) and fidelity ( ~96%4) between two network nodes have been demonstrated separately in this system.

Despite all these advances achieved so far, currently it is still very difficult to demonstrate a quantum repeater with three nodes or a quantum network which can utilize more than one pair of remote entanglement, when the separation between different nodes reaches metropolitan scale ( ~10 km). A requisite for this outstanding goal is the rate of remote entanglement generation between different nodes should be higher than the memory decoherence rate of each network node, as the remote entangling operation is in a probabilistic way5,6. This stringent requirement can also be interpreted as the ‘link efficiency’ ηlink should be larger than unity3,26. Currently, ηlink >1 can only be achieved in a lab-scale quantum network26,27. For all the heralded entanglement between two nodes over a metropolitan-scale fiber ( >10 km), the link efficiency is still less than 0.01.

One of the most important obstacles that limits the efficiency for a metropolitan-scale quantum network lies in the round-trip heralding time in each remote entangling attempt. For a 10 km fiber, the time cost for each entangling attempt is at least 2L/c = 100 μs (L is the fiber length and c is the light speed), which is two orders of magnitude higher than the value in a lab-scale case4,27. To resolve this issue, multimode quantum repeater7,28 has been proposed, which is able to accelerate the remote entangling operation via a multiplexing scheme. Currently, multiplexed quantum network node has been demonstrated in several different physical systems for quantum memories15,20,29,30,31,32,33,34,35,36,37,38,39. Multiplexing-enhanced heralded atom-photon entanglement over a metropolitan-scale fiber has been demonstrated on neutral atomic ensemble system recently, and a spin-photon entanglement efficiency (ratio of remote spin-photon entangling rate to memory decoherence rate) as high as 0.46 has been achieved35.

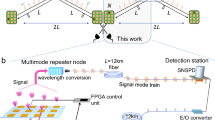
In this work, we experimentally realize a highly multiplexed trapped-ion quantum network node which can distribute heralded ion-photon entanglement with a high rate and protect the quantum information stored locally. We demonstrate different multiplexing schemes for three different fiber lengths at 3 m (lab size), 1 km (campus size), and 12 km (metropolitan size). The heralded ion-photon entanglement distribution rate is improved by 3-fold, 5-fold, and 16-fold over the single-mode case, respectively. For the 12 km case, a hybrid scheme combining both the multiple excitation and ion shuttling is employed to boost the remote ion-photon entangling rate to 4.28 s−1, which is already higher than the rate of memory decoherence 3.69 s−1 and yields a record-high ratio of remote ion-photon entangling rate to memory decoherence rate of 1.16 over a metropolitan-scale fiber. Besides, with the dual-type encoding40,41,42,43, the local quantum information stored in the memory qubit is not influenced by the noisy operations (such as cooling, pumping, and photon excitation) during the ion-photon entangling attempts, which is also a requisite for building a multi-node ( > 2) quantum network and quantum repeater. In addition, the spontaneous emission error in the memory qubit can be detected by a mid-circuit measurement, demonstrating another important capability regarding the purification and error correction needed in a future large-scale quantum network3. With all these achievements, this functional and highly-multiplexed trapped-ion quantum network node will contribute to the realization of a multi-node metropolitan-scale quantum network (Fig. 1a) in the future.

Fig. 1: A multiplexed quantum network.
figure 1

a The schematic of a multiplexed trapped-ion quantum network. There are two kinds of qubits in each network node. The communication qubits (green, red, blue, orange) are used for distributing heralded entanglement between different nodes, and the memory qubits (grey) are responsible for storing local quantum information or carrying out local computing tasks. Entanglement between distant nodes is heralded via interfering the photons on a beamsplitter in the middle point of the two nodes. The entanglement distribution task can be accelerated via different multiplexing schemes. In this work, multiplexing-enhanced ion-photon entanglement is realized as highlighted in the dashed box (other parts are not realized). b The protocol of a time-bin multiplexing scheme. Totally N temporal modes are excited in one run of entangling attempts, and the corresponding heralding signal returns to the node after a round-trip travel time of \(\frac{2L}{c}\) following the excitation. c Enhancement factor in time-bin multiplexing. The enhancement factor M starts saturating when the duty cycle of the entangling attempts reaches 50%. Here \({N}_{0}=(\frac{2L}{c}+{T}_{{{{\rm{ovh}}}}})/\Delta t\) is the characteristic number when the duty cycle reaches 50% (Tovh is the averaged time overhead in each round which mainly include the initialization and cooling period in the experiment).

Full size image

Results

Enhancement factor of time-bin multiplexing

There are already several different multiplexing schemes demonstrated so far, which exploit the time-bin, frequency, orbital angular momentum (OAM), or other dimensions of a flying qubit. A multiplexing scheme effectively reduces the averaged time cost of each entangling attempt, thus accelerates the entanglement distribution process. For a time-bin multiplexing scheme shown in Fig. 1b, the averaged time cost for each entangling attempt can be expressed as:

$${T}_{{{{\rm{eff}}}}}=\left(\frac{2L}{c}+{T}_{{{{\rm{ovh}}}}}+N\Delta t\right)/N=\frac{\frac{2L}{c}+{T}_{{{{\rm{ovh}}}}}}{N}+\Delta t$$
(1)

where \(\frac{2L}{c}\) is the round-trip travel time in the long fiber (L is the fiber length and c is the light speed in fiber), Tovh is the averaged time overhead in each round of N entangling attempts (including communication time in control system, initial cooling before each entangling round starts, sympathetic cooling in the entangling process, and all other overhead in the sequence), N is the number of modes used in each round of entangling attempts, and Δt is the time interval between two successive modes. Usually, we have \(\frac{2L}{c}+{T}_{{{{\rm{ovh}}}}}\gg \Delta t\). In the limit of a large N, the effective time cost for an entangling attempt Teff will be dominated by Δt, as shown in Eq. (1). To achieve a high effective attempting rate 1/Teff in the process of remote entangling, we need to improve the number of time-bin modes (N) and select an appropriate time interval between them (Δt). It is also noteworthy that the frequency or OAM multiplexing can be considered as a special case with Δt = 0 in this model.

Based on Eq. (1), we can derive the enhancement factor of multiplexing as:

$$M={T}_{\!\!{{{\rm{0}}}}}/{T}_{\!\!{{{\rm{eff}}}}}$$
(2)

where \({T}_{0}=\frac{2L}{c}+{T}_{{{{\rm{ovh}}}}}+\Delta t\) is the averaged time cost of each entangling attempt with a single-mode quantum memory. Note that here we assume the success probabilities in all the modes are the same. We illustrate the multiplexing enhancement versus mode number in Fig. 1c. One can see that given a fixed time interval Δt, the multiplexing enhancement M increases with N and saturates around \({N}_{0}=\frac{\frac{2L}{c}+{T}_{{{{\rm{ovh}}}}}}{\Delta t}\), where the duty-cycle of entangling attempts reaches 50% (duration for entangling attempts NΔt is equal to all the waiting time \(\frac{2L}{c}+{T}_{{{{\rm{ovh}}}}}\)). In this case a multiplexing enhancement of \(M=\frac{{N}_{0}+1}{2}\approx \frac{{N}_{0}}{2}\) can be achieved. This 50% duty cycle can be regarded as an indication that ‘sufficient’ multiplexing has been employed, as further increase of N can only improve the multiplexing enhancement by a factor of less than twice.

In the realistic case, the success probabilities for different modes are usually not the same due to the inevitable inhomogeneity in the system. Therefore, the effective multiplexing enhancement of a multi-mode quantum network over a single-mode case needs a more complicated evaluation. However, the simplified model in Eq. (1) still reveals the essentials and is able to provide a quick estimation of the effectiveness of multiplexing. More detailed calculation of multiplexing enhancement with mode inhomogeneity considered is described in the Supplementary Information.

Two different multiplexing methods

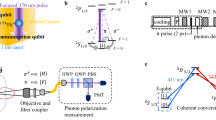
We use the dual-type scheme to build our trapped-ion quantum network node40,41,42,43. Following the scheme demonstrated in ref. 41 and Fig. 2, we can implement the cooling, pumping, state detection, and ion-photon entanglement excitation with 397 nm and 866 nm lasers in a closed three-level communication qubit subspace consisting of \(\vert {S}_{1/2}\rangle\), \(\vert {D}_{3/2}\rangle\), and \(\vert {P}_{1/2}\rangle\) levels of 40Ca+. During the dissipative operations such as cooling, pumping, detection, and ion-photon entangling, the local quantum information can be faithfully stored in the memory qubit subspace (\(\vert {D}_{5/2}\rangle\) level), without being influenced due to large spectral separation over THz. The coherent conversion between these two subspaces can be implemented by a 729 nm quadruple transition or an 850 nm/854 nm Raman transition with high fidelities41. We generate ion-photon entanglement via a strong 397 nm pulse which excites the ion from the \(\vert {S}_{1/2}\rangle\) level to the \(\vert {P}_{1/2}\rangle\) level. We then collect the spontaneously emitted 866 nm photon and the ion decays to three sub-levels of \(\vert {D}_{3/2}\rangle\) in this process. We then merge sub-levels in \(\vert {D}_{3/2}\rangle\) and transfer the ion internal state to \(\vert {D}_{5/2}\rangle\) level by three successive Raman pulses. After these Raman transitions, we end up with a maximally entangled Bell state,

$$\vert \Psi \rangle=\frac{1}{\sqrt{2}}(\vert {\uparrow }_{c}\rangle \vert H\rangle+\vert {\downarrow }_{c}\rangle \vert V\rangle )$$
(3)

The detailed process of the ion-photon entanglement generation and the Raman operations can be found in Supplementary Note 1.

Fig. 2: Experimental setup, encoding scheme, and multiplexing protocols.
figure 2

a In this experiment, a 5-ion (including 4 communication qubits and 1 memory qubit) crystal is confined in a linear blade trap. The magnetic field is perpendicular to the ion chain. An 866 nm objective, aligned perpendicular to the magnetic field, collects single photons in ion photon entangling process. Four DC electrodes are employed to shuttle the ion chain for multiplexing. A 729 nm addressing beam is able to drive each ion individually. Other beams such as the 397 nm σ+ optical pumping, 397 nm picosecond pulse for entangling, two sets of Raman beams, and the cooling and pumping beams (not shown in this figure) are all global. b Dual-type encoding of the communication qubits and memory qubits. The communication qubits are encoded in a closed three-level subspace consisting of \(\vert {S}_{1/2}\rangle\), \(\vert {D}_{3/2}\rangle\), and \(\vert {P}_{1/2}\rangle\), which is able to carry out cooling, pumping, ion photon entangling, and detection without influencing the memory qubit subspace \(\vert {D}_{5/2}\rangle\). Coherent conversions between these two subspaces can be realized with 729 nm quadruple transition or a 850 nm/854 nm Raman transition. Another 866 nm/866 nm Raman transition is used for rotation in the \(\vert {D}_{3/2}\rangle\) level41 (see Supplementary Note 1 for detailed description of Raman transitions). c The multiplexing scheme of multiple excitation. We squeeze the population out of the \(\vert {S}_{1/2}\rangle\) level by multiple ion-photon entangling pulses and this can effectively increase the branching ratio of the 866 nm transition from 6% to `unity'. After several excitation pulses, the population accumulated in \(\vert {S}_{1/2},m=-1/2\rangle\) is cleaned by an intermediate optical pumping. As the ion can also decays to \(\vert {D}_{3/2}\rangle\) during the optical pumping, the optimal branching ratio we can achieve is 54.4%. The detailed process of ion-photon entanglement generation can be found in Supplementary Note 1.

Full size image

The photon we collect in ion-photon entanglement generation is from the \(\vert {P}_{1/2}\rangle\) to \(\vert {D}_{3/2}\rangle\) transition in 866 nm wavelength, which is very suitable for being converted to telecom C band with high efficiency and low noise via the difference frequency generation (DFG) in a Periodically Poled Lithium Niobate (PPLN) waveguide. However, the small branching ratio of 6% limits the efficiency of the ion-photon entanglement generation. Therefore, in the first multiplexing scheme, we demonstrate how to resolve this issue by a method of multiple excitation.

The idea is that we can reuse the ion after the unsuccessful excitation. Each time when the ion is excited to the \(\vert {P}_{1/2}\rangle\) level, the ion decays back to the initial state \(\vert {S}_{1/2},m=+ 1/2\rangle\) with a probability of roughly \(\frac{2}{3}\times (1-6\%)\approx 63\%\), to \(\vert {D}_{3/2}\rangle\) level (emitting an 866 nm photon simultaneously) with a probability of 6%, and to the other Zeeman level of \(\vert {S}_{1/2},m=-1/2\rangle\) with a probability of \(\frac{1}{3}\times (1-6\%)\approx 31\%\) (see Fig. 2c). In addition, the ion will not be influenced by the 397 nm excitation pulse if it has already decayed to \(\vert {D}_{3/2}\rangle\) state. Thus the ion returns to the initial state with a high probability after an unsuccessful excitation and will not be excited again after a successful excitation. Therefore, we can iteratively excite the communication ion by successive excitation pulses until all the population in the initial state has been removed. This scheme effectively improves the branching ratio of the 866 nm transition and we call this method ‘pushing the branching ratio to unity’. During the process of multiple excitation, a time-bin train of 866 nm photonic pulses are emitted and collected (see Fig. 3), which can be employed to enhance the efficiency of ion-photon entanglement generation.

Fig. 3: Experimental results of multiplexing-enhanced ion photon entanglement in 3 m case.
figure 3

a Experimental protocol. We apply a spin echo sequence of τ on the memory qubit. Meanwhile, the ion-photon entangling attempts are applied to the communication qubit. In each τ/2, the blocks of entangling attempts are repeated for 238 and 231 times. In each block, series of 8 ion photon entangling attempts are repeated for 60 times. State analysis of the communication qubit can be executed directly after the heralding event or delayed until later computational tasks with the memory qubit. The protocol restarts if no photon is detected. b The histogram of the photon detection events in the ion photon entangling attempts. The photon is in 866 nm. The photon detection events between 150 ns and 250 ns are induced by the intermediate optical pumping. c The reconstructed density matrix of the ion-photon entanglement. The measured fidelity is 96.8 ± 0.4%. By applying real-time phase adjustment, we can yield the same ion-photon entangled state no matter which of the 8 modes is excited. d Merging \(\vert {2}_{C}\rangle\) and \(\vert {1}_{C}\rangle\) by a 866 nm/866 nm Raman pulse (see Fig. 2b and ref. 41). A \(\frac{2}{3}\pi\)-pulse is first used to scan the phase for merging the levels, as indicated in the inset. A subsequent fine scan on time is performed at the optimal phase. This measurement yields a merging fidelity of 98.5 ± 1.1%. e The memory qubit under different mutually unbiased bases (MUBs). The memory qubit is initialized to six MUBs which are also the eigenstates of σx, σy and σz. By scanning the phase or time of the 729 nm pulse, we can perform the single qubit state tomography and get the fidelity of each stored qubit. Mid-circuit detection is employed to detect the errors ϵ caused by the finite lifetime of \(\vert {D}_{5/2}\rangle\) state. If a decay event is detected in the mid-circuit measurement, this trial is aborted and the protocol starts over again. With a success rate of 89%, the memory qubit fidelity averaged over six MUBs reaches 93.3 ± 0.9%. Error bars represent one standard deviation in this figure.

Full size image

After a series of four successive excitation pulses, most of the population in \(\vert {S}_{1/2},{m}_{S}=+ 1/2\rangle\) is pumped to \(\vert {S}_{1/2},{m}_{S}=-1/2\rangle\) and \(\vert {D}_{3/2}\rangle\) level, and then the excitation probability becomes low. As most of the population is accumulated in \(\vert {S}_{1/2},{m}_{S}=-1/2\rangle\) level, we can pump the ion back to the initial state via a 397 nm σ+ transition (see Fig. 2c). Note that unlike the initial pumping, here 866 nm laser is not applied to protect the state in \(\vert {D}_{3/2}\rangle\). Iteratively, other series of excitation pulses and intermediate optical pumpings are applied, until most of the population are in \(\vert {D}_{3/2}\rangle\) level. In this way, we can generate a time-bin train of 866 nm photonic pulses, which is temporally separable and can be employed to enhance the efficiency of ion-photon entanglement generation. Note that as the ion can also decay to \(\vert {D}_{3/2}\rangle\) level in the intermediate optical pumping, thus not all the ion population in \(\vert {D}_{3/2}\rangle\) level is related to photon emission event in the ion-photon entangling attempts. However, this does not influence the quality of ion-photon entanglement as the 866 nm photon emitted in the optical pumping will not be collected. In addition, the already created ion-photon entanglement will not be influenced by the following intermediate pumping as the ion is already in \(\vert {D}_{3/2}\rangle\) state in this case. Therefore, the intermediate pumping will not induce false heralding or ruin the established ion-photon entangled state. Ideally, the branching ratio of the 866 nm emission in the ion-photon entangling can be ‘improved’ to 54.4% considering the optical pumping processes, and the multiplexing enhancement factor saturates with N = 10 modes approximately. In the future, we can shelve the state in \(\vert {D}_{3/2}\rangle\) to \(\vert {D}_{5/2}\rangle\) and apply 866 nm laser in the intermediate optical pumping, by which we can achieve an effective branching ratio of 100%. Currently, we are limited by the laser power to realize this fast shelving. The detailed analysis on this issue can be found in the Supplementary Information.

Another scheme to realize multiplexing enhancement is ion shuttling. Through this scheme, one can successively generate temporally multiplexed ion-photon entanglements via shuttling different ions to the interaction region of the optical interface38,39,44,45,46. In our experiment, the time cost for ion shuttling is Δt = 25 μs (see Supplementary Information).

Multiplexing-enhanced ion-photon entanglement in three different cases

In this section, we demonstrate the realization of multiplexing-enhanced ion-photon entanglement via the two multiplexing schemes mentioned above, at different fiber lengths of 3 m, 1 km, and 12 km.

For the 3 m case, the round-trip travel time for heralding an ion-photon entanglement is \(\frac{2L}{c}=30\) ns and the averaged overhead Tovh is below 1 μs in our experiment. In this situation of small overhead and short fiber, a small Δt is necessary to achieve a high multiplexing enhancement factor. Therefore, it is not suitable to use the ion-shuttling method in this case as the 25 μs shuttling time is much higher than the total overhead \(\frac{2L}{c}+{T}_{{{{\rm{ovh}}}}}\approx 1\,\mu\) s. Here we use a 2-ion chain (one for communication qubit and the other for memory qubit) and employ the multiple excitation method to accelerate the generation of heralded ion-photon entanglement. As the enhancement factor of this method has an upper limit of \(\frac{54.4\%}{6\%}\approx 9\) (all the population is pushed to \(\vert {D}_{3/2}\rangle\) level), which means the enhancement factor already saturates roughly at N ≈ 9. Therefore, we need to reduce Δt to a value as small as possible, in order to guarantee \(N\Delta t\approx 9\Delta t\approx \frac{2L}{c}+{T}_{{{{\rm{ovh}}}}}\) and achieve a high enhancement factor (see the analysis in Section II A). Therefore, here we use the fastest multiple excitation scheme in which we apply a series of four consecutive pulses from a mode-locked pulse laser to excite the ion. The time interval between consecutive pulses is 13 ns which is the reciprocal of the laser repetition rate at 76 MHz. After 4 consecutive pulses, we pump the ion back to the initial state by a 397 nm pulse (intermediate pumping). Another set of 4 consecutive pulses is applied after the intermediate optical pumping. A total number of 8 excitations are applied to generate 8 photonic time-bin modes (see Fig. 3). Upon any of the 8 time-bin modes is detected by the photon detector, our control system can identify which mode is excited via the arrival time of the photon detection signal. Followed by dynamical adjustment of the ion phase, the finally yielded ion-photon entangled state \(\frac{\vert \uparrow \rangle \vert H\rangle+{e}^{i\phi }\vert \downarrow \rangle \vert V\rangle }{\sqrt{2}}\) always has the same phase ϕ no matter which mode is actually excited. The heralded ion-photon entanglement has a fidelity of 96.8 ± 0.4% to the closest maximally entangled state. The total time cost of the 8 excitation pulses and the intermediate pumping is about 340 ns, and the entangling rate is enhanced by a factor of M = 3.4 compared to the single-mode case. The entanglement generation rate in this case is about 263 s−1. As the time interval between the excitation pulses 13 ns is comparable to the spontaneous decay time of \(\vert {P}_{1/2}\rangle\) at 7 ns, it is possible that the ion is still in the excited state when the next excitation pulse arrives. However, this only induces a slight efficiency loss but does not influence the quality of the heralded entanglement, which is discussed in the Supplementary Information. The memory qubit fidelity averaged over six mutually unbiased bases (MUBs)40,41 is measured to be 93.3 ± 0.9% after 100 ms storage.

As a functional quantum network node should be capable of storing quantum information during the ion-photon entangling attempts, we use the dual-type scheme to encode quantum information in a memory qubit in \(\vert {D}_{5/2}\rangle\) level for this task40,41,43. It is shown that the coherence time of the quantum information in the memory ion is 366 ± 11 ms and the crosstalk of operations on communication qubit has negligible influence on the memory qubit, as shown in Fig. 4. In this case, the memory coherence time is roughly 100 times longer than the ion-photon entanglement generation time of \(\frac{1}{263{{{{\rm{s}}}}}^{-1}}=3.8\) ms.

Fig. 4: Coherence time and crosstalk.
figure 4

a Protocol to measure the coherence time of communication qubit and memory qubit. We prepare the memory qubit in \(\vert {+}_{M}\rangle=\frac{\vert {\downarrow }_{M}\rangle+\vert {\uparrow }_{M}\rangle }{\sqrt{2}}\) (Fig. 2b), and apply a Ramsey measurement with a spin echo in the middle. We measure the memory qubit coherence time in both the case with ion-photon entangling (IPE) performed on the communication qubit (yellow shaded sequence) and the case without IPE (green shaded sequence). For the communication qubit, we prepare the communication qubit in \(\vert {+}_{C}\rangle=\frac{\vert {\downarrow }_{C}\rangle+\vert {\uparrow }_{C}\rangle }{\sqrt{2}}\) and apply a Ramsey measurement without spin echo (blue shaded sequence). b Measurement results. For the communication qubit, a fitting of Gaussian decay yields a coherence time of 5.8 ± 0.1 ms (blue triangle). The yellow square and the fitted curve show the fidelity decay in the memory qubit with all the noisy operations on the communication qubits applied. The extracted coherence time is 366 ± 11 ms. The green circle is the memory qubit fidelity in the case of no operations on the communication qubits, and the fitted coherence time is 368 ± 9 ms. The coherence time of memory qubit with or without operations on communication qubits cannot be faithfully distinguished considering the statistical error. The red diamonds characterize the spontaneous decay of the memory qubit after different storage times. The fitted lifetime of \(\vert {D}_{5/2}\rangle\) is 958 ms. The small discrepancy between our measurement result and the theoretical value ( ~1 s) can be attributed to the leaked 854 nm laser. All the coherence time is fitted by a Gaussian decay \(F=a\,{e}^{-{(x/\tau )}^{2}}+1/2\). Error bars represent one standard deviation in this figure.

Full size image

For the 1 km case, the total overhead \(\frac{2L}{c}+{T}_{{{{\rm{ovh}}}}}\) is slightly higher than 10 μs. As the total overhead is still small compared to the 25 μs switching time of ion shuttling, we still use the multiple excitation method as in the 3 m case, and only one communication qubit is used. However, now we can set the time interval Δt to a larger value of around 200 ns to avoid the efficiency loss in the 13 ns interval case, as the population in the excited state is negligible after 200 ns. The pulse sequence in this case is shown in Fig. 5a, in which totally 12 excitation pulses are applied to excite ion-photon entanglement in a total duration of 3.3 μs, including the four optical pumping in between. In this case, the generation rate of heralded ion-photon entanglement is 40 s−1, enhanced by a factor of 5.1 via multiplexing. The fidelity of the yielded ion-photon entanglement after feedforward on heralding signal is measured to be 94.6 ± 0.7%, as shown in Fig. 5c. The memory fidelity averaged over six MUBs is 88.5 ± 1.1% after 240 ms storage.

Fig. 5: Experimental results of the multiplexing-enhanced ion photon entanglement in 1 km case.
figure 5

a Experimental protocol. Unlike the 3 m case, we increase the time interval between successive excitation pulses to around 200 ns. We apply a series of 3 − 3 − 2 − 2 − 2 excitation pulses and 4 optical pumpings in between (detailed ion-photon entangling sequence can be found in Supplementary Note 2). b Histogram for photon detection events. The time interval between different modes is set to 200 ns. Four intermediate optical pumpings are inserted between excitation pulses. c Reconstructed density matrix of the ion-photon entanglement. The measured fidelity is 94.6 ± 0.7%. d The fidelity of the merging operation is 98.2 ± 1.1%. e The memory qubit measurements in six mutually unbiased bases (MUBs). The survival rate of memory qubit is about 79%, and the averaged fidelity over six MUBs is 88.5 ± 1.1% after 240 ms storage. Error bars represent one standard deviation in this figure.

Full size image

For the case in which the fiber length is 12 km, the total overhead \(\frac{2L}{c}+{T}_{{{{\rm{ovh}}}}}\) is larger than 120 μs, which is already longer than the switching time of ion shuttling. In this case, we accelerate the remote entangling process via a hybrid of both multiplexing methods mentioned in Section II B, as shown in Fig. 6. Unlike the 3 m and 1 km cases, here we increase the number of communication qubits from 1 to 4 as shown in Fig. 2a, and convert the 866 nm photon to 1558 nm via DFG41. We first use the similar time-bin multiplexing method as in the 1 km case to generate 11 time-bin pulses from ion 1. Then we shuttle the ion chain to move ion 2 to the focus of the objective and generate another 11 time-bin pulses from ion 2, and later ion 3 and ion 4. For the communication qubits not in the focus of the objective, their population in \(\vert {D}_{3/2}\rangle\) level are shelved to \(\vert {D}_{5/2}\rangle\) during the excitation of other communication qubits to avoid the crosstalk influence. After all the excitations, we shuttle the ion chain back to the initial position. The total duration of the ion-photon entangling attempts lasts for 87 μs with totally 44 time-bin modes emitted. The remote entanglement generation rate is 4.28 s−1 and the multiplexing enhancement factor is 15.6 compared with the single-mode case. Here we still use the arrival time of photon detection events for feedforward and yield the same ion-photon entanglement no matter which of the 44 modes is excited, and the final heralded ion-photon entanglement has a fidelity of 89.8 ± 1.1%. The dephasing time of the memory qubit is 366 ± 11 ms (see Fig. 4), which is already longer than the expected entanglement generation time about \(\frac{1}{4.28\,{{{{\rm{s}}}}}^{-1}}=234\) ms. Thus with multiplexing enhancement we can achieve a ratio of the remote entangling rate to the memory decoherence rate (also known as ‘spin-photon entanglement efficiency’) of \(\frac{1}{234\,{{{\rm{ms}}}}}/\frac{1}{366\,{{{\rm{ms}}}}}\times 74\%=1.16 > 1\) (74% is the survival rate of memory qubit, see Fig. 6 and the analysis below), which is an important threshold for the scale-up of a quantum network and sets the record for metropolitan-scale fiber so far.

Fig. 6: Experimental results of the multiplexing-enhanced ion photon entanglement in 12 km case.
figure 6

a Experimental protocol. In this case, we use a hybrid multiplexing method which combines the multiple excitation scheme used in the cases of 3 m and 1 km, and the ion shuttling scheme. In one round of excitation, each of the 4 communication quibt is excited by 11 times and emits in 11 time-bin photonic modes via multiple excitation scheme, and totally 44 modes are emitted after all the 4 communication qubits are excited via ion shuttling (detailed ion-photon entangling sequence can be found in Supplementary Note 2). A 650 μs sympathetic cooling is applied after 10 rounds of excitation. In this protocol, we apply on-demand shuttling and addressing for the measurement of communication qubits and memory qubit. b The histogram of the 44 photonic modes. c The measured ion-photon entanglement fidelity is 89.8 ± 1.1%. d The fidelity of merging operation on the 4 communication qubits. Here we fix the pulse area to 2/3 π and scan the phase for the merging pulse. This merging transition is sensitive to magnetic field, and we can use this property to check the magnetic field inhomogeneity on the 4 communication qubits (see Supplementary Information for details). This measurement yields a fidelity of 96.7 ± 3.3%. e The memory qubit measurement in six mutually unbiased bases (MUBs). The survival rate of memory qubit is about 74%, and the averaged fidelity over six MUBs is 78.7 ± 1.4% after 300 ms storage. Error bars represent one standard deviation in this figure.

Full size image

As the memory qubit is encoded in \(\vert {D}_{5/2}\rangle\) state which has a finite lifetime of 958 ms in our experiment (see Fig. 4b), the qubit stored in the memory qubit will suffer from considerable spontaneous emission error when the protocol time is close to the lifetime. However, this error can be detected via a mid-circuit measurement, thus it will not influence the quality of the quantum storage but only reduces the success probability of the task41. In this experiment, we still use this mid-circuit measurement scheme to detect and avoid the influence of the spontaneous emission error. The spontaneous decay error happens with a probability of 11%, 21%, and 26% in the 3 m, 1 km, and 12 km cases, respectively (see Figs. 3e, 5e, and 6e). The error budget of the ion-photon entanglement is listed in Table 1 and the detailed analysis is provided in Supplementary Note 10.

Table 1 Error budget in ion-photon entanglement
Full size table

Discussion

In summary, we have experimentally realized a highly-multiplexed trapped-ion quantum network node, which is capable of delivering heralded ion-photon entanglement with an entangling rate higher than the memory decoherence rate over a metropolitan-scale fiber. The remarkable enhancement factor of about 16-fold is achieved via the hybrid of a novel multiple excitation scheme which is demonstrated for the first time in this work and the ion shuttling scheme. Besides, the stored quantum information in the memory qubit is protected from the dissipative operations on the communication qubit via dual-type encoding, and the spontaneous emission error in the memory qubit can be detected via a mid-circuit meansurement. Here we also analyze the expected performance of ion-ion entanglement with the multiplexing schemes demonstrated in this work, as discussed in Supplementary Note 8 in detail. It is shown that the expected performance via our multiplexing scheme can reach or exceed the performances of current best experimental realization. Our multiplexing method is also compatible with the cavity enhancement, and the combination with high finesse optical cavity in the future would further improve the performance (see Supplementary Notes 7 and 8). In the future, the generation rate of the heralded ion-photon entanglement can be further improved by optimizing the efficiency of wavelength conversion from 12% in this experiment to the current best 57%47. Currently, the ion shuttling speed is limited by the bandwidth of the low-pass filter for the trap electrodes, and future improvement to a shuttling time of less than 3 μs is possible by replacing the filter. The entanglement generation rate can also be largely enhanced if high-finesse cavity is applied in the future48. With all these improvements, we believe a multi-node, metropolitan-scale trapped-ion quantum network could be realized in the future based on the multiplexed quantum network node demonstrated in this work.

Methods

Experimental setup

We fabricate a linear Paul trap consisting of five segments in each blade. A pair of blades are driven by an identical radio-frequency electric field, which provides the radial confinement for the ion chain. The other pair of blades generates the DC electric field to provide axial confinement and necessary static electric field for radial trapping, with the four outermost electrodes of this pair of blades being used for ion chain shuttling.

The global 397 nm, 866 nm and 854 nm lasers are used for Doppler cooling of the ion chain. By detuning the 397 nm laser by Γ/2 and setting the power to the half-saturation intensity, we achieve optimal cooling of the 15 phonon modes of the five-ion chain. The 866 nm and 854 nm re-pump lasers are employed to repump the population remaining in the D manifolds. To further improve state preparation and measurement (SPAM) performance, we employ global 397 nm σ+-polarized coupling light and π-polarized probe light to perform electromagnetically induced transparency (EIT) cooling. By providing two driving components for the probe light, we can achieve efficient cooling of all axial and radial modes simultaneously.

The state preparation is achieved by optically pumping the ions into the \(\vert {\uparrow }_{s}\rangle\) state using the σ+ polarized 397 nm laser. The laser frequency is tuned to resonance to maximize the state preparation rate, thereby increasing the repetition rate of entanglement generation.

A single 794 nm pulse with a temporal width of 6 ps, far shorter than the 7 ns P1/2 state lifetime, is selected from the pulse train produced by a mode-locked Ti:sapphire laser with a repetition rate of 76 MHz. This 794 nm pulse is frequency doubled using a β-barium borate (BBO) crystal to generate a 397 nm pulse, which is then combined with the σ+ polarized continuous-wave 397 nm laser mentioned above via a Wollaston prism before entering the trap. This setup is specifically used for photon excitation during the entanglement generation process.

Our system consists of two objectives. The objective with a numerical aperture (NA) of 0.52 is used to collect 866 nm single photons for the generation of ion-photon entanglement. The objective with a numerical aperture of 0.33 is mainly used for ion imaging and 729 nm laser addressing.

We employ a crossed AOD pair to achieve one-dimensional addressing. By providing the same driving signal to both AODs, this setup ensures that no additional phases are introduced into the qubit. A detailed discussion of our 729 nm addressing technique can be found in the Supplementary Information. 729 nm addressed laser enables individual shelving of ions into the D5/2 state. On one hand, this can be used for shelving detection in 40Ca+. On the other hand, it serves as a method to protect neighboring communication qubits during entanglement generation. Additionally, it serves as one of the bridges between the communication qubit subspace and the memory qubit subspace, as well as for the ion-photon entanglement state tomography and subsequent computational tasks.

The 850 nm, 854 nm and 866 nm lasers are generated by external cavity diode lasers (ECDLs) and locked to the same ULE (ultra-low expansion) Fabry-Pérot cavity, enabling transitions between the D3/2 and D5/2 states, as well as the Zeeman levels within the D3/2 manifold.

Quantum state tomography

For ion-photon entanglement tomography, we perform measurements on totally 36 bases \(\{{\sigma }_{x\pm }^{I},{\sigma }_{y\pm }^{I},{\sigma }_{z\pm }^{I}\}\otimes \{{\sigma }_{x\pm }^{P},{\sigma }_{y\pm }^{P},{\sigma }_{z\pm }^{P}\}\) for both the ion and photon subsystems. By performing these measurements we can reconstruct the density matrix of the entangled quantum state. For photon projection measurements, we use a pre-calibrated set of waveplates and a polarizing beam splitter (PBS). For ion measurements, we measure the off-diagonal elements by applying a π/2 pulse and adjusting the phase of the 729 nm drive, while the diagonal elements are measured using a π pulse. We perform state reconstruction using an iterative algorithm based on maximum likelihood estimation (MLE).