Accurate imputation of pathway-specific gene expression in spatial transcriptomics with PASTA

Abstract

Mapping the entire transcriptome at single-cell resolution under its natural spatial context is essential for investigating the oncogenesis and progression of diseases. The recently emerged targeted in-situ technologies retain the spatial organization of cells at high resolution, although they remain limited in the number of genes that can be simultaneously measured. To overcome this obstacle, numerous computational methods have been developed to predict unmeasured gene expression in spatial transcriptomics data by leveraging scRNA-seq data. Most of these methods focus on the expression of individual genes and usually generate highly variable predictions. In this study, we introduce PASTA (PAthway-oriented Spatial gene impuTAtion), a spatial pathway expression imputation method that leverages cell type and spatial proximity to enhance prediction accuracy. PASTA assumes that nearby cells and cells of the same type exhibit similar expression patterns, along with pathway information integrated into the imputation process, which improves prediction robustness and enhances biological relevance in spatial transcriptomics data. We demonstrate PASTA’s superior performance across both simulated and real-world datasets, highlighting its ability to impute pathway gene expression with improved stability and biological significance.

Introduction

Named “Method of the Year 2020” by Nature Methods, spatial transcriptomics (ST) opened the way to quantify gene expression with spatial context¹. Unlike traditional RNA sequencing methods, which average gene expression across dissociated cells, ST preserves the spatial relationships between cells, enabling the study of gene expression patterns in situ. This advancement is particularly significant for understanding tissue architecture, cellular heterogeneity, and the molecular micro-environments of complex tissues^2,3,4.

ST is becoming more accessible due to the development of commercialized technologies. Different ST technologies cover spatial content using different methods. For example, Visium and Stereo-seq are sequencing-based, which rely on spatially barcoded DNA; CosMx and MERFISH are imaging-based and rely on in situ hybridization⁵. However, most of the technologies still suffer from low sensitivity and resolution by limiting their detection to a set of pre-selected genes, which leads to the emergence of computational methods for gene imputation, especially the methods integrating the whole transcriptomic profiling from single-cell RNA-sequencing (scRNA-seq) data. For example, k-nearest neighbors (k-NN) has been used in several existing methods to predict uncovered genes with direct alignment between ST and scRNA-seq data, such as Spatial Gene Enhancement (SpaGE)⁶ and stPlus⁷. Another method, Tangram, adopted a different approach through a deep learning framework to map scRNA-seq data directly to ST spots⁸. This strategy minimizes the distance at both feature and sample levels and improves the imputation accuracy. Along this thread, other existing works also used diffusion model or other deep learning approaches to borrow information from scRNA-seq and predict the gene expression coverage in ST data, including stDiff⁹, SpotDiff¹⁰, and SPRITE¹¹.

The current ST imputation methods share several limitations, such as overestimation of spatial smoothness, uncertainty of the imputed biological accuracy, and reliance on the additional data. None of the methods aims on or is driven by biological pathway information. Pathway analysis has gradually become a standard way to discover and interpret biological functions based on omics datasets. For example, pathway enrichment analysis has been used in understanding the genesis of diseases^12,13, detecting druggable targets^14,15, and improving the therapeutic effects in patients with insomnia¹⁶, myocardial infarction¹⁷, and cerebral ischemia¹⁸. Many existing tools are available to help researchers move beyond individual gene-level changes to understand the broader biological processes and molecular functions affected by differential gene expression, providing insight into how these genes collectively contribute to disease mechanisms, cellular responses, or physiological changes¹⁹. Thus, obtaining pathway expression from ST data can facilitate the translation of spatial findings into clinical and therapeutic applications. Moreover, existing methods generally suffer from high noise level and low accuracy in their imputation results. Combining multiple functionally similar genes from a pathway can improve imputation robustness. Additionally, current imputation methods rarely integrate cell type information, although it has been widely acknowledged that cells belonging to the same cell type have more similar expression levels. Missing this critical knowledge in the imputation process introduces extra noise in the prediction results.

In this paper, we present PAthway-oriented Spatial gene impuTAtion (PASTA), a pathway expression imputation tool for ST data that simultaneously leverages cell type and spatial coordinate information while borrowing information from scRNA-seq data (Fig. 1A). PASTA constructs a mapping matrix between the scRNA-seq reference and ST data by assuming nearby cells and cells from the same cell type share similar expressions. During the mapping, pathway information is provided to guide the training process. In general, gene expression is highly sparse in both scRNA-seq and ST data. In contrast, incorporation of pathway aggregates multiple genes that have more similar behaviors and provides more stable and precise prediction for further analysis. In addition, the pathway-level expression across the ST landscape can offer more biologically related interpretations and conclusions, which reduces the efforts for downstream pathway analysis. PASTA shows its consistent performance in simulated datasets with different pathways and reference data settings. Applied to several real ST datasets, PASTA demonstrates its ability on pathway expression imputation compared with existing methods that serve similar purposes.

Fig. 1: Overview of the PASTA algorithm.

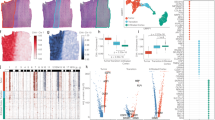
A The schema of PASTA algorithm. PASTA takes ST and scRNA-seq data as input. It computes a mapping matrix to impute the uncovered pathway-specific genes with assumptions: 1. Cells from the same cell type have more similar expression. 2. Cells within a neighborhood have more similar expression. B–E Simulation results of different pathway settings. Box-plots represent the distribution across 30 independent simulation runs. The center bar represents the median value, and the upper/lower bound of the box shows the 25%/75% quartile with whiskers extending to the minimum and maximum values. Each dot in the box represents a correlation value between the imputed and the true pathway value. B Results of the simulation where ScRNA-seq data and ST data are selected randomly. C Results of the simulation where scRNA-seq data and ST data are selected from different regions. D Results of the simulation where scRNA-seq data and ST data are selected from different subjects. E Results of the simulation where scRNA-seq data and ST data are selected from different types of cells. Source data are provided as a Source Data file.

Results

Simulation

We carefully performed comprehensive simulations to compare PASTA with several other existing popular ST imputation methods^20,21. The simulation datasets were generated based on Stereo-seq datasets using the Axolotl Regenerative Telencephalon²². Compared with other ST technologies, Stereo-seq can measure the whole genome transcriptomic information at single-cell resolution. To begin, we focused on a relatively straightforward scenario: Each simulated ST dataset contains 3000 cells and 1000 genes, which are randomly selected from the Stereo-seq dataset; ScRNA-seq data was obtained from the unselected cells in the same Stereo-seq dataset. This setting ensured that the scRNA-seq and ST datasets maintained similar gene expression distributions. The pathways were constructed by randomly selecting genes from the simulated ST datasets. To summarize pathway expression, we calculated the summation of the expression of the genes in each pathway. In our initial simulations, we opted for a simple but relatively uncommon case where all genes within a pathway were observed in the ST dataset. We then compared the performance of our proposed method against several other established methods, using metrics Mean Squared Error (MSE), Pearson correlation, and Spearman correlation to assess the prediction accuracy. Our results showed that PASTA consistently outperformed the alternatives, achieving the highest correlations and the lowest MSE (Fig. 1B). However, we did observe a slight decline in performance as the number of genes within each pathway increased, suggesting that pathway size can influence imputation accuracy. However, the decline did not continue if we increased  the pathway size (Fig. S1). This observation aligns with expectations, as more complex pathways naturally introduce additional variability, making imputation more challenging. Next, we extended our analysis to a more realistic scenario, where only a subset of randomly selected pathway genes were observed in the ST dataset, with the remaining genes coming from the unmeasured portion of the scRNA-seq data. In this partially observed pathway setting, performance across all methods declined, as expected. Nevertheless, our proposed method continued to demonstrate superior performance compared to the other approaches, maintaining the best correlations and lowest MSE (Figs. 1B and  S2), no matter whether the genes was observed or not originally (Fig. S3). The ability to handle missing information and still achieve strong results highlights the robustness of PASTA.

We then evaluated the proposed method under some more challenging conditions. In one scenario, we simulated a situation where the reference scRNA-seq data and the ST data were collected from the same subject but different regions (Fig. 1C). The number of genes in a pathway was fixed at 35, and all of them were observed in the simulated ST dataset. This was designed to introduce more variability in cells between the reference and query datasets, as cells from different regions are likely to exhibit distinct expression patterns. Despite this increased complexity, PASTA demonstrated notable stability, consistently providing accurate predictions even in the presence of this variability. In practical applications, collecting data from the same tissue is common, but obtaining both ST and scRNA-seq data from the same subject can be logistically challenging. To address this, we further constructed another scenario where the scRNA-seq data originated from a different subject. After generating the simulated ST data, we down-sampled scRNA-seq data from different individuals’ Stereo-seq datasets. Our proposed method continued to exhibit superior performance, maintaining accuracy and stability despite the increased complexity (Fig. 1D). We also conducted another situation where the scRNA-seq data and the ST data contain cells belong to different cell types. Under this condition, several existing methods, such as Seurat, struggled to produce stable predictions, reflecting their sensitivity to variability between cell types. However, although compared to the other scenario PASTA saw a bit of decline on the performance, it still shows satisfactory prediction precision (Fig. 1E). These results highlight the robustness of PASTA in dealing with the variability inherent in real-world data collection.

We also observed that the performance of our proposed model is not substantially affected by the size of the scRNA-seq reference dataset (Fig. S4), except when the number of reference cells is relatively small (e.g.,  <2000), in which case increasing the reference size improves imputation accuracy. However, this improvement stops once a sufficient number of reference cells is reached. With respect to the ST data, major cell types tend to exhibit slightly better imputation performance, although the differences are modest (Fig. S5). Since our method borrows information from neighboring cells, a higher number of cells can provide more context and improve the imputation process. Notably, we found that over-clustering of cells introduces unnecessary heterogeneity, which can obscure shared biological signals and reduce the stability of pathway-level imputation (Fig. S6).

Analyzing xenium dataset from human lung cancer tissue

We first collected an ST dataset from human lung cancer tissue with 480 genes processed by 10× Genomics Xenium²³. We annotated the dataset manually referring to the PanglaoDB²⁴ for the seven clusters that Xenium provides. The corresponding scRNA-seq dataset was collected from the UCSC cell Browser website²⁵, which is from human lung tissue and contains 26485 genes.

To demonstrate the effectiveness of PASTA in predicting pathway expression, in addition to the methods we used in simulation studies, we expanded our comparison to a few more recently developed tools, including SpaGE, gimVI²⁶, stDiff, stPlus, and stAI²⁷. We examined 44 pathways from the Hallmark gene set collection, which is known to be associated with cancer progression²⁸. We summarized pathway expression by aggregating the expression levels of genes within each pathway and used the overlapping genes between the pathways and the ST data as the ground truth. The predicted pathway expression was visualized by projecting the results into the spatial profiles (Figs. 2 and S7). We did not include stAI in Fig. 2 due to its inability to predict the entire tissue slice; specifically, it requires over 100 GB of GPU memory, which exceeds our available computational resources. Overall, PASTA significantly achieved higher pathway correlations (Figs. 3B and S8): Compared to SpaGE, predictions of our model showed higher accuracy in 79.5% of the pathways. Compared to Tangram, our model generated better predictions in all pathways. Notably, for certain pathways, such as the Hedgehog signaling pathway involved in regulating cancer stem cells, the correlation reached as high as 0.9. Despite the overall pathway distribution among all cells, within each cell type PASTA shows homogeneous high accuracy in terms of the pathway expression distribution.

Fig. 2: Patterns of imputed pathway expression by PASTA and six other existing methods using a human lung cancer ST data.

Three pathways are presented: MYOGENESIS, XENOBIOTIC METABOLISM, and HEDGEHOG SIGNALING (from top to bottom, respectively). PASTA-imputed pathway expression shows consistently higher correlations with true values, as indicated by the strong resemblance between the predicted and actual pathway expression patterns. Notably, for the Hedgehog signaling pathway involved in regulating cancer stem cells, the correlation between the PASTA-imputed expression and the true value reach 0.907. Source data are provided as a Source Data file.

Fig. 3: Further comparison between PASTA and other methods using the human lung cancer ST data.

A Cell annotation of the lung cancer data. We annotated the cells manually referring to the PanglaoDB. B Correlation between the imputation and the truth of pathway genes from PASTA and existing methods over 44 biological pathways. Each Dot represents a correlation value. The center bar represents the median value, and the upper/lower bound of the box shows the 25%/75% quartile with whiskers extending to the minimum and maximum values. Two sided Wilcoxon rank sum test shows significantly better predictions from PASTA compared to the other methods (P < 0.0001, *** shows significant differences). C Pathway enrichment in each cell type. D Comparison of the cell annotation, IRIS cluster, and K-means cluster in three representative areas. E Predicted hallmark pathway expression in tumor and the abjection area from PASTA. Source data are provided as a Source Data file.

We further checked how the predicted pathways connected to different cell types. Figure 3C illustrates the enrichment of hallmark pathways across various cell types, where each dot represents a significant pathway enrichment in a particular cell type. The size of the dot indicates the significance level, with larger dots corresponding to more significant enrichment. PASTA predicted that cancer cell development-related pathways, MYC TARGETS V1 and V2, are enriched in tumor cells. Additionally, PASTA identified immune-related pathways, including INFLAMMATORY RESPONSE, IL2-STAT5 SIGNALING, and ALLOGRAFT REJECTION, as highly expressed in T cells and macrophages, while using only the measured genes failed to capture correct enrichment patterns across cell types. In addition to pathway analysis, we applied PASTA to predict meta-programs (MPs)–gene sets defined by Gavish et al.²⁹ that are upregulated in specific subpopulations of tumor cells. These MPs capture diverse cellular processes underlying intratumor heterogeneity. PASTA predicted that nearly all MPs are highly expressed in basal cells within the tumor area (Fig. S9).

Pathways provide more comprehensive and biologically meaningful information than single genes. We illustrated this by clustering the dataset using pathway expression. We first applied Integrative and Reference-Informed Tissue Segmentation (IRIS)³⁰ to detect the tumor region within the data set. IRIS integrates scRNA-seq data and biological knowledge to identify domains in the ST dataset, and we set the number of domains as two during the application. Next, we performed K-means clustering on a pathway-by-cell matrix, where each row represents pathway-level expression. For the K-means cluster, we also set the number of clusters to two aiming to distinguish tumor cells from the rest of the dataset. To evaluate clustering performance, we selected three representative regions and compared cell type annotation, pathway-based clustering results, and IRIS-defined clusters (Fig. 3D, from top to bottom). While IRIS grouped all cells within the tumor region into a single cluster, pathway-based clustering achieved a finer separation, effectively distinguishing tumor cells within a tumor-infiltrating lymphocyte environment. In addition, we also observed that pathway expression shows more spatial structure compared to the single gene expression (Fig. S10): It can accurately show the tissue structure, while single gene may fail on capturing it.

Among the two domains detected by IRIS, one mainly contained fibroblasts and immune cells, while the other primarily comprised basal cells. We defined the latter as the “tumor domain." The HALLMARK pathway expression aligned well with the tumor cells distribution (Fig. 3E). We extracted the cells from the tumor domain, and constructed trajectory analysis using the R package Monocle3³¹, which can reflect the sequence of biological expression changes among cells. Instead of using the original gene-by-cell expression matrix, we still used the pathway-by-cell matrix as we used for K-means clustering. The pathway-by-cell matrix reduces the computational complexity. It also removes potential gene noises, which can make the trajectory clearer and more robust, providing a more coherent picture of biological processes over time that can make it easier to interpret shifts in cell states along the trajectory. Following the standard process provided by Monocle3, we generated a principal graph and ordered the cells by their pseudo-development time (pseudotime) using the first principal component as the root to get the trajectory. We then classified the cells into “early stage" and “late stage" based on their pseudotime. The predictions from our proposed method and Tangram showed distinct patterns (Fig. S11): Our method revealed that more developed tumor cells were concentrated in the center, whereas Tangram’s predictions placed them at the right edge. To further validate these results, we examined the expression of the MET gene, which is associated with abnormal cell proliferation. The distribution of the gene expression aligned closely with our method’s predictions, demonstrating that our approach effectively captures the underlying biological development among the tumor cells.

Analyzing merfish mouse brain ST data

We collected an adult mouse brain dataset processed by Merfish technology (Zhuang-ABCA-3, brain section: Zhuang-ABCA-3.010)³². The dataset contains 82075 cells with a panel of 1122 genes. The cell types were identified by the authors manually, including mostly neurons. The corresponding mouse primary visual cortex scRNA-seq data is collected from the Allen Institute.

We first examined how PASTA and the other spatial feature imputation methods perform on pathway imputation. The ground truth was defined as the summation of the genes’ expression common to both the pathway and the ST dataset. We chose the GOBP pathways related to mouse brain development. Overall, we observed that PASTA achieved the highest correlations between predicted pathway expression and the ground truth (Figs. 4B and S12). Particularly, for the BRAINSTEM DEVELOPMENT pathway, the correlation achieved 0.958 (Fig. 4A).

Fig. 4: Pathway imputation of a mouse brain dataset.

A Overview of the mouse brain cells and the predicted pathway expression. We grouped the cells into three main clusters. B Summary of correlation between the predicted and the true pathway expressions over 24 pathways. Each Dot represents a correlation value. The center bar represents the median value, and the upper/lower bound of the box shows the 25%/75% quartile with whiskers extending to the minimum and maximum values. PASTA shows significant better predictions compared to other methods except for Tangram (Two-sided Wilcoxon rank sum test, P = 0.0002 compared to StAI, P < 0.0001 for the others. *** indicates significant comparisons). C UMAP of the layer cells. D Pseudo-development time of the layer cells (111 L2 cells, 2909 L2/3 cells, 1789 L4/5 cells, and 438 L6 cells) estimated using pathway expression matrix from PASTA and Tangram. Each Dot represents a pseudo-development time value, and the center bar represents the median value. E K-means cluster using the pathway expression matrix from PASTA. F Major cell distributions of the K-means clusters using the pathway expression matrix from PASTA, Tangram, Seurat. Astro-Epen astrocyte and ependymal-like cells, GABA Gamma-aminobutyric acid, Glut glucose transporters, CB cerebellum, IT-ET inhibitory-excitatory, IMN immature neurons, DG dentate gyrus, OEC olfactory ensheathing cell, OPC oligodendrocyte progenitor cells. Source data are provided as a Source Data file.

The trajectory analysis revealed that pathway expressions can be referred for cell development information. We extracted the inhibitory neurons from the data, and then only kept the layer cells for the trajectory analysis. Four groups of cells are shown in Fig. 4C, which are layer 2 cells (L2), layer 2 or 3 cells (L2/3), layer 4 or 5 cells (L4/5), and layer 6 cells (L6). These layers are formed during a specific developmental process known as inside-out neurogenesis, where neurons in deeper layers (L5 and L6) are generated first, followed by neurons in the more superficial layers (L4, L3, and L2)³³. We used the predicted GOBP pathways to construct a pathway-by-cell matrix to infer the cells’ development. Using the pathways predicted by PASTA, the estimated pseudotime follows the theoretical inside-out development pattern (Fig. 4D). However, trajectory analysis with pathways predicted by Tangram failed on predicting the time shift. (Fig. 4D).

We then clustered the cells using the pathway expression matrix predicted by different methods. The cluster and cell distributions from PASTA are shown in Fig. 4E, F, along with the cell distributions generated from Tangram and Seurat. We found that pathways predicted by PASTA can generate clear cell distribution in the clusters: Cluster 1 consists of astrocyte and ependymal-like cells, oligodendrocyte precursor cells, and vascular cells; Cluster 2 consists of the other cells. Astrocytes and oligodendrocytes play a vital role in providing metabolic support to neurons. Both astrocytes and vascular cells are crucial components of the blood-brain barrier. However, clusters generated from pathways predicted by Tangram and Seurat have cell mixture. K-means cluster results of the other existing methods are presented in Fig. S13.

Analyzing mouse primary visual cortex data

Another dataset that we examined is collected from mouse primary visual cortex^34,35. There are three tissue slices, and the largest contains 119 genes profiled from 82785 cells. We clustered the dataset using Seurat and annotated each cluster manually referring to the PanglaoDB. The corresponding primary visual cortex scRNA-seq data is collected from the Allen Institute, including 15413 cells with the expressions of thousands of genes.

We evaluated the performance of PASTA against other spatial feature imputation methods, including Tangram, SpaGE, gimVI, stDiff, stPlus, and Seurat, to assess its ability to predict pathway expression through checking the correlation between predictions and the ground truth. During the training process, we did not incorporate cell type information for PASTA, as the majority of the cells were neurons that are distributed across the spatial domain. We summarized pathway expression by aggregating the expression levels of pathway genes. We focused on GOBP pathways, particularly those involved in neuron development. The ground truth was defined as the overlapping genes between each pathway and the ST data. Overall, our model achieved the highest correlations in predicting pathway expression, especially for pathways related to brain activity (Fig. 5A, B). We did not include stAI in Fig. 5B due to its inability to predict the entire tissue slice. We observed that some methods, such as SpaGE and Seurat, struggled to predict the pathway expression. In contrast, our model and Tangram showed better performance among all the methods. Our model showed better performance in around 70% of the checked pathways compared to Tangram. We found that our method generated non-satisfactory predictions in some pathways, such as actin-mediated cell contraction and adult behavior pathways, which were expected as the pathway selves did not have a strong relevance with the dataset source.

Fig. 5: Predicted pathway expression of mouse frontal cortex data.

A Pathway predictions. PASTA and Tangram showed superior performance. B Overall correlations between the predictions and the ground truth derived from 26 pathways. Each Dot represents a correlation value. The center bar represents the median value, and the upper/lower bound of the box shows the 25%/75% quartile with whiskers extending to the minimum and maximum values. Two sided Wilcoxon rank sum test shows significantly better predictions from PASTA compared to the other methods except for Tangram (P < 0.0001, *** shows significant differences). C Pathway enrichment among each cell type. Seurat generates some false positives under the cluster of endothelial cells. D Pseudotime estimation from PASTA and Tangram predictions projected in UMAP coordinates. The UMAP and the trajectory analysis were conducted using the predicted “pathway-by-cell" matrix. Source data are provided as a Source Data file.

To check whether the predicted spatial gene expression is biologically meaningful, we first examined how the predicted pathways are enriched in the cells. We found that a variety of neuron-related pathways are highly expressed among the neuron cells, which is accurately detected by the imputation methods. However, some methods, such as Seurat, generated false positive enrichment among the Epithelial cells (Fig. 5C). Additionally, we constructed developmental trajectories using the R package Monocle3 to reveal the progression of cell states. The proposed method and Tangram produced different developmental patterns: our method highlighted early and late stages across the spatial domain, while Tangram predictions were impacted by spatial coordinates, resulting in a uniformly distributed pseudotime in UMAP (Fig. 5D, E). It is rare to have uniformly distributed pseudotime, which might be led by overfit or over-relies on the spatial coordinates during the imputation. If the model prioritizes spatial smoothness, it may impose coordinate-based trends, especially when information from actual gene expression data is limited. In contrast, our method balanced spatial smoothing with biologically informed patterns, capturing the biological characteristics of the dataset in a more meaningful way.

We also applied the imputation methods on the other two additional ST slices. The proposed method still shows advantages in predicting the pathway information (Fig. S14).

Analyzing human frontal cortex ST data

We collected a large data set that contains 18,686 cell profiles from human frontal cortex tissue. The corresponding scRNA-seq data are collected from a study related to the developmental atlas of the human prefrontal cortex³⁶ with 24153 genes leveled from 2394 cells.

The cells in the dataset were identified to 13 clusters, including oligodendrocytes and layer cells. We evaluated the performance of our proposed model against other spatial feature imputation methods: Tangram, SpaGE, gimVI, stDiff, stPlus, and Seurat. The ground truth was defined as the summation of the expression levels of genes common to both the pathways and the ST dataset. With more than 6000 genes present in the spatial dataset, almost all pathway genes were represented. We would like to note that imputation may not be necessary for high-resolution ST datasets, although sparse ST datasets can still benefit from imputation (Fig. S15). We focused on GOBP pathways related to brain development. Our proposed method demonstrated superior performance, in around 70% of the examined pathways, achieving the highest correlations between predicted pathway expression and the ground truth, followed by Tangram and GimVi (Fig. 6A, B). We did not include stAI in Fig. 6B due to its inability to predict the entire tissue slice. The brain renin angiotensin system pathway from GOBP database aligns with the astro cells correctly than highly expressed genes among astro cells (Fig. S16). To further illustrate how the predicted pathways capture biological processes, we analyzed cortical layer cells, specifically L2 cells (outer granular layer), L3 cells (outer pyramidal layer), L4 cells (inner granular layer), and L6 cells (polymorphic layer). The development of the layer cells in the brain follows an inside-out pattern, from L6 to L2. We integrated the predicted expression levels from over 200 GO pathways into a matrix and applied the R package Monocle3 for trajectory construction. By selecting L6 cells as the development root, we ordered the cells according to their pseudotime. The predicted cell development order aligned with biological expectations: L4 cells developed after L6 cells, while L2 and L3 cells developed at the very end (Fig. 6E).

Fig. 6: Pathway imputation comparison of PASTA and six other methods for CosMX human frontal cortex data.

A True pathway expressions and the predictions from different methods. B Correlation of the predicted and true pathway expressions over 40 pathways. Each Dot represents a correlation value. The center bar represents the median value, and the upper/lower bound shows the 25%/75% quartile. Two sided Wilcoxon rank sum test shows significant better predictions from PASTA compared to the other methods (P < 0.001, *** indicates significant comparisons). C Calibration scores for different methods. We calculated the calibration score for each of the 13 cell types, and summarized the medians in this box plot. The center bar represents the median value, and the upper/lower bound of the box shows the 25%/75% quartile with whiskers extending to the minimum and maximum values. D The distribution of calibration score of all cells. E Pesudotime of 14449 layer 2 cells (L2, outer granular layer) and layer 3 cells (L3, outer pyramidal layer), 8801 layer 4 cells (L4, inner granular layer), and 7609 layer 6 cells (L6, polymorphic layer) from the trajectory analysis. Each Dot represents a pseudo-development time, and the center bar represents the median value. Source data are provided as a Source Data file.

We evaluated the predictions using the recently developed calibration score presented by TISSUE³⁵. The calibration score measures imputation uncertainty and is defined as the ratio between the absolute prediction error and the variability within cell neighborhoods, which integrates both spatial and gene expression similarity. Following the standard procedure outlined by TISSUE, we examined the overall distribution of calibration scores as well as the distribution within each of the 13 cell subsets. Across all cells, our proposed method achieved a calibration score comparable to Tangram and StDiff (Fig. 6C, D). Within individual cell subsets, our method consistently showed lower calibration scores. Overall, the lower median calibration score from PASTA indicates more stable spatial gene expression estimation.

Discussion

In this study, we introduced PASTA (PAthway-oriented Spatial gene imputaTAtion), a framework for imputing pathway expression in ST data. By integrating both cell type information and spatial proximity, PASTA enhances the biological relevance and interpretability of spatial analyses. In contrast to existing methods that primarily operate at the gene level, PASTA directly models pathway-level expression by aggregating signals from functionally related genes, thereby reducing noise and improving the downstream biological interpretation.

We systematically evaluated PASTA through simulations and four real-world datasets generated using diverse ST platforms, including Xenium, MERFISH, ISS, and CosMx. Across all technologies, PASTA consistently outperformed state-of-the-art methods such as SpaGE, StPlus, and Tangram in accurately imputing pathway-level expression, proven by the downstream analysis, including pathway enrichment and trajectory inference. While we observed potential applicability to spot-level ST data, such data typically capture transcriptomes from multiple neighboring cells, resulting in cell type mixtures within individual spots. In these cases, coupling PASTA with specialized denoising tools designed for larger or mixed-resolution ST may further enhance accuracy and biological interpretability of the imputed pathway signals.

PASTA shares several limitations common to most imputation methods. A key challenge lies in its dependence on the quality and completeness of the reference scRNA-seq data. Biases or missing information in the reference, particularly involving pathway genes, may impact imputation accuracy. Moreover, pathway selection is critical: pathways derived from the same tissue type or disease context tend to yield better performance. PASTA also assumes that spatial proximity and cell type are reliable proxies for gene expression similarity, an assumption that may not always hold in complex or heterogeneous biological environments.

Future directions for PASTA could focus on further improving its robustness and expanding its applicability to more diverse tissue types and conditions. One potential avenue of exploration is the integration of additional biological layers, such as proteomics or metabolomics data, to enhance the imputation accuracy. Another promising direction could involve refining the model to better handle cases where pathway behavior deviates from spatial organization, allowing for a more robust prediction process. As ST technologies continue to advance, PASTA’s pathway-oriented approach provides a solid foundation for pathway imputation, with potential applications in translational research and clinical diagnostics.

Methods

Method overview

In this section, we will introduce the algorithm of PASTA. We would like to impute the missing pathway expression, i.e., the summation of genes within the pathway, through borrowing information form scRNA-seq dataset. The expression of a single gene in ST data is generally sparse with high variance. Pathway expression, in contrast, aggregates multiple genes that are more functionally similar. Thus, incorporating the pathway information in the imputation process would stabilize the prediction and provide more accurate estimations. Additionally, pathway information adds known biological knowledge to the results, allowing for easier interpretation and more straightforward downstream analysis.

Let $T\in {R}^{{n}_{T}\times {G}_{T}}$ denote the ST gene expression matrix measured at n_T cells for G_T genes (denoted as ${{{{\mathscr{G}}}}}_{T}$), and $S\in {R}^{{n}_{S}\times {G}_{S}}$ be the scRNA-seq gene expression matrix measure for the (usually larger) G_S genes (denoted as ${{{{\mathscr{G}}}}}_{S}$) in n_S single cells. The two assays share the subset of genes ${{{\mathscr{O}}}}={{{{\mathscr{G}}}}}_{T}\cap {{{{\mathscr{G}}}}}_{S}$. We focus on a curated collection of P pathways, for each pathway l its full gene list is ${{{{\mathscr{G}}}}}_{l}\subseteq {{{{\mathscr{G}}}}}_{S}$. Within ${{{{\mathscr{G}}}}}_{l}$ we distinguish the part observed in ST as ${{{{\mathscr{G}}}}}_{l}^{obs}$ from the remaining part missing in ST but present in scRNA-seq as ${{{{\mathscr{G}}}}}_{l}^{miss}$.

Our goal is to predict at every spatial location, the sum of expression of the entire pathway gene set ${{{{\mathscr{G}}}}}_{l}$ even when many of its genes are unmeasured in ST. To do so, we first learn a trainable alignment matrix $\widetilde{A}\in {R}^{{n}_{s}\times {n}_{T}}$, after row-wise soft-max transformation, its entries are converted into ${A}_{ik}=\frac{\exp ({\widetilde{A}}_{ij})}{{\sum }_{{j}^{{\prime} }=1}^{{n}_{T}}\exp ({\widetilde{A}}_{i{j}^{{\prime} }})}$, which form a probability distribution that maps each scRNA-seq cell i onto spatial location j in ST. and S* = A^TS is therefore the single cell informed gene expression estimation in ST.

For a given pathway l, we define its imputed expression as ${T}_{l}=[{S}_{:,{{{{\mathscr{G}}}}}_{l}}^{ * }]{{{\boldsymbol{1}}}}$, where T_l is a n_T by 1 pathway activity vector on the tissue slide. Here we are not simply imputing genes one-by-one, we aim to aggregate real ST knowledge and scRNA-seq information into a robust pathway activity measurement.

At each time we focus on one pathway l, the alignment matrix is learned by minimizing a weighted sum of four loss functions that each serves a distinct role. The first reconstruction loss is:

$${L}_{recon}={\sum }_{j=1}^{{n}_{T}}MSE\left({\left({A}^{T}{S}_{:,{{{{\mathscr{G}}}}}_{l}^{obs}}\right)}_{N(j)},{\left({T}_{:,{{{{\mathscr{G}}}}}_{l}^{obs}}\right)}_{N(j)}\right),$$

(1)

which aligns the pathway expression within each spatial location’s neighboring cells from the same cell type. This is because spatial expression changes smoothly within the same cell type but can jump sharply across different cell types; therefore, for each focal spatial location j, we consider its k-nearest neighboring cells from the same cell type as N(j), k = 10 by default.

The global similarity loss is

$${L}_{global}=- \mathop{\sum}_{g\in {{{\mathscr{O}}}}}Co{s}_{sim}\left({S}_{:,g}^{ * },{T}_{:,g}\right),$$

(2)

which enforces transcriptome-wide agreement on all shared genes to enable mapping between scRNAseq with ST.

The pathway similarity loss is:

$${L}_{pathway}=-{\sum}_{j=1}^{{n}_{T}}Co{s}_{sim}({S}_{j,{{{{\mathscr{G}}}}}_{l}^{obs}}^{ * },{T}_{j,{{{{\mathscr{G}}}}}_{l}^{obs}}),$$

(3)

which narrows down to the current pathway’s own genes, preventing them from being washed out by highly expressed genes in the global similarity loss, and ensuring the alignment is still optimized for pathways that are under-represented in ST.

The neighborhood similarity loss is:

$${L}_{neigthbor}=- {\sum}_{j=1}^{{n}_{T}}Co{s}_{sim}({S}_{N(j),{{{{\mathscr{G}}}}}_{l}^{obs}}^{*},{T}_{N(j),{{{{\mathscr{G}}}}}_{l}^{obs}}),$$

(4)

which encourages cell-type-coherent expression patterns in each cell’s immediate cellular neighborhoods.

Taking together, the total loss is

$$L={\lambda }_{1}{L}_{recon}+{\lambda }_{2}{L}_{global}+{\lambda }_{3}{L}_{pathway}+{\lambda }_{4}{L}_{neighbor}.$$

(5)

We minimized the loss function through gradient-based optimization using the PyTorch library. After model training, we obtain the predicted pathway T_l.

As demonstrated by the ablation analysis, all components of the loss function contribute meaningfully to the overall performance of PASTA (Fig. S17). Sensitivity analysis further revealed that the algorithm is particularly responsive to the pathway loss weight: assigning a higher value to this parameter generally leads to improved imputation accuracy. Additionally, performance benefits from a reasonably large learning rate and moderate values for the other loss regularization terms (Fig. S18). By default, the algorithm sets λ₁ and λ₃ to 1, λ₂ to 2, and λ₄ to 10.

Our method is inspired by Tangram, a well-established tool for spatial gene expression prediction. However, we simplified its assumptions by focusing more on individual cells and incorporating neighbor cells and cell type information, aiming to produce more accurate and interpretable imputed pathway expression.

Real datasets

Xenium human lung cancer dataset

We collected 161,000 ST cells from human lung cancer tissue processed by 10× Genomics’ high-plex Xenium In Situ technology. The dataset includes 480 genes. Cell annotations were performed manually based on features identified by K-means clustering (K = 7) referring to the PanglaoDB (Human, including tumor/cancer samples and cell lines). Annotation details can be found in the next section. The dataset includes 31249 basal cells, 28866 fibroblasts, 27453 T cells, 21975 macrophages, 18946 plasma cells, 18046 epithelial cells, and 13913 endothelial cells. The corresponding reference scRNA-seq data was obtained from the UCSC Cell Browser. This reference dataset includes all cell types observed in the ST dataset, along with 30 additional cell types.

Merfish mouse brain data

The dataset is downloaded through the Allen Brain Cell Atlas. We extracted the cells with brain section number brain section labeled “Zhuang-ABCA-3.010". Cell type annotations were provided by the original authors, and we filtered out cell types with fewer than 40 cells. The final dataset contains 82,075 cells from 27 cell types. The corresponding scRNA-seq data was collected from the Allen Institute, comprising 15,413 cells with the expression of ten thousands of genes.

ISS mouse primary visula cortex dataset

We analyzed an in situ sequencing (ISS) dataset from the mouse primary visual cortex^34,35. This dataset includes three slices: the largest contains 119 genes profiled from 82,785 cells, while the other two contain 136 genes profiled from 14,066 and 15,823 cells, respectively. We clustered the dataset using Seurat and manually annotated each cluster based on the PanglaoDB. Details can be found in the next section. The corresponding scRNA-seq data was collected from the Allen Institute, comprising 15,413 cells with the expression of ten thousands of genes.

CosMx Human frontal cortex dataset

We analyzed a large dataset containing 188,686 cells from human frontal cortex tissue. Using the CosMx Spatial Molecular Imager technique, over 6000 genes were characterized from human frontal cortex FFPE tissue. The dataset mainly contains 7 cell types, which are astrocytes, inhibitory neuron, endothelial, cortical layer cells, microglia, oligodendrocyte, oligodendrocyte progenitor cells (OPCs). The corresponding scRNA-seq data was obtained from a study on the developmental atlas of the human prefrontal cortex³⁶, which includes 24,153 genes from 2394 cells, including six major cell types: neural progenitor cells, excitatory neurons, interneurons, astrocytes, OPCs, and microglia, which are intersected with the cell types in the spatial dataset.

Cell type annotation for the real datasets

Xenium human lung cancer dataset

The clusters and their features were provided by Xenium (https://www.10xgenomics.com/datasets/ffpe-human-lung-cancer-data-with-human-immuno-oncology-profiling-panel-and-custom-add-on-1-standard). We used the K-means cluster with K = 7. For each cluster, we ranked features by p-value and log2 fold change, selecting the top five to annotate each cluster using PanglaoDB. The annotation was performed with species set to human, including tumor/cancer samples, cell lines, as well as non-adult and non-primary samples.

ISS mouse primary visual cortex dataset

We annotated this dataset using the Seurat R package, following its standard workflow for normalization and feature selection, with the number of variable features set to 2000. Clustering was performed at a resolution of 0.2, and marker genes for each cluster were identified using the Wilcoxon rank-sum test. Markers were ranked by p-value and log2 fold change, and the top five features were used for cluster annotation, referring to PanglaoDB with species set to mouse, including non-adult and non-primary samples.

Pathway selection

Selecting appropriate pathways is crucial for obtaining accurate and interpretable results. In general, pathway selection should consider dataset characteristics such as source tissue and disease context. We recommend using well-curated pathway databases, such as KEGG and Reactome, and selecting pathways with an appropriate level of detail. Broad pathways may be less informative for datasets focused on a specific biological process. To improve robustness, pathway relevance can be validated using independent datasets.

For the human lung cancer dataset, we used 49 hallmark pathways which has overlapped genes with the ST dataset. For the mouse brain and primary cortex dataset, we used GOBP pathways, particularly, we included the pathways related to brain development. For the human cortex dataset, we checked 40 brain development-related pathways collected from GOBP sets. An example table of the pathways we examined was included in the supplementary file.

Benchmarking

Compared methods

We compared our proposed model with several state-of-art methods, including Tangram, StDiff, gimVI, Seurat, SpaGE, stPlus, and stAI. These methods are all imputation tools for gene expression. After we get the gene expression, we will compute the pathway expression by aggregating the pathway genes for each cell.

Tangram aligns scRNA-seq profiles with ST data to impute the missing genes in it. For different levels of resolution, it voxels the spatial volume differently. For example, a voxel for Visum technology is an individual spots, but for MERFISH is an individual cell. It minimizes an imputation loss function by incorporating gene-by-voxel and voxel-by-gene expressions, as well as the cell density in each voxel. In our implementation, we used the default parameter settings, except for adjusting the voxel-gene regularization term to 2.

StDiff introduces a diffusion model for ST gene imputation referring to scRNA-seq data. Instead of seeking similarity between the scRNA-seq and ST data, the model leverages the rules behind the scRNA-seq data to impute the missing genes in ST data, which can reduce the potential technical noise introduced by the two different experimental platforms. In summary, the model uses two interconnected Markov chains: the forward chain adds noise to the scRNA-seq data. All genes in scRNA-seq data undergoes noise perturbation, then the unique genes in scRNA-seq data will be added a time-dependent noise. Then the shared genes and unique gene part are concatenated to train the model to predict the noise. After the model is trained, unique genes in scRNA-seq data will be set as zero values in ST data and combine with the shared genes’ values in the ST data to be fed into the model to do the prediction. The usage of diffusion model is under explored in bioinformatics analysis. We expect that the model can capture local dependencies in ST data where gene expression patterns are often highly dependent on location. For real-world datasets, we prepared the inputs of spatial and scRNA-seq data in H5AD format and ran the program with default settings.

GimVI uses a variational inference framework to optimize the joint likelihood of scRNA-seq data and ST data. For scRNA-seq data, it uses zero-inflated negative binomial or negative binomial distribution to sample gene expressions, assumed conditionally independent on a latent variables. For ST data, it uses Poisson or negative binomial distribution to sample the gene expressions, assumed conditionally independent on a latent variable. Then, variational inference approximates the posterior distributions, from which missing genes will be imputed. We trained and ran Gimvi with default parameters.

Seurat, a widely used R package initially designed for scRNA-seq analysis and visualization, has been adapted to impute missing genes in ST datasets. It first jointly reduces the dimension of both scRNA-seq and ST datasets using canonical correlation analysis (CCA) with a L2-normalization on the canonical correlation vectors. Mutual nearest neighbors were used in the low-demensional space to get the “anchors", which refer as the cell pairs between scRNA-seq data and ST data. Then, a weighted matrix is constructed between each query cell (ST dataset) and each anchor to impute the missing genes. We followed the standard Seurat workflow, normalizing the data and using CCA by setting the dimension argument as 30 for anchor detection. Then principal component analysis (PCA) was set to impute the missing genes, as projecting a query dataset onto an existing PCA structure is more efficient in cases working with a large reference dataset and can eliminate the potential batch differences.

SpaGE follows a two-step process: it first applies domain adaptation to align ST and scRNA-seq data in a shared space. Then, for each cell in the ST data, neighbor cells from the scRNA-seq data are defined. Then missing genes’ expressions of that cell are predicted as a weighted average of the expressions of the neighbor cells, where the weight is associated with the cosince distance between cells. We trained the SpaGE model using the ST datasets with their corresponding scRNA-seq reference and imputed the missing genes by setting the number of principal vectors in SpaGE equal to 30.

StPlus jointly embeds ST and scRNA-seq data into a common space using an autoencoder. It then predicts the missing gene expression of a spatial cell by computing the weighted average of its neighborhood scRNA-seq cells. We performed pathway gene imputation using its default parameters, setting the random seed to 10.

stAI is a deep learning-based model which extracted sharing features of ST and scRNA-seq data through an encoder-decoder-based backbone framework. Missing genes in ST data were imputed through a weighted linear combination of the genes in the near cells from scRNA-seq data. The method can also perform cell annotation for ST data. We performed pathway gene imputation using its example parameters.

Evaluations

After the gene imputation, we performed the downstream analysis to explore the rationality of the results.

Correlation

To evaluate the performance of pathway imputation, we computed the Pearson correlation between the observed and imputed pathway expression in the ST dataset. For a given pathway, the ground truth was defined as the expression summation of its genes measured in the ST dataset, while the predicted values corresponded to the imputed expression summation of these same genes. By quantifying the correlation between observed and imputed pathway expression, we assessed the extent to which the imputation methods preserved pathway expression patterns within the spatial context.

TISSUE calibration score

The goal of the TISSUE framework³⁵ is to calibrate the predictions of gene expression in ST, incorporating a measure of uncertainty to reflect the confidence in these predictions. The formula of the score is

$${s}_{ij}=\, \frac{{X}_{ij}-{\hat{X}}_{ij}}{{U}_{ij}},\\ {U}_{ij}=\, 1+\sqrt{\frac{{\sum }_{k\in {N}_{i}}{W}_{ik}{({\hat{X}}_{kj}-{\hat{X}}_{ij})}^{2}}{{\sum }_{k\in {N}_{i}}{W}_{ik}}},\\ {W}_{ik}=\, exp\left(\frac{{\hat{X}}_{i:}\cdot {\hat{X}}_{k:}}{| | {\hat{X}}_{i:}| | | | {\hat{X}}_{k:}}| | \right).$$

(6)

The X_ij denotes the gene expression for cell i and gene j, and ${\hat{X}}_{ij}$ is the corresponding predicted expression. U_ij is a cell-centric variability that measures the deviation between the predicted expression of a cell and its neighborhood cells, with a weight of the exponential cosine similarity between that cell and its neighbors.

During our implementation, the input of the algorithm was pathway-by-cell matrix. The calibration score could reflect how well the model’s predicted probabilities (and uncertainties) align with the true spatial pathway expression data, which can be a fair measurement for the imputation methods.

Trajectory analysis

We aim to use pathway information to infer the temporal dynamics of biological processes through trajectory analysis. Since pathway expression reflects underlying biological activity, we hypothesize that trajectory analysis based on pathway profiles can effectively capture the progression of biological states in ST data. We perform this analysis using the R package Monocle3, which is designed to model cell state transitions in scRNA-seq data, particularly in contexts such as differentiation, development, and disease progression. In our analysis, the input to Monocle3 is a cell-by-pathway expression matrix, where each row corresponds to a pathway’s expression. We originally included 49 pathways for the Xenium lung cancer dataset and 292 pathways for the CosMx frontal cortex dataset. The number of pathways used can vary depending on tissue complexity and heterogeneity; incorporating a broader and biologically relevant set of pathways generally improves the resolution and robustness of trajectory inference. In practice, including several dozen to around a hundred well-chosen pathways often yields more meaningful and stable trajectories. Following the standard Monocle3 workflow, we preprocess the data and construct developmental trajectories. The root cells of the trajectory are assigned for the theoretically early-developed cells.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.