Fast superconducting qubit control with subharmonic drives

Abstract

Increasing the fidelity of single-qubit gates requires a combination of faster pulses and increased qubit coherence. However, these requirements can be contradictory. Additionally, increasing the drive power can heat the qubit’s environment and degrade coherence. In this work, we circumvent this issue and achieve rapid gates by pumping a transmon’s native Kerr at approximately one third of the qubit’s resonant frequency. The subharmonic Rabi rate of the process is proportional to applied drive amplitude cubed, allowing for rapid gates. In addition, we demonstrate that filtering can be used to protect the qubit’s coherence while performing rapid gates. Single qubit gates as short as 37.4 ns are demonstrated with fidelity of 99.91%. We present theoretical calculations indicating that drive induced multi-photon decay will not limit qubit lifetime; calculated power absorption also indicates that this technique could reduce cryostat heating for fast gates, a vital requirement for large-scale quantum computers.

Introduction

High-fidelity single qubit control is one of the fundamental requirements for gate-based quantum computing. While many factors can limit gate fidelity, such as cross-talk^1,2 and leakage to non-computational states³, the most fundamental are gate speed and qubit coherence^4,5,6,7,8, with recent improvements driven more by increased coherence than enhanced speed^9,10. However, for superconducting qubits, single qubit gates typically use resonant driving of a qubit transition, in which the requirements for fast gates and coherent qubits are contradictory.

For instance, to protect the qubit coherence time, weakly coupled drive ports and heavily attenuated lines are typically used to suppress qubit photon leakage, thermal noise^10,11, and out of band radiation¹². As qubit coherence increases, there is a trend towards more thorough and careful filtering. The increased losses of filtering and weaker qubit-drive line couplings together result in longer gate times at a given drive strength. However, achieving high gate fidelity requires we maintain or increase the ratio of qubit lifetime to gate time and so we attempt to compensate by increasing drive strength, which in turn increases heating of the cryostat. Heating of filter elements and drive lines¹³ can degrade the qubit by creating an excess thermal population at the qubit transition or higher frequencies (for example, at the superconducting gap) and/or heating the entire cryostat by exceeding the cooling capacity of the dilution refrigerator¹⁴. Moreover, the thermal time constants (in the millisecond range) are much slower than the pulses (roughly 10s of nanoseconds range) or qubit coherence times ( ~ 100 μs to 1 ms), and can produce effects which accumulate and persist across many experiments¹³. This situation is exacerbated by the necessity of scaling to larger quantum machines and thus increased qubit count and associated heating⁷.

To combat these limitations, better heat handling of each component, especially the attenuators on the control lines, has proven useful^11,13. Another solution is to break the symmetry between input control drives and out-going qubit photon decay in the power domain using a non-linear filter¹⁵. In this paper, we propose breaking the link between qubit coherence and driving by separating the two processes in frequency space, proposing and demonstrating a new single qubit control scheme based on parametric driving, which we term subharmonic driving.

In subharmonic driving we operate a transmon, a commonly used fixed-frequency qubit, by parametrically driving it at one third of its $| g\left.\right\rangle \leftrightarrow | e\left.\right\rangle$ transition frequency. Similar controlling methods are widely used in other systems, such as parametric amplification^16,17 and parametric qubit-cavity¹⁸, multi-cavity^19,20,21 and multi-qubit gates^22,23. In each of these scenarios, far off-resonant terms in the Hamiltonian are utilized, consuming pump photons to produce effective lower-order interaction Hamiltonians which need not satisfy energy conservation. The benefits of parametric driving include strong interactions and high on/off ratios; the use of reflective filters to protect mode frequencies while allowing strong driving is also well established^21,24,25.

The dominant nonlinear term in a transmon, the self-Kerr, is generated from the fourth order term of the Josephson junction’s cosinusoidal potential, with magnitude typically ranging from -150 to -250 MHz²⁶. We pick the 4^th order term ${\hat{q}}^{{{\dagger}} }\hat{q}\hat{q}\hat{q}+h.c.$, where ${\hat{q}}^{{{\dagger}} }$ is the qubit creation operator, and parametrically drive the qubit at near one third of the qubit transition frequency. Under these drive conditions, the chosen term annihilates three drive photons to create one qubit photon. The effect of the drive is described by the effective Hamiltonian $\sim {\eta }^{3}{\hat{q}}^{{{\dagger}} }+h.c.$, where η is the dimensionless amplitude of the coherent drive. We note that the potential energy contains many other terms; however, these terms are suppressed as they are fast-rotating as can be seen by applying the rotating wave approximation (RWA). We emphasize that the term we use is both ubiquitous and of very similar strength in every transmon qubit. This scheme can also be adapted to other qubits and systems by choosing an appropriate source of nonlinearity, for instance, 3^rd or 5^th order terms in qubits with asymmetric Josephson elements²⁷, and thus can be applied widely in superconducting circuits.

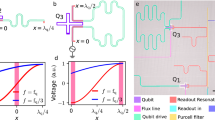
The proposed control scheme has two main advantages. The first advantage is that the drive frequency is separated from the qubit transition frequency. It allows us to suppress a primary relaxation channel in the system without affecting the ability to control the qubit by engineering the impedance at two widely separated frequencies. To this end, we placed a reflective low-pass filter (LPF) with low absorption (S11(ω_d)=0.2 dB) and good isolation in the stop band (S21(ω_q)=61 dB) at the qubit drive port, as shown in Fig. 1a. This suppresses qubit photon leakage to the environment through resonant decay while allowing low-frequency drive photons to pass freely. Therefore, the drive port can be more strongly coupled to the qubit for fast control without increasing the qubit’s direct relaxation rate. The second advantage of subharmonic control is that the Rabi rate is proportional to the drive amplitude cubed because it is a three-photon driving process, which allows us to rapidly improve qubit gate speed with only a moderate increase of drive power.

Fig. 1: Subharmonic driving schematic.

a A transmon qubit (at left in blue) and a λ/2 resonator for readout (at right in orange) are supported on a sapphire chip inside an aluminum tube. A low-pass filter (in green) is placed at the qubit drive port to suppress qubit photon leakage to the environment while allowing fast single qubit control at low frequencies. b The frequency distribution of the subharmonic drive ω_d (red), qubit frequency ω_q (blue), and the readout resonator frequency ${\omega }_{{{{\rm{res}}}}}$ (orange). Only the subharmonic drive is within the pass-band of the LPF (green). The dashed, shifted peak of ω_q represents the ac-Stark effect during the subharmonic drive. c The energy level diagram of subharmonic driving. The ac-Stark effect induced by subharmonic drive creates a detuning δ_d between the qubit’s un-driven and driven frames. Flat-top pulses are used to control the qubit state.

In this paper, we experimentally demonstrate the concept of single qubit, subharmonic control and achieve gates as fast as 37.4 ns with gate fidelities up to 99.91% on a typical, unoptimized transmon qubit. We also present calculations which address two key questions about practical implementation of subharmonic gates. First, we present a theoretical study of the effects of the low frequency lossy environment on the qubit’s coherence, finding that this coupling offers a negligible decay channel even for very strong couplings. Second, based on both theoretical calculations and measured parameters of our system, we find that the combination of low loss at base with realistic filter losses should allow high fidelity qubit gates with heating lower than conventional direct qubit drives.

Results

Subharmonic driving theory

The displaced Hamiltonian of a transmon under an off-resonant drive $\varepsilon (t)\cos ({\omega }_{d}t)$ can be written as

$${\hat{H}}^{D}/\hslash=({\omega }_{q}-\alpha ){\hat{q}}^{{{\dagger}} }\hat{q}+\frac{\alpha }{12}{(\hat{q}+\eta {e}^{-i{\omega }_{d}t}+h.c.)}^{4},$$

(1)

where η = iβ(ω_d)ε(t) is the dimensionless drive strength, and $\beta=2{\omega }_{d}/[{({\omega }_{q}-\alpha )}^{2}-{\omega }_{d}^{2}]$ (see Supplement Sec. I A). Expanding the Hamiltonian ${\hat{H}}^{D}$, we find numerous 4^th-order terms corresponding to different parametric processes of the transmon, which can be individually activated by driving at the correct frequencies. For example, driving the term $4\eta {e}^{i{\omega }_{d}t}\hat{q}\hat{q}\hat{q}+h.c.$ at 3(ω_q + α) activates the three-photon transition $| g\left.\right\rangle \leftrightarrow | h\left.\right\rangle$ (where $| h\left.\right\rangle$ is the third excited state), while the two-photon transition $| g\left.\right\rangle \leftrightarrow | f\left.\right\rangle$, commonly seen in transmon spectroscopy (usually termed gf/2), can be activated by driving the term $6{({\eta }^{*}{e}^{i{\omega }_{d}t})}^{2}\hat{q}\hat{q}+h.c.$ near (2ω_q + α)/2. For subharmonic driving, the term we are interested in is $4{({\eta }^{*}{e}^{i{\omega }_{d}t})}^{3}\hat{q}+h.c.$ Moving to the rotating frame at 3ω_d ≈ ω_q and performing the RWA, we acquire the desired single qubit Rabi drive term, as well as a term proportional to (ηη^*)q^†q, which represents the ac-Stark effect during subharmonic drive.

In the end, the Hamiltonian has the form:

$${\hat{H}}_{{{{\rm{sub}}}}}^{R}/\hslash=(2\alpha | \eta {| }^{2}-3\delta ){\hat{q}}^{{{\dagger}} }\hat{q}+\frac{1}{2}\alpha {\hat{q}}^{{{\dagger}} }{\hat{q}}^{{{\dagger}} }\hat{q}\hat{q}+\frac{1}{3}\alpha \left({\eta }^{3}{\hat{q}}^{{{\dagger}} }+{\eta }^{*3}\hat{q}\right),$$

(2)

with the drive detuning $\delta={\omega }_{d}-\frac{1}{3}{\omega }_{q}$. Eq. (2) shows two important properties of subharmonic driving: the Rabi rate of the process Ω is proportional to ∣η∣³, and the ac-Stark shift Δω during the subharmonic drive is proportional to ∣η∣². The ac-Stark effect also adds a drive-dependent phase on the qubit when performing a gate, which needs to be considered and calibrated in all experiments, as the qubit frequency changes in response to the amplitude of the drive.

One potential concern about subharmonic driving is qubit photon decay through the drive line at low frequencies via multi-photon processes, which could limit coherence when we couple the transmon and drive line very strongly. We perform a detailed calculation in the Supplement Sec. I G and summarize key results here. For a transmon qubit coupled to a low-frequency lossy environment, the system-bath coupling strength is

$$\lambda (\nu )=\Theta (\nu )\frac{{C}_{c}}{\sqrt{{C}_{r}c}}\sqrt{\frac{{\omega }_{q}\nu }{2\pi v}},$$

(3)

where C_c is the coupling capacitance between the qubit and the transmission line, C_r is the capacitance of the qubit, c is the characteristic capacitance of the transmission line, and v is the speed of light in the transmission line²⁸. In our case, we put a cut-off (filter) function Θ(ν) to suppress the high-frequency system-bath coupling. Specifically, the filter function is modeled as

$$\Theta (\nu )=\left\{\begin{array}{ll}1 &\nu \le {\omega }_{q}/3+\vartheta \\ 0 &\nu > {\omega }_{q}/3+\vartheta,\end{array}\right.$$

(4)

where ω_q/3 + ϑ is the bandwidth of the filter pass band. The decay rate through a three photon decay process can then be written as

$${\Gamma }_{3}=\frac{243}{32{\pi }^{2}}\frac{{\gamma }_{1}^{3}| \alpha {| }^{2}}{{\omega }_{q}^{4}}{\left(\frac{\vartheta }{{\omega }_{q}}\right)}^{2}$$

(5)

where γ₁ = 2πλ², λ is the system-bath coupling strength. For a transmon system with typical properties, because α and γ₁ are both much smaller than ω_q, the subharmonic decay rate Γ₃ is orders of magnitude smaller than the decay rate through resonant decay via internal losses or residual coupling to drive ports. Therefore, Γ₃ can be safely neglected even for very strong couplings.

Gate tune up and calibration

The subharmonic driving scheme was tested on a single qubit-resonator system, which had a transmon qubit and a λ/2 stripline resonator²⁹ with parameters commonly used in the field. Specifically, a transmon qubit (ω_q/2π = 4.237 GHz, α/2π = − 148.7 MHz, T₁/T_2R/T_2E = 41/21/72 μs) and a ${\omega }_{{{{\rm{res}}}}}/2\pi=6.498\,\,{\mbox{GHz}}\,$ readout resonator were housed inside a 4 mm diameter aluminum tube. The coupling rate of the resonator is κ_ext/2π = 1.44 MHz and the cross-Kerr between the qubit and the resonator is χ/2π = 0.77 MHz. This system was chosen to represent a general transmon-cavity system without any special engineering or specific design requirements, demonstrating that the subharmonic driving scheme is widely applicable to transmon-based quantum processors.

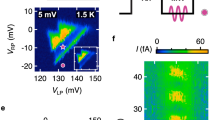
To better understand subharmonic driving, we first performed Rabi experiments, sweeping the drive frequency and amplitude on the qubit to observe its population oscillating between two states. Figure 2 shows qubit response vs. drive frequency, amplitude, and initial state. The pulse used here was a 100 ns flat-top pulse with smoothed edges (see Supplement Sec. I B). Preparing the qubit in the states $| g\left.\right\rangle$, $| e\left.\right\rangle$ and $| f\left.\right\rangle$, we see the four-wave mixing ge/3, ef/3 and fh/3 processes, respectively, by activating the term q^†qqq + h. c. . They are separated by a frequency of α/3. Furthermore, the 8-wave mixing processes gf/6 and eh/6 can be observed, with the term q^†q^†q⁶ + h. c. activated. The gf/6 process is the subharmonic correspondence of the gf/2 peak that is often seen in qubit spectroscopy.

Fig. 2: Parametric processes near one third of the qubit frequency.

a-c prepare the transmon’s initial state in $| g\left.\right\rangle$, $| e\left.\right\rangle$, and $| f\left.\right\rangle$ respectively. Multiple transitions can be activated by sweeping drive amplitude and frequency. The numerator and denominator of labels mean the levels and the number of drive photon involved in the transitions. The drive voltage V_p represents the peak amplitude of a pulse at the base stage of the dilution refrigerator.

We also observe a state-dependent upper boundary above which the coherent oscillations disappear and the transmon population moves to higher excited states. Such a boundary puts a maximum speed limit of our subharmonic gates, but is beyond the scope of this paper and the subject of a separate investigation³⁰. Within this upper boundary, all of these parametric processes can be used to perform qubit controls without appreciable degradation of the qubit’s coherence. In this work, we focus on the ge/3 process and use it to build fast single-qubit gates.

Our next step is driving the qubit with fixed power (and hence ac-Stark shift) and variable pulse duration at a given pulse amplitude to find the Rabi rate and frequency. As shown in Fig. 3a, the subharmonic Rabi oscillation versus time shows a chevron pattern similar to the pattern observed using a resonant drive. By fitting the data, we extract both the ac-Stark shift induced by the off-resonant drive on the qubit and the Rabi rate at the given drive strength.

Fig. 3: Rabi rate and ac-Stark shift vs. subharmonic driving strength.

a A Rabi experiment for subharmonic driving of the qubit as a function of pulse duration and drive frequency at fixed drive amplitude of 6.47 × 10⁻⁵ mV/MHz. At this amplitude, the Rabi rate is 2π × 13.55 MHz and the drive-induced qubit ac-Stark shift is 2π × -81.25 MHz, equivalent to 0.55 times of the transmon anharmonicity α. b Rabi rate and qubit ac-Stark shift vs. drive amplitude. The Rabi rate (red squares) is proportional to drive amplitude cubed. The ac-Stark shift (blue stars) is proportional to drive amplitude squared. A single fit function describes both sets of data with only one free parameter, the scaling factor k converting pulse amplitude βV_p to the effective driving strength η.

The experiment was then repeated with other pulse amplitudes. The drive amplitude in millivolts is the pulse peak amplitude at the base stage of the dilution refrigerator. The microwave configuration on the input line is shown in Supplementary Fig. 11. The method of calibrating the pulse amplitude in the base stage is discussed in the Supplement Sec. II B. After calibration, we assume that the voltage is linearly proportional to the drive strength η on the qubit. As shown in Fig. 3b, with a drive amplitude of 1.67 × 10⁻⁵ mV/MHz, the slowest Rabi rate was only 2π × 0.27 MHz. When the drive amplitude was increased by 7.1 times to 1.11 × 10⁻⁴ mV/MHz, the Rabi rate reached 2π × 68.04 MHz, which increased by around 250 times. The qubit also experiences an ac-Stark shift around 1.6 times of its anharmonicity. The Rabi rate Ω(V_d) and the ac-Stark shift Δω(V_d) as a function of drive strength V_d are fitted simultaneously with a single free parameter k, which relates the room temperature and cryogenic drive voltages:

$$\left\{\begin{array}{ll}\Delta \omega ({V}_{d}) &=2\alpha {(k\beta {V}_{d})}^{2}\\ \Omega ({V}_{d}) &=\frac{2}{3}\alpha {(k\beta {V}_{d})}^{3},\end{array}\right.$$

(6)

where the transmon self-Kerr α and β are known parameters measured using qubit spectroscopy. In Fig. 3b, the ac-Stark shift is normalized by the transmon anharmonicity α and the data fit well with the fitting function, with k = 2π × 1.25 × 10³ MHz/mV. The data point with the highest drive amplitude is plotted but not used in the fitting. In general, the details of the qubit response at the very strongest drives, here with a Rabi rate approaching the qubit anharmonicity, is subject to a number of complicating factors and requires further investigation in future work.

These Rabi experiments demonstrate subharmonic driving can perform fast controls on quite standard transmon qubits. To use this scheme practically, we also need to develop a procedure for calibrating a high-fidelity single-qubit gate with well-defined parameters. For on-resonance driving, both deterministic tune-up³¹ and randomized benchmarking procedures have been well developed⁵. However, these procedures cannot be directly applied to subharmonic gates tune-up without first addressing the issue of drive-induced frequency shift. When the generator frame and the qubit frame are rotating at different speeds, phase tracking is required. In the case of subharmonic driving, as shown in Eq. (2) and Fig. 3, the qubit frequency is shifted. Therefore, the qubit frame rotates at a different speed relative to the generator frame during the drive and effectively adds a phase shift φ_i to the qubit. Such phase shift can be calculated as

$${\varphi }_{i}=\int_{{t}_{i}}^{{t}_{i+1}}{\omega }_{q}+\Delta \omega (t)-3{\omega }_{d}(t)dt,$$

(7)

where t_i and t_i+1 are the starting time and ending times of gate i. One way to correct the phase shift is by applying a virtual-Z gate after the pulse³². Alternately, we can apply a time-varying frequency modulation to the pulse, which changes the instantaneous frequency of the pulse based on the qubit’s ac-Stark shift. Ideally, a frequency-modulated pulse can always satisfy 3ω_d(t) = ω_q + Δω(t), which makes phase tracking unnecessary. However, in experiments, we found that phase tracking is usually still required to remove residual errors over many pulses.

Additionally, applying a fixed-frequency pulse with large ac-Stark shifts can cause direct excitation to non-computational states. For example, as shown in Fig. 4a, when the qubit is prepared in the ground state and driven at fixed frequency ω_d = ω_q/3 + δ, the gf/6 process can be activated during the ramp up/down period of a pulse if the detune δ is larger than one sixth of the transmon anharmonicity α. By following the transmon frequency during a drive, chirped pulses avoid directly crossing and activating unwanted processes, and thus reduce leakage. Figure 4b shows the Rabi experiment with frequency modulation using a quadratic model Δω = 2α∣η∣², as predicted by the 4^th-order truncated Hamiltonian. The ac-Stark shift of the transmon is mostly removed. The remaining distortion of the Rabi fringes arises primarily from imperfect pulse envelopes and the mismatch of instantaneous frequency and drive amplitude. We can reduce the distortion by performing pulse envelope correction and including higher-order Hamiltonian terms to obtain a more accurate modulation model.

Fig. 4: Amplitude-dependent frequency modulation of the drive frequency.

a With the drive frequency following the ac-Stark shift of the transmon (red trace), a frequency chirped pulse is always resonant with the subharmonic process. Compared with fixed-frequency drive (blue trace), it avoids directly crossing other processes. b A power Rabi experiment with frequency chirping. The frequency axis here is the initial frequency of the pulse.

To benchmark our subharmonic single qubit gates, we choose the usual π and π/2 rotation over the X, Y, and Z axes as the basic operations. Rotation about the Z axis is realized through VZ gate, which has no cost and fidelity close to one³². For the X and Y gates, the drive amplitude needs to be balanced between errors due to qubit decay, leakage to non-computational states, hardware limitations, and other factors. Because of control hardware limitations, we found best results when performing rotations of π and π/2 with 50.9 ns and 37.4 ns long smoothed flat-top pulses. The details of a gate sequence-based calibration procedure that calibrates each parameter are explained in Supplement Sec. II C.

Randomized benchmarking and interleaved randomized benchmarking^33,34,35 are used to calibrate the average fidelity of all Clifford gates and the fidelity of specific gates, including X, $\sqrt{X}$, Y and $\sqrt{Y}$ gates. The fidelity of the interleaved gate is calculated using³⁵,

$$1-F=\frac{1-{p}_{{{{\rm{gate}}}}}/{p}_{{{{\rm{ref}}}}}}{2}.$$

(8)

As shown in Fig. 5, the average Clifford gate fidelity is 99.604(9)%, and the gate fidelities of X, $\sqrt{X}$, Y, and $\sqrt{Y}$ are 99.79(1)%, 99.91(1)%, 99.76(2)%, 99.91(1)% respectively. To maintain this fidelity, a stable environment for room-temperature control hardware is crucial. The subharmonic gates are three times more sensitive to the amplitude and phase drift than resonant gates, because of the Rabi rate’s cubic dependence on drive amplitude. To reduce pulse parameter drifting, we stabilized the room-temperature equipment’s environment by sealing it in a PID controlled temperature stabilizing box, which is discussed in detail in Methods and Supplement Sec. II D.

Fig. 5: Randomized gate benchmarking.

Gate fidelities are calibrated with randomized and interleaved randomized benchmarking. The red trace shows the average fidelity of Clifford gates using subharmonic driving. The green and blue traces show the average fidelity of random sequences with a specific interleaved Clifford gate (X and $\sqrt{X}$ here), respectively, and are used to extract the fidelities of individual gates.

Potential for reduced heating and fast subharmonic gates

We have shown experimentally that a subharmonic drive can perform fast and high-fidelity single qubit control, and found theoretically that strong couplings to low-frequencies are not associated with enhanced qubit losses. Of far greater concern is the behavior of the low-pass filter, which protects the qubit. The filter’s figures of merit are the absorptive losses in reflection and insertion loss at the qubit’s transition frequency (which protect the qubit from the environment noise and Purcell decay into the filter) and the losses in transmission at the drive frequency (which contribute to cryostat heating).

Measurements of the filter used in this experiment (Mini-circuits ZLSS-A2R8G-S+) at room temperature show that the impedance is 6.66 − 123.3i Ω at the qubit g − e frequency ω_q. By performing the finite element simulation using Ansys HFSS, we estimate that the filter reduces the decay rate through the qubit port at ω_q from κ(ω_q)/2π = 0.55 kHz to κ_LPF(ω_q)/2π = 18.2 Hz. The subharmonic decay rate κ_sub is much smaller than κ_LPF and can be neglected. To verify the performance of the LPF, we measured three qubits with lowpass filters on the qubit drive port and one qubit without the filter. These four qubits were fabricated on the same wafer, went through the same fabrication processes and had similar design. Therefore, their coherence times should be similar. Although the improvement of the qubit coherence times are not as good as theory predicts, we still see a clear improvement (see Supplement Sec. II A). The discrepancy is likely due to the loss and electrical length of the cable between the qubit and the filter. A low loss on-chip filter^36,37 could further reduce photon loss and improve filter protection.

Subharmonic driving also offers new possibilities to address cryostat and component heating. It is a common practice to attenuate the input signal by 60 dB or higher to reduce thermal noise to a very small residual photon occupancy in the drive lines at the readout resonator and qubit frequencies^38,39.

These attenuators put a heat load on the refrigerator and can become a limitation for near-term quantum machines. Because the heat load is usually limited by the cooling power at the base stage of the dilution refrigerator, we focus on the drive line configuration at the base stage. Figure 6 shows an estimate of the heat dissipated at the base stage of a dilution refrigerator with various drive line configurations. Because the drive power is also related to the coupling strength of the drive port to the qubit, the coupling strength is designed to limit the qubit lifetime to T₁ = 1 ms, which is estimated using finite element circuit modeling and filter data measured at room temperature. As shown in Fig. 6, with a conventional high-attenuation drive line, approximately -30 dBm of power is dissipated at the base stage to achieve a π-pulse time of 10 ns. The current limited cooling capacity of our dilution refrigerator ( ~ 10 μW at 20 mK) allows only tens of single-qubit drives in parallel before significantly heating the base stage. Moreover, the attenuator itself as a dissipative element can be heated and generate broadband thermal radiation in turn. Commercial attenuators have been shown to cool much slower than the typical experiment repetition rates, creating further complications¹³. It would be advantageous to simply remove these components.

Fig. 6: Resonant drive vs. subharmonic drive.

The heat dissipated at base stage vs. Rabi rate Ω with different input line configurations and driving methods is compared. Using the subharmonic drive method, the attenuators at base stage can be reduced and replaced with reflective filters. The coupling to drive lines limits qubit coherence time T₁ around 1 ms. Conventional resonant drives are shown as dashed lines, subharmonic drives are shown as solid lines.

As shown in Fig. 6, we compare conventional drive lines with a line that has 20 dB base attenuation and a LPF, which is close to our experiment configuration, and a line with 3 dB attenuation and a LPF at base. The configuration with 3 dB attenuation further alleviates the heat dissipation at the base stage by completely removing attenuators from the base plate. The remaining 3 dB attenuation represents our estimate of realistic losses on components other than RF attenuators, such as coaxial cables and Eccosorb filters, which dominate over the insertion loss of the LPF. Reducing the losses at the base stage allows us to take full advantage of subharmonic driving; at a Rabi rate of 50 MHz, heat dissipation for subharmonic drive configuration with 3 dB attenuation is reduced by around 20 dB relative to the conventional drive configuration, allowing 100 times more qubits to be controlled for the same dissipated power and realistic assumptions about the drive line configuration.

Discussion

In conclusion, we have shown that subharmonic driving is a new single-qubit control scheme with fast gate speed and high fidelity. By breaking the symmetry between drive and decay of a qubit in the frequency domain, we protect the qubit from resonant relaxation and control the qubit without any need for resonant access. In addition, the cubic dependence of the gate speed on the drive strength could reduce the heat dissipated during qubit driving for appropriately designed reflective drive lines.

In the experiment single-qubit gates with fidelity of 99.9% are realized. However, higher gate fidelity can be achieved. The gate time currently used to achieve 99.9% fidelity is much slower than the maximum Rabi rate that we measured in this experiment. This is because of the pulse distortion and imprecise control of FPGA hardware, we believe gate times of 10 ns or lower are possible to achieve. In addition, DRAG correction or other pulse engineering techniques^3,40,41 can be implemented to reduce gate error and improve gate speed. With moderate improvement in qubit coherence times and gate time of 10 ns, gate fidelities of 99.99% or higher are achievable, and, together with reduced cryostat heating, make subharmonic gates a compelling method for single-qubit control in future large-scale quantum computers.

Methods

Experiment setup

The metal block housing the qubit and cavity’s tube is made of Al-6061 alloy with a 4 mm diameter hollow tube and two coupling ports. One of the ports is coupled to the transmon for single qubit control. The other port is coupled to the resonator for the dispersive readout. The transmon qubit and the λ/2 stripline resonator are fabricated on a 421 μm thick sapphire substrate with around 200 nm Ta film except for the Josephson junction of the transmon, which is a Al/AlO_x/Al junction.

The experiment setup is shown in the Supplementary Fig. 11. We used a low-pass filter, Mini-circuits ZLSS-A2R8G-S+, to protect the qubit and perform subharmonic drives. The sample is mounted on the base plate of the dilution refrigerator, which is operated at around 20 mK. The qubit driving pulses and readout pulses are generated by direct digital synthesis (DDS) using the Xilinx RFSoC ZCU216 based on the QICK⁴². For the qubit drive, before the signal is sent to the sample, a small fraction is split using a directional coupler, then sent back to the digitizer for monitoring pulse stability.

Temperature stabilization

The performance of room temperature electronics depends on their operating status and environment. For example, the gain of a power amplifier changes as environment temperature changes. In monitoring our pulse properties, we found the operating temperature, which is regularly perturbed by air-conditioning cycles in the room air, has the most significant effect on our system performance. A clear dependence on devices’ temperature can be observed, As shown in the supplement Sec. II D, While a few percents of relative variation in power and phase can often be ignored in simple one or two pulse protocols, such as T₁ or T₂ measurements, it is a limiting factor for high-fidelity quantum control, and it is important for building a stable quantum computer without frequent pulse calibration. Also, this is especially important for subharmonic driving, since it is three times more sensitive to the fluctuation of pulses’ magnitude and phase.