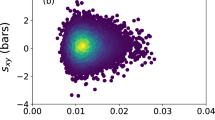
Abstract
Elucidating mechanical deformation in glassy materials at the atomic level is challenging due to their disordered atomic structure. Using our frozen-atom analysis of the simulation data, we reveal that anelastic deformation in CuZr metallic glasses is fundamentally driven by cooperative atomic motions of tens of atoms elastically linked to one another, forming trigger groups. They initiate localized rearrangements, which can cascade into plastic flow. These cores show no clear structural or elastic precursors in the initial configuration, challenging the idea that deformation occurs in defective regions. Instead, deformation events are highly stochastic and transient, driven by collective atomic motion. This finding not only reshapes our understanding of glassy material deformation mechanisms but also highlights cooperative motion as a key factor in avalanche-like phenomena governing the behavior of disordered systems across multiple scales.
Similar content being viewed by others
Data availability
The data underlying the figures, including atomic structure data and associated derived quantities, have been deposited in Zenodo with DOI 10.5281/zenodo.1795899458. The complete set of atomic configurations exceeds 1 TB and cannot be deposited in a public repository due to size limitations. These data are preserved by the authors and may be accessed for non-commercial academic research by contacting the corresponding author (shiihara@toyota-ti.ac.jp). Requests will receive a response within 2 weeks, and the data will remain available for at least 5 years after publication.
Code availability
The implementations of the frozen-atom analysis are available in a Code Ocean capsule at DOI 10.24433/CO.2573501.v159.
References
Greer, A., Cheng, Y. & Ma, E. Shear bands in metallic glasses. Mater. Sci. Eng. R: Rep. 74, 71 (2013).
Nicolas, A., Ferrero, E. E., Martens, K. & Barrat, J.-L. Deformation and flow of amorphous solids: insights from elastoplastic models. Rev. Mod. Phys. 90, 045006 (2018).
Richard, D. et al. Predicting plasticity in disordered solids from structural indicators. Phys. Rev. Mater. 4, 113609 (2020).
Hansen, N. Hall–Petch relation and boundary strengthening. Scr. Mater. 51, 801 (2004).
Meyers, M., Mishra, A. & Benson, D. Mechanical properties of nanocrystalline materials. Prog. Mater. Sci. 51, 427 (2006).
Johnson, W. L. & Samwer, K. A universal criterion for plastic yielding of metallic glasses with a \({(T/{T}_{g})}^{2/3}\) temperature dependence. Phys. Rev. Lett. 95, 195501 (2005).
Argon, A. & Kuo, H. Plastic flow in a disordered bubble raft (an analog of a metallic glass). Mater. Sci. Eng. 39, 101 (1979).
Delogu, F. Effects of compression cycles on the atomic mobility in metallic glasses. Phys. Rev. B 79, 064205 (2009).
Liu, Z. Y. et al. Temperature dependent dynamics transition of intermittent plastic flow in a metallic glass. II. Dynamics analysis. J. Appl. Phys. 114, 033521 (2013).
Shang, B. S., Li, M. Z., Yao, Y. G., Lu, Y. J. & Wang, W. H. Evolution of atomic rearrangements in deformation in metallic glasses. Phys. Rev. E 90, 042303 (2014).
L, M. & Sen Gupta, B. Characteristics and correlations of nonaffine particle displacements in the plastic deformation of athermal amorphous materials. Soft Matter 18, 8626 (2022).
Adam, G. & Gibbs, J. H. On the temperature dependence of cooperative relaxation properties in glass-forming liquids. J. Chem. Phys. 43, 139 (1965).
Cohen, M. H. & Grest, G. S. The nature of the glass transition. J. Non-Cryst. Solids 61–62, 749 (1984).
Blackburn, F., Cicerone, M. T., Hietpas, G., Wagner, P. A. & Ediger, M. Cooperative motion in fragile liquids near the glass transition: probe reorientation in o-terphenyl and polystyrene. J. Non-Cryst. Solids 172–174, 256 (1994).
Donati, C. et al. Stringlike cooperative motion in a supercooled liquid. Phys. Rev. Lett. 80, 2338 (1998).
Zhang, H. et al. Role of string-like collective atomic motion on diffusion and structural relaxation in glass forming Cu–Zr alloys. J. Chem. Phys. 142, 164506 (2015).
Jaiswal, A. et al. Onset of cooperative dynamics in an equilibrium glass-forming metallic liquid. J. Phys. Chem. B 120, 1142 (2016).
Falk, M. L. & Langer, J. S. Dynamics of viscoplastic deformation in amorphous solids. Phys. Rev. E 57, 7192 (1998).
Sethna, J. P., Dahmen, K. A. & Myers, C. R. Crackling noise. Nature 410, 242 (2001).
Antonaglia, J. et al. Bulk metallic glasses deform via slip avalanches. Phys. Rev. Lett. 112, 155501 (2014).
Antonaglia, J. et al. Tuned critical avalanche scaling in bulk metallic glasses. Sci. Rep. 4, 4382 (2014).
Malandro, D. L. & Lacks, D. J. Molecular-level mechanical instabilities and enhanced self-diffusion in flowing liquids. Phys. Rev. Lett. 81, 5576 (1998).
Maloney, C. E. & Lemait̂re, A. Amorphous systems in athermal, quasistatic shear. Phys. Rev. E 74, 016118 (2006).
Berthier, L. & Kob, W. Static point-to-set correlations in glass-forming liquids. Phys. Rev. E 85, 011102 (2012).
Barbot, A. et al. Local yield stress statistics in model amorphous solids. Phys. Rev. E 97, 033001 (2018).
Bhowmik, B. P., Chaudhuri, P. & Karmakar, S. Effect of pinning on the yielding transition of amorphous solids. Phys. Rev. Lett. 123, 185501 (2019).
Xu, D., Zhang, S., Liu, A. J., Nagel, S. R. & Xu, N. Discontinuous instabilities in disordered solids. Proc. Natl. Acad. Sci. USA 120, e2304974120 (2023).
Cheng, Y. & Ma, E. Atomic-level structure and structure–property relationship in metallic glasses. Prog. Mater. Sci. 56, 379 (2011).
Egami, T. & Srolovitz, D. Local structural fluctuations in amorphous and liquid metals: a simple theory of the glass transition. J. Phys. F: Met. Phys. 12, 2141 (1982).
Fan, Y., Iwashita, T. & Egami, T. Evolution of elastic heterogeneity during aging in metallic glasses. Phys. Rev. E 89, 062313 (2014).
Lieou, C. K. C. & Egami, T. Relevance of structural defects to the mechanism of mechanical deformation in metallic glasses. Sci. Rep. 13, 15979 (2023).
Iwashita, T., Nicholson, D. M. & Egami, T. Elementary excitations and crossover phenomenon in liquids. Phys. Rev. Lett. 110, 205504 (2013).
Langer, J. S. Dynamics of shear-transformation zones in amorphous plasticity: formulation in terms of an effective disorder temperature. Phys. Rev. E 70, 041502 (2004).
Iwashita, T. & Egami, T. Atomic mechanism of flow in simple liquids under shear. Phys. Rev. Lett. 108, 196001 (2012).
Wei, D. et al. Revisiting the structure–property relationship of metallic glasses: common spatial correlation revealed as a hidden rule. Phys. Rev. B 99, 014115 (2019).
Wei, D. et al. Assessing the utility of structure in amorphous materials. J. Chem. Phys. 150, 114502 (2019).
Bapst, V. et al. Unveiling the predictive power of static structure in glassy systems. Nat. Phys. 16, 448 (2020).
Dahmen, K. A., Ben-Zion, Y. & Uhl, J. T. Micromechanical model for deformation in solids with universal predictions for stress–strain curves and slip avalanches. Phys. Rev. Lett. 102, 175501 (2009).
Dahmen, K. A., Ben-Zion, Y. & Uhl, J. T. A simple analytic theory for the statistics of avalanches in sheared granular materials. Nat. Phys. 7, 554 (2011).
Uhl, J. T. et al. Universal quake statistics: from compressed nanocrystals to earthquakes. Sci. Rep. 5, 16493 (2015).
Thompson, A. P. et al. LAMMPS—a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 271, 108171 (2022).
Cheng, Y. Q., Ma, E. & Sheng, H. W. Atomic level structure in multicomponent bulk metallic glass. Phys. Rev. Lett. 102, 245501 (2009).
Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 81, 511 (1984).
Hoover, W. G. Canonical dynamics: equilibrium phase-space distributions. Phys. Rev. A 31, 1695 (1985).
Nakamura, T., Kawamoto, S. & Shinoda, W. Precise calculation of the local pressure tensor in Cartesian and spherical coordinates in LAMMPS. Comput. Phys. Commun. 190, 120 (2015).
Lobzenko, I., Shiihara, Y., Iwashita, T. & Egami, T. Shear softening in a metallic glass: first-principles local-stress analysis. Phys. Rev. Lett. 124, 085503 (2020).
Yang, Z.-Y., Wei, D., Zaccone, A. & Wang, Y.-J. Machine-learning integrated glassy defect from an intricate configurational-thermodynamic-dynamic space. Phys. Rev. B 104, 064108 (2021).
Cubuk, E. D. et al. Identifying structural flow defects in disordered solids using machine-learning methods. Phys. Rev. Lett. 114, 108001 (2015).
Baggioli, M., Kriuchevskyi, I., Sirk, T. W. & Zaccone, A. Plasticity in amorphous solids is mediated by topological defects in the displacement field. Phys. Rev. Lett. 127, 015501 (2021).
Wakeda, M., Shibutani, Y., Ogata, S. & Park, J. Relationship between local geometrical factors and mechanical properties for Cu–Zr amorphous alloys. Intermetallics 15, 139 (2007).
Jin, W., Datye, A., Schwarz, U. D., Shattuck, M. D. & O’Hern, C. S. Using delaunay triangularization to characterize non-affine displacement fields during athermal, quasistatic deformation of amorphous solids. Soft Matter 17, 8612 (2021).
Lobzenko, I., Tsuru, T., Shiihara, Y. & Iwashita, T. First-principles atomic level stresses: application to a metallic glass under shear. Mater. Res. Express 10, 085201 (2023).
Tsamados, M., Tanguy, A., Goldenberg, C. & Barrat, J.-L. Local elasticity map and plasticity in a model Lennard–Jones glass. Phys. Rev. E 80, 026112 (2009).
Şopu, D., Stukowski, A., Stoica, M. & Scudino, S. Atomic-level processes of shear band nucleation in metallic glasses. Phys. Rev. Lett. 119, 195503 (2017).
Richard, D., Kapteijns, G., Giannini, J. A., Manning, M. L. & Lerner, E. Simple and broadly applicable definition of shear transformation zones. Phys. Rev. Lett. 126, 015501 (2021).
Dasgupta, R., Hentschel, H. G. E. & Procaccia, I. Microscopic mechanism of shear bands in amorphous solids. Phys. Rev. Lett. 109, 255502 (2012).
Fan, Z. & Ma, E. Predicting orientation-dependent plastic susceptibility from static structure in amorphous solids via deep learning. Nat. Commun. 12, 1506 (2021).
Shiihara, Y., Iwashita, T., Todaka, T., Adachi, N. & Egami, T. Data for: cooperative atomic motion during shear deformation in metallic glass. Zenodo https://doi.org/10.5281/zenodo.17958994 (2025).
Shiihara, Y., Iwashita, T., Todaka, T., Adachi, N. & Egami, T. Frozen-atom analysis code. Code Ocean https://doi.org/10.24433/CO.2573501.v1 (2025).
Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO—the open visualization tool. Model. Simul. Mater. Sci. Eng. 18, 015012 (2009).
Acknowledgements
This work was supported by Grant-in-Aid for Transformative Research Areas B, “Rheology of disordered structures: establishing Anankeon dynamics", JSPS KAKENHI Grant Numbers 22B206, 22H05041, 22H05042, 22H05040, and 23K28105. T.E. was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division.
Author information
Authors and Affiliations
Contributions
Y.S. and T.I. conceived the research. Y.S. developed the modeling framework. Y.S. and T.I. performed the simulations and conducted the data analysis. Y.S. and T.E. developed further interpretation of the data and wrote the manuscript. N.A. and Y.T. provided advice on the physics of the system. All the authors discussed the results and contributed to the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Yun-Jiang Wang and the other anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Shiihara, Y., Iwashita, T., Adachi, N. et al. Cooperative atomic motion during shear deformation in metallic glass. Nat Commun (2026). https://doi.org/10.1038/s41467-026-68308-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-026-68308-4