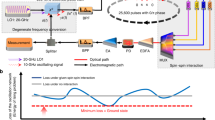
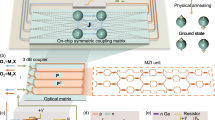
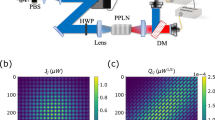
Abstract
Time-multiplexed networks of degenerate optical parametric oscillators have demonstrated remarkable success in simulating coupled Ising spins, thus providing a promising route to solving complex combinatorial optimization problems. In these systems, referred to as coherent Ising machines, spins are encoded in the oscillator phases, and measured at the system output using phase-sensitive techniques, making intricate phase stabilization necessary. Here, we introduce an optical Ising machine based on spontaneous polarization symmetry breaking in a coherently driven fiber Kerr nonlinear resonator. In our architecture, the spins are encoded in the polarization state, allowing robust, all-intensity readout with off-the-shelf telecom components. By operating in a newly-discovered regime where nonlinearity and topology lock the system’s symmetry, we eliminate drift and bias, enabling uninterrupted Ising trials at optical speeds for over an hour, without manual intervention. This all-fiber platform not only simplifies the hardware but also opens a path to more stable, high-throughput coherent optical optimization devices for applications from finance to drug design and beyond.
Similar content being viewed by others
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon request.
Code availability
The code that supports the plots within this paper and other findings of this study are available from the corresponding author upon request.
References
Lucas, A. Ising formulations of many NP problems. Front. Phys. 2, 5 (2014).
Perdomo-Ortiz, A., Dickson, N., Drew-Brook, M., Rose, G. & Aspuru-Guzik, A. Finding low-energy conformations of lattice protein models by quantum annealing. Sci. Rep. 2, 571 (2012).
Tanahashi, K., Takayanagi, S., Motohashi, T. & Tanaka, S. Application of Ising machines and a software development for Ising machines. J. Phys. Soc. Jpn. 88, 061010 (2019).
Matsubara, S. et al. Digital annealer for high-speed solving of combinatorial optimization problems and its applications, In 2020 25th Asia and South Pacific Design Automation Conference (ASP-DAC), 667–672 (IEEE, 2020).
Crawford, D., Levit, A., Ghadermarzy, N., Oberoi, J. S. & Ronagh, P. Reinforcement learning using quantum Boltzmann machines. Quantum Inf. Comput. 18, 51–74 (2018).
Hauke, P., Bonnes, L., Heyl, M. & Lechner, W. Probing entanglement in adiabatic quantum optimization with trapped ions. Front. Phys. 3, 21 (2015).
Pagano, G. et al. Quantum approximate optimization of the long-range Ising model with a trapped-ion quantum simulator. Proc. Natl. Acad. Sci. USA 117, 25396–25401 (2020).
Barends, R. et al. Digitized adiabatic quantum computing with a superconducting circuit. Nature 534, 222–226 (2016).
Chou, J., Bramhavar, S., Ghosh, S. & Herzog, W. Analog coupled oscillator based weighted Ising machine. Sci. Rep. 9, 14786 (2019).
Pierangeli, D., Marcucci, G. & Conti, C. Large-scale photonic Ising machine by spatial light modulation. Phys. Rev. Lett. 122, 213902 (2019).
Dutta, S. et al. An Ising Hamiltonian solver based on coupled stochastic phase-transition nano-oscillators. Nat. Electron. 4, 502–512 (2021).
Jin, Y. et al. A Kerr soliton Ising machine for combinatorial optimization problems.Preprint at arXiv https://doi.org/10.48550/arXiv.2508.00810 (2025).
Wang, Z., Marandi, A., Wen, K., Byer, R. L. & Yamamoto, Y. Coherent Ising machine based on degenerate optical parametric oscillators. Phys. Rev. A 88, 063853 (2013).
Barahona, F., Grötschel, M., Jünger, M. & Reinelt, G. An application of combinatorial optimization to statistical physics and circuit layout design. Oper. Res. 36, 493–513 (1988).
Kanamaru, S. et al. Efficient Ising model mapping to solving slot placement problem, In 2019 IEEE International Conference on Consumer Electronics (ICCE), (2019).
Marandi, A., Wang, Z., Takata, K., Byer, R. L. & Yamamoto, Y. Network of time-multiplexed optical parametric oscillators as a coherent Ising machine. Nat. Photon. 8, 937–942 (2014).
Inagaki, T. et al. A coherent Ising machine for 2000-node optimization problems. Science 354, 603–606 (2016).
McMahon, P. L. et al. A fully programmable 100-spin coherent Ising machine with all-to-all connections. Science 354, 614–617 (2016).
Clements, W. R. et al. Gaussian optical Ising machines. Phys. Rev. A 96, 043850 (2017).
Wang, T., Wu, L., Nobel, P. & Roychowdhury, J. Solving combinatorial optimisation problems using oscillator based Ising machines. Nat. Comput. 20, 287–306 (2021).
Inagaki, T. et al. Large-scale Ising spin network based on degenerate optical parametric oscillators. Nat. Photon. 10, 415–419 (2016).
Honjo, T. et al. 100,000-spin coherent Ising machine. Sci. Adv. 7, eabh0952 (2021).
Takesue, H. & Inagaki, T. 10 GHz clock time-multiplexed degenerate optical parametric oscillators for a photonic Ising spin network. Opt. Lett. 41, 4273–4276 (2016).
Hamerly, R. et al. Experimental investigation of performance differences between coherent Ising machines and a quantum annealer. Sci. Adv. 5, eaau0823 (2019).
Böhm, F., Verschaffelt, G. & Van der Sande, G. A poor man’s coherent Ising machine based on opto-electronic feedback systems for solving optimization problems. Nat. Commun. 10, 3538 (2019).
Haelterman, M., Trillo, S. & Wabnitz, S. Polarization multistability and instability in a nonlinear dispersive ring cavity. J. Opt. Soc. Am. B 11, 446–456 (1994).
Garbin, B. et al. Asymmetric balance in symmetry breaking. Phys. Rev. Res. 2, 023244 (2020).
Garbin, B. et al. Dissipative polarization domain walls in a passive coherently driven Kerr resonator. Phys. Rev. Lett. 126, 023904 (2021).
Coen, S. et al. Nonlinear topological symmetry protection in a dissipative system. Nat. Commun. 15, 1398 (2024).
Quinn, L. et al. Random number generation using spontaneous symmetry breaking in a Kerr resonator. Opt. Lett. 48, 3741–3744 (2023).
Casilli, N. et al. Floquet-based Ising machines escape local minima in QUBO problems. Res. Sq. 10.21203/rs.3.rs-6870975/v1 (2025).
Fatome, J. et al. Temporal manipulation of period-2 polarization domain wall solitons in a nonlinear fiber Kerr resonator. Opt. Commun. 537, 129810 (2023).
Yamamoto, Y. et al. Coherent Ising machines—optical neural networks operating at the quantum limit. npj Quantum Inf. 3, 49 (2017).
Böhm, F., Van Vaerenbergh, T., Verschaffelt, G. & Van der Sande, G. Order-of-magnitude differences in computational performance of analog Ising machines induced by the choice of nonlinearity. Commun. Phys. 4, 149 (2021).
Syed, M. & Berloff, N. G. Physics-enhanced bifurcation optimisers: All you need is a canonical complex network. IEEE J. Sel. Top. Quantum Elec. 29, 7400406 (2023).
Haribara, Y., Ishikawa, H., Utsunomiya, S., Aihara, K. & Yamamoto, Y. Performance evaluation of coherent Ising machines against classical neural networks. Quantum Sci. Technol. 2, 044002 (2017).
Leleu, T. et al. Scaling advantage of chaotic amplitude control for high-performance combinatorial optimization. Commun. Phys. 4, 266 (2021).
Shokraneh, F., Geoffroy-Gagnon, S. & Liboiron-Ladouceur, O. The diamond mesh, a phase-error- and loss-tolerant field-programmable MZI-based optical processor for optical neural networks. Opt. Express 28, 23495–23508 (2020).
Gray, R. M. et al. Large-scale time-multiplexed nanophotonic parametric oscillators. Newton 1, 100108 (2025).
Fujiwara, M. et al. Optical carrier supply module using flattened optical multicarrier generation based on sinusoidal amplitude and phase hybrid modulation. J. Lightwave Technol. 21, 2705–2714 (2003).
Nielsen, A. U., Garbin, B., Coen, S., Murdoch, S. G. & Erkintalo, M. Emission of intense resonant radiation by dispersion-managed Kerr cavity solitons. APL Photonics 3, 120804 (2018).
Haelterman, M. Ikeda instability and transverse effects in nonlinear ring resonators. Opt. Commun. 100, 389–398 (1993).
Menyuk, C. Pulse propagation in an elliptically birefringent Kerr medium. IEEE J. Quantum Elec. 25, 2674–2682 (1989).
Agrawal, G. P. Nonlinear Fiber Optics, 5th ed. (Academic Press, 2013).
Acknowledgements
We acknowledge the financial support provided by The Royal Society of New Zealand in the form of Marsden Funding (18-UOA-310 and 23-UOA-053). Additional financial contributions were kindly provided by CNRS through the IRP Wall-IN project and the Conseil Régional de Bourgogne Franche-Comté.
Author information
Authors and Affiliations
Contributions
L.Q. performed all of the experiments with the assistance of Y.X. Numerical simulations were completed by L.Q. with the help of S.C. and M.E. The first draft was written by L.Q. with subsequent editing and review completed by M.E. and S.C. The theory and concept were developed by G.O., J.F., M.E. and S.C. Additional support and supervision were provided by S.G.M. The overall project was supervised by M.E and S.C.
Corresponding author
Ethics declarations
Competing interests
The authors declare no conflicts of interest.
Peer review
Peer review information
Nature Communications thanks Alessia Pasquazi, and Guy Verschaffelt their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Quinn, L., Xu, Y., Fatome, J. et al. Coherent Ising machine based on polarization symmetry breaking in a driven Kerr resonator. Nat Commun (2026). https://doi.org/10.1038/s41467-026-68794-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-026-68794-6