Introduction

Brain aging is a complex and multifaceted process caused by the loss of neural circuits and synaptic plasticity, which is associated with cognitive decline and structural changes1. These changes are often associated with an increased susceptibility to neurodegenerative diseases2 including Alzheimer’s disease3 (AD), Parkinson’s disease4, and Huntington’s disease5. Structural and functional alterations associated with neurodegenerative diseases are currently considered largely irreversible. Furthermore, validated diagnostic biomarkers remain scarce; while a few exist for diseases with a known genetic etiology6, those for sporadic forms are only beginning to develop or gain early regulatory approval7,8. AD develops at the culmination of a chronic pathophysiological process, with preclinical stages appearing decades earlier in life9. Therefore, understanding the links between brain aging process and the mechanism of neurodegenerative disease can significantly improve the early detection of these conditions.

Moreover, AD is believed to be a slowly evolving process that begins years to decades prior to the appearance of clinical symptoms10. This highlights the need of a cheap and efficient biomarker for AD and brain aging. Underlying structural changes may exist even in cognitively unimpaired individuals, and longitudinal studies using structural magnetic resonance imaging (MRI) indicate indicates these changes are associated with an increased risk of cognitive decline3,11. A novel biomarker to measure subtle changes of the brain structure can help the detection and early intervention of AD. While brain aging itself is a primary risk factor for the onset of these debilitating conditions, the exact mechanisms underlying the transition from normal brain aging to pathological neurodegeneration remain unclear.

Advanced neuroimaging tools allowed delineation of complex structural and functional changes of the brain12. MRI is a noninvasive structural imaging tool of the brain that is routinely used for both research and clinical purposes. While high-resolution T1 weighted MRI scans maximize the contrast difference between components of the brain and are commonly used to study brain structure12, 2D MRI scans commonly available in clinical practice are essential for the diagnosis and monitoring of various brain conditions. In clinical practice, radiologists and clinicians identify brain atrophy by visually assessing the enlargement of the lateral ventricles, the sulcal widening between gyri, and the width of the temporal horn around the hippocampus, which increase linearly with age in healthy subjects, irrespective of sex13. However, these visual assessments lack accuracy compared to quantitative analyses due to the absence of objective metrics. Consequently, there is a need for accessible quantitative method to analyze dynamics of changes in the aging brain using 2D T1 imaging in clinical practice.

Recently, the term ‘brain age’ is widely being used as the predicted age from structural MRI scans of the brain14,15. The development of deep learning models allowed model architectures that perform well on natural images to be applied on domain-specific tasks. Most notably, convolutional neural network (CNN) models showed good performance on MRI scans14,16. A positive brain age gap or delta, defined as the age difference between predicted brain age and chronological age, is shown to indicate deviation from healthy aging in multiple studies17,18. Research-grade 3D T1 weighted MRI scans are mainly used to train brain age prediction models16. Only recently the importance of models targeted to two dimensional (2D) MRI scans more commonly used in clinical settings were highlighted19,20,21. However, these models were trained using in-house 2D MRI scans, and focused on modalities other than T1 weighted images19 or T1 weighted images of healthy children aged 0 to 5 years old21. When a 2D CNN architecture (VGG1622)-based brain age model trained successfully with 3D T1 weighted brain MRI scans23 was applied to 2D T1 weighted scans, it showed significant brain age bias and mean absolute error (MAE) of 8.12 [7.19, 9.29] years even after age bias correction20. Another study suggested an alternative approach to train the same VGG16-based brain age prediction model23 by using a mixture of actual research-grade 3D MRI scans and synthetic 1 mm isotropic MP-RAGE from clinical 2D MRI scans of various modalities24. Although the model failed to predict brain age of clinical MRIs accurate enough for clinical use, the study demonstrated that it is feasible to incorporate research-grade and clinical MRI scans for model training. Therefore, to accurately train the brain age prediction model targeted for clinical 2D T1 weighted MRI scans, development of both the model and an adequate MRI scan preprocessing pipeline for training are required.

In this study, we aim to build a 3D CNN based brain age prediction model specialized for clinical 2D axial T1 weighted MRI scans, by training it with publicly available research grade 3D T1 weighted MRI scans. To achieve this, we created a novel preprocessing pipeline that first slices research grade 3D scans into 2D axial scans, then interpolates the 2D axial scans back into 3D scans to use for training. This is intended to overcome the heterogenic nature of 2D axial scans caused by the larger slice thickness compared to other dimensions. We then tested the model on an independent test set of actual clinical 2D scans from healthy subjects. When the model is applied on actual clinical 2D scans, the scans are again interpolated into 3D scans. Finally, the model was tested on neurodegenerative disease cohorts to evaluate the association of brain age gap with different stages of neurodegenerative diseases.

Results

Training brain age prediction model with research grade 3D MRI scans

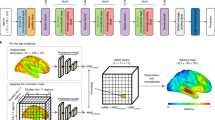
The biggest challenge of training models intended for clinical grade 2D MRI scans is the lack of publicly available routine clinical 2D MRI datasets. To overcome this problem, we collected 8681 research grade 3D MRI scans from the Samsung Medical Center (SMC) and 24 publicly available datasets (age mean ± SD: 51.76 ± 21.74, range: 16.22–95) and sliced the scans with axial gaps larger than 7 mm to mimic clinical grade 2D scans. The overall framework for training the model using 3D MRI scans and applying it to routine clinical 2D MRI scans are shown in Fig. 1.

Fig. 1: Brain age prediction model architecture and overall research framework.
figure 1

a The age prediction model is based on the 3D version of DenseNet-169. b The process for creating the training dataset from research grade 3D T1-weighted MRI scans. The 3D scans are first sliced to generate synthetic 2D axial scans, then interpolated back into a common 3D voxel space. c Applying the trained model to inference brain age of actual clinical-grade 2D T1-weighted MRI scans. The 2D scans are interpolated into 3D scans for initial brain age prediction, then age bias correction is applied to produce the final prediction.

Full size image

The 3D DenseNet-169 based model for brain age prediction was successfully trained using interpolated 2D axial T1-weighted MRI scans created from slicing research grade 3D T1-weighted MRI scans (Fig. 2a). When the best model was selected using the validation dataset, MAE averaged over 5-fold cross-validation was 1.53 years with 95% CI [1.22, 1.84] and showed high correlation with chronological age (Pearson’s r = 0.996 [0.994, 0.998]) during training and MAE 3.66 years with 95% CI [3.50, 3.81], r = 0.974 [0.970, 0.978] during validation. The trained model demonstrated accurate brain age prediction for the test dataset with MAE 3.68 years with 95% CI [3.52, 3.83] and showed high correlation with chronological age (r = 0.973 [0.970, 0.977]) (Fig. 2b). Minimal brain age bias by chronological age was observed during the training process (Fig. 2c). When the MAE for the test dataset was compared across the source datasets, we observed minimal variation for the performance of the model indicating the model was able to generalize across different age groups or demographics (Supplementary Table 1).

Fig. 2: Training brain age prediction model using interpolated 2D axial T1-weighted MRI scans created from research grade 3D T1-weighted MRI scans.
figure 2

95% confidence intervals are shown with MAE averaged over 5-fold cross-validation. a The 3D DenseNet-169 based model was successfully trained using 3D scans interpolated from the 2D axial scans (Training dataset: 55,602 scans created from 6903 research grade 3D scans, training MAE = 1.53 years with 95% CI [1.22, 1.84], Pearson’s r = 0.996 [0.994, 0.998]). b The validation dataset was used for early stopping, and no further adjustments were made to the model output (Validation dataset: 7035 scans created from 863 research grade 3D scans, validation MAE = 3.66 [3.50, 3.81] years, r = 0.974 [0.970, 0.978]; Test dataset: 6961 scans created from 863 research grade 3D scans, test MAE = 3.68 [3.52, 3.83] years, r = 0.973 [0.970, 0.977]). c Minimal brain age gap bias by chronological age was observed.

Full size image

Clinical grade axial 2D T1-weighted MRI scans from SMC

The model also successfully predicted brain age from clinical grade axial 2D T1-weighted MRI scans of cognitively unimpaired subjects (Fig. 3a). For 175 axial 2D scans, the model achieved average 5-fold test MAE of 2.73 years with 95% CI [2.54, 2.92] after bias correction (r = 0.918 [0.901, 0.936]), and when using the ensemble of all 5 models from each CV runs the MAE was further reduced to 2.23 years. When applied to 199 axial 2D scans from patients diagnosed with AD, the model predicted positive brain age gap where mean corrected brain age gap was 3.10 [2.52, 3.67] years (Fig. 3b). Brain age gap was significantly higher in patients diagnosed with AD than cognitively unimpaired subjects (Fig. 3c; p < 0.001, Two sample Z-test). Brain age gap showed minimal brain age bias after linear bias correction (Fig. 3d), with mean corrected brain age gap of 0.09 [−0.66, 0.85] years. The trend of positive brain age gap was stronger in relatively younger individuals (Fig. 3e).

Fig. 3: Brain age prediction of clinical grade axial T1-weighted MRI scans (2D scans).
figure 3

95% confidence intervals across 5-fold cross-validation are shown with error bars. a When the trained model was tested on cognitively unimpaired individuals from an independent dataset from SMC, the model successfully predicted brain age after brain age bias correction using oldest and youngest 5% individuals (Test dataset: 175 2D axial scans, test MAE = 2.73 years with 95% CI [2.54, 2.92] after bias correction, Pearson’s r = 0.918 [0.901, 0.936]; when using ensemble of all 5 models from each CV runs - MAE = 2.23 years). b Individuals diagnosed with Alzheimer’s disease showed positive brain age gap and this trend was stronger in relatively younger individuals (CU: n = 175, mean corrected brain age gap = 0.09 [−0.66, 0.85] years; AD: n = 199, mean corrected brain age gap = 3.10 [2.52, 3.67] years). c Brain age gap was significantly higher in individuals diagnosed with AD compared to CU individuals (p < 0.001, Two sample Z-test). d Brain age gap in CU individuals after linear age bias correction. Dotted lines indicate 95% confidence bands of regression lines used in bias correction. e Brain age gap in individuals diagnosed with AD after age bias correction with coefficients learned from CU individuals.

Full size image

Guided backpropagation analysis showed that the model focus on cerebrospinal fluid (CSF) regions and their adjacent regions to predict brain age (Fig. 4a). This includes the lateral ventricle, the 3rd and 4th ventricles, and region involving the insula. For MRI scans from patients with Alzheimer’s disease, the model correctly overestimates brain age by focusing on the larger CSF volumes due to brain atrophy (Fig. 4b). Full visualization of the guided backpropagation analysis is shown in Supplementary Fig. 1.

Fig. 4: Visualization of brain age prediction model using guided backpropagation.
figure 4

Clinical grade axial T1-weighted MRI scans (2D scans) from (a) a cognitively unimpaired individual and (b) an individual diagnosed with Alzheimer’s disease were used. The model seems to focus on cerebrospinal fluid spaces and their adjacent regions including the lateral ventricle, 3rd and 4th ventricles, and region involving the insula.

Full size image

Brain age prediction on neurodegenerative disease cohorts

For the ADNI dataset, our model predicted brain age MAE of 2.05 years after age bias correction for cognitively unimpaired (CU) subjects with mean corrected brain age gap of 0.57 years (Fig. 5a). Brain age was then predicted for subjects in the mild cognitive impairment (MCI) and Alzheimer’s disease (AD) cohorts with bias correction using coefficients learned from the CU cohort. The cohorts showed significantly different mean brain age gap (p < 0.001, Welch’s ANOVA; brain age gap: 0.57 vs 2.15 vs 2.47 years in CU vs MCI vs AD cohorts). Further post hoc analysis showed the brain age gap of patients diagnosed with MCI or AD were significantly greater than CU subjects (p < 0.001, Pairwise Games–Howell test). Brain age gap was also significantly greater in patients with AD compared to patients with MCI (p < 0.05, Pairwise Games–Howell test).

Fig. 5: Brain age prediction on neurodegenerative disease cohorts.
figure 5

a The ADNI dataset contains brain MRI scans of cognitively unimpaired (CU; n = 6921), mild cognitive impairment (MCI), and Alzheimer’s disease (AD) cohorts. The cohorts showed significantly different mean brain age gap (p < 0.001, Welch’s ANOVA; brain age gap: 0.57 vs 2.15 vs 2.47 years in CU vs MCI vs AD cohorts). Brain age gap of patients diagnosed with MCI or AD were significantly greater than CU subjects (p < 0.001, Pairwise Games–Howell test). Brain age gap was significantly greater in patients with AD compared to patients with MCI (p < 0.05, Pairwise Games–Howell test). b The PPMI dataset contains brain MRI scans of cognitively unimpaired (CU), prodromal (PRO), and Parkinson’s disease (PD) cohorts. The cohorts showed significantly different mean brain age gap (p < 0.001, Welch’s ANOVA; brain age gap: 1.03 vs 1.42 vs 2.23 years in CU vs PRO vs PD cohorts). Brain age gap of patients in PRO or PD cohorts were significantly greater than CU subjects (p < 0.001, Pairwise Games–Howell test). Brain age gap was significantly greater in patients diagnosed with PD compared to patients in the PRO cohort (p < 0.01, Pairwise Games–Howell test). Dotted lines are drawn at the mean brain age gap values of each cohort.

Full size image

To study further clinical implications of the model, we tested correlations between predicted brain age gap and the Mini-Mental State Examination (MMSE) score in patients with AD. From 2D MRI scans of patients with AD obtained from SMC, we observed a significant negative correlation between brain age gap and MMSE score (Supplementary Fig. 2a; r = -0.25, p < 0.001). However, this correlation was not statistically significant in 3D MRI scans of patients with AD in the ADNI dataset (Supplementary Fig. 2b; r = -0.066, p = 0.18)

The PPMI dataset contains 3D research grade T1-weighted MRI scans for (1) subjects with no neurologic disorder and no first degree relative with PD (cognitively unimpaired cohort; CU), (2) participants who are at risk of Parkinson’s based on clinical features, genetic variants, or other biomarkers (prodromal cohort; PRO), and (3) patients diagnosed with Parkinson’s disease (PD cohort). Our brain age model predicted brain age MAE of 2.59 years after age bias correction for the CU cohort with mean corrected brain age gap of 1.03 years (Fig. 5b). Mean corrected brain age gap was 1.42 years for subjects in the PRO cohort and 2.23 years for patients in the PD cohort. The cohorts showed significantly different mean brain age gap (p < 0.001, Welch’s ANOVA). Further post hoc analysis showed the brain age gap of subjects in the PRO or PD cohort were significantly greater than CU subjects (p < 0.001, Pairwise Games–Howell test). Brain age gap was also significantly greater in patients diagnosed with PD compared to subjects in the prodromal phase (p < 0.01, Pairwise Games–Howell test).

Discussion

In this study, we have demonstrated accurate brain age prediction on clinical grade 2D axial T1 weighted MRI scans using a 3D DenseNet based model trained with research grade 3D T1 weighted MRI scans. This training pipeline can potentially be applied to MRI scans of other modalities. Our model achieved MAE of 3.68 years in brain age prediction for axial-sliced 3D T1 weighted MRI scans, and MAE of 2.73 years after age bias correction for clinical grade 2D axial MRI scans. This is a great improvement compared to previous brain age prediction models targeted for clinical grade 2D T1 weighted MRI scans, and even comparable to the performance of state-of-the-art models that uses entire research grade 3D MRI scans14. We were able to achieve such performance with a dataset covering a wide range of age distribution with range from 16.22 to 95 years, and standard deviation of 21.74 years. While previous studies using 2D CNN architecture models or trained with in-house 2D axial T1 scans have failed to accurately predict brain age of clinical grade 2D axial T1 weight MRI scans20,24, we overcame this problem by (1) employing a 3D CNN architecture and (2) developing a pipeline to leverage widely available research grade 3D MRI scans for training. Given common use of axial 2D MRI scans in routine clinical examinations and primary healthcare settings, our findings provide a reliable result for precise brain age prediction, potentially enabling early detection of neurological abnormalities and improving patient outcomes. Increase in brain age gap (i.e., older predicted brain age) of our model was associated with disease progression in both Alzheimer’s disease and Parkinson’s disease. The results of this study show the feasibility of utilizing brain age gap as a screening tool to assess the risk of neurodegenerative diseases during routine clinical examinations. Negative correlation between brain age gap from clinical 2D MRI scans and MMSE was observed in the AD cohorts of the SMC dataset, suggesting additional clinical values of our brain age prediction model. However, this correlation was weaker and not statistically significant when calculated for the 3D MRI scans in the AD cohorts from the ADNI dataset. One possible explanation for this discrepancy could be due to the difference of the homogeneity of the datasets. The SMC dataset hold data obtained from a single center with the same scanner and protocol whereas the ADNI dataset is a collection of datasets from various centers, and this could introduce biases in both MRI imaging and MMSE scoring.

Another important consideration when developing models for routine clinical use is inference speed and computation resource usage. Although 2D CNN models have cheaper computational cost, our trained 3D DenseNet based model takes only 1.3 seconds to (1) load the model and a clinical 2D axial scan saved in NIfTI format, then (2) predict brain age. This experiment was performed using a NVIDIA L40S GPU and required less than 1GB of GPU memory. Therefore, using a pretrained 3D CNN model only for brain age inference would not be a challenge in clinical settings.

Guided backpropagation reveled CSF and their adjacent regions are important in predicting brain age for our model. This involves multiple major CSF regions, indicating that overall CSF volume is important in predicting brain age. Previous study using clinical grade 2D T2 weighted MRI scans to predict brain age also showed that CSF regions are associated with brain age prediction19. One possible explanation for this is that overall brain atrophy from aging leads to larger CSF volumes.

Generalizability of a model is a critical factor in developing brain age prediction models. Scans from different scanner vendors or hospitals contain inherent heterogeneity, which leads to suboptimal predictions. Thus, accurately predicting the brain age of unrepresentative data has been a major challenge for brain age prediction models. Our model showed great generalizability during training since the training dataset was collected from various sources. The model was able to accurately predict brain age in the validation and test datasets, and minimal brain age bias was observed. However, when the model was applied to clinical 2D axial datasets, age bias correction had to be performed. This may be due to the innate differences between research grade 3D MRI scans and clinical 2D MRI scans. Although our preprocessing pipeline to convert research grade 3D MRI scans into the training dataset tried to imitate clinical 2D MRI scans, these innate differences may have led to regression dilution or attenuation bias. Without age bias correction, the model will overestimate the brain age of MRI scans from younger individuals and underestimate the brain age of MRI scans from older individuals. Therefore, an accurate age bias correction step is required for clinical application on 2D MRI scans. We showed that this is possible using only a few scans from cognitively unimpaired individuals.

There are some limitations of this study. First, further validation of the model using clinical 2D scans from various sources is required. Since significant brain age bias correction was required when applying the model to the SMC clinical axial 2D MRI scan dataset, slight adjustments to the learned linear bias correction coefficients may be necessary for scans from different sources. Furthermore, to use the model as a screening tool for measuring risk of neurodegenerative diseases, training the model to classify healthy subjects and patients could enhance its performance. When trained sorely to predict brain age, it does not necessarily learn the features of neurodegenerative diseases. While our model successfully predicted greater brain age gap in neurodegenerative disease cohorts compared to healthy subjects, training a model targeted specifically for a particular neurodegenerative disease could lead to the development of a specialized model for risk assessment for that disease.

In conclusion, we have demonstrated that it is possible to accurately predict brain age of clinical grade 2D axial T1 weighted MRI scans by training a 3D DenseNet based model with publicly available research grade 3D T1 weighted MRI scans. The same training pipeline can possibly be used MRI scans of other modalities. The high performance and fast inference speed of the model show potential for application in clinical situations, pending further validation with additional clinical 2D MRI scans.

Methods

Datasets

A total of 8681 research grade 3D T1-weighted MRI scans were acquired from 8495 cognitively unimpaired subjects from the Samsung Medical Center (SMC) and 24 publicly available datasets: Alzheimer’s Disease Neuroimaging Initiative25 (ADNI; http://adni.loni.usc.edu/), Cambridge Centre for Ageing and Neuroscience (Cam-CAN) data repository26,27, Calgary-Campinas-359 (CC-359) dataset28, Dallas Lifespan Brain Study (DLBS), International Consortium for Brain Mapping29 (ICBM; www.loni.usc.edu/ICBM), Information eXtraction from Images (IXI; http://brain-development.org/ixi-dataset/), Open Access Series of Imaging Studies-3 (OASIS-3)30, Parkinson’s Progression Markers Initiative (PPMI)31, Southwest University Adult Lifespan Dataset32 (SALD), and 15 datasets33,34,35,36,37,38,39,40,41,42,43,44,45,46,47 from OpenNeuro48 (Table 1). The description of each cohort and information about image protocols and scanners are described in Supplementary Information 1. Scans taken from a same subject were collected if the scans were taken more than 5 years apart. Otherwise, only the scan taken from the earliest timepoint was selected. Of the 8681 3D scans, 4821 scans were from female subjects and the mean age of the scans was 51.76 (±21.74) years with a range from 16.22 to 95.

Table 1 Training dataset composed of research grade 3D T1-weighted MRI scans from cognitively unimpaired individuals
Full size table

The study protocol received approval from the Institutional Review Board of SMC, and all procedures were conducted in accordance with the approved guidelines. Written consent was obtained from each participant prior to their involvement in the study. To test the model’s performance on clinical grade axial 2D T1-weighted MRI scans, 175 scans from cognitively unimpaired subjects and 199 scans from patients diagnosed with AD were also collected from SMC (Table 2). The mean age of the SMC 2D cognitively unimpaired cohort was 65.06 (±8.67) with a range of 41 to 85, and 111 out of the 175 subjects were female. The mean age of the SMC 2D AD cohort was 72.83 (±8.64) with a range of 47 to 89, and 133 out of the 199 subjects were female. The cognitively unimpaired subjects in the test dataset do not overlap with the subjects in the SMC cohort in the training dataset. Further details of the SMC 2D dataset are described in Supplementary Information 1.

Table 2 Test dataset composed of clinical grade axial 2D T1-weighted MRI scans from SMC and 3D MRI scans of neurodegenerative disease cohorts from public datasets
Full size table

Image processing

All scans were converted into NIfTI format then skull stripped49. Since the model was targeted for clinical grade axial 2D MRI scans, the 3D scans used for training were first sliced to generate synthetic axial 2D scans. The axial gap between these slices was set to the smallest integer multiple of the axial gap of the original 3D scan that was greater than or equal to 7 mm. The synthetic 2D scans were then interpolated back into common voxel space of 2 mm x 2 mm x 2 mm. To normalize for the different MR signal ranges from different devices, the intensity of each scan was normalized by subtracting the mean and dividing by standard deviation. Then the background values were subtracted to every voxel to set background intensity to 0. The mean and standard deviation were computed using voxels between the 1st and 99th percentiles after excluding background voxels. To remove outliers, all voxels with intensity above the 99.9th percentile was replaced with the 99.9th percentile value. Finally, the scans were cropped in the center or padded into a common size (sagittal x coronal x axial 160 mm x 240 mm x 80 mm). No spatial registration or bias field correction was applied. To filter out corrupted scans containing only parts of the brain, scans with more than 92% background voxels were removed. The final training dataset composed of 69,598 3D scans interpolated from 2D axial T1-weighted MRI scans created from slicing 8629 research grade 3D T1-weighted MRI scans.

For the clinical grade axial 2D T1-weighted MRI scans, the same preprocessing was applied excluding the axial slicing procedure. Open access tools were used for preprocessing: dcm2niix50 was used to convert scans from DICOM to NIfTI format; HD-BET49, a brain extraction tool built with open access python libraries was used for skull stripping; MONAI51, an open-source project built on PyTorch was used to interpolate 2D scans into 3D scans; Python libraries NiBabel, and Numpy were used for all other preprocessing procedures.

Brain age prediction model

A 3D DenseNet-169 based model52 was used for brain age prediction. DenseNet concatenates learned features from all preceding layers to each layer to prevent the vanishing gradient problem and improve information flow. It was previously used to successfully predict brain age from research grade 3D T1-weighted MRI scans53, and clinical grade axial T2-weighted or diffusion-weighted scans. For application in this study, the last transitional layer was removed due to smaller input size (80x120x40 compared to 224 x 224 x 224 of the original model). The softmax layer within the classification layer was replaced with a fully connected layer where the output is a single scalar for the predicted brain age. LeakyReLU with negative slope 0.01 was used for the activation layers instead of ReLU. All other configurations including convolution kernel sizes, stride, dense block configurations, and the growth rate was set to values in the original paper. An illustration of the model architecture is shown in Fig. 1a. Our final model contained 20.4 million parameters. 5-fold cross validation with training 80%, validation 10%, test 10% splits were conducted where the validation dataset was used to select the best model. To prevent data leakage, the dataset was split at the research grade 3D T1-weighted MRI scan level.

He initialization using the Kaiming normal distribution was used for weight initialization54. The Adam optimizer with β1 = 0.9 and β2 = 0.9 and weight decay λ = 1e−4 was used to minimize the mean squared error loss between predicted and chronological age. Initial learning rate was set to 1e−4 and was scheduled to be reduced by a factor of 2 when no improvement in validation loss is observed for 5 epochs. To prevent overfitting, three data augmentation methods were applied during model training. For every training epoch, the training batch is (1) randomly shifted by up to 2 voxels in the axial direction, and up to 10 voxels in the sagittal and coronal directions, (2) mirrored with respect to the sagittal plane with 50% probability, and (3) gamma correction with ɣ ~ U(0.7, 1.3) and intensity was multiplied with by factor of ɑ ~ U(0.7, 1.3) for data augmentation. Mini batch size was set to 32, and total epoch number was set to 70. We observed stability in the model after an iteration of 70 epochs. Training time per epoch was approximately 200 s, and the entire training time including validation and testing was approximately 4.2 h when using one NVIDIA L40S GPU for training. Model implementation, training, and testing were done using PyTorch55. Python scripts for model implementation and inference will be made available under GNU General Public License version 3 upon request to the corresponding author.

Applying model on clinical grade axial 2D T1-weighted MRI scans

The model was applied on clinical grade axial 2D T1-weighted MRI scans collected from SMC (Table 2). Brain age gap, defined as the difference between predicted age (y) and chronological age (x), is known to be overestimated in younger individuals and underestimated in older individuals due to regression dilution56. Although our model showed minimal brain age bias during training, brain age bias was apparent when applied on clinical grade axial 2D scans. This may be due to the innate differences of clinical grade axial 2D images and research grade 3D images. Therefore, linear bias correction using scans from oldest and youngest 5% cognitively unimpaired subjects was added after model prediction. A linear regression y = ax + b is first fit using these subjects, then the corrected prediction y’ was calculated as y’ = y + [x - (ax + b)] for all subjects. The coefficients a and b learned from cognitively unimpaired subjects are used for age bias correction for age prediction results of the MRI scans from patients with Alzheimer’s disease. Brain age gap of cognitively unimpaired subjects was compared to patients with Alzheimer’s disease using the two sample Z-test.

Guided backpropagation is a gradient based method to visualize how deep networks predict. It gives a detailed, pixel-space heatmap of importance on model prediction57. Guided backpropagation was used to visualize important regions of the brain on predicting brain age of clinical grade 2D MRI scans from cognitively unimpaired subjects and patients with Alzheimer’s disease.

Brain age prediction on neurodegenerative disease cohorts

Multisite large-scale studies often provide datasets including MRI scans from different stages of a neurodegenerative disease (Table 2). The Alzheimer’s Disease Neuroimaging Initiative (ADNI) provides various types of MRI scans from cognitively unimpaired subjects, mild cognitive impairment, to Alzheimer’s disease. The Parkinson’s Progression Markers Initiative (PPMI) dataset includes scans across all stages of Parkinson’s disease. The same linear bias correction method as previously described was applied for each study to ensure correct prediction of brain age gap. The linear bias coefficients learned from cognitively unimpaired subjects are used for neurodegenerative disease cohorts from the same study. Given the model was originally tasked to predict brain age of cognitively unimpaired subjects and thus learn features of normal brain aging, the model does not necessarily learn features of neurodegenerative diseases. However, if greater brain age gap is observed in subjects with neurodegenerative disease, it could potentially highlight the role of the brain age prediction model in accessing risk for neurodegenerative diseases.

The brain age gap of subjects from different stages of the disease was compared with the brain age gap of cognitively unimpaired subjects using Welch’s analysis of variance (ANOVA) with pairwise Games–Howell post hoc test. All statistical analysis were performed using the open-source Pingouin Python package58.