Introduction

In the realm of heterogeneous catalysis, the construction of surface phase diagrams (SPDs) is central for revealing the relationship between the most stable thermodynamic state of the catalyst surface and the state variables. In reactive environments, the surface can often be assumed to be in a thermodynamic equilibrium with the ambient medium, characterized by its surface free energy1,2,3,4. The lowest surface free energy configuration is relevant as it represents the most thermodynamically favored state of a reaction system, and is hence useful for deriving the surface structures of all reaction intermediates. Traditional approaches rely on chemical intuition and brute-force search to determine the most thermodynamically favored configuration of surface adsorbates. As a result, the adsorbate-catalyst configurations under study are often highly if not overly simplified compared to their experimental counterparts5. In most cases, however, additional complexity must be introduced in order to obtain meaningful results that are comparable to experiments.

In general, the complexity of deriving SPDs may stem from 3 main sources – catalyst, adsorbate and reaction condition. In the simplest case, a SPD can be constructed by performing electronic structure calculations for a set of adsorbate-catalyst configurations with representative adsorbate coverage patterns on an unchanged catalyst surface6,7. However, for alloy systems which we target in this paper, further degrees of freedom are introduced to the chemical composition and ordering of the catalyst, and consequently the chemical environment of the adsorption sites. Also, a catalyst modelled by a stepped surface or a nanoparticle (NP) may present a lot more symmetry-inequivalent adsorption sites than on a flat surface. In the matter of adsorbate effects, a change in adsorbate coverage can potentially alter the reaction mechanism due to variations in adsorbate-adsorbate interactions8,9,10,11,12,13 and potentially adsorbate-induced surface reconstruction14,15,16,17,18,19,20,21. Under certain reaction conditions (especially phase transition regions), the thermodynamically favored state may accommodate a co-adsorption of mixed adsorbate species22,23,24,25, adding further complexity to the surface chemistry. Moreover, alloy catalysts may undergo dramatic adsorbate-induced segregation26,27,28,29,30,31, suggesting that a search for the most stable adsorbate-alloy configuration must optimize the catalyst and the adlayer holistically. Finally, different reaction conditions may lead to very different free energy landscapes, thereby completely different reaction mechanisms.

Determining the most stable adsorbate-alloy configuration under a certain reaction condition is already an open question. A realistic and sophisticated description of the system requires the account of a plethora of degrees of freedom, e.g., the composition and ordering of the alloy, the coverage and arrangement of the adsorbates, and even the composition and ordering of the adlayer if multiple adsorbate species are considered. All degrees of freedom jointly contribute to the ‘combinatorial explosion’ of the search space of all possible adsorbate-alloy configurations. When searching through such a huge space, the reliability of the putative global minimum configuration depends on the accuracy and efficiency of the energy evaluator, as well as the efficiency of the global optimization algorithm. One can of course use a small unit cell to limit the search space, but this will inevitably affect the quality of the alloy SPD that one can obtain, owing to the limited possible variations of the adsorbate coverage and the surface chemical ordering.

Despite being challenging, a handful of endeavors have been made in the past to search for the most stable adsorbate-alloy configuration under a given condition. The majority of theoretical studies rely on Monte Carlo (MC) simulations to search for the stationary states of alloy catalysts in the presence of adsorbates32,33,34,35,36,37,38,39,40. Recently, evolutionary algorithm (EA) emerges as an alternative solution to search for the most stable adsorbate-alloy configuration41,42,43. As a stochastic optimization method, EA is highly suitable for determining the lowest-energy configuration since it is not constrained to the sample space according to a distribution. In the matter of the energy evaluator, coupled-lattice cluster expansion33,34,44,45 is the conventional approach for describing the energetics of such adsorbate-alloy systems and are commonly used in conjunction with MC simulations33,34,35,37,38. Nevertheless, the feasibility of this method is limited by the number of different adsorbate species it can treat, which is further exacerbated when various types of adsorption site are considered46. Moreover, cluster expansion models describe the energy of a relaxed system as a linear combination of many-body interactions defined on a fixed ideal lattice, which may yield spurious predictions for very complex adsorbate-alloy systems, especially when the atoms undergo drastic displacement during local optimization47. On the other hand, most EA studies are coupled with expensive but accurate density functional theory (DFT) calculations, which becomes intractable when the search space is too vast.

To study the dependency of alloy stability on reaction condition, it is important to map out the most stable adsorbate-alloy configurations to various reaction conditions and illustrate in alloy SPDs. The research so far has mainly relied on three structure generation strategies for deriving such diagrams: (i) systematically enumerating an exhaustive set of adsorbate-alloy configurations3,48,49, (ii) manually selecting a subset of adsorbate-alloy configurations based on human intuition50,51,52,53,54,55, or (iii) separately searching for the most stable adsorbate-alloy configurations under different reaction conditions32,36,37,38. The first strategy often restricts the surface model into a small unit cell, which essentially excludes many possible (and potentially stable) adsorbate-alloy configurations. The second strategy is easy to implement but lacks reliability unless there are strong theoretical or experimental backing. The last strategy is comparatively more robust, but one obvious drawback is the waste of computational resources by repeating the search multiple times with essentially the same total search space. Although this can be eased by parallelization, the resolution of a SPD still largely depends on the number of probing conditions. Moreover, when there are multiple state variables jointly influencing the chemical potentials, it can become intractable to perform separate searches for a combinatorial set of reaction conditions.

In general, the thermodynamic stability of a surface configuration x can be considered as a black-box fitness function f(x) characterized by n bounded parameters representing the state variables. The task of deriving a SPD can then be seen as a global optimization problem with the goal of finding a set of configurations that contains the fittest (i.e. most stable) candidate for any combination of the n parameters constrained by their bounds. This type of optimization problem belongs to the definition of multifactorial (or multitask) optimization, i.e., to simultaneously progress multiple optimization tasks (which may or may not be interdependent) in a unified search space56. Despite having multiple fitness functions for each individual, this is not to be confused with a multi-objective optimization where the goal is to locate the Pareto front of multiple competing objectives. Gupta et al.56 first proposed the idea of evolutionary multitasking (EM) to address multifactorial optimization problems by performing multiple EA tasks in a single population. A canonical EA progresses a population of evolving candidate solutions by performing genetic operations including crossover, mutation and selection. Apart from the efficiency offered by the parallelism of the population-based EA search, EM can also harness underlying relationships between different tasks via genetic transfer, which is a direct benefit offered by the unified search space56,57. The good thing about the EM application in materials science is that the search spaces of all tasks are often naturally unified. In the context of deriving alloy SPDs, genetic transfer can be achieved by a crossover between the alloy surface of one structure and the adlayer of another. In particular, a SPD often involves surface configurations with adsorbate coverages varying from low to high, and consequently from a small to large number of possible coverage-specific configurations. Compared to performing a standard EA search at a condition where high adsorbate coverage is favored, it can be even faster to find the solution by performing an EM search at multiple conditions, where the low-coverage tasks can quickly find superior structural traits (e.g. the favored adsorption sites, adsorbate species and alloy surface ordering) and then pass to the higher-coverage tasks successively, all thanks to the cross-task genetic transfer. In Gupta’s formulation, an EM algorithm, namely multifactorial EA (MFEA), was devised to limit the total number of function evaluations by evaluating at only a single task for each individual based on genetic heuristics56. However, the problem of deriving SPDs falls into a different setting, where only a single expensive electronic structure calculation is required for each observation regardless of the number of tasks. It is then trivial to calculate fitness for all tasks thanks to the efficient vectorization on modern CPUs. Hence there is no need to trade off accuracy for efficiency by evaluating fewer tasks as is in the MFEA. Instead, we describe in the Methods section a novel EM algorithm that follows a dynamic niching routine designed specifically for deriving phase diagrams.

For an adsorbate-alloy system, the magnitude of the total search space is tantamount to the number of variations for distributing K different adsorbate species and vacancies on S adsorption sites while also distributing M different metal species in an N-atom surface, which leads to (K+1)S ⋅ MN possible configurations. If we consider a typical adsorbate-alloy system consisting of 3 possible adsorbate species, 2 possible metal components and a 4 × 4 × 4 surface slab with 64 high-symmetry adsorption sites, the total search space then comprises 6.3 × 1057 configurations. Although the configurational search space is unified in an EM search for the SPD, a premature convergence is still likely to happen when searching through such an enormous space. With the implementation of symmetry-constrained genetic operators, we have recently made it possible to search for the ground-state 5 nm nanoalloy in a high-symmetry subspace under vacuum condition58. In this work, we have extended the concept of symmetry constraints to the genetic operations that involves adsorbates, taking the assumption that the most stable surface configuration will likely have adsorbates arranged in a somewhat ordered manner. Based on the same idea of grouping, we describe in the Supplementary Information (SI) a new set of symmetry-constrained genetic operators that are specifically designed to reduce the search space of adlayer patterns by exploiting the lattice symmetry of adsorption sites. Besides, the search space can be further reduced by constraining the minimum adsorbate-adsorbate distance and eliminating duplicates. In this work, we have devised a structure comparator based on graph automorphism to prevent duplicate adsorbate-alloy configurations from entering the EA population, as discussed in the Methods section.

Surrogate models have been employed in EAs to minimize the number of expensive electronic structure calculations required in a global structural optimization59,60. Bayesian EA (BEA) is a typical type of surrogate-assisted EA that uses a Gaussian process (GP) model to perform Bayesian inference based on the a posteriori knowledge of the evaluated observations59,60,61,62. Importantly, GP provides the benefit of uncertainty quantification, which can be readily incorporated into the fitness function of a BEA to balance between exploration and exploitation59. To efficiently obtain mean prediction and uncertainty of the relaxed energy for each surface structure, we consider using a GP model that can perform the so-called direct initial structure to relaxed energy (IS2RE) tasks63. Such a model requires encoding adsorbate-alloy configurations into unique fingerprints that are invariant to the small coordinate changes resulting from the geometry relaxation. In the Methods section, we describe a GP model that employs a graph kernel to directly predict the relaxed energies without the need of explicitly encoding each structure.

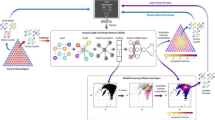
In the present work, we propose a Bayesian EM (BEM) framework (see Fig. 1), serving as a new strategy for finding the most stable adsorbate-alloy configurations under various reaction conditions ‘once and for all’. By leveraging graph theory, lattice symmetry constraints, Bayesian active learning and EM, our framework is capable of tackling all aforementioned complexity ascribed to alloys, adsorbates and reaction conditions, thereby deriving alloy SPDs with good efficiency and accuracy. In particular, the combination of Bayesian active learning and EM brings an additional benefit of balancing between exploration and exploitation automatically. The works most related to ours are probably those of Ulissi et al.64 and Ghanekar et al.49, in which they both derived surface Pourbaix diagrams through active learning. Specifically, they considered the problem of selecting a minimum subset from thousands of candidate adsorbate-catalyst configurations to be evaluated by DFT. Although the BEM framework also uses the concept of active learning, we would like to underline that it is designed to solve a much more complex problem, i.e., to let the algorithm automatically search in an unknown space and generate the structures that contribute to the SPD with as few energy evaluations as possible. Another notable difference is that we not only consider the variation of the adlayer patterns, but also the change of the alloy catalyst itself, which often results in a search space comprising an astronomical number of adsorbate-catalyst configurations.

Fig. 1: Schematic illustration of the BEM framework.
figure 1

Constructing an alloy SPD can be seen as performing k global optimization tasks with a unified search space of all possible adsorbate-alloy configurations, where k represents the number of sampled reaction conditions. The goal of each task is to optimize an expensive black-box function derived from the first-principles potential energy surface (PES). The BEM framework takes in knowledge of graph theory, lattice symmetry, Bayesian active learning and EM to perform all k tasks simultaneously, and to eventually find the most stable adsorbate-alloy configuration for every task.

Full size image

The ability of our BEM method is demonstrated by two binary alloy systems in the context of two heterogeneous catalytic reactions. The first case study involves the construction of the surface Pourbaix diagram for the electrochemical oxygen reduction reaction (ORR) on a Pd-doped Ag(111) catalyst. A semi-empirical effective medium theory (EMT) potential65, as implemented in the Atomic Simulation Environment (ASE)66, is used as a toy calculator to first benchmark our methods. This is followed by a DFT-based study on the same system. In the second case, we consider a Pt-doped Ni nanocatalyst in contact with the gas phase under various steam methane reforming (SMR) conditions. This case is of special interest since it has been reported experimentally that doping Ni NPs with a tiny amount of Pt can lead to a significant boost in the catalytic activity for SMR67,68,69. Compared to the extended surfaces, NPs introduce additional complexity of size and shape, making this study even more challenging. In reactive environments, the shape of a NP can change drastically due to the presence of adsorbates on different facets, which is a phenomenon known as ‘NP reshaping upon ligand adsorption’70. Our goal is then to study how the shape of the Pt-Ni nanoalloy changes as a function of the reaction condition. Global optimization of nanoalloys in reactive environment is a daunting task due to the large length scale of NPs. Instead, one can derive the phase diagram of a nanoalloy by first determining the SPD of each low-index facet, then predicting the equilibrium shape using the Gibbs-Wulff construction71,72 that takes the surface free energies of the lowest-energy adsorbate-alloy configurations for all facets into account. Specifically, we consider the two most dominant low index facets – (111) and (100) – as well as a stepped (311) facet representing the step-edge interface of (111) and (100). To test the robustness of our BEM framework, we consider a wide range of SMR conditions. From the DFT-based SPDs derived by the BEM, we are able to show the effects of coking and sulfur poisoning which are known to be the main causes for the deactivation of SMR73.

Results and discussion

BEM active learning workflow

The general BEM active learning (BEM-AL) workflow for deriving SPDs is shown in Fig. 2. The active learning starts by generating an initial population of surface configurations (with adsorbates). A fraction of the initial population are then relaxed by electronic structure calculations to construct an initial dataset. In each BEM iteration, a GP surrogate first learns from the latest dataset (consisting of relaxed structures and the corresponding electronic energies), then acts as a high-throughput function evaluator in the EM to efficiently suggest a set of fittest surface configurations that contribute to the fitness upper envelope. Only the newfound fittest configurations are sent to be further evaluated by electronic structure calculations. Every time a new set of data points is obtained, the GP model can benefit from re-tuning the hyperparameters and retraining the model. We can then restart the BEM with the final population of the previous run while employing an improved GP surrogate. The whole BEM-AL scheme terminates when the BEM cannot suggest any new configurations on the fitness upper envelope, or there is no progression in the lower envelope of the calculated surface free energies for a successive number of BEM iterations.

Fig. 2: BEM-AL workflow for deriving SPDs.
figure 2

As specified in the text, the convergence of the BEM-AL scheme is governed by the predicted fitness upper envelope and the lower envelope of the calculated surface free energies.

Full size image

The BEM-AL scheme mainly involves two alternating tasks – electronic structure calculations and BEM global optimization. Typically, an EA-based global optimization of alloy catalysts requires the generation of an initial pool of alloy configurations and a set of genetic operators to generate new configurations. When coupled with adsorbates, the generation of the initial catalyst configurations requires additional automated identification of the adsorption sites to allow placing adsorbates. Meanwhile, the optimization now also requires automated surface analysis of adsorbate-catalyst configurations to derive their fitness. As for genetic operations, the imposition of symmetry constraints can significant accelerate the global optimization of alloy catalysts with or without adsorbates58. To this end, we have developed computational tools for automating structure generations and accelerating EAs (including EM), which are integrated into a general workflow as presented in Fig. 3. The integration is done by packing all the tools into an open-source Python package named Alloy Catalysis Automated Toolkit (ACAT), which is freely accessible at https://gitlab.com/asm-dtu/acat. The code is written for general use with the support of a wide variety of crystal structures, which should be broadly useful for the community of computational heterogeneous catalysis. A detailed description of ACAT can be found in the SI.

Fig. 3: Schematic of the workflow for a global optimization task of an adsorbate-alloy system automated by ACAT.
figure 3

The two main features of ACAT are (a) structure generation and (b) EA (including EM). ACAT is generalized for various surfaces and NPs, and offers complementary features such as adsorption site identification and symmetry constraints.

Full size image

Pd-Ag SPDs for ORR

To benchmark our methods, we have used an efficient EMT calculator to carry out different types of EA for deriving the Pd-Ag(111) surface Pourbaix diagram for ORR. In detail, we consider a reversible hydrogen electrode potential (URHE) window from -0.5 to 0.5 V and a fixed temperature of 300 K. We also consider a pure Nernstian shift in potential with pH, which means the lowest-energy surface configurations are independent of the concentration of protons6. First, we have separately performed standard EAs using EMT at 11 different electrode potentials (0.1 V apart). The results are then compared with the EMT-based EM, where the global optimization is performed at all 11 electrode potentials simultaneously. With the goal of minimizing the number of energy evaluations by EMT, we have tested our BEM-AL approach in four different hyperparameter settings: the exploration factor κ taking values at 0, 1, 2 and multitasking at all three values (i.e. ‘exploration-exploitation-balanced’ sampling). To avoid anomalies, all EA runs start with the same initial population and use the same stopping criterion, and each run is repeated five times. Besides, symmetry constraints are applied to all adsorbate-related genetic operations for all EAs in order to explore the configurational space more efficiently (see Fig. 4c for comparison).

Fig. 4: EMT benchmark results for EM and BEM-AL.
figure 4

a depicts the putative EMT-based Pd-Ag(111) surface Pourbaix diagram at pH = 0 according to all calculations. b shows the EMT-based Pd-Ag(111) surface Pourbaix diagram at pH = 0 found by different EAs (including standard EA, EM and BEM-AL with different hyperparameter settings). c compares the evolution of the global minimum surface free energy in a standard EA search at URHE = 0 V with and without symmetry constraints. d shows the average number of EMT energy evaluations required in different EAs. The error bars in (b, d) and the shaded areas in (b) represent the standard deviations from five repeated searches.

Full size image

According to the EMT-based surface Pourbaix diagram displayed in Fig. 4a, the Pd-Ag(111) surface favors a 1 monolayer (ML) H* coverage at all hcp sites within the URHE window from -0.5 to -0.1 V, while a 1 ML O* coverage with the same pattern is favored at higher electrode potentials. Also, diamond-shaped Pd clusters are found at the surface and the subsurface for both structures. As shown in Fig. 4b, the standard EAs struggle to find these two structures at almost all electrode potentials while 3 out of 5 EM runs have found them, which may be attributed to the fact that EM can benefit from knowledge transfer across tasks. In regard to the BEM-AL, setting κ = 0 results in a premature convergence in all 5 runs, which is as expected since the GP surrogate only learns from the initial training data. By setting κ to 1 and 2, we are able to obtain similar results as in the EMT-based EM. The best performance is found with the ‘balanced’ BEM-AL strategy, where all 5 runs are able to reproduce the true EMT-based Pd-Ag(111) surface Pourbaix diagram. Efficiency-wise, we have found that an EM run on average takes a comparable number of energy evaluations to converge w.r.t. a standard EA. In general, a larger population size is recommended for EM, so that every task has sufficient good candidates present in the population. For the BEM-AL, although the ‘balanced’ runs sample more configurations in each BEM iteration, they end up costing a similar number of energy evaluations as in the κ = 1 and κ = 2 runs due to the fewer iterations required to converge. In particular, the ‘balanced’ BEM-AL takes an average of 94 energy evaluations to converge, which is a 27-fold reduction compared to a ‘brute-force’ EM using the EMT potential.

We have also obtained the DFT-based surface Pourbaix diagram of the Pd-Ag(111) surface by performing the ‘balanced’ BEM-AL, taking only 76 DFT relaxations in total. Here we have considered 11 URHE values ranging from 0.5 to 1.5 V. As shown in Fig. 5a, water oxidation starts at URHE = 1.29 V, forming a single-atom alloy (SAA) surface structure due to the O-induced surface Pd segregation. The adsorption of oxygen atoms first leads to the formation of a c(2 × 4) orthogonal overlayer pattern (0.25 ML coverage) and quickly stabilizes at 0.38 ML coverage when increasing the electrode potential. Considering the dissolution of Ag, the desirable reaction condition for the Pd-Ag(111) electrocatalyst is probably at pH = 14 with a standard hydrogen electrode (SHE) potential window from 0.46 to 0.61 V (see Fig. 5b). Note that here we have not considered the hydrogen bonds between the surface and the water layer which may potentially stabilize the surface OH* species6.

Fig. 5: DFT-based Pd-Ag(111) surface Pourbaix diagrams derived by BEM-AL.
figure 5

a shows the DFT-based Pd-Ag(111) surface Pourbaix diagram at pH = 0. b shows the DFT-basd 2-dimensional Pd-Ag(111) surface Pourbaix diagram (USHE vs. pH) including Ag dissolution effects. Different on-envelope configurations are shown in different colors.

Full size image

Pt-Ni SPDs for SMR

We have performed the ‘balanced’ BEM-AL to derive the DFT-based Pt-Ni(111), (100) and (311) SPDs under a large set of SMR conditions that are both experimentally and industrially relevant. Specifically, we consider four S/C ratios (β) ranging from 1 to 4, seven total pressures (P) ranging from 1 to 30 bar, eight temperatures (T) ranging from 573 to 1273 K, and seven H2S concentrations (c) ranging from 0 to 2000 ppm, which are combined into a total number of 1568 tasks. This set is further expanded to 15,253 tasks by taking into account the CH4 conversion (a) ranging from 0 to equilibrium with a binning interval of 0.05 for each task.

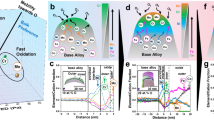
As a big picture, we showcase in Fig. 6 the ‘balanced’ BEM-AL workflow for constructing the Pt-Ni(111) SPD. To provide an intuitive view of how the most stable adsorbate-alloy configuration evolves as the SMR reaction moves toward equilibrium, we keep track of the lower envelope of the DFT-calculated surface free energies as a function of the CH4 conversion under a common lab-scale SMR condition of c = 0, β = 2, P = 1 bar and T = 973 K. We have performed 8 iterations of BEM, coupled with 9 DFT iterations (345 DFT relaxations in total). A relatively large initial training set of 100 DFT-relaxed configurations is used to ensure that adequate data are collected before updating the GP posterior, so that the surrogate model can describe the high-dimensional PES of such complex system decently well to begin with. The ‘balanced’ sampling strategy is illustrated in Fig. 6g, where the pure exploitative (κ = 0) tasks return configurations that are predicted to be the most stable according to the mean predictions of the current GP model, while the more explorative tasks (κ = 1, 2) look for configurations that have higher uncertainty. The progress of each BEM search is reflected by the constant elevation of the fitness upper envelope until convergence. After each DFT iteration, we estimate the predictive power of the graphical GP model by comparing the GP-predicted energies and the actual DFT-evaluated energies. As can be seen in Fig. 6d, the mean absolute error (MAE) trends down from 46.9 to 8.6 meV/atom over the course of the BEM-AL. Note that since all surface free energies are calculated by DFT, the accuracy of the GP surrogate only reflects the confidence of finding the actual most stable adsorbate-alloy configurations. As the GP model is constantly improved, the fittest configurations suggested by the BEM also become more and more stable with increasing number of iterations. This is reflected by the constant descent of the lower envelope of the calculated surface free energies, while the adlayer patterns displayed by the on-envelope configurations also become visibly more ordered.

Fig. 6: BEM-AL workflow for deriving the DFT-based Pt-Ni(111) SPD.
figure 6

The blue block shows the evolution of the lower envelope of the DFT-calculated surface free energies w.r.t. CH4 conversion after (a) 1, (b) 2 and (c) 9 DFT iterations. d shows the MAE between the GP-predicted potential energies and the DFT-evaluated potential energies of the fittest structures derived in each iteration. The red block shows the BEM global optimization process in the first BEM iteration, where the evolution of the fitness upper envelope is depicted for the pure exploitative task from (e) the initial generation to (f) the 104th generation, and (g) depicts the `balanced' sampling strategy for 3 tasks with a = 0.5 and κ = 0, 1, 2. Different on-envelope configurations are shown in different colors. The perspective is fixed at the SMR condition of c = 0, β = 2, P = 1 bar, T = 973 K.

Full size image

According to the Pt-Ni(111) SPD w.r.t. CH4 conversion, as depicted in Fig. 6c, a CO* coverage of 0.5 ML is strongly favored by the Pt-Ni(111) surface when the conversion is below 0.45. The Pt atoms are not present on the surface, but instead form a c(2 × 4) orthogonal pattern in the subsurface. As the reaction progresses, a lower CO* coverage of 0.25 ML with the c(2 × 4) pattern is favored, while the Pt atoms start to segregate to the surface to form the same c(2 × 4) pattern. As the reaction approaches equilibrium, the c(2 × 4) pattern of surface Pt remains stable, while only a small amount of H* is present on the surface. In general, CO* always prefers binding to all-Ni 3-fold hollow sites. The CO* coverage trends down as the reaction progresses, which makes room for the subsurface Pt to segregate to the surface. Interestingly, both the Pt and CO* prefer to form orthogonal lattices despite the fact that a hexagonal unit cell is used. A previous study has reported that coke is unlikely to form on the Ni(111) surface74. We have shown that this is likely also the case for the Pt-doped Ni(111) surfaces.

The SPDs and the most stable adsorbate-alloy configurations obtained by the BEM-AL for the Pt-Ni(100) and (311) surfaces are depicted in Supplementary Fig. 11. Severe coking is observed on the Pt-Ni(100) surface, where C* gradually replaces CO* at the surface 4-fold hollow sites and forms a distorted 0.5 ML all-C* adlayer pattern (known as the ‘clock’ reconstruction75) for CH4 conversions above 0.5. Pt atoms tend to abandon the surface as the C* coverage increases. Coke is also found on the Pt-Ni(311) surface at the beginning of SMR, blocking half of the 4-fold sites. The coke formation targets the 4-fold sites due to the high valency of C, while low valency species such as CO* tends to adsorb on the bridge and hcp sites, which is in good agreement with a previous theoretical study on the stepped Ni(211) surface74. Pt segregation is observed at the surface terrace sites as the CH4 conversion reaches 0.1, while a stable 0.5 ML hexagonal CO* adlayer pattern is formed on the surface step sites. At higher conversion, Pt atoms further segregate to the step sites, while the CO* coverage stabilizes at 0.25 ML with a triangular pattern.

Next, we illustrate the effect of sulfur poisoning on the Pt-Ni SPDs in Supplementary Fig. 12. As can be seen, a small amount of H2S impurity (100 ppm) can lead to the poisoning of all 3 Pt-Ni surfaces at the early stage of SMR. S* are found to block 25% of the fcc sites on the (111) surface, 50% of the 4-fold hollow sites on the (100) surface and 50% of the B5 sites on the (311) surface. This blocking effect is detrimental for the (311) surface since the B5 sites are reported to be the most active step-edge sites for SMR on Ni catalysts74,76. Notably, the surface Pt and S* both favor a hexagonal (2 × 2) lattice on the Pt-Ni(111) surface instead of the orthogonal lattice observed without H2S.

For a more holistic view of the high-dimensional Pt-Ni SPDs obtained by the BEM-AL, we map CH4 conversion onto other state variables such as S/C ratio, total pressure and temperature, as illustrated in the 2-dimensional phase diagrams for the three surfaces (see Fig. 7a–c, Supplementary Fig. 13 and 14). The stable Pt-Ni(111) and (311) surfaces are predominantly covered by pure CO* under a wide range of reaction conditions, while the Pt-Ni(100) surface favors either a mixture of CO* and C*, or the carbon-induced ‘clock’ reconstruction phase as noted in Supplementary Fig. 13. The stability of the Pt-Ni alloy surfaces is generally less sensitive to the S/C ratio and the pressure than to the CH4 conversion and the temperature. Besides, an earlier poisoning is observed on the Pt-Ni surfaces when increasing the H2S concentration.

Fig. 7: DFT-based Pt-Ni alloy SPDs concerning various state variables, derived by BEM-AL.
figure 7

The most stable Pt-Ni(111) surface configurations obtained after 9 DFT iterations are plotted in different colors in (a) β-a, (b) P-a and (c) T-a phase diagrams under the SMR condition of c = 0 with 2 of the 3 other state variable values: β = 2, P = 1 bar, T = 973 K. In the bottom half of the figure, the lower envelopes of the calculated surface free energies w.r.t. CH4 conversion under the SMR conditions of (d) c = 0 and (e) c = 100 ppm (both with β = 2, P = 1 bar, T = 973 K) are shown for the Pt-Ni(111), (100) and (311) surfaces after 9, 8 and 8 DFT iterations, respectively. The equilibrium nanoalloy shapes are obtained at CH4 conversions of 0.1 and 0.6 by Gibbs-Wulff constructions, where the facet colors are consistent with the corresponding lower envelopes.

Full size image

Based on the lower envelopes of the calculated surface free energies of the Pt-Ni(111), (100) and (311) surfaces obtained by the BEM-AL, we are able to perform Gibbs-Wulff constructions (using the Wulffpack package77) under various reaction conditions to understand how the nanoalloy shape changes in response to the chemical environment. As depicted in Fig. 7d and e, the equilibrium shape of the Pt-doped fcc Ni NP is probed at two CH4 conversions (0.1 and 0.6) under the SMR conditions of 0 and 100 ppm H2S. Without the presence of H2S, the close-packed (111) facet dominates at higher CH4 conversion, while the higher adsorption energies at the more open facets such as (311) lead to a rounding of the crystallite at low conversion. In contrast to the rather low stability of the (100) facet under c = 0 condition, the sulfur-poisoned (100) facet quickly becomes so stable that the NP is reshaped into almost a cube with the presence of only 100 ppm H2S in the gas phase. This reshaping phenomenon, which has already been reported experimentally78, indicates that the sulfur poisoning not only deactivates reactions by blocking the active sites, but also by faceting the active Ni crystal planes into less active ones.

We conclude this section with a discussion of the limitation of our BEM method. First, despite the fact that the graphical GP model is always trained on the relaxed structures and a discrepancy in the graph representation is allowed between the relaxed and the unrelaxed structures, the hope is that the discrepancy is not too large so that the model training can still benefit the predictions on the unrelaxed structures generated automatically during the BEM. However, this may become problematic if there are drastic events happening at the surface, e.g. dealloying and leaching79,80. Furthermore, the accuracy of the BEM approach depends on the thermodynamic formulation of the fitness function. The thermodynamic equilibrium assumption directly affects the results one can get from the BEM. Also, since the role of configurational entropy becomes increasingly important as the temperature elevates, an alloy surface (including adsorbates) may favor disordered configurations over ordered ones at sufficiently high temperatures. In the SMR case study, we have used a mean-field approximation for the configurational entropy which only distinguishes between different compositions. This means that our BEM will favor mixed compositions at higher temperatures, but still tends to find the most ordered configuration at that composition. An accurate estimation of the configurational entropy, however, requires a prohibitively large number of energy calculations to evaluate the configurational density of states81, which is intrinsically incompatible with our BEM high-throughput global optimization scheme.

Methods

Evolutionary multitasking via dynamic niching

Let f(x) denote the general fitness function that describes the thermodynamic stability of a configuration x, let θ1, …, θn denote the n continuous state variables, the construction of a phase diagram then requires finding a set of solutions X* that maximizes a global fitness function F(X), defined as the multiple integral of the upper envelope (i.e. pointwise maximum) of the set of fitness functions given by configurations X over the n-dimensional domain of all bounded state variables:

$$F(X)={\int}_{{{{{\mathcal{D}}}}}_{1}}\cdots {\int}_{{{{{\mathcal{D}}}}}_{n}}\mathop{\max }\limits_{x\in X}f\left(x,{\theta }_{1},\ldots ,{\theta }_{n}\right)\ {{{\rm{d}}}}{\theta }_{1}\,\cdots {{{\rm{d}}}}{\theta }_{n}$$
(1)

where \({{{{\mathcal{D}}}}}_{1},\ldots ,{{{{\mathcal{D}}}}}_{n}\) are the bounded domains of the n state variables θ1, …, θn, respectively. As it is intractable to solve for X* directly in the whole configurational space, we resort to EM heuristics to derive a set of ‘good enough’ solutions for all possible combinations of the n bounded state variables.

For multifactorial optimization problems with continuous parameters, one can achieve multitasking by binning the parameters into B1, …, Bn discrete points over the corresponding domains of \({{{{\mathcal{D}}}}}_{1},\ldots ,{{{{\mathcal{D}}}}}_{n}\). This will generate \(k=\mathop{\prod }\nolimits_{i = 1}^{n}{B}_{i}\) tasks in total, where each task represents a unique condition. The binning can be applied evenly or unevenly, but the choice of the interval directly affects the resolution of the final result. A general rule is to bin each parameter based on the sensitivity of the fitness function to that parameter. Binning with small intervals can potentially find more solutions while inevitably slows down the search.

Given the multimodality of our multifactorial global optimization problem, it is natural to apply niching82 in EM to maintain the diversity of the population. In a niching scheme, each task t can be conveniently assigned to a unique niche represented by an n-dimensional vector \({{{{\bf{n}}}}}_{t}=({\theta }_{1}^{t},\ldots ,{\theta }_{n}^{t})\). By assigning equal fitness to the fittest candidates across k niches, we can end up locating a set of solutions that covers all possible conditions irrespective of their relative fitness82. A classical niche EA, however, is no longer suitable for multifactorial global optimization problems due to the fact that there is no intrinsic property (e.g. composition) for classifying the individuals. Instead, we introduce a maximum-gain dynamic niching (MGDN) algorithm for EM, as described in Supplementary Algorithm 1.

Given k niches, there are also k tiers of fitness evaluation associated with each individual x. The gist of the MGDN algorithm is to assign each new individual to only one dominating niche that has undergone the maximum gain in raw fitness w.r.t. the upper envelope before adding the individual to the database, and then apply a standard niching routine. To generate offsprings, parents are selected based on the individual ranking within the niche they are assigned to. After adding a new individual, the assigned niche of every existing individual is renewed by its maximum-gain niche (or, more precisely, minimum-loss niche) w.r.t. the updated upper envelope. The existing individuals are also subject to niche migration, depending on whether the assigned niche is a dominating niche. An effective fitness, given by the minimum difference between the raw fitness of the assigned niche and the updated upper envelope, is then used as the criterion for evaluating individual merits. In a MGDN-EM, we track the number of individuals in the database, d, and store the raw fitness of each individual at each niche in a d × k matrix F. Subsequently, we use a d × k dynamic matrix that only allows one entry per row, namely Feff, to record the effective fitness and the assigned niche for each individual x. Similar to a standard EA, the MGDN-EM converges when the population is stagnated for a number of generations successively.

To exemplify, we illustrate in Fig. 8 the evolution of the assigned niches and the effective fitness during the consecutive addition of 3 individuals x1, x2 and x3 when applying the MGDN algorithm. Once the first individual x1 enters the database, it is assigned to the maximum-gain niche n1, where the effective fitness is calculated to be 0. Likewise, the next added individual x2 is assigned to n3 with an effective fitness of 0. The addition of x2 does not change the effective fitness of x1 since they both contribute to the upper envelope. After adding x3, however, the fitness of x1 and x2 are completely dominated by x3 over all 3 niches. As a result, x3 is assigned to n3 with an effective fitness of 0, while the effective fitness of x1 and x2 are now calculated to be negative at n1 – the niche with the minimum fitness loss. Finally, we apply fitness sharing by forcing the assigned niches of x1 and x2 to both migrate to the dominating niche assigned with x3. This ensures that the merits of the 3 individuals are compared within a same niche n3, i.e., comparing all effective fitness scores in the third column of Feff.

Fig. 8: Illustration of the MGDN-EM algorithm.
figure 8

The raw fitness, effective fitness and the niche assignment are depicted as 3 new configurations, (a) x1, (b) x2 and (c) x3, being added consecutively into the database in a 1-factorial (i.e. θ) global optimization employing the MGDN-EM algorithm. Different on-envelope configurations are depicted in different colors. The dominating niche with the maximum gain after adding each configuration is indicated by the red arrow. F and Feff are the matrices storing the raw fitness and the effective fitness, respectively.

Full size image

Graphical Gaussian process surrogate

Given an adsorbate-alloy configuration x, we can represent it as a graph G by converting the atoms into nodes V and assigning unweighted edges \({{{\mathcal{E}}}}\) between nodes that are not apart more than a cutoff. We can then assign an initial label to each node by a label function \({\ell }_{0}:V\to {{{{\mathcal{L}}}}}_{0}\) based on the type of the corresponding atoms. In the next iteration h = 1, a new label function ℓ1 is obtained by performing a procedure named color refinement (also known as the 1-dimensional Weisfeiler-Lehman algorithm)83, shown in Supplementary Algorithm 3. This procedure is then reiterated until reaching the maximum iteration H, where the nodes in each graph are labeled with distinct ‘colors’ in each iteration h. This approach was originally proposed as a test of graph isomorphism83, but was recently implemented as graph kernels in kernel-based models for mainly classification tasks84.

Since the color refinement takes the neighborhood (i.e. the 1-hop neighbors) of each node into consideration, the node labels after each iteration can thus serve as fingerprints of the local chemical environment of the corresponding atoms. With more iterations, the local environment can be refined by message passing from longer distances. We hereby generalize a feature vector x for the graph in each iteration by counting the nodes in each ‘color’. For each iteration h > 0, we adapt the feature vector to our regression task by assigning a weight wh bounded between 0 and 1. The kernel function between two configurations x and \({x}^{{\prime} }\) can then be defined as a linear combination of the inner products of the feature vectors x and \({{{{\bf{x}}}}}^{{\prime} }\) at all iterations:

$$K(x,{x}^{{\prime} })={{{{\bf{x}}}}}_{0}^{{\mathsf{T}}}{{{{\bf{x}}}}}_{0}^{{\prime} }+\mathop{\sum }\limits_{h=1}^{H}{w}_{h}{{{{\bf{x}}}}}_{h}^{{\mathsf{T}}}{{{{\bf{x}}}}}_{h}^{{\prime} }$$
(2)

Since the weights are all non-negative, the kernel still returns an inner product of the transformed feature vectors and therefore is a valid Mercer kernel85.

Using Eq. (2) as the kernel function, we employ a graphical GP regression model as the surrogate in our BEM. Given some DFT-relaxed adsorbate-alloy configurations X and the corresponding electronic energies y, we can estimate directly the relaxed electronic energy of a new configuration x by the mean function of the GP,

$$\mu (x)={{{{\bf{k}}}}}_{xX}^{{\mathsf{T}}}{\left({{{{\bf{K}}}}}_{XX}+\lambda {{{\bf{I}}}}\right)}^{-1}{{{\bf{y}}}}$$
(3)

with an uncertainty quantification given by the variance

$${\sigma }^{2}(x)=K(x,x)-{{{{\bf{k}}}}}_{xX}^{{\mathsf{T}}}{\left({{{{\bf{K}}}}}_{XX}+\lambda {{{\bf{I}}}}\right)}^{-1}{{{{\bf{k}}}}}_{xX}$$
(4)

where kxX is the covariance vector between the new configuration x and the training configurations X, KXX is the Gram matrix of X, λ is a regularization term accounting for the noise of the training observations. Both λ and the weighting factors w1, …, wH are treated as hyperparameters θ and are jointly optimized by maximizing the log marginal likelihood of the N training data (X, y):

$$\begin{array}{rcl}\log p({{{\bf{y}}}}| {{{\bf{X}}}},{{{\boldsymbol{\theta }}}})&=&-\frac{1}{2}{\left({{{\bf{y}}}}-\mu ({{{\bf{X}}}})\right)}^{{\mathsf{T}}}{\left({{{{\bf{K}}}}}_{XX}+\lambda {{{\bf{I}}}}\right)}^{-1}\left({{{\bf{y}}}}-\mu ({{{\bf{X}}}})\right)\\ &&-\frac{1}{2}\log \left\vert {{{{\bf{K}}}}}_{XX}+\lambda {{{\bf{I}}}}\right\vert -\frac{N}{2}\log 2\pi \end{array}$$
(5)

Given the unit cell size of our surface atomistic models, we find that a maximum iteration H = 3 is sufficient to distinguish between any non-automorphic adsorbate-alloy configurations. This suggests that the automorphic duplicates generated throughout the BEM can be easily identified by checking the following equality for every pair of configurations:

$$K(x,{x}^{{\prime} })=\sqrt{K(x,x)K({x}^{{\prime} },{x}^{{\prime} })}$$
(6)

Besides, this also gives the important implication that our graphical GP model is able to describe any adsorbate-adsorbate interactions. As an example, we illustrate in Fig. 9 how the color refinement process generates different feature vectors for two adsorbate-catalyst configurations with slightly different adsorbate-adsorbate interactions. At iteration 0, the feature vectors are identical for both configurations as they both contain 9 Ni atoms and 2 O atoms. After one color refinement step, the feature vectors start to deviate, and become more disparate at higher iterations. With an increasing number of different adsorbate species, the feature vectors will be prolonged in each iteration, but the dimensionality of the general kernel function will not be affected thanks to the form of inner product.

Fig. 9: Illustration of the color refinement.
figure 9

The graph representations and feature vectors after 0, 1 and 2 iterations of color refinement are depicted for 2 similar adsorbate-catalyst configurations (a) and (b). Different types of atoms are encoded into different integers and are represented as differently colored nodes. In each color refinement iteration, all nodes and their 1-hop neighbors are further compressed into new integers to refine the colors of the nodes.

Full size image

Fitness function for alloy surface stability

For a binary alloy system consisting of a dopant metal A and a host metal B, we can model the alloy surface by an asymmetric periodic slab with the bottom layer fixed to the positions and composition of a bulk reference. The surface can then be assumed to be in equilibrium with underlying bulk and liquid/gas phase reservoirs3. In this 3-component system, the alloy surface is allowed to exchange metal atoms with the bulk reservoirs, meanwhile the adsorbates can exchange atoms with the liquid/gas phase reservoirs. This formulation allows an explicit assessment of the thermodynamic stability of an A-B alloy surface structure x in reactive environments using the surface free energy at a given reaction condition (θ1, …, θn):

$$\begin{array}{rcl}\gamma (x,{\theta }_{1},\ldots ,{\theta }_{n})&=&\frac{1}{{A}_{{{{\rm{surf}}}}}}\left[{G}_{{{{\rm{ads/slab}}}}}(x)-{N}_{{{{\rm{A(slab)}}}}}(x)\cdot {\mu }_{{{{\rm{A}}}}}-{N}_{{{{\rm{B(slab)}}}}}(x)\cdot {\mu }_{{{{\rm{B}}}}}\phantom{{\sum }_{i}}\right.\\ &&-\left.\mathop{\sum}\limits_{i}\left({N}_{i{{{\rm{(ads)}}}}}(x)\cdot {\mu }_{i}({\theta }_{1},\ldots ,{\theta }_{n})\right)\right]-{\gamma }_{{{{\rm{ref}}}}}\end{array}$$
(7)

where Asurf is the cross-sectional surface area of the slab’s unit cell, Gads/slab(x) is the total Gibbs free energy of the adsorbate-covered slab, NA(slab)(x) and NB(slab)(x) are the numbers of dopant and host metal atoms in the slab, μA and μB are the corresponding metal chemical potentials, Ni(ads)(x) is the number of non-metal atom i present in the surface adsorbates, μi(θ1, …, θn) is the chemical potential of this atom at the given reaction condition, and γref is the surface free energy of the reference clean slab (representing the bottom surface) which needs to be subtracted from the total surface free energy. We can calculate γref as

$${\gamma }_{{{{\rm{ref}}}}}=\frac{1}{2{A}_{{{{\rm{surf}}}}}}\left({G}_{{{{\rm{ref(slab)}}}}}-{N}_{{{{\rm{slab}}}}}{\mu }_{{{{\rm{ref(bulk)}}}}}\right)$$
(8)

where Gref(slab) is the Gibbs free energy of the reference slab, Nslab is the total number of atoms in the slab, μref(bulk) is the chemical potential of the bulk reference.

In this work, we use the pure host metal B as the reference. To relate the chemical potentials of both metals to the underlying bulk B reservoir, we can rewrite Eq. (7) by replacing the chemical potentials of every metal atom in the surface with that of the bulk B, then accounting for the free energy change arisen from doping A:

$$\begin{array}{rcl}\gamma (x,{\theta }_{1},\ldots ,{\theta }_{n})&=&\frac{1}{{A}_{{{{\rm{surf}}}}}}\left[{G}_{{{{\rm{ads/slab}}}}}(x)-{N}_{{{{\rm{slab}}}}}{\mu }_{{{{\rm{B(bulk)}}}}}-{N}_{{{{\rm{A(slab)}}}}}(x)\cdot \Delta {\mu }_{{{{\rm{A-B}}}}}\phantom{{\sum }_{i}}\right.\\ &&\left.-\mathop{\sum}\limits_{i}\left({N}_{i{{{\rm{(ads)}}}}}(x)\cdot {\mu }_{i}({\theta }_{1},\ldots ,{\theta }_{n})\right)\right]-{\gamma }_{{{{\rm{B}}}}}\end{array}$$
(9)

where ΔμA−B = μA − μB is the chemical potential difference between A and B. According to the derivation in Ref. 3, the value of ΔμA−B essentially reflects the changing rate of the chemical potential of the bulk B in response to an increment of A content. In this work, since we consider doping A at low levels into B, the A content in the bulk is assumed to be no higher than 25%. This allows us to approximate ΔμA-B by referencing to the chemical potentials of the bulk B and the stoichiometric AB3 bulk alloy (which serves as another stable bulk reservoir):

$$\Delta {\mu }_{{{{\rm{A-B}}}}}=-\frac{{\mu }_{{{{{\rm{AB}}}}}_{{{{\rm{3(bulk)}}}}}}-{\mu }_{{{{\rm{B(bulk)}}}}}}{3/4-1}=4\left({\mu }_{{{{{\rm{AB}}}}}_{{{{\rm{3(bulk)}}}}}}-{\mu }_{{{{\rm{B(bulk)}}}}}\right)$$
(10)

Next, the Gibbs free energy of the surface, including the adsorbates, can be written as

$${G}_{{{{\rm{ads/slab}}}}}={E}_{{{{\rm{ads/slab}}}}}^{{{{\rm{elec}}}}}+{F}_{{{{\rm{ads}}}}}^{{{{\rm{vib}}}}}+{F}_{{{{\rm{slab}}}}}^{{{{\rm{vib}}}}}-T\left({S}_{{{{\rm{ads}}}}}^{{{{\rm{conf}}}}}+{S}_{{{{\rm{slab}}}}}^{{{{\rm{conf}}}}}\right)+PV$$
(11)

where \({E}_{{{{\rm{ads/slab}}}}}^{{{{\rm{elec}}}}}\) is the electronic energy of the adsorbate-covered slab, \({F}_{{{{\rm{ads}}}}}^{{{{\rm{vib}}}}}\) and \({S}_{{{{\rm{ads}}}}}^{{{{\rm{conf}}}}}\) are respectively the vibrational free energy term (including zero-point energies) and the configurational entropy of the adsorbates, \({F}_{{{{\rm{slab}}}}}^{{{{\rm{vib}}}}}\) and \({S}_{{{{\rm{slab}}}}}^{{{{\rm{conf}}}}}\) are those of the surface, and PV is the volume term that can be neglected for transition metal alloy systems86. Combining Eqs. (8) to (11), we arrive at

$$\begin{array}{lll}\gamma (x,{\theta }_{1},\ldots ,{\theta }_{n})=\frac{1}{{A}_{{{{\rm{surf}}}}}}\left[{E}_{{{{\rm{ads/slab}}}}}^{{{{\rm{elec}}}}}(x)+{F}_{{{{\rm{ads}}}}}^{{{{\rm{vib}}}}}(x)+{F}_{{{{\rm{slab}}}}}^{{{{\rm{vib}}}}}(x)-{N}_{{{{\rm{slab}}}}}{\mu }_{{{{\rm{B(bulk)}}}}}\right.\\\qquad\qquad\qquad\quad\;\;\, -\,4{N}_{{{{\rm{A(slab)}}}}}(x)\cdot \left({\mu }_{{{{{\rm{AB}}}}}_{{{{\rm{3(bulk)}}}}}}-{\mu }_{{{{\rm{B(bulk)}}}}}\right)\\\qquad\qquad\qquad\quad\;\;\,-\mathop{\sum}\limits_{i}\left({N}_{i{{{\rm{(ads)}}}}}(x)\cdot {\mu }_{i}({\theta }_{1},\ldots ,{\theta }_{n})\right)-T\left({S}_{{{{\rm{slab}}}}}^{{{{\rm{conf}}}}}(x)\right.\\\qquad\qquad\qquad\quad\;\;\, \left.\left.+\,{S}_{{{{\rm{ads}}}}}^{{{{\rm{conf}}}}}(x)\right)-\frac{1}{2}\left({E}_{{{{\rm{B(slab)}}}}}^{{{{\rm{elec}}}}}+{F}_{{{{\rm{B(slab)}}}}}^{{{{\rm{vib}}}}}-{N}_{{{{\rm{slab}}}}}{\mu }_{{{{\rm{B(bulk)}}}}}\right)\right]\end{array}$$
(12)

Regarding the vibrational free energy terms for the adsorbates, since there is no significant variation between different types or chemical environment of the sites, we will only distinguish between different adsorbate species. For each species considered, we calculate the vibrational free energy term in the harmonic limit with the adsorbate bound to a representative site (see SI for DFT-calculated terms). At high coverages, the total vibrational free energy of all adsorbates is simply approximated by summing all individual terms. For the vibrational free energy terms of the surface and the bulk structures, we here assume they do not vary much with different metal compositions. Moreover, pairs of terms involving vibrational free energy calculations, e.g., \({F}_{{{{\rm{slab}}}}}^{{{{\rm{vib}}}}}(x)-{N}_{{{{\rm{slab}}}}}{\mu }_{{{{\rm{B(bulk)}}}}}\), \({\mu }_{{{{{\rm{AB}}}}}_{{{{\rm{3(bulk)}}}}}}-{\mu }_{{{{\rm{B(bulk)}}}}}\) and \({F}_{{{{\rm{B(slab)}}}}}^{{{{\rm{vib}}}}}-{N}_{{{{\rm{slab}}}}}{\mu }_{{{{\rm{B(bulk)}}}}}\), can cancel out one another to a large extent. Therefore, we decide to neglect all vibrational free energy terms for the surface and the bulk structures to avoid computationally expensive phonon calculations. This gives us the final working equation for the surface free energy of a dilute A-B alloy system:

$$\begin{array}{rcl}\gamma (x,{\theta }_{1},\ldots ,{\theta }_{n})&=&\frac{1}{{A}_{{{{\rm{surf}}}}}}\left[{E}_{{{{\rm{ads/slab}}}}}^{{{{\rm{elec}}}}}(x)+{F}_{{{{\rm{ads}}}}}^{{{{\rm{vib}}}}}(x)-{N}_{{{{\rm{slab}}}}}{E}_{{{{\rm{B(bulk)}}}}}^{{{{\rm{elec}}}}}-4{N}_{{{{\rm{A(slab)}}}}}(x)\cdot \phantom{{\sum }_{i}}\right.\\ &&\left({E}_{{{{{\rm{AB}}}}}_{{{{\rm{3(bulk)}}}}}}^{{{{\rm{elec}}}}}-{E}_{{{{\rm{B(bulk)}}}}}^{{{{\rm{elec}}}}}\right)-\mathop{\sum}\limits_{i}\left({N}_{i{{{\rm{(ads)}}}}}(x)\cdot {\mu }_{i}({\theta }_{1},\ldots ,{\theta }_{n})\right)\\ &&\left.-T\left({S}_{{{{\rm{slab}}}}}^{{{{\rm{conf}}}}}(x)+{S}_{{{{\rm{ads}}}}}^{{{{\rm{conf}}}}}(x)\right)-\frac{1}{2}\left({E}_{{{{\rm{B(slab)}}}}}^{{{{\rm{elec}}}}}-{N}_{{{{\rm{slab}}}}}{E}_{{{{\rm{B(bulk)}}}}}^{{{{\rm{elec}}}}}\right)\right]\end{array}$$
(13)

where \({E}_{{{{\rm{B(bulk)}}}}}^{{{{\rm{elec}}}}}\) and \({E}_{{{{{\rm{AB}}}}}_{{{{\rm{3(bulk)}}}}}}^{{{{\rm{elec}}}}}\) are the per-atom electronic energies of the bulk structures.

Under the assumption that the surface is in equilibrium with the liquid/gas phase, one can directly link the surface free energy to the reaction condition, (θ1, …, θn), through the chemical potential of each type of non-metal atom i, μi. Details of how we relate these chemical potentials to various reaction conditions in ORR and SMR can be found in the SI. We also provide discussions in the SI regarding the treatment of configurational entropy and the equivalence of our thermodynamic formulation to a semi-grand canonical MC.

In our BEM scheme, we ascribe a probability distribution of the relaxed electronic energy, \({E}_{{{{\rm{ads/slab}}}}}^{{{{\rm{elec}}}}}(x)\), to each adsorbate-alloy configuration x. This enables us to formulate the fitness function of the BEM using a Bayesian acquisition function commonly used in Bayesian optimization. Here we combine the Upper Confidence Bound (UCB) acquisition function with the surface free energy formulation in Eq. (13), and arrive at our task-dependent raw fitness function in the form of

$$\begin{array}{rcl}f(x,\kappa ,{\theta }_{1},\ldots ,{\theta }_{n})&=&-\frac{1}{{A}_{{{{\rm{surf}}}}}}\left[\mu (x)-\kappa \sigma (x)+{F}_{{{{\rm{ads}}}}}^{{{{\rm{vib}}}}}(x)-{N}_{{{{\rm{slab}}}}}{E}_{{{{\rm{B(bulk)}}}}}^{{{{\rm{elec}}}}}-4{N}_{{{{\rm{A(slab)}}}}}(x)\cdot \phantom{{\sum }_{i}}\right.\\ &&\left({E}_{{{{{\rm{AB}}}}}_{{{{\rm{3(bulk)}}}}}}^{{{{\rm{elec}}}}}-{E}_{{{{\rm{B(bulk)}}}}}^{{{{\rm{elec}}}}}\right)-\mathop{\sum}\limits_{i}\left({N}_{i{{{\rm{(ads)}}}}}(x)\cdot {\mu }_{i}({\theta }_{1},\ldots ,{\theta }_{n})\right)\phantom{{\sum }_{i}}\\ &&\left.-T\left({S}_{{{{\rm{slab}}}}}^{{{{\rm{conf}}}}}(x)+{S}_{{{{\rm{ads}}}}}^{{{{\rm{conf}}}}}(x)\right)-\frac{1}{2}\left({E}_{{{{\rm{B(slab)}}}}}^{{{{\rm{elec}}}}}-{N}_{{{{\rm{slab}}}}}{E}_{{{{\rm{B(bulk)}}}}}^{{{{\rm{elec}}}}}\right)\right]\end{array}$$
(14)

where κ is the trade-off parameter that determines the weight of uncertainty over the predicted mean. Note that when the search space is not completely shared by all tasks, a large penalty must be imposed to the fitness function for tasks that represent a mismatch between the queried configuration and the corresponding search space, e.g. the presence of S* under zero H2S conditions.

As has been discussed in ref. 59, one can control the balance between exploiting more stable configurations and exploring uncertain configurations by varying κ. A BEA run with a low κ value tends to stagnate its population much faster than those with higher κ values, while it also has a propensity to stuck in a local optimum and consequently suffering from a premature convergence. Since it is non-trivial to know the optimal κ beforehand, the common practice is to perform multiple BEA runs with various κ values ranging from low to high. However, learning from the idea of EM, we can simply consider κ as an additional ‘state variable’ and perform an ‘exploration-exploitation-balanced’ BEM in a single run by incorporating a vectorized κ with different values. Any other acquisition function with a trade-off parameter, e.g., expected improvement (EI), would also be applicable in such a multitasking setup.

Computational details

All DFT calculations have been performed using VASP87,88 with the spin-polarized revised Perdew-Burke-Ernzerhof89 (RPBE) exchange-correlation functional. The force convergence criterion for relaxation tasks is set to 0.05 eV/Å. The valence electrons are treated explicitly and the ionic cores are described by the projector augmented wave (PAW) potentials90. A plane-wave basis set is used with a kinetic energy cutoff of 500 eV and a Gaussian smearing with a width of 0.1 eV. The energy convergence criterion is set to 10−6 eV. For each adsorbate-alloy configuration, we model the system by a 4 × 4 × 4 periodic slab with a 10 Å vacuum layer in the z-direction and sample the first Brillouin zone by a 5 × 5 × 1 Monkhorst-Pack k-point mesh91. Vibrational frequencies for gas phase molecules and surface bound adsorbate species are calculated using the finite difference method with a step size of 0.01 Å.

We have carried out BEM searches using our ACAT implementation in conjunction with ASE66. To generate unweighted graph representations for the graphical GP model, we use a cutoff of rc = r1 + r2 + 0.75 Å, where r1 and r2 are the covalent radii of two neighboring atoms. When training the graphical GP model, we also jointly optimize all hyperparameters (w1, w2, w3 and λ) using a GP hyperparameter tuning implementation (A. L. Vishart, personal communication, August 9, 2021). All structure generation and BEM runs are performed with symmetry constraints using ACAT. In detail, we use the RandomOrderingGenerator (for alloy surfaces) and OrderedPatternGenerator (for adlayer patterns) to generate the initial population, the RandomSlabPermutation and RandomCompositionMutation operators to mutate respectively the chemical ordering and the composition of alloy surfaces, the AdsorbateGroupSubstitute, AdsorbateGroupPermutation and ReplaceAdsorbateSpecies operators to mutate adlayer patterns with symmetry constraints, and the CatalystAdsorbateCrossover operator to mate between the catalyst of one structure and the adlayer of another. To ensure the symmetry constraints can be applied to all adsorbate-alloy configurations generated during the BEM, we search and predict energetics strictly on the unrelaxed structures, whereas the graphical GP surrogate is always trained w.r.t. the relaxed structures. A WLGraphComparator is used to identify duplicate adsorbate-alloy configurations. Optimally, the hyperparameters of a BEM run, in particular the task settings and the population size, should be chosen according to the solution space of the system. However, one would not know the actual solutions without completing the full BEM-AL. Here we instead heuristically set the hyperparameters based on the solutions found in the first BEM iteration (i.e. employing the initial GP model). The parameters of the tasks are set to their most chemically-relevant ranges and the tasks are generated by binning evenly with a predefined resolution. As for the population size, we start from testing a large population size of 400, and then gradually reduce the size until the BEM cannot find the same number of solutions. Using this rule, we have set the population size to 50 and 300 in the BEM search of the alloy SPDs for ORR and SMR, respectively. H*, O* and OH* are considered as possible adsorbate species in the ORR case, while H*, C*, O*, S*, CH*, OH* and CO* are considered in the SMR case. In both cases, only a maximum of two different adsorbate species are allowed to present on each surface. We also set the minimum adsorbate-adsorbate distance allowed in the BEM search to 2 Å by removing all neighboring sites within a 2 Å radius (e.g. 1 neighboring shell for fcc(111) sites and 2 neighboring shells for fcc(100) sites), which effectively sets the coverage upper bound to 1 ML. Note that the minimum coverage is set to 0, i.e., clean slabs are still allowed. No bridge sites are considered for fcc(111) surfaces, as they are found to be unstable when binding the considered adsorbate species. The dopant is only allowed to enter the top 3 surface layers and its content is limited to be no higher than 25% in each layer considering the low dopant loading. This is also to prevent the surface energy from being strongly affected by the strain effect. Each EA run (including standard EA, EM and BEM) converges after the whole population stagnates for 2 consecutive generations. The BEM-AL for the ORR and the SMR case studies proceeds until there is no update to the lower envelope for 5 and 2 consecutive iterations, respectively.