Introduction

Ferroic materials are a family of materials that exhibit switchable order parameters, including electric polarization, spin polarization, or strain, in which the order parameters can be switched by external fields like electric fields, magnetic fields, or stress fields1. Multiferroic materials with the coexistence of electric and spin polarizations have garnered substantial attention due to the application in magnetoelectric functionality2,3,4,5. However, they are not abundant in nature due to the mutual exclusive origin of the two order parameters in most instances (empty d shells for electric polarization and partially filled d shells for spin polarization)6. In general, there are two types of multiferroics. The multiferroics whose electric polarization and spin polarization occur independently are defined as type-I, in which two kinds of ferroic orders exhibit weak coupling. In contrast, type-II multiferroics show strong coupling of their electric polarization and spin polarization7. The research for multiferroics had been focused on three-dimensional (3D) materials at first, leading to the discovery of various type-I and type-II multiferroics. Type-I multiferroics include the distortion induced by lone pair electrons in BiFeO38,9 and PbNiO310, geometric ferroelectricity in YMnO311,12 and Ca3Mn2O713, charge ordering in LuFe2O414 and Fe3O415. Type-II multiferroics, such as TbMnO316,17 and YBaCuFeO518, exhibit polar ordering driven by magnetic ordering.

In the past decade, significant breakthroughs have been made in the field of two-dimensional (2D) ferroics, including 2D ferroelectric (FE) materials like SnTe, MX (M = Ge, Sn, X = S, Se), In2Se3, CuInP2S619,20,21,22,23,24,25,26, and 2D ferromagnetic (FM) materials like CrI3 and Fe3GeTe227,28,29,30. Inspired by the progress in 2D FE and FM materials, the research on 2D multiferroics has gained attention, and several 2D multiferroics have been investigated, including Hf2VC2F2, CuMP2X6 (M = Cr, V, X = S, Se), ReWCl6, Cr(pyz)2, Co2CF2, VOX2 (X = Cl, Br, I)31,32,33,34,35,36,37,38. Recently, the study on one-dimensional (1D) ferroic materials has also emerged. Several 1D FE materials, such as GeS/SnS, WOX4 (X = F, Cl, Br), NbOX3 (X = Cl, Br, I), and VOF3 have been theoretically studied39,40,41,42. Besides, the research for 1D FM materials also makes breakthrough, for example CrSbSe3 and Ca2MnO3X (X = Cl, Br)43,44.

However, the exploration of intrinsic multiferroicity, characterized by the coexistence of ferroelectricity and ferromagnetism in 1D materials, is still yet to be realized. The realization of such materials is crucial for understanding the relationship between low-dimensionality and FE/FM ordering, and these studies can provide potential candidates for the development of high-density information storage devices. In this work, we predicted the existence of robust type-I multiferroicity in 1D MoOBr3 nanowires whose bulk phase has been successfully synthesized in experiments. Our findings indicate that this material exhibits spontaneous polarization (PS) along the wire axis, with high Curie temperature (~570 K) far above room temperature (300 K) and small coercive electric field (~0.56 MV/cm). This material, in addition, also possesses antiferroelectric (AFE) structures, which are metastable compared to FE structures. Both FE and AFE structures exhibit FM properties with calculated FM Curie temperatures for the FE and AFE structures are 9.5 and 9.3 K, respectively. We also found that tensile strain (~5%) can distinctly boost the ferroelectric polarization (~40%) and compress strain may readily switch the easy axis of FE MoOBr3 nanowires. To further demonstrate the multiferroicity in molybdenum oxytrihalides family, we also performed calculations for MoOCl3 and MoOI3 nanowires. This study marks the first reported analysis of intrinsic type-I multiferroicity in 1D materials. Our findings propose a novel 1D system encompassing both inherent electric and spin polarizations, offering significant promise for developing new electronic and spintronic devices based on 1D multiferroics.

Results and discussion

Structural and ferroelectric properties

The chemical synthesis of 1D transition metal oxytrihalides MOX3 in bulk phase, wherein M represents a transition metal and X denotes a halogen element, was initiated at an early stage, for instance MoOBr3, WOX3 and NbOX3 (X = Cl, Br, I)45,46,47. Recently, a modified method has been successfully employed to synthesize bulk phase of van der Waals 1D MoOBr3 nanowires, followed by a comprehensive investigation of its magnetic properties48. Sublimation method has been successfully utilized to extract a single van der Waals nanowire from bulk phase49,50, and this method makes obtaining a purely single MoOBr3 nanowire possible.

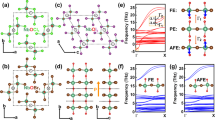
Here, we employ first-principles calculations to investigate the FE and FM properties of 1D MoOBr3 nanowires. The bulk phase structure of MoOBr3, presented in Fig. 1a, is characterized by a tetragonal crystal lattice with the P42nm space group. There are two MoOBr3 nanowires within a bulk unit cell (dash line square), and the calculated alignment of polarization directions in both MoOBr3 nanowires suggests that the bulk structure of MoOBr3 demonstrates FE behavior. This phenomenon is distinguished from bulk of 1D SnS/GeS that exhibit an AFE bulk phase39, so it is likely that FE polarization can be detected in bulk MoOBr3 without the necessity of exfoliation (See detail in Supplementary Fig. 1). In order to ascertain the potential for exfoliating MoOBr3 nanowires from bulk phase, the binding energy was calculated and found to be 0.102 J/m2, which is much smaller than the binding energies of black phosphorene (~0.358 J/m2)51 and MoS2 (~0.422 J/m2)52. For 1D MoOBr3 nanowires, the axis direction, also referred to as the periodic direction, is along the ‘a’ direction (Fig. 1b). There exhibits two MoO2Br4 octahedral units in one unit cell, with two Br atoms shared between the octahedral units situated at the central position along the ‘b’ (long radius) direction, as depicted in Fig. 1b. In the fully relaxed structure of MoOBr3 nanowires, it is observed that two Mo atoms, denoted as Mo1 and Mo2, possess displacements along the axis direction, so the structure breaks its centrosymmetry and exhibits a polar symmetry space group known as Pmm2. To quantify the displacements, we define the distortion distances d1 and d2, which represent the respective magnitudes of distortion of Mo1 and Mo2. In Fig. 1c, we define d1 = d2 > 0 ( < 0) as phase A (A’) that is a polar structure with polarization P1 = P2 > 0 ( < 0). In addition, we name the structure as phase B (B’) when d1 = −d2 > 0 ( < 0), accompanied by a polarization P1 = −P2 > 0 ( < 0), and phase B (B’) is characterized by a nonpolar space group identified as P2/m. The intermediate phase between A (B) and A’ (B’), denoted as the phase C, maintains centrosymmetry with d1 = d2 = 0 and corresponds to the space group Pmmm. By performing free-energy calculations and analyzing the parameter space of d1 and d2 (Fig. 1d), it is found that the Mo-displaced polar phases A and A’ are indeed the ground states with degeneracy in energy, and these two phases are separated by the Mo-nondisplaced centrosymmetric phase C along the counter-diagonal direction (d1 = d2). More importantly, the energy curve exhibits a characteristic anharmonic double-well shape commonly observed in FE materials in the counter-diagonal direction. Besides, the Mo-displaced nonpolar phases B and B’ also exhibit energy degeneracy and are separated by phase C along the main diagonal direction (d1 = −d2). However, it is critical to note that B and B’ are metastable phases as their anharmonic energy double-well is approximately 5 meV shallower than that of A and A’, and both of B and B’ do not possess polarization throughout the entire unit cell due to the equal and opposite nature of P1 and P2.

Fig. 1: Structural configurations and energy map.
figure 1

a The side view of MoOBr3 bulk phase, where Mo atoms show as green balls, O atoms show as red balls and Br atoms show as brown balls. The periodic direction of MoOBr3 nanowires is along ‘a’ direction, and the dash line shows one unit bulk cell. b The three-dimensional (3D) view (top panel), top view (middle panel) and front view (bottom panel) of a single MoOBr3 nanowire, and dash line indicates one unit cell in which two Mo atoms are named Mo1 and Mo2, respectively. c Top views of two energy degenerate Mo-displaced polar structures with opposite polarization (phases A and A’), two energy degenerate Mo-displaced nonpolar structures without polarization (phases B and B’) and Mo-nondisplaced centrosymmetric structure (phase C). d The free energy contour plot of single MoOBr3 nanowires as a function of displacement of Mo1 (d1) and displacement of Mo2 (d2). The positions of phases A’, A, B, B’ and C are indicated on the contour plot.

Full size image

The presence of ferroelectricity is often associated with the existence of soft optical modes in the Brillouin zone center of the corresponding centrosymmetric structure53,54,55. To thoroughly investigate the potential polar structures in MoOBr3, the Mo-nondisplaced centrosymmetric structure (phase C) is defined as paraelectric (PE) structure, in which four Mo-O bonds, four Mo-Br bonds in middle, and four Mo-Br bonds in edge are equivalent, respectively, and all O-Mo-Br bond angles are 90°. It is obvious that the positive and negative charge center are coincident in the paraelectric structure. In PE structure, Fig. 2a illustrates that there are two soft optical modes, denoted as λ1 and λ2, located in the Brillouin zone center, and these soft modes indicate the dynamical instability of 1D PE MoOBr3 system. Further analysis of soft modes vibration reveals that λ1 and λ2 correspond to the displacements of two Mo atoms along axis the direction, in which the displacements can be either in the same direction (λ1) or in opposite directions (λ2). Remarkably, the presence of these soft modes induces spontaneous transitions towards either phase A (A’) or phase B (B’), as is shown in Fig. 2b. As for phase A (A’), although four Mo-Br bonds in middle and four Mo-Br bonds in edge are still equal respectively, four Mo-O bonds are not equal (2.153 Å for two longer Mo-O bonds and 1.687 Å for two shorter Mo-O bonds) due to the displacements of two Mo atoms, leading to the separation of positive and negative charge centers. What’s more, this separations in two MoO2Br4 octahedral units are the same and there exhibits polarization in a whole MoOBr3 unit cell, so phase A (A’) is named as FE structure. With regard to phase B (B’), although Mo atoms have displacements, the polarization directions are inverse in both MoO2Br4 octahedral units. Therefore, the whole MoOBr3 unit cell does not show FE polarization, and we define phase B (B’) as AFE structure. The phonon spectra were thoroughly analyzed to ascertain the dynamical stability of FE and AFE structures, and there is no negative frequency is observed in the phonon spectra (Fig. 2a), providing further confirmation of the stability of the FE and AFE structures.

Fig. 2: Dynamical analysis and ferroelectric properties.
figure 2

a Phonon spectra for FE, PE and AFE structures from left to right, in which λ1 and λ2 indicates two soft optical phonon modes. b The vibrational modes of the imaginary mode λ1 and λ2 in a. c Two different FE switching paths and their energy barriers. d Free energy as a function of polarization. Red dots are the DFT results and blue line is from model fit. e Ferroelectric polarization as a function of temperature (red). The differential curve of polarization with respect to temperature (blue). f The FE hysteresis loop simulated by Monte Carlo calculations at room temperature (300 K).

Full size image

The polarization switching phenomenon plays a significant role in FE materials, as it enables desirable functionalities and applications. In this study, we designed and investigated two distinct paths for polarization switching in FE MoOBr3, as illustrated in Fig. 2c. Path-I indicates the displacements of two Mo atoms reverse synchronously, passing through the PE structure (phase C), and the polarization switching occurs concomitantly with the collective movement of the two Mo atoms. In contrast, Path-II demonstrates the displacements of two Mo atoms reverse independently. One Mo atom undergoes a reversal in displacement, while the other remains unchanged, resulting in an intermediate AFE state (phase B). Subsequently, the unchanged Mo atom also reverses its displacement, realizing the transition from phase A to A’. As is shown in Fig. 2c, the calculated energy barriers for path-I and path-II are 147.54 and 75.25 meV respectively, underscoring path-II is greater feasibility and efficiency in polarization switching compared to path-I.

To demonstrate the FE properties of MoOBr3, we have calculated the FE dipole value of MoOBr3 nanowires to be 3.81 eÅ per unit cell (u.c.) based on Berry phase method56,57. The PS value is defined as the FE dipole value divided by pure nanowire volume without the inclusion of vacuum, and the PS is aligned with the axis direction with a value of 0.61 C/m2, which is larger than that of 2D SnTe (~0.22 C/m2)19 and CuInP2S6 (~0.15 C/m2)24. For practical applications, it is crucial to ensure that the critical temperature, TC, of 1D FE MoOBr3 is sufficiently high to maintain polarization above room temperature. To investigate the impact of finite temperature, Monte Carlo (MC) simulations are performed, in which the Landau-Ginzburg-type expansion with the polarization serving as the order parameter20 is adopted to explore the variation of the free energy:

$$\begin{array}{l}\,E=\sum \limits_{i}\left[\frac{A}{2}\left({P}_{i}^{2}\right)+\frac{B}{4}\left({P}_{i}^{4}\right)+\frac{C}{6}\left({P}_{i}^{6}\right)\right]+\frac{{D}_{a}}{2}\sum\limits _{{\left\langle i,j\right\rangle }_{a}}{\left({P}_{i}-{P}_{j}\right)}^{2}\\\qquad+\,\frac{{D}_{b}}{2}\sum _{{\left\langle i,j\right\rangle }_{b}}{\left({P}_{i}-{P}_{j}\right)}^{2}\end{array}$$
(1)

in which i and j represent different MoO2Br4 octahedral units. The first three terms describe the energy contribution from polarization in each MoO2Br4 octahedral unit, capturing the anharmonic double-well potential depicted in Fig. 2d. The dipole-dipole coupling in the nearest-neighbor along the ‘a’ and ‘b’ directions, represented by coefficients Da and Db respectively, is crucial for stabilizing the FE ordering. The calculation methods of Da as well as Db are shown in Supplementary Fig. 3, and the values of coefficients A, B, C, Da and Db are summarized in Supplementary Table 2. Figure 2e illustrates the average polarization values as a function of temperature (red dots), in which blue line exhibits a sharp drop of polarization at a temperature near TC ( ~ 570 K), indicating the occurrence of a phase transition39. More significantly, the predicted TC is much higher than the experiment reported TC of 2D FE SnTe (~270 K)19 and CuInP2S6 (~320 K)24. To verify the thermal stability of FE and AFE MoOBr3 structures, ab initio molecular dynamics (AIMD) simulations are employed, and the results (Supplementary Fig. 4) confirm the thermal stability of both structures at room temperature (300 K). Figure 2f shows the MC simulated hysteresis loop of FE MoOBr3 nanowires at room temperature, and the coercive electric field is around 0.56 MV/cm. Compared to the coercive electric field of 2D FE In2Se3 (~10 MV/cm)23 and CuInP2S6 (~10 MV/cm)24, the small coercive electric field of MoOBr3 nanowires indicates its great potential for low power FE devices. The structural and FE parameters of both FE and AFE structures are summarized in Table 1 as below.

Table 1 Calculated lattice parameter a (Å), Mo displacement d (Å), and spontaneous polarization PS (C/m2) in one unit cell of 1D FE and AFE MoOBr3 nanowires, FE Curie temperature TC (K) of and coercive electric field EC (MV/cm) at room temperature (300 K) of 1D FE MoOBr3 nanowires
Full size table

Electronic and ferromagnetic properties

In addition to the studies of FE properties, we also investigated the electronic band structures of MoOBr3 nanowires. The valence states of Mo, O, and Br are +5, −2, and −1 respectively, so magnetism may appear because Mo-4d orbitals have an unbonded electron. Figure 3a displays the band structure of FE MoOBr3 with a FM ground state, which will be further discussed in subsequent sections. It is noteworthy that FE MoOBr3 behaves as a semiconductor with an indirect band gap of approximately 0.81 eV. All three structures (FE, AFE, and PE structures) exhibit FM spin polarization, with a total magnetic moment of 1 μB per MoO2Br4 octahedral unit. The partial density of states (PDOS) depicted in Fig. 3b reveals the DOS of the band structure in Fig. 3a, and PDOS results of AFE and PE MoOBr3 refer to the Supplementary Figure 5. To gain further insights, a real-space charge distribution analysis of the top two valence bands is conducted (Fig. 3c), along with a cross-section analysis of the partial charge distribution (Fig. 3d). These investigations indicate that the magnetic moment predominantly arises from the Mo-dyz orbitals. The coupling between the Mo-dyz and O-p orbitals is negligible within the Slater-Koster approximation58, therefore, the movement of Mo along the axis direction is not hindered by the Mo-dyz orbitals. Considering the configuration of Mo−Br−Mo, which approximates a right angle, and applying the Goodenough-Kanamori-Anderson rules59,60,61, it is inferred that a superexchange occurs in the Mo-Br-Mo bond via the py or pz orbitals of Br, favoring FM ordering (Fig. 3e). In accordance with the crystal field effects observed in octahedral complexes, the \({d}_{{z}^{2}}\) and \({d}_{{x}^{2}-{y}^{2}}\) orbitals (eg orbitals) lie directly in the path of the approaching ligands62. Electrons in these orbitals experience a greater force of repulsion compared to those in the dyz, dxy, and dxz orbitals (t2g orbitals) that are directed in the space between the approaching ligands. Consequently, the energy of the eg orbitals increases due to the greater repulsion, while that of the t2g orbitals decreases. The splitting of the Mo-d orbitals is illustrated in Fig. 3f, and it can be deduced that the dyz orbital exhibits a spin-up electron occupation, consistent with the previous partial charge analysis.

Fig. 3: Electronic results for ferroelectric MoOBr3 nanowires.
figure 3

a, b The band structure and partial density of states. c, d The partial charge distribution with isosurface equals to 0.004 e/Bohr3 and the cross section for partial charge of top two valance bands. e The nearly 90°superexchange diagram for Br-Mo-Br which describes the short-range magnetic ordering along the ‘b’ direction. f Left: The 3D view of MoO2Br4 octahedral unit. Right: The corresponding Mo-d orbitals splitting and occupation for MoO2Br4 octahedral unit.

Full size image

Like FE phase transition, the Curie temperature for FM phase transition is also a crucial parameter. To determine the energetically preferred magnetic ordering in MoOBr3, we employed a double cells configuration along the axis direction, where FM configuration and three antiferromagnetic (AFM) configurations were considered to explore the long-range magnetic ordering in FE MoOBr3, as illustrated in Fig. 4a. The presence of magnetic anisotropy is essential for stabilizing long-range magnetic ordering in 2D and 1D materials, as it overcomes the Mermin-Wagner restriction63, so we took the spin-orbit coupling (SOC) into account to evaluate the magnetic anisotropy energy (MAE) of MoOBr3. The magnetization direction was set along the ‘a’, ‘b’, and ‘c’ (short radius) directions respectively, among them that the most stable state corresponds to the ‘b’ direction while the highest energy state aligns along the ‘a’ direction. In order to effectively describe the FM interactions in MoOBr3, we constructed the following spin Hamiltonian:

$$\,\widehat{H}=-\sum _{\left\langle {ij}\right\rangle }{J}_{1}{\vec{S}}_{i}{{\,\cdot\, }}{\vec{S}}_{j}-\sum _{\left\langle {kl}\right\rangle }{J}_{2}{\vec{S}}_{k}{{\,\cdot\, }}{\vec{S}}_{l}-\sum _{\left\langle {mn}\right\rangle }{J}_{3}{\vec{S}}_{m}{{\,\cdot\, }}{\vec{S}}_{n}+\,K\sum _{\left\langle i\right\rangle }{({\vec{S}}_{i}^{z})}^{2}$$
(2)

in which the summation <ij> and <kl> include all the nearest-neighbor exchange interactions along ‘b’ and ‘a’ direction respectively, and the summation <mn> includes the next-nearest-neighbor exchange interactions. Last term denotes the magnetic anisotropy, which is defined as the energy difference per Mo atom of the hard axis and easy axis. The parameters J1, J2, J3, and K were extracted from the first-principles calculations, yielding values 3.964, 0.412, 0.161, and 0.269 meV, respectively (more details are given in Supplementary Information). The FM transition temperature was estimated using the MC simulations based on this spin model, and the obtained FM transition temperature for FE MoOBr3 is around 9.5 K64. For AFE MoOBr3, the corresponding FM transition temperature is approximately 9.3 K (Supplementary Fig. 6).

Fig. 4: Ferromagnetic properties.
figure 4

a The considered four magnetic configurations, including ferromagnetic state and three antiferromagnetic (AFM) states. Yellow and blue isosurfaces of 0.02 e/Bohr3 are corresponding to positive and negative spin density, respectively. b The average value of magnetization changes with temperature for FE MoOBr3 (red). The differential curve of magnetization with respect to temperature (blue). c The energies difference among three AFM states and FM state in a change with MoOBr3 from PE (normalized value is 0) structure to FE structure (normalized value is 1), in which the energy value of FM is set as reference value of zero. d The magnetic anisotropy energies (MAE) per Mo atom change with MoOBr3 from PE structure (normalized value is 0) structure to FE structure (normalized value is 1).

Full size image

Moreover, we made a tentative evaluation of the magnetoelectric coupling by monitoring the magnetism response to variations in FE polarization, achieved by transitioning Mo atoms from PE state to FE state. Figure 4c illustrates the corresponding energy dependence of the four magnetic configurations relative to FE structures, in which the ground state consistently maintains the FM ordering for FE MoOBr3 while the lowest energy AFM state exhibits AFM2 ordering. As MoOBr3 transitions from PE to FE structure, the energy difference between AFM2 state and FM state decreases, and the FM easy axis shifts from ‘c’ direction to ‘b’ direction. Additionally, the MAE for magnetization along the ‘a’ direction is always the highest, as depicted in Fig. 4d. The relative results of MoOBr3 transitioning from PE to AFE structure exhibit similarities to the consequences observed during the transition from PE to FE structure (details can be found in Supplementary Fig. 6). The FM parameters of both FE and AFE structures are concluded in Table 2 as below.

Table 2 Calculated band gap Eg (eV), magnetic exchange coupling parameters J1, J2, and J3 (meV), magnetic anisotropy energy K (meV), FM Curie temperature TC-FM (K) of 1D FE and AFE MoOBr3 nanowires
Full size table

Regulation of multiferroicity by strain

Strain is a highly effective method for regulating FE polarization and exerting influence on magnetic properties of materials, and the axis strain is applied to FE MoOBr3 to investigate the change of FE and FM properties, as illustrated in Fig. 5a. The comprehensive results clearly demonstrate positive correlations between both the displacements of Mo atoms and the polarization value with strain, and a 40% increase in the polarization value is observed when strain reaches 5% (Fig. 5b). To illustrate the significance of this finding, we compared our results to 2D systems with comparable FE switch barrier and FE dipole value, using the well-studied 2D α-GeSe as an example (barrier: ~137 meV, dipole: ~3.95 eÅ/u.c.). In the case of α-GeSe, an increase of approximately 10% in polarization value is observed under a uniaxial 5% strain applied along the polarization direction21, highlighting the giant response of polarization to strain in our FE MoOBr3 nanowires. With regards to the magnetic properties, the material maintains FM state when the strain varies from −3% to 5%. However, a notable finding emerges when the strain exceeds 2%, the energy of AFM3 state becomes lower than that of AFM1, despite AFM2 exhibiting the lowest energy among the three AFM states (Fig. 5c). Throughout the range of strains from −3% to 5%, a remarkable switch of the easy axis from ‘c’ direction to ‘b’ direction is observed when the strain is around −2%, and ‘c’ direction even become the hardest axis if the strain larger than 4%, as depicted in Fig. 5d.

Fig. 5: Regulation of multiferroicity by strain.
figure 5

a Strain direction for FE MoOBr3 nanowires. b Alteration of Mo’s displacement with regard to strain (red). Variation of polarization changes with strain (blue). c The energy difference among three AFM states and FM state as functions of strain. d Change of the MAE per Mo atom with regard to strain, in which red dots indicate MAE between ‘c’ and ‘b’ directions and blue dots represent MAE between ‘a’ and ‘b’ directions.

Full size image

Finally, we can confirm the type of multiferroicity exhibited in 1D MoOBr3 nanowires by discussing the origin and coupling of ferroelectricity and ferromagnetism. Based on the previous results, it is evident that ferroelectricity of MoOBr3, which combines contributions of ionic polarization and electronic polarization, arises from the displacements of Mo atoms. In this case, it is noteworthy that the absolute value of ionic polarization (0.95 C/m2) is approximately three times larger than that of electronic polarization (0.34 C/m2), despite their opposite directions (refer to the Supplementary Figure 2 for more details). On the other hand, ferromagnetism in MoOBr3 can be attributed to the presence of half-filled Mo-dyz orbitals, as indicated by electronic analysis. Importantly, MoOBr3 system consistently maintains a FM state as it transitions from PE structure to FE/AFE structure, though the magnetic easy axis changes from PE to FE structure. Therefore, we can conclude that there is an intrinsic type-I multiferroicity presenting in 1D MoOBr3 nanowires, in which the electric polarization and spin polarization show weak coupling. What’s more, the Dzyaloshinskii-Moriya interaction may exist in FE MoOBr3 nanowires (Supplementary Fig. 8), based on the investigation on 2D type-I multiferroic VOI265,66. To further broaden the multiferroicity in MoOX3 (X = Cl, Br, I) family, we also performed calculations for MoOCl3 and MoOI3 nanowires (see results in Supplementary Information).

In summary, our study has presented the prediction of intrinsic type-I multiferroicity in one-dimensional MoOBr3 nanowires. The nanowires exhibit both ferroelectric and antiferroelectric structures, the polarization arises from the displacements of Mo atoms, and the ferroelectric MoOBr3 nanowires possess above room temperature ferroelectric TC and small coercive electric field. Additionally, we have also discovered the presence of ferromagnetic ordering along the radius direction in both ferroelectric and antiferroelectric MoOBr3 nanowires due to the half-filled Mo-dyz orbitals, leading to the inherent coexistence of ferroelectricity and ferromagnetism in one-dimensional materials. Further investigation indicated that strain can evidently boost ferroelectric polarization and readily switch ferromagnetic easy axis of ferroelectric MoOBr3 nanowires. Our findings not only realize intrinsic one-dimensional multiferroicity, but also provide a practical platform for the development of nanoscale devices.

Methods

First-principles calculations details

Our first-principles calculations are performed within the density functional theory (DFT) formalism, and the calculation software package is the Vienna Ab-initio Simulation Package (VASP)67. The projector augmented wave (PAW)68 method is employed to model the ionic potentials, treating the Mo 4p 5 s 4d, O 2 s 2p, and Br 4 s 4p as valence electrons. The exchange and correlation energy are treated with the Perdew–Burke–Ernzerhof (PBE)69 realization of the generalized gradient approximation (GGA) and the GGA + U70 method is applied for the 4d orbitals of Mo atoms with Ueff = 2 eV. The Heyd-Scuseria-Ernzerhof (HSE06)71,72 functional is also adopted to compare with the GGA + U results. The energy cut-off is set to 500 eV, and a vacuum region larger than 15 Å is introduced to avoid interactions between neighboring nanowires. The van der Waals (vdW) correction is considered by DFT-D3 approach73. All the atoms are allowed to relax until the calculated forces were converged to 0.01 eV Å-1, and the energy precision was set to be 10-5 eV. The energy precision was set to be 10-7 eV for MAE calculations. The k-point grid of 13 × 1 × 1 in the Monkhorst-Pack scheme74 is used to sample the Brillouin zone for relaxation and self-consistent calculations. The spin−orbit coupling (SOC)75 effect is taken into consideration for MAE calculations. The Nudged Elastic Band (NEB) method76 is used to study the ferroelectric phase transition. Lattice dynamics calculations are performed with the Phonopy package77, which uses the supercell finite-displacement method to obtain sets of second-order force constant matrices. The force constant matrices are calculated using 4 × 1 × 1 supercells for the FE, AFE and PE phase.

Monte Carlo simulations details

MC simulations are performed for a periodic 1D supercell containing 103 unit cells. The 4 × 105 MC steps are used for equilibration, and every simulation is repeated 3 × 105 times.

Molecular dynamics simulations details

Ab initio molecular dynamics (AIMD) simulations are studied by taking NVT ensemble with Nosé thermostat78 at finite temperature by VASP code67. Calculations are performed on 8 × 1 × 1 supercells, for a total of 6000 fs with a 1.5 fs time resolution.