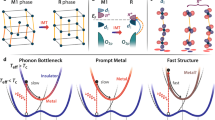
Abstract
Transition metal d-electron oxides with an odd number of electrons per unit cell are expected to form metals with partially occupied energy bands, but exhibit in fact a range of behaviors, being either insulators, or metals, or having insulator-metal transitions. Traditional explanations involved predominantly electron-electron interactions in fixed structural symmetry. The present work focuses instead on the role of symmetry breaking local structural motifs. Viewing the previously observed V-V dimerization in VO2 as a continuous knob, reveals in density functional calculations the splitting of an isolated flat band from the broad conduction band. This leads past a critical percent dimerization to the formation of the insulating phase while lowering the total energy. In VO2 this transition is found to have a rather low energy barrier approaching the thermal energy at room temperature, suggesting energy-efficient switching in neuromorphic computing. Interestingly, sufficient V-V dimerization suppresses magnetism, leading to the nonmagnetic insulating state, whereas magnetism appears when dimerization is reduced, forming a metallic state. This study opens the way to design novel functional quantum materials with symmetry breaking-induced flat bands.
Similar content being viewed by others
Introduction
Unlike metal sp-orbital oxides, cation d-orbital oxides manifest a specific selectivity between being either persistent insulators, or persistent metals, or transitioning between the two phases. For example, under ambient conditions, the early 3d metal oxides LaTiO3 and LaVO3 are persistent insulators both below and above the magnetic ordering temperature1,2,3, whereas SrVO3 and CaVO34 are persistent metals, while VO25,6,7,8,9 shows reversible insulator-metal transition (IMT) near room temperature holding promising applications for neuromorphic computing. Understanding such distinct choices made by undoped quantum materials has occupied physical chemists and condensed matter theorists1,2,3 for a long time. Such trends can be gleaned phenomenologically from the composition-weighted sum of formal valence charges (FVC). In conventional sp-electron oxides—such as Al2MgO4—the FVC is zero, consistent with being charge-neutral insulator with the Fermi level (EF) located between the occupied valence and empty conduction bands. Yet, in Sr2+V5+(O2−)3, La3+Ti4+(O2−)3 or V5+(O2−)2 the FVC are +1. Thus, in the absence of any structural or magnetic symmetry breaking, these FVC > 0 compounds would be expected to have a metallic band structure with EF residing in the principal conduction band. Whether or not symmetry breaking is sufficient to convert the initial hypothetical metal into a real insulator10,11,12, depends on the balance between the energy gained by lowering EF from the conduction band into the gap region vs. the energy invested in breaking bond symmetry. For example, the fact that LaTiO3 and LaVO3 are persistent insulators under ambient conditions could be explained by magnetic symmetry breaking in the antiferromagnetic and paramagnetic phases10,12; whereas SrVO3 remains metallic has been explained10,11 by the insufficient magnitude of the magnetic and octahedral (tilting) symmetry breaking.
Attempts to understand the origin of insulating as well as metallic phase of vanadium dioxide has attracted interests for over 60 years5, in part because its transition temperature (TIMT) is conveniently positioned near room temperature (340 K5), offering interesting applications9,13,14. The foregoing discussion raises the dilemma of why the quintessential insulator-metal transition system VO2 is an insulator at low T and metal at higher T even though it is believed to lack magnetic symmetry breaking6,7,15,16 or octahedral (tilting) symmetry breaking. The current paper studies this question, pointing to relevant mechanisms for the existence of both insulating (Fig. 1a) and metallic (Fig. 1b) phases in VO2, namely the emergence of “split-off flat bands” as a consequence of symmetry breaking, as well as potential hidden magnetism.
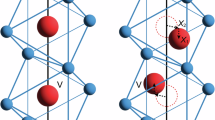
a Monoclinic (M) VO2 (space group: \(P{2}_{1}/c\))48 with alternating short (shown by blue bond) and long (shown by dashed line) V-V bonds along the V chain (in the direction of the a axis of the monoclinic lattice) due to V-V dimerization. b Rutile (R) VO2 (space group: \(P{4}_{2}/{mnm}\))46 with uniform V-V bond length along the V chain (in the direction of the c axis of the rutile lattice) and absence of V-V dimerization. The cartesian axes used in electronic structure calculations are given (a, b).
Early density functional theory (DFT) band structure calculations of non-magnetic monoclinic VO2 by Wentzcovitch, Schulz, and Allen15 predicted a vanishing band gap despite the assumed presence of V-V dimers that might have produced a Peierls band gap. Also, photoemission measurements by Shin et al. 17 indicated that the measured d-d bonding-to-antibonding splitting in the insulating phase is ~2.5 eV, which was much larger than the value of ~0.5 eV found in the molecular cluster calculation of Sommers and Doniach18. These discrepancies between experiments5,6,7,17 and mean field calculations (lacking strong correlation)15,18 drew attention to alternative explanation of the electronic structure of VO2, such as strong electron correlation1,3 where on-site electronic Coulomb correlation U plays a dominant role. For example, as the different types of insulating phases of VO2 with different dimerization arrangements are found to have comparable interband transition energies across the band gap, ref. 19 concludes that V-V dimerization may not be an important factor for opening the band gap. However, such conclusions may be premature given that they were based on calculations with large U values (5.7 eV) that could overwhelm other symmetry breaking effects. (Indeed, it was noted recently that applying large U terms to DFT could lead to insulating electronic structures even in the otherwise metallic rutile phase20). A compromise hybrid approach of Coulomb-assisted mechanism for the phase transition in VO2 was offered recently16,21. However, other density functional band calculations of dimerized and nonmagnetic monoilinic phase with a better description of the compactness of d orbitals excluding the on-site coulomb repulsion term U predicted correctly the monoclinic phase to be an insulator22,23,24. These theoretical advances15,22,23,24 implied that neither strong correlation nor long-range ordered magnetism are necessarily required to form the gap in monoclinic VO2. However, how the electronic states associated with insulator-metal transition are influenced by V-V dimerization and magnetism, and how V-V dimerization interacts with magnetism in VO2 still remain unclear.
In the present work we study insulating and metallic phases in VO2 by using the monoclinic and rutile periodic structures (Fig. 1) in the framework of mean-field-like density functional theory. Whereas this approach can include (electron-gas like) correlation effects, it does not include degeneracy-removal “strong correlation”25. A popular application of DFT band theory involves using as input a high symmetry ‘averaged configuration’, often deduced by X-Ray Diffraction. However, it is possible to extend such DFT applications by allowing structural or magnetic symmetry breaking, should it lower the total (internal) energy of the system. We thus start from the symmetry unbroken nonmagnetic rutile phase of VO2, and study the symmetry breaking associated with atomic positions (V-V dimerization) or magnetic moments (paramagnetism) in the initial insulating and final metallic phases. We take this approach specifically to examine whether local structural and/or magnetic symmetry breaking effects, can explain the mechanism of insulating vs metallic phases. Such effects might include different degrees of V-V bond alternation as well as different distributions of local magnetic moments in the supercell26. Details of the method of calculation are provided in the Methods section.
We find that, in the framework of DFT, as V-V dimers form in VO2, rather narrow “flat bands” split off the partially occupied broad metallic conduction band of the symmetry unbroken structure (Fig. 2a), resulting in occupied isolated d bands below the now empty conduction band. This process of forming split-off flat bands due to structural symmetry breaking creates the insulating phase (Fig. 2b, where the yellow highlight indicated the insulating band gap). The d-d bonding-to-antibonding splitting predicted in our DFT study without U is consistent with the experimental measurement17. We find that strong dimerization will suppress the magnetism, leading to the nonmagnetic insulating state with split-off flat bands. In contrast, magnetism appears when dimerization is weakened, indicating hidden magnetism in the transient monoclinic phases during the insulator-metal transition as well as the metallic rutile phase. We predict a rather low energy barrier between the nonmagnetic monoclinic phase and the magnetic rutile phase from DFT approaching the thermal energy at room temperature. The present study suggests the existence of hidden magnetism in the process of insulator-metal transition in VO2, and reveals the interplay between the hidden magnetism and V-V dimerization as well as their roles in the transition associated with the formation of split-off flat bands. This opens the way of designing functional quantum materials with exotic physical properties enabled by split-off flat bands.
a, b Electronic structures of nonmagnetic VO2 from the revised Perdew-Burke-Ernzerhof (PBE) exchange-correlation functional (R-PBE)51. DBA = 0% corresponds to the symmetry unbroken rutile structure in the M-like unit cell subject to structural minimization with R-PBE. ∆Eint in a indicates the internal gap between the principal conduction band and the principal valence band. DBA = 25.6% in b was obtained via structural minimization of the M phase with R-PBE. Bold red curves indicate the bands that are split off from the principal conduction band as the DBA increases. The yellow highlight in b indicates the gap between the lowest conduction band and the highest, split-off valence band. c Partial charge density of the split-off bands shown by bold red curves in b (isosurface: 0.01 \(\left|{\rm{e}}\right|{{\rm{bohr}}}^{-3}\)).
Results and discussion
Structural symmetry breaking in VO2 without magnetism
Flat Bands splitting off from the metallic principal conduction band in response to V-V dimerization
We first focus on the physical properties of the nonmagnetic VO2 phases. As pointed out by Koster and Slater27, isolated subbands can split off from a continuum of bands into a band gap region in response to specific perturbations, once the latter exceed a critical miniml magnitude. The structural perturbation (V-V dimerization) in VO2 leads to a V chain with alternating short and long V-V bonds (see Fig. 1a), where all V atoms are dimerized. We define the “degree of bond alternation” (DBA) as
based on the two V-V bond lengths (\({d}_{{\rm{V}}-{\rm{V}}}^{{\rm{long}}}\) and \({d}_{{\rm{V}}-{\rm{V}}}^{{\rm{short}}}\)). The DBA is denoted in percentage for clarity. The maximal value of DBA in VO2 is estimated to be 81.8% based on the hard-sphere model of the monoclinic phase by using the ionic radii28 of 0.58 Å for V4+ and 1.36 Å for O2-, with the minimum value being zero for the rutile phase. To explore the electronic structure by continuously monitoring its variation at different DBA values, we appoint the rutile phase (see Fig. 1b) and the monoclinic phase (Fig. 1a) as two end-point structures, which are relaxed by DFT, and averagely separate the different corresponding atomic positions of the two end-point structures into a number of “snapshots” of intermediate structures.
Figure 2a shows the electronic structure of the symmetry unbroken phase (DBA = 0%), where the Fermi level EF lies in a broad principal conduction band, leading to a metallic electronic structure. The k-path used is shown in Supplementary Fig. 1 and the structure used (rutile phase in M-like unit cell) is shown in Supplementary Fig. 2. Note in Fig. 2a the existence of an “internal energy separation” ∆Eint between the principal conduction band (V-d) and the principal valence band (O-p). This provides an incentive for symmrty breaking by lowering EF from the conduction band into the internal gap area. We see that as the DBA increases, two narrow V-d bands split off from the broad conduction bands, forming isolated split-off “flat bands” that become the occupied upper valence band (the bold red curves in Fig. 2b). The squared wavefunction of the occupied split-off flat bands, shown in Fig. 2c, are localized near the V atoms and V-V bonds of the V-V dimers (tilted away from the direction of the V chains, see also Fig. 1a) trapping V-d electrons. It is interesting to study the effect of the tilting of V-V dimers on the electronic structure of VO2. We find that when changing the orientations of the V-V dimers into the direction of the V chains in the M structure while maintaining the DBA, the split-off flat bands are maintained and the insulating band gap changes negligibly, as shown in Supplementary Fig. 3. Our results suggest the robustness of the insulating states against variations of the V-V dimer orientations in monoclinic VO2. We will thus focus on the effect of DBA on the formation of the insulating states.
Figure 3 follows the process of emergence of flat bands from the continuum as the DBA increases gradually [see Fig. 3a–c for the density of states (DOS) of monoclinic VO2 with given % dimerization]. Supplementary Fig. 2 demonstrates that the rutile structure in the monoclinic-like unit-cell is connected to the monoclinic structure by small atomic distortions and small cell-shape variations. The intermediate structures with different DBA values calculated in Fig. 3 are generated by gradually applying these atomic distortions and cell-shape variations to the rutile structure as a linear interpolation between the rutile and monoclinic structures. As the degree of bond alternation increases, a portion of the V-d states gradually split off the continuum conduction band forming the isolated split-off flat bands with a band gap opened between the split-off flat bands and the conduction bands (see Fig. 3c from R-PBE and Supplementary Fig. 4 from HSE). Fig. 3d shows the energy gap between the occupied split-off states and the empty above continuum V-d states as a function of V-V dimerization. Different exchange-correlation functionals have different threshold DBA values at which the perturbation is large enough to split off flat bands into the principal gap. This is reminiscent of the way that impurity levels split off the continuum broad band past a critical impurity potential strength in the Koster-Slater work27. As shown in Fig. 3d, the Heyd-Scuseria-Ernzerhof (HSE) functional29 has the minimal threshold DBA to expel flat bands from the continuum into the gap, followed by the strongly constrained and appropriately normed (SCAN) meta-GGA functional30 and the local density approximation (LDA)31. Note that the LDA functional requires a larger DBA than the value used in the LDA study of ref. 15, which may explain why ref. 15 did not produce a band gap. Details of band gaps from preceding theoretical studies are provided in Supplementary Table 1.
a–c Density of states from R-PBE exchange-correlation functional of nonmagnetic monoclinic VO2 with given degrees of bond alternation. The crystal structures with different DBA values are generated by linear interpolation of the relaxed (by R-PBE) rutile and monoclinic structures. The majority states are indicated in a–c. Blue area indicates the occupied states. The split-off flat-band states in c are indicated by bold red boundary, which have a band width of 0.43 eV and are separated from the other d states in the conduction band by 0.14 eV (Eg). \(\triangle {d}_{{\rm{||}}}\) in c indicates the splitting energy between the bonding and antibonding \({d}_{{\rm{||}}}\) bands mainly consisting of \({a}_{1g}\) states. d Band gaps of the monoclinic structures generated by linear interpolation of the R and M structures as a function of DBA from different types of exchange-correlation functionals29,30,31,51,55 without U.
One might have thought that the appearance of relatively narrow bands is not unexpected in systems with d orbitals that have the capacity to be localized, and that this finding is therefore not surprising or new. In our view this is, however not the correct expectation. Note that the conduction band of VO2 in the absence of symmetry breaking dimerization is a rather broad band (Figs. 2a and 3a) even though it contains significant d-orbital character that has the capacity to localize. Thus, a system of d orbitals of ions such as V4+ can be intrinsically delocalized and cannot be expected to represent “heavy bands”. What is, in our view, new and surprising, is that a threshold magnitude of symmetry breaking (measured by the DBA in Fig. 3d) splits from this broad delocalized empty metallic band a much narrower sub-band (highlighted by the bold red band in the band structure of Fig. 2b and the bold red DOS peak in Fig. 3c), which becomes the flat band-like valence band maximum in the insulating phase. It is this sub-band, that is created by symmetry breaking—not via topology (as in Kagome lattices32,33,34,35) or via strong correlation (we use U = 0) that gives rise to the insulating phase. In this respect the study of the electronic structure as a function of the DBA provides conceptually new insight into the insulator-metal transition of VO2.
Difference between symmetry breaking-induced split-off flat bands and flat topological bands (FTBs)
The symmetry breaking-induced split-off flat bands presented here are different from the flat topological bands (i.e. flat bands with nontrivial topological properties) discussed recently in the literature32,33,34,35. The FTBs are analyzed via model Hamiltonians for certain lattice topologies32. For example, the bipartite lattice (AnBm)32,36, as one of the topological lattice geometries, does not consider homopolar A-A or B-B bonds that are formed by symmetry breaking, such as metal-metal dimerization. Indeed, the FTBs originate from the geometrical topology and weak atomic orbital couplings32,33, and are often connected by dispersion to other bands32. In contrast, the isolated split-off flat bands found here in VO2, arise from structural symmetry breaking that creates homopolar bonds (V-V dimerization). The FTBs predicted in the symmetry unbroken phase of VO2 are different in many ways from the symmetry breaking-induced flat bands. For example, the FTBs predicted in the symmetry unbroken rutile phase of VO2 is the lowest principal conduction band with a wide overall band width of ~1.2 eV32,36. Whereas, the isolated split-off flat bands in the symmetry broken monoclinic phase are the upper valence bands with a much narrower overall band width of 0.43 eV (17 meV along the Z-E k-line) (see Fig. 2b and Fig. 3c). Furthermore, the isolated split-off flat bands in the monoclinic phase can be switched on and off by tuning the magnitude of symmetry breaking as a knob. On the other hand, the FTBs persist for certain lattice topologies32,33,34,35.
The appearance of magnetism with reduced V-V symmetry breaking
V-V dimerization counters magnetism
In the above section, we assumed that the monoclinic phase with strong V-V dimerization to be nonmagnetic. The following issue is how dimerization influences magnetism and when magnetism is suppressed. We test the three ordered magnetic configurations with zero global magnetic moment in the monoclinic unit cell (see the Insets to Fig. 4a), and examine such magnetic configurations in the M phase with strong dimerization. We find the initial non-zero local magnetic moments on the V sites are all relaxed to zero, which demonstrates that strong V-V dimerization suppresses magnetism. We further examine the disordered magnetic moments by applying the spin special quasi-random (spin-SQS) magnetic configurations on the 1 × 2 × 2 supercell (48 atoms) of the monoclinic structure. The initial local magnetic moments on the V sites are also relaxed to zero. The initial and final states of the above supercell calculations are given in Supplementary Fig. 5. Our results coincide with the fact that the ground state monoclinic phase of VO2 is believed to be nonmagnetic6,7,15,16.
a Energy barriers for the transition paths between rutile and monoclinic VO2 obtained from climbing image nudged elastic band with R-PBE. The relaxed (by R-PBE) rutile structure in the M-like unit cell and the monoclinic structure are used as the endpoints for the nudged elastic band calculations. The nonmagnetic configuration and the three magnetic configurations with zero global moment in the monoclinic-like unit cell (see Insets) are considered. b Average magnetic moment magnitudes over the V4+ ions in VO2 that are equivalent for the nonmagnetic configuration but can separate into non-equivalent groups for magnetic configurations along the phase transition paths for the three magnetic configurations shown in a. c Band gaps of VO2 along the phase transition paths for the three magnetic and nonmagnetic configurations.
Next, we investigate whether magnetism can appear in VO2 when V-V dimerization is reduced. To address this issue, we employ the climbing image nudged elastic band (NEB) method37 to search for the minimum-energy transition path between the monoclinic phase and rutile phase (see Fig. 4a) and monitor the local magnetic moments (Fig. 4b) as well as band gaps (Fig. 4c) along the path. The structures derived by linear interpolation of the relaxed rutile (in M-like unit cell) and monoclinic structures are used as initial structures for the NEB calculations. We consider the three ordered magnetic configurations (see the Insets in Fig. 4a) by using the relaxed rutile structure in the monoclinic-like unit cell and the monoclinic structure as the two endpoint phases for the nudged elastic band calculations. The structural transition from the rutile to the monoclinic phase along the minimum-energy paths of the nudged elastic band calculations is demonstrated in Supplementary Figs. 2, 6, 7, which also show the intermediate images that are the local maxima of the minimum-energy paths. We find that although the strong V-V dimerization in monoclinic VO2 leads to a nonmagnetic phase, when the dimerization is significantly reduced, e.g., in the rutile phase, non-zero local magnetic moments are found in DFT calculations. Certain types of magnetism lead to interesting spin splitting in the energy bands, named non-relativistic spin splitting (NRSS)38,39,40. We find large NRSS in the calculated electronic structure of the Mag-2 configuration (see Fig. 4a) of the rutile phase as shown in Supplementary Fig. 8. Furthermore, Fig. 4b shows that: (i) the overall magnitudes of the local magnetic moments for the three magnetic configurations (Mag-1, 2, 3, see Insets of Fig. 4a) at the same DBA are close to each other; (ii) the local magnetic moments fall down towards vanishing as DBA increases up to the threshold around 20%. Our results based on DFT without U demonstrate the compensation between V-V dimerization and magnetism, i.e., strong dimerization suppresses local magnetic moments whereas weak or zero dimerization enhances the formation of magnetic moments, leading to hidden forms of magnetism in the transient phases during IMT as well as the final metallic rutile phase. The spin splitting and spin polarization arising from the hidden magnetism can be switched on (off) by the forward (backward) insulator-metal transition, shedding light on the potential technological application of the hidden spin physics in the IMT of VO2.
Ultra-low energy barrier for the insulator-metal transition from the nonmagnetic monoclinic phase to the magnetic rutile phase
We next discuss the phase transition between nonmagnetic monoclinic to magnetic rutile phase. The rutile phase is found to be metallic with or without magnetism (see Fig. 4c). As shown in Fig. 4a, the phase transition barrier between monoclinic and rutile VO2 in the Mag-1 (Mag-2 or Mag-3) ordered configuration is found to be 0.041 (0.034 or 0.040) eV per dimer from R-PBE, lower than the phase transition barrier (0.046 eV per dimer) for the nonmagnetic configuration. Such ultra-low phase transition barriers approaching the thermal energy of the insulator-metal transition temperature (kBTIMT, TIMT = 340 K5) not only coincide with the low TIMT of VO2 but also suggest the low energy cost of IMT in VO2 near room temperature. It is interesting to notice that for the Mag-2 configuration (see Fig. 4a), the structure with a medium DBA (~11.5%) is a metallic local minimum on the phase transition path—such higher-energy metallic magnetic monoclinic phase could be detected during the process of photoinduced phase transition41,42,43.
Possible paramagnetism in the rutile phase
Due to the small energy difference between nonmagnetic and ordered magnetic configurations (4–9 meV per f.u., see Fig. 4a), the rutile phase is not likely to be magnetically ordered near TIMT (340 K5). Recent magnetic susceptibility (χ) measurements reported a sharp drop at TIMT from a temperature-dependent large χ to a negligible χ as temperature decreases, suggesting a transition from a high-T paramagnetic state to a low-T nonmagnetic or weakly magnetic state44,45. To model the paramagnetic rutile phase, we construct a spin-SQS on the 2 × 2 × 2 supercell of the experimental rutile phase46, and find that the local magnetic moment on V (μV) in the relaxed structure has an average magnitude of 0.75 μB with a distribution of 0.35 μB ~ 1.00 μB. As shown in Fig. 5a, the paramagnetic rutile phase is metallic with the Fermi level residing in the principal conduction band, although the strong variation of magnetization density across the crystal reflects the symmetry breaking induced by paramagnetism (see Fig. 5b). The failure to open the band gap in the paramagnetic rutile phase shows that paramagnetism is still not strong enough to shift the localized states within the principal conduction band down to form split-off bands. Our results demonstrate that the metallic rutile phase with zero V-V dimerization is paramagnetic with non-zero μV. Therefore, the IMT in VO2 is a transition from the nonmagnetic insulating phase (Fig. 3c) to the paramagnetic metallic phase (Fig. 5a), which is different from the transitions in other IMT systems8.
a Density of states of the paramagnetic rutile phase of VO2 modelled by the cell-internal relaxed (by R-PBE) spin-SQS structure of the 2 × 2 × 2 supercell (48-atom) of the experimental rutile structure with R-PBE exchange-correlation functional. The majority states are indicated in a. b Magnetization density of the paramagnetic rutile phase from R-PBE. Yellow (blue) iso-surface indicates positive (negative) magnetization density (isosurface: 0.02 \(\left|{\rm{e}}\right|{{\rm{bohr}}}^{-3}\)).
Comparing with experiments and the role of hidden magnetism on the band width of the split-off bands
Next, we compare the fundamental physical properties arising from symmetry breaking in VO2 with experimental values. The calculated band gap for symmetry broken nonmagnetic monoclinic phase depending on the exchange-correlation functional used is in the range of 0.66 eV to 0.14 eV, in comparison with the experimental optical band gap of 0.6–0.7 eV7 [see the density of states of monoclinic VO2 from HSE (with optimized large DBA = 26.3%) in Supplementary Fig. 4 and those from R-PBE (with optimized large DBA = 25.6%) in Fig. 3c, respectively, demonstrating the band gaps]. As shown in Fig. 4a, the magnetic configurations with zero global moment in the monoclinic unit cell (antiferromagnetic) relax into the above nonmagnetic configuration. On the other hand, the relaxed ferromagnetic configuration of the monoclinic phase has a rather small DBA compared to the experimental value as well as a metallic electronic structure (see Supplementary Section 2).
Figure 3c also indicates for large DBA a large energy splitting between d-d bonding and anti-bonding states (shown by \({\triangle d}_{{\rm{||}}}\) in Fig. 3c) that were observed by photoemission measurements17. Information regarding the orbital components are provided in Supplementary Fig. 9. This splitting is formed by the \({a}_{1g}\) states: the V ions in VO2 reside in the VO6 octahedral local environment, which splits the V-d orbital into \({t}_{2g}\) and \({e}_{g}\) states. The crystal field in the monoclinic phase further splits the \({t}_{2g}\) and \({e}_{g}\) states into the \({a}_{1g}\), \({e}_{g}^{\pi }\), and \({e}_{g}^{\sigma }\) states. The formation of V-V dimer results in a strong coupling between two equivalent V ions and a pronounced repulsion between the bonding and anti-bonding \({a}_{1g}\) states (also referred to as the bonding and anti-bonding \({d}_{{\rm{||}}}\) states), leading to a large d-d bonding and anti-bonding splitting \(\triangle {d}_{{\rm{||}}}\). The R-PBE results in Fig. 3c give a d-d splitting \(\triangle {d}_{{\rm{||}}}\) of 2.10 eV, while the HSE results in Supplementary Fig. 9 gives a \({\triangle d}_{{\rm{||}}}\) of 2.59 eV, in good agreement with the experimental value 2.5 eV17.
On the other hand, we find that the experimentally measured band width of the split-off bands in monoclinic VO2 ( > 1 eV)47 is much larger than the value predicted from DFT calculations (0.43 eV, see Fig. 3c). The increase of the band width of split-off bands could be related to the above discussed hidden magnetism in the monoclinic phases with reduced V-V dimerization. As shown in Fig. 4, we found that from the insulating monoclinic phase to the metallic rutile phase, as the V-V dimerization is gradually reduced, local magnetic moments appear. At ambient conditions, there could be dynamic variation of V-V dimerization and the associated variation of local magnetic moments. For paramagnetic rutile VO2, such dynamic process could constantly change the local magnetic moments, making the material behave like a Pauli paramagnet as discussed in experiments44,45, which however possesses hidden magnetization. Such dynamic process could also induce weak magnetism in the monoclinic phase as demonstrated by the temperature-dependent magnetic susceptibility observed in experiments44,45. Further investigation of the magnetoresistance and magnetic susceptibility along with resistivity in VO2 with tuned V-V dimerization could reveal rich spin physics from hidden magnetism in the transient phases of the insulator-metal transition as well as a type of paramagnetism in the rutile phase that behaves like both Curie-Weiss paramagnetism and Pauli paramagnetism. To study the effect of such hidden magnetism on the electronic structure of monoclinic VO2, we performed a constrained theoretical calculation by modelling the potential transient magnetic monoclinic phase with a spin-SQS structure on the 1 × 2 × 2 supercell of the experimental monoclinic structure48 from HSE using the fixed crystal structure from experiments. The density of states of such magnetic monoclinic phase, as shown in Fig. 6, in comparison with those of the nonmagnetic configuration of the fixed experimental monoclinic structure, demonstrates the increase of the split-off band width by a factor of two (from 0.58 eV to 1.14 eV) due to the appearance of magnetism.
a Nonmagnetic phase. b Paramagnetic phase as modelled by the spin-SQS structure of the 1 × 2 × 2 supercell (48-atom) of the experimental monoclinic structure. The majority states are indicated in a, b. Blue area indicates the occupied states, among them the split-off flat-band states are indicated by bold red boundary.
The increase of band width of the isolated split-off bands arises from the quasirandom distribution of magnetic moments in the magnetic monoclinic phase with reduced V-V dimerization. Such magnetic monoclinic phase hosts the local magnetic environment with spin parallel V-V dimers that induce large band width for the isolated split-off bands (see the wide-spread partial density of states of the isolated split-off bands on a spin-up V ion belonging to a spin parallel V-V dimer in Supplementary Fig. 10). In the spin parallel V-V dimers, the two \({a}_{1g}\) states from the two V ions have the same spin and strongly couple with each other, leading to the increased band width. Whereas, in spin anti-parallel V-V dimer, the two \({a}_{1g}\) states from the two V ions have opposite spins and no strong coupling. A schematic diagram illustrating the strong (weak) coupling between the two \({a}_{1g}\) states of spin parallel (anti-parallel) V-V dimers is provided in Supplementary Fig. 11. Such mechanism for magnetism enhanced split-off band width could be related to the experimentally observed broad band width of the split-off bands in monoclinic VO247. Direct observation of the hidden magnetism in this flat band material could open the door to the rich physics of potential hidden magnetism in transition-metal flat band systems.
Discussion
We studied the symmetry breaking associated split-off flat bands and insulator-metal transition in VO2 based on DFT free from the strong correlation interactions. We found that once the structural symmetry breaking (V-V dimerization) exceeds a threshold magnitude, narrow “flat bands” split off from the broad principal conduction band giving an insulating phase. We predicted rather low phase transition barrier for the insulator-metal transition and found an interesting compensation effect between magnetic symmetry breaking and structural symmetry breaking during the IMT, i.e., strong dimerization suppresses magnetic moments whereas reduced dimerization enhances the formation of magnetic moments, leading to the hidden magnetism in the transient phases of the IMT as well as the final metallic rutile phase. Such hidden magnetism is a result of the interplay between magnetic and structural symmetry breaking. The interplay between different types of symmetry breaking is commonly found in quantum materials such as YNiO349. The interplay of magnetic and structural symmetry breaking is extremely strong in VO2 as the structural symmetry breaking has the capability to completely quench the magnetic symmetry breaking (see Fig. 4b). Such strong interplay in VO2 leads to a type of magnetic system that has a phase transition from the paramagnetic phase with non-zero local magnetic moments to the nonmagnetic phase as temperature decreases. This type of magnetic systems could offer knobs to completely switch off a random distribution of magnetic moments and then switch on another distribution with promising applications in stochastic computing. Our study reveals the roles of V-V dimerization and magnetism in the insulator-metal transition in VO2 associated with the formation of isolated split-off flat bands, shedding light on the phase transition mechanism in this prototypic IMT system that does not require the degeneracy-removal strong correlation25, bringing this essential quantum material closer to the technologically essential semiconductors, opening the arena for designing novel functional quantum materials with split-off flat bands for energy-efficient neuromorphic computing.
Methods
Electronic structure method
To evaluate the electronic structures of the insulating and metallic phases of VO2, we apply the generalized gradient approximation (GGA) to density functional theory using the projector-augmented wave (PAW) pseudopotential50 with the revised Perdew-Burke-Ernzerhof exchange-correlation functional51 as implemented in the Vienna Ab initio Simulation Package (VASP)52,53, without the on-site electronic Coulomb correlation term U. We use the basis set energy-cutoff of 520 eV, and reciprocal space grids of 8 × 10 × 10 and 8 × 5 × 5 for the monoclinic structure and its 1 × 2 × 2 supercell (as well as the 2 × 2 × 2 supercell of the tetragonal rutile structure), respectively. For the calculation of density of states in metals (insulators), we use the Gaussian smearing method with a width of smearing of 0.05 eV (tetrahedron method with Blöchl corrections54). In addition to R-PBE, we employ the HSE hybrid functional29 to evaluate the electronic structures of the relaxed (by HSE) monoclinic structure with a mixing parameter α = 0.1 to reproduce the experimental band gap7. The same mixing parameter is applied to evaluate the electronic structure of the unrelaxed 1 × 2 × 2 supercell of the experimental monoclinic structure48 from HSE. As a comparison, we also use the PBE functional55, the LDA functional31, and the SCAN meta-GGA functional30 to evaluate the electronic structures of nonmagnetic VO2. The VO2 crystal structures were drawn by using the VESTA software56.
Nudged elastic band method
To study the insulator-metal transition in VO2, we employ the climbing image nudged elastic band method37 in the framework of the generalized solid-state NEB57, as implemented for VASP in the VASP Transition State Theory (VTST) code58. We perform NEB calculations to locate the minimum-energy paths for the phase transition between the rutile and monoclinic phases, based on the optimization of the total energy for each image with the R-PBE exchange-correlation functional while maintaining equal spacing to neighboring images. We use the rutile structure in the monoclinic-like unit cell as well as the monoclinic structure, both relaxed by using R-PBE, as the endpoints for nudged elastic band calculations. As macroscopic magnetic moment has not been observed in both the monoclinic and rutile phases of VO244,45, we consider the nonmagnetic configuration and the three magnetic configurations with zero global moment in the monoclinic structure (see Insets of Fig. 4a) for the nudged elastic band simulations, to study the effect of magnetism on the insulator-metal transition in VO2.
Special quasirandom structures
As weak magnetism without long-range ordering has been observed in experiments44,45, we model the potential paramagnetic states of VO2 by constructing the spin special quasirandom structures26 via decorating a supercell with spin-up and spin-down magnetic moments to create a global zero-moment configuration closest to the high-temperature limit of a random spin paramagnet59, generated by using the Alloy Theoretic Automated Toolkit60 with perfect match. The paramagnetic rutile phase of VO2 (see Fig. 5b) is modelled by the spin-SQS structure of the 2 × 2 × 2 supercell (48-atom) of the experimental rutile structure46 with cutoff distances of 5.7 Å and 11.4 Å for pairs and triplets, respectively. The paramagnetic monoclinic phase of VO2 (see Supplementary Fig. 5a) is modelled by the spin-SQS structure of the 1 × 2 × 2 supercell (48-atom) of the experimental monoclinic structure48 with cutoff distances of 5.3 Å and 10.6 Å for pairs and triplets, respectively.
Data availability
The authors declare that the data supporting the findings of this study are available within the paper and its supplementary information.
Code availability
The underlying code for this study is not publicly available for proprietary reasons.
References
Mott, N. F. Metal-Insulator Transitions. (Taylor and Francis, 1990).
West, A. R. Solid State Chemistry and its Applications. (John Wiley & Sons, 1998).
Imada, M., Fujimori, A. & Tokura, Y. Metal-insulator transitions. Rev. Mod. Phys. 70, 1039–1263 (1998).
Zhang, L. et al. Correlated metals as transparent conductors. Nat. Mater. 15, 204–210 (2016).
Morin, F. J. Oxides Which Show a Metal-to-Insulator Transition at the Neel Temperature. Phys. Rev. Lett. 3, 34–36 (1959).
Goodenough, J. B. Direct Cation-Cation Interactions in Several Oxides. Phys. Rev. 117, 1442–1451 (1960).
Berglund, C. N. & Guggenheim, H. J. Electronic Properties of VO2 near Semiconductor-Metal Transition. Phys. Rev. 185, 1022–1033 (1969).
Georgescu, A. B. et al. Database, Features, and Machine Learning Model to Identify Thermally Driven Metal-Insulator Transition Compounds. Chem. Mater. 33, 5591–5605 (2021).
Schofield, P. et al. Harnessing the Metal-Insulator Transition of VO2 in Neuromorphic Computing. Adv. Mater. 35, 2205294 (2023).
Varignon, J., Bibes, M. & Zunger, A. Origin of band gaps in 3d perovskite oxides. Nat. Commun. 10, 1658 (2019).
Wang, Z., Malyi, O. I., Zhao, X. G. & Zunger, A. Mass enhancement in 3d and s-p perovskites from symmetry breaking. Phys. Rev. B 103, 165110 (2021).
Malyi, O. I., Zhao, X.-G. & Zunger, A. Insulating band gaps both below and above the Néel temperature in d-electron LaTiO3, LaVO3, SrMnO3, and LaMnO3 perovskites as a symmetry-breaking event. Phys. Rev. Mater. 7, 074406 (2023).
Zimmers, A. et al. Role of Thermal Heating on the Voltage Induced Insulator-Metal Transition in VO2. Phys. Rev. Lett. 110, 056601 (2013).
Yi, W. et al. Biological plausibility and stochasticity in scalable VO2 active memristor neurons. Nat. Commun. 9, 4661 (2018).
Wentzcovitch, R. M., Schulz, W. W. & Allen, P. B. VO2 - Peierls or Mott-Hubbard - a View from Band Theory. Phys. Rev. Lett. 72, 3389–3392 (1994).
Biermann, S., Poteryaev, A., Lichtenstein, A. I. & Georges, A. Dynamical singlets and correlation-assisted peierls transition in VO2. Phys. Rev. Lett. 94, 026404 (2005).
Shin, S. et al. Vacuum-Ultraviolet Reflectance and Photoemission-Study of the Metal-Insulator Phase-Transitions in VO2, V6O13, and V2O3. Phys. Rev. B 41, 4993–5009 (1990).
Sommers, C. & Doniach, S. First Principles Calculation of Intra-Atomic Correlation Energy in VO2. Solid State Commun. 28, 133–VO135 (1978).
Huffman, T. J. et al. Insulating phases of vanadium dioxide are Mott-Hubbard insulators. Phys. Rev. B 95, 075125 (2017).
Stahl, B. & Bredow, T. Critical Assessment of the DFT plus U Approach for the Prediction of Vanadium Dioxide Properties. J. Comput. Chem. 41, 258–265 (2020).
Nájera, O., Civelli, M., Dobrosavljevic, V. & Rozenberg, M. J. Resolving the VO2 controversy: Mott mechanism dominates the insulator-to-metal transition. Phys. Rev. B 95, 035113 (2017).
Eyert, V. VO2: A Novel View from Band Theory. Phys. Rev. Lett. 107, 016401 (2011).
Grau-Crespo, R., Wang, H. & Schwingenschlogl, U. Why the Heyd-Scuseria-Ernzerhof hybrid functional description of VO2 phases is not correct. Phys. Rev. B 86, 081101(R) (2012).
Mondal, W. R. et al. Role of V-V dimers on structural, electronic, magnetic, and vibrational properties of VO2 by first-principles simulations and Raman spectroscopic analysis. Phys. Rev. B 103, 214107 (2021).
Perdew, J. P., Ruzsinszky, A., Sun, J. W., Nepal, N. K. & Kaplan, A. D. Interpretations of ground-state symmetry breaking and strong correlation in wavefunction and density functional theories. Proc. Natl Acad. Sci. USA 118, e2017850118 (2021).
Zunger, A., Wei, S. H., Ferreira, L. G. & Bernard, J. E. Special Quasirandom Structures. Phys. Rev. Lett. 65, 353–356 (1990).
Koster, G. F. & Slater, J. C. Simplified Impurity Calculation. Phys. Rev. 96, 1208–1223 (1954).
Shannon, R. D. Revised Effective Ionic-Radii and Systematic Studies of Interatomic Distances in Halides and Chalcogenides. Acta Crystallogr. A 32, 751–767 (1976).
Heyd, J., Scuseria, G. E. & Ernzerhof, M. Erratum: “Hybrid functionals based on a screened Coulomb potential” [J. Chem. Phys. 118, 8207 (2003)]. J. Chem. Phys. 124, 219906 (2006).
Sun, J. W., Ruzsinszky, A. & Perdew, J. P. Strongly Constrained and Appropriately Normed Semilocal Density Functional. Phys. Rev. Lett. 115, 036402 (2015).
Perdew, J. P. & Zunger, A. Self-Interaction Correction to Density-Functional Approximations for Many-Electron Systems. Phys. Rev. B 23, 5048–5079 (1981).
Regnault, N. et al. Catalogue of flat-band stoichiometric materials. Nature 603, 824–828 (2022).
Calugaru, D. et al. General construction and topological classification of crystalline flat bands. Nat. Phys. 18, 185–189 (2022).
Kang, M. G. et al. Dirac fermions and flat bands in the ideal kagome metal FeSn. Nat. Mater. 19, 163–169 (2020).
Li, Z. et al. Realization of flat band with possible nontrivial topology in electronic Kagome lattice. Sci. Adv. 4, eaau4511 (2018).
Bernevig, B. A. et al. Materials Flatband Database. https://www.topologicalquantumchemistry.fr/flatbands (2024).
Henkelman, G., Uberuaga, B. P. & Jonsson, H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 113, 9901–9904 (2000).
Yuan, L. D., Wang, Z., Luo, J. W., Rashba, E. I. & Zunger, A. Giant momentum-dependent spin splitting in centrosymmetric low-Z antiferromagnets. Phys. Rev. B 102, 014422 (2020).
Yuan, L. D., Wang, Z., Luo, J. W. & Zunger, A. Prediction of low-Z collinear and noncollinear antiferromagnetic compounds having momentum-dependent spin splitting even without spin-orbit coupling. Phys. Rev. Mater. 5, 014409 (2021).
Yuan, L. D. & Zunger, A. Degeneracy Removal of Spin Bands in Collinear Antiferromagnets with Non-Interconvertible Spin-Structure Motif Pair. Adv. Mater. 35, 2211966 (2023).
Morrison, V. R. et al. A photoinduced metal-like phase of monoclinic VO2 revealed by ultrafast electron diffraction. Science 346, 445–448 (2014).
Liu, H. W. et al. Unifying the order and disorder dynamics in photoexcited VO2. Proc. Natl Acad. Sci. USA 119, e2122534119 (2022).
Johnson, A. S. et al. Ultrafast X-ray imaging of the light-induced phase transition in VO2. Nat. Phys. 19, 215–VO220 (2023).
Yin, C. Y. et al. Unusual magnetic transition near metal-insulator transition and paramagnetic anomaly in VO2. Appl. Phys. Lett. 110, 172404 (2017).
Zhang, R. et al. Understanding of metal-insulator transition in VO2 based on experimental and theoretical investigations of magnetic features. Sci. Rep. 8, 17093 (2018).
Mcwhan, D. B., Marezio, M., Remeika, J. P. & Dernier, P. D. X-Ray-Diffraction Study of Metallic VO2. Phys. Rev. B 10, 490–VO495 (1974).
Okazaki, K. et al. Photoemission study of the metal-insulator transition in VO2/TiO2(001): Evidence for strong electron-electron and electron-phonon interaction. Phys. Rev. B 69, 165104 (2004).
Longo, J. M. & Kierkegaard, P. A Refinement of the Structure of VO2. Acta Chem. Scandinavica 24, 420–VO426 (1970).
Malyi, O. I. & Zunger, A. Rise and fall of Mott insulating gaps in YNiO3 paramagnets as a reflection of symmetry breaking and remaking. Phys. Rev. Mater. 7, 044409 (2023).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).
Hammer, B., Hansen, L. B. & Norskov, J. K. Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof functionals. Phys. Rev. B 59, 7413–7421 (1999).
Kresse, G. & Furthmuller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).
Kresse, G. & Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Blochl, P. E., Jepsen, O. & Andersen, O. K. Improved Tetrahedron Method for Brillouin-Zone Integrations. Phys. Rev. B 49, 16223–16233 (1994).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Momma, K. & Izumi, F. for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 44, 1272–1276 (2011).
Sheppard, D., Xiao, P. H., Chemelewski, W., Johnson, D. D. & Henkelman, G. A generalized solid-state nudged elastic band method. J. Chem. Phys. 136, 074103 (2012).
Henkelman, G. et al. VASP Transition State Theory code. https://theory.cm.utexas.edu/vtsttools (2024).
Gambino, D., Malyi, O. I., Wang, Z., Alling, B. & Zunger, A. Density functional description of spin, lattice, and spin-lattice dynamics in antiferromagnetic and paramagnetic phases at finite temperatures. Phys. Rev. B 106, 134406 (2022).
van de Walle, A., Asta, M. & Ceder, G. The Alloy Theoretic Automated Toolkit: A user guide. Calphad 26, 539–553 (2002).
Acknowledgements
The work on structural symmetry breaking and polymorphous spin special quasirandom structure calculations was supported by the U.S. National Science Foundation DMREF program through Grant No. DMREF-1921949. This work used resources of Stampede2 system at Texas Advanced Computing Center through allocation PHY180030 from the Advanced Cyberinfrastructure Coordination Ecosystem: Services & Support (ACCESS) program, which is supported by National Science Foundation grants #2138259, #2138286, #2138307, #2137603, and #2138296. The nudged elastic band simulation of the insulator-metal transition trajectory in this work were supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division under Award # DE-SC0010467. This work also used resources from the National Energy Research Scientific Computing Center, which was supported by the Office of Science of the U.S. Department of Energy.
Author information
Authors and Affiliations
Contributions
A.Z. conceived and supervised the project. X.Z. and J.-X.X. developed the idea and designed the research. X.Z. performed the density functional theory calculations and plotted the figures. J.-X.X. performed the analysis of the split-off flat bands and the non-relativistic spin splitting. X.Z., J.-X.X., and A.Z. analyzed the calculated results and wrote the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhang, X., Xiong, JX. & Zunger, A. Hidden magnetism and split off flat bands in the insulator metal transition in VO2. npj Comput Mater 10, 217 (2024). https://doi.org/10.1038/s41524-024-01382-8
Received:
Accepted:
Published:
Version of record:
DOI: https://doi.org/10.1038/s41524-024-01382-8