Introduction

The global imperative for sustainable and green energy solutions has intensified the search for efficient hydrogen storage materials. With the highest energy density among fuels1, hydrogen represents a promising alternative to fossil sources that can be produced with zero CO2 emissions powered by surplus renewable energy2, through methods such as electrolysis3,4,5. The main barrier preventing a future economy based on hydrogen energy is the cost of production, and the absence of a green, safe, and efficient way to store and transport it. Solid-state hydrogen storage technologies are the most studied in this regard, being the safest, offering higher volumetric densities6 than cryogenic or high-pressure gaseous alternatives7,8,9. Despite these advantages, the technology remains in its early stages and the search for materials allowing large-scale applications, like in the automotive industry10, remains open11,12.

Metal hydrides currently represent promising efficient and economical solutions13. Particularly, Magnesium stands out for its excellent hydrogen storage capacity14, environmental friendliness, and natural abundance, displaying theoretical storage capacities as high as 7.6% wt15. However, the slow kinetics of hydrogen in magnesium-based compounds still pose a limit to possible applications. Therefore, understanding and optimizing hydrogen diffusion pathways through theoretical modeling16,17,18 and experimental studies19,20,21 is crucial in order to improve performances of future Mg-based hydrogen storage materials. Despite numerous efforts over the past decade, modeling hydrogen dynamics in solid-state compounds remains challenging22,23,24,25. The low hydrogen diffusivity in magnesium requires prolonged simulation times, in the order of nanoseconds, for accurate studies using ab-initio Molecular Dynamics (MD). Consequently, ab-initio transition state calculations, such as the nudged elastic band (NEB) method, have emerged as the most effective approaches to reproduce and interpret the experimental data documented in the literature to date17. However, this technique is cumbersome and often impracticable for systems with high defect concentrations, or complex potential energy landscapes: manually describing all possible paths required by NEB may be very challenging and virtually impossible17.

Recently, Machine Learning accelerated MD (MLMD) has revolutionized the world of MD by making accurate simulations of large systems accessible over long time scales26. The application of such approach to study hydrogen-defective systems is of high interest27, since the prediction of dynamical properties would highly expand the limited landscape offered by today’s transition state computations. MLMD does allow the study of multi-component systems28 and can efficiently account for interaction between defects29. However, developing accurate interatomic potentials, especially for hydrogen-defective materials, is notoriously challenging25,30. Still, the field is rapidly growing and several new approaches were proposed to explore new and complex phase spaces. On one side, various pre-trained universal solutions31,32 start to be available, aiming to offer a convenient and versatile way of tackling the problem. However, as discussed in this work, while their training datasets are rich in chemical compositional space, the limited configurational sampling can significantly compromise their accuracy on previously unseen defected, metastable and transition states, leading to ungranted generalization capabilities. On the other side, active-learning approaches based on Bayesian force fields are showing a large versatility thanks to the construction of on-the-fly databases33,34. The error-oriented sampling of configurations allows these models to easily collect high-quality data widely spanning the configurational space, thus making them highly accurate despite their architecture, constrained compared to neural networks. The current study aims at illustrating a systematic procedure for ML-potentials applications in diffusive dynamics conditions, which can be used to enhance the study of different embedded defects, without departing from ab-initio accuracy. This procedure specifically consists in improving ML-based pre-trained models’ performance via actively learned configurations, generated by on-the-fly training of the Vienna Ab Initio Simulation Package Bayesian ML Force-Field (VASP-MLFF)33,34. We consider four different concentrations (MgH0.03125, MgH0.046875, MgH0.0625 and MgH0.078125) and compute the hydrogen diffusion coefficient at three different temperatures (300 K, 480 K, and 673 K), employing a proper methodology which ensures accurate analysis of unbiased dynamical properties. Two different Universal Interatomic Potentials (UIPs), CHGNet31 and MACE32, were considered. Dynamical properties were computed for VASP-MLFF alongside the pre-trained and fine-tuned versions of the UIPs. The comparison between the different results and experimental data showed excellent agreement, both with VASP-MLFF and fine-tuned potentials, while the pre-trained versions fail to reach a satisfactory accuracy. Interestingly, the fine-tuned potentials outperform VASP-MLFF by correctly predicting the temperature dependence of the diffusion coefficient.

Results

Validation of the ML-potentials

The results reported in Fig. 1 show how the predictions of the VASP-MLFF achieve an accuracy below 0.3 meV/atom for energies and below 10 meV/Å for forces, respectively, as reasonably expected compared to other studies involving MLFF-MD35,36,37,38. On the other hand, the UIPs pre-trained on the MP-database, respectively named on CHGNet_MP and MACE_MP, failed to reach such level of accuracy by more than one order of magnitude. The discrepancy was significantly reduced after fine-tuning the two models on the VASP-generated database: the error obtained shows that the CHGNet_FT performance reaches a level comparable with the VASP-MLFF, and MACE_FT even outperforms it. The performance differences between CHGNet_FT and MACE_FT may stem from the equivariant architecture employed by the latter. MACE turned out to be highly data-efficient, leading to better fine-tuning results over small datasets, compared to the more data-hungry architectures like CHGNet. The MACE model was also trained from scratch on the VASP-DFT configurations (MACE_TR), achieving slightly smaller errors on forces with respect to MACE_FT. Please note that all energy values at concentrations different from the training concentration exhibit a systematic shift dependent on the hydrogen content. However, the underlying physics of hydrogen dynamics is unaffected, as this shift remains consistent throughout simulations with a constant number of particles and does not influence the forces. Consequently, the models are still capable of accurately describing the hydrogen dynamics. For completeness, we also present the pristine validation and the corresponding R2 values, as shown in Supplementary Fig. SF2.

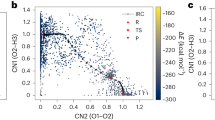
Fig. 1: Validation results for different ML-potentials.
figure 1

a RMSE values for the predictions of energies and forces on the validation set from every model considered in the study. These results are given at different concentrations, obtained using a supercell with a variable number of H atoms, removing the corresponding constant energy shift by setting the mean of all the configurations at the same concentration to zero. The subscript ’MP’ refers to the pre-trained model on the Material Project database, ’TR’ to the one trained from scratch and ’FT’ to the fine-tuned version. b Energy barrier values associated to the hydrogen transition between different octahedral (Oi) and tetragonal (Ti) sites, obtained through ciNEB calculations, using different ML-potentials and DFT reference (in yellow).

Full size image

The climbing-image nudged elastic band (ciNEB) calculations conducted with the ML-potentials, allowed to estimate the transition energy barrier Eb between various octahedral and tetragonal hydrogen interstitial sites, and to further validate the accuracy of the ML-potentials. In fact, we compared the obtained Eb values through these methods with the VASP-DFT benchmark results. Our findings, shown in Fig. 1b, reveal that the universal potentials perform significantly less accurately in predicting the energy barriers. However, the performance of the trained and fine-tuned counterpart dramatically improves, producing results that are much closer to the VASP-DFT reference values. The VASP-MLFF method also gave excellent agreement with the DFT benchmark. As expected, the model with better accuracy on the validation set, especially on the forces, obtained results closer to the DFT values.

Diffusion coefficient and dynamical analysis

The diffusion coefficient D predicted for every model, using the methodology described in the “Methods” section, is reported in Fig. 2a, and compared with experimental19 and NEB17 results, at each investigated temperature. The experimental data from Nishimura et al. were collected in the temperature range of 474–493 K and then extrapolated at higher and lower temperatures using an Arrhenius relation. The results clearly show that our procedure provides multiple solutions with excellent experimental agreement, outperforming NEB computations16 that until now have represented the standard for such applications. This holds true for the MACE_FT potential in particular, which not only predicts the correct order of magnitude across all temperatures, but significantly agrees at 480 K. The VASP-MLFF instead, shows a good agreement at 480 K and 673 K, while missing the room temperature by one order of magnitude. Concerning CHGNet_FT, it provides remarkable agreement with the experimental value at 480 K, but at the lowest temperatures underestimates the result by one order of magnitude. As expected from the error analysis on energies and forces, both the pre-trained versions of the UIPs result in much lower agreement, with deviations of at least one order of magnitude from experimental values at most temperatures. A closer inspection of the temperature dependence of the diffusion coefficients, as shown in Fig. 2b, reveals that CHGNet_FT still outperforms the VASP-MLFF by better reproducing the Arrhenius curve observed in the experiments, while the MACE_FT solutions outperform both. This shows how with smaller errors, the deep networks are capable of better representing the shape of the energy landscape, with respect to the Bayesian alternative. In this regard, further quantitative analysis can be provided by comparing the predicted value of the activation energy Ea, obtained from the linear fits in the Arrhenius plots. In particular, we achieved values of 0.4 eV for VASP-MLFF, 0.19 eV for CHGNet_FT and 0.28 eV for MACE_FT, where the experiment value corresponds to 0.25 eV19. MACE_FT clearly excels at representing the energy landscape of the system.

Fig. 2: Simulations results for different ML-potentials.
figure 2

a Diffusion coefficient values of hydrogen in MgH0.0625 at three different constant average temperatures of 380 K, 480 K and 673 K, and the corresponding activation energy, comparing results achieved via different potentials in our investigations, and previous studies17,19. The number in parentheses indicates the Standard Error of the Mean (SEM) in the last significant digit of the value. The colorbar highlights in logscale the relative deviation with respect to the experimental values. b Comparison between the dependence of the diffusion coefficient with temperature, for ML-models, the NEB17 and experimental results19. The experimental curve is extrapolated from data obtained at 474–493 K. c Radial distribution function of atom pairs at 673 K during 1 ns long NVE simulations. VASP-MLFF and MACE show a remarkable agreement over the whole domain for every pair, while CHGNet starts to differ at larger distances.

Full size image

Furthermore, we computed D at various hydrogen concentrations using MACE_FT, along with the associated Ea, as shown in Fig. 3a. The results reveal a decrease in hydrogen mobility with increasing concentration, leading to a corresponding reduction in the diffusion coefficient. Simultaneously, the activation energy increases with higher hydrogen densities. The evaluation of D across different concentrations enabled a comparison with experimental values, demonstrating that the results for lower concentrations, specifically MgH0.03 and MgH0.045, show the best alignment. It should be noted that Nishimura et al.19 did not report the hydrogen concentration within their samples. These findings suggest that the target hydrogen concentration in Nishimura’s experiments may be lower than 0.0625, assumed in previous DFT studies17.

Fig. 3: Results obtained from runs at different hydrogen content using MACE_FT.
figure 3

a Diffusion coefficients at different temperatures and H concentration, on top, and obtained activation energy at different concentrations, on the bottom. The target experimental value from ref.19 is reported as the dashed line in every plot. b Comparison of the simulated hydrogen pair distributions (np occurrences, bars) with theoretical Poisson distributions (points and dashed lines) at three temperatures (300 K, 480 K, and 673 K) for varying hydrogen concentrations. The lower panel shows the λ parameter (average number of pairs) as a function of temperature and concentration.

Full size image

Further analysis has been performed on the dynamics of the system by evaluating the radial distribution function (RDF) in all of the NVE runs performed. We report in Fig. 2c the predicted behavior by the best performing models in the system at 673 K, while other temperature cases can be found in Supplementary Fig. SF6. A very good agreement between MACE_FT and VASP-MLFF is found, while the RDF of CHGNet_FT departs from the others at larger distances, by smoothing out peaks. From such curves it is possible to retain information about the behavior of hydrogen during the simulation. Proceeding in order with increasing distance radius, the first peak appears just before 2 Å in the Mg–H curve, in correspondence of the average distance of one Magnesium atom from the center of the nearest octahedral sites on which hydrogen tend to sit16. The second peak, belonging to the H–H pair, is very pronounced at around 2.6 Å, reflecting a correlation between hydrogen atoms at this distance. This behavior finds agreement in the literature for molecular dynamics with magnesium hydride nanoclusters30. In fact, the distance of 2.6 Å corresponds to the one between two octahedral sites along the c-direction16, as also reported in literature30, implying how hydrogen tends to sit on near sites. To highlight such behavior, we also report in Fig. 4 the extensive diffusion path of a representative hydrogen atom within the magnesium matrix during a 100 ps simulation, at 673 K. The trajectory is unwrapped in the replicas of the periodic images to enhance visibility and interpretation. The color-gradient serves as a temporal marker, with blue indicating the initial position of the hydrogen atom at the beginning of the simulation (t = 0 ps) and red indicating its position at the end of the studied interval (t = 100 ps). Intermediate colors (cyan, green, yellow, and orange) represent the progression of time between these two extremes, providing a visual cue for the temporal evolution of the atom’s diffusion path. The black circles highlight interstitial regions where the hydrogen atom tends to oscillate around the magnesium sites, indicating temporary trapping sites within the lattice structure, before continuing its diffusion trajectory. The third significant peak in the RDF is observed around 3 Å in the Mg–Mg curve, consistently with the typical magnesium distances in hcp structures. Multiple smaller peaks indicate further neighbor interactions in the crystal lattice. Analogous results were found in the RDF at 300 K and 480 K, where the peaks are sharper due to the reduced effect of thermal motion, see Supplementary Fig. SF6. In particular, a higher pronounced RDF at lower temperature indicates that hydrogen tends to spend more time in the vicinity of Magnesium, and diffuse less in the crystal structure.

Fig. 4: Diffusion path of a representative hydrogen atom in MgH0.0625 during 100 ps at 673 K, depicted using a color-gradient line to represent the progression of time, from blue to red.
figure 4

The black circles highlight the interstitial regions where H atoms tend to oscillate around Mg lattice site before continuing their diffusing trajectory.

Full size image

The analysis of hydrogen pair (np) distributions presented in Fig. 3b provides a clear insight into the dependence of pair formation on temperature and concentration. At elevated temperatures, such as 480 K and 673 K, the simulated distributions align closely with the theoretical Poisson distribution, calculated as:

$$f({n}_{p};\lambda )=\frac{{e}^{-\lambda }{\lambda }^{{n}_{p}}}{{n}_{p}!},$$
(1)

where λ represents the average number of pairs. This agreement demonstrates the random nature of hydrogen pairing, indicating a lack of correlation and independence from the initial atomic configuration. Furthermore, the convergence of λ values for different concentrations as temperature increases underscores this intrinsic randomness. Conversely, at 300 K, a deviation from the Poissonian behavior emerges, with λ showing a stronger dependence on hydrogen concentration. This behavior can be attributed to the reduced mobility of hydrogen atoms at low temperatures, where the thermal energy is insufficient to overcome the energy barriers for interstitial site transitions. Consequently, the hydrogen atoms remain in proximity to their initial positions, leading to non-equilibrated pair distributions within the simulation timescale. These results suggest that, while the system approaches a random distribution at higher temperatures, longer simulations would be required to achieve equilibration and Poissonian behavior at room temperature for low-mobility regimes.

Discussion

To summarize, our investigation enabled us to thoroughly characterize the kinetic properties and mobility of hydrogen within a structured environment, such as pure magnesium, across various temperatures through a rigorous and efficient methodology. We performed a systematic and comparative study of ML-based interatomic potential MD schemes, particularly focusing on Bayesian versus equivariant and graph neural networks (MACE and CHGNet), under different training modes (universal and fine-tuned). The results were validated by estimates of the diffusion coefficient and the activation energy values, which showed excellent agreement with experimental data. The obtained results proved that the VASP-DFT configurations, collected during the MLFF on-the-fly training, represent a complete set for the accurate modeling of interatomic interactions, between hydrogen and magnesium atoms. This strategy could be consistently applied to generate a comprehensive dataset for the proper training of existing or forthcoming potentials. In fact, we identified the limitations of pre-trained UIPs in studying materials with diffusing defects, due to the absence of representative high temperatures, defective and metastable states in their datasets. Particularly, we demonstrated the ability of state-of-the-art machine learning models to achieve DFT-level accuracy, after fine-tuning on actively learned DFT configurations, highlighting the importance of focusing on efficient dataset-building methods and their quality. Specifically, the importance of including defected and transition state configurations, as well as the role of transfer-learning, allowing pre-trained solutions to adapt to new systems. The obtained data offer valuable new insights into the collective dynamical properties at varying hydrogen concentrations, accurately predicting a decrease in hydrogen mobility as concentration increases. Additionally, the statistical analysis of hydrogen pair distributions indicates the system approaches a random distribution at higher temperatures. However, longer simulations would be necessary to achieve equilibration and Poissonian behavior at room temperature in low-mobility regimes.

These progresses not only improves our understanding of hydrogen interactions in magnesium, but also paves the way for future research into a broader range of multi-component systems and defected compositions. This is especially significant for systems with complex potential energy surfaces, where traditional ab-initio methods become impractical. Successfully modeling the hydrogen diffusion mechanism in magnesium via machine learning-accelerated molecular dynamics could facilitate the study and discovery of new, more efficient materials for hydrogen storage and beyond it, contributing to the transition towards a greener and more sustainable energy future.

Methods

MLFF-MD

The Density Functional Theory (DFT), MLFF-MD and climbing-image-NEB39 (ciNEB) calculations were performed using VASP version 6.4.2 and version 6.4.333,34,40,41, respectively. We utilized a 4 × 4 × 4 supercell, shown in Fig. 5, comprising 128 Mg atoms in hcp crystal symmetry, with 8 H atoms (MgH0.0625) randomly distributed in the lattice. We performed non-spin-polarized calculations, at the Perdew-Burke-Ernzerhof (PBE) functional level of theory42, using an energy cutoff of 600 eV and a 4 × 4 × 4 k-points grid, with convergence threshold of 0.1 meV, employing a Gaussian smearing with a sigma value of 0.05 eV. To ensure consistency and avoid any discrepancies with our database, we adopted the same convergence parameters as those used in the Materials Project Database. For VASP-MLFF we used the default parameters. The temperature was incrementally raised from 0 to 700 K over a 0.2 ns interval with VASP on-the-fly MLFF-MD. In this setup, derived configurations-including structure energy, forces acting on each atom, atomic coordinates, stress tensor, and lattice parameters-were used to train the interatomic potential. Whenever the Bayesian error surpassed the set fixed threshold, VASP reverted to DFT to generate a new configuration in the database. Such on-the-fly procedure allows the model to use the accumulated ab-initio configurations to gradually improve the predictions on subsequent steps. The threshold value of 5 meV/Å has been set to ensure a collection of diverse and well-spread representation of structures in the database from the explored configurational phase space. During the thermalization phase, we opted for an NpT ensemble while constraining the cell shape, employing the Langevin thermostat with a friction coefficient for the lattice and atomic degrees-of-freedom equal to 10 ps−1. We applied zero external pressure and a time step of 1 fs. At key temperatures of 300 K, 480 K and 673 K, we conducted further 100 ps long NpT simulations in training mode to accumulate additional configurations. A total of over 3700 ab-initio configurations have been stored, fewer than 1000 being recorded at each constant temperature, and the remaining configurations captured during the ramping phase. Subsequently, we switched to MLFF-MD in run mode and determined the average lattice volume over a 100 ps period at fixed temperatures of 300 K, 480 K, and 670 K. The average volume configurations were then utilized to conduct NVT simulations. Following the 100 ps NVT simulation, we extracted three structures with an energy close to the average value of the NVT run. To avoid any correlations, we ensured that the time interval between each of them was at least 10 ps. Subsequently, starting from those, we performed three distinct NVE simulations, where we computed the mean squared displacements (MSD) of hydrogen atoms as the ensemble average of

$${\rm{MSD}}(t)=\frac{1}{T-t}\mathop{\int}\nolimits_{0}^{T-t}{[{\bf{r}}(t+\Delta )-{\bf{r}}(\Delta )]}^{2}d\Delta .$$
(2)

Where T is the total simulation time, and r is the trajectory of the atoms under analysis. During the final NVE run a reduced time step of 0.5 fs was employed to reduce energy fluctuations. All the MSD were constructed over NVE trajectories of 1 ns, and used to extract the diffusion coefficient D by fitting the linear part of the function with the Einstein relation

$${\rm{MSD}}(t)=6Dt$$
(3)

by fitting the initial 0.2 ns linear region of the simulation. The value of D at each temperature was computed as the average value of the three NVE replicas. The associated uncertainty was computed as the standard error of the mean SEM = SD/\(\sqrt{3}\), where SD is the standard deviation, and 3 the number of our collected predictions. An example of MSD fitting procedures is included in Supplementary Fig. SF1.

Fig. 5: Perspective view of a MLFF-MD frame, at 673 K, of the 4 × 4 × 4 MgH0.0625 supercell employed in the calculations.
figure 5

Mg atoms are displayed in orange and H atoms in pink.

Full size image

The ciNEB calculations were performed using a 2 × 2 × 2 supercell with one Hydrogen positioned along the main paths between interstitial sites identified in the literature17. A visualization of those sites is reported in Supplementary Fig. SF3. Also, every computation was performed using ten images and a 0.01 eV/Å forces convergence criterion.

Universal interatomic potentials UIPs

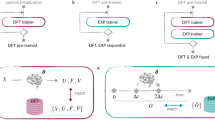
We consider two state-of-the-art best performing43 pre-trained UIPs: MACE44, based on an equivariant message passing neural network, and CHGNet31, a graph-based neural network. The models are imported in their pre-trained versions on the Materials Project (MP) relaxation trajectories database45, comprising 1.6 million crystal structures with the associated energies, forces, stresses, and magnetic moments. In order to tackle the predicted dynamical properties from such UIPs, we followed the same NEB and MD procedure (excluding the on-the-fly training phase) as explained in the previous section. Subsequently, CHGNet and MACE were fine-tuned on the VASP-DFT generated data obtained during the on-the-fly MLFF-MD. MACE was also trained from scratch on the dataset. Both training and fine-tuning of all the models were performed using the standard procedure and parameters suggested by the developers in the respective github repositories. During CHGNet’s MD simulations, we observed the need of a 0.5 fs time step to stabilize the dynamics also in the NPT and NVT runs, avoiding drifts in temperature for NVE. In this regard, we show examples of temperature oscillations during NVE simulations from 0.5 fs and 1.0 fs cases in Supplementary Figs. SF4 and SF5. To perform the MD simulations we employed LAMMPS46 and ASE47, for MACE and CHGNet respectively. A schematic view of the employed workflow is represented in Fig. 6. Furthermore, using the best performing model, (MACE_FT), we followed the same protocol to estimate D at three additional hydrogen concentrations, containing 10 H (MgH0.078125), 6 H (MgH0.046875) and 4 H (MgH0.03125), respectively. To assess the performance of every model, we evaluated the Root Mean Square Errors (RMSE) for the prediction of energy and forces over a test dataset of 1200 configurations. These were randomly sampled, with proper equal spacing in time, from the NVE replicas of the MACE_FT model, with 400 samples for each temperature. This validation process was independently repeated for each different hydrogen content to test the models’ accuracy beyond the training concentration. At last, NEB calculation on the same path studied using VASP were performed with every model using the ciNEB implementation of ASE employing the same number of images and convergence criteria.

Fig. 6: Methodological protocol employed to improve the performance of interatomic potentials and obtain dynamical properties.
figure 6

The database of configurations is built both during NpT-MD thermalizations of the system from 0 K to 700 K via active learning of the VASP-MLFF, and at target temperatures (300 K, 480 K, and 673 K). Subsequently, the machine learned potentials are fine-tuned or trained, and after system-equilibration the MSD and the diffusion coefficient D at fixed T are computed.

Full size image