Introduction

Many state-of-the-art solid-state high performance materials are composed of several different types of elements sharing the same lattice sites. Examples for application areas are, but not limited to, energy conversion and storage systems1,2,3,4,5,6,7,8,9,10,11 as well as other special-purpose applications12,13,14,15,16. In some of the most interesting materials for these applications (e.g., layered oxides, ionic conductors), numerous element types with various concentration ratios are combined in a single-crystal phase. While such compositions can be represented with the help of partial site occupations, the configurational complexity becomes a severe challenge for simulation methods that require structural models with integer site occupations, such as commonly used density functional theory (DFT)17,18. The problem of determining reasonable atomistic configurations out of all possible configurations therefore constitutes a serious challenge for modelling and simulation19,20,21,22,23,24. To represent complex compositions with integer occupations the so-called supercell approach is frequently employed, where multiple periodic images of the unit cell are treated explicitly. For computational studies it is often of interest to determine low(est)-energy atomistic configurations which can be a hard combinatorial problem for large supercells. For complex compositions it is generally infeasible to evaluate all possible configurations (even when accounting for symmetry), especially when using high-level methods such as DFT. Therefore, special techniques such as the Coherent Potential Approximation (CPA)25, Special Quasirandom Structure (SQS)26, Cluster Expansion (CE)27,28, Virtual Crystal Approximation (VCA)29, or Small Set of Ordered Structures (SSOS)30 have been developed that approximate the energy and/or are able to find special atomistic configurations that have relevant properties for further investigations. Approximations such as CE where many-particle interaction terms up to a certain order are taken into account can reduce the computational demand drastically31. Other approaches that try to mimic highly accurate energies at low computational costs include machine-learned potentials and/or try to reduce the amount of configurations that must be evaluated with other machine learning approaches, e.g., active learning32,33,34,35,36,37.

Naturally, the number of possible configurations becomes higher if the supercell contains more sites, more positions per site, and also when more elements can occupy a site, especially when elements are mixed in equimolar amounts. All of these factors generally apply to novel energy materials and yield a combinatorial explosion of the total number of possible configurations. For highly symmetric cells, this number can be reduced by several orders of magnitude if symmetry operations are taken into account and only symmetrically irreducible configurations are considered38. There are several software packages and methods such as the site-occupancy disorder (SOD) code39, ENUMLIB40 (also accessible through PYMATGEN41), the solid-solution tools42,43 in the commercial CRYSTAL code44, the so-called SUPERCELL software45, the DISORDER code46 and its recently published tree search algorithm38, and the SHRY package47 that all focus explicitly on determining symmetry in-equivalent structures. The number of available software and considerable computational effort spent highlights the importance of the atomistic combinatorial problem in computational materials research.

For ionic crystals, the Coulomb energy with ionic point charges represents a simple energy model allowing to evaluate numerous atomistic configurations with limited computational resources. In practice, the model requires the assignment of the ion valencies and the electrostatic energy is calculated by Ewald summation48 to obtain the exact Coulomb energy of the periodic lattice49. This allows to consider plenty of atomistic configurations explicitly and, in some cases, even the complete enumeration of all possible configurations for practical simulation supercells. This full enumeration approach, sometimes also referred to as brute force method or exhaustive sampling, is implemented with Coulomb energy evaluation in the so-called SUPERCELL software45. More recently, the EWALDSOLIDSOLUTION software50 was released offering the brute-force approach with an option for sparser sampling of the density of states based on Coulomb energy evaluation. In addition, EWALDSOLIDSOLUTION also features a post-processing gradient-descent-like algorithm for optimizing atomistic configurations. However, treating complex combinatorial problems as they appear in modern energy materials by brute forcing is computationally very demanding, even for simple Coulomb energy evaluation. Therefore, classical optimization approaches and the use of heuristics is commonly required.

The atomistic combinatorial sampling can be considered as a general optimization problem and commonly used meta heuristics can be applied. Do Lee et al.51 applied some well-known heuristics, including genetic algorithms, particle swarm optimization, harmony search, cuckoo search, bayesian optimization, and deep Q-networks, to configurational optimization in argyrodite utilizing Coulomb energies. Out of the vast amount of meta heuristics especially the Genetic Algorithm (GA)52 should be mentioned that is known to be effective for the atomistic combinatorial problem51,53, as well as for global optimization of complex chemical structures in general54. Next to these classical approaches, more physically motivated approaches such as Monte Carlo (MC)55 simulations were also shown to be efficient in approaching the atomistic configurations problem32,56,57,58, with the respective Monte Carlo methods implemented, e.g., for determination of SQS in the MCSQS code59 as part of the ALLOY THEORETIC AUTOMATED TOOLKIT (ATAT)60 or for general cluster expansions within the recently released STATISTICAL MECHANICS ON LATTICES package61. Binninger et al.56 recently also demonstrated that the configuration problem can be solved on existing quantum-computing hardware by formulating it as a binary optimization problem that can be mapped onto a quantum annealer.

The aforementioned software and approaches for determining lowest energy atomistic configurations are either effectively or explicitly limited in the size of the configurational space39,41,42,43,45,51,56,61 or do not specifically aim to determine the low(est) Coulomb energy structures by optimization38,40,46,50,59. As modern high-performance materials introduce more and more species, approaches are required that can reliably and quickly optimize even large combinatorial problems comprising of ten to the power of several hundreds of configurations. For that purpose, either heuristics or general-purpose optimization software can be used while the latter one bears the opportunity for exact global optimization within limited computational resources. Even though some works already employed heuristic optimization methods to the configuration problem, as discussed before, there is still, to the best of our knowledge, no published tool that allows for optimization of such complex problems yet. Efficient energy evaluation methods, even faster than the commonly applied Ewald summation, along with specifically tailored heuristics must be employed to achieve optimization in difficult atomistic combinatorial problems within reasonable computation time. Creating optimized atomistic configurations for complex problems in a high-throughput manner allows for efficient structure pre-selection for computational studies, such as DFT calculations, of novel materials and thereby offers the opportunity to enhance computational materials discovery in several important research fields.

In this work, we therefore approach the atomistic combinatorial problem in novel energy materials as an optimization problem utilizing a basic but reformulated Coulomb energy model. We present a Python-based code, termed GOAC (Global Optimization of Atomistic Configurations by Coulomb), that enables to interface any configuration problem of ions with distinctive valancies given as a crystallographic information file (CIF)62 to existing (free or commercial) optimization software. CIFs are read with help of the PYMATGEN41 package. Moreover, we introduce several Fortran-based routines that can be called from the Python code to apply various heuristics to the configurational optimization problem, including GA and MC. To provide a highly efficient implementation, the Coulombic energy is expressed by a binary optimization problem and the optimization heuristics are parallelized using OpenMP63. The methodological details of the implementations and the capabilities of the GOAC code are discussed in the next section, followed by a discussion of the results and benchmarking to alternative methods.

Results

Implementation and theoretical background

A supercell is assumed comprising S sites with partial occupations and each site having Ps positions within the cell. Moreover, a site should be occupied by Ns,e ions of the element e while in total Es elements can occupy the given site s. The total number of possible configurations C in the supercell, without considering any symmetries, is then given by:

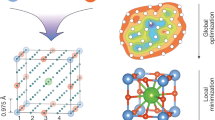
$$C=\mathop{\prod }\limits_{s=1}^{S}\frac{{P}_{s}!}{\mathop{\prod }\nolimits_{e = 1}^{{E}_{s}}{N}_{s,e}!}.$$
(1)

For a given problem, the Global Optimization of Atomistic Configurations by Coulomb (GOAC) code aims to determine low(est) energy atomistic configuration(s) out of all possible configurations by employing various optimization techniques. To this end, GOAC offers a command line interface to provide a CIF with partial occupations and assumed charge states (valencies) for the different ions. The general workflow of GOAC is sketched in Fig. 1.

Fig. 1
figure 1

Schematic workflow of the GOAC code and connection to external packages.

Full size image

In a first step, GOAC calculates the required pairwise Ewald energy matrix-elements, which is discussed in the next section. Then, a binary optimization problem is constructed by expansion to site-specific terms that can be either interfaced to external optimizers, e.g., the GUROBI solver64, or solved by internal Fortran heuristics. Both approaches are discussed in the following sections. Finally, the n lowest energy atomistic configurations are outputted as a CIF along with the respective Coulomb energies. It should be noted that, in its current implementation, GOAC is not able to identify symmetry-equivalent structures and all optimizers run on the full configurational space. However, filtering by energy is possible to only include structures that are different in energy, which can be useful for many problems but might exclude symmetry in-equivalent structures in some problems.

Pre-calculation of Coulomb energy terms

As optimization methods generally require evaluating the energy of many different atomistic configurations, GOAC implements an ionic Coulomb energy model due to the low computational demand. Naturally, such simple point charge models cannot account for quantum mechanical effects and there is no guarantee that the order of different ionic configurations by Coulomb energy is aligned with the one obtained by more accurate calculations, e.g., based on DFT. However, several studies showed that structures with a low Coulomb energy are often also good candidates for low DFT energies50,51,56,58,65. As an example, a satisfactory correlation between DFT and Coulomb energies at randomly selected configurations is shown in Fig. 2 for ionic configurations in the layered oxide Na[Li0.33Mn0.67]O2 (assumed ionic charges: Na: +1; Li: +1; Mn: +4; O: −2) that was synthesized by Wang et al.66. The relative energies show a strong correlation between DFT and Coulomb models and the linear fit well matches the diagonal representing perfect correlation. A commonly employed approach therefore consists in pre-selecting a certain number of low Coulomb energy structures to be used for more accurate DFT calculations and eventually determine low DFT energy configurations65,67,68,69,70.

Fig. 2: Correlation between relative DFT (details are described in the Method section) and Coulomb energies of different ionic configurations for Na[Li0.33Mn0.67]O2.
figure 2

Coulomb energies were obtained with the following ionic valencies: Na: +1; Li: +1; Mn: +4; O: −2. A linear fit of the data points is shown as a red dashed line, along with the ideal correlation diagonal (black solid line).

Full size image

Following this approach, GOAC utilizes point-charge Coulomb energies and expands them into a binary optimization model with site coefficients up to the second order. We note that for the specific case of the point-charge Coulomb energy this expansion is exact due to the pairwise character of Coulomb point-charge interactions. This allows for an efficient evaluation of different atomistic configurations during optimization as the energy can be expressed as a sum of pre-calculated coefficients. In periodic systems, Coulomb energies are, however, difficult to converge and the Ewald summation technique is required for the energy calculation.

The procedure of expressing the atomistic combinatorial problem as a binary optimization problem is sketched in Fig. 3. The total energy (Etot) of a given atomistic configuration can be expressed as a sum of the energy of the fixed ions (zero-order term, Econst), the interaction of each placed iterative ion with the fixed ions as well as its self-interaction due to periodic boundary conditions (first-order term, α), and all particle-particle interactions between all placed iterative sites (second-order term, β). All interactions in the resulting binary optimization model can be pre-calculated for efficient energy evaluation during optimization. In order to do this, the elements of the pairwise interaction matrix of the Ewald energy xtotal can be calculated by71:

$${x}_{ij}^{\,{\text{real}}\,}={q}_{i}{q}_{j}\sum _{{\bf{L}}}\frac{\,{\text{erfc}}\,(\eta \cdot {d}_{ij})}{{d}_{ij}}$$
(2)
$${x}_{ij}^{\,\text{recip}\,}=\frac{{q}_{i}{q}_{j}}{\pi V}\sum _{{\bf{k}}}\frac{\exp \left(\frac{-{\left\vert \dot{k}\right\vert }^{2}}{4{\eta }^{2}}\right)}{{\left\vert \dot{k}\right\vert }^{2}}\cdot \cos \left(\dot{k}\left({\dot{r}}_{i}-{\dot{r}}_{j}\right)\right)$$
(3)
$${x}_{ii}^{\,\text{self}\,}=\frac{-{q}_{i}^{2}\eta }{\sqrt{\pi }}$$
(4)
$${x}_{ij}^{\,\text{total}}={x}_{ij}^{{\rm{real}}}+{x}_{ij}^{{\rm{recip}}}+{x}_{ij}^{\text{self}\,}$$
(5)
Fig. 3: The energy calculation approach.
figure 3

Schematic visualization of the expansion approach to binary variables for iterative sites for the energy calculation of atomistic configurations along with the simplified energy formula and an example on how to map specific atomistic configurations on a binary vector. Arrows indicate pairwise interaction terms in the Ewald matrix while for the constant term only interactions for one site are shown exemplary.

Full size image

In these equations i and j are the indices of two sites, \(\dot{r}\) is their position, q their charge, and dij the Euclidean distance between them. The cell volume is denoted as V, L is the sum over all real-space lattice vectors and k over (non-zero) reciprocal-space lattice vectors within the respective cut-off radii and η is the screening length. While the theory and implementation of Ewald summation is already extensively discussed in the literature, for example by Faber et al.71, we want to highlight that for the energy calculation of configurational optimization problems, the real-space and reciprocal-space terms can be split into an charge-dependent (q-dependent) and position-dependent (r-dependent or d-depended) term. The computationally demanding parts are in the position-depended expressions as the sum over all real-space (L) and reciprocal-space (k) lattice vectors has to be considered. As the pre-calculation of all pairwise interactions of a configurational optimization problem requires to evaluate multiple charges on fixed positions, the position-dependent terms of the real- and reciprocal-parts only have to be considered once for each site-pair. This can result in an additional speed-up compared to standard Ewald summations of different configurations as not just every pairwise interaction is only considered once, but also the computationally demanding summations over lattice vectors are only performed once for each pair of different positions. GOACs implementation to calculate the pairwise interaction Ewald summation energy matrix for configurational optimization problems utilizes this shortcut and in addition parallelizes the calculation of the matrix elements. From the Ewald summation matrix it is straight forward to construct the binary optimization problem by summing up the matrix elements that correspond to the black arrows in Fig. 3 to obtain the values for Econst and all expansion coefficients α and β. We note, that this expansion can be considered as special case of a general second-order cluster expansion without the requirements for any distance cut-offs as periodic pair-wise interactions are considered exactly by Ewald summation. Thus, cutting the expansion at the second interaction order yields the exact Coulomb energy of a configuration.

GOAC also allows to consider Gaussian smeared charges instead of point-charges by applying to following correction to the point-charge energy-terms72:

$${x}_{ij}={x}_{ij}^{Point}-\frac{1}{2}{q}_{i}{q}_{j}\sum _{{\bf{L}}}\frac{\,{\text{erfc}}\,\left(\frac{{\sigma }_{i}{\sigma }_{j}}{\sqrt{{\sigma }_{i}^{2}{\sigma }_{j}^{2}}}{d}_{ij}\right)}{{d}_{ij}}.$$
(6)

In this equation σ is related to the smearing width \(\hat{\sigma }\) of the Gaussian shaped charge by \(1/(\sqrt{2}\sigma )\). It should be noted that no correction to the self-energy is applied to ensure a convergence towards the point-charge energy for \(\hat{\sigma }\to 0\). This does practically also do not influence the configuration search as the self-energy cancels out when two different configurations are compared.

For the exemplary problem in Fig. 3 with two sites that are both occupied by 50% by two different species, all possible configurations can be expressed by a binary solution vector x that has a position for each site for each species. A possible solution would than have a 1 on every position where a species is placed and a 0 everywhere else. By that, the total energy of a given instance becomes a simple sum of products of pre-calculated first-order (α) and second-order (β) coefficients and the binary solution vector x. To ensure that only second-order terms are counted where both ions are placed, the β-coefficients are multiplied by the two corresponding positions in the binary solution vector. Due to the pairwise character of Coloumb energies such an expansion to a binary optimization problem is able to give the correct periodic energy for each configuration by pre-calculated coefficients.

For implementing the binary optimization problem, a slight reformulation of the equation in Fig. 3 appears to be practical where the solution vector x has two dimensions, one for the site-species (i) and one for the positions this site-species can occupy (j). Consequently, the expansion coefficients α and β become higher in dimensionality as well. By reformulation of the sums it is ensured that each interaction is only counted in one direction and just one half of the diagonal α and β matrices must be stored. Lastly, for a full optimization problem the constraints have to be defined. Beyond the binary constraint for the x variables (Eq. (10)) it must be also ensured by additional constraints that the desired total occupancy (Oi) is matched for each site-species i (Eq. (8)) and that a certain position j is not occupied by multiple species i (Eq. (9)). In summary, the optimization problem of atomistic configurations is implemented in GOAC as shown in Eqs. (7–10).

$$\mathop{\min }\limits_{{E}_{tot}}\quad {E}_{tot}={E}_{const}+\mathop{\sum }\limits_{i=1}^{S}\mathop{\sum }\limits_{j=1}^{{P}_{i}}{\alpha }_{i,j}\cdot {x}_{i,j}+$$
(7)
$$\begin{array}{l}\mathop{\sum }\limits_{i=1}^{S}\mathop{\sum }\limits_{j=1}^{{P}_{i}}\mathop{\sum }\limits_{l=j+1}^{{P}_{i}}{\beta }_{i,j,i,l}\cdot ({x}_{i,j}\cdot {x}_{i,l})+\\ \mathop{\sum }\limits_{i=1}^{S}\mathop{\sum }\limits_{j=1}^{{P}_{i}}\mathop{\sum }\limits_{k=i+1}^{S}\mathop{\sum }\limits_{l=1}^{{P}_{k}}{\beta }_{i,j,k,l}\cdot ({x}_{i,j}\cdot {x}_{k,l})\end{array}$$

subject to:

$$\mathop{\sum }\limits_{j=1}^{{P}_{i}}{x}_{i,j}={O}_{i}\quad \,\forall i\in S$$
(8)
$$\mathop{\sum }\limits_{i=1}^{S}{x}_{i,j}\le 1\quad \quad \forall j\in {P}_{i}$$
(9)
$${x}_{i,j}\in \{0;1\}\quad \quad \forall i\in S;\quad \forall j\in {P}_{i}$$
(10)

Even though Coulomb (Ewald summation) calculations are computationally comparably inexpensive, for high-throughput evaluations of atomistic configurations Eqs. (7–10) represent a significant speed-up compared to a full Ewald summation for each atomistic configuration. Moreover, by storing the expansion coefficients (α and β), the pre-calculated energy terms conveniently allow to test multiple optimization approaches without performing energy calculations every time.

Optimization strategies for atomistic configurations

Two main categories of optimizers, namely exact and heuristic optimizers, can be distinguished. A successful run of an exact optimizer guarantees that the global optimum is found or, if specified, not just the global optimum but the n lowest energy structures while n can be freely chosen by the user. The heuristic optimizers guarantee to output a valid, low energy structure that might be the global minimum or just a local minimum or no minimum at all, depending on the optimizer. The focus of heuristics is to create valid, high-quality solutions fast, while exact optimizers spend significant effort on proving optimality without improving the actual minimum solution. Depending on the needs of the user, both approaches can be valuable and are accessible via the GOAC code as described in the next sections.

Interfacing to external exact optimizers

Generally speaking, Eqs. (7–10) describe a so-called mixed integer non-linear programming (MINLP) problem with the special circumstance that all variables are not just integer but binary variables which technically allows for a reformulation to a mixed integer linear programming (MILP) problem. Problems of the same type frequently appear in the context of business economics under the collective term Operations Research, where the aim is, e.g., to determine the optimal (shortest/fastest) delivery route73 or to optimize production planning74. Due to the economic value connected to this problem type plenty of optimizers exist75. Their aim is to find the global optimum and also prove that the global optimum was found employing advanced mathematical strategies that can be faster than a full enumeration of all possible solutions (brute forcing), which, by definition, is also an exact optimization method.

For a given atomistic combinatorial problem, GOAC can create a standard MINLP with the help of the licensed Gurobi64 software and the full problem statement is written to a standard MPS (Mathematical Programming System) file. By default, GOAC passes this MINLP also to Gurobi for solving, however, it should be noted that the MPS file can be used to run the problem in other (commercial or free) optimization software. GOAC supports interfacing to the Gurobi optimizer and its solver parameters. It is worth noting that Gurobi (and other software) is technically capable of linearizing the quadratic terms in the MINLP to an MILP due to the binary character of the integer variables. This is not done by default in GOAC but was found to be efficient for some problems. Such a reformulation can also allow the use of other standard optimization software that are not capable of general MINLPs. However, results for exact optimizations presented in this work were obtained with the default Gurobi parameter set in GOAC, which was found to be most robust for different configuration problems. It should be noted that the MPS file of the problem can be also handed to non-exact heuristic solvers.

Internal Fortran heuristics in GOAC

The core of the GOAC code offers different heuristic optimizers for the atomistic combinatorial problem that are all tailored for this specific problem and implemented in Fortran. All of these heuristics are capable of generating valid low energy structures. The following methods are currently supported in the GOAC code: a random structure generator, a Greedy Heuristic, a Gradient Descent algorithm (GD), a Metropolis Monte Carlo code (MC)55, a simulated annealing extension of the MC code (SA), a Replica Exchange Monte Carlo scheme (REMC)76, and a Genetic Algorithm (GA)52 with roulette wheel selection77. The random structure generation occupies sites randomly and resulting structures are not as random as structures obtained by, e.g., SQS. It is also possible to combine some of the aforementioned heuristics to a hybrid approach. Such combinations were already proposed and proven successful for chemical optimization problems78,79 and a combination of the REMC and GA heuristic is benchmarked and referred to as HY in the following. The functionalities of the different algorithms are discussed in more detail in the manual and the code can be directly accessed within the project repository (see Code Availability Statement).

Most heuristics that are directly implemented in the GOAC code are of stochastic nature and it can be useful to run the same heuristic multiple times. By that procedure, the probability and confidence that the global minimum and other low energy structures are found can be increased. For convenience, GOAC allows to run the same heuristic multiple times in parallel with the help of OpenMP63 which allows to achieve an statistic ensemble over multiple runs with the same heuristic. Moreover, trivial parallelizations such as, e.g., parallelization over the different temperatures in REMC are also implemented via OpenMP in GOAC to further boost the performance of the code. The scaling behaviour of the different algorithms is also sketched in Supplementary Fig. 1. Finally, the internal heuristics in GOAC offer abortion by run time or heuristic steps without improvement on the global minimum. More detailed descriptions of GOAC’s features and how to employ them can be found in the manual inside the project repository (see Code Availability Statement).

Performance of exact optimization methods

As explained above, GOAC has the possibility to interface to external optimization software for exact optimization of atomistic configurations. For this benchmark, the Gurobi optimizer, which utilizes an advanced branch-and-cut method, is employed with the default parameter set GOAC uses to interface to Gurobi. This parameter set enforces strong pre-solving of the model (Presolve = 2) along with a focus on proving optimality (MIPFocus = 2). It also ensures that the n lowest energy structures are found by setting the convergence boundaries to zero (MIPGap = 0 and MIPGapAbs = 0) and the “PoolSearchMode” to 2. To the best of our knowledge, the existing software for exact optimization of configurations, i.e., including proof of optimality, employ the full enumeration approach. An efficient implementation of the latter can be found in the SUPERCELL software, which is used as a reference for timings of full enumeration. Here it should be noted that the SUPERCELL software only considers the symmetry in-equivalent structures which reduces the number of explicitly considered atomistic configurations drastically compared to the total number of configurations when ignoring symmetry.

The SUPERCELL software and the optimization with Gurobi of the model prepared by GOAC were tested on a layered-oxide sodium-ion-battery cathode material (Na[Li1/3Mn2/3]O2)66 with one layer in the c-direction and partial occupations in both the transition-metal and sodium-ion sites, cf. Fig. 4. By changing the sodium-ion stoichiometry from 1.0 to 0.52, configuration combinatorics with steadily increasing number of total possible configurations ranging from ca. 107 to 1014 were created and evaluated by both approaches. Such variation of the sodium concentration is also a practical example as it is a common task of battery material simulations to find sodium configurations at various concentrations that are suitably low in energy to predict accurate operation voltages80. Charge states of Na+, Li+, Mn4+ and a variable oxidation state of oxygen ranging from −2.0 (for a Na stoichiometry of 1) to −1.75926 (for a Na stoichiometry of 0.52) to ensure charge-neutrality were assumed as the compound is reported to show anionic redox from O2− to On− (n < 2)66. As both approaches guarantee to determine the global optimum after a successful run, it is only of interest to benchmark the run time of both methods. The timings on 128 physical processor cores are plotted against the total number of configurations in Fig. 4. For smaller problem instances with up to ca. 109 configurations, full enumeration was faster than optimization due to the overhead of interfacing to an external optimization code combined with the capability of the SUPERCELL software to reduce the solution space to just symmetry in-equivalent structures. However, it should be noted that timings on these problem instances are well below 10 s and therefore computationally inexpensive in both approaches. For more complex problems the full enumeration approach scales perfectly linearly while run time of the branch-and-cut optimization method increased more irregularly from the small offset caused by the overhead. In general, the computation time of the branch-and-cut optimization was significantly lower for more complex instances of this problem and also appeared to scale lower towards problems with many configurations. Overall, a speed-up of up to three orders of magnitude was achieved by the optimization with Gurobi compared to full enumeration with the SUPERCELL software at the most difficult considered problem instance with ca. 1014 total configurations. The respective run times to find the global optimum atomistic configuration in Coulomb energy were ca. 18 h by full enumeration versus ca. 1.5 min by Gurobi optimization.

Fig. 4: Scaling of full enumeration versus optimization.
figure 4

\({\log }_{10}\)-\({\log }_{10}\) representation of run time (estimated from outputted timings of the software) to find the global optimum atomistic configuration versus number of total possible configurations using the full enumeration approach and external optimization software.

Full size image

Figure 4 clearly highlights the computational advantages that can be accessed by using GOAC to formulate a general optimization problem for the combinatorial ground-state search that can be handed to external optimization software. However, extrapolating the scaling behaviour to much larger problems also reveals that even with the significant speed up achieved, still only problems of intermediate difficulty/size can be tackled. It must be also noted that the actual performance of the branch-and-cut optimization is very much problem dependent. By introducing (slight) changes to the presented problem (e.g., more species per site or more sodium sites by using a P-type layered structure81), problems can be constructed where optimization of the complete configuration space is even slower than full enumeration of symmetry in-equivalent structures or problems that formally have as many as 10230 configurations, but are being optimized within seconds, might be obtained.

In summary, the performance of applying standard optimization software to the atomistic combinatorial problem is strongly problem (material) dependent. However, our results indicate that especially for problems of intermediate difficulty (ca. 1010 to 1020 possible configurations), such as configuration of charge carriers in rechargeable energy storage materials, optimization can give a significant computational advantage over full enumeration approaches, even if the full enumeration method accounts for symmetry equivalents.

Benchmark of heuristics in GOAC

As the heuristics do not guarantee to find the global minimum, a suitable benchmark could either compare the lowest energy that is found within given computational resources or the time that it takes to find a known global optimum. However, the implemented heuristics are of stochastic nature which makes it important to average their performance over multiple runs. Such comparisons of the different internal heuristics in GOAC are discussed for several examples with various complexity in the following. Moreover, an additional benchmark of FeSbO4 is shown in the supplementary information (Supplementary Table 1). All examples in the following were executed on the same hardware and run times (given in real time) were estimated by the CPU time required to perform each calculation.

Atomistic configurations in NaCl

The site occupation in NaCl is not a true combinatorics problem as the unit cell contains two distinctive sites, one for Na and one for Cl. However, for testing purposes both sites can be modified such that each site is occupied by 50% of each species, yielding an atomistic combinatorial problem. With this model, in a 3 × 3 × 3-supercell the total number of possible configurations is ca. 1064, a rather difficult combinatorial problem. As the global optimum still remains trivial, a perfectly alternating pattern of Na and Cl in all dimensions, this problem statement is a rather suitable benchmark. Moreover, calculation of the Madelung constant82,

$${M}_{C}=\frac{4\pi \times {\epsilon }_{0}\times r\times | E| }{{N}_{{\rm{Ions}}}/2\times e},$$
(11)

is straight forward and convergence to the literature value of M = 1.74756…83 can be tracked for the different heuristics over run time. In this equation, ϵ0 is the electric constant, r the lattice distance of two neighbouring sites (2.81 Å), E the Coulomb energy of the considered structure, Nions the total number of ions in the structure (216), and e the elementary charge.

The convergence towards the Madelung constant for the heuristics implemented in GOAC is plotted in Fig. 5. It is observed that the Gradient Descent heuristic requires some time before the first solutions can be obtained. In this algorithm, the first solution is written as soon as the local minimization from a random starting point is finished and then the next random starting structure is optimized. The time required to reach this first solution is also different for random starting structures as different amounts of optimization steps are necessary to reach a local minimum. Therefore, in the beginning of the GD plot, averages over less than 16 runs are contained, which also explains the drop in the average caused by more independent runs that obtained their first solution being included. Even though the average becomes flatter and standard deviations as well as min-max differences become smaller towards the end of the 5 minutes run time, no run was able to find the global minimum. This highlights the problem of this algorithm as it guarantees to find a local minimum but on shallow energy surfaces with many local minima it becomes highly unlikely to find the global minimum as there is a high chance to get trapped in another local minimum. However, in other use cases one might also be interested in studying these local minima.

Fig. 5: Heuristic optimization in NaCl.
figure 5

Single-Core (1 physical CPU core, 1 OpenMP thread) performance of the MC (a), SA (b), REMC (c), GD (d), GA (e), and HY (f) approaches as implemented in GOAC on the atomistic combinatorial problem of NaCl in a 3 × 3 × 3-supercell with 1064 possible configurations. All heuristics were run for 300 seconds and averages over 16 independent runs along with their statistics (standard deviations, minimum, maximum) and the obtained minimum structure are shown in the plots. For MC, averages and standard deviations over 16 runs are visualized for 10 different temperatures, respectively. The temperature evolution for SA is shown in the respective inset and the REMC parallel temperatures are indicated in the corresponding plot.

Full size image

The same tendency can be observed in Fig. 5 for Monte Carlo performed at low temperatures (ca. 0.1–0.5 eV) as the average quickly flattens to a constant value since the algorithm gets trapped in local minima at a low sampling temperature, similar to the outcome of the GD method. At higher temperatures (ca. 0.6–0.8 eV), however, the averages are observed to get closer to the Madelung constant (corresponding to the global energy minimum) over time as local barriers can be passed with a certain probability to eventually find lower minima. At high temperatures (ca. 0.9–1.0 eV) the algorithm is able to pass even higher energy barriers, thus spending only short times for local optimization and resulting in a decrease of average performance. In this example, the best result (on average) was obtained at a temperature of 0.8 eV and the performance was quite sensitive to the simulation temperature, even though multiple runs at various temperatures were able to find the global optimum within five minutes of run time. To overcome these temperature sensitivity, methods that make use of temperature variation to improve the optimization performance are discussed next.

The average performance of Simulated Annealing was similar to that of MC at lower to intermediate temperatures with a relatively high variance in solutions, as some runs returned the global optimum. This behaviour can be explained by the rather fast cooling rate chosen, which exponentially decreased from an initial simulation temperature of 1.0 eV to almost 0 eV during the run time (cf. inset in Fig. 5). Such a high cooling rate, which was required to scan a sufficiently large temperature range within the given run time limit, makes it more unlikely that a sufficient temperature is present at the crucial optimization steps leading to a high risk of local minima trapping. Nevertheless, SA was able to find the global optimum in some runs.

The last tested approach from the MC family, namely Replica Exchange Monte Carlo, shows a better performance than SA. The algorithm showed a pronounced optimization, especially in the first ca. 100 s, before almost constant values for average, standard deviation, and min-max were reached. This behaviour indicates that the optimization got trapped in local minima for some runs, while in other runs the global optimum was successfully reached. As only about one third of the run time (ca. the first 100 s) was effectively used for optimization, the performance might be improved by using more than four temperatures in REMC, including also largely-different and higher temperatures. Compared to the other heuristics, REMC performed very well within the given run time.

Among the approaches compared in Fig. 5, the Genetic Algorithm shows the slowest increase in average performance versus run time. Several generations and selection procedures are required to obtain more optimized structures resulting in the steep improvement of average energy. Even though some GA runs successfully reached the global optimum, the average over all runs was still substantially below the correct Madelung constant after 300 s of run time, showing that some runs got trapped in local minima. The trapping also goes along with high standard deviations and a large min-max difference. This occurs if the structural variation in the generations becomes low and centred around a deep local minimum. Another problem can be that the generation consists of symmetry equivalents of the same local minimum or if the local minimum is so deep that it can not be exited at small mutation rates which are required for a systematic optimization.

To overcome these limitations the Hybrid approach can be employed which provided the best performance among the methods compared in Fig. 5. Here, a pre-trained (from REMC) generation was used for the GA which greatly improved the average performance within the first seconds of the run. Moreover, the REMC steps between the GA runs can help to improve the variation in the generation pool of the GA. Vice versa, the GA offers a systematic procedure to make rather large steps on the potential energy surface that cannot be efficiently achieved by pure REMC. Therefore, both approaches can complement each other and the results demonstrate that HY was very effective with the average of 16 independent runs being fairly close to the correct Madelung constant after just 5 minutes of run time and with many runs ending in the global optimum. Moreover, the average kept increasing at longer run times indicating that most of the runs would eventually converge to the global optimum. Notably, the HY strategy performed better than the two individual approaches (GA and REMC) and was the best out of all investigated methods, indicating that a beneficial synergy effect between GA and REMC was achieved.

Li-site occupation and Ta doping in LLZO

Li7La3Zr2O12 (LLZO) is a widely studied electrolyte for all-solid-state batteries and therefore of high practical interest. However, the global minimum energy structure or in general low energy configurations are rather hard to approach computationally due to its large unit cell (8 formula units). The computational challenge becomes even more severe when dopants and defects are introduced that require even larger supercells. For these cases, the configurational space is extremely large, representing an interesting test for GOAC to obtain optimized atomistic configurations in terms of Coulomb energies. As an example, we consider Li6La2.969Zr0.906Ta1.094O12 (Charges: Li1+, La3+, Zr4+, Ta5+, O2−) which can be modelled by a 2 × 2 × 1 supercell (32 formula units). The modelled composition is in good agreement with the experimental one reported by Redhammer et al.84. We define the structure such that all lithium ions can be placed in both the tetrahedral and octahedral sites, resulting in a total of ca. 10159 possible atomistic configurations. The corresponding structure model is also shown in Supplementary Fig. 2.

Performances over 10 independent optimization runs are visualized for each heuristic of GOAC in Fig. 6. As discussed previously at the example of NaCl, the GD algorithm requires some time before the first local optimizations are finished and therefore the average plot begins at ca. 1000 s in Fig. 6. The overall performance of GD was found to be among the worst out of the GOAC heuristics. The GA solutions converged to a similar average energy as GD, but also had the largest variation between the best and worst independent runs, hinting at local minima trapping. This behaviour might be reasoned by the different parallelization approaches as discussed in the supplementary information and the code documentation in the project repository (see Code Availability statement). However, averages shown in Fig. 6 are still a fair comparison of optimization performance versus CPU time, revealing that the heuristics including some sort of MC are more efficient than a pure GA for LLZO.

Fig. 6: Heuristic optimization in LLZO.
figure 6

Average (a) and min/max (b) energies per ion for the LLZO atomistic combinatorial problem with ca. 10159 configurations over 10 independent runs of 1 h at 128 physical CPU cores (128 OpenMP threads) for GD, MC, SA, REMC, GA, and HY as implemented in GOAC. In the upper plot, also the average temperature profile used for the SA simulations is shown. The structure inset in the lower plot corresponds to the minimum energy structure that was obtained across all optimizations. An enlarged version of the minimum energy structure is also given in Supplementary Fig. 3.

Full size image

The MC approach returned an intermediate average energy per ion, while the SA and REMC methods yielded significantly lower energies after one hour of run time. For most heuristics the convergence was rather flat beyond the first ca. 500 s, but SA showed an exponential decrease over the whole run time which was matching the exponential decrease of the respective simulation temperature from ca. 12,000 K to almost 0 K (cf. Fig. 6). Interestingly, also the variance between the best and worst runs became rather small for the SA approach. In contrast to the results obtained for NaCl, SA performed well for the present example due to the longer run times that allowed for a slower cooling rate. The final average energies obtained from SA and REMC were similar, but the energy of the best REMC run was slightly lower than that of the best SA run, and the corresponding minimum-energy structure is shown in Fig. 6. The superior performances of SA and REMC over the other methods demonstrate that MC approaches with some temperature variation are very effective for the complex LLZO configuration problem. While in this example, the HY approach was not able to improve on the performance of REMC, still a much lower average energy than for the pure GA was found. The overall performance of HY might be increased by longer run times and adjusted heuristic parameters.

The determined minimum energy structure can be analysed in terms of the ratio of lithium ions in tetrahedral versus octahedral coordination of oxygen as all lithium ions were freely iterated over both classes of sites during optimization. A ratio of \(\frac{77}{115}\approx 0.67\) is obtained which is in very good agreement with the ratios of 0.74, 0.64, and 0.59 (after different treatments) and an average of 0.66 reported from experiments84. This highlights again the predictive quality of point-charge Coulomb energies for the configuration of ions in complex structures and validates the approach of pre-selecting atomistic low energy configurations by Coulomb energies for higher-level calculations. It should be mentioned that in a practical study one might be interested in the n lowest energy configurations as the material probably encounters some disorder in experiment. However, referencing to the lowest energy configuration is desirable to assess which meta-stable configurations might exist at a given temperature. Moreover, the discussed LLZO example can hardly be approached by exact optimization or computationally more demanding energy evaluation models proving the practicability of heuristic optimization with Coulomb energies. To the best of our knowledge, heuristic configurational optimization of Coulomb energies has not been reported before for any comparably complex atomistic combinatorial problem. However, it should be mentioned that heuristic optimization was carried out on different, more complex problem settings beyond site-configurational optimization and Coulomb energies such as, e.g., protein folding85.

Layered oxide cathode materials

To further demonstrate the optimization capabilities of GOAC, we addressed the atomistic combinatorial problem in a high-entropy layered sodium-ion-battery cathode material. The composition of O3-Na2/3[Li1/6Fe1/6Co1/6Ni1/6Mn1/3]O2 was recently proposed by Yao et al.86, while O3 indicates that the structure has three layers in the c-direction and octahedral coordination of the sodium ions81. We modelled the system in a \(\sqrt{3}\)-unit cell (a = 5.0 Å, c = 19.2 Å) assuming ionic charges of Na+, Li+, Fe2.5+, Co3.5+, Ni2+, Mn4+, and O1.75−. The cationic charges were chosen to agree with the ones observed in experiment86 while the charge of Fe was decreased by 0.5 and the one of Co was increased by 0.5 to ensure that all configurations are distinguishable in Coulomb energy. The oxygen charge was set to achieve a overall charge-neutral compound and can be reasoned by the experimentally reported oxygen redox. All sodium ions were iterated over all sodium positions in every layer (one sodium site in the whole structure with nine positions in the unit cell) and all ions in the transition metal layers were iterated over all positions in each layer (one transition metal site in the whole structure with nine positions in the unit cell), allowing for the maximal configurational space. To highlight the scalability and limitations of GOAC, this configuration problem was solved in supercells of different sizes ranging from 4 unit cells (2 × 2 × 1, Na24[Li6Fe6Co6Ni6Mn12]O72) to 108 unit cells (6 × 6 × 3, Na648[Li162Fe162Co162Ni162Mn324]O1944). Structure models for the smallest and largest considered supercells are visualized in Supplementary Fig. 4. Results for optimizing the atomistic configurations with the heuristics in GOAC within a given run time (given computational resources) are summarized in Table 1.

Table 1 Energies per ion of the lowest energy structures obtained for differently sized supercells of O3-Na2/3[Li1/6Fe1/6Co1/6Ni1/6Mn1/3]O2 with the different heuristics implemented in GOAC (all calculations performed on 128 physical CPU cores and using 128 OpenMP threads)
Full size table

Remarkably, all solvers were capable to find the same minimum, likely the global minimum, for the smallest problem of a 2 × 2 × 1 supercell within just one hour of run time. It should be also noted that most heuristics identified this minimum within the first minutes (cf. the convergence versus run time plots in Supplementary Figs. 5–10). Compared to the exact solvers presented in the previous section, this represents a huge speed up as a problem with 1031 total configurations would be (almost) impossible to solve with an exact solver in a reasonable run time, especially not within just one hour. This highlights the practicability of GOAC as problems of this size regularly appear when high-entropy structures or similarly complex structures are to be pre-selected for DFT calculations. The suitability to pre-select low(est) energy structures for DFT calculations was also checked by performing single-point DFT calculations on the 10 lowest energy configurations obtained by the REMC approach (Supplementary Fig. 11). This is particularly practical as one is usually interested in selecting a sufficiently low or several low energy configurations but in the following just the global minimum is discussed to better compare the performances of the different heuristic optimizers.

For the next larger problem, a 2 × 2 × 2 supercell, only the more advanced heuristics, namely SA, REMC, GA, and HY, were able to find the same lowest energy structure, which makes it again a likely candidate for the global minimum in Coulomb energy. The respective minimum energy is lower than the minimum energy obtained for the smaller problem, because the increased problem size allows for larger, energetically more favourable superstructures. The same applies to the 4 × 4 × 1 supercell where SA, REMC, and HY obtained the same best candidate configuration for the global minimum. As the periodicity is extended in a different direction compared to the 2 × 2 × 2 supercell, the minimum energy is still lower than for the 2 × 2 × 1 case but higher than for the 2 × 2 × 2 supercell. For a 4 × 4 × 2 supercell, only SA and REMC were capable to find a likely candidate for the global minimum. The respective minimum energy is identical to the one of the 2 × 2 × 2 problem as both consider the same periodicity, and thus same degrees of freedom, in the c-direction. The additional degrees of freedom in a and b-direction, on the other hand, did not seem to allow for the formation of lower energy superstructures. These findings highlight another aspect why it is important to consider sufficiently large supercells in the construction of structural models with occupational disorder, because suitable supercell sizes are required for lowest energy superstructures. To efficiently select suitable supercell sizes and to account for the fact that it becomes increasingly hard to obtain the lowest energy configuration in larger supercells even if it is already known from a smaller commensurately cell, GOAC also allows to systematically scan for increasing supercell sizes to find low(est) energy configurations.

For an even larger 6 × 6 × 1 supercell, the GD heuristic was not able to reach any local minimum within the given run time since more complex problems not only increase the expected number of optimization steps required to reach a local minimum from a random starting structure but also heavily increase the amount of neighbouring structures that need to be evaluated to follow the steepest descent path. Within the given framework, 10269 configurations seemed to be the maximum where GD could be applied within reasonable computational resources, which is arguably already a quite large configurational space. For the 6 × 6 × 1 supercell, REMC returned the lowest energy structure, lower in energy than the 2 × 2 × 1 minimum, which was expected given that the 6 × 6 × 1 is a multiple of the 2 × 2 × 1 supercell. SA also returned a low-energy solution, albeit not the same minimum, probably because the cooling rate was too fast for the given problem size and run time limitation.

For all supercells larger than 6 × 6 × 1, SA found the lowest energy structure out of all heuristics implemented in GOAC. However, the obtained minima did not correspond to the respective global minima as they were higher in energy than the minimum energy structures of one of the smaller problems with matching multiplicity. While it is still possible to run optimizations on these extremely large problems, the results show the limitations of the heuristics implemented in GOAC as one cannot expect to find lowest energy configurations within reasonable run times for such large configurational spaces. Due to the combinatorial explosion in large cells it is also not surprising that it is nearly impossible to find minimum energy structures in configurational spaces with up to 10920 configurations, a number even larger than the estimated total number of atoms in the entire universe87 to the power of ten (The actual number of atoms in the universe must be estimated from measured densities and hydrogen/helium distributions and is in the range of ca. 1080 atoms).

The pure MC heuristic performed inferior to the more elaborate SA and REMC extensions for all problem sizes. As it was shown for NaCl, the MC method is quite sensitive to the simulation temperature which was not re-optimized for every problem in the benchmark (fixed to 0.75 eV). The GA performed rather poor for problems with a complexity of 10269 or more in its current implementation. Combining the GA with REMC in the HY approach did not resolve this issue for the larger problem sizes as the gain in performance compared to the pure GA stemmed almost exclusively from the REMC part. Therefore, the overall performance of the HY method was still inferior to using all computational resources on REMC. More advanced HY combination schemes or different crossing strategies in the GA might resolve this under-performance in the future.

Discussion

In this work, we showed that the problem of finding low(est) energy configurations in the huge configurational space of modern energy materials can be effectively approached by using advanced optimization methods in combination with Coulomb energy models. The Coulomb energy variations between different configurations often align well with energies from higher levels of theory, e.g., DFT, and sampling by Coulomb energies is therefore an attractive method to pre-select low-energy structure candidates. As a tool for conveniently and effectively exploring the vast configurational space of atomistic configurations in complex materials, we introduced the GOAC code that can be conveniently accessed as a command line tool.

The calculation of energies of different configurations was significantly sped up by expressing the Coulomb energy cost function as an expansion to a binary optimization problem, which enables the use of pre-calculated coefficients in the optimization procedure, thus providing significant improvements over performing Ewald summations at each optimization step. This reformulation transforms the atomistic combinatorial problem statement into an MINLP problem and allows to employ various advanced optimization methods. We showed that the exact optimization of the MINLP, interfaced via GOAC to existing optimization software, was several orders of magnitude faster than the full enumeration approach often applied for the atomistic combinatorial problem, allowing to exactly solve configuration problems for larger system sizes.

Due to the combinatorial explosion of the configurational space in complex multi-element materials, exact solving strategies cannot be applied to more complex materials. For such problems, we implemented several heuristics in GOAC, including Gradient Descent, Monte Carlo, Simulated Annealing, Replica Exchange Monte Carlo, Genetic Algorithms, and hybrid approaches. With these heuristics, GOAC produced high-quality low-energy structures within limited computational resources for extremely large configuration problems, which is of interest to model complex compositions and identify possible superstructures. As a highlight, we showed that GOAC was able to find likely candidates for global minimum structures of problems with 10303 configurations in just about 2 h of run time on 128 CPU cores. It should be mentioned that this usually implies that also the n lowest energy configurations that are of interest for further computational studies are obtained as well. Moreover, it was demonstrated that for problem combinatorics up to 10920, it was still possible to perform optimizations using the GOAC package even though finding minimum energy configurations in reasonable computation time cannot be expected at such large problems.

For the results presented in this work, simple point-charge Coulomb energies were employed, which represent a rough estimation that does not guarantee to coincide in the lowest energy configuration with higher level of theory approaches, e.g., DFT. Moreover, atomistic combinatorial problems with charge-neutral ions (atoms) or ions with identical valencies cannot be optimized on the basis of Coulomb energies alone. In general, one can expect to get reasonable energetic alignments of DFT and Coulomb when the charges are more localized as this is more well-described by point-charges. When studying systems with more delocalized charges, e.g., highly charged cathode materials, the alignment of DFT and Coulomb energies might decrease. To potentially overcome the issue of too delocalized charges and also allow to treat different ions with the same charge, GOAC also supports Gaussian smeared charges. Future studies will show if or how smearing out the point-charges can improve the accuracy of the Coulomb model in cases with strong delocalization and help to deal with different species that have the same valency.

Finally, it should be mentioned that GOAC can perform well on several other research questions concerning configurations, also beyond the scaling tests and configurational selections shown in this work. For example, GOAC might be employed to study charge-ordering of ions that disproportionate into different valances (cf. Supplementary Fig. 12) or charge-ordering in general. In fact, results at the example of a layered oxide sodium-ion cathode material in Supplementary Fig. 13 indicate that a strong correlation of energies of charge-orderings of differently charged Mn ions exists between Coulomb and DFT energies. In the case of layered oxide cathodes GOAC optimizations also allow to study transition metal layer charge-orderings and Na-orderings in a coupled fashion to get an idea if and how theses two orderings are coupled. The examples presented in Supplementary Fig. 14 indicate that GOAC might also be successfully applied to this problem setting as DFT calculations show similar trends to the GOAC optimizations. Further studies might show in more detail how GOAC can be employed to study various types of orderings in layered oxide materials and how well the results match selected references, e.g., DFT calculations. Lastly, GOAC was recently also applied to study the single-phase — two-phase charging characteristics of lithium iron phosphate (LFP)88. Results showed that electrostatic optimization can reproduce the critical particle size from experiment for the switch from the single-phase to the two-phase charging mechanism as well as the energetically most favourable interface orientation between the two phases. This indicates that GOAC could be used to study similar materials in the future.

In summary, GOAC can be a valuable tool for computational research on novel energy materials and other complex materials to determine likely candidate structures for low or lowest energy atomistic configurations with comparably little computational resources.

Methods

DFT reference calculations

The DFT reference calculations shown in Fig. 2 were performed with the VIENNA AB INITIO SIMULATION PACKAGE (VASP)89 in the projector augmented wave (PAW) scheme90 with the Perdew–Burke–Ernzerhof (PBE) exchange-correlation functional91. An energy cut-off of 520 eV along with a convergence criterion of 10−4 eV, a 1 × 1 × 2 Γ-centred k-point grid, and spin-polarization was employed. Single-point calculations without any geometry optimization were performed to allow for a fair comparison to Coulomb energies. The exact geometries can be found in the “Examples” folder of the project repository (see Data Availability statement). Structure models in this work were visualize with the VESTA software92.