Introduction

Novel functional materials are crucial in advancing technology across various fields, including energy1, electronics2, and manufacturing3. However, the discovery or optimization of these materials, especially in complex multi-component systems, is a challenging and time-consuming process. Traditional trial-and-error approaches are inadequate due to the complexity of multicomponent systems and the vast parameter space involved4,5. High-throughput synthesis, characterization, and analysis in a combinatorial fashion offer an alternate solution6,7. A combinatorial library containing a large number of compositionally varying samples, enables rapid screening within certain composition spaces, facilitating the identification of promising candidate materials with desired properties8. The high-throughput approach has the potential to enable automated or even autonomous materials development9,10,11.

Extracting material information from combinatorial libraries using various characterization techniques is a crucial step in establishing the composition–structure–property relationship12,13. Powder X-ray diffraction (XRD) is one of the most common structural characterization techniques, as the diffraction patterns contain rich material information. Basic information includes the number, identity, and fraction of the phases present in each sample, while advanced information includes the lattice changes, texture, defects, and solid solutions, etc. Analyzing diffraction patterns and correctly extracting this material information is a key step in the high-throughput combinatorial materials development loop14.

Analyzing diffraction patterns requires significant domain-specific knowledge, including crystallography, X-ray diffraction, thermodynamics, kinetics, and solid-state chemistry. Experienced specialists arrive at the “most reasonable” solutions not only based on the fitting quality of diffraction patterns but also by leveraging their comprehensive understanding of the investigated materials system and materials chemistry. For instance, intensity deviations from the calculated diffraction pattern of a known phase may indicate crystallographic texture with preferential orientation or the coexistence of a polymorphic phase15. Low-intensity peaks may suggest the presence of minor phases or arise from random background noise. Multiple candidate crystal structures may be assigned to an unknown phase, but only a few are valid solutions considering the bonding characters of certain ions16. Moreover, the constituent phase information in most experimental combinatorial libraries lacks a ground-truth solution, while a universally accepted evaluation criterion to assess the quality of solutions has yet to be established. Minimizing the difference between observed and reconstructed diffraction patterns appears to be a straightforward optimization objective. However, this does not guarantee a trustworthy solution with “chemical reasonableness“17. In many cases, manual assessment by human experts remains essential.

Given the large number of samples in a typical combinatorial library, rapid analysis of high-throughput XRD patterns and automated extraction of material information are highly desirable. Typical combinatorial library diffraction datasets contain hundreds to thousands of samples. Manual analysis of diffraction patterns one by one is impractical, and is incompatible with the autonomous synthesis–characterization–analysis loop. However, these datasets are considered “small datasets” in the machine learning field, making it difficult to apply cutting-edge large models18. Various algorithms have been developed to solve the phase mapping problem based on limited XRD data11,19,20,21,22,23,24,25,26. Long et al. introduced non-negative matrix factorization (NMF) as an unsupervised approach to tackle the phase mapping problem27, followed by the development of various NMF extensions20,21,28. Suram et al. applied convolutional NMF and successfully identified the constituent phases and revealed the lattice parameter change information in a V–Nb–Mn oxide library21. Despite their success, NMF approaches usually require prior determination of the number of phases by human experts. The accuracy of this predetermined number significantly affects the quality of the solutions. Chen et al. developed an unsupervised pattern demixing model using deep reasoning networks and incorporating prior scientific knowledge as constraints23. Lee et al. adopted a convolutional neural network (CNN) and built a supervised model to solve a synthetic experimental dataset29, which contains only three constituent phases but with available ground truth. Recently, a supervised ensemble model named XCA was designed to produce probabilistic classifications of present phases22. Despite these advancements, performing phase mapping tasks on complex experimental combinatorial libraries and ensuring that the solutions are physically reasonable remains challenging.

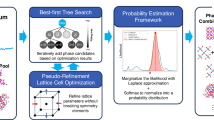
In this paper, we present AutoMapper, a fully automated workflow designed to solve experimental high-throughput XRD patterns in combinatorial libraries. We outline our approach to incorporating domain-specific knowledge during the preprocessing, solving, and refinement stages. By leveraging the powerful fitting capability of optimization-based neural networks models, our solver can reach solutions that are guaranteed to be physically reasonable. The integration of thermodynamic data from first-principles calculation databases aids in filtering plausible candidate phases, and we enforce restrictions on chemical composition and phase rules by incorporating corresponding terms into the loss function. Iterative fitting by considering samples with similar chemical compositions speeds up the solving process and avoids local minimum traps. Furthermore, our automated solver provides texture information for major phases for the first time. We apply our algorithm to three experimental library datasets and find reasonable solutions in each case: V–Nb–Mn oxide, Bi–Cu–V oxide, and Li–Sr–Al oxide systems, which differ in chemistry, preparation method, sample number, texture, microstructure, and diffractometer. We identified α-Mn2V2O7 and β-Mn2V2O7 phases in the V–Nb–Mn oxide system, which were absent in a previous solution21. For the first time, we provide texture information for major phases using an automated solver. We underscore the importance of domain-specific knowledge in both the design of the automated workflow and the evaluation of solution quality.

Results

Datasets

We analyzed three previously published combinatorial libraries: the V–Nb–Mn oxide21, the Bi–Cu–V oxide23, and the Li–Sr–Al oxide systems29, which contain 317, 307, and 50 samples, respectively. All three datasets include the XRD patterns and associated cation composition information (the oxygen content remains unknown). The first two systems were prepared by sputter deposition and characterized using a synchrotron X-ray source, known for its high intensity and strong polarization. The Li–Sr–Al oxide system was prepared by blending three compounds (Li2O, SrO, and Al2O3), and characterized on a laboratory X-ray diffractometer, which we assume has an unpolarized X-ray source.

For the Bi–Cu–V oxide system, we opted not to utilize the background-subtracted data directly, which was performed by a machine learning model in the previous work23. Instead, we worked with the raw XRD data and applied background removal using the rolling ball algorithm30. Besides, in contrast to subtracting diffraction peaks from the SnO2 substrate in a preprocess step23, we retained the diffraction peaks from the substrate during the solving process. The rationale for using raw diffraction data and reapplying background removal will be elaborated upon in the discussion section.

Identification of valid candidate phases

Collecting all relevant candidate phases in the investigated chemistry system is a prerequisite for a successful phase mapping process (Fig. 1). Entries were collected from two commonly used inorganic material databases: the International Centre for Diffraction Data (ICDD) and the Inorganic Crystal Structure Database (ICSD). Only oxide entries are included because all three libraries are prepared under ambient conditions. A total of 1262, 499, and 231 entries were collected in the V–Nb–Mn oxide, Bi–Cu–V oxide, and Li–Sr–Al oxide systems, respectively (Table S1). Entries that are identical or very similar in both composition and diffraction pattern are considered duplicates, and thus are grouped and regarded as a single candidate phase (Table S1).

Fig. 1: Workflow of AutoMapper.
figure 1

The experimental library dataset comprises hundreds of samples with diffraction patterns and cation compositions. Our solver first fetches all relevant entries in the chemical system of interest (e.g., V–Nb–Mn oxide system) from inorganic material databases (ICSD and ICDD). All fetched entries undergo a cleaning process, eliminating duplicates and excluding highly unstable phases. Simulated diffraction patterns of candidate phases are then employed in the subsequent solving process. An encoder-decoder framework optimizes a loss function that accounts for both XRD pattern fitting quality and composition agreement. Solutions from compositional neighboring samples are iteratively used to enhance the solution quality and speed. In the refinement stage, the solver conducts texture analysis to identify the preferred orientation of major phases. Finally, the solver reaches a set of satisfied solutions and outputs information on the identified phases, fractions, shifts, widths, and texture.

Full size image

Phases that are highly thermodynamically unstable based on first principles calculations31 were further excluded. 49 highly unstable entries (energy above the convex hull >100 meV/atom) are eliminated in this step (Table S1). We believe that either these eliminated entries relate to phases under non-ambient conditions, or their associated structures are physically unreasonable. In fact, by carefully examining these eliminated phases, we surprisingly found that a few recorded entries (related to the β-Mn2V2O7 phase) from the database have incorrect structures (More details in “Discussion”). Finally, 140, 130, and 34 entries were included as candidate phases for the V–Nb–Mn oxide, Bi–Cu–V oxide, and Li–Sr–Al oxide systems, respectively (Table S2).

Automated phase mapping

Encoding the domain-specific knowledge as constraints into a loss function for optimization is the key to a successful automated phase mapping algorithm. Our loss function is a weighted sum of three components: LXRD, Lcomp, and Lentropy. LXRD quantifies the fitting quality of the reconstructed diffraction profile, which employs the functional form of the weighted profile R-factor (Rwp) as commonly used in Rietveld refinement. Lcomp describes the consistency between the reconstructed and experimentally measured cation composition, which is calculated by their squared distance within the composition space. Lentropy is an entropy-based regularization term to mitigate the risk of overfitting (Details in method).

Instead of treating phase mapping as a demixing problem21,23,27, we directly used simulated XRD patterns of the candidate phases to fit the experimental diffraction patterns. The polarization of the X-ray beam from different diffractometers has a significant impact on the intensity of diffraction peaks. We assume that the incident beam from a synchrotron source is fully plane-polarized, whereas the incident beam from a laboratory X-ray source is unpolarized. A pseudo-Voigt function is used to simulate the diffraction-line broadening. The candidates are initially pruned by the cation composition and XRD patterns (Supplementary Information (SI)). Subsequently, only the remaining candidates are retained for the next step of the solving process (Fig. 1 and Fig. S1). We solve the phase fractions of all constituent phases and peak shifts with an encoder-decoder structure by minimizing the loss (More details in SI and Fig. S2).

In principle, the above approach can be performed on each sample independently and in parallel. However, “difficult” samples that are located at the phase region boundaries and contain three or more major phases can be trapped in local minima and lead to solution failure. In contrast, “easy” samples containing only one or two major phases usually converge to plausible solutions within a few iterations. To deal with difficult-to-solve samples, iterative optimizations were performed by using the identified major phases in the compositional neighboring samples (Fig. 1), which helps to avoid local minima and to reach the most plausible solutions.

Texture analysis and diffraction pattern refinement

Powder diffraction patterns from crystallites that have a non-random distribution of orientation, which is common in thin-film samples, can exhibit intensity deviations from calculated profiles that assume random orientations32. Extracting texture information is important to understand the investigated chemical system (e.g., strength, reflectivity, chemical reactivity, magnetic susceptibility) and further improve the fitting quality. In the refinement step (Fig. 1), we build multiple versions of simulated diffraction patterns of identified major phases with different degrees of preferred orientation adopting the March-Dollase function form33. Refinement was performed and the version with the lowest loss was selected.

The phase mapping solution by AutoMapper

AutoMapper was deployed to solve all three datasets (V–Nb–Mn oxide, Bi–Cu–V oxide, and Li–Sr–Al oxide) and successfully identified 9, 13, and 3 phases present, respectively (Fig. S3). Since the ground truth solution of phase information is partially or completely unavailable for these datasets, manual inspection was performed to ensure that our solutions are chemically plausible, as advised in a common Rietveld refinement routine.

For the V–Nb–Mn oxide system, we identified two previously missing phases: α-Mn2V2O7 and β-Mn2V2O7 (Fig. 2a and Fig. S3a). β-Mn2V2O7 is identified as a major phase present in 187/317 samples (Table S4) with a maximum phase fraction of 70.92%, while α-Mn2V2O7 is identified as a minor polymorph coexisting with β-Mn2V2O7. Interestingly, the Mn3V2O8 phase (Table S6), which was previously identified as a major phase using the automated NMF-based solver of Suram et al.21, is absent in the solution from our automated solver. The 9 identified phases are: Nb2MnO6, Mn2O3, β-Mn2V2O7, MnV2O6, Mn3O4, V4Nb18O55, VNbO5, α-Mn2V2O7, and V2O5. Except the aforementioned manganese vanadate phases, all seven of the other present phases that we identified are consistent with previous solutions21. Nb2MnO6 has a maximum content of 47.72% across all samples, and appears in 270/317 samples (Table S4) with a relatively large single-phase region. The large single-phase region Nb2MnO6 is accompanied by the lattice contraction of up to 1.5%, suggesting the formation of a solid solution.

Fig. 2: Manually constructed phase diagrams and representative reconstructed PXRD patterns from each dataset.
figure 2

Phase diagrams of a V–Nb–Mn oxide and b Bi–Cu–V oxide systems. Each sample is represented by a mini pie chart located at the sample’s chemical composition. Within each pie chart, each slice represents a constituent phase. The size of the slice represents phase fraction, and different phases are distinguished by color. The nine identified phases in V–Nb–Mn oxide system and 13 identified phases in Bi–Cu–V oxide system are present by solid circles. The dashed line indicates a solid solution region. Representative observed and reconstructed PXRD patterns from each of the c V–Nb–Mn oxide, d Bi–Cu–V oxide, and e Li–Sr–Al oxide systems. Parity plots comparing ground-truth and reconstructed height fraction for f Li2O, g SrO, and h Al2O3 in the Li–Sr–Al oxide system.

Full size image

We also compared the ternary phases that our automated solver identified with previously reported experimental phase diagrams. For the Mn2O3–Nb2O5 subsystem, Nb2MnO6 is the only identified ternary phase, consistent with previous experimental reports34. For the V2O5–Mn2O3 subsystems, three ternary compounds were identified by our solver, namely MnV2O6, β-Mn2V2O7, and α-Mn2V2O7. Two of which, MnV2O6 and β-Mn2V2O7, are consistent with earlier experimental studies at high temperature34,35. Besides, β-Mn2V2O7 can go through a phase transition to its polymorph α-Mn2V2O7 at room temperature36, which explains the co-existence of both Mn2V2O7 phases as observed in our solution. V2O5–Nb2O5 is the only subsystem that deviates from the previously reported experimental phase diagram. VNb9O25, the only previously reported stable ternary phase37, is absent in our solutions. The two identified phases VNbO5 and V4Nb18O55 were reported as metastable phases. Both of them are very difficult to synthesize via the conventional solid-state reaction method, but can form due to precursor decomposition in a specific temperature window38.

For Bi–Cu–V oxide system, we identified 13 constituent phases, consistent with the previous solution by DRNets23. In contrast, the NMF method23 only identified five major phases (Table S6). Differences in the presence and fraction of the minor phases were observed compared to the previous solution, especially at the phase boundary regions (Fig. 2b and Fig. S3b). Identified phases comprise four major phases (BiVO4, Cu2BiVO6, CuO, and Cu3Bi4V2O14) and 9 minor phases (Bi8V2O17, Bi12V2O23, Cu2V2O7, CuBi2O4, Cu5V2O10, Cu3V2O8, Bi4V2O11, Cu11V6O26, and CuV2O6). The 4 major phases constitute 21.77%, 21.62%, 16.75%, and 15.04% of the total fractions and are present in 105, 138, 177, and 110 out of 307 samples, respectively (Table S4). All identified binary and ternary phases are consistent with previous phase diagram reports in Bi2O3–CuO, Bi2O3–V2O5, CuO–V2O5 subsystems39,40,41. Our automated texture analysis revealed that a few phases in this system exhibit strong texturing. The identified preferred orientations are (013), (011), (006), and (210) for BiVO4, Bi8V2O17, Bi12V2O23, and Cu2V2O7, respectively (Table S5). The SnO2 substrate was also identified to have a preferred orientation in (200) direction (Table S5).

For the V–Nb–Mn oxide and Bi–Cu–V oxide systems, we manually constructed phase diagrams and plotted phase boundaries that closely align with the results from our phase mapping algorithm. Solid single-color circles represent identified phases, tie-lines indicate two-phase regions, and triangles denote three-phase regions. The dashed line between Nb2MnO6 and MnV2O6 signifies a solid solution within this region (Fig. 2a). Across most of the composition space covered by the combinatorial libraries, the manually constructed phase diagrams agree well with the phase mapping results. However, minor discrepancies were observed near phase boundary regions. For example, Mn2V2O7 is almost absent in samples that are closest to its composition stoichiometry. Similar phenomena were observed in a series of copper vanadates: CuV2O6, Cu2V2O7, Cu3V2O8, Cu11V6O26, and Cu5V2O10, of which the identified phases from diffraction patterns always seem to appear in a more V-rich region. The cation composition was measured using EDS and XRF, both of which are semi-quantitative. We suspect that the measured compositions may have a systematic error from their actual compositions.

For Li–Sr–Al oxide system, we identified 3 present phases (Li2O, SrO, and Al2O3) that match the ground truth (Fig. S3c and Fig. S4). Despite this being the smallest dataset with only 50 samples, our solver shows robust performance. Our solution agrees well with the ground truth29 (Fig. 2f-h and Fig. S5), and the Pearson correlation coefficients for Li2O, SrO, and Al2O3 are 93%, 98%, and 98%, respectively, suggesting that both the phase identities and the phase fractions are correctly solved.

Our solver achieves an average Rwp factor of 12.20%, 18.15%, and 17.73% for V–Nb–Mn oxide, Bi–Cu–V oxide, and Li–Sr–Al oxide systems, respectively, indicating robust fitting quality. Representative reconstructed PXRD patterns from the three datasets are shown (Fig. 2c–e). Additionally, we have compiled all the reconstructed XRD patterns into a supplementary dataset for comprehensive reference. Visual inspection further confirms the reasonableness of our solution. Note that we did not enforce a hard constraint on the connectivity of constituent phases; instead, we used neighboring samples merely to accelerate the solving process. Nevertheless, our solution still largely adheres to phase connectivity (Fig. S3). The identified preferred orientation is also consistent among compositional neighboring samples, providing additional validation for the physical reasonableness of our solutions (Table S5).

Discussion

The goal of phase mapping is to correctly extract materials information, aiding researchers in understanding the material system and guiding subsequent experiments. This principle holds true for any automated solver. The incorporation of domain-specific knowledge is crucial for generating solutions that are “chemically reasonable”. In the following examples, we illustrate why including such knowledge is essential and highlight the material insights that can be gained.

Identification of plausible candidate phases is a prerequisite for successfully solving the phase mapping problem. Entries in two mainstream inorganic material databases, ICSD and ICDD, exhibit a range of quality and reliability. Incorrect entries that exist in the databases can potentially lead to failures in phase mapping. By performing first-principles calculations, we found a β-Mn2V2O7 entry (ICDD 00-038-0034, quality mark: star) having a highly unstable structure with exceptionally high energy above the convex hull (205 meV/atom). We believe that the structure for this entry is incorrect, wherein Mn2+ and V5+ were accidentally swapped, and occupy each other’s Wyckoff positions. Although this arrangement yields a similar diffraction profile (Fig. 3a), it contradicts the fact that Mn2+ has a stronger preference than V5+ to occupy octahedral positions with a six-fold coordination16. First-principles calculations confirm that the correct structure (with Mn and V positions swapped) is stable, i.e., on the convex hull (Table S2). Additionally, a Mn3V2O8 entry (ICDD 00-039-0091, quality mark: low precision) that appeared as a major phase in a previous solution21 is absent in our solution. To the best of our knowledge, its associated diffraction patterns do not agree with any other available literature reports. We excluded this entry because of its low reliability. We assert that a thermodynamic assessment of candidate entries with first-principles calculations is essential, as no other standardized quality assessment is available.

Fig. 3: Illustration of the effect of incorporating domain-specific knowledge in developing an automated phase mapping solver.
figure 3

a Crystal structures and associated XRD patterns of erroneous (ICDD 00-038-0034) and correct (ICDD 00-052-1266) entries for β-Mn2V2O7 in ICDD database. Blue, orange, and pink spheres represent the Mn, V, and O atoms, respectively. b Coexisting phases of α-Mn2V2O7 and β-Mn2V2O7 observed in sample #275 in V–Nb–Mn oxide. The inset shows the presence of two polymorphs in the composition space. c Diffraction pattern of sample #249 in Bi–Cu–V oxide system. The background-subtracted data in previous work23 and this work, as well as the raw data, are compared. d Our automated texture analysis revealed that Cu2V2O7 exhibits a strong preferred orientation in (210) direction in sample #33 in Bi–Cu–V oxide system.

Full size image

The Gibbs phase rule states that for systems under thermodynamic equilibrium, the number of constituent phases is bounded by the number of elements. Most state-of-the-art automated solvers enforce the Gibbs phase rule as a soft or hard constraint to ensure solutions are physically reasonable14,21,23. In fact, whether the solutions obey the Gibbs phase rule is sometimes employed as a metric to evaluate the validity of solutions14,23.

However, the Gibbs phase rule can be violated in combinatorial libraries, as we observed in the V–Nb–Mn oxide system. The major constituent phases at the Mn-rich region are Mn2O3 and Mn3O4 (Fig. 2a and Fig. S3a). If the system is assumed to be in equilibrium with the ambient atmosphere, meaning temperature, total pressure, and oxygen partial pressure are all fixed, the Gibbs phase rule imposes a strict constraint, limiting the system to a single phase. However, the transition temperature from Mn3O4 to Mn2O3 in air is approximately 1000 to 1100 °C, indicating that the equilibrium oxygen partial pressure for this transition is lower than that of the ambient environment. Also, two polymorphs of Mn2V2O7 (α and β phases) were identified as coexisting phases present in our solution (Fig. 3b and Fig. S6), also violating the Gibbs phase rule. The reason for the discrepancy is that the Gibbs phase rule requires thermodynamic equilibrium conditions, which often does not hold for these combinatorial systems. During the annealing process, phases that are thermodynamically favored at high temperature are likely to form during heating, and remain in the sample after quenching down due to kinetics. Mn3O4 is more stable at high temperature and under low oxygen partial pressure, and loses its thermodynamic advantage to Mn2O3 when the temperature decreases42. Similarly, β-Mn2V2O7 is more stable than α-Mn2V2O7 when the temperature is above 30 °C43. The phase transition towards equilibrium can be incomplete due to kinetics, hence leading to samples in which the Gibbs phase rule is violated. Therefore, a strict enforcement of the Gibbs phase rule is not physically plausible, and may actually hinder an accurate solution of some experimental datasets.

The choice of loss function can affect the performance of automated solver significantly. When quantifying the quality of reconstructed diffraction patterns, “chemical reasonableness” is more important than a lower “loss”17, and is a non-trivial task even in manual refinements17. We adopted weighted profile R-factor (Rwp) as used in Rietveld refinement, which lowers uncertainties in the fit parameters when errors are purely statistical17. Rwp is more sensitive to low-intensity locations in the observed diffraction patterns compared to L1 or L2 loss. Different loss function forms can lead to discrepancies in minor phases (Fig. S7).

We evaluated the performance of AutoMapper using different loss functions (L1, L2, and Rwp) in the Li–Sr–Al oxide system, where ground truth is available. We used an illustrative example (sample #47) from this system to demonstrate that different loss functions result in discrepancies in minor phases (Fig. S7). When the LXRD is Rwp (Fig. S7a), we identified the three phases, Li2O, SrO, and Al2O3, which are consistent with the ground truth. In contrast, when the LXRD is L1 or L2 loss (Fig. S7b, c), two different polymorphs Li2O (ICSD 108886) and Al2O3 (ICSD 43732) were incorrectly identified. It indicates that the Rwp shows greater sensitivity to low-intensity locations in the observed diffraction patterns.

The raw diffraction data also contain background signals, including a relatively smooth baseline and diffraction peaks from the substrate if a crystalline substrate is used (as observed in Bi–Cu–V oxide system23). If minor diffraction peaks are accidentally eliminated as background, it will lead to a significant increase in Rwp, which may prevent the solver from finding the correct solutions. We found that the previous background removal algorithm44 removed a minor peak when subtracting peaks from SnO2 substrate (q = 17.8 nm−1 sample #249, Bi–Cu–V oxide system), leading to a severe distortion of the diffraction peaks from the Cu3Bi4V2O14 phase (ICDD 04-011-5345) (Fig. 3c). In our approach, we subtracted the background from the raw diffraction data using rolling ball algorithm, and retained the diffraction peaks from the SnO2 substrate in the whole spectrum fitting. As a result, minor diffraction peaks from Cu3Bi4V2O14 are not affected, which is important for the solving procedure.

Extracting texture information of major phases plays not only a crucial role in finding accurate solutions to XRD datasets, but also in establishing the composition–structure–property relationship. Strong texture, which is common in thin film samples22,45, is one of the major challenges of using simulated XRD patterns to directly fit the experimental data in an automated algorithm. The intensity of diffraction peaks can be affected by the diffractometer choice, non-random distribution of preferred orientation, defects, solid solutions, etc. By accounting for the degree of polarization of X-rays, our approach avoids systematic intensity deviations of simulated diffraction patterns. By building multiple versions of simulated patterns with different degrees of preferred orientation, we can reveal texture information to understand the orientation distribution of polycrystalline materials. In the Bi–Cu–V oxide library, our automated texture analysis found that Cu2V2O7 exhibits a strong texture in the (210) direction (Fig. 3d), and this orientation preference is consistent in all compositional nearby samples, indicating that the revealed texture is chemically reasonable.

In this work, we developed an unsupervised phase mapping solver, AutoMapper, to address the phase mapping challenge in high-throughput X-ray diffraction datasets. Besides leveraging the robust fitting ability of machine learning algorithms, our approach integrates first-principles calculation thermodynamic data, crystallographic principles, X-ray diffraction concepts, texture analysis, and other material information and knowledge. We demonstrated our approach across three different datasets. In the one dataset where the ground truth is known, our approach correctly identified not only the number, identity, and fraction, of the phases present, but also the peak shifts due to lattice change, and texture information. For cases where no ground truth is known, our approach identified chemically plausible solutions for all of these quantities. We emphasize the importance of understanding and integrating material information correctly as constraints for automated solvers, which should be beneficial for the development of future automated characterization tools. Our work paves the way for the future development of the automated synthesis-characterization-analysis loop of materials innovation. Furthermore, we strongly advocate for the community to produce and provide more experimental/synthetic datasets, which will be beneficial for advancing this field.

Methods

Generate candidate pool

In this work, the V–Nb–Mn oxide, Bi–Cu–V oxide, and Li–Sr–Al oxide systems were investigated and all relevant entries were extracted from the ICDD and ICSD databases. We collected 868, 99, and 37 corresponding entries in the ICDD, and 394, 400, and 194 entries in the ICSD. The stick patterns corresponding to each crystal structure were calculated by the XRDCalculator module in Pymatgen, an open-source toolbox for materials analysis46. The shape of each peak in the patterns was altered using a pseudo-Voigt profile function. Due to the diverse quality and reliability of the entries, all collected entries were cleaned and only plausible candidate phases were used for the following phase mapping task. The cleaning process consists of three steps. First, hypothetical and deleted ICDD entries were excluded. ICDD entries with a blank or low-precision quality mark, or tagged with non-ambient conditions, were removed. The number of removed entries is listed in Table S1. Second, since both databases contain duplicates, entries that are identical or very similar in both composition and XRD pattern were grouped and regarded as a single candidate phase. Finally, the stabilities of the remaining entries were computed using DFT to exclude highly unstable phases (energy above the convex hull >100 meV/atom) and generate our pool of candidates. In the end, there are 140, 130, and 34 candidates for the V–Nb–Mn oxide, Bi–Cu–V oxide, and Li–Sr–Al oxide systems, respectively.

Density-functional theory (DFT) calculations

The DFT calculations were performed using the Vienna Ab initio Simulation Package (VASP)47 with Projector Augmented Wave (PAW) pseudopotentials48 and the GGA-PBE exchange-correlation functionals49. And it followed the standard Open Quantum Materials Database (OQMD)31 workflow. Ionic relaxations were carried out until force converged to 10−2 eV/Å. This was followed by static calculations with a 520 eV cutoff energy and 8000 KPPRA to obtain accurate energies. The stability analyses were based on the convex hull energies referenced from the OQMD.

Encoder-decoder framework

The mathematical optimization encoder-decoder framework is a type of neural network used to get efficient data coding in an unsupervised manner, which is not a learning-based approach but rather an optimization-based model. The aim is to optimize a representation (encoding) for a set of data, typically for dimensionality reduction. The neural network consisting of an automatic encoder and manual decoder was adopted for phase mapping and the encoded matrix after optimization is the solution matrix. Simulated diffraction profiles of candidate phases are discretized into vector representations. Three ensuing fully connected layers followed the activation function ReLu as hidden layers were used to encode the phase fraction and peak shift amount into a filter matrix. The CNN filter could shift XRD diffraction patterns. The decoder includes one convolutional layer. The reconstruction of the XRD pattern is the 2D-convolution product of the basis XRD pattern matrix and the filter matrix. The dimensional transformations of model parameters across the encoding and decoding process are summarized in Table S3.

The framework derives a phase mapping solution by minimizing a designed loss function that incorporates physical constraints. The loss function is a weighted sum of three components: LXRD, Lcomp, and Lentropy. LXRD quantifies the fitting quality of the reconstructed diffraction profile by Rwp, which is a weighted profile residual, commonly used in Rietveld refinement. Lcomp describes the consistency between the reconstructed cation composition and experimentally measured cation composition. Lentropy is designed to penalize overfitting, and is calculated based on phase fractions. The equation is as follows:

$$L={w}_{1}\cdot {R}_{\mathrm{wp}}^{2}+{w}_{2}\cdot {\left({c}_{\exp }-{c}_{\mathrm{recon}}\right)}^{2}+{w}_{3}\cdot {\sum }_{p}{f}_{p}\log \left({f}_{p}\right),$$
(1)

The cexp and crecon are the normalized experimental and reconstruction compositions of cations, since only cation compositions are known. All compositions were normalized to sum to 1. The last item is an entropic form to penalize overfitting. \({f}_{p}\) are the phase fractions which range between 0 and 1 (and sum to 1).

Texture analysis

The preferred orientation was determined using the texture coefficient of the plane, which indicates the degree of deviation from the standard sample and suggests preferred growth. The calculation for this is as follows:

$${TC}=\frac{{I}_{{hkl}}/{I}_{{hkl}}^{0}}{(1/n)\cdot {\sum }_{{h}^{{\prime} }{k}^{{\prime} }{l}^{{\prime} }}{I}_{{h}^{{\prime} }{k}^{{\prime} }{l}^{{\prime} }}/{I}_{{h}^{{\prime} }{k}^{{\prime} }{l}^{{\prime} }}^{0}},$$
(2)

where TC is the texture coefficient of selected planes specified by Miller indices (hkl). \(I\) and \({I}^{0}\) are the experimental and standard integrated intensities (random orientation), respectively, for a given peak and n is the number of diffraction reflections. A TC value of 1 indicates randomly oriented crystallites, whereas values of TC > 1 indicate that the crystallites are preferentially oriented in a specific direction. Within the experimental q domain, a reflection plane was selected, and the degree of texturing, as defined by the March parameter, was randomly varied.

Solving details

Each experimental XRD pattern in our used datasets is optimized independently by the encoder-decoder framework. There is no transfer of model parameters between samples during optimization. In our setting, the \({w}_{1}\), \({w}_{2}\), and \({w}_{3}\) of loss function are 6, 2, and 0.1 (V–Nb–Mn oxide and Bi–Cu–V oxide)/0.01(Li–Sr–Al oxide), respectively.