Entanglement transitivity problems

Abstract

One of the goals of science is to understand the relation between a whole and its parts, as exemplified by the problem of certifying the entanglement of a system from the knowledge of its reduced states. Here, we focus on a different but related question: can a collection of marginal information reveal new marginal information? We answer this affirmatively and show that (non-) entangled marginal states may exhibit (meta)transitivity of entanglement, i.e., implying that a different target marginal must be entangled. By showing that the global n-qubit state compatible with certain two-qubit marginals in a tree form is unique, we prove that transitivity exists for a system involving an arbitrarily large number of qubits. We also completely characterize—in the sense of providing both the necessary and sufficient conditions—when (meta)transitivity can occur in a tripartite scenario when the two-qudit marginals given are either the Werner states or the isotropic states. Our numerical results suggest that in the tripartite scenario, entanglement transitivity is generic among the marginals derived from pure states.

Introduction

Entanglement¹ is a characteristic of quantum theory that profoundly distinguishes it from classical physics. The modern perspective considers entanglement as a resource for information processing tasks, such as quantum computation^2,3,4,5,6, quantum simulation⁷, and quantum metrology⁸. With the huge effort devoted to scaling up quantum technologies⁹, considerable attention has been given to the study of quantum many-body systems^10,11, specifically the ability to prepare and manipulate large-scale entanglement in various experimental systems.

As the number of parameters to be estimated is huge, entanglement detection via the so-called state tomography is often impractical. Indeed, significant efforts have been made for detecting entanglement in many-body systems^10,11 using limited marginal information. For example, some tackle the problem using properties of the reduced states^{12,13,14,15,16,17,18,19,20,21,22,23}, while others exploit directly the data from local measurements^{24,25,26,27,28,29,30,31,32,33,34,35}. Despite their differences, they can all be seen as some kind of entanglement marginal problem (EMP)³⁶, where the entanglement of the global system is to be deduced from some (partial knowledge of the) reduced states.

The entanglement of the global system, nonetheless, is not always the desired quality of interest. For instance, in scaling up a quantum computer, one may wish to verify that a specific subset of qubits indeed get entangled, but this generally does not follow from the entanglement of the global state (recall, e.g., the Greenberger-Horne-Zeilinger states³⁷). Thus, one requires a more general version of the problem: Given certain reduced states, can we certify the entanglement in some other target (marginal) state? We call this the entanglement transitivity problem (ETP). Since the global system is a legitimate target system, ETPs include the EMP as a special case.

As a concrete example beyond EMPs, one may wonder whether a set of entangled marginals are sufficient to guarantee the entanglement of some other target subsystems. If so, inspired by the work³⁸ on nonlocality transitivity of post-quantum correlations³⁹, we say that such marginals exhibit entanglement transitivity. Indeed, one of the motivations for considering entanglement transitivity is that it is a prerequisite for the nonlocality transitivity of quantum correlations, a problem that has, to our knowledge, remained open.

More generally, one may also wonder whether separable marginals alone, or with some entangled marginals could imply the entanglement of other marginal(s). To distinguish this from the above phenomenon, we say that such marginals exhibit metatransitivity. Note that any instance of metatransitivity with only separable marginals represents a positive answer to the EMP. Here, we show that examples of both types of transitivity can indeed be found. Moreover, we completely characterize when two Werner-state⁴⁰ marginals and two isotropic-state⁴¹ marginals may exhibit (meta)transitivity.

Results

Formulation of the entanglement transitivity problems

Let us first stress that in an ETP, the set of given reduced states must be compatible, i.e., giving a positive answer to the quantum marginal problem^42,43. With some thought, one realizes that the simplest nontrivial ETP involves a three-qubit system where two of the two-qubit marginals are provided. Then, the problem of deciding if the remaining two-qubit marginal can be separable is an ETP different from EMPs.

More generally, for any n-partite system S, an instance of the ETP is defined by specifying a set ${{{\mathcal{S}}}}=\{{{{{\rm{S}}}}}_{i}:i=1,2,\ldots ,k\}$ of k marginal systems S_i (each in its respective state ${\sigma }_{{{{{\rm{S}}}}}_{i}}$) and a target system ${{{\rm{T}}}}\,\notin\, {{{\mathcal{S}}}}$. Here, ${{{\mathcal{S}}}}$ is a strict subset of all the 2ⁿ possible combinations of at most n subsystems, i.e., k < 2ⁿ. Then, ${{{\boldsymbol{\sigma }}}}:=\{{\sigma }_{{{{{\rm{S}}}}}_{i}}\}$ exhibits entanglement (meta)transitivity in T if for all joint states ρ_S compatible with σ, the reduced state ρ_T is always entangled while (not) all given ${\sigma }_{{{{{\rm{S}}}}}_{i}}$ are entangled. Formally, the compatible requirement reads as: ${{{{\rm{tr}}}}}_{{{{\rm{S}}}}\backslash {{{{\rm{S}}}}}_{i}}({\rho }_{{{{\rm{S}}}}})={\sigma }_{{{{{\rm{S}}}}}_{i}}$ for all ${{{{\rm{S}}}}}_{i}\in {{{\mathcal{S}}}}$ where S\S_i denotes the complement of S_i in the global system S.

Notice that for the problem to be nontrivial, there must be (1) some overlap among the subsystems specified by S_i’s, as well as with T, and (2) the global system S cannot be a member of ${{{\mathcal{S}}}}$. However, the target system T may be chosen to be S and if all ${\sigma }_{{{{{\rm{S}}}}}_{i}}$ are separable, we recover the EMP³⁶ (see also refs. ^19,23 for some strengthened version of the EMP). Hereafter, we focus on ETPs beyond EMPs, albeit some of the discussions below may also find applications in EMPs.

Certification of (meta)transitivity by a linear witness

Let ${{{\mathcal{W}}}}(\rho )$ be an entanglement witness²⁶, i.e., ${{{\mathcal{W}}}}(\rho )\,\ge \,0$ for all separable states in T, and ${{{\mathcal{W}}}}(\rho ) \,<\, 0$ for some entangled states. We can certify the (meta)transitivity of ${{{\mathcal{S}}}}$ in T if a negative optimal value is obtained for the following optimization problem:

$$\mathop{\max }\limits_{{\rho }_{{{{\rm{S}}}}}}{{{\mathcal{W}}}}({\rho }_{{{{\rm{T}}}}}),{{{\rm{s.t.}}}}{{{{\rm{tr}}}}}_{{{{\rm{S}}}}\backslash {{{{\rm{S}}}}}_{i}}({\rho }_{{{{\rm{S}}}}})={\sigma }_{{{{{\rm{S}}}}}_{i}}\forall \,\,{{{{\rm{S}}}}}_{i}\in {{{\mathcal{S}}}},\,\,{\rho }_{{{{\rm{S}}}}}\succcurlyeq 0,$$

(1)

where ${{{\rm{tr}}}}({\rho }_{{{{\rm{S}}}}})=1$ is implied by the compatibility requirement and “ ≽ ” denotes matrix positivity. Then, ${{{\mathcal{W}}}}$ detects the entanglement in T from the given marginals in ${{{\mathcal{S}}}}$.

Consider now a linear entanglement witness, i.e., ${{{\mathcal{W}}}}({\rho }_{{{{\rm{T}}}}})={{{\rm{tr}}}}\left[{\rho }_{{{{\rm{S}}}}}({W}_{{{{\rm{T}}}}}\otimes {{\mathbb{I}}}_{{{{\rm{S}}}}\backslash {{{\rm{T}}}}})\right]$ for some Hermitian operator W_T, where ${\rho }_{{{{\rm{T}}}}}={{{{\rm{tr}}}}}_{{{{\rm{S}}}}\backslash {{{\rm{T}}}}}({\rho }_{{{{\rm{S}}}}})$ is the reduced state of ρ in T. In this case, Eq. (1) is a semidefinite program⁴⁴. Interestingly, its dual problem⁴⁴ can be seen as the problem of minimizing the total interaction energies among the subsystems S_i while ensuring that the global Hamiltonian is non-negative, see Supplementary Note 1.

Hereafter, we focus, for simplicity, on T being a two-body system. Then, a convenient witness is that due to the positive-partial-transpose (PPT) criterion^45,46, with ${W}_{{{{\rm{T}}}}}={\eta }_{{{{\rm{T}}}}}^{{{\Gamma }}}$, where η_T ≽ 0 and Γ denotes the partial transposition operation. Further minimizing the optimum value of Eq. (1) over all η_T such that ${{{\rm{tr}}}}({\eta }_{{{{\rm{T}}}}})=1$ gives an optimum λ^* that is provably the smallest eigenvalue of all compatible ${\rho }_{{{{\rm{T}}}}}^{{{\Gamma }}}$ (see Supplementary Note 1). Hence, λ^* < 0 is a sufficient condition for witnessing the entanglement (meta)transitivity of the given σ in T.

Three remarks are now in order. Firstly, the ETP defined above is straightforwardly generalized to include multiple target systems {T_j: j = 1, …, t} with ${{{{\rm{T}}}}}_{j}\,\notin\, {{{\mathcal{S}}}}$ for all j. A certification of the joint (meta)transitivity is then achieved by certifying each T_j separately. Secondly, other entanglement witnesses²⁶ may be considered. For instance, to certify the entanglement of a two-body ρ_T that is PPT⁴⁷, a witness based on the computable cross-norm/ realignment (CCNR) criterion^48,49,50,51, may be employed. Finally, for a multipartite target system, a witness tailored for detecting the genuine multipartite entanglement in ρ_T (see, e.g., Refs. ^14,16) is surely of interest.

A family of transitivity examples with n qubits

As a first illustration, let $\left|{{{\Psi }}}^{+}\right\rangle =\frac{1}{\sqrt{2}}(\left|10\right\rangle +\left|01\right\rangle )$ and consider:

$${\rho }_{n}(\gamma )=\left(\frac{n-2\gamma }{n}\right)\left|00\right\rangle \,\left\langle 00\right|+\frac{2\gamma }{n}\left|{{{\Psi }}}^{+}\right\rangle \,\left\langle {{{\Psi }}}^{+}\right|,\quad n\,\ge \,3,$$

(2)

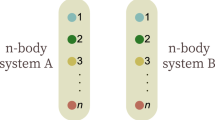
which is a two-qubit reduced state of ${{{\Omega }}}_{n}(\gamma )=\gamma \left|{W}_{n}\right\rangle \,\left\langle {W}_{n}\right|+(1-\gamma )\left|{0}^{n}\right\rangle \,\left\langle {0}^{n}\right|$, i.e., a mixture of $\left|{0}^{n}\right\rangle$ and an n-qubit W state $\left|{W}_{n}\right\rangle =\frac{1}{\sqrt{n}}\mathop{\sum }\nolimits_{j = 1}^{n}\left|{1}_{j}\right\rangle$, where 1_j denotes an n-bit string with a 1 in position j and 0 elsewhere. Now, imagine drawing these n qubits as vertices of a tree graph⁵² with (n − 1) edges, see Fig. 1, such that every edge corresponds to a pair of qubits in the state ρ_n(γ), that is,

$${{{{\rm{tr}}}}}_{{{{\rm{S}}}}\backslash {{{{\rm{S}}}}}_{i}}(\rho )={\sigma }_{{{{{\rm{S}}}}}_{i}}={\rho }_{n}(\gamma )\,\,\forall \,\,{{{{\rm{S}}}}}_{i}\in {{{\mathcal{S}}}},$$

(3)

where ${{{\mathcal{S}}}}$ represents the set of edges. Then we prove the following result:

Fig. 1: Tree graph.

A tree graph is any undirected acyclic graph such that a unique path connects any two vertices. Graph a and b are the only two nonisomorphic trees with (n − 1) edges for n = 4. Graph c is not a tree because it is disconnected and has a cycle.

Theorem 1

For any tree graph with n vertices that satisfies Eq. (3), ${{{\Omega }}}_{n}(\gamma )=\gamma \left|{W}_{n}\right\rangle \,\left\langle {W}_{n}\right|+(1-\gamma )\left|{0}^{n}\right\rangle \,\left\langle {0}^{n}\right|$ is the unique global state and all the two-qubit reduced states are ρ_n(γ).

The details of its proof can be found in Supplementary Notes 2. Thus, these ρ_n(γ) exhibit transitivity for any of the $\frac{(n-1)(n-2)}{2}$ pairs of qubits that are not linked by an edge. Indeed, the symmetry of Ω_n(γ) implies that all its two-qubit marginals are ρ_n(γ), and the smallest eigenvalue of ρ_n(γ)^Γ is ${\lambda }^{* }=\frac{(n-2\gamma )-\sqrt{{(n-2\gamma )}^{2}+4{\gamma }^{2}}}{2n} \,<\, 0$ for γ ∈ (0, 1].

We should clarify that the transitivity exhibited by ρ_n(γ) requires a tree graph only in that it represents the minimal amount of marginal information for the global state to be uniquely determined. Any other n-vertex graph with equivalent marginal information or more leads to the same conclusion.

These examples involve only entangled marginals. Next, we present examples where some of the given marginals are separable. In particular, we provide a complete solution of the ETPs with the input marginals being a Werner state⁴⁰ or an isotropic state⁴¹.

Metatransitivity from Werner state marginals

A Werner state⁴⁰ W_d(v) is a two-qudit density operator invariant under arbitrary U ⊗ U unitary transformations, where U belongs to the set of d-dimensional unitaries ${{{{\mathcal{U}}}}}_{d}$ for finite d. Let ${P}_{{{{\rm{s}}}}}^{d}({P}_{{{{\rm{as}}}}}^{d})$ be the projection onto the symmetric (antisymmetric) subspace of ${{\mathbb{C}}}^{d}\otimes {{\mathbb{C}}}^{d}$. Then we can write qudit Werner states as the one-parameter family⁴⁰

$${W}_{d}(v)=v\frac{2}{d(d+1)}{P}_{{{{\rm{s}}}}}^{d}+(1-v)\frac{2}{d(d-1)}{P}_{{{{\rm{as}}}}}^{a},v\in [0,1].$$

(4)

Consider a pair of Werner states σ = {W_d(v_AB), W_d(v_AC)} that are the marginals of some joint state ρ_ABC. Then the Werner-twirled state⁵³ ${\widetilde{\rho }}_{{{{\rm{ABC}}}}}=\int d{\mu }_{U}(U\otimes U\otimes U){\rho }_{{{{\rm{ABC}}}}}{(U\otimes U\otimes U)}^{{\dagger} }$, where μ_U is a uniform Haar measure over ${{{{\mathcal{U}}}}}_{d}$, is trivially verified to be a valid joint state for these marginals. Moreover, ${\widetilde{\rho }}_{{{{\rm{ABC}}}}}$ has a Werner state W_d(v_BC) as its BC marginal.

Importantly, the aforementioned twirling bringing ρ_ABC to ${\widetilde{\rho }}_{{{{\rm{ABC}}}}}$ is achievable by local operations and classical communications (LOCC). Since LOCC cannot create entanglement from none, if the BC marginal ${\widetilde{\rho }}_{{{{\rm{BC}}}}}$ of ${\widetilde{\rho }}_{{{{\rm{ABC}}}}}$ is entangled, so must the BC marginal ρ_BC of ρ_ABC. Conversely, since ${\widetilde{\rho }}_{{{{\rm{ABC}}}}}$ is a legitimate joint state of the given marginals σ, if ${\widetilde{\rho }}_{{{{\rm{BC}}}}}$ is separable, by definition, the given marginals σ cannot exhibit transitivity. Without loss of generality, we may thus restrict our attention to a Werner-twirled joint state ${\widetilde{\rho }}_{{{{\rm{ABC}}}}}$. Then, since a Werner state W_d(v) is entangled if and only if (iff)⁴⁰ $v\in [0,\frac{1}{2})$, combinations of Werner state marginals W_d(v_AB) and W_d(v_AC) leading to ${\widetilde{\rho }}_{{{{\rm{BC}}}}}={W}_{d}({v}_{{{{\rm{BC}}}}})$ with ${v}_{{{{\rm{BC}}}}} \,<\, \frac{1}{2}$ must exhibit entanglement (meta)transitivity.

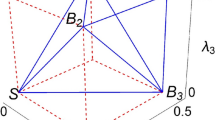
Next, let us recall from Ref. ⁵⁴ the following characterization: three Werner states with parameters $\overrightarrow{v}=({v}_{{{{\rm{AB}}}}},{v}_{{{{\rm{AC}}}}},{v}_{{{{\rm{BC}}}}})$ are compatible iff the vector $\overrightarrow{v}$ lies within the bicone given by $f(\overrightarrow{v})\,\ge \,g(\overrightarrow{v})$ and $3-f(\overrightarrow{v})\,\ge \,g(\overrightarrow{v})$, where $f(\overrightarrow{v})={v}_{{{{\rm{AB}}}}}+{v}_{{{{\rm{AC}}}}}+{v}_{{{{\rm{BC}}}}}$ and $g(\overrightarrow{v})=\sqrt{3{({v}_{{{{\rm{AC}}}}}-{v}_{{{{\rm{AB}}}}})}^{2}+{(2{v}_{{{{\rm{BC}}}}}-{v}_{{{{\rm{AB}}}}}-{v}_{{{{\rm{AC}}}}})}^{2}}$. To find the (meta)transitivity region for (v_AB, v_AC), it suffices to determine the boundary where the largest compatible ${v}_{{{{\rm{BC}}}}}=\frac{1}{2}$. These boundaries are found (see Supplementary Note 3) to be the two parabolas ${({v}_{{{{\rm{AB}}}}}-{v}_{{{{\rm{AC}}}}}-\frac{1}{2})}^{2}=2(1-{v}_{{{{\rm{AB}}}}})$ and ${({v}_{{{{\rm{AB}}}}}+{v}_{{{{\rm{AC}}}}}-\frac{1}{2})}^{2}=4{v}_{{{{\rm{AB}}}}}{v}_{{{{\rm{AC}}}}}$, mirrored along the line v_AB + v_AC = 1, as shown in Fig. 2. It also shows the compatible regions of (v_AB, v_AC) obtained directly from Ref. ⁵⁴, and the desired (shaded) regions exhibiting the (meta)transitivity of these marginals. In particular, the lower-left region corresponds to (a) while the top-left and bottom-right regions correspond to (b) in Fig. 4. Remarkably, these results hold for arbitrary Hilbert space dimension d ≥ 2 (but for d = 2, the lower-left shaded region does not correspond to compatible Werner marginals).

Fig. 2: Parameter space for a pair of Werner state marginals with, respectively, weight v_AB and v_AC on the symmetric subspace.

For d ≥ 3 the compatible region for the pair is enclosed by the solid red line, but for d = 2 it is restricted to the portion above the dotted line. The blue curves (being parts of two parabolas) describe boundaries where the largest compatible v_BC is $\frac{1}{2}$. Regions exhibiting (meta)transitivity are shaded in (gray) cyan.

Metatransitivity from isotropic state marginals

An isotropic state⁴¹ is a bipartite density operator in ${{\mathbb{C}}}^{d}\otimes {{\mathbb{C}}}^{d}$ that is invariant under $U\otimes \overline{U}$ (or $\overline{U}\otimes U$) transformations for any unitary $U\in {{{{\mathcal{U}}}}}_{d}$; here, $\overline{U}$ is the complex conjugation of U. We can write qudit isotropic states as a one-parameter family⁴¹

$${{{{\mathcal{I}}}}}_{d}(p)=p\left|{{{\Phi }}}_{d}\right\rangle \,\left\langle {{{\Phi }}}_{d}\right|+\frac{1-p}{{d}^{2}-1}\left({{\mathbb{I}}}_{{d}^{2}}-\left|{{{\Phi }}}_{d}\right\rangle \,\left\langle {{{\Phi }}}_{d}\right|\right),$$

(5)

where $\left|{{{\Phi }}}_{d}\right\rangle =\frac{1}{\sqrt{d}}\mathop{\sum }\nolimits_{j = 0}^{d-1}\left|j\right\rangle \left|j\right\rangle$ and p gives the fully entangled fraction^55,56 of ${{{{\mathcal{I}}}}}_{d}(p)$.

Consider now a pair of isotropic marginals ${{{\boldsymbol{\sigma }}}}=\{{{{{\mathcal{I}}}}}_{d}({p}_{{{{\rm{AB}}}}}),{{{{\mathcal{I}}}}}_{d}({p}_{{{{\rm{AC}}}}})\}$ as the reduced states of some joint state τ_ABC. Then the “twirled” state ${\widetilde{\tau }}_{{{{\rm{ABC}}}}}=\int d{\mu }_{U}(\overline{U}\otimes U\otimes U){\tau }_{{{{\rm{ABC}}}}}{(\overline{U}\otimes U\otimes U)}^{{\dagger} }$, which has a Werner state marginal W_d(v_BC) in BC, is easily verified to be a valid joint state for the given marginals. As in the case of given Werner states marginals, it suffices to consider ${\widetilde{\tau }}_{{{{\rm{ABC}}}}}$ in determining the region of (p_AB, p_AC) that demonstrates metatransitivity.

To this end, note that two isotropic states and one Werner state with parameters $\overrightarrow{p}=({p}_{{{{\rm{AB}}}}},{p}_{{{{\rm{AC}}}}},{v}_{{{{\rm{BC}}}}})$ are compatible iff⁵⁴ the vector $\overrightarrow{p}$ lies within the convex hull of the origin ${\overrightarrow{p}}_{0}=(0,0,0)$ and the cone given by ${\alpha }_{+}\,\le \,1+\frac{1}{d}(\beta +1)$ and $d{\alpha }_{+}-\beta \,\ge \,d\sqrt{{\left({\alpha }_{+}+\beta \right)}^{2}+\left(\frac{d+1}{d-1}\right){\alpha }_{-}}$, where α_± = p_AB ± p_AC and β = 2(v_BC − 1). To find the metatransitivity region for (p_AB, p_AC) we again look for the boundary where the largest compatible ${v}_{{{{\rm{BC}}}}}=\frac{1}{2}$, which we show in Supplementary Note 4 to be $4{p}_{{{{\rm{AB}}}}}{p}_{{{{\rm{AC}}}}}={({p}_{{{{\rm{AB}}}}}+{p}_{{{{\rm{AC}}}}}-1+\frac{1}{d})}^{2}$. The resulting regions of interest are illustrated for the d = 3 case in Fig. 3, and they correspond to (b) in Fig. 4.

Fig. 3: Parameter space for a pair of isotropic state marginals with, respectively, fully entangled fraction p_AB and p_AC.

The compatible region for the pair is enclosed by the solid red line. The blue curves (shown for the case of d = 3) marks the boundary where the largest compatible v_BC is $\frac{1}{2}$. Regions exhibiting metatransitivity are shaded in gray, which shrink with increasing d, as the upper red curve flattens towards the dashed black line and the blue curves approach the two axes.

Fig. 4: A schematic diagram for the metatransitivity examples.

Each row describes the known bipartite marginals in a 3- or 4-partite system and the target subsystems where metatransitivity are exhibited.

Metatransitivity with only separable marginals

Curiously, none of the infinitely compatible pairs of marginals given above result in the most exotic type of metatransitivity, even though there are known examples where separable marginals imply a global entangled state (see, e.g., refs. ^12,24,25,36). In the following, we provide examples where the entanglement of a subsystem is implied by only separable marginals. This already occurs in the simplest case of a three-qubit system. Consider the rank-two mixed state ${\chi }_{{{{\rm{ABC}}}}}=\frac{1}{4}\left|{\chi }_{1}\right\rangle \,\left\langle {\chi }_{1}\right|+\frac{3}{4}\left|{\chi }_{2}\right\rangle \,\left\langle {\chi }_{2}\right|$ where

$$\begin{array}{lll}\left|{\chi }_{1}\right\rangle &=&{\left(\frac{1}{3},\frac{1}{12},-\frac{\sqrt{7}}{12},0,\frac{\sqrt{7}}{12},-\frac{1}{3},-\frac{3}{4},\frac{1}{3}\right)}^{{{{\rm{T}}}}},\\ \left|{\chi }_{2}\right\rangle &=&{\left(-\frac{1}{2},\frac{\sqrt{5}}{24},\frac{1}{6},\frac{1}{8},-\frac{1}{3},-\frac{3}{4},\frac{\sqrt{5}}{24},\frac{1}{8}\right)}^{{{{\rm{T}}}}}.\end{array}$$

(6)

It can be easily checked that the AB and BC marginals of χ_ABC are PPT, which suffices⁴⁶ to guarantee their separability, while Eq. (1) with the PPT criterion can be used to confirm that AC is always entangled. Thus, this example corresponds to (c) in Fig. 4. Likewise, examples exhibiting different kinds of transitivity can also found in higher dimensions (with bound entanglement⁴⁷) or with more subsystems, see Supplementary Note 5 for details.

Here, we present one such example to illustrate some of the subtleties of ETPs in a scenario involving more than three subsystems. Consider the four-qubit pure state

$$\begin{array}{ll}{\left|\xi \right\rangle }_{{{{\rm{ABCD}}}}}=\Big(\frac{1}{45},-\frac{1}{3},\frac{1}{3},\frac{1}{9},\frac{2}{9},-\frac{1}{4},-\frac{2}{5},\frac{1}{9}, \\ \qquad\qquad\quad {\frac{\sqrt{10}}{36},\frac{1}{9},-\frac{1}{9},-\frac{1}{4},-\frac{1}{2},\frac{1}{9},-\frac{1}{9},\frac{1}{3}\Big)}^{{{{\rm{T}}}}}.\end{array}$$

(7)

One can readily check that its AB, BC, and CD marginals are PPT and are thus separable. At the same time, one can verify using Eq. (1) with the PPT criterion that these three marginals together imply the entanglement of all the three remaining two-qubit marginals. Thus, this corresponds to (d) in Fig. 4.

At this point, one may think that the entanglement in the AC marginal already follows from the given AB and BC marginals, analogous to the tripartite examples presented above. This is misguided: the CD marginal is essential to force the AC marginal to be entangled. Similarly, the AB marginal is indispensable to guarantee the entanglement of BD. Thus, the current metatransitivity example illustrates a genuine four-party effect that cannot exist in any tripartite scenario. For completeness, an example exhibiting the same four-party effect but where all input two-qubit marginals are entangled is also provided in Supplementary Note 5.

Metatransitivity from marginals of random pure states

Naturally, one may wonder how common the phenomena of (meta)transitivity is. Our numerical results based on pure states randomly generated according to the Haar measure suggest that transitivity is generic in the tripartite scenario: for local dimension up to five, all sampled pure states have only non-PPT marginals and demonstrate entanglement transitivity. However, with more subsystems, (meta)transitivity seems rare. For example, among the 10⁵ sampled four-qubit states, only about 7.32% show transitivity while about 3.38% show metatransitivity. For a system with even more subsystems or with a higher d, we do not find any example of (meta)transitivity from random sampling (see Table 1 for details).

Table 1 Summary of various features of uniformly sampled n-partite pure states of local dimension d according to the Haar measure.

Next, notice that for the convenience of verification, some explicit examples that we provide actually involve marginals leading to a unique global state. However, uniqueness is not a priori required for entanglement (meta)transitivity. For example, among those quadripartite (meta)transitivity examples found for randomly sampled pure states, >73% of them (see Supplementary Note 5) are not uniquely determined from three of its two-qubit marginals (cf. refs. ^57,58,59). In contrast, most of the tripartite numerical examples found appear to be uniquely determined by two of their two-qudit marginals, a fact that may be of independent interest (see, e.g., refs. ^60,61,62,63).

Discussion

The example involving noisy W-state marginals demonstrate that the transitivity can occur for arbitarily long chain of quantum systems. This leads us to consider metatransitivity with only separable marginals. Beyond the example given above, we present also in Supplementary Note 5 a five-qubit example with four separable marginals and discuss some possibility to extend the chain. For future work, it could be interesting to determine if such exotic metatransitivity examples exist at the two ends of an arbitrarily long chain of multipartite system. For the closely related EMP, we remind that an explicit construction for a state with only two-body separable marginals and an arbitrarily large number of subsystems is known²³ (see also ref. ³⁶).

So far, we have discussed only cases where both the input marginals and the target marginal are for two-body subsystems. If entanglement can be deduced from two-body marginals, it is also deducible from higher-order marginals that include the former from coarse graining. Hence, the consideration of two-body input marginals allows us to focus on the crux of the ETP. As for the target system, we provide—as an illustration—in Supplementary Note 5 an example where the three two-qubit marginals of Fig. 1(b) imply the genuine three-qubit entanglement present in BCD. Evidently, there are many other possibilities to be considered in the future, as entanglement in a multipartite setting is known^1,26 to be far richer.

Our metatransitivity examples also illustrate the disparity between the local compatibility of probability distributions and quantum states. Classically, probability distributions P(A, B) and P(B, C) compatible in P(B) always have a joint distribution P(A, B, C) (this extends to the multipartite case for marginal distributions that form a tree graph⁶⁴). One may think that the quantum analogue of this is: compatible ρ_AB and ρ_BC must imply a separable joint state, and hence a separable ρ_AC. However, our metatransitivity example (as with nontrivial instances of tripartite EMPs), illustrates that this generalization does not hold. Rather, as we show in Supplementary Note 8, a possible generalization is given by classical-quantum states ρ_AB and ρ_BC sharing the same diagonal state in B—in this case, metatransitivity can never be established.

Evidently, there are many other possible research directions that one may take from here. For example, as with the W-states, we have also observed transitivity in n ≤ 3 ≤ d ≤ 6 for qudit Dicke states^65,66,67, which seems to be also uniquely determined by its (n − 1) bipartite marginals. To our knowledge, this uniqueness remains an open problem and, if proven, may allow us to establish examples of transitivity for an arbitrarily high-dimensional quantum state that involves an arbitrary number of particles. From an experimental viewpoint, the construction of witnesses specifically catered for ETPs are surely welcome.

Finally, notice that while ETPs include EMPs as a special case, an ETP may be seen as an instance of the more general resource transitivity problem (CYH, GNT, YCL), where one wishes to certify the resourceful nature of some subsystem based on the information of other subsystems. In turn, the latter can be seen as a special case of the even more general resource marginal problems⁶⁸, where resource theories are naturally incorporated with the marginal problems of quantum states.

Methods

Metatransitivity certified using separability criteria

As mentioned before, we can certify the entanglement (meta)transitivity of a given set of marginals in a bipartite target system T by demonstrating the violation of the PPT separability criterion. We can show this by solving the following convex optimization problem:

$$\begin{array}{l}\mathop{\max }\limits_{{\rho }_{{{{\rm{S}}}}}}\qquad \qquad \qquad \lambda \\ {{{\rm{subj.}}}}\,{{{\rm{to}}}}\quad {{{{\rm{tr}}}}}_{{{{\rm{S}}}}\backslash {{{{\rm{S}}}}}_{i}}({\rho }_{{{{\rm{S}}}}})={\sigma }_{{{{{\rm{S}}}}}_{i}}\,\,\forall \,\,{{{{\rm{S}}}}}_{i}\in {{{\mathcal{S}}}},\\ {\rho }_{{{{\rm{S}}}}}\succcurlyeq 0,\quad {\rho }_{{{{\rm{T}}}}}^{{{\Gamma }}}\succcurlyeq \lambda {\mathbb{I}},\end{array}$$

(8)

which directly optimizes over the joint state ρ_S with marginals ${\sigma }_{{{{{\rm{S}}}}}_{i}}$ such that the smallest eigenvalue λ of ${\rho }_{{{{\rm{T}}}}}^{{{\Gamma }}}$ is maximized. Because a bipartite state that is not PPT is entangled^45,46, if the optimal λ (denoted by λ^⋆ throughout) is negative, the marginal state in T of all possible joint states ρ_S must be entangled.

In the Supplementary Notes, we compute the Lagrange dual problem to Eq. (1) with a linear witness W_T. A similar calculation for Eq. (8) shows that it is equivalent to a dual problem with $W={\eta }_{{{{\rm{T}}}}}^{{{\Gamma }}}$, where η_T being an additional optimization variable subjected to the constraint of η_T ≽ 0 and ${{{\rm{tr}}}}({\eta }_{{{{\rm{T}}}}})=1$.

Meanwhile, to certify genuine tripartite entanglement in the target tripartite marginal T, we use a simple criterion introduced in ref. ⁶⁹. Consider the density operator ρ_AB on ${{\mathbb{C}}}^{m}\otimes {{\mathbb{C}}}^{n}$ to be an m × m block matrix of n × n matrices ρ^(i, j). Let $\widetilde{{\rho }_{AB}}$ denote the realigned matrix obtained by transforming each block ρ^(i, j) into rows. The CCNR criterion^48,49 dictates that for separable σ_AB, $\parallel \widetilde{{\sigma }_{{{{\rm{AB}}}}}}{\parallel }_{1}\le 1$.

Now, let A∣BC denote a bipartition of a tripartite system ABC into a bipartite system with parts A and BC. Finally, for any tripartite state ρ_ABC on ${{\mathbb{C}}}^{d}\otimes {{\mathbb{C}}}^{d}\otimes {{\mathbb{C}}}^{d}$, define

$$\begin{array}{ll}M({\rho }_{{{{\rm{ABC}}}}}):=\frac{1}{3}\left(\parallel {\rho }_{{{{\rm{ABC}}}}}^{{{{{\rm{T}}}}}_{{{{\rm{A}}}}}}{\parallel }_{1}+\parallel {\rho }_{{{{\rm{ABC}}}}}^{{{{{\rm{T}}}}}_{{{{\rm{B}}}}}}{\parallel }_{1}+\parallel {\rho }_{{{{\rm{ABC}}}}}^{{{{{\rm{T}}}}}_{{{{\rm{C}}}}}}{\parallel }_{1}\right)\\ N({\rho }_{{{{\rm{ABC}}}}}):=\frac{1}{3}\left(\parallel \widetilde{{\rho }_{{{{\rm{A}}}}| {{{\rm{BC}}}}}}{\parallel }_{1}+\parallel \widetilde{{\rho }_{{{{\rm{B}}}}| {{{\rm{CA}}}}}}{\parallel }_{1}+\parallel \widetilde{{\rho }_{{{{\rm{C}}}}| {{{\rm{AB}}}}}}{\parallel }_{1}\right),\end{array}$$

(9)

where T_X means a partial transposition with respect to the subsystem X. It was shown in ref. ⁶⁹ that for any biseparable ρ_ABC, we must have

$$\max \{M({\rho }_{{{{\rm{ABC}}}}}),N({\rho }_{{{{\rm{ABC}}}}})\}\,\le \,\frac{1+2d}{3}.$$

(10)

This means that if any of M(ρ_ABC), N(ρ_ABC) is larger than $\frac{1+2d}{3}$, ρ_ABC must be genuinely tripartite entangled.

Therefore in the metatransitivity problem, we can use this, cf. Eq. (8) for the bipartite target system, for detecting genuine tripartite entanglement. This is done by minimizing M and N of the target marginal and taking the larger of the two minima. To this end, note that the minimization of the trace norm can be cast as an SDP⁷⁰. Further details can be found in Supplementary Notes 1.

Certifying the uniqueness of a global compatible (pure) state

A handy way of certifying the (meta)transitivity of marginals $\{{\sigma }_{{{{{\rm{S}}}}}_{i}}\}$ known to be compatible with some pure state $\left|\psi \right\rangle$ is to show that the global state ρ_S compatible with these marginals is unique, i.e., ρ_S is necessarily $\left|\psi \right\rangle \,\left\langle \psi \right|$. This can be achieved by solving the following SDP:

$$\begin{array}{l}\mathop{\min }\limits_{{\rho }_{{{{\rm{S}}}}}}\qquad \qquad \qquad \left\langle \psi \right|{\rho }_{{{{\rm{S}}}}}\left|\psi \right\rangle \\ {{{\rm{subj.}}}}\,{{{\rm{to}}}}\quad {{{{\rm{tr}}}}}_{{{{\rm{S}}}}\backslash {{{{\rm{S}}}}}_{i}}({\rho }_{{{{\rm{S}}}}})={\sigma }_{{{{{\rm{S}}}}}_{i}}\,\,\forall \,\,{{{{\rm{S}}}}}_{i}\in {{{\mathcal{S}}}}\,{{{\rm{and}}}}\,{\rho }_{{{{\rm{S}}}}}\succcurlyeq 0\end{array}$$

(11)

The objective function here is the fidelity of ρ_S with respect to the pure state $\left|\psi \right\rangle$. If this minimum is 1, then by the property of the Uhlmann-Jozsa fidelity⁷¹, we know that the only compatible ρ_S is indeed given by $\left|\psi \right\rangle\!\left\langle \psi \right|$.

For the numerical results that show how typical transitivity is for the bipartite marginals of a pure global state, the marginals are obtained from a uniform random n-qudit state, which is obtained by taking the first column of a dⁿ-dimensional Haar-random unitary.