Introduction

Non-Hermitian physics has garnered significant attention for its ability to capture dissipative and open-system dynamics beyond traditional quantum mechanics1,2. Among its intriguing phenomena, EPs3,4,5 —special parameter regimes where eigenvalues and eigenvectors coalesce—offer profound implications in a range of applications, from enhancing sensitivity in sensors6,7,8 to controlling light-matter interactions9,10,11. While EPs are well-studied in classical systems12,13,14,15,16, the investigation of their quantum counterparts is still at an initial stage. Using methods such as extended Hilbert spaces17 and quantum trajectories18 to construct effective non-Hermitian Hamiltonians, or using the Liouvillian superoperator formalism within the Lindblad master equation framework19,20, which explicitly incorporates quantum jump effects, recent work has realized EPs in various quantum systems such as optical systems21,22,23, superconducting circuits18,24,25,26, ion traps27,28,29, nitrogen-vacancy centers17,30,31 and ultracold atoms32,33. The coexistence of the non-Hermiticity and quantum properties makes them promising platforms for establishing the relationship between quantum correlations and EPs in few-body systems34,35,36,37.

Extending to the investigation of the broader implications of non-Hermitian physics in multimode systems, previous research has revealed intriguing phenomena in classical regime, such as exceptional topology5, enhanced sensing via higher-order EPs38,39, and the dynamic behavior of first-order moments40,41,42,43,44,45. However, the investigation of second-order moments, which are crucial for understanding quantum correlations46,47, remains largely unexplored. Instead of addressing the quantum jump effects in dissipative quantum systems18,19,20, the bosonic chains with mode-hopping and squeezing interactions48,49,50,51,52,53,54,55 provide an efficient route to construct non-Hermitian dynamics without dissipation in Hermitian quantum systems. With advances in optomechanics56,57,58,59,60 and mechanical systems61,62,63,64, the implementation of the desired bosonic chains offers a timely opportunity to explore multimode quantum correlations in the non-Hermitian framework. This leads to a fundamental question: Can non-Hermitian physics, especially EPs, help us uncover deeper insights into multimode quantum correlations in an N-mode bosonic network?

In this work, we explore the connection between non-Hermiticity and entanglement in bosonic chains with mode-hopping and squeezing interactions. Using the BdG framework to describe the equations of motion, we identify the conditions for second-order and higher-order EPs and analyze their effects on quantum entanglement dynamics. Importantly, we find that EPs divide the parameter space into three distinct regions, characterized by purely imaginary, purely real, and mixed eigenvalue spectra, along with entanglement exhibiting exponential, oscillatory, or hybrid behaviors. Furthermore, we demonstrate that higher-order EPs can significantly enhance the degree of multimode entanglement when parameter are optimally tuned. These results deepen our understanding of the connections between non-Hermitian spectral properties and entanglement dynamics in bosonic systems, offering a practical foundation for utilizing EPs to control quantum correlations in complex dynamical processes.

Results

Our model

We consider a network of N bosonic modes with nearest-neighbor hopping and squeezing terms, as illustrated in Fig. 1a. The Hamiltonian takes the form (ℏ = 1)

$$\widehat{H}=\mathop{\sum }\limits_{j=1}^{N}\frac{\eta }{2}{\widehat{a}}_{j}^{2}+\mathop{\sum }\limits_{j=1}^{N-1}(g{\widehat{a}}_{j}^{\dagger }{\widehat{a}}_{j+1}+J{\widehat{a}}_{j}^{\dagger }{\widehat{a}}_{j+1}^{\dagger })+h.c.,$$
(1)

where \({\widehat{a}}_{j}\) and \({\widehat{a}}_{j}^{\dagger }\) denote the mode annihilation and creation operators. Here, g (gj = g), J (Jj = J), and η (ηj = η) represent the uniform beam-splitter (BS), two-mode squeezing (TMS), and single-mode squeezing (SMS) rates, respectively. The presence of the squeezing terms (either TMS or SMS) significantly changes the system’s nonequilibrium behaviors. In addition to modifying the dynamics, leading to non-reciprocal and non-Hermitian behavior44,58,59,60, the squeezing terms are also well-known for generating entanglement. This raises the question: What is the connection between the non-Hermiticity of the dynamic matrix and entanglement?

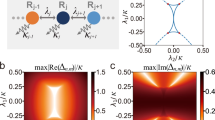
Fig. 1: Schematic of N-mode bosonic chain and the dynamical spectrum divided by EPs.
figure 1

a Schematic of an N-mode bosonic chain with nearest-neighbor mode-hopping and squeezing terms. The system is represented graphically using the BdG formalism, which includes BS (g), TMS (J), and SMS (η) interactions (Supplementary Note 1). b, c Illustration of the dynamical spectrum (M) change affected by the EPs. For a system with only BS and TMS terms, the spectrum is divided into two regions by X-fold EP2s appearing at g = g0. In contrast, the introduction of the SMS term splits the X-fold EP2s into X-unfold EP2s located in the region of \({g}_{0}^{-}\le g\le {g}_{0}^{+}\), corresponding to three different regions of the spectrum. Here X = N for even N and X = N − 1 for odd N.

Full size image

To address it, we consider the dynamic matrix M describing the nonequilibrium behavior of the system through the Heisenberg equation of motion i(d/dt)Φ(t) = MΦ(t). Using the vector \(\Phi ={[a,{a}^{\dagger }]}^{T}\) with \(a={[{\widehat{a}}_{1},{\widehat{a}}_{2},\ldots ,{\widehat{a}}_{N}]}^{T}\), the dynamic matrix M takes the form of a bosonic BdG matrix

$$M(g,\eta ,J)=\left[\begin{array}{cc}{\mathcal{A}}(g) & {\mathcal{B}}(\eta ,J)\\ -{{\mathcal{B}}}^{* }(\eta ,J) & -{{\mathcal{A}}}^{* }(g)\end{array}\right],$$
(2)

where \({\mathcal{A}}(g)\) and \({\mathcal{B}}(\eta ,J)\) are N × N parameter matrices (see detailed expressions in Supplementary Note 1). Crucially, the presence of the squeezing terms ensures \({\mathcal{B}}(\eta ,J)\ne 0\), which induces non-Hermitian dynamics without dissipation even though the Hamiltonian itself remains Hermitian1,58,59. This approach fundamentally differs from both the construction of effective non-Hermitian Hamiltonians17,18 and the use of the Liouvillian superoperator formalism19,20, as it generates effective dynamical non-Hermiticity through quantum coherence and parametric driving under BdG framework.

By transforming the non-Hermitian matrix M into its Jordan normal form, the structure of EPs in the dynamical spectrum can be identified through its block structure (see details in Supplementary Note 2). For the minimal system size N = 2, the eigenvalues of the conventional bosonic Kitaev chain (BKC) with nearest-neighbor hopping and paring interaction (g, J ≠ 0 and η = 0) are \({\lambda }_{1,2}=\sqrt{{g}^{2}-{J}^{2}}\) and λ3,4 = − λ1,2. These eigenvalues reveal two degenerate second-order EPs (2-fold EP2s) at g = g0 = J, dividing the spectrum into two distinct regions: purely imaginary eigenvalues for g < g0 and purely real eigenvalues for g > g0. This degeneracy of 2-fold EP2s can be broken by adding the SMS term. As shown in Fig. 1b, c, the 2-fold EP2s are split into two separate EP2s at \(g={g}_{0}^{-}=| J-\eta |\) and \(g={g}_{0}^{+}=| J+\eta |\), respectively. This splitting creates three distinct regions: (I) a purely imaginary region (\(g < {g}_{0}^{-}\)), (II) a purely real region (\(g > {g}_{0}^{+}\)), and (III) an intermediate region (\({g}_{0}^{-} < g < {g}_{0}^{+}\)), where the eigenvalues are mixed, with two being real and the other two being imaginary [Fig. 2a, b].

Fig. 2: Exceptional points and entanglement dynamics for the two-mode system.
figure 2

The real part (a) and imaginary part (b) of four eigenvalues of M versus g/J with η/J = 0.2. The spectrum is divided into three regions by two EP2s at \({g}_{0}^{-}/J=0.8\) and \({g}_{0}^{+}/J=1.2\). c The time evolution of ν− for g/J = 0.79 (blue), g/J = 1.19 (orange) and g/J = 1.59 (red), showing three distinct types of the entanglement dynamics, i.e., exponential behavior in region I (blue), oscillatory behavior in region II (red) and mixed behavior in region III (orange). d The long time evolution of ν−, to show more difference between region II (red) and III (orange). Other parameters are the same as (c). e The values of ν− versus g/J and t/J with η/J = 0.2. The representative parameters (g/J = 0.79 and g/J = 1.19) near the EP2s in (c) are chosen to illustrate the contrasting entanglement dynamics across these regions, while g/J = 1.59 is just chosen to ensure a consistent parametric spacing.

Full size image

Extending to the multimode BKC with N being even, N-fold EP2s are observed at g = g0, separating the purely imaginary region (I, g < g0) from the purely real region (II, g > g0). The addition of SMS term breaks the degeneracy at g = g0, splitting the N-fold EP2s into N-unfold EP2s. For example, in the case of N = 4, four non-degenerate EP2s can be found, satisfying \({g}_{0}^{-}={g}_{1} < {g}_{2} < {g}_{3} < {g}_{4}={g}_{0}^{+}\). The spectrum in this case exhibits three regions: (I) the purely imaginary region (\(g < {g}_{0}^{-}\)), (II) the purely real region (\(g > {g}_{0}^{+}\)), and (III) an intermediate region (\({g}_{0}^{-} < g < {g}_{0}^{+}\)), where eigenvalues mix real and imaginary parts. For systems with N being odd, (N − 1)-fold EP2s are found. Unlike the case with even N, odd-number-mode chains do not feature a purely real spectrum after adding SMS term. Instead, it contains imaginary eigenvalues in all regions, resulting in scalable entanglement over time (see details in Supplementary Note 2).

Nonequilibrium entanglement dynamics divided by EPs

Multimode systems can present complex entanglement structures, whose characterization poses significant challenges. We focus here on bipartite entanglement, namely entanglement between two partitions of the system, such as between one mode and the rest of the system, which we denote as (1∣N − 1). The entanglement is characterized by the covariance matrix (CM), which describes second-order moments and serves as a common criterion of bipartite entanglement for Gaussian systems46,47. The CM σ of an N-mode state \(\widehat{\rho }\) is expressed as a 2N × 2N real symmetric matrix with elements \({\sigma }_{ij}=\langle {\widehat{\beta }}_{i}{\widehat{\beta }}_{j}+{\widehat{\beta }}_{j}{\widehat{\beta }}_{i}\rangle -2\langle {\widehat{\beta }}_{i}\rangle \langle {\widehat{\beta }}_{j}\rangle ,\) where \(\beta ={({\widehat{X}}_{1},{\widehat{P}}_{1},\ldots ,{\widehat{X}}_{N},{\widehat{P}}_{N})}^{\top }\). The operators \({\widehat{X}}_{i}=(\widehat{a}+{\widehat{a}}^{\dagger })/\sqrt{2}\) and \({\widehat{P}}_{i}=-i(\widehat{a}-{\widehat{a}}^{\dagger })/\sqrt{2}\) represent the amplitude and phase quadratures of the ith mode, respectively. Quantification of bipartite entanglement can be achieved through the minimal symplectic eigenvalue, denoted as ν−, of the CM after performing a partial transpose. Specifically, ν− < 1 signifies the presence of entanglement, with smaller values of ν− indicating stronger entanglement. This allows us to track the time evolution of ν−(t) in different parameter regions.

For the two-mode model without SMS interaction,

$${\nu }_{-}(t)=\sqrt{\xi (t)-\sqrt{\xi {(t)}^{2}-\det \widetilde{\sigma }(t)}},$$
(3)

where \(\xi (t)=({g}^{2}-{J}^{2}\cos (4ct))/{c}^{2},\,c={\lambda }_{1,2}=\sqrt{{g}^{2}-{J}^{2}}\) and \(\widetilde{\sigma }(t)\) is the partial transposed CM (PCM), as can be seen in Methods. The time evolution of the parameter ν− shows different behaviors in the region of purely imaginary eigenvalues (g/J < 1) and purely real eigenvalues (g/J > 1), corresponding to a change from exponentially decaying to oscillatory. When adding SMS interaction, the entanglement dynamics become more complex while maintaining close connections to the spectral bifurcations. In the purely imaginary region (region I) as shown in Fig. 2a, b, the entanglement witness ν− exhibits an exponential decay, indicating a monotonic increase in entanglement over time [blue line in Fig. 2c]. In contrast, in the purely real region (region II), entanglement exhibits oscillatory behavior over time [red line in Fig. 2c, d], markedly different from the behavior in region I. In the intermediate region (region III), where the eigenvalues are a mixture of real and imaginary parts, the entanglement dynamics combine exponential-like and oscillatory behaviors [orange line in Fig. 2c, d]. We classify these dynamics into three distinct types: type-I, type-II, and type-III [Fig. 2e], corresponding to regions I, II, and III, respectively. Each type exhibits unique nonequilibrium behaviors in both the time and frequency domains (see details in Supplementary Note 3). Extending the analysis to a multimode chain and considering the translation invariance of the bulk modes, a similar transition in bipartite entanglement dynamics induced by EP2s can be observed. These entanglement transitions align well with the spectral bifurcation points, as detailed in Supplementary Note 3.

Enhanced entanglement by higher-order EPs

Beyond second-order EPs, we demonstrate that N-mode chains have the potential to exhibit higher-order EPs, which can induce stronger entanglement compared to the case of second-order EPs. In previous work, higher-order EPs can be generated by the evolution matrices of system operator higher-order moments20. Here, we use an alternative method to achieve higher-order EPs of bosonic BdG matrix by introducing a non-integer-π hopping phase, efficiently constructing a dynamical matrix with a higher-dimensional Jordan block (see details in Supplementary Note 2). Considering an N-mode BKC, 2-fold highest-order EPs (EPNs) emerge in the dynamical spectrum when the phase ϕ of the BS terms satisfies ϕ ≠ mπ (\(m\in {\mathbb{Z}}\)) with g/J = 1 (For g/J ≠ 1, the system is not operated at EP regardless of the phase ϕ. See details in Supplementary Note 2). Conversely, X-fold EP2s arise at ϕ = mπ as discussed before. Under the same parameter condition, we observe that the degree of multimode entanglement is significantly higher when the system operates at EPNs compared to EP2s. As illustrated in Fig. 3a, the (1∣N-1)-bipartite entanglement degree increases to its maximum as the hopping phase varies from 0 to π/2. The corresponding ν−(ϕ, t) in the N-mode system is expressed as

$${\nu }_{-}(\phi ,t)=\sqrt{{\xi }_{N}(\phi ,t)-\sqrt{{\xi }_{N}^{2}(\phi ,t)-1}},$$
(4)

with \({\xi }_{N}(\phi ,t)=1+{\sum }_{j=1}^{N-1}{c}_{j}{J}^{2j}{t}^{2j}{\sin }^{2(j-1)}(\phi )\), where the coefficient sequence {cj} remains consistent across different N (see details in Supplementary Note 3). Obviously, a non-integer-π phase induces higher-order terms in ξN leading to enhanced entanglement and thereby directly demonstrating the connection between the order of EPs and entanglement dynamics. Besides, We can find that \(-\log ({\nu }_{-})\) increases monotonically with the phase distance from ϕ = 0 to π/2.

Fig. 3: Entanglement enhancement by higher-order EPs.
figure 3

a Logarithmic negativity \(-\log {\nu }_{-}\) of N-mode BKC model as a function of hopping phase ϕ for N = 2 (blue), N = 3 (light blue), N = 4 (yellow), N = 5 (orange), and N = 6 (red). Here, we set Jt = 3.5 and any point on the solid line corresponds to 2-fold EPNs except for ϕ = 0, π (X-fold EP2s instead). b The time evolution of optimized entanglement enhancement ratio \(R(t)=\log [{\nu }_{-}(\pi /2,t)]/\log [{\nu }_{-}(0,t)]\) with different lengths of N = 3 (light blue), N = 4 (yellow), N = 5 (orange) and N = 6 (red). The inset shows the ratio R as a function of N (2 ~ 30) with fixed time, i.e., Jt = 3.5, which can be fitted as R ≈ − 4.11e−0.4633N + 2.493, revealing a trend of nearly 2.5 times enhancement by highest-order EPs in thermodynamic limits. The other parameters are fixed at g/J = 1 and η = 0.

Full size image

Moreover, the degree of multimode entanglement in the highest-order EPs accumulates with increasing time, as shown in Fig. 3b. The improvement of the optimized multimode entanglement (the maximum at ϕ = π/2) induced by EPNs for the N-mode BKC can be quantified by the ratio \(R(t)=\log [{\nu }_{-}(\pi /2,t)]/\log [{\nu }_{-}(0,t)]\), which exhibits exponential growth with the order of EPs [see Fig. 3b inset]. As N increases, we find that multimode entanglement induced by the highest-order EPs can reach up to ~ 2.5 times that of the EP2s case at the fixed time Jt = 3.5. The saturation feature observed here is caused by the coefficients cj which decrease by orders of magnitude as j increases. More specifically, although the highest power (Jt)2(N−1) grows rapidly with N, its contribution is suppressed by the small prefactor cj (See details in Supplementary Note 3). So, as N increases, the additional gain from higher-order terms diminished for a fixed Jt, leading to the observed saturation of R.

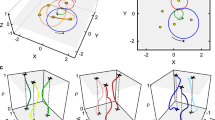
Besides adding a non-integer-π hopping phase, tuning BS (TMS) interaction strengths being unequal, i.e., gi ≠ gj (Ji ≠ Jj), can also be applied to construct the highest-order EPs. Taking a 3-mode BKC as an example [Fig. 4a], the condition for generating EPs requires \({g}_{1}^{2}+{g}_{2}^{2}={J}_{1}^{2}+{J}_{2}^{2}\) (For \({g}_{1}^{2}+{g}_{2}^{2}\ne {J}_{1}^{2}+{J}_{2}^{2}\), the system is not operated at EPs. See details in Supplementary Note 2). Unlike the emergence of third-order EPs induced by the hopping phase, 2-fold third-order exceptional surfaces (ESs) can be observed with zero hopping phases. The degenerate ESs divide the parameter space into two distinct regions: one where all eigenvalues are purely imaginary (above the ESs) and another where they are purely real (below the ESs). Additionally, the parameter space of the degenerate ESs includes a boundary line (red line), corresponding to the case where g1 = J1 and g2 = J2. This condition generates the second-order exceptional arcs (EAs)65.

Fig. 4: Exceptional points and entanglement dynamics in the nonuniform BKC.
figure 4

a Schematic of a three-mode system and the corresponding conditions for EPs in parameter space. The light red surface represents the 2-fold third-order ESs, where each point corresponds to 2-fold EP3s, except for the EAs (red line) consisting of 2-fold EP2s. The parameter space is divided into two regions: eigenvalues are purely imaginary above the ESs, while they are purely real below the ESs, with the exception of two eigenvalues always being 0. The light blue cut at J1/J2 = 1 is shown as a visual guide for the data presented in (b). b The entanglement witness \({\nu }_{-}^{13| 2}\) at Jt = 5 versus interaction strengths, along the blue cut in (a). In region I, entanglement evolves exponentially, while in region II, it oscillates. The white dashed line, marking the intersection of the light red surface and the light blue plane, indicates the positions of EPs, with φ representing the angle between EP3s and EP2s. c Entanglement witness \(-\log ({\nu }_{-}^{13| 2})\) as a function of φ along the white dashed line in (b). The degree of entanglement increases as φ moves further from EP2s. d Time evolution of \(-\log ({\nu }_{-}^{13| 2})\) at φ = 0 (blue line), φ = π/8 (orange line), and φ = π/4 (red line), with other parameters being the same as in (c).

Full size image

Figure 4b illustrates the entanglement behavior under varying hopping strengths [along the light blue cut in Fig. 4a, J1 = J2 = J]. By calculating \({\nu }_{-}^{13| 2}\) to measure the bipartite entanglement between mode a2 and modes a1,3, the degree of entanglement displays two distinct behaviors, separated by the EPs (white dashed line). When \({g}_{1}^{2}+{g}_{2}^{2} < 2{J}^{2}\), an exponentially decaying trend (type I) is observed, while oscillations (type II) occur for \({g}_{1}^{2}+{g}_{2}^{2} > 2{J}^{2}\). This behavior aligns with the entanglement dynamics governed by EPs in the BKC with identical interaction strengths, as discussed earlier. Similar patterns are observed for the other two bipartite entanglements, \({\nu }_{-}^{12| 3}\) and \({\nu }_{-}^{23| 1}\), further indicating the presence of genuine tripartite entanglement. The entanglement gain induced by the highest-order EPs can be quantified by varying the interaction strengths along the white dashed line, as described by the equation: \({\nu }_{-}^{13| 2}(\varphi ,t)={({\xi }_{n-id}(\varphi ,t)-\sqrt{{\xi }_{n-id}^{2}(\varphi ,t)-1})}^{1/2}\), with \({\xi }_{n-id}(\varphi ,t)=32{J}^{4}{t}^{4}{\sin }^{2}\varphi +16{J}^{2}{t}^{2}+1.\) Here, the parameter \(\varphi =\pi /4-\arctan ({g}_{2}/{g}_{1})\) represents the angle between EP3s and the EP2s (see details in Supplementary Note 3). The degree of entanglement as a function of φ and t is shown in Fig. 4c, d, which exhibits the stronger entanglement induced by higher-order EPs.

Discussion

Non-Hermitian physics has garnered considerable attention in recent years, driving advancements in sensing and wave manipulation. As quantum techniques develop, it has become feasible to simulate non-Hermitian dynamics within quantum systems, attracting both theoretical and experimental interest in how to harness quantum resources under non-Hermitian conditions effectively. By constructing a non-Hermitian BdG framework to understand multimode entanglement dynamics, our work provides a foundational and distinct mechanism to utilize entanglement resources efficiently. We present two examples to demonstrate its potential applications. In quantum metrology, for a parameter χ encoded in an initial state, the metrological power of the corresponding final quantum state can be quantified by its quantum Fisher information (QFI) Qχ, which sets a bound on the precision (Δχ)2 to estimate χ, i.e., (Δχ)2 ≥ 1/(νQχ) with ν being the number of independent measurements. Thus, a larger QFI indicates greater metrological power. We can find that the QFI Qχ in our three-mode BKC is significantly enhanced in the parameter regimes where all nonzero eigenvalues are purely imaginary, while it remains relatively low in the purely real regimes. This demonstrates that distinct behaviors of QFI on the two sides of EP2s can be observed and the states in purely imaginary region can provide a higher accuracy for parameter estimation. Another application is to detect multimode entanglement under noise. For a fixed evolution time, we can find the entanglement in our three-mode BKC quickly vanishes as the thermal noise increases in the purely real spectral region. In contrast, in the region where all nonzero eigenvalues are purely imaginary, the entanglement only diminishes slightly and remains detectable, revealing a more resilient parameter regime for implementing and observing multimode entanglement under noise (see detailed calculations in Supplementary Note 4).

To discuss the possible implementation of our model, we note that the rapid progress in quantum technologies—particularly in bosonic platforms—offers promising avenues for realizing both mode-squeezing and mode-exchange interactions. Optical and mechanical systems are especially well-suited for this purpose, as their photonic and mechanical degrees of freedom naturally support continuous-variable quantum information processing and bosonic quantum simulations. For instance, integrated optical chips have recently emerged as powerful platforms capable of implementing frequency-mode exchange and pair-squeezing interactions among quantum modes66,67. In optomechanics58,59,60, exchange (squeezing) couplings can be engineered by modulating the intensity of the drive laser using multiple harmonic tones with frequencies that approximate the frequency differences (sums) of mechanical modes. Moreover, two- and three-mode hopping and single-mode squeezing interactions were demonstrated in a gigahertz-frequency multimode mechanical resonator coupled to a superconducting qubit62,63. By controlling the qubit’s driving frequency, these exchange and squeezing couplings can also be extended to a large-scale multimode setting. Additionally, superconducting quantum circuits also offer a natural environment for realizing hopping and pairing terms in the synthetic dimensions of a multimode superconducting parametric cavity51.

In summary, our work studies the entanglement behavior driven by EPs in multimode bosonic models. By mapping the Heisenberg equations to the non-Hermitian BdG framework, we uncover a variety of EPs, from second-order to highest-order, separating distinct spectral regimes characterized by purely imaginary, purely real, or mixed eigenvalue spectra. These EPs directly determine nonequilibrium entanglement transitions, giving rise to exponential, oscillatory, or hybrid entanglement dynamics. Remarkably, by comparing to the multimode entanglement achievable in the EP2s case, we demonstrate that the highest-order EPs, obtained through non-integer-π hopping phases or nonuniform interaction strengths, can be designed to enhance the entanglement degree when operated optimally. Our findings provide new insights into the relationship between non-Hermitian features and quantum entanglement, with the potential applications for further engineering quantum correlations as well as enhancing sensitivity in photonic66,67, optomechanical58,59,60, and mechanical platforms61,62,63,64.

Looking forward, several intriguing questions remain open. For example, (i) while we provide a connection between second-order quadrature correlations (covariance matrix) and the dynamical matrix, it is unclear whether a deeper connection can be established between the dynamical matrix and higher-order quadrature correlations. This would be valuable, as it may offer a path to better understand multimode non-Gaussian entanglement dynamics68 (i.e., entanglement beyond second-order quadrature correlations), which is considered as a necessary resource for quantum computation and metrology69,70. (ii) The introduction of the squeezing terms may also induce rich topological phases48,51,60. Given the strong connection between the topological phases and the dynamics of first-order moments40,41,42,43,44,45, the investigations of the connection with the CM could provide valuable insights into a deeper understanding of quantum correlations in a topological framework. (iii) It would also be interesting to extend dissipation-free bosonic chains to Markovian17,18,19,20 and non-Markovian71 regimes and investigate the connection between the non-Hermiticity and quantum correlations in open quantum systems.

Methods

The positive partial transpose criterion

Here, we introduce the entanglement criterion we used to describe the multimode entanglement in our model. For Gaussian systems, the positive partial transpose (PPT) criterion is widely applied to measure the bipartite entanglement46,47. Specifically, considering a nA × mB bipartite Gaussian state ρAB, we can obtain its CM σAB with matrix elements \({\sigma }_{ij}=\langle {\widehat{\beta }}_{i}{\widehat{\beta }}_{j}+{\widehat{\beta }}_{j}{\widehat{\beta }}_{i}\rangle -2\langle {\widehat{\beta }}_{i}\rangle \langle {\widehat{\beta }}_{j}\rangle\), where we define vector \(\beta =({\widehat{X}}_{1}^{A},{\widehat{P}}_{1}^{A},\ldots ,{\widehat{X}}_{n}^{A},{\widehat{P}}_{n}^{A},{\widehat{X}}_{1}^{B},{\widehat{P}}_{1}^{B},\ldots ,{\widehat{X}}_{m}^{B},{\widehat{P}}_{m}^{B})\). As a bona fide CM, it should satisfy

$${\sigma }_{AB}+i\Omega \ge 0,$$
(5)

or equivalently

$${\nu }_{i}^{AB}\ge 1\,(\forall i=1,\ldots ,{n}_{A}+{m}_{B}),$$
(6)

where \({\nu }_{i}^{AB}\) is the symplectic eigenvalue of σAB and Ω is the symplectic form

$$\Omega =\mathop{\oplus}_{k=1}^{N}\omega ,\,\omega =\left[\begin{array}{cc}0 & 1\\ -1 & 0\end{array}\right].$$
(7)

Correspondingly, the PCM \({\widetilde{\sigma }}_{AB}={\theta }_{AB}{\sigma }_{AB}{\theta }_{AB}\) with

$${\theta _{AB}} = {{diag}}\left\{ {\underbrace {1,1, \ldots ,1,1}_{2{n_A}},\underbrace {1, - 1, \ldots ,1, - 1}_{2{m_B}}} \right\},$$
(8)

which means mapping \({\widehat{P}}_{B}\) to \(-{\widehat{P}}_{B}\). PPT criterion indicates that if the new matrix \({\widetilde{\sigma }}_{AB}\) isn’t a bona fide CM, i:e

$${\widetilde{\sigma }}_{AB}+i\Omega < 0,$$
(9)

or equivalently

$${\widetilde{\nu }}_{i}^{AB} < 1\,(\exists i\in \{1,\ldots ,{n}_{A}+{m}_{B}\}),$$
(10)

the subsystem SA composed of nA modes is entangled with the subsystem SB composed of nB modes. To be clear, the PPT criterion is the sufficient and necessary condition for all (nA × 1)-mode Gaussian states but not for generic cases. However, it still can be used to measure the entanglement in nA × mB bipartite Gaussian state once \({\widetilde{\sigma }}_{AB}\) isn’t a bona fide CM. Moreover, we can used the logarithmic negativity \({E}_{{\mathcal{N}}}\) to quantify the violation of the PPT criterion,

$${\mathrm{i.e.,E}}_{{\mathcal{N}}}=\left\{\begin{array}{ll}-\mathop{\sum }\limits_{k}\log {\widetilde{\nu }}_{k}, & for\,k:{\widetilde{\nu }}_{k} < 1\\ 0, & if\,{\widetilde{\nu }}_{i}\ge 1\forall i.\end{array}\right.$$
(11)

Namely, the logarithmic negativity \({E}_{{\mathcal{N}}}\) is a good choice to measure entanglement. By the way, there is a lemma that at most \({N}_{\min }\equiv \min \{{n}_{A},{m}_{B}\}\) symplectic eigenvalues \({\widetilde{\nu }}_{k}\) of \({\widetilde{\sigma }}_{AB}\) can violate the PPT inequality for a nA × mB bipartite Gaussian state. Especially, for all (nA × 1)-mode Gaussian states, we can directly use \({\nu }_{-}\equiv \min \{{\widetilde{\nu }}_{i}\}\) to measure entanglement as we apply to measure the entanglement between one mode and the rest of the system, denoted as (1∣N − 1), in the main text. When ν− < 1, the system has entanglement. Otherwise, it’s separable. Furthermore, the closer ν− to zero, the greater the entanglement.