Deciphering cell-fate trajectories using spatiotemporal single-cell transcriptomic data

Abstract

Cellular processes evolve dynamically across time and space. Single-cell and spatial omics technologies have provided high-resolution snapshots of gene expression, greatly expanding the capability to characterize cellular states. This review summarizes recent modeling strategies for time-series and spatiotemporal transcriptomic data, emphasizing links between dynamical systems, generative modeling, and biological insight. These approaches illustrate how computational tools can deepen our understanding of the dynamic nature of single cells.

Introduction

Biological processes are inherently dynamic. From lineage bifurcations in embryogenesis to the gradual remodeling of tissues in regeneration and disease, cells continuously evolve across both time and space. Understanding these transitions requires not only high-resolution molecular measurements but also computational methods that can connect static observations into continuous trajectories^{1,2,3,4,5,6,7,8,9}. In recent years, the development of single-cell and spatial omics technologies has greatly expanded our ability to measure cellular states. Single-cell RNA sequencing (scRNA-seq)^10,11,12 has revealed the diversity of cell types and states, while temporally resolved scRNA-seq^4,13,14 enables sampling across multiple time points. Spatial transcriptomics (ST)^{15,16,17,18,19,20,21,22} has introduced spatial context into these measurements, and the emergence of time series ST²³ offers the opportunity to investigate how cellular organization changes simultaneously across time and space. Together, these technologies mark an important step from static cellular atlases toward dynamic, spatiotemporal reconstructions of biological processes, and constitute the foundation of the recent efforts to build the AI-empowered virtual cells^24,25,26.

Despite these progresses, the majority of omics-based data remain fragmented. For instance, snapshot-based scRNA-seq provides only a single-time-point measurement of each cell. Methods such as pseudotime inference^27,28,29 and RNA velocity^{30,31,32,33,34} have therefore been developed to infer dynamics from these static data, ordering cells along latent trajectories or inferring velocity directions of change based on splicing kinetics. These approaches, while highly valuable, are inherently designed for single-time-point snapshot data. Meanwhile, time-series data, such as temporally resolved scRNA-seq or time series ST, directly capture population-level changes across multiple time points and hold the potential to reconstruct faithful cellular trajectories and regulatory mechanisms. Using these richer datasets requires dedicated mathematical and computational frameworks that extend beyond single snapshot-based tools.

A wide range of dynamical modeling strategies have then been proposed, including formulations based on dynamical systems (e.g., ordinary differential equations, ODEs; stochastic differential equations; and partial differential equations) as well as generative frameworks such as optimal transport^{14,35,36,37,38}, flow matching^{39,40,41,42,43,44}, unbalanced transport^45,46,47,48, Schrödinger bridges (SB)^49,50,51, and mean-field approaches^52,53,54,55. These methods provide powerful tools to couple distributions across time and to account for proliferation, death, noise, and cell-cell interactions. Each framework offers distinct advantages and is well-suited to the analysis of multi-time-point or spatiotemporal data.

Several reviews have provided comprehensive summaries of this rapidly developing field. For instance, recent surveys have reviewed or benchmarked pseudotime inference methods^56,57, summarized RNA velocity approaches^31,56,58,59, and highlighted optimal transport theory in single-cell or spatial omics^4,5,14,60. In³⁷, it systematically discussed how concepts from dynamical systems and generative modeling can be applied to spatiotemporal single-cell data. Other reviews have highlighted complementary perspectives, including developmental landscapes and energy-based formulations^1,3,9.

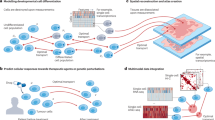
This review takes a distinct perspective. We concentrate specifically on methods designed to analyze time-series single-cell and ST data, including temporally resolved scRNA-seq and spatiotemporal ST. We aim to provide a unified, biologically accessible framework: (i) introducing the mathematical concepts and foundations in intuitive terms, (ii) reviewing key algorithms with a focus on their data requirements, design principles and practical applications, and (iii) offering practical guidelines for selecting, applying, and interpreting these methods in real biological studies. By clarifying the connections between data types, modeling choices, and biological insights, this review will serve as a bridge between theoretical advances and experimental practice, empowering the community to more effectively integrate dynamical modeling into their research. To this end, we introduce the idea of spatiot emporal Dynamical Generative Model (stDGM), a framework that conceptually encompasses the methods discussed (Fig. 1) and implemented in our accompanying software package CytoBridge.

Fig. 1: Overview of the spatiotemporal dynamical generative model (stDGM) framework.

A The analysis starts with raw data from single-cell sequencing, which is converted into a time-resolved, unpaired gene expression and then projected into a low-dimensional embedding. B stDGM model the evolution of the initial cell distribution to a target distribution over time. This approach accounts for key biological processes, including cell differentiation, growth/ death, stochastic effects, and cell-cell interactions. C The trained model enables a rich suite of downstream analyses, such as (a) visualizing velocity streamlines; (b) generating cell states and trajectories at unobserved time points; (c) identifying regions of high cellular proliferation; (d) mapping cell fate stability via a Waddington-like potential landscape; (e) inferring fate probabilities; and (f) constructing gene regulatory networks and predicting the effects of perturbations. The Figure was created in BioRender. Zhang, Z. (2025) under the license https://BioRender.com/f6etpat.

This paper is organized as follows. Section mathematical foundation introduces the mathematical principles of dynamical modeling. Section Algorithms Implementation reviews key algorithmic approaches for temporally resolved single-cell data and spatiotemporal data. Section Practical Guidelines provides practical guidelines for method selection and interpretation. Finally, we summarize the insights and conclude with future perspectives and open challenges in Section Conclusion and Future Directions.

Mathematical foundation

In this section, we summarize the mathematical foundations that underpin trajectory inference and spatiotemporal data integration in single-cell biology (Table 1). The core idea is to treat observed cell populations as samples from distributions that evolve over time and to transport one distribution into another in a way that respects biological constraints in reality. These theories form a hierarchical toolbox, ranging from deterministic to stochastic, from mass-conserving to unbalanced, and from individual to interacting populations. Together, they offer principled ways to decode developmental trajectories and tissue organization from spatiotemporal single-cell data. The historical lineage of key mathematical theories of stDGM is summarized in (Fig. 2A).

Fig. 2: Historical evolution of mathematical foundations and algorithmic landscape for stDGM.

A Timeline traces the conceptual lineage from 18th-century static optimal transport to the recent unbalanced mean-field Schrödinger bridges, incrementally relaxing assumptions to match biological complexity. B The contemporary algorithmic zoo is compactly charted along three axes: data assumption, modeling strategy, and training method. The dense grid of named tools demonstrates a fast-evolving ecosystem where theoretical advances have already been packaged into practical, user-ready implementations. The algorithms are still in rapid expansion, and due to the limitation of the authors' scope, some relevant algorithms might not be included.

Table 1 A comparative table of mathematical framework for modeling spatiotemporal scRNA-seq data

Static optimal transport

Static optimal transport (static OT) provides a principled way to relate two unpaired cellular populations sampled at distinct time points⁶¹. Formally, let ${\bf{X}}\in {{\mathbb{R}}}^{N\times G}$ and ${\bf{Y}}\in {{\mathbb{R}}}^{M\times G}$ be the gene expression matrices collected at two distinct time points t₁ and t₂, where each row represents a cell embedded in the G-dimensional transcriptomic space. Then, one can define two marginal distributions ν₀ ∈ C_N and ν₁ ∈ C_M at t₁ and t₂, respectively, on the probability simplex ${C}_{N}=\{{\bf{a}}\in {{\mathbb{R}}}^{N}| \sum {a}_{i}=1,{\bf{a}}\ge 0\}$. The well-known Kantorovich formulation⁶² of the static OT task is to find the nonnegative coupling ${\boldsymbol{\pi }}\in {{\mathbb{R}}}_{\ge 0}^{N\times M}$ that minimizes the total transportation cost:

$${{\mathcal{L}}}_{{\rm{stat}}}({\boldsymbol{\pi }}):=\langle {\boldsymbol{\pi }},{\boldsymbol{c}}\rangle =\sum _{ij}{c}_{ij}{\pi }_{ij},$$

(1)

where the transport plan ${\boldsymbol{\pi }}\in {{\mathbb{R}}}^{N\times M}$ must satisfy the marginal constraints π1_M = ν₀ and π^⊤1_N = ν₁. Each entry c_ij: = c(x_i, y_j) of the cost matrix c = [c_ij] quantifies the dissimilarity between the transcriptomic profiles of cell i at time t₁ and cell j at time t₂, typically chosen as the squared Euclidean distance. The resulting optimal coupling π assigns each cell from ν₀ to ν₁ in the least-cost fashion where π_ij denotes the mass transported from cell i to j.

Intuitively, the OT model assumes that similar cell states in gene expression space are more likely to be coupled in the cell-fate decision process across time points. Using such a method⁶³, identifies the heterogeneous EMT responses in a scRNAseq time course data of MCF10A cells treated by TGF-beta.

Dynamical optimal transport

Developmental biology seeks to understand how one cell population continuously reshapes itself into another. To generate continuous trajectories from cells at any time point and with different expressions rather than merely assigning pseudotime to all cells in static snapshots, dynamical optimal transport presents a continuous mechanistic modeling framework. By treating cell-state transitions as a smooth, mass-preserving flow, this approach recasts lineage progression in the language of continuum fluid dynamics. In the Benamou-Brenier framework⁶⁴, the single-cell trajectories satisfy the ODE dX_t = b(X_t, t)dt, where b(X_t, t) describes the nonlinear gene regulatory dynamics that drive the cell-state transitions, analogous to the concept of RNA velocity^30,31,34. Suppose the gene expression matrices are sampled from a smooth and time-dependent probability density function ρ(x, t), the spatiotemporal dynamics of the density are governed by the continuity equation

$${\partial }_{t}\rho ({\bf{x}},t)+{\nabla }_{{\bf{x}}}\cdot ({\bf{b}}({\bf{x}},t)\rho ({\bf{x}},t))=0\quad \forall t\in [0,1],\,{\bf{x}}\in {{\mathbb{R}}}^{G},$$

where ${\bf{b}}({\bf{x}},t)\in {{\mathbb{R}}}^{G}$ here naturally could be reinterpreted as the velocity field of the density movement. The transport map from the initial to final conditions is not unique; OT resolves this ambiguity by choosing the one that minimizes the total kinetic energy, resulting in the Wasserstein distance between two probability distributions. This is expressed as a minimization with the cost:

$${{\mathscr{L}}}_{{\rm{dyn}}}(\rho ,{\bf{b}}):={\int_{0}^{1}}{\int_{{{\mathbb{R}}}^{G}}}\frac{1}{2}\Vert{\bf{b}}({\bf{x}},t){\Vert}^{2}\rho ({\bf{x}},t)\,{\rm{d}}{\bf{x}}\,{\rm{d}}t\quad \,{\rm{subject}}\, {\rm{to}}\,\,\rho (\cdot ,0)={\nu }_{0},\,\rho (\cdot ,1)={\nu }_{1}$$

(2)

and the continuity equation constraint. One important feature of dynamical OT type methods is that they serve as natural generative models. After the vector field in cell state space is learned, the processes of single cells at unobserved temporal points could be simulated through the inferred model. Theoretically, it has be shown that this dynamical OT is equivalent to the static OT when the cost c_ij = ||x_i− y_j||²⁶⁴.

Combining dynamical OT with other biological priors, such as RNA velocity or cell growth, TrajectoryNet generates continuous, nonlinear trajectories in both simulated and real biological systems, uncovering cell differentiation paths in human embryoid-body data that align with previously reported biological findings⁶⁵.

Unbalanced dynamical optimal transport

To faithfully model biological systems in which cells proliferate (mass creation) and undergo apoptosis (mass destruction), one needs to relax the classical assumption of strict mass conservation, that is, the number of cell is permitted to change over time. Such biological constraints have motivated the introduction of unbalanced optimal transport, which is increasingly popular for connecting a time series of densities with different masses. To explicitly and continuously encode cell growth and death, unbalanced dynamical optimal transport introduces a spatiotemporal variable growth rate function $g({\bf{x}},t):{{\mathbb{R}}}^{G}\times [0,1]\to {\mathbb{R}}$, which acts as a source-sink term in the continuity equation^45,46:

$${\partial }_{t}\rho ({\bf{x}},t)+{\nabla }_{{\bf{x}}}\cdot ({\bf{b}}({\bf{x}},t)\rho ({\bf{x}},t))=g({\bf{x}},t)\rho ({\bf{x}},t)\quad \forall t\in [0,1],{\bf{x}}\in {{\mathbb{R}}}^{G}$$

(3)

and the initial and final conditions: ρ( ⋅ , 0) = ν₀, ρ( ⋅ , 1) = ν₁. In this setup, Wasserstein and Fisher-Rao (WFR) distance^45,66 has been used to optimize transport dynamics with respect to both velocity and growth energy. It minimizes the combined WFR metrics defined as:

$$\begin{array}{l}{{\mathcal{L}}}_{{\rm{WFR}}}(\rho ,{\bf{b}},g):={\int_{0}^{1}}{\int_{{{\mathbb{R}}}^{G}}}\left[\frac{1}{2}\Vert{\bf{b}}({\bf{x}},t){\Vert}^{2}+\alpha \,{g}^{2}({\bf{x}},t)\right]\rho ({\bf{x}},t)\,{\rm{d}}{\bf{x}}\,{\rm{d}}t,\\\qquad\quad\,\,\,\rho (\,\cdot \,,0)={\nu }_{0},\,\rho (\,\cdot \,,1)={\nu }_{1}\end{array}$$

subject to the continuity Eq. (3).

Powered by dynamical unbalanced optimal transport, TIGON⁶⁷ reconstructs cell-state transition dynamics during EMT and detects the cellular proliferation peak at the intermediate stage, consistent with the biology that intermediate-state cells transiently reacquire stem-like potency^{68,69,70,71,72}.

Schrödinger bridge problem (SB)

To capture the prevalent stochasticity of single-cell trajectories during the cell-fate decision process⁷³, the SB framework explicitly models random fluctuations rather than relying on purely deterministic transport. It seeks to determine the most probable evolution between a specified initial distribution ν₀ and a terminal distribution ν₁ relative to a prescribed reference stochastic process. Formally, the problem is described as an optimal control problem whose objective is to minimize the Kullback-Leibler (KL) divergence D_KL, an idea that traces back to Schrödinger (1932) and subsequent stochastic control treatments^74,75:

$$\mathop{\inf }\limits_{{\mu }_{0}^{{\bf{X}}}={\nu }_{0},{\mu }_{1}^{{\bf{X}}}={\nu }_{1}}{D}_{{\rm{KL}}}\left({\mu }_{[0,1]}^{{\bf{X}}}\,\parallel \,{\mu }_{[0,1]}^{{\bf{Y}}}\right),$$

(4)

where ${\mu }_{[0,1]}^{{\bf{X}}}$ is the probability measure on ${\mathcal{C}}([0,1],{{\mathbb{R}}}^{G})$ induced by the stochastic process ${\{{{\bf{X}}}_{t}\}}_{0\le t\le 1}$. At each time t, the one-time marginal of measure ${\mu }_{[0,1]}^{{\bf{X}}}$ is denoted ${\mu }_{t}^{{\bf{X}}}$ and possesses the density ρ(x, t). Concretely, each cell’s gene expression state ${{\bf{X}}}_{t}\in {{\mathbb{R}}}^{G}$ can be assumed to evolve as dX_t = b(X_t, t) dt + σ(X_t, t) dW_t, where ${\{{{\bf{W}}}_{t}\}}_{t\ge 0}$ is a standard multidimensional Brownian motion (with dimension G) and $\sigma :{{\mathbb{R}}}^{G}\times [0,1]\to {{\mathbb{R}}}^{G\times G}$ denotes the diffusion coefficient. The reference measure ${\mu }_{[0,1]}^{{\bf{Y}}}$ is generated by the uncontrolled diffusion dY_t = σ(Y_t, t) dW_t. Simply put, it aims to identify the cell-state transition dynamics from purely stochastic motion to dynamics driven by both clear gene regulation forces and stochastic components either intrinsically from gene expression process or from the fluctuating environment. In this formulation, the problem can be equivalently transformed to minimizing the cost^50,51,75,76:

$${{\mathcal{L}}}_{{\rm{SB}}}(\rho ,{\bf{b}}):=\mathop{\int}\nolimits_{0}^{1}{\int}_{{{\mathbb{R}}}^{G}}\frac{1}{2}\left[{{\bf{b}}}^{T}({\bf{x}},t)\,{{\bf{a}}}^{-1}({\bf{x}},t){\bf{b}}({\bf{x}},t)\right]\,\rho ({\bf{x}},t)\,{\rm{d}}{\bf{x}}\,{\rm{d}}t,\,$$

(5)

where a(x, t) = σ(x, t)σ^⊤(x, t) and the optimization is taken over all pairs of functions ρ satisfying ρ( ⋅ , 0) = ν₀, ρ( ⋅ , 1) = ν₁. Additionally, the pair (ρ, b) needs to satisfy the Fokker-Planck Equation:

$${\partial }_{t}\rho ({\bf{x}},t)+{\nabla }_{{\bf{x}}}\cdot ({\bf{b}}({\bf{x}},t)\rho ({\bf{x}},t))=\frac{1}{2}{\nabla }_{{\bf{x}}}^{2}:\,({\bf{a}}({\bf{x}},t)\rho ({\bf{x}},t)),$$

(6)

where ${\nabla }_{{\bf{x}}}^{2}:({\bf{a}}\rho )={\sum }_{ij}{\partial }_{ij}({{\bf{a}}}_{ij}\rho )$, coupled with asymptotic vanishing boundary condition: ${\lim }_{| {\bf{x}}| \to \infty }\rho ({\bf{x}},t)=0$.

Inspired by SB, SF2M reconstructed high-dimensional trajectories of differentiating mouse embryonic stem cells from five unpaired scRNA-seq time-points and accurately predicted an unseen day-6 population⁷⁷. Its built-in Brownian-bridge noise term captured the probabilistic bifurcation of pluripotent cells into mesoderm and ectoderm lineages.

Regularized Unbalanced Optimal Transport (RUOT)

In the study of cellular dynamics, where both random changes and processes such as cell growth and death occur, the RUOT framework offers a natural advancement of traditional optimal transport models^51,78,79. Specifically, when the diffusion coefficient is isotropic, i.e., a(x, t) = σ²(t)I, the density evolution follows the Fokker–Planck equation with a source term:

$${\partial }_{t}\rho ({\bf{x}},t)+{\nabla }_{{\bf{x}}}\cdot ({\bf{b}}({\bf{x}},t)\rho ({\bf{x}},t))=\frac{1}{2}{\sigma }^{2}(t){\Delta }_{{\bf{x}}}\rho ({\bf{x}},t)+g({\bf{x}},t)\rho ({\bf{x}},t),$$

(7)

where g(x, t) denotes the net growth rate and the boundary condition ${\lim }_{| x| \to \infty }\rho ({\bf{x}},t)=0$ ensures integrability. The corresponding optimization problem seeks to minimize an action functional that balances kinetic energy against a growth penalty:

$${{\mathcal{L}}}_{{\rm{RUOT}}}(\rho ,{\bf{b}},g):=\mathop{\int}\nolimits_{0}^{1}{\int}_{{{\mathbb{R}}}^{G}}\left[\frac{1}{2}\parallel {\bf{b}}({\bf{x}},t){\parallel }^{2}+\alpha \Psi \left(g({\bf{x}},t)\right)\right]\rho ({\bf{x}},t)\,{\rm{d}}{\bf{x}}\,{\rm{d}}t$$

(8)

subject to the dynamics (7) and marginal constraints ρ( ⋅ , 0) = ν₀, ρ( ⋅ , 1) = ν₁. Here $\Psi :{\mathbb{R}}\to [0,+\infty ]$ is a convex penalty that controls deviations from mass conservation. Note that in the definition if $\Psi \left(g\right)=+\infty$ unless g = 0 and $\,\Psi \left(0\right)=0$, then it implies g(x, t) = 0 and the RUOT problem is equivalent to the special case of the SB Problem, characterized by a(x, t) = σ²(t) I. If σ(t) → 0 and $\Psi \left({\bf{x}},t\right)=| g({\bf{x}},t){| }^{2}$, this degenerates to the unbalanced dynamic optimal transport with WFR metrics.

Based on such framework, DeepRUOT⁵¹ also traces the unbalanced continuous epithelial-intermediate-mesenchymal path with greater accuracy, illustrating how the method merges RNA-velocity drift, genuine growth/death, and stochastic effects to achieve smooth temporal cell population interpolation in real scRNA-seq data.

Hamilton-Jacobi-Bellman (HJB) Equation and Optimal Transport

The Hamilton-Jacobi-Bellman (HJB)^80,81 equation is a fundamental tool in the field of stochastic optimal control, providing an effective framework for solving optimization problems involving stochastic processes. In the context of optimal transport, the HJB equation plays a crucial role in characterizing the optimal control strategies that minimize the cost of transporting one probability distribution to another. When solving optimal transport and its variants, the Fokker-Planck equation serves as a constraint that can be incorporated into the optimization objective via Lagrange multipliers. Taking the RUOT problem as an example⁵¹, the augmented objective function is given by:

$${\mathcal{L}}={\int_{0}^{1}}{\int_{{{\mathbb{R}}}^{G}}}\rho \left[\frac{1}{2}\Vert{\bf{b}}{\Vert}^{2}+\alpha \Psi (g)+\lambda \left({\partial }_{t}\rho +{\nabla }_{{\bf{x}}}\cdot ({\bf{b}}\rho )-\frac{1}{2}{\sigma }^{2}(t){\Delta }_{{\bf{x}}}\rho -g\rho \right)\right]{\rm{d}}{\bf{x}}\,{\rm{d}}t.$$

(9)

Then the problem can be treated as an unconstrained optimization problem, with variational derivatives with respect to ρ, b and g yielding three optimality conditions. In particular, the optimality condition obtained from the variation with respect to ρ provides the evolution equation for the Lagrange multiplier over time, which is the HJB equation. By deriving the optimality condition, one can show that only one scalar field λ(x, t) needs to be trained⁴⁸, sparing us from learning the RNA velocity drift b, the growth rate g and the density ρ (or the associated energy landscape, the score function) separately, yielding the faster and more stable optimization. The optimality condition and HJB equation for the RUOT problem is:

$$\frac{\partial \lambda }{\partial t}+\frac{1}{2}\parallel {\nabla }_{{\bf{x}}}\lambda {\parallel }^{2}+\frac{1}{2}{\sigma }^{2}{\Delta }_{{\bf{x}}}\lambda +\lambda g-\alpha \,\Psi (g)=0,{\bf{b}}={\nabla }_{{\bf{x}}}\lambda ,\alpha {\Psi }^{{\prime} }(g)=\lambda .$$

(10)

When g = 0, this equation reduces to the HJB equation for the SB problem. When σ = 0 with $\Psi (g)=\frac{1}{2}{g}^{2}$, it reduces to the HJB equation for the Dynamical Unbalanced OT problem that employs the WFR metric.

In mouse blood hematopoiesis, Var-RUOT⁴⁸ reaches the smallest action, trains faster and shows lower variance, all benefitted from learning one scalar field that simultaneously produces the straighter lineage-splitting trajectory and the accurate upstream-to-downstream decay of cellular growth rate, which is consistent with the knowledge of proliferating stem cells in biology.

Mean-Field Schrödinger Bridge (MFSB)

The classical SB problem reconstructs the most-probable trajectory between two observed distributions under the assumption that the underlying cells (i.e., particles) are independent. In comparison, biological reality is shaped by persistent cell-cell communications that couple individual fates into a collective process. To capture this coupling, the bridge problem can be extended to a mean-field setting^82,83. Consider N particles evolving under the influence of a kernel of symmetric interaction K. The discretized McKean-Vlasov stochastic dynamics⁸⁴ has the form

$${\rm{d}}{{\bf{X}}}_{t}^{i,N}=\frac{1}{N}\mathop{\sum }\limits_{k=1}^{N}{\bf{K}}\left({{\bf{X}}}_{t}^{i,N},{{\bf{X}}}_{t}^{k,N}\right)\,{\rm{d}}t+\sigma {\rm{d}}{{\bf{W}}}_{t}^{i},\qquad i=1,\ldots ,N,$$

where the first term captures the interactions between particles quantified by the interacting kernel K, and the second term involves ${{\bf{W}}}_{t}^{i}$, which are independent standard Brownian motions for i = 1, …, N. The empirical measures at t = 0 and t = 1 are observed to be close to the prescribed probability measures ν₀ and ν₁, respectively. The discrete system has a mean field limit with density ρ(x, t) satisfies the McKean-Vlasov PDE ${\partial }_{t}\rho +{\nabla }_{{\bf{x}}}\cdot \left(\rho \,{\mathbb{K}}\rho \right)=\frac{1}{2}{\sigma }^{2}(t){\Delta }_{{\bf{x}}}\rho$ with ${\mathbb{K}}\rho ({\bf{x}},t):={\int}_{{{\mathbb{R}}}^{G}}{\bf{K}}({\bf{x}},{\bf{y}})\rho ({\bf{y}},t){\rm{d}}{\bf{y}}$.

In the context of the mean-field SB, one also seeks for a velocity field b(x, t) that drives the continuity equation

$${\partial }_{t}\rho +{\nabla }_{{\bf{x}}}\cdot \left[\rho \,({\bf{b}}+{\mathbb{K}}\rho )\right]=\frac{1}{2}{\sigma }^{2}(t){\Delta }_{{\bf{x}}}\rho$$

(11)

between the prescribed marginals ν₀ and ν₁. Here one chooses the reference process as the mean-field Mckean-Vlasov dynamics instead of the Brownian motion in Section. By incorporating a prescribed interaction kernel k(x, y) which modulates how strongly position y influences position x (e.g., nearest neighbor kernel or Gaussian kernel) in (11), one can approximate the interaction kernel K by taking the ansatz K(x, y) = − k(x, y) ∇_xV(x − y), where V is a scalar interaction potential to be learned. Among all velocity fields b, one that minimizes the action functional, which is exactly Eq. (2) in the dynamical OT, is selected.

Optimizers of this MFSB problem characterize the most probable collective evolution of an interacting cellular population that is consistent with the observed initial and final statistics.

Unbalanced Mean-Field Schrödinger Bridge (UMFSB)

To simultaneously account for (i) collective cell-cell interactions, (ii) stochastic single-cell dynamics, and (iii) unbalanced mass changes driven by proliferation and death, the Mean-Field SB is unified with the regularized unbalanced optimal transport framework, resulting in the UMFSB model⁵⁴. This model seeks the most-probable collective evolution point clouds of dynamically interacting cells between observed snapshots whose total mass may differ. Formally, UMFSB is a variational problem.

$${{\mathcal{L}}}_{{\rm{UMFSB}}}(\rho ,{\bf{b}},g,{\bf{K}}):={\int_{0}^{1}}{\int_{{\mathbb{{R}^{G}}}}}\left[\frac{1}{2}\Vert{\bf{b}}({\bf{x}},t){\Vert}^{2}+\alpha \,\Psi \left(g({\bf{x}},t)\right)\right]\rho ({\bf{x}},t)\,{\rm{d}}{\bf{x}}\,{\rm{d}}t$$

(12)

subject to the Fokker-Planck equation of McKean-Vlasov process

$${\partial }_{t}\rho +{\nabla }_{{\bf{x}}}\cdot \left[\rho \,({\bf{b}}+{\mathbb{K}}\rho )\right]=\frac{1}{2}{\sigma }^{2}(t){\Delta }_{{\bf{x}}}\rho +g\rho ,\qquad \rho (\cdot ,0)={\nu }_{0},\,\rho (\cdot ,1)={\nu }_{1},$$

where ${\mathbb{K}}\rho ({\bf{x}}):={\int}_{{{\mathbb{R}}}^{G}}{\bf{K}}({\bf{x}},{\bf{y}})\rho ({\bf{y}},t){\rm{d}}{\bf{y}}$, $\Psi :{\mathbb{R}}\to [0,\infty ]$ is a convex penalty, typically Ψ(g) = g² that regulates mass deviations, and α > 0 balances transport energy against growth cost. In the limit σ → 0 with Ψ(g) = g² UMFSB reduces to unbalanced dynamic optimal transport; with g ≡ 0 and Ψ(g) = + ∞ unless g = 0 it becomes the Mean-Field SB; and when both σ → 0 and g ≡ 0 classical optimal transport with interaction is recovered.

Using the UMFSB framework,⁵⁴ reveals the interaction force that draws transcriptionally similar cells closer together in mouse hematopoiesis data. Especially compared the single-cell drift b with the interaction force ${\mathbb{K}}\rho$, the correlation shows a clear time-dependence: early in the time-course the attraction nudges progenitors toward differentiation, whereas later it restrains them from completing terminal stage. These results show both the necessity of embedding cell-cell interactions in dynamic models and the model’s capacity to learn those interactions directly from data.

Gromov-Wasserstein Optimal Transport (GWOT)

GWOT provides a principled way to compare or align two populations of cells, even when they are measured in entirely different feature spaces or different biological samples across time points^36,85,86,87. In essence, GW transport asks how one cellular population could be “morphed” into another while preserving the internal relationships between cells, rather than depending on shared coordinates or matched features. This flexibility makes GW particularly appealing for single-cell biology, where distinct experimental conditions, temporal points, modalities, or technologies often produce data embedded in incompatible measurement spaces. By contrast, classical optimal transport (OT) assumes that both datasets lie in the same coordinate system and directly penalizes the cost of moving cellular mass from one point to another in that shared space.

In the GWOT formulation one posits two discrete metric-measure spaces ${{\mathcal{X}}}_{0}=({{\bf{X}}}_{{\bf{0}}},{d}_{{{\bf{x}}}_{{\bf{0}}}},{\nu }_{0})$ and ${{\mathcal{X}}}_{1}=({{\bf{X}}}_{{\bf{1}}},{d}_{{{\bf{x}}}_{{\bf{1}}}},{\nu }_{1})$. Here ${{\mathcal{X}}}_{0}$ and ${{\mathcal{X}}}_{1}$ are finite sets of cells, ${d}_{{{\bf{x}}}_{{\bf{0}}}}$ and ${d}_{{{\bf{x}}}_{{\bf{1}}}}$ are intrinsic distance matrices (they might be Euclidean, diffusion, or correlation distances), and ν₀, ν₁ are probability vectors that weight each cell, possibly reflecting sequencing depth or prior knowledge. The GW problem seeks a coupling matrix ${\boldsymbol{\pi }}\in {{\mathbb{R}}}_{\ge 0}^{N\times M}$ whose marginals recover the prescribed masses and that minimizes the total structural distortion

$${{\mathcal{L}}}_{GW}({\boldsymbol{\pi }})=\sum _{i,j,k,\ell }{\left\vert {d}_{{{\bf{X}}}_{{\bf{0}}}}\left({{\bf{x}}}_{i}^{0},{{\bf{x}}}_{k}^{0}\right)-{d}_{{{\bf{X}}}_{{\bf{1}}}}\left({{\bf{x}}}_{j}^{1},{{\bf{x}}}_{\ell }^{1}\right)\right\vert }^{p}\,{\pi }_{ij}{\pi }_{k\ell },$$

(13)

Intuitively, whenever cells ${{\bf{x}}}_{i}^{0}$ and ${{\bf{x}}}_{k}^{0}$ are far apart in their own geometry, the cells ${{\bf{x}}}_{j}^{1}$ and ${{\bf{x}}}_{\ell }^{1}$ to which they are coupled should be far apart in the second geometry, and vice-versa. The exponent p (usually p = 2) controls the sensitivity to large mismatches. The resulting matrix π can be read as a soft many-to-many assignment, producing lineage-like correspondences across experiments without any gene-wise alignment.

Using a fused GWOT framework, MOSCOT³⁶ reconstructed spatiotemporal organogenesis trajectories in mouse embryogenesis especially for the heart and brain region, mapping how cells migrate, differentiate, and reorganize across both position and developmental stages.

Rigid Body Transformation Invariant Optimal Transport (RBTI-OT) and Spatiotemporal Dynamics Learning (stVCR)

In contrast to the GW framework, which preserves relational structures without imposing explicit alignment of the underlying spaces, rigid body transformation invariant optimal transport (RBTI-OT)⁸⁸ explicitly models the deformation between the two measure spaces as a rigid body transformation, comprising only rotations and translations, to unify them into a common coordinate system. This approach is particularly suited to scenarios like aligning ST data across time points, where differences in the measurement spaces of the data are assumed to be alignable solely through rigid body transformations, enabling direct comparison in a shared Euclidean space rather than relying on intrinsic distances alone⁸⁹. Formally, given two discrete spaces ${{\mathcal{X}}}_{0}=({{\bf{Z}}}_{{\bf{0}}},{\nu }_{0})$ and ${{\mathcal{X}}}_{1}=({{\bf{Z}}}_{{\bf{1}}},{\nu }_{1})$, where Z₀ and Z₁ are sets of points in potentially misaligned coordinate systems (Z is the coordinate variable in ST), RBTI-OT seeks a coupling matrix ${\boldsymbol{\pi }}\in {{\mathbb{R}}}_{\ge 0}^{N\times M}$ with marginals matching ν₀ and ν₁, along with an optimal transformation G = (R, r) from the set ${\mathcal{G}}$ of rotations R and translations r, minimizing the total transportation cost

$$({{\boldsymbol{\pi }}}^{\star },{G}^{\star})=\mathop{{\rm{arg}}\,{\min}}\limits_{G\in {\mathcal{G}},{\boldsymbol{\pi }}}\langle C(G),{\boldsymbol{\pi }}\rangle \mathop{=}\limits^{{\rm{def.}}}\mathop{\sum }\limits_{i=1}^{M}\mathop{\sum }\limits_{j=1}^{N}{\pi }_{ij}{\left\Vert {{\boldsymbol{z}}}_{0,i}-G({{\boldsymbol{z}}}_{1,j})\right\Vert }_{2}^{2},$$

(14)

where G(z_j): = Rz_j + r. Both RBTI-OT and GW are designed for data in distinct measurement spaces, dispensing with the need for shared features or coordinates in classical OT; however, RBTI-OT’s explicit parameterization of ${\mathcal{G}}$ as rigid motions allows for recovery of the transformation itself, whereas GW achieves flexibility through relational invariance but at a higher computational cost due to its quartic objective and lack of coordinate unification. The problem is solved via alternating minimization: first updating π as a static OT problem with fixed G, then solving for G as a weighted Procrustes alignment⁹⁰ given π. Extensions to affine transformations or other constrained deformations are straightforward, and entropic regularization can be similarly applied to smooth the optimization. Finally, since RBTI-OT unifies the distributions into a common space, it becomes easier to extend it to the dynamic OT framework. Formally, we minimize

$${{\mathcal{L}}}_{{\rm{RBTI}}\text{-}{\rm{OT}}}(\rho ,{\bf{b}},G):=\mathop{\int}\nolimits_{0}^{1}{\int}_{{{\mathbb{R}}}^{G}}\frac{1}{2}\parallel {\bf{b}}({\bf{z}},t){\parallel }^{2}\,\rho ({\bf{z}},t)\,{\rm{d}}{\bf{z}}\,{\rm{d}}t$$

(15)

subject to

$$\begin{array}{l}{\partial }_{t}\rho ({\bf{z}},t)+{\nabla }_{{\bf{z}}}\cdot ({\bf{b}}({\bf{z}},t)\rho ({\bf{z}},t))=0\quad \forall t\in [0,1],\\\rho (\cdot ,0)={\nu }_{0},\quad \rho (\cdot ,1)=G({\nu }_{1}),\quad G\in {\mathcal{G}}.\end{array}$$

An application of this dynamic RBTI-OT is the spatiotemporal Video Cassette Recorder (stVCR) framework⁸⁹, which reconstructs cell differentiation, migration, and proliferation/apoptosis from time-series ST data that jointly measure gene expression ${\{{{\bf{X}}}_{i}\}}_{i = 0}^{K}$ and spatial coordinates ${\{{{\bf{Z}}}_{i}\}}_{i = 0}^{K}$. In stVCR, the authors solve a minimization problem with the cost

$${{\mathcal{L}}}_{{\rm{stV}}\;{\rm{CR}}}\left(\rho ,{\bf{b}},{\bf{g}},{\{{G}_{i}\}}_{i = 1}^{K}\right):={\int_{0}^{{t}_{K}}}{\int_{{{\mathbb{R}}}^{G+{d}_{s}}}}\,\,\frac{1}{2}\left[\Vert{{\bf{b}}}_{{\bf{x}}}{\Vert}^{2}+{\tau }_{1}\Vert {{\bf{b}}}_{{\bf{z}}}{\Vert}^{2}+{\tau }_{2}{g}^{2}\right]\rho \,{\rm{d}}{\bf{x}}\,{\rm{d}}{\bf{z}}\,{\rm{d}}t$$

(16)

subject to

$$\begin{array}{l}{\partial }_{t}\rho ({\bf{x}},{\bf{z}},t)+\nabla \cdot \left(\left({{\bf{b}}}_{{\bf{x}}}({\bf{x}},{\bf{z}},t),{{\bf{b}}}_{{\bf{z}}}({\bf{x}},{\bf{z}},t)\right)\rho ({\bf{x}},{\bf{z}},t)\right)=g({\bf{x}},{\bf{z}},t)\rho ({\bf{x}},{\bf{z}},t),\,\forall t\in [0,1],\\\qquad\qquad\rho (\cdot ,0)={\nu }_{0},\quad \rho (\cdot ,{t}_{i})={G}^{i}({\nu }_{i}),\quad {G}^{i}\in {\mathcal{G}}.\end{array}$$

where b = (b_x, b_z) characterizes the migration velocity in coordinate space and gene space, respectively. In addition, stVCR incorporates optional biological priors, including known cell-type transitions and spatial structure-preserving priors. These priors are introduced as constraints on the reconstruction dynamics, effectively guiding the model based on established biological knowledge. In scenarios with sparsely sampled time-point data, the inclusion of such biological priors is indispensable and significantly enhances the accuracy of the dynamical reconstruction.

stVCR has been applied to reconstruct the continuous spatiotemporal dynamics of brain regeneration in the Mexican axolotl following injury⁹¹. It has also been used to model the 3D development of Drosophila embryos and organs, particularly the central nervous system and midgut, capturing the spatiotemporal dynamics from 7 to 10 hours post-fertilization^92,93, especailly at unseen time points. These applications demonstrate stVCR’s ability to recover complex biological processes with high temporal and spatial resolution, providing insights into tissue regeneration and organogenesis.

Algorithms implementation

In this section, we summarize the existing trajectory inference algorithms that are implemented based on the mathematical theories described above (Fig. 2B, Table 2). Often, these methods aim to learn the “optimal" mapping from one distribution to another, which can be induced by point-to-point correspondences or continuous flows within the data space, and is determined by the form of the “action" defined for the cell state-transition process. We categorize these trajectory inference methods based on three characteristics: Data Assumption, Modeling Strategy, and Training Methods.

Table 2 A comparative table of algorithms for modeling spatiotemporal scRNA-seq Data

Data assumption

Different trajectory inference methods rely on distinct assumptions about the input data, reflecting diverse types of biological priors. For example, several methods propose considering the effects of cell division and death, which lead to an unnormalized total mass in the distribution (Unbalanced Data). In such cases, one assumes that the distribution follows an unbalanced Fokker-Planck equation and uses the static unbalanced OT distance or the WFR distance as the action (Eq. (3), Eq. (8)). Typical methods that adopt the Unbalanced Data Assumption include TIGON⁶⁷, DeepRUOT⁵¹, and stVCR⁸⁹.

In scRNA-seq data, the gene expression count numbers are inherently discrete, typically following count distributions such as the Poisson or negative binomial (Count Data). As a result, data points cannot evolve continuously within the data space. To nevertheless capture the continuous evolution of the continuous cell fates, one approach is to model the dynamics of a parameterized probability measure and employ the geodesic distance, e.g., defined via the Fisher information metric on a finite-dimensional statistical manifold as the action functional, and then adopt the least action method to calculate the transitional paths. For instance, Euclidean VAE⁹⁴ adopts the idea by assuming that the VAE’s decoder is a smooth mapping from the latent space to the probability measure manifold, and directly considering the evolution trajectory in the latent space.

Most computational methods assume that data reside in a Euclidean space; however, scRNA-seq data are often governed by intrinsic biological structures and thus are better represented as lying on a low-dimensional manifold (Low-Dim Manifold). For example, although gene expression measurements are collected in a G-dimensional gene space, cellular states typically occupy only a restricted region determined by regulatory programs, developmental lineages, or other biological constraints⁹⁵. Consequently, the effective dimensionality of the data is substantially much lower than G. Methods like MIOFlow⁹⁶ and Metric FM⁹⁷ exploit the low-dimensional manifold structure underlying the data and perform geodesic interpolation in this manifold rather than in Euclidean space. Wasserstein Lane-Riesenfeld (WLR) algorithm⁹⁸ approximates B-spline curves in the Wasserstein space through iterative averaging of geodesics. In the meantime, methods such as Topological SB⁹⁹ treat each dimension of the data vector as a feature on the vertices of an undirected graph, thus designating the diffusion on the graph as the reference process in the SB problem.

At times, the data points analyzed are sampled from different modalities (e.g., transcriptomic, proteomic, or morphological measurements) or from distinct biological systems (e.g., samples collected across individuals, tissues, or developmental time points) with different metric spaces (Cross-Domain Mapping), making the optimal transport problem directly on these data points not well defined. A typical theory used for analyzing and processing such cross-space data is GWOT (Eq. (13)), which computes a transport plan using the geodesic distance between data points on each manifold, therefore assessing the similarity of the two manifolds’ geometric structures. Building on this framework, methods such as MOSCOT³⁶, GENOT¹⁰⁰, and SCOT+¹⁰¹ apply GWOT theory to address multi-modal and cross-system integration challenges in trajectory inference tasks.

In single-cell omics, a special type of data is ST data, which includes not only gene expression counts within cells but also the physical spatial location information of each cell (Spatial Data). Methods like stVCR⁸⁹, Dest-OT¹⁰² and STORIES¹⁰³ are specifically designed to handle such data. Both DeST-OT and STORIES adopt Fused Gromov-Wasserstein OT (FGWOT) to model ST across time. More specifically, DeST-OT incorporates cell proliferation by employing semi-unbalanced OT within the static OT framework, while STORIES directly uses FGWOT as the loss function to reconstruct gene expression dynamics. Instead of using GWOT-related theory, stVCR applies RBTI-OT to model spatial coordinates, which makes it possible to simultaneously reconstruct cell differentiation, migration, and proliferation dynamics in a continuous setting. Besides, other related applications for spatiotemporal data have also been developed. For example, PASTE¹⁰⁴ and PASTE2¹⁰⁵ align adjacent tissue slices by employing the Gromov-Wasserstein OT framework. CODA¹⁰⁶ uses an image registration-based approach to align histological images and reconstruct 3D tissues from serial sections. Furthermore, other methods focus on inferring spatial locations for scRNA-seq data; for example, STALocator¹⁰⁷ uses a supervised auto-encoder to localize single cells onto ST data, while iSORT¹⁰⁸ maps gene expressions to spatial locations via transfer learning.

Lastly, in perturbation studies, the gene expression matrices are often accompanied by categorical labels or other experimental conditions (e.g., treatment type, dosage, or time point), which needs to be explicitly incorporated during training or inference (Conditional Modeling). Methods such as CFGen¹⁰⁹ and CellFlow¹¹⁰ enable the generation of cell states under specified perturbations, while MMFM¹¹¹ extends trajectory inference frameworks to account for conditional information.

Modeling strategy

Trajectory inference methods also differ in the dynamical models they adopt, which could be formulated in either discrete or continuous time and space. The choice of dynamical model specifies the underlying structure of the governing equations, while the inference procedure estimates the unknown components (typically time-dependent scalar or vector fields). When the continuous temporal evolution of the distribution is not of primary interest, one may instead employ discrete-time dynamics, focusing on the mapping of cell states observed at an initial time point to those at a subsequent one (Eq. (1)). Methods such as Waddington OT³⁵, MOSCOT³⁶ and Multistage OT¹¹² adopt this setting. In particular, optimal transport between Gaussian mixtures admits an analytical solution, which scEGOT¹¹³ takes advantage of. Moreover, OTVelo¹¹⁴ attempts to estimate RNA Velocity using the solution of discrete OT. Discrete OT also has several variants. For example, HM-OT¹¹⁵ can handle partially observed data by learning a latent representation for each data point and determining the transition matrix in the latent representation. By harmonizing discrete and continuous-time modeling, the CT-OT Flow method¹¹⁶ estimates finer-grained time labels from the data, and then proceeds to solve the OT problem and reconstruct the continuous ODE/SDE dynamics.

In practice, cellular processes are subject to numerous unobserved perturbations and intrinsic variability, and coarse-graining of underlying deterministic dynamics naturally gives rise to stochastic dynamics. A principled framework for inferring such stochastic dynamics is provided by the SB (Eq. (4), Eq. (5), Eq. (6)). This formulation augments single-particle dynamics with a Brownian motion term and introduces a diffusion term into the corresponding Fokker-Planck equation, while retaining an action functional equivalent to that of Dynamical Optimal Transport. Methods like SB between Gaussian¹¹⁷, SF²M⁷⁷, PISDE¹¹⁸, FBSDE Model¹¹⁹, Probability Flow Inference¹²⁰ and Likelihood Training SB¹²¹ discuss various solutions for the SB problem. Among them, SB between Gaussian provides an analytical solution for cases with Gaussian Mixture marginal distributions; Likelihood Training SB mimics the Likelihood Training in score matching to offer a framework for solving the SB problem. Several methods are proposed solve more generalized SB problems. For example, Lagrangian SB¹²² allows for solving the evolution of particle distributions in any given potential field; mvOU-OTFM¹²³ sets the reference process of the SB to an OU process; and Smooth SB¹²⁴ adopts a smooth Gaussian process as the reference process. In order to handle branching data for improved downstream tasks such as cell fate prediction, Branched SB¹²⁵ matches a single initial distribution to multiple terminal distributions with unequal weights. Moreover, to simultaneously address the previously mentioned Unbalanced Distribution and Stochastic Dynamics, Pseudo Dynamics¹²⁶ uses the Fokker-Planck equation with diffusion and non-equilibrium terms, and employs maximum likelihood estimation to determine the parameters; Unbalanced Diffusion SB¹²⁷ proposes a SB that incorporates growth and death; ARTEMIS¹²⁸ solves such a SB in the latent space of a VAE, further enhancing the model’s expressive capacity ; DeepRUOT⁵¹ adopts the RUOT framework (Eq. (7), Eq. (8)), where the Fokker-Planck equation includes both diffusion and unbalanced terms, using the WFR Distance as the action.

Compared to the commonly used first-order dynamical frameworks, incorporating momentum dynamics allows modeling of more complex cellular processes, where the history or “inertia” of transcriptional changes influences future cell states. Methods such as 3MSBM¹²⁹ explicitly account for this effect. Moreover, many existing approaches assume that cells evolve independently; however, in biological systems this assumption is often violated. Cell-cell interaction dynamics arising from processes such as ligand-receptor signaling or cell-cell contact can play a central role in shaping cell-fate trajectories. To address this, methods including MetaFM¹³⁰, scIMF⁵⁵, GraphFP¹³¹, and CytoBridge⁵⁴ incorporate intercellular interactions into trajectory inference.

Training methods

Trajectory inference methods also differ in their training paradigms. A foundational class of approaches builds on the Neural ODE framework^132,133. For instance, TrajectoryNet⁶⁵ and scNODE¹³⁴ approximate population dynamics by evolving an empirical particle system, where velocity fields are parameterized by neural networks to capture the underlying transcriptional dynamics. The associated action functional and distribution-matching error can be computed from this neural ODE formulation and incorporated into the loss function for backpropagation-based training. A recent alternative, Cell-MNN¹³⁵, learns a locally linearized ODE representation of dynamics by predicting the system’s linear operator. To further address the challenge of highly unbalanced cell state distributions, TIGON⁶⁷ employs a weighted particle system by additionally parameterizing growth rate to approximate the evolution of both cellular mass and densities. To solve stochastic dynamics, PISDE¹¹⁸ and Var-RUOT⁴⁸ also adopt the neural SDE methods¹³⁶.

However, neural ODE or SDE-based methods require iterative numerical integration of continuous dynamics during training, which leads to computational overhead. As a result, their scalability is limited when applied to high-dimensional gene expression spaces or large-scale single-cell datasets. In response, a series of simulation-free training methods exemplified by Conditional Flow Matching^39,40,137 have emerged. These methods are typically designed based on analytical solutions for simple cases (for instance, mapping a Dirac distribution to another Dirac distribution), allowing for the direct estimation of the target scalar or vector fields without simulating ODEs. SF²M⁷⁷ employs the Flow Matching method to solve the SB problem; Score-Based NF¹³⁸ uses the Flow Matching method to solve the velocity field of the PF-ODE in Score Matching; Unbalanced Monge Map¹³⁹ and VGFM⁴¹ combine Unbalanced Optimal Transport with Flow Matching. In particular, VGFM can simultaneously learn v and g in the Unbalanced Dynamical Optimal Transport framework to address Unbalanced Distribution. Curly FM¹⁴⁰ is capable of learning non-gradient velocity fields, while Metric FM⁹⁷ first estimates geodesics on a low-dimensional manifold and then performs geodesic interpolation. Furthermore, Wasserstein FM¹⁴¹ performs interpolation directly in the space of probability measures and has proven to be effective in generating high-dimensional distributions; MMSFM¹⁴² allows the connection of data between time points via multi-marginal SB.

Furthermore, the first-order optimality conditions for optimal transport and its variants can be derived via variational principles (Eq. (9) and Eq. (10)), providing the foundation for designing efficient computational algorithms. PRESCIENT¹⁴³,Action Matching¹⁴⁴ and PISDE¹¹⁸ constrain the dynamic search space to the set of gradients of a scalar field, where the HJB equation is enforced as a loss term in PISDE. Wasserstein Lagrangian Flow¹⁴⁵ solves optimal transport and its variants by fitting covariant vectors on the probability measure manifold along with parameterized probability measures. GraphFP¹³¹ designs a gradient descent method based on the Pontryagin Maximum Principle for solving optimal control laws. HJ-Sampler¹⁴⁶ employs the Cole-Hopf transformation to convert the nonlinear problem into a tractable linear or semi-linear form, then derives the control law by solving the HJB equation, ultimately obtaining the posterior distribution of the data. Recently, Var-RUOT⁴⁸ further demonstrated that it is sufficient to solve the RUOT problem by merely parametrizing a single scalar function based on the HJB framework.

Practical guidelines

To help researchers utilize the proposed Spatiotemporal Dynamical Generative Model (stDGM) framework, here we outline the guidelines for applying dynamical generative modeling tools, covering the entire workflow from data input to biological discovery, as summarized in Fig. 3. Specifically, to put these principles into practice, we are actively developing CytoBridge, a Python package that integrates this entire workflow, and we invite contributions from the community to help shape its future. Below we describe the design philosophy and the workflow of applying the CytoBridge into spatiotemporal omics data analysis. We also provide a case study in Box 1 to demonstrate the stDGM workflow using CytoBridge.

Fig. 3: A practical workflow for Spatiotemporal Dynamical Generative Model (stDGM) analysis.

The analysis pipeline starts with data preprocessing. Following preprocessing, a suitable model is configured by selecting from four primary components offered by the CytoBridge package: velocity for cell differentiation, growth for cell proliferation, score for stochasticity, and interaction for cell-cell communication. Different combinations of these components correspond to distinct theoretical frameworks and enable specific downstream analyses.

Box 1A Demo for stDGM Analysis with CytoBridge

This box provides a practical guide to using the CytoBridge Python package for analyzing time-series single-cell data, corresponding to the workflow outlined in Fig. 3. We use a mouse hematopoiesis dataset¹⁶³ as a conceptual example to demonstrate how to perform the stDGM analysis. This dataset combines time-series single-cell RNA-sequencing with barcoding to link the initial transcriptomic states of mouse hematopoietic progenitors to their clonal fates after differentiation, which contains 49,302 cells with lineage tracing information collected at three time points.

Steps

1. Data Loading and Preprocessing

The first step is to load the data into an AnnData object. We then use the built-in CytoBridge preprocessing function, which handles normalization, highly variable genes selection, and dimensionality reduction. In the following example code, the dimensions are reduced to 50 using PCA. The parameter time_key='Time' specifies the column name in adata.obs that contains the sampling time for each cell. dim_reduction='PCA' specifies the method for dimensionality reduction. The processed features will be stored in adata.obsm['X_latent'] for model training.

adata = scanpy.read_h5ad("mouse_hematopoiesis_data.h5ad")

cytobridge.pp.preprocess(adata,time_key='Time',dim_reduction='PCA')

2. Model Configuration and Training

Next, we select a model from the stDGM framework and train it. This is done through the cytobridge.tl.fit function, where the config parameter allows the user to choose the appropriate theoretical model based on their biological assumptions. For the mouse hematopoiesis dataset, the study’s protocol involves culturing progenitor cells and sampling them at days 2, 4, and 6, with cells being replated after the initial time point to allow for continued proliferation and differentiation. This ensures that the observed increase in cell numbers is a direct result of biological growth, a dynamic that the unbalanced framework is specifically designed to model. Thus, we choose the Dynamical Unbalanced OT framework for stDGM analysis.

cytobridge.tl.fit(adata, config='unbalanced_ot')

The trained dynamical model is stored back into adata.uns, which can be conveniently loaded for later downstream analysis.

3. Downstream Analysis and Visualization

The basic downstream analysis at this stage is the visualization of learned velocity and growth rate of cells from the original dataset. These quantities can be calculated by loading the previously trained model using functions from the cytobridge.tl.analysis module.

cytobridge.tl.analysis.compute_velocity(adata)

cytobridge.tl.analysis.compute_growth(adata)

The calculated velocity and growth rate will be automatically stored in adata.obsm['velocity_latent'] and adata.obsm['growth_rate'], which can be subsequently plotted on UMAP coordinates. For the mouse hematopoiesis dataset, the velocity streamline plot (Fig. 1a) clearly shows distinct differentiation trajectories, which is in line with different cell fates. The predicted growth rate (Fig. 1c) can also be validated by comparing with lineage information from the dataset⁶⁷. Specifically, regions predicted to have higher growth rates correspond to undifferentiated progenitor cells, which are expected to produce larger clones as identified by shared barcodes at later time points. Given the calculated velocity and growth rates, more advanced downstream analysis can be conducted by combining these quantities with scVelo and CellRank.

4. Trajectory Generation

To reconstruct entire cell-trajectory sequences, we have implemented generative and visualization routines in cytobridge.tl.analysis and CytoBridge.pl.plot.

cytoBridge.tl.generate_ode_trajectories(adata=adata)

cytoBridge.pl.plot_ode_trajectories(adata)

These routines simulate and visualize multi-step trajectories under a dynamical model driven by velocity and growth in this case study, thereby preserving the full continuity of cell-state transitions (Fig. 4). These generated trajectories provide a dynamic visualization of differentiation in the mouse hematopoiesis dataset, detailing the continuous process of cells moving from their initial progenitor states toward diverse lineage-specific fates. Notably, generate_ode_trajectories reads the instantaneous growth rate, assigns each cell a weight. The weight change ratio r guides decisions: cells with r > 1 probabilistically generate descendant cells, while those with r < 1 are retained or eliminated based on random sampling. This logic accurately simulates the probabilistic division and death of cells in the mouse hematopoiesis system (Fig. 4).

Data preprocessing

stDGM is primarily applied to temporally-resolved scRNA-seq data or spatial-transcriptomic data. The required input is a gene expression matrix accompanied by metadata for each cell, crucially specifying its sampling time point, and spatial coordinates if available. The initial step, data preprocessing, is essential for minimizing technical noise. This process involves normalizing the gene expression data to correct for library size variations, and aligning spatial coordinates across different time points. Then, feature selection of highly variable genes is utilized to isolate signals driving cellular change¹⁴⁷. Subsequently, the gene expression data is projected into a low-dimensional space. Methods like PCA and AutoEncoders are recommended because they are reversible, they allow vectors to be projected from the reduced space back to the original gene expression space. This property is vital for enabling the downstream analysis of specific genes and pathways. Generally, this projected space should be kept below 100 dimensions, as higher dimensionality can obscure the key factors driving cell differentiation. These preprocessing steps can be carried out using CytoBridge, as shown in Step 1 of Box 1.

Tools selection

With a clean and properly structured dataset in hand, the core analysis begins: applying and configuring the dynamical models. These methods reconstruct trajectories from discrete time-point snapshots by using neural networks to model the driving factors of cellular state changes. The CytoBridge package supports four primary modeling components: velocity network, growth network, score network, and interaction network. Each of these components corresponds to a specific stDGM-based framework. Then, a crucial step is selecting the appropriate dynamical model, a choice guided by the biological assumptions one makes about the system.

The first consideration is the cell growth term. If changes in the number of cells across time points are not significant, or due to technical sampling artifacts, or not of biological interest, a standard dynamical OT formulation focused only on matching probability distributions can be applied. Representative methods include MioFlow⁹⁶ or OT-CFM⁴⁰. However, users still need to be cautious of the false-positive transitions incurred by unbalanced sample sizes^35,51,67 and certain resampling strategies could be considered. Indeed, if population size changes are significant, or reflect genuine biological processes like development, including the growth term is recommended to gain deeper insights and more accurate inference. This places the analysis within the unbalanced optimal transport framework, often requiring an additional neural network to model growth, as implemented in tools like TIGON⁶⁷ and the recently proposed simulation-free method VGFM⁴¹. In such methods, velocity and growth networks are used to simultaneously match both the distribution and the number of cells across different time points. An example of leveraging the dynamical unbalanced OT framework can be found in Step 2 of Box 1.

A second consideration is stochasticity. To capture the inherent randomness of biological processes, the problem can be framed as a SB Problem if the growth term is not considered. This can be addressed by directly simulating neural SDE with methods like PI-SDE¹¹⁸, or by augmenting a deterministic velocity field with a score-matching network to model probability densities, as seen in SF²M⁷⁷. For systems exhibiting both unbalanced growth and stochasticity, Regularized Unbalanced Optimal Transport (RUOT) frameworks, implemented in methods like DeepRUOT⁵¹ and Var-RUOT⁴⁸, are appropriate.

Most recently, the scope of modeling has expanded to include cell-cell interactions through the newly proposed Unbalanced Mean Field Schrödinger Bridge (UMFSB) problem⁵⁴. The UMFSB framework can simultaneously infer interactions, growth, and stochastic effects. Built upon this theory, the CytoBridge package is aimed at serving as a unified toolkit. It enables users to selectively deactivate the interaction, growth, or stochastic terms, thereby tailoring the analysis precisely to their specific dataset and biological questions.

Downstream analysis

The next stage of the workflow is the downstream analysis and interpretation. Visualization is often the first step, where the inferred velocity can be projected onto a low-dimensional embedding like a UMAP¹⁴⁸. This provides an intuitive view of the developmental flow and the major predicted lineage paths (Fig. 1C (a)). Moreover, the growth network, if available, can reveal the specific cell types that exhibit higher growth rates (Fig. 1C (c)). The score network identifies high-density regions corresponding to stable cell fates, which are analogous to the valleys in the Waddington epigenetic landscape^{4,51,149,150,151,152,153,154,155,156,157,158} (Fig. 1C (d)). The usage of basic visualization using CytoBridge can be found in Step 3 of Box 1. Beyond visualization, the trained neural networks are interpretable models that enable powerful quantitative analysis. The learned velocity field, for instance, can be used to infer Gene Regulatory Networks (GRNs) by computing its Jacobian⁶⁷ (Fig. 1C (f)). Similarly, the gradient of the growth network can identify key genes driving cell proliferation. This principle extends to models that include cell-cell interactions. Methods modeling cellular interactions can distinguish a cell’s intrinsic differentiation drive from the influence of intercellular communication. By analyzing the properties of the interaction forces, it’s possible to identify which genes are most responsive to neighborly signaling and to characterize the nature of the interactions themselves by calculating the spatial autocorrelation of the similarity of interacting forces to the intrinsic drift⁵⁴. For these analyses, the results from the low-dimensional space can be projected back to the original gene space to ensure biological interpretability. The lists of high-impact genes generated from these different analyses, whether they are GRN hubs, proliferation drivers, or interaction targets, can be subjected to Gene Set Enrichment Analysis¹⁵⁹. This step connects the individual genes to the broader biological pathways and functions they collectively represent, completing the bridge from data to mechanistic insights. Thus, in-silico perturbations to specific driver genes can be applied in a straightforward way. It is also noteworthy that the overall drift, which integrates velocity, score, and interaction terms if available, provides a comprehensive representation of cellular dynamics. This drift is compatible with other downstream analysis tools such as scVelo³⁴, and thus can be used to compute a cell-to-cell transition matrix and velocity graph. The constructed graph can be subsequently applied to CellRank¹⁶⁰ to infer fate probabilities or driver genes (Fig. 1C (e)). The seamless integration of these stDGM methods with the broader ecosystem of downstream analysis tools opens the door to a wider array of analytical possibilities.

Trajectory generation

A fundamental advantage of the stDGM methods discussed here, distinguishing them from static methods, is their formulation as generative models. This generative capability allows one to simulate entire cellular trajectories forward in time from an initial population distribution. Consequently, these models can not only reconstruct the observed cell distributions at discrete time points but also interpolate to predict cell states at previously unobserved times (Fig. 1C (b)). Therefore, a final step in the workflow focuses on this trajectory reconstruction. Once trajectories are built, they provide an explicit mapping of an individual cell’s fate, revealing which cell state evolves into another. This enables the direct analysis of how cell types transition along a lineage. To achieve this, a cell annotation step is typically required, where a classifier is trained to predict a cell’s type from its gene expression vector. By applying these labels to the simulated trajectories, a complete lineage fate map can be constructed, offering interpretability into the underlying biological mechanisms of development and differentiation. For example, TrajectoryNet⁶⁵ used the generated trajectory on an embryoid body dataset¹⁶¹ to identify how early the gene expression profiles of cells destined for different fates began to diverge. On the same dataset, MIOFlow⁹⁶ generated and decoded trajectories back to the full gene space to accurately reconstruct complex, non-monotonic expression dynamics for individual genes, which align with known biology. TIGON⁶⁷ interpolated data at unmeasured time points in an epithelial-to-mesenchymal transition (EMT) dataset¹⁶², revealing the changes of cell-cell communication patterns over time. We show CytoBridge’s function of generating trajectories in Step 4 of Box 1, and also visualize the generated trajectory of the mouse hematopoiesis dataset using CytoBridge in Fig. 4.

Fig. 4: Illustration of the dynamical generative function of CytoBridge.

In the mouse hematopoiesis dataset that includes samples from Day 2, Day 4, and Day 6, CytoBridge reconstructs continuous dynamic trajectories to elucidate cellular dynamics. Specifically, based on the initial sampling at Day 2, it generates 100 time-step hypothetical cell trajectories from Day 2 to Day 6, depicted as red lines, with the states for Days 3, 4, 5, and 6 individually highlighted. At every time point, cells that arise from division during the generation interval are shown in orange. These data and figures are produced by calling Cytobrdige fit funciton with the unbalanced mode.

However, there remain several key limitations inherent to current generative models. A primary challenge is temporal generalization. While models may excel at interpolation within the training time ranges, their accuracy often degrades when forecasting far beyond it, as the underlying biological regulatory dynamics may shift. Another potential issue is the sensitivity to initial conditions and sampling noise; errors or biases in the early time point data can be amplified throughout the simulation, leading to divergent and biologically implausible trajectories. Furthermore, generalization across different cell types can be limited; a model trained on specific differentiation pathways may be unable to predict the emergence of a rare or previously unseen cell lineage. Rigorously validating generated trajectories remains a challenge. Experimental lineage tracing, when available, can serve as a standard for confirmation.

Conclusion and future directions

In this review, we have discussed recent progress toward the $\underline{{\bf{s}}}{\rm{patio}}\underline{t}{\rm{emporal}}$ Dynamical Generative Model (stDGM) for single-cell and ST, with a particular emphasis on dissecting cell-fate trajectories from time-series scRNA-seq and spatiotemporal data. We first introduced the mathematical foundations of dynamical systems and generative modeling, including optimal transport and SB foundation formulations, highlighting how these concepts provide a framework for reconstructing and generating cellular dynamics. We then reviewed algorithmic advances that implement these frameworks in practice. Finally, we offered practical guidelines to help researchers select and apply methods to different types of application scenarios. By integrating mathematical principles, computational methods, and biological applications, our aim is to provide a systematic and accessible perspective for the study of cellular dynamics.

Looking forward, an important direction is the integration of richer data modalities, where transcriptomic time series are combined with epigenomic, proteomic, and imaging measurements to provide more comprehensive views of regulatory dynamics. Another promising direction is the incorporation of lineage tracing and clonal recording technologies^{163,164,165,166,167,168}, which will allow computationally inferred trajectories to be validated and refined with experimentally observed ancestry, thus strengthening the biological interpretation of fate decisions. Advances in spatial and temporal resolution will also make it possible to explicitly couple intracellular dynamics with cell-cell interactions^{169,170,171,172,173,174,175} and tissue-level organization. Importantly, integrating studies of cell mechanics will help model cellular morphogenesis in physical space^176,177,178, offering multiscale perspectives on development and disease. Finally, the continued refinement of computational packages into user-friendly and accessible tools will be critical for enabling a broader community of biologists to apply these methods in practice. Together, these developments point toward a future in which dynamical modeling is not only a theoretical framework but also a practical component of experimental biology, deepening our understanding of cellular dynamics in development, regeneration, and pathology.