Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Asynchronous abundance fluctuations can drive giant genotype frequency fluctuations

Nature Ecology & Evolution volume 9, pages 166–179 (2025)Cite this article

Subjects

Abstract

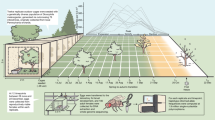
Large stochastic population abundance fluctuations are ubiquitous across the tree of life, impacting the predictability and outcomes of population dynamics. It is generally thought that abundance fluctuations with a Taylor’s law exponent of two do not strongly impact evolution. However, we argue that such abundance fluctuations can lead to substantial genotype frequency fluctuations if different genotypes in a population experience these fluctuations asynchronously. By serially diluting mixtures of two closely related Escherichia coli strains, we show that such asynchrony can occur, leading to giant frequency fluctuations that far exceed expectations from genetic drift. We develop an effective model explaining that the abundance fluctuations arise from correlated offspring numbers between individuals, and the large frequency fluctuations result from (even slight) decoupling in offspring number correlations between genotypes. The model quantitatively predicts the observed abundance and frequency fluctuation scaling. Initially close trajectories diverge exponentially, suggesting that chaotic dynamics may underpin the excess frequency fluctuations. Our findings suggest that decoupling noise is also present in mixed-genotype Saccharomyces cerevisiae populations. Theoretical analyses demonstrate that decoupling noise can strongly influence evolutionary outcomes, in a manner distinct from genetic drift. Given the generic nature of these frequency fluctuations, we expect them to be widespread across biological populations.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on SpringerLink
  • Instant access to the full article PDF.

USD 39.95

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Observation of large genotype frequency fluctuations.
Fig. 2: Model of population fluctuations.
Fig. 3: Within-cycle chaotic dynamics of genotype frequencies.
Fig. 4: Quantifying the relative strength of intrinsic noise, extrinsic noise and the effect of sharing mother cultures.
Fig. 5: Extrinsic and intrinsic decoupling noise found in barcoded S. cerevisiae populations.
Fig. 6: Theoretical evolutionary implications of decoupling noise.

Similar content being viewed by others

Data availability

All data presented in this manuscript are available via GitHub at https://github.com/joaoascensao/giantpopflucts and Zenodo at https://doi.org/10.5281/zenodo.13787815 (ref. 63). All strains presented in this paper are available upon request.

Code availability

All code presented in this manuscript is available via GitHub at https://github.com/joaoascensao/giantpopflucts and Zenodo at https://doi.org/10.5281/zenodo.13787815 (ref. 63).

References

  1. Fisher, R. A. XXI. On the dominance ratio. Proc. R. Soc. Edinb. 42, 321–341 (1923).

    Article  Google Scholar 

  2. Haldane, J. B. S. A mathematical theory of natural and artificial selection, part V: selection and mutation. Math. Proc. Cambridge Philos. Soc. 23, 838–844 (1927).

    Article  Google Scholar 

  3. Kimura, M. On the probability of fixation of mutant genes in a population. Genetics 47, 713–719 (1962).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  4. Uecker, H. & Hermisson, J. On the fixation process of a beneficial mutation in a variable environment. Genetics 188, 915–930 (2011).

    Article  PubMed  PubMed Central  Google Scholar 

  5. Barrick, J. E. & Lenski, R. E. Genome dynamics during experimental evolution. Nat. Rev. Genet. 14, 827–839 (2013).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  6. Kimura, M. Diffusion models in population genetics. J. Appl. Probab. 1, 177–232 (1964).

    Article  Google Scholar 

  7. Ohta, T. Slightly deleterious mutant substitutions in evolution. Nature 246, 96–98 (1973).

    Article  CAS  PubMed  Google Scholar 

  8. Okada, T. & Hallatschek, O. Dynamic sampling bias and overdispersion induced by skewed offspring distributions. Genetics 219, iyab135 (2021).

    Article  PubMed  PubMed Central  Google Scholar 

  9. Kimura, M. Evolutionary rate at the molecular level. Nature 217, 624–626 (1968).

    Article  CAS  PubMed  Google Scholar 

  10. Fisher, R. A. The distribution of gene ratios for rare mutations. Proc. R. Soc. Edinb. 50, 204–219 (1931).

    Article  Google Scholar 

  11. Hallatschek, O. Selection-like biases emerge in population models with recurrent jackpot events. Genetics 210, 1053–1073 (2018).

    Article  PubMed  PubMed Central  Google Scholar 

  12. Anderson, R. M., Gordon, D. M., Crawley, M. J. & Hassell, M. P. Variability in the abundance of animal and plant species. Nature 296, 245–248 (1982).

    Article  Google Scholar 

  13. Taylor, L. R. & Woiwod, I. P. Comparative synoptic dynamics. I. Relationships between inter- and intra-specific spatial and temporal variance/mean population parameters. J. Anim. Ecol. 51, 879–906 (1982).

    Article  Google Scholar 

  14. George, A. B. & O’Dwyer, J. Universal abundance fluctuations across microbial communities, tropical forests, and urban populations. Proc. Natl Acad. Sci. USA 120, e2215832120 (2023).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  15. Taylor, L. R. Aggregation, variance and the mean. Nature 189, 732–735 (1961).

    Article  Google Scholar 

  16. Cobain, M. R. D., Brede, M. & Trueman, C. N. Taylor’s power law captures the effects of environmental variability on community structure: an example from fishes in the North Sea. J. Anim. Ecol. 88, 290–301 (2019).

    Article  PubMed  Google Scholar 

  17. Cohen, J. E. & Xu, M. Random sampling of skewed distributions implies Taylor’s power law of fluctuation scaling. Proc. Natl Acad. Sci. USA 112, 7749–7754 (2015).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  18. Xu, M. Taylor’s power law: before and after 50 years of scientific scrutiny. Preprint at https://doi.org/10.48550/arXiv.1505.02033 (2016).

  19. Eisler, Z., Bartos, I. & Kertész, J. Fluctuation scaling in complex systems: Taylor’s law and beyond. Adv. Phys. 57, 89–142 (2008).

    Article  CAS  Google Scholar 

  20. Melbinger, A. & Vergassola, M. The impact of environmental fluctuations on evolutionary fitness functions. Sci. Rep. 5, 15211 (2015).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  21. Hanski, I. Spatial patterns and movements in coprophagous beetles. Oikos 34, 293–310 (1980).

    Article  Google Scholar 

  22. Perry, J. N. Chaotic dynamics can generate Taylor’s power law. Proc. Biol. Sci. 257, 221–226 (1994).

    Article  Google Scholar 

  23. Ballantyne, F. IV. The upper limit for the exponent of Taylor’s power law is a consequence of deterministic population growth. Evol. Ecol. Rev. 7, 1213–1220 (2005).

  24. Ballantyne, F. IV. & Kerkhoff, J. A. The observed range for temporal mean-variance scaling exponents can be explained by reproductive correlation. Oikos 116, 174–180 (2007).

  25. Ewens, W. J. Mathematical Population Genetics 1: Theoretical Introduction (Springer Science & Business Media, 2004).

  26. Wright, S. Classification of the factors of evolution. Cold Spring Harb. Symp. Quant. Biol. 20, 16–24D (1955).

    Article  CAS  PubMed  Google Scholar 

  27. Buri, P. Gene frequency in small populations of mutant Drosophila. Evolution 10, 367–402 (1956).

    Article  Google Scholar 

  28. Cavalli-Sforza, L. L., Menozzi, P. & Piazza, A.The History and Geography of Human Genes (Princeton Univ. Press, 1994).

  29. Ascensao, J. A., Wetmore, K. M., Good, B. H., Arkin, A. P. & Hallatschek, O. Quantifying the local adaptive landscape of a nascent bacterial community. Nat. Commun. 14, 248 (2023).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  30. Rozen, D. E. & Lenski, R. E. Long-term experimental evolution in Escherichia coli. VIII. Dynamics of a balanced polymorphism. Am. Nat. 155, 24–35 (2000).

    Article  PubMed  Google Scholar 

  31. Rozen, D. E., Schneider, D. & Lenski, R. E. Long-term experimental evolution in Escherichia coli. XIII. Phylogenetic history of a balanced polymorphism. J. Mol. Evol. 61, 171–180 (2005).

    Article  CAS  PubMed  Google Scholar 

  32. Rozen, D. E., Philippe, N., Arjan de Visser, J., Lenski, R. E. & Schneider, D. Death and cannibalism in a seasonal environment facilitate bacterial coexistence. Ecol. Lett. 12, 34–44 (2009).

    Article  PubMed  Google Scholar 

  33. Le Gac, M., Plucain, J., Hindré, T., Lenski, R. E. & Schneider, D. Ecological and evolutionary dynamics of coexisting lineages during a long-term experiment with Escherichia coli. Proc. Natl Acad. Sci. USA 109, 9487–9492 (2012).

    Article  PubMed  PubMed Central  Google Scholar 

  34. Good, B. H., McDonald, M. J., Barrick, J. E., Lenski, R. E. & Desai, M. M. The dynamics of molecular evolution over 60,000 generations. Nature 551, 45–50 (2017).

    Article  PubMed  PubMed Central  Google Scholar 

  35. Plucain, J. et al. Epistasis and allele specificity in the emergence of a stable polymorphism in Escherichia coli. Science 343, 1366–1369 (2014).

    Article  CAS  PubMed  Google Scholar 

  36. Lenski, R. E. Experimental evolution and the dynamics of adaptation and genome evolution in microbial populations. ISME J. 11, 2181–2194 (2017).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  37. Bartlett, M. S. Some notes on insecticide tests in the laboratory and in the field. Supplement to the Journal of the Royal Statistical Society 3, 185 (1936).

    Google Scholar 

  38. Takahata, N., Ishii, K. & Matsuda, H. Effect of temporal fluctuation of selection coefficient on gene frequency in a population. Proc. Natl Acad. Sci. USA 72, 4541–4545 (1975).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  39. Vasi, F., Travisano, M. & Lenski, R. E. Long-term experimental evolution in Escherichia coli. II. Changes in life-history traits during adaptation to a seasonal environment. Am. Nat. 144, 432–456 (1994).

    Article  Google Scholar 

  40. Rocabert, C., Knibbe, C., Consuegra, J., Schneider, D. & Beslon, G. Beware batch culture: seasonality and niche construction predicted to favor bacterial adaptive diversification. PLoS Comput. Biol. 13, e1005459 (2017).

    Article  PubMed  PubMed Central  Google Scholar 

  41. Ascensao, J. A. et al. Rediversification following ecotype isolation reveals hidden adaptive potential. Curr. Biol. 34, 855–867.e6 (2024).

    Article  PubMed  Google Scholar 

  42. Rosenstein, M. T., Collins, J. J. & De Luca, C. J. A practical method for calculating largest Lyapunov exponents from small data sets. Physica D 65, 117–134 (1993).

    Article  Google Scholar 

  43. Elowitz, M. B., Levine, A. J., Siggia, E. D. & Swain, P. S. Stochastic gene expression in a single cell. Science 297, 1183–1186 (2002).

    Article  CAS  PubMed  Google Scholar 

  44. Kinsler, G. et al. Extreme sensitivity of fitness to environmental conditions: lessons from #1BigBatch. J. Mol. Evol. 91, 293–310 (2023).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  45. Venkataram, S. et al. Development of a comprehensive genotype-to-fitness map of adaptation-driving mutations in yeast. Cell 166, 1585–1596.e22 (2016).

    Article  PubMed  PubMed Central  Google Scholar 

  46. Gillespie, J. H. Natural selection with varying selection coefficients—a haploid model. Genet. Res. 21, 115–120 (1973).

    Article  Google Scholar 

  47. Gillespie, J. H. Natural selection for within-generation variance in offspring number. Genetics 76, 601–606 (1974).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  48. Kimura, M. The number of heterozygous nucleotide sites maintained in a finite population due to steady flux of mutations. Genetics 61, 893–903 (1969).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  49. Griffiths, R. C. The frequency spectrum of a mutation, and its age, in a general diffusion model. Theor. Popul. Biol. 64, 241–251 (2003).

    Article  CAS  PubMed  Google Scholar 

  50. Evans, S. N., Shvets, Y. & Slatkin, M. Non-equilibrium theory of the allele frequency spectrum. Theor. Popul. Biol. 71, 109–119 (2007).

    Article  PubMed  Google Scholar 

  51. Ramsayer, J., Fellous, S., Cohen, J. E. & Hochberg, M. E. Taylor’s law holds in experimental bacterial populations but competition does not influence the slope. Biol. Lett. 8, 316–319 (2012).

    Article  PubMed  Google Scholar 

  52. Kinsler, G., Geiler-Samerotte, K. & Petrov, D. Fitness variation across subtle environmental perturbations reveals local modularity and global pleiotropy of adaptation. eLife 9, e61271 (2020).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  53. Rogers, T., Johnson, B. & Munch, S. Chaos is not rare in natural ecosystems. Nat. Evol. Ecol. 6, 1105–1111 (2022).

    Article  Google Scholar 

  54. Costantino, R. F., Desharnais, R. A., Cushing, J. M. & Dennis, B. Chaotic dynamics in an insect population. Science 275, 389–391 (1997).

    Article  CAS  PubMed  Google Scholar 

  55. Benincà, E. et al. Chaos in a long-term experiment with a plankton community. Nature 451, 822–825 (2008).

    Article  PubMed  Google Scholar 

  56. Becks, L., Hilker, F. M., Malchow, H., Jürgens, K. & Arndt, H. Experimental demonstration of chaos in a microbial food web. Nature 435, 1226–1229 (2005).

    Article  CAS  PubMed  Google Scholar 

  57. Graham, D. W. et al. Experimental demonstration of chaotic instability in biological nitrification. ISME J. 1, 385–393 (2007).

    Article  CAS  PubMed  Google Scholar 

  58. Benincà, E., Ballantine, B., Ellner, S. P. & Huisman, J. Species fluctuations sustained by a cyclic succession at the edge of chaos. Proc. Natl Acad. Sci. USA 112, 6389–6394 (2015).

    Article  PubMed  PubMed Central  Google Scholar 

  59. Tilman, D. & Wedin, D. Oscillations and chaos in the dynamics of a perennial grass. Nature 353, 653–655 (1991).

    Article  Google Scholar 

  60. Ushio, M. et al. Fluctuating interaction network and time-varying stability of a natural fish community. Nature 554, 360–363 (2018).

    Article  CAS  PubMed  Google Scholar 

  61. Peng, F. et al. Effects of beneficial mutations in pykF gene vary over time and across replicate populations in a long-term experiment with bacteria. Mol. Biol. Evol. 35, 202–210 (2018).

    Article  CAS  PubMed  Google Scholar 

  62. Stan Development Team. Stan modeling language users guide and reference manual (2023).

  63. Ascensao, J. A., Lok, K. & Hallatschek, O. joaoascensao/giantpopflucts: Publication. Zenodo https://doi.org/10.5281/zenodo.13787815 (2024).

Download references

Acknowledgements

We thank A. Arkin, K. Buttrey, B. Good, J. Denk, K. Wetmore, Q. Q. Yu, J. Ye, D. Nayak and all members of the Hallatschek lab (past and present) for helpful comments and advice on the project. We thank R. Lenski for sending us the LTEE-derived strains and populations, along with experimental advice and feedback. We thank T. Cooper for sending us the REL606 ΔpykF mutant. Research reported in this publication was supported by a National Science Foundation CAREER Award (grant no. 1555330 to O.H.). This work was supported by the National Institute of General Medical Sciences of the NIH under award R01GM115851 (O.H.) and by a Humboldt Professorship of the Alexander von Humboldt Foundation (O.H.). J.A.A. acknowledges support from an NSF graduate research fellowship, a Berkeley fellowship (from UC Berkeley) and Lloyd and Brodie scholarships (from UC Berkeley Dept of Bioengineering). We thank M. West of the Cell and Tissue Analysis Facility (CTAF) at UC Berkeley. This work was performed in part in the QB3 CTAF, that provided the ThermoFisher Attune Flow Cytometer (2017 model).

Author information

Author notes

  1. Kristen Lok

    Present address: Department of Biomedical Engineering, Duke University, Durham, NC, USA

Authors and Affiliations

  1. Department of Bioengineering, University of California Berkeley, Berkeley, CA, USA

    Joao A. Ascensao & Kristen Lok

  2. California Institute for Quantitative Biosciences, University of California Berkeley, Berkeley, CA, USA

    Joao A. Ascensao

  3. Department of Physics, University of California Berkeley, Berkeley, CA, USA

    Oskar Hallatschek

  4. Department of Integrative Biology, University of California Berkeley, Berkeley, CA, USA

    Oskar Hallatschek

  5. Peter Debye Institute for Soft Matter Physics, Leipzig University, Leipzig, Germany

    Oskar Hallatschek

Authors
  1. Joao A. Ascensao
    View author publications

    Search author on:PubMed Google Scholar

  2. Kristen Lok
    View author publications

    Search author on:PubMed Google Scholar

  3. Oskar Hallatschek
    View author publications

    Search author on:PubMed Google Scholar

Contributions

J.A.A. and O.H. designed the project. J.A.A. and K.L. performed the experiments and analysed the data. J.A.A. and O.H. wrote and revised the paper.

Corresponding author

Correspondence to Oskar Hallatschek.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Ecology & Evolution thanks Ivana Cvijovic, Michael Lässig and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

Extended Data Fig. 1 Simulations of chaotic dynamics in a simple two-genotype system.

(A) We model the dynamics of two genotypes, A and B, as coupled logistic maps (in discrete time). The model we analyse here is not intended to represent the underlying dynamics of the S/L system, but rather serves to demonstrate generic properties of chaotic dynamics. The parameters KA and KB are the carrying capacities of strains A and B, respectively. When the coupling parameter, c, goes to zero, we recover standard, independent logistic maps. Here, we consistently use r = 3.9, which puts the populations in the chaotic regime. (B-C) Examples of the abundance and genotype frequency dynamics. Here, we use c = 0.1. Even though the abundance dynamics are mildly coupled to each other, we still see fluctuations creeping into the genotype frequency dynamics. (D-E) Mean-variance scaling behaviors of the population abundance and genotype frequency. In both cases, we see power-law scaling with exponents of two, indicating the presence of effective offspring number correlations and decoupling noise. We varied the carrying capacities over several orders of magnitude to change the abundance and frequency. We computed the mean and variance of trajectories ran for 105 iterations, and discarded the first 104 iterations (to control for transient behaviors). We see that the degree of coupling does not affect the power-law exponent, but can change the intercept (as expected).

Extended Data Fig. 2 Correlated fluctuations between barcoded clones, from Venkataram et al. data.

Using the previously analyzed barcoded S. cerevisiae data45, we computed the pairwise correlation in log-displacement between every pair of high-frequency clones over every time point, replicate, and batch, that is corr \((\Delta \log {f}_{i,t},\Delta \log {f}_{j,t})\). Points represent correlation coefficients for every pair of clones, and bars represent the average (n = 3321, 190, 1640; left to right). Error bars represent 95% CIs. We see that, on average, pairs of haploid clones have highly correlated displacements, followed by pairs of diploid clones, and then pairs consisting of one haploid and one diploid clone.

Supplementary information

Supplementary Information

Supplementary theory, methods and figures.

Reporting Summary

Peer Review File

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ascensao, J.A., Lok, K. & Hallatschek, O. Asynchronous abundance fluctuations can drive giant genotype frequency fluctuations. Nat Ecol Evol 9, 166–179 (2025). https://doi.org/10.1038/s41559-024-02578-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Version of record:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41559-024-02578-3

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing