Main

Explaining the origin of compositional diversity within alkaline–silicate igneous complexes is an ongoing petrological problem because silica-undersaturated compositions are thought to be separated from feldspathoid-free compositions by a thermal divide over typical crustal pressures in the canonical clinopyroxene–nepheline–olivine–quartz ‘basalt tetrahedron’1,2. This divide means that a single crystallizing melt should be unable to generate both evolved silica-oversaturated and silica-undersaturated rocks during crystallization over a range of crustal pressures. Despite this well-established concept, isotopic evidence in some alkaline–silicate complexes indicates that a diversity of compositions can form from a shared parental melt at crustal pressures3,4,5.

Numerous processes have therefore been invoked to explain the observed compositional diversity, including volatile addition, variation in mantle melting degree, high-pressure fractional crystallization (≳9 kbar) and melt contamination, for example, via continental crust assimilation2,3,6,7,8,9,10,11. However, the global applicability of these processes to explain geochemical diversity in alkaline–silicate complexes remains unclear (for example, isotope data are not always consistent with assimilation12, or estimated crystallization pressures are shallow13,14). Understanding the petrogenesis of the alkali-rich, silica-undersaturated components is particularly important since they often record the highest concentrations of rare earth elements (REEs) and, in some cases, host REE deposits, particularly when melts have become extremely peralkaline (‘agpaitic’)15,16,17.

Phase equilibria modelling is a powerful tool for mineral assemblage analysis within igneous rocks18. Until recently, such modelling could not be applied to alkali-rich compositions due to the lack of thermodynamic models for their constituent phases. However, with recent thermodynamic models for silica-undersaturated melt and feldspathoid minerals, phase equilibria modelling can now be used to explore the petrogenesis of both alkali- and silica-rich igneous rocks in volatile-free systems19. In addition, the MAGEMin software20 allows for efficient implementation of fractional (open-system) crystallization calculations. In this Article, we apply these modelling advances to explore how a single mafic melt can generate the compositional diversity of alkaline–silicate igneous rocks seen in nature, using the Blatchford Lake Igneous Complex (BLIC) as a case study.

Blatchford Lake Igneous Complex

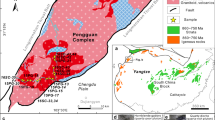
The BLIC is an ~2.2-billion-year-old intrusive suite consisting of two lobes of cogenetic silica-oversaturated and silica-undersaturated rocks intruded into the southwestern margin of the Slave Craton, Northwest Territories, Canada (Fig. 1 and Supplementary Discussion)4. The most primitive unit is the Caribou Lake gabbro (CLG; light blue shades, Fig. 1b,c), which forms part of the BLIC’s western lobe, alongside diorite, quartz-syenite and granite (dark blue symbols, Fig. 1c)14,21. Basal cumulate peridotite and clinopyroxenite layers within the gabbro indicate early olivine and clinopyroxene fractionation. The western lobe units are suggested to be directly related via a liquid line of descent, with reported Al-in-hornblende barometry indicating final mid-crustal crystallization at 3.5–4.9 kbar (ref. 14) (range across 15 samples; ±0.6 kbar (refs. 22,23)). Drill-core and gravity modelling indicate that the CLG has extensive lateral and vertical continuations beyond its surface expression24,25. The BLIC’s eastern lobe (orange shades, Fig. 1b,c) contains granite, syenite and agpaitic nepheline syenite (the Nechalacho Layered Suite (NLS))14.

Fig. 1: Location, geology and whole-rock geochemistry of BLIC, Canada.
figure 1

a, Overview map of Canada, in Albers projection. b, BLIC geology. c, Whole-rock geochemistry12,14,28 for BLIC (coloured symbols) in total alkali–silica space43. Background data in grey (n = 9,499) are global alkaline igneous rock compositions from GEOROC; see Supplementary Discussion for compilation details. Sample outlined in black is the bulk composition used for modelling. Panel b adapted with permission from ref. 12, Oxford Academic/Oxford Univ. Press.

Full size image

The diversity of silica-undersaturated and silica-oversaturated compositions in the BLIC follows that seen in other worldwide alkaline–silicate igneous complexes (for example, Kangerlussuaq and Ilimaussaq, Greenland11; Mt Brome, Canada3) and includes primitive gabbros (Fig. 1c). Therefore, this complex provides an ideal case study for investigating controls on the formation of cogenetic silica-undersaturated and silica-oversaturated melts. Existing geochemistry, geochronology and petrology suggest that intrusive phases of the BLIC represent emplacement of separate magma batches, each derived from the same mantle-derived parental melt that underwent progressive mid- to lower-crustal fractionation4,12,14,21. Although crustal assimilation (yielding silica-oversaturated magmas) and magma recharge with alkalis or volatiles (yielding silica-undersaturated magmas) have been invoked to explain the cogenetic suites of silica-oversaturated and silica-undersaturated rocks4,12,14,21, isotope data argue against substantial assimilation in eastern lobe granites12.

Forming compositional diversity

We model endmember batch and fractional BLIC crystallization using the most primitive reported CLG sample (highest MgO, excluding cumulate peridotite/pyroxenite) as the starting bulk composition (the silica-saturated gabbro CLG-1075C; Methods, Supplementary Table 1 and Extended Data Fig. 1). The pressure–temperature (P–T) pseudosection for this composition (representing batch crystallization) and corresponding phase proportions during batch and fractional crystallization at high (10 kbar) and low (1 kbar) pressures are shown in Fig. 2.

Fig. 2: Phase assemblages during isobaric crystallization of a primitive CLG bulk composition.
figure 2

a, P–T pseudosection. Zero mode isolines are highlighted for clinopyroxene (green), olivine (pink), garnet (yellow) and liquid (bold). Dashed lines and legend show pressures and phase colours for mode boxes in panels b–e. b–e, Supra-solidus mode boxes at 10 kbar (b,c) and 1 kbar (d,e) for batch (b,d) and fractional (c,e) crystallization. Colour-coded vertical lines show appearance of each phase. cpx, clinopyroxene; g, garnet; ilm, ilmenite; liq, liquid; mgt, magnetite; ol, olivine; opx, orthopyroxene; pl, plagioclase; qz, quartz; ru, rutile; spl, spinel.

Full size image

The compositional evolution of the melt in total alkali–silica (TAS) space during batch and fractional crystallization at different pressures (the latter to 95 vol%) is shown in Fig. 3a. Final in situ batch crystallization of this fractionated melt for a subset of pressures, considering that continued fractionation at small melt fractions may be unrealistic, is shown in Fig. 3b. The 95% crystallization transition from fractional to batch was chosen because further melt evolution at intermediate pressures (~4–5 kbar) undergoes a sharp divergence, as discussed in the following, but changing the transition point does not change our conclusions (Extended Data Fig. 2). We classify the modelled fractionated melts as silica-undersaturated (feldspathoid-bearing), silica-saturated (neither feldspathoid- nor quartz-bearing) or silica-oversaturated (quartz-bearing) on the basis of their equilibrium solidus assemblage. Melt compositions in other oxides during fractionation at 4–5 kbar, crystallization assemblages and mineral compositions are given in Extended Data Figs. 3 and 4.

Fig. 3: Evolution of melt compositions during isobaric batch and fractional crystallization of a primitive CLG bulk composition, shown in total alkali–silica space.
figure 3

Whole-rock geochemistry12,14,28 for BLIC shown in coloured symbols following Fig. 1: orange shades for eastern lobe of the NLS (circle), Thor Lake syenite (diamond), Grace Lake granite (cross); blue shades for western lobe of Hearne Channel/Mad Lake granite (upward triangle), Whiteman Lake syenite (pentagon) and CLG (inverted triangle). Grey squares show the composition of selected phase endmembers; see text for discussion. a, Main axes show fractional crystallization; inset shows batch crystallization. Crosses mark the first 50, 75 and 90 vol% of crystallization. b, Crystallization continues from 95% fractionation in a (dotted lines showing evolution up to that point) at 4.0 and 5.0 kbar, with additional calculations at 0.5 kbar intervals; 3.5 kbar included as lower limit of reported BLIC pressures14. aeg, aegirine; ab, albite; cpx, clinopyroxene; di, diopside; fsp, feldspar; Fo, forsterite; hd, hedenbergite; ol, olivine.

Full size image

Batch crystallization modelled at pressures ≤7.0 kbar produces olivine as the first liquidus phase, followed by augitic clinopyroxene, plagioclase feldspar, ilmenite and magnetite (Fig. 2a,d). At higher pressures, clinopyroxene replaces olivine as the liquidus phase, with olivine unstable above ~8 kbar, and spinel becomes the oxide phase (Fig. 2a,b). At the highest considered pressures (>12 kbar), garnet is also stabilized near the solidus. Typical 1σ uncertainties on such phase equilibria calculations are ±1 kbar, ±50 °C (refs. 19,26,27). Batch crystallization results in a moderate increase in total alkalis (<5 wt%) and restricted variation in the silica content of the melt (Fig. 3a).

Fractionation to 95% crystallization results in similar mineral assemblages to batch crystallization (Fig. 2c,e and Extended Data Fig. 4). Low-pressure fractionation (≤4 kbar) generates silica-oversaturated melts (marked with squares in Fig. 3), whereas higher-pressure fractionation generates silica-undersaturated melts (stars in Fig. 3). Fractionating melts record extensive variation away from the starting composition as fractionation drives a continually evolving bulk composition, with strong pressure sensitivity reflecting differences in early-crystallizing assemblage (for example, projecting away from olivine at low pressures, or clinopyroxene at higher pressures; grey squares in Fig. 3a). Isobaric fractional crystallization across the pressure range previously estimated for the BLIC (3.5–4.9 ± 0.6 kbar (ref. 14)) yields melt evolution from gabbroic to dioritic and syenitic, as recorded in the BLIC (Fig. 1c). These fractionation paths also reproduce trends in other major-element oxide abundances (Extended Data Fig. 3) and are consistent with observed mineral assemblages and cumulate microstructures in BLIC gabbros14,28. The high crystallization degree of a mafic melt required to generate the observed extreme alkali enrichment is consistent with previous modelling in other complexes29. The suggestion of extensive fractionation is also consistent with drill-core and gravity modelling, which indicate large volumes of gabbro at depth24,25.

Given this compositional and barometric match, we now focus on evolved (95% fractionation) melts that span from silica-oversaturation to silica-undersaturation (transition from paths marked as squares versus stars in Fig. 3a) and model their continuing in situ batch crystallization (Fig. 3b). Silica-oversaturated residual melts at 4.0 kbar crystallize to a final assemblage of Fe-rich clinopyroxene, alkali feldspar, ilmenite and quartz (Extended Data Fig. 4). During this final crystallization, equilibrium melts become syenitic and granitic (Fig. 3b). Silica-undersaturated melts at 5.0 kbar produce a similar final assemblage as at 4.0 kbar, with the addition of fayalitic olivine, and nepheline instead of quartz (Extended Data Fig. 4). The 4.5–5.0 kbar equilibrium melts become increasingly alkali-rich nepheline-syenitic (Fig. 3b). At pressures between 4.0 and 4.5 kbar there is a sharp divergence in final melt composition towards high silica or high alkalis that define a critical narrow ‘tipping point’ for generating silica-undersaturated and silica-oversaturated evolved melts (typical 1σ pressure uncertainties of ±1 kbar (refs. 19,26,27)). The small differences in mineral assemblage (and mineral compositions) across the tipping point result in residual melts lying either side of the ‘tie-line’ between albite and bulk solid assemblages dominated by clinopyroxene, olivine, oxides and plagioclase. Consequently, residual melts are driven to either high silica or high alkalis as the crystallizing plagioclase becomes more albite-rich (Extended Data Fig. 4). If no final batch crystallization is considered or if the transition to batch crystallization occurs earlier (for example, at 90% fractionation), the residual melts range from silica-undersaturated to silica-oversaturated across the same pressure range (Extended Data Fig. 2).

Sensitivity to bulk composition

Although the initial bulk composition for modelling was chosen avoiding samples reported as cumulates (Extended Data Fig. 3b), even fine-grained gabbro samples probably record some crystal accumulation14,30, complicating primitive melt identification. To explore the sensitivity of the tipping point to starting composition, we considered four additional BLIC bulk compositions (Supplementary Tables 1 and 2): two lower MgO gabbros, including the fine-grained CLG type specimen28, and two ‘cumulate-corrected’ compositions calculated by removing olivine and olivine plus clinopyroxene from the original bulk (Supplementary Discussion). Our results (Extended Data Fig. 5) show that the transition pressure between evolved silica-oversaturated and silica-undersaturated melts varies between 3 and 5 kbar among these compositions, consistent with the 4.0–4.5 ± 1 kbar range proposed in the preceding, suggesting that the tipping-point estimate is robust despite potential cumulate processes. Some of this pressure variation may also result from varying oxidation state, as discussed in the following.

Sensitivity to oxidation state and water

The model described in the preceding considers crystallization of an anhydrous system (consistent with the rarity of hydrous phases reported in the gabbro28) at a given initial redox condition. However, oxidation state (considered as xFe3+, molar Fe3+/[Fe2++Fe3+]) and volatiles (especially water) could either remove or affect the pressure of the tipping point by impacting the crystallizing assemblage. Therefore, we explore the impact of these two variables on melt composition and subsequently tipping-point behaviour.

First, xFe3+ was varied from 0.10 to 0.18 (versus 0.13 used for Figs. 2 and 3) to slightly extend beyond the viable 0.11–0.17 range on the basis of reported oxide assemblage30 (Extended Data Fig. 1 and Methods). Our model shows that increasing xFe3+ results in a higher-pressure tipping point, from ~3.5 kbar when xFe3+ = 0.10 to 4.5–5.0 kbar when xFe3+ = 0.18 (Fig. 4). This behaviour is driven by the crystallizing assemblage (particularly earlier modelled oxide crystallization at higher xFe3+; Extended Data Fig. 6), resulting in shallower melt paths in TAS space at higher xFe3+ for a given pressure. However, across the modelled range of bulk xFe3+ (0.10–0.18 here, 0.13–0.23 in bulks used to explore cumulate processes described in the preceding), the tipping point remains within 3–5 kbar.

Fig. 4: Evolution of melt compositions during isobaric crystallization of the primitive CLG bulk composition at varying initial xFe3+.
figure 4

a,b, Initial xFe3+ = 0.10 (a) and initial xFe3+ = 0.18 (b). Modelled crystallization is fractional up to 94–95 vol.% (dashed lines) followed by final in situ batch crystallization (solid lines), as in Fig. 3. Whole-rock geochemistry12,14,28 for the BLIC shown in coloured symbols following Fig. 1: orange shades for eastern lobe of the NLS (circle), Thor Lake syenite (diamond) and Grace Lake granite (cross); blue shades for western lobe of Hearne Channel/Mad Lake granite (upward triangle), Whiteman Lake syenite (pentagon) and CLG (inverted triangle).

Full size image

Second, we consider the impact of water in our model system. The thermodynamic melt model calibrated for alkaline (and sub-alkaline) systems19 does not include water, so we necessarily use a different melt model31,32 to investigate the effects of water. This alternative melt model is strictly calibrated only for hydrous sub-alkaline systems and hence is not used primarily in this study. The newer anhydrous melt model was developed from this precursor hydrous model and includes all of the anhydrous constraints used to calibrate this older model, so produces similar results in sub-alkaline conditions31,32. Given the importance of melt behaviour during the early stages of crystallization in determining eventual silica-saturation state, the use of the hydrous sub-alkaline melt model is sufficient to determine the first-order control of water on the tipping point. In Extended Data Fig. 7, we show anhydrous melt evolution to confirm that melt model choice does not lead to systematic differences in early melt evolution, and then show results for 0.25–1.00 wt% H2O. As water content increases, melt evolution trends in TAS space at a given pressure become shallower, and consequently, the tipping point shifts to higher pressure, for example, to ~5 kbar with 0.5 wt% H2O. This varying melt composition occurs because of earlier evolution to albite-rich plagioclase and earlier oxide crystallization with increasing water (Extended Data Fig. 8), with a consequently shallower residual melt–fractionating solid vector for the majority of crystallization. With sufficient water (1 wt% H2O), the effect is exacerbated by edenitic to pargasitic amphibole crystallization (from ~70% fractionation), which suppresses alkali enrichment in residual melts.

In the BLIC, the rarity of reported amphibole in the gabbro suggests <1 wt % H2O, and the modelled late appearance of biotite in evolved melts with 0.25–0.50 wt% H2O is consistent with reported mineral assemblages in the granites and syenites14. We note that the presence of water suppresses solidus temperatures and generates evolved compositions at lower fractionation degrees. Under these hydrous conditions, our results still support the mid-crustal tipping point for the formation of silica-undersaturated and silica-oversaturated BLIC melts. However, because this hydrous model is not calibrated for alkaline systems, we do not further quantify the tipping point in the hydrous system and note that further investigation of the suggested deepening of the tipping point with increasing water (for example, for application to arc settings) will require calibration of a hydrous alkaline melt model.

Overall, our results show that crystallization of batches of a primitive BLIC melt at mid-crustal pressures (3–5 kbar, also consistent with existing barometry estimates from the BLIC14) can generate the range of silica-undersaturated to silica-oversaturated compositions observed, including agpaitic nepheline syenite. Mafic recharge, crustal assimilation or melt-peridotite reaction is not required12,14,33, although they are not ruled out by our results. The results presented in the preceding indicate that at least two crystallization pressures (above and below the tipping point) are required to generate the reported major-element compositional diversity. If a uniform emplacement pressure is imposed as a constraint for the two BLIC lobes (for example, based on field relations14), the identified critical fractionation pressure remains relevant. In this instance, some fractionation deeper than the tipping point must occur, with final emplacement at shallower pressures. After a certain point during deep fractionation, melts become silica-undersaturated and remain so even during later, shallower, emplacement. Therefore, silica-oversaturated final melts can be extracted early from a deeper chamber. The required amount of deep fractionation depends on the pressure of each crystallization step; for example, higher emplacement pressures require lower amounts of crystallization to reach silica-undersaturated compositions (Extended Data Fig. 9).

Implications for rare earth element enrichment

Reported REE concentrations in the BLIC increase throughout increasingly evolved gabbro and syenite units4,12,14,34. The REE enrichment culminates in the silica-undersaturated NLS, which contains substantial REE deposits35. Since the major-element behaviour of the BLIC suggests that fractionation pressure has controlled the formation of silica-undersaturated rocks, we additionally model magmatic lanthanum (La) and ytterbium (Yb) behaviour (representative of light/heavy REEs (LREE/HREE), respectively) during fractionation at varying pressures by combining our phase equilibrium models with mineral-melt partition coefficients (for example, refs. 36,37; Methods).

Our models produce the continual REE enrichment expected for broadly incompatible elements during isobaric fractional crystallisation (Fig. 5a). An upper limit on the fractionation pressure of BLIC melts is provided by garnet crystallization at ~12 kbar as this phase efficiently sequesters HREEs38 (Fig. 5b). With increasing fractionation pressure from 5–12 kbar (5 kbar being the lower fractionation pressure limit to generate silica-undersaturated melts for this bulk composition; Fig. 3), the Yb/La ratio decreases in response to increasing clinopyroxene abundance at the expense of plagioclase (Fig. 5b).

Fig. 5: Modelled melt REE enrichment during crystallization of the primitive CLG.
figure 5

a, Residual enrichment in melt (concentrationliquid (Cl)/concentrationinitial(Ci)) for La and Yb at 5 kbar. Solid lines show results using the preferred mineral-melt partition coefficients (Methods and Supplementary Table 3), but dashed lines show comparison using an alternative clinopyroxene model44 since clinopyroxene, alongside plagioclase feldspar, drives most of the residual enrichment. Shaded grey bars show enrichment of La and Yb measured in evolved BLIC units relative to sample CLG-1075C (see Supplementary Discussion for the sample details). Crystallization percentages of evolved samples estimated from their position in Fig. 3. b, Residual enrichment of Yb relative to La in fractionating melt at different pressures.

Full size image

Our fractional crystallization models generate the observed range of REE concentrations in non-mineralized BLIC rocks relative to primitive CLG (which has mid-ocean-ridge basalt (MORB)-like REE concentrations; Supplementary Fig. 1) at their predicted crystallization fractions (Fig. 5). These results support our petrogenetic model for the BLIC although minor phases outside the model system (for example, monazite) will also influence whole-rock REE concentrations. Reported negative Eu anomalies in BLIC rocks12 (Supplementary Fig. 1) are consistent with modelled extensive plagioclase fractionation. We do not model continued REE enrichment in evolved NLS units because of the absence of thermodynamic models for relevant minerals (for example, sodalite). Nevertheless, we note the model prediction that ~5 kbar fractionation, as proposed for the BLIC, generates the highest magmatic HREE/LREE enrichment in silica-undersaturated melts and is consistent with the NLS being reported as HREE-rich39.

Global implications

Using thermodynamic models, we have quantified a mid-crustal tipping point (~3–5 kbar) for fractional crystallization that controls the ultimate evolution of mafic melts to silica-oversaturation or silica-undersaturation (Fig. 6). For a given bulk composition, fractionation over a narrow ~0.5 kbar range within that window generates compositional diversity representative of that seen in alkaline–silicate igneous systems worldwide (Fig. 1c). This critical pressure is not unique to the BLIC: equivalent calculations for primary MORB and an ocean island basalt show the same tipping point in melt evolution (Extended Data Fig. 10). Such behaviour is expected for any silica-saturated mafic melt (with ≲1 wt% H2O) where olivine and clinopyroxene crystallize early if extreme fractional crystallization can occur, as clinopyroxene abundance will increase at the expense of olivine with increasing pressure, consequently changing the melt evolution from higher silica to higher alkali enrichment. New thermodynamic models are required to understand the evolution of more hydrous primitive melts.

Fig. 6: Schematic of the mid-crustal tipping point separating the formation of silica-undersaturated or silica-oversaturated magmas from silica-saturated primitive melts.
figure 6

Deeper fractionation than the tipping point yields silica-undersaturated magmas (red shades), and shallower fractionation yields silica-oversaturated (yellow shades) magmas.

Full size image

Early experimental work also suggested that an increasing ratio of early-crystallizing pyroxene to olivine with increasing pressure in silica-saturated melts would generate increasingly alkali-rich residual melts6, as observed in our results. However, the ability of a fractionating melt to overcome the thermal divide between silica-saturation and silica-undersaturation was suggested to be limited to high pressures where the divide disappeared (~8–9 kbar (refs. 1,2,40)). This result was constrained by 4.5 and 9.0 kbar experiments2,6 with pyroxene replacing olivine as a liquidus phase at ≥9 kbar (ref. 2) although it was also qualitatively suggested that early clinopyroxene fractionation before plagioclase could enable residual melts to cross the thermal divide at lower pressures40. The lower mid-crustal pressure indicated by our modelling quantitatively supports this latter hypothesis and is notable because it can explain the juxtaposition of cogenetic silica-undersaturated and silica-oversaturated rocks where fractionation has been suggested to occur across the mid- to upper crust (for example, ref. 11). This pressure is consistent with the depth of geophysical anomalies interpreted as extensive mafic intrusions beneath some of the world’s largest alkaline–silicate igneous complexes (for example, Ilimaussaq, Greenland)16,41,42. Our results can also account for complexes where final upper-crust emplacement is suggested (for example, ref. 13) by indicating that variable amounts of earlier fractionation deeper than the same tipping point could generate the observed diversity (Extended Data Fig. 9). These cogenetic silica-undersaturated and silica-oversaturated residual melts may feasibly be emplaced together at shallower pressures (Fig. 6), suggesting a key role for mid-crustal mafic staging chambers in forming igneous complexes with cogenetic silica-undersaturated and silica-oversaturated rocks.

Methods

Phase equilibria modelling

Modelling was performed in the volatile-free ten-component Na2O–CaO–K2O–FeO–MgO–Al2O3–SiO2–TiO2–Fe2O3 ± Cr2O3 model system for most of the calculations presented, with thermodynamic database ds6.36 (ref. 45, as modified in ref. 19). Calculations were performed using the composition-dependent equations of state (x-eos) for silicate melt, nepheline, ilmenite, clinopyroxene, orthopyroxene and garnet presented in ref. 19, feldspar from ref. 46, olivine from ref. 31 and spinel from ref. 47. For Extended Data Figs. 7 and 8, modelling was performed in the hydrous 11-component Na2O–CaO–K2O–FeO–MgO–Al2O3–SiO2–H2O–TiO2–Fe2O3–Cr2O3 model system with thermodynamic database ds6.36 (ref. 45, as modified in ref. 32, following ref. 31). Composition-dependent x-eos for olivine, garnet, spinel, feldspar, clinopyroxene and ilmenite are as outlined in the preceding, with the addition of biotite and hydrous melt from ref. 32 and amphibole from ref. 26. We note that nepheline exists in the database as a pure phase. Pseudosections were constructed using THERMOCALC v.3.51s.

The bulk composition modelled in this work is that of natural sample CLG-1075C14 (Supplementary Table 1). This sample was selected as it contains the highest MgO content (that is, most primitive) of published CLG samples14,28 and is therefore considered the best available composition to capture the earliest evolution of the BLIC. The sample selection excluded those classified as cumulate peridotite/pyroxenite14, as these are not representative of instantaneous melts, and a sample recorded as being rich in pyrite28 due to S not being in the model system. As discussed in the main text, other high-MgO samples were also investigated, alongside ‘corrections’ for crystal accumulation, to confirm that our results are not sensitive to cumulate processes in the gabbro, which despite our sample screening are hard to avoid completely14,28,30. The sample compositions were converted to the model system (Supplementary Table 2) by ignoring elements outside the model system. The Fe3+/FeT ratio of 0.13 for CLG-1075C was determined using a T–xFe3+ diagram at 4 kbar (Extended Data Fig. 1), whereby reported co-existing magnetite and ilmenite in CLG samples30 constrains viable molar Fe3+/FeT to between ~0.11 and 0.17. When xFe3+ was considered as a variable (Fig. 4), values of 0.10 and 0.18 were chosen to just bracket this range. No petrographic description of sample CLG-1075C is available for comparison with the pseudosection results, but descriptions of general CLG petrography indicate that samples typically comprise olivine, clinopyroxene, plagioclase and oxides (including magnetite and ilmenite) with variable orthopyroxene and other accessory phases14,21,30, broadly consistent with Fig. 2 below 9 kbar. A primary normal MORB (NMORB) composition48 and primary Kilauea (Hawai‘i) melt49 are used as a comparison with the CLG. Fe3+/FeT in NMORB is taken as 0.14 (ref. 50), and a typical value measured in glasses of 0.10 was used for Kilauea51.

We used MAGEMin20 (MAGEMin_C version 1.7.6) to perform fractional crystallization calculations. Fractional crystallization was simulated via stepwise crystallization in 1 °C intervals from liquidus temperatures, taking the liquid composition remaining at each interval as the bulk composition for the next calculation. Volatile-bearing phases such as amphibole and biotite are also important to model in detail the end stages of crystallization of evolved melt compositions and are present in the evolved portions of the BLIC12,14,28. Nevertheless, the volatile-free system used herein is suitable for modelling most of the petrogenetic history of the BLIC as volatile-bearing phases are recorded only rarely and/or interstitially in the CLG rocks covered by up to 95% fractionation in our model12,28 (the fractionation range within which an evolution to silica-undersaturation versus silica-oversaturation is determined). However, we do consider results in a hydrous model system to confirm the impact on the tipping point, although note that since the hydrous model is not calibrated for alkaline systems, the volatile-free results are mostly used throughout the text. In all our modelling, uncertainties of ±1 kbar for a pressure-sensitive boundary, or ±50 °C for a temperature-sensitive boundary, are considered to represent a 1σ uncertainty in a boundary that introduces a phase that can reach substantial proportions. The presence or absence of accessory phases at a given pressure–temperature coordinate carries higher uncertainty because they contribute so little to the Gibbs energy of the assemblage26,27.

Model melts are labelled as silica-undersaturated (feldspathoid-bearing), silica-saturated (neither quartz nor feldspathoid-bearing) or silica-oversaturated (quartz-bearing) according to their equilibrium (batch) solidus mineral assemblage at the relevant pressure (that is, if completely crystallized).

Rare earth element enrichment modelling

Mineral-melt partitioning for REEs is calculated using the mineral assemblage and mineral composition information during crystallization. Clinopyroxene and plagioclase feldspar partitioning is implemented using composition-, temperature-, and pressure-dependent Dmineral-melt models36,37. For spinel and magnetite, a temperature-dependent Dmineral-melt is used52, and for all other minerals fixed Dmineral-melt are used (nepheline53, olivine53, ilmenite54, garnet38; Supplementary Table 3). The Dclinopyroxene-melt model36 used here was chosen due to the variety of calibrated clinopyroxene compositions, including an NLS sample. For comparison, results using an alternative Dclinopyroxene-melt model44 are also shown in Fig. 5, demonstrating that the choice of model does not affect the conclusions of this study.

Bulk Dsolid-melt is calculated by mass balance using the modal phase abundances from the phase equilibrium models. Residual enrichment (for batch crystallization), Cliquid/Cinitial, is calculated as 1/(F + D(1 – F)) where D is bulk Dsolid-melt and F is the fraction of liquid present. For fractional crystallization, the preceding calculation refers to the enrichment at each 1 °C fractionation step (effectively a series of batch calculations), giving enrichment relative to the previous step. Therefore, overall residual enrichment (relative to the starting composition) at each step, i, is calculated as 1/(F + D(1 – F))i × 1/(F + D(1 – F))i−1.