Acoustic metasurfaces

Abstract

Acoustic metasurfaces derive their characteristics from the interaction between acoustic waves and specifically designed materials. The field is driven by the desire to control acoustic wave propagation using compact devices and is governed by fundamental and physical principles that provide the design rules and the functionality of a wave. Acoustic metasurfaces have added value and unusual functionalities compared with their predecessor in materials science, namely, acoustic metamaterials. These rationally designed 2D materials of subwavelength thickness provide a new route for sound wave manipulation. In this Review, we delineate the fundamental physics of metasurfaces, describe their different concepts and design strategies, and discuss their functionalities for controllable reflection, transmission and extraordinary absorption. In particular, we outline the main designs of acoustic metasurfaces, including those based on coiling-up space, Helmholtz-resonator-like and membrane-type structures, and discuss their applications, such as beam focusing, asymmetrical transmission and self-bending beams. We conclude with an outlook of the future directions in this emerging field.

Introduction

Wave manipulation using artificial materials is a central topic in materials physics. The design of a material has an important role in determining the characteristics of waves inside and outside the material and in achieving such manipulation. Since 2011, a family of thin, 2D artificial materials, namely, metasurfaces, has emerged. The concept of metasurfaces was introduced to the materials science and physics communities for optical waves via the generalized Snell’s law, which opened up opportunities for optical wave manipulation and led to new applications¹. Inspired by this pioneering work, and because acoustic waves also follow Snell’s law, a flurry of activity^{2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25} has revealed acoustic metasurfaces as suitable materials for controlling sound and has led to new applications in acoustics. However, mapping the success of electromagnetic metasurfaces to the acoustic domain is challenging, primarily owing to the intrinsic differences between electromagnetic and acoustic waves, for example, the mechanical nature of acoustic waves and the difficulty of efficiently coupling acoustic waves to very thin structures^5,25,26.

Acoustic metasurfaces are 2D materials of subwavelength thickness capable of providing non-trivial local phase shifts (or amplitude modulation) or extraordinary sound absorption. The uniqueness of metasurfaces lies in their ability to freely tailor the wave fields such that the phase and/or amplitude is fully controlled. The acoustic metasurface concept is based on arrays of subwavelength units, including (but not limited to) Helmholtz resonators³, membranes⁷ and coiling-up space structures^5,11,27. These units can be used to realize and showcase fascinating wavefront engineering features, including self-bending beams⁴, a twisted wavefront (for example, acoustic vortices)^28,29, non-diffraction beams³⁰, diffuse reflection^8,31, asymmetric transmission³², beam focusing³, artificial Mie resonances¹² and near-perfect absorption^7,9,33,34.

Building on the success of bulk metamaterials in the past decade^{35,36,37,38,39,40}, acoustic metasurfaces have significantly advanced the field of wave manipulation, enabling the design of miniaturized materials and devices with complex and unprecedented functionalities. One of the main reasons for the interest in acoustic metasurfaces is the challenge of using bulk acoustic metamaterials to manipulate the sound of long wavelengths in air and water. The use of metasurfaces — in the form of thin and lightweight structures — is an ingenious way to overcome this problem.

The subwavelength units of acoustic metasurfaces are on the millimetre and sub-millimetre scales and therefore are challenging to fabricate using traditional machining methods. With the development of additive manufacturing technologies, especially 3D printing techniques, the subwavelength units can be readily realized, making the related experimental demonstration straightforward. Indeed, thanks to the large impedance mismatch between air and solids, the plastic or resin materials used in 3D printing are sufficient to provide highly reflective boundaries for airborne sound. Therefore, common 3D printing techniques, such as fused deposition modelling or stereolithography, which offer excellent nominal precision down to 0.01 mm, provide a perfect manufacturing strategy for fabricating acoustic metasurfaces that can operate at frequencies below 10 kHz.

There are numerous contributions in the acoustics community that predate the concept of acoustic metasurfaces but are closely associated with acoustic metasurfaces. One example is the sound diffuser^41,42,43 in architectural acoustics, which is an engineered surface designed to scatter sound in a uniform manner. The optimal sound diffuser was proposed by Schroeder in the 1970s^44,45. Other examples include tuned mass dampers for narrowband absorption or vibrations^46,47, bass traps (air-backed panel absorbers)⁴⁸, quarter-wave or Helmholtz resonator systems as subwavelength absorbers^49,50,51, acoustic holography⁵² and Alberich absorbers for underwater sound⁵³.

In this Review, we delineate advances in the field of acoustic metasurfaces and identify the challenges as well as future directions for fundamental research and applications. We emphasize the physics of metasurfaces and their unique abilities of wavefront shaping for achieving controllable transmission and reflection, and near-perfect absorption.

The physics of acoustic metasurfaces

Classic acoustics informs us that the refraction and reflection of acoustic plane waves impinging on a planar boundary separating two media obey Snell’s law. Snell’s law predicts equal angles of incidence and reflection as well as the relationship between the angles of incidence and refraction. This relationship between the angles depends on the difference between the refractive indices of the two media. However, such a well-established physical law relies on the assumption that the phase shift of waves accumulates gradually along the propagation path. It is possible, as we prove here, to revisit Snell’s law and control transmitted and reflected sound waves in a manner beyond what is offered by conventional interfaces between two natural media (for example, water, air and metal). This enhanced control of sound waves is achieved by introducing abrupt phase shifts in the acoustic path by adding periodic structures into a planar interface at subwavelength scales.

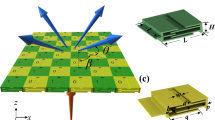
Consider an incident acoustic plane wave illuminating an artificially structured interface such that an additional phase shift, which is a continuous function of the position along the interface, is introduced to the acoustic waves transmitted or reflected from the interface (Fig. 1). If the interface is located in the plane of z = 0, it is able to create a phase discontinuity, denoted as ϕ(x) (for a 1D interface) or ϕ(x, y) (for a 2D interface), for the incident wave as it is reflected or passes through the interface. For simplicity, we consider 1D cases and derive the relationship between the angles of incidence and reflection from Fermat’s principle. This principle governs the propagation of acoustic waves. More specifically, it states that the acoustic path length (defined as the physical length multiplied by the refractive index of the medium) of a ray of an acoustic wave from point A to point B after being reflected off the interface (or to point C after being refracted into a different medium) is a minimum (Fig. 1). From wave theory, the difference in the length of the acoustic path is equivalent to the variation of the propagation phase. Hence, Fermat’s principle can also be understood by considering that the trajectory taken by the acoustic wave between two points, for example, A and B (or C), should be the path of least phase change.

Fig. 1: Schematics of the generalized Snell’s law and acoustic metasurface.

By artificially engineering the interface between two media 1 and 2, an abrupt phase shift dependent on the position along the interface is introduced in the acoustic path, giving rise to the generalized Snell’s law of reflection and refraction. Such an artificial interface can be realized by a monolayer of meta-atoms with subwavelength thickness, namely, a metasurface. θ_i, angle of incidence; θ_r, angle of reflection; θ_t, angle of transmission; ϕ(x), phase discontinuity.

For the reflection case, it can be derived that when we desire a ray of an acoustic wave to leave point A located at (x_A, z_A), impinge on point O located at (x, 0) with an angle of incidence θ_i and then bounce back to point B located at (x_B, z_B), the total phase variation along this path taken by the acoustic wave should be:

$${\Psi }_{{\rm{r}}}\left(x\right)=\phi \left(x\right)+{k}_{1}\sqrt{{\left(x-{x}_{{\rm{A}}}\right)}^{2}+{z}_{{\rm{A}}}^{2}}+{k}_{1}\sqrt{{\left({x}_{{\rm{B}}}-x\right)}^{2}+{z}_{{\rm{B}}}^{2}}$$

(1)

where an abrupt phase discontinuity ϕ(x) is introduced owing to the contribution of the engineered interface. λ₁ = c₁/f is the wavelength in medium 1, where c₁ and f are the speed of sound and the frequency, respectively. To obtain the expression that needs to be satisfied by the coordinates of point O, we differentiate Ψ_r(x) with respect to x and let it be equal to zero to have a minimum for the acoustic path length, which yields:

$$\begin{array}{c}\frac{d{\Psi }_{{\rm{r}}}\left(x\right)}{dx}=\frac{d\phi \left(x\right)}{dx}+\frac{{\lambda }_{1}\left(x-{x}_{{\rm{A}}}\right)}{2{\rm{\pi }}\sqrt{{\left(x-{x}_{{\rm{A}}}\right)}^{2}+{z}_{{\rm{A}}}^{2}}}\\ -\frac{{\lambda }_{1}\left({x}_{{\rm{B}}}-x\right)}{2{\rm{\pi }}\sqrt{{\left({x}_{{\rm{B}}}-x\right)}^{2}+{z}_{{\rm{B}}}^{2}}}=0\end{array}$$

(2)

Simplification of equation 2 yields:

$$\frac{d\phi \left(x\right)}{dx}+\frac{{\lambda }_{1}}{2{\rm{\pi }}}\left(sin{\theta }_{{\rm{i}}}-sin{\theta }_{{\rm{r}}}\right)=0$$

(3)

Hence, the reflection of acoustic waves on such an interface is governed by the following generalized Snell’s law of reflection, which gives a nonlinear relationship between the angle of incidence θ_i and the angle of reflection θ_r:

$$sin{\theta }_{{\rm{r}}}-sin{\theta }_{{\rm{i}}}=\frac{{\lambda }_{1}}{2{\rm{\pi }}}\frac{d\phi \left(x\right)}{dx}$$

(4)

Note that equation 4 is in stark contrast to the conventional specular reflection. The phase change for the transmitted wave from point A in medium 1 to point C in medium 2 through refraction at point O between the two media can be derived in a similar manner:

$${\Psi }_{{\rm{t}}}\left(x\right)=\phi \left(x\right)+\frac{2{\rm{\pi }}}{{\lambda }_{1}}\sqrt{{\left(x-{x}_{{\rm{A}}}\right)}^{2}+{z}_{{\rm{A}}}^{2}}+\frac{2{\rm{\pi }}}{{\lambda }_{2}}\sqrt{{\left({x}_{{\rm{C}}}-x\right)}^{2}+{z}_{{\rm{C}}}^{2}}$$

(5)

where (x_C, z_C) is the position of point C and λ₂ = c₂/f is the wavelength in medium 2, with c₁ being the speed of sound. Consequently, the angle of incidence θ_i and the angle of transmission θ_t can be obtained by solving for the shortest acoustic path, as given below:

$$\frac{d{\Psi }_{{\rm{t}}}\left(x\right)}{dx}=\frac{d\phi \left(x\right)}{dx}+\frac{2{\rm{\pi }}}{{\lambda }_{1}}sin{\theta }_{{\rm{i}}}-\frac{2{\rm{\pi }}}{{\lambda }_{2}}sin{\theta }_{{\rm{t}}}=0$$

(6)

By simplifying equation 6, we derive the generalized Snell’s law of refraction as:

$$\frac{1}{{\lambda }_{2}}sin{\theta }_{{\rm{t}}}-\frac{1}{{\lambda }_{1}}sin{\theta }_{{\rm{i}}}=\frac{1}{2{\rm{\pi }}}\frac{d\phi \left(x\right)}{dx}$$

(7)

When Φ(x) is independent of x, equation 4 and equation 7 recover the conventional Snell’s law. However, if ϕ(x) is chosen to have a linear dependence on x, more specifically, ϕ(x) = βx, then equations 4 and 7 can be simplified to:

$$sin{\theta }_{{\rm{r}}}-sin{\theta }_{{\rm{i}}}=\frac{{\lambda }_{1}}{2{\rm{\pi }}}\beta $$

(8)

$$\frac{1}{{\lambda }_{2}}sin{\theta }_{{\rm{t}}}-\frac{1}{{\lambda }_{1}}sin{\theta }_{{\rm{i}}}=\frac{1}{2{\rm{\pi }}}\beta $$

(9)

In this case, the reflected (transmitted) wave has a specific angle of reflection (refraction), giving rise to the anomalous reflection and refraction governed by the generalized Snell’s law. Equation 8 means that the values of θ_r and θ_t can be controlled by adjusting the parameter β. It is worth noting that according to the generalized Snell’s law, the angles of reflection (or refraction) for incidence angles of +θ_i and −θ_i are not the same, which is fundamentally different from the case of a conventional interface between natural media. Furthermore, if ϕ(x) is designed to be a nonlinear function of x, then the angles of reflection and refraction depend on the position along the interface, which can be easily understood in the context of geometrical acoustics. This theory suggests the possibility of producing arbitrary manipulation over the reflected and transmitted acoustic beams by controlling the nonlinear function such that the local acoustic response at each point behaves differently.

In practice, such interfaces capable of imprinting phase discontinuities on propagating acoustic waves can be implemented by using a monolayer of unit cells of artificial structures, which is called an acoustic metasurface. It is worth stressing that acoustic metasurfaces do not have zero or near-zero thicknesses but rather subwavelength thicknesses; indeed, the unit cells constituting metasurfaces can be of arbitrary shapes and have vanishing dimensions only when compared with the wavelength. With extended wave-steering functionalities at reduced dimensions, acoustic metasurfaces are empowered with physics distinctly different from that of bulk metamaterials and thus enable new applications.

Although the concepts of the generalized Snell’s law and metasurfaces were first proposed in the realm of optics¹, a translation from optical metasurfaces to acoustic metasurfaces is not trivial owing to the innate differences between acoustic waves and electromagnetic waves. For example, despite the existence of an acoustic analogue of electromagnetic plasmonic layers for scattering cancellation, there is no direct acoustic counterpart of the resonant oscillation of conduction electrons at the interface, which is known as plasmonic resonance and is the mechanism of numerous optical metasurfaces^54,55. In addition, the effects associated with acoustic metasurfaces, which are not found in optic systems, must be carefully considered. For example, thermoviscous losses, which are frequency-dependent, are unique effects in acoustic systems with narrow channels. Although these losses are well-known phenomena in acoustics, the influence of these losses on acoustic metamaterials and acoustic metasurfaces requires further investigation⁵⁶. These losses can be accounted for numerically⁵⁷ or analytically⁵⁸, and their influence on the performance of acoustic metasurfaces has been investigated⁵⁸. Another effect found in acoustic systems is the acoustic–structure interaction, which occurs when sound impinges on the non-rigid boundary (or wall) of an acoustic metasurface⁵⁹. However, it has been revealed that the acoustic–structure interaction has a less significant impact than thermoviscous loss. The realization of acoustic metasurfaces can therefore be expected to still be challenging and require the exploration of fundamentally new physics^9,60,61,62.

In this Review, we overview the theory of acoustic metasurfaces and introduce the major types of acoustic metasurface devices, including the coiling-up space structure for elongating the propagating path^2,10, the hybrid structure comprising Helmholtz resonators and straight pipes for controlling the propagation phase while maintaining near-unity transmission³ and membrane-type metasurfaces with hybrid resonances⁷ (Box 1).

Box 1 Designs of acoustic metasurfaces

Coiling-up space structure

Acoustic metasurfaces based on coiling-up space structures with subwavelength dimensions force acoustic waves to propagate along a coiled path, which is substantially longer than the physical dimensions of the structure (see the figure, panel a). This longer path length allows the modulation of reflected waves and for the reflected phase shift to be tailored within the full 0–2π range. The effectiveness and simplicity of these acoustic metasurfaces have resulted in them receiving considerable attention since their inception. However, the zigzag structure must be designed to avoid excessive thermoviscous losses and for optimal impedance matching.

Helmholtz-resonator-like structure

In contrast to reflection-type acoustic metasurfaces, which have intrinsically high reflectivity, the problem of impedance matching is considerably more important when manipulating transmissive acoustic waves. The first attempt to simultaneously realize a high refractive index and high transmission was the design of a transmission-type metasurface unit cell comprising four Helmholtz resonators for flexible phase control and a straight pipe for introducing hybrid resonances that compensate for the impedance mismatch (see the figure, panel b). The resulting metasurface produces a tunable phase velocity and a near-unity transmission efficiency, and, remarkably, features a deep-subwavelength width that ensures fine spatial resolution of the phase profile.

Membrane-type structure

An acoustically reflecting surface can be modified to eliminate reflection by using a simple configuration (see the figure, panel c). By producing two resonances in a deep-subwavelength layer with weak absorption, extra impedance is added to the decorated membrane resonator to hybridize the two resonances. The resulting metasurface enables perfect absorption at a frequency close to the anti-resonance, despite the deep-subwavelength thickness. Although previous designs have realized narrowband sound absorption with thin absorbers without additional lossy materials^104,129, these designs need to dissipate the incident acoustic energy by exploiting the thermoviscous effect in the resonant cavities or narrow channels. By contrast, the membrane-type structure enables large variance in membrane displacement and therefore leads to total absorption when a very weak absorption coefficient is multiplied by a large energy density.

Metasurfaces for controllable reflection

In contrast to an electromagnetic wave, airborne sound is a scalar wave and propagates freely without a cut-off frequency inside a waveguide with rigid walls. This assumption is reasonable owing to the large difference in impedance between air and a solid, enabling an extreme elongation of the propagating path of the wave by using coiling-up space with labyrinthine configurations^{63,64,65,66,67,68,69,70}.

As a consequence of the association of the reflected phase shift with the propagating path, a coiling-up space structure with a tunable propagating path is a feasible way to construct acoustic-reflection-type metasurfaces^{2,10,11,71,72,73,74,75,76,77}. A simple type of coiling-up space structure, namely, a labyrinthine-like structure, constitutes the building block of an acoustic metasurface for controlling sound reflection (Fig. 2a). Acoustic waves enter the labyrinthine structure through the inlet, propagate in the coiled channel, are completely reflected by the hard boundary, backtrack inside the channel and finally exit the inlet, forming the reflected field. In a free space, the length of the propagating path from the inlet to the outlet is 2a_x. However, after introducing the space-coiling structure, the propagating path contains two zigzags, and its length is significantly increased. As a result, the reflected phase provided by the labyrinthine block is significantly delayed, which enables full control of the phase shift. Unsurprisingly, by varying the geometry of the coiled channel (for example, by changing the parameter t), the reflected phase can be tuned over a range of 2π (Fig. 2b). More specifically, a_x and a_y are fixed at λ₀/8, with λ₀ = 0.1 m being the working wavelength, which ensures the deep-subwavelength feature for the resulting metasurface.

Fig. 2: Acoustic-reflection-type metasurface.

a | A schematic of a specific labyrinthine unit (of width a_x and height a_y) that forms part of an acoustic-reflection-type metasurface. The labyrinthine unit consists of identical plates arranged to create a labyrinthine channel of width d. The channel is sealed in the y direction by using two additional plates (of thickness t). b | The phase shifts of waves reflected by four different types of labyrinthine units. The label (3, 2) indicates that three plates from the top and two plates from the bottom are used for the unit (as shown in panel a). c | Eight 3D-printed labyrinthine units capable of providing fully controlled reflected wave phase delay, with the parameters indicated by the dots in panel b. d | An analytical pressure field theoretically predicted for a beam-focusing metasurface. The rectangle indicates the area within which measurements (results shown in panel e) are performed. e | An experimental pressure field of a beam-focusing metasurface. φ, phase shift; λ, wavelength; p_i, incident phase; p_r, reflected phase. Adapted with permission from ref.¹⁰, APS.

To minimize the loss induced by viscous friction and thermal conduction inside narrow regions, four different types of labyrinthine unit (each with a specific number of plates and having a reasonable width) are used to provide sufficient phase delays. In this system, the notation (3, 2) refers to a labyrinthine unit with 3 and 2 plates extruding from the top and bottom, respectively (Fig. 2a). This configuration is sufficient to achieve a 2π-span phase delay by varying h, as evidenced by the red line in Fig. 2b. However, the width of the coiled channel, d, for the (3, 2) configuration is very small owing to the large number of plates. This small width implies greater dissipative losses than those in wider channels; therefore, it is not optimal to exclusively use the (3, 2) structure. If the number of plates is reduced, for example, in the (2, 2), (2, 1) and (1, 1) structures, building units with desired phase delays but wider channels and hence lower loss can be constructed. With this design strategy, eight labyrinthine units, whose geometrical parameters are indicated by the dots in Fig. 2b, are selected to provide the fully controlled phase shift with increments of π/4. The labyrinthine units are fabricated using fused deposition modelling (Fig. 2c).

With these eight labyrinthine units, any phase profile can be constructed. For example, the required phase profile along the y direction can be retrieved from the desired focusing field (Fig. 2d). The entire metasurface can then be formed by fitting the predefined phase profile using the eight units. The analytical results show that after incidence, the wave reflected from the metasurface focuses at the desired spot (Fig. 2d). This effect is confirmed by the experimental results (Fig. 2e). With a unique wave-steering ability, the metasurface opens exciting possibilities for designing compact acoustic components and may find applications ranging from ultrasound imaging to caustic engineering, where designing the shape of a focused trajectory of sound is needed.

In addition to the coiled-up labyrinthine structure, a planar surface using Helmholtz resonators can generate double reflections: an ordinary reflection and an extraordinary one that follows the generalized Snell’s law of reflection⁷². Considering the resonant nature of labyrinthine units, such designs inevitably have a limited working bandwidth. This limitation can be overcome by the fabrication of a reflective metasurface consisting of grooves with subwavelength width, which can arbitrarily control reflected wave fields without considerable bandwidth limitation⁷⁸.

Considering the importance of wavefront manipulation in acoustics, acoustic metasurfaces with exotic acoustical properties and reduced dimensionalities are expected to reveal new applications and may even revolutionize existing techniques. An example is the acoustic diffuser, which scatters sound energy in all directions and improves the quality of sound^{41,42,43,44,45}. More specifically, widely commercialized Schroeder diffusers proposed over 40 years ago have very bulky structures composed of an array of gratings whose depths may reach half the wavelength of the lowest-pitched sound to be diffusely scattered. This large depth limits their application in the low-frequency and even mid-frequency range⁸. However, using the concept of acoustic metasurfaces, an ultrathin Schroeder diffuser that is approximately ten times thinner than the conventional Schroeder diffuser has been developed (Fig. 3). The ultrathin diffuser consists of a 2D array of locally resonant elements (Helmholtz-resonator-like structures), with each being properly designed to produce a specific phase shift according to a certain quadratic residue sequence delineated by Schroeder’s theory. The simulation and experimental results show that the metasurface-based diffuser is highly efficient and has a performance similar to that of commercialized diffusers. However, the ultrathin diffuser uses less material and may result in lighter, more-compact and lower-cost diffusers. This metasurface-based diffuser may provide a roadmap to reflective wave manipulation and have far-reaching implications in architectural acoustics and noise control.

Fig. 3: A metasurface-based Schroeder diffuser.

a | A schematic of a 2D Schroeder diffuser (SD), including an inset (bottom) showing the cross section of the unit cells. b | A schematic of the proposed metasurface-based SD (MSD), including an inset (bottom) showing the cross section of a unit cell. c | The analytical and simulated relationship between the phase shift and the geometric parameter w at the centre (6,860 Hz) of the working frequency band. d | Simulated and measured diffusion coefficient (d_n) values for normal incidence (left) and 45° incidence (right) in the x–z plane versus frequency (f) for the broadband MSD (BMSD) and the conventional SD, respectively. λ, wavelength; D, width of a unit cell; w, neck width of the cavity. Adapted with permission from ref.⁸, APS.

Metasurfaces for controllable transmission

Acoustic metasurfaces are also capable of modulating the transmitted wavefront to achieve interesting properties, such as beam steering, focusing and the conversion of propagating waves into surface waves. In a similar fashion to the reflective case, fine phase modulation plays a key role in the design of transmissive acoustic metasurfaces. Another feature of transmissive cases, which may not be required for reflective cases, is the matching of impedance between the metasurface and its ambient environment. A natural solid is typically opaque for airborne sound because of the large impedance mismatch between the solid and air, which significantly suppresses the transmission efficiency of an acoustic device. Therefore, to enhance the performance of a transmissive acoustic metasurface, its unit must be tailored to minimize the impedance mismatch with respect to its surrounding material (for example, air).

A common way to demonstrate transmissive acoustic metasurfaces is to showcase a phenomenon called anomalous refraction (Fig. 1). Classical refraction derived from Snell’s law obeys the rule that the accumulated phase change across the interface is continuous. However, in an acoustic metasurface, the phase gradient on the surface adds an additional term to Snell’s law, as described by equation 7, and the refractive angle becomes different from the classical angle. This qualitative theory indicates that engineering the surface phase gradient enables the realization of almost any kind of wavefront modulation, including beam deflection^5,6,79 (Fig. 4a,b), focusing^64,80,81,82 (Fig. 4c) and conversion from propagating into surface-bound modes^5,6,79 (Fig. 4a,b). From a detailed theoretical analysis based on a mode-coupling theory⁶, it is possible to quantitatively evaluate the transmittance of an acoustic metasurface comprising periodically repeated supercells, whose units are designed to cover a phase change of 2π while maintaining high transmission.

Fig. 4: Transmissive metasurfaces.

a | A fabricated supercell of an acoustic metasurface consisting of tapered labyrinthine structures. b | The measured field pattern of a sound wave transmitted through the metasurface at normal incidence (left). The dashed line indicates the surface normal, and the solid line indicates the direction of the transmitted wave. The near-field evanescent mode on the transmitted side of the metasurface is measured for an incident angle of 25° (right). c | Focusing of a normal incident plane wave through a metasurface. d | A self-bending beam through a metasurface. λ, wavelength; ξ, phase gradient. Panels a, b are adapted from ref.⁵, Springer Nature Limited. Panel c is adapted with permission from ref.⁸¹, AIP. Panel d is adapted with permission from ref.³, APS.

Similar to the reflective wave case, space-coiling structures^36,65,66 are promising candidates for engineering a surface phase gradient across a subwavelength thickness. However, the impedance of a space-coiling structure or its declination, namely, a labyrinthine structure, is usually poorly matched to the impedance of air^63,65,66. To overcome this limitation, various designs have been proposed, such as tapered labyrinthine metamaterials⁸³, spatially varied coiling-slit units^79,84 and impedance-matching layers of gradient index⁸⁵.

Tapered structures, for example, horns, are widely used in musical systems and loudspeakers for optimizing impedance matching and increasing the operating bandwidth. The gradually varying cross-sectional area of a horn-like structure diminishes the mismatch of the transverse wave component caused by a sudden change in the cross-sectional area and therefore significantly enhances the efficiency of power transmission. For example, a horn-like labyrinthine metamaterial with a spiral-shaped geometry, high transmission efficiency and non-resonant dispersion has been proposed and investigated^5,83. A supercell containing six types of such horn-like labyrinthine cells with different levels of spirallings (Fig. 4a) is able to cover a phase change range of 2π while maintaining a uniform subwavelength thickness in the frequency range of 2,500–3,500 Hz (ref.⁵). A 1D periodic array of the supercell forms a metasurface whose phase gradient is approximately 2π/p, where p is the array period of the supercell. A supercell made from acrylonitrile butadiene styrene thermal plastics via the fused filament fabrication 3D printing method revealed several unique properties, including the conversion of propagating waves into surface waves, beam steering and apparent negative refraction (Fig. 4a).

In a different approach, a spatially varying coiling-slit was used as the building unit of the metasurface⁷⁹. Each unit consisted of a number of rigid horizontal bars. By changing the number and geometry of these horizontal bars, the effective air path and the impedance can be adjusted, offering control of the amplitude and phase response. A supercell with eight units of the same thickness but different numbers of rigid bars was designed for a working frequency of 2,550 Hz. Each unit supports almost unitary transmission, and the phase shift increases with a step of approximately π/4 between the nearest neighbours; as a consequence, the supercell covers the entire 2π phase range. Similar to the previous horn-like case, a metasurface was constructed by a 1D array of the supercell, whose transverse phase gradient was again determined by 2π/p. The anomalous refraction of airborne sound for various incidence angles was experimentally verified with a sample fabricated with thermoplastics via 3D printing.

In addition to space-coiling structures, acoustic Helmholtz resonators, a common element in acoustic devices, have been considered as building blocks for acoustic metasurfaces. Although a single Helmholtz resonator provides a limited phase shift, four Helmholtz resonators connected in series can achieve a wide range of phase shifts³. However, this connection increases the impedance mismatch with respect to air compared with a single Helmholtz resonator, which leads to lower transmission. To address this problem, Helmholtz resonators connected in series are coupled with a straight pipe of a tunable height and a fixed width of λ/2. The transmission is enhanced owing to the coupling between the Helmholtz resonance and Fabry–Perot resonance of the pipe. A self-bending beam is experimentally demonstrated using a metasurface fabricated from thermoplastics via 3D printing (Fig. 4d).

Although anomalous refraction by engineering the phase gradient was the initial interest of studying transmissive acoustic metasurfaces, other intriguing applications have been realized. Three examples of such applications are discussed here: asymmetric sound transmission, acoustic holography and acoustic vortex.

Asymmetric acoustic transmission refers to unusual wave phenomena characterized by different transmission efficiencies of a specific mode, such as a plane wave mode incident from two opposite directions in rationally designed linear systems, where reciprocity still holds. There has been a surge of interest in the physics and applications of this phenomenon because such materials affect incident sound waves from opposite directions unequally. Artificial materials engineered with the asymmetric acoustic transmission characteristic may be useful for noise control and energy-harvesting applications⁸⁶. Asymmetric sound transmission can be achieved using acoustic metasurfaces by integrating a near-zero-index metasurface (ZIM) with a gradient-index metasurface (GIM)^23,27. A plane wave impinging normally on the GIM is deflected by an angle dictated by the generalized Snell’s law (Fig. 5a). Then, the deflected beam experiences total reflection owing to the near-zero critical angle of the ZIM. However, a plane wave impinging normally on the ZIM will pass through both metasurfaces.

Fig. 5: Applications of transmissive metasurfaces.

a | The principle of a metasurface for asymmetric transmission. b | The measured transmitted sound fields show asymmetric transmission. The acoustic fields of the negative direction (left) and positive direction (right) are shown. A photo of a prototype of an asymmetrical transmissive metasurface is also shown (lower). c | The top panel indicates that the phase distribution shown will produce a letter A at the image plane. The simulation and experimental results at different planes (middle and bottom panels, respectively). The letter A can be seen on the image plane. d | A schematic of the metasurface with eight sections assigned with different phase shifts. The vortex sound field produced from the metasurface shows spiral phases. θ, rotation angle of metasurface relative to the original position; λ, wavelength; ASA, angular spectrum approach. Panel a is adapted with permission from ref.²⁷, AIP. Panel b is adapted with permission from ref.³², APS. Panel c is adapted from ref.⁹², Springer Nature Limited. Panel d is adapted with permission from ref.²⁹, APS.

A simpler method for asymmetric acoustic transmission using a single acoustic metasurface has been proposed³² (Fig. 5b). In contrast to the previous method, this simpler route works only for oblique angles of incidence. Another reason for the success of this route is the intrinsic loss in the GIM, which was either ignored or minimized in previous GIM-based designs. For negative incidence, high-order diffraction can be excited under oblique angle incidence, and because multiple reflection is associated with high-order diffraction, the transmission loss is amplified, leading to very small transmission. Conversely, for positive incidence, high-order diffraction is not excited; therefore, the transmission is not significantly weakened and can be as much as 10 dB higher than for negative incidence. It is noted that these two methods do not rely on breaking the reciprocity, which may require active acoustic components⁸⁷ or nonlinearity. Other routes are available for asymmetric sound transmission based on acoustic metasurfaces^88,89,90.

Acoustic holography enables the recording and reconstruction of information related to the acoustic field^52,91. Acoustic holography is a challenging task because conventional approaches rely on complicated and expensive active phased arrays. In a recent study⁹², acoustic holography was realized by using a 2D array of metasurface unit cells. A set of 12 unit cells, each representing a certain phase shift, was used to form the 2D passive array, operating at a frequency of 4 kHz. The array consisted of 512 3D-printed unit cells, and the unit cells covered a phase change of 2π across the metasurface. The unit cells were arranged such that their phase shifts followed a distribution determined by a modified weighted Gerchberg–Saxton algorithm. The resulting phase distribution produces a desired pressure field pattern on a predetermined plane parallel to the array, such as a letter A (Fig. 5c) or a multi-foci pattern. The device functions in free space but can also produce desired wave fields in inhomogeneous media. For example, the metasurface array can replace active arrays to focus ultrasound through the skull to ablate brain tumours or disintegrate clots in the treatment of stroke⁹³. The accuracy of acoustical holography is improved if both the phase and amplitude can be modulated^84,94.

Acoustic vortices have been generated using metasurfaces²⁹. Such systems are formed by dividing the source plane into equal segments (similar to a pie chart with uniform slices) and assigning growing phase shifts to each segment. For example, a metasurface divided into eight sections with phase shifts ranging from 0 to 7π/4 with increments of π/4 (Fig. 5d) can produce a metasurface with a first-order acoustic vortex with spiral phases and orbital angular momentum. Other set-ups have been proposed^28,95,96,97, and applications of acoustic vortices have been studied^{98,99,100,101,102}.

Metasurfaces for acoustic absorption

Reducing noise levels preserves our hearing for longer periods and lowers our annoyance to noise, resulting in a higher quality of life. Currently, these issues are more important owing to transportation in cities, with low-frequency noise being especially pernicious. Sound absorption is the main way to abate noise, but this is not effective over the entire noise spectrum. Classical sound-absorbing materials have fixed absorption spectra, which can be adjusted only by increasing or decreasing the thickness, resulting in bulky and heavy absorbers³⁴. It is desirable to create a new generation of sound absorbers that can be tailored to fit the noise spectrum, having a reduced-size feature and a deep-subwavelength thickness for better accommodation.

Acoustic absorption and attenuation in the low-frequency regime (50–500 Hz) have been a scientific and technological challenge for physicists and engineers. More specifically, the absorption and attenuation of low-frequency sound are challenging because the intrinsic dissipation of materials is typically weak in the low-frequency regime³³. The conventional means of acoustic absorption, such as viscoelastic materials, porous and fibrous materials¹⁰², gradient-index materials¹⁰³ and microperforated plates with cavities behind them¹⁰⁴, are either bulky or structurally weak^33,105,106. In addition, such conventional absorbers usually have dimensions comparable to the larger wavelengths of low-frequency waves, making them impractical for low-frequency implementations.

Since the 2000s, the field of acoustic metamaterials has expanded to include a wide range of material properties and functionalities as well as new applications, including the absorption, attenuation and mitigation of acoustic waves^26,35,40. Currently, few demonstrations of acoustic absorption or attenuation have been made in the low-frequency regime^{37,105,106,107,108,109,110,111,112,113}. These demonstrations are based on (but not limited to) two configurations, namely, membrane-type and plate-type metamaterials, which are either structurally weak or operate at frequencies slightly higher than the targeted range. More recently, sound-absorbing structures based on the causality constraint have been reported, with the direct relation between the absorption spectrum and the structure thickness being discussed and a design strategy for tailoring broadband acoustic absorbers being proposed³⁴.

2D materials with subwavelength thicknesses can provide some intriguing functionalities that have enabled the development of a new generation of acoustic absorbers. In this section, sound-absorbing acoustic metasurfaces for the low-frequency regime based on impedance-matched metasurfaces with hybrid resonances and coiling-up space geometry are discussed. We delineate their concepts, underlying physical mechanisms and absorbing properties.

Impedance-matched metasurface absorbers

Acoustic absorbers based on an impedance-matched surface with hybrid resonances arise if an acoustically reflecting surface becomes impedance-matched to incoming sound waves⁷ (Fig. 6a). Incident waves on such surfaces generate no reflection, and no transmission is allowed⁷. Hence, the metasurface almost perfectly absorbs the energy of the incident acoustic wave. The simple design of this metasurface incorporates a reflecting membrane resonator consisting of an elastic membrane decorated with a platelet and a reflecting hard surface, between which a gas with a small adiabatic index is sealed (Fig. 6a). The decorated membrane resonator is characterized by two resonant modes: one mode related to the oscillation of the platelet and the other mode related to the oscillation of the surrounding elastic membrane (Fig. 6b). The sealed gas and reflecting surface add extra impedance in series to the decorated membrane resonator and, as a result, the resonance conditions are changed. The resonances of the decorated membrane resonator are forced to hybridize, forming new resonant hybrid modes in which the absorption conditions are realized. This hybrid resonance-based design requires only material with weak intrinsic dissipation to achieve total absorption, which sets apart the physical mechanism underlying the absorption from the traditional absorption mechanisms involved when using lossy materials. More specifically, the mechanism is that the variance of membrane displacement is decoupled from the radiation mode; this variance can be very large despite the low dissipation coefficient of the material. This large variance of membrane displacement leads to total absorption when a small absorption coefficient is multiplied by a large energy density. The absorption properties of impedance-matched metasurfaces show an extremely sharp and almost perfect absorption peak, confirming the impedance match with air. This constructed impedance-matched absorbing metasurface typically has a deep-subwavelength thickness and can operate at very low frequencies (~150 Hz)⁷. Nonetheless, the applicability of the metasurfaces in some scenarios could be challenging owing to their fragility and narrowband property.

Fig. 6: Absorbing metasurfaces.

a | A schematic of an impedance-matched metasurface composed of a decorated membrane (with radius a) and a reflecting hard surface, between which a gas is sealed in a cell (of depth s). Here, k represents the incident wavevector. b | An illustration of the two lowest-frequency eigenmodes of a decorated membrane, where W is the normal displacement of the membrane, normalized to the sound wave amplitude W_s. The flat rectangle indicates the platelet, and the red and blue curves the membrane. c | A schematic of a coiled-up metasurface composed of a perforated plate (grey region; thickness t, hole diameter d and lateral dimension a) and a coiled back-chamber (blue region; thickness w and coiled beam thickness b). d | Theoretical results showing perfect absorption at a frequency of 125 Hz. e | A coiled metasurface (acoustic absorber) with a thickness of 1 cm and diameter of 10 cm. f | Numerical and experimental results for the fabricated acoustic absorber. Panels a, b are adapted from ref.⁷, Springer Nature Limited. Panels c, d are adapted with permission from ref.⁹, AIP.

Ultrathin acoustic absorbers

Ultrathin, near-perfect acoustic absorbers have been developed based on coiled absorbing metasurfaces, which rely on sound waves being effectively slowed down in high-refractive-index materials⁹. This slowing-down-of-sound effect is achieved by coiling up the wave propagation space through curled channels (for example, spirals, labyrinths or zigzags), creating substantial phase delays^63,67. The most important function of this concept is its ability to shrink bulky structures to the deep-subwavelength scale while also causing large dissipation of the impinging acoustic energy, generating a near-perfect absorption provided that resonance and impedance-matching conditions are satisfied. Therefore, there has been a growing effort over the past few years to explore acoustic absorption based on the concept of coiled metasurfaces, which could overcome the challenges related to the low-frequency airborne sound regime.

For example, a coiled absorbing metasurface for very low frequencies is based on a soundless spiral⁹ (Fig. 6c–f). The metasurface is composed of a centred perforated plate and a coiled coplanar air chamber. To realize perfect or near-perfect absorption, this metastructure was designed to simultaneously satisfy two conditions: a resonant state and impedance matching with the surrounding air. These conditions cause all the acoustic energy to be transferred into the coiled chamber, rather than reflected, and to be finally absorbed within the perforated hole owing to thermoviscous losses. Acoustic waves travel through the channel, which increases the total propagation length of the wave, leading to a low sound velocity and high acoustic refractive index. This promotes the dissipation of the acoustic energy through conversion into heat. This near-perfect absorber consisting of a coiled metasurface operates like an acoustic sink. All the impinging sound energy is completely redirected and absorbed within the perforated hole and dissipated as heat (Fig. 6c,e). It is worth noting that the properties and functionalities of the metasurface depend only on the design of its structure rather than the nature of its composition. Indeed, in this so-called materials-by-design approach, an acoustic absorber can be tailored and fabricated from any rigid material.

The implementation of such a coiled absorbing metasurface in a noisy environment and for a myriad of applications is straightforward. Its resistance, reliability and flexibility to be made of any rigid material make this concept one of the most elegant systems for addressing low-frequency sound absorption. Similar to the impedance-matched metasurface with hybrid resonances, the coiled metasurface has to be further investigated to increase its working bandwidth.

Design strategy of acoustic metasurfaces

The strategy for the design of acoustic metasurfaces depends on the targeted physical properties and applications (reflection, transmission and absorption). A thorough assessment of the design choice should take place before tackling specific applications. The main metasurface designs are based on the Helmholtz-resonator-like structure, membrane-type structure and coiling-up space structure. Metasurfaces based on Helmholtz-resonator-like elements have the advantage of being easily fabricated and tunable. The metasurfaces based only on Helmholtz resonators are mostly suitable for controllable reflection (more specifically, reflection, retroreflection¹¹⁴ and diffuse reflection). Metasurfaces based on Helmholtz-resonator-like elements depend on the local resonance and, in general, are thinner and simpler in design than their coiling-up space counterparts. However, the advantages of coiling-up space structures are in non-transmission applications owing to impedance mismatch, generating dissipation in labyrinthine channels and slowing down the effective phase velocity. In most cases, such a concept requires a trade-off between the thickness of the metasurface and thermoviscous dissipation induced by the coiled channels, the constituent materials and the fabrication process owing to the complexity of the design. Concerning the membrane-type metasurface configuration, it has been proved that such a metasurface yields the advantage of being very thin and particularly efficient for sound absorption in the low-frequency regime. It nevertheless exhibits a significant disadvantage of being flimsy and more complex to fabricate.

Outlook

The field of acoustic metasurfaces has rapidly grown over the past 5 years and is propelled by the desire to control the propagation of acoustic waves by compact structures. In the designs of acoustic metasurfaces for reflection, transmission and absorption applications, precise control of the phase and amplitude of acoustic wave propagation is required. This task can be achieved by using existing acoustic artificial structures of either a resonating or non-resonating nature. Typical structures include Helmholtz-resonator-like structures, coiling-up space structures and membrane-type structures.

Despite great achievements, more remains to be done in the quest for sound manipulation at will with thin materials. An overarching challenge is the practical implementation of acoustic metasurfaces. Most acoustic metasurfaces are narrowband and operate at low frequencies (below 10 kHz). To enhance their performance over a broad bandwidth, many acoustic metasurfaces with different working frequencies can be integrated. However, this strategy may increase the size of the structure and defeat the purpose of acoustic metasurfaces. Thus, new design principles are needed to create compact acoustic metasurfaces that can operate over a broad frequency range. One candidate is an active material^115,116 (for example, a piezoelectric material), which is emerging as an important direction in the field of acoustic metamaterials¹¹⁷. Effective material responses that are not possible with passive materials are realized and can even be tuned by active materials^118,119. Meanwhile, the realization of high-frequency acoustic metasurfaces calls for more sophisticated fabrication techniques. Advances in additive manufacturing and 3D printing, which have been crucial for the development of mechanical and acoustic metamaterials, may be the origin of such techniques^120,121.

Another challenge is the intrinsic thermoviscous loss arising from the deep-subwavelength channels in these metasurface structures, which affects the performance of the acoustic metasurface^56,58. This loss may be circumvented by creating active metasurfaces. The classical ones, which are passive and generally have a fixed geometry, are hindered by the bandwidth of the working frequency and the invariable functionality. With active control, for example, soft metasurfaces controllable with tension can enrich the functionalities and performances of the metasurfaces. Another exciting prospect in the field of metasurfaces is parity-time (PT)-symmetrical and non-Hermitian acoustics¹²². It is well known that intrinsic losses inside metasurfaces can hinder their properties and performance, leading to, for example, low transmitted energy. With the emergence of PT-symmetrical and non-Hermitian acoustics, integration of a gain material in metasurfaces to compensate for their intrinsic loss could lead to metasurfaces with new functionalities, for example, the ability to access the exceptional points (a hallmark in PT-symmetry physics) and topologically protected one-way propagation. To a similar extent, acoustic metasurfaces can also benefit from the development of Willis coupling^123,124, which is another emerging topic in wave physics.

In addition to acoustic metasurfaces for airborne sound, acoustic metasurfaces that can operate in water or other fluids may be used in underwater acoustics, cloaking¹²⁵ and medical applications, including bioimaging and therapeutics^126,127. Compared with air, water has a lower contrast in acoustic properties to most solid materials, which favours the design of structures with a desired phase and an impedance matched to the water environment. However, the rigid-wall assumption, which is crucial in many metasurface unit cells, becomes less accurate, and the viscous layer complicates the propagation path and increases loss.

Another approach to improve acoustic metasurface functionalities can be realized by introducing functional materials as constituents to produce so-called multifunctional metasurfaces. On the basis of recent advances in additive manufacturing, the idea is to complement acoustic metasurfaces using piezoelectric or thermoelectrical material coatings to produce and improve new physical and engineering effects, such as simultaneous sound absorption and acoustic energy harvesting. This feature can be an innovative way to conceptualize the next generation of acoustic metasurfaces.

New ideas in the field of acoustic metasurfaces, beyond those reviewed here, will certainly emerge in the near future, with more powerful abilities to manipulate sound waves in various ways that are closely related to our everyday life, such as acoustic energy harvesting^11,73,128 and noise abatement. Thus, we conclude that the future of acoustic metasurfaces is sound and bright.