Main

V1298 Tau is a young (10–30 Myr), approximately solar-mass star (1.10 ± 0.05 M⊙) in the Taurus star-forming region2,4,5,6,7,8. Observations by NASA’s Kepler space telescope in its extended K2 mission9 revealed transits of the star by four different planets, each larger than Neptune2,3. The V1298 Tau planets occupy a sparsely populated region of the observed exoplanet period versus radius plane. As a young system of large planets, it provides a crucial snapshot of planetary architecture just after formation, serving as the ‘missing link’ between protoplanetary disks and the mature systems found by Kepler3. Measuring their masses and orbits is, therefore, a key test of planet formation theories and allows us to witness early evolutionary processes, such as atmospheric mass loss, that sculpt planetary systems over billion year timescales.

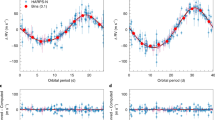
Between 2019 and 2024, we observed 43 other transits of all four planets using both space- and ground-based telescopes. This campaign successfully recovered the previously lost outermost planet, V1298 Tau e, and resolved a long-standing period ambiguity10 (Methods). We performed homogeneous and self-consistent modelling of all transit data from 2015 to 2024. After determining the transit shape parameters, we fit the midpoint of each transit individually (Methods). The transit-timing variations (TTVs) are shown in Fig. 1. All planets exhibit significant TTVs with amplitudes ranging from  approximately 50 min to 100 min. Moreover, the TTVs of the c–d pair are anticorrelated, as are those of the b–e pair. This indicates that the c–d and b–e interactions dominate over other pairwise interactions.

Fig. 1: TTVs in the V1298 Tau system.
figure 1

Top left, points show the transit times of planet c measured against a reference linear ephemeris; error bars represent 1σ uncertainties. Grey curves show credible transit times drawn from the N-body models described in the text. Bottom left, same as above but for planet d. The interactions between c and d are nearly sinusoidal and anticorrelated. Top and bottom right, the same but for planets b and e. The TTVs of b and e are also sinusoidal and anticorrelated.

Full size image

Previous works have developed analytic models of TTVs applicable to certain orbital configurations11,12. Other works have developed N-body TTV models based on a dynamical integration of the star–planet system subject to Newtonian gravity (for example, refs. 13,14,15). Analytic models are generally faster to evaluate, have fewer free parameters and offer a clearer connection between the system properties and the TTV waveform. N-body models, with more free parameters, are slower to evaluate but can completely describe any star–planet system.

Most TTV studies in the literature treat planets from the 4-year Kepler mission. These studies had the benefit of near-continuous sampling over a full TTV period. The sparse sampling of our dataset presents different challenges. We, therefore, used analytic models to build our intuition of the system dynamics before undertaking a full N-body analysis. The nature of TTV interactions depends on the proximity to resonance Δ, defined as \(\varDelta =\frac{{P}_{2}}{{P}_{1}}\frac{j-1}{j}-1\), where P1 and P2 are the orbital periods of the inner and outer planets, respectively, and j is a positive integer defining the resonance, with smaller Δ associated with larger TTVs. In this system, Δcd = 0.2%, Δdb = −2.7% and Δbe = 0.8%. Given the strength of the c–d and b–e interactions over d–b interactions, we used analytic models to treat the c–d and b–e interactions separately. The analytic models indicated low masses and low eccentricities (Methods).

Guided by our analytic results, we then performed a full N-body dynamical fit to the transit times to derive a final, robust set of planet parameters. This model accounts for all gravitational interactions in the system simultaneously, including subtle, higher-order TTVs that can help break degeneracies inherent in our analytic models. Details of our N-body model, Bayesian statistical framework and Markov chain Monte Carlo sampling are provided in Methods.

Figure 1 shows a selection of credible models drawn from our posterior samples, along with the timing data. The models fit the data well, with increased scatter where observations are sparse. The credible range of each planetary parameter is listed in Table 1. We find masses Mc = 4.7 ± 0.6 M⊕, Md = 6.0 ± 0.7 M⊕, Mb = 13.1 ± 5.3 M⊕ and Me = 15.3 ± 4.2 M⊕ (the uncertainties correspond to the 68% highest density intervals of the marginal posteriors). In addition, the planetary eccentricities are all  less than about 1%. A detailed dynamical analysis (Methods) confirms that this solution corresponds to a long-term stable and non-resonant orbital architecture. The N-body results are consistent with the analytic results at 2σ or better with smaller uncertainties. The N-body model is a more complete description of the planetary dynamics than our analytic models and includes effects like synodic chopping16 and d–b interactions. It exhibits root mean square (r.m.s.) values of 4–11 min, consistent with our analytic models. Henceforth, we adopt and interpret the N-body results. The masses of planets b and e have substantial fractional uncertainties but are distinct from zero; they are larger than 4.8 M⊕ and 7.8 M⊕ to 95% confidence. The broad uncertainties stem from the well-known mass versus eccentricity degeneracy11. Extremely low masses and high eccentricities would produce b–d interactions that are inconsistent with the data.

Table 1 Planetary parameters
Full size table

The combination of low planet masses with the youth of the host star makes Doppler mass measurements challenging. The expected semi-amplitudes of the radial velocity are  approximately 1–2 m s−1, which are two orders of magnitude smaller than the stellar activity signal. For comparison, the measured r.m.s. values of the radial velocity in existing datasets for V1298 Tau are 260 m s−1, 197 m s−1 and 195 m s−1 for HARPS-N, CARMENES VIS and CARMENES NIR, respectively7. The challenge of this high stellar activity has been a central theme in recent studies of the system17,18,19,20. Reference 7 simultaneously modelled planetary and activity radial velocity variations, reporting masses of 203 ± 60 M⊕ and 367 ± 95 M⊕ for planets b and e, an order of magnitude larger than our TTV results. However, ref. 21 found that the planet-activity model is biased towards over-predicting planet masses when stellar activity dominates. Given these challenges and the risk of systematic bias, a TTV-only analysis provides, at present, the most robust and unbiased mass constraints for this system. Notably, our dynamical mass for planet b is consistent with independent atmospheric constraints. A recent analysis of transmission spectra captured by the James Webb Space Telescope by ref. 22 inferred a mass from the atmospheric scale height that is in excellent agreement with our TTV result. That two independent methods—one based on gravitational dynamics and the other on atmospheric structure—yield such consistent results provides a powerful validation of our measurement.

The planetary densities that we measured in the V1298 Tau system are among the lowest exoplanet densities recorded. The only known multi-planet system exhibiting comparably low densities is, perhaps not coincidentally, the young (approximately 300 Myr) transiting system Kepler-51, for which mass measurements were also made through TTVs23,24,25,26,27, although V1298 Tau is significantly younger and more compact. Figure 2 places the V1298 Tau planetary system in the context of the broader, mature exoplanet population. Figure 2a shows these young planets positioned above the radius gap28. To trace their future evolution, we overplot the ‘fluffy’ planet scenarios from ref. 29, which are the most relevant analogues. These models bracket a range of possibilities by assuming two different core masses (5 M⊕ and 10 M⊕) and two stellar extreme-ultraviolet activity levels that result in different degrees of atmospheric mass loss. The 5 M⊕ scenario is a particularly strong analogue, as our own interior structure modelling (Methods) constrains the core masses of planets c and d to be 4–6 M⊕ (1σ). The resulting tracks indicate that some planets will contract across the gap to become super-Earths, whereas others will become sub-Neptunes, thus directly tracing the formation of the bimodal radius distribution observed by Kepler. Figure 2b reveals substantial H/He envelopes30, although their final evolved states may have densities that are degenerate with water worlds31.

Fig. 2: Planetary radius versus orbital period and planetary mass.
figure 2

a,b, Planetary radius versus orbital period (a) and planetary radius versus planetary mass (b) for the V1298 Tau system (red filled circles); error bars represent 1σ uncertainties. The low-density planets of the Kepler-51 system are shown for comparison (purple squares), along with kernel density estimates of the distributions of well-characterized exoplanets (shaded contours), drawn from the NASA Exoplanet Archive (n = 624 planets with mass and radius uncertainties less than 20%, P < 150 days and host Teff = 4,500–6,500 K to exclude M dwarfs). The parameters of the Kepler-51 planets were sourced from the ‘outside 2:1’ solution in Table 6 of ref. 27. Theoretical radius evolution tracks from ref. 29 are shown as vertical dashed lines. The terminal radii at 5 Gyr from that work are shown as open triangles. The colour indicates the assumed core mass (red for 5 M⊕ and black for 10 M⊕). The orientation represents the stellar extreme-ultraviolet activity level (upwards for high activity and downwards for low activity). The black dashed line in a depicts the observed location of the radius valley28. Theoretical mass–radius relations for different planet compositions from ref. 31 are shown in b as dashed lines. Grey dotted lines indicate theoretical mass–radius relations for Earth-like cores with H/He envelopes with various mass fractions from ref. 30, calculated for an age of 100 Myr and an insolation of 10 F⊕.

Full size image

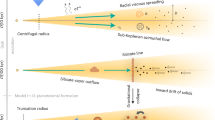
The low masses and densities of the V1298 Tau planets have significant ramifications for planet formation theory. Theoretical modelling indicated that planet c (Mc = 4.7 ± 0.6 M⊕) was one of the best targets for constraining its formation history: a mass higher than 10 M⊕ would be consistent with standard core-accretion models, whereas a mass lower than 6 M⊕ would require a ‘boil-off’ phase during protoplanetary disk dispersal32. Such a phase occurs when the pressure support of the disk is removed swiftly, triggering profuse atmospheric mass loss through a Parker wind and rapid cooling, leaving behind an envelope with lower entropy and a longer Kelvin–Helmholtz timescale compared with predictions from standard core-accretion models33,34.

To explore the possible formation channels for the V1298 Tau planets, we modelled the planets as two-layer objects consisting of an Earth composition rocky core ensheathed in a H/He envelope. The initial envelope entropy is parameterized by its Kelvin–Helmholtz contraction timescale. We ran a dense grid of models spanning core mass, initial envelope mass fraction and initial envelope entropy at the location of each planet in the system and evolved them to the current age of the system.

Figure 3 shows posterior distributions for the initial properties of all four planets, providing a deeper insight into the system architecture. The right panel confirms that the inner planets c and d require low-entropy initial states (much greater than 30 Myr Kelvin–Helmholtz cooling times), whereas the less-irradiated outer planets b and e remain unconstrained. The left panel, however, reveals a notable uniformity: all four planets are consistent with having similar core masses (approximately 4–6 M⊕) and initial envelope mass fractions (approximately 0.1–0.2). This indicates that the system is an exemplar of the ‘peas in a pod’ phenomenon at formation35, implying its present-day size diversity is a transitory phase driven by different levels of photoevaporation.

Fig. 3: Posterior distributions for the initial properties of the V1298 Tau planets.
figure 3

The posteriors were derived by applying the planetary evolution and mass loss framework of ref. 32 to our measured masses and radii for planets c (red), d (orange), b (green) and e (blue). Left, initial envelope mass fraction versus core mass. Right, initial Kelvin–Helmholtz cooling timescale versus core mass. Contours show the 1σ and 2σ credible regions. (Note that the jagged appearance of some contours is a numerical artefact of the discrete core mass grid used in our analysis; see Methods for more details). The vertical dotted line in the right panel at 10 Myr marks the approximate upper limit for standard high-entropy formation models. These models are strongly disfavoured for the inner planets c and d, whereas for the less-irradiated outer planets b and e, the method lacks the statistical power to distinguish between high- and low-entropy scenarios.

Full size image

Extended Data Fig. 1 shows that the measured masses and radii of planets c and d lie outside the region of parameter space accessible to standard, high-entropy core-accretion models. As the illustrative tracks in the figure demonstrate, only lower-entropy (boil-off) models can simultaneously satisfy both the mass and radius constraints after accounting for 23 Myr of evolution and mass loss. During boil-off, the planetary envelope becomes over-pressurized and expands hydrodynamically, carrying away significant internal energy and leaving behind a cooler interior33,34,36. Although our measurements support boil-off for the inner planets, recent atmospheric retrievals indicating a high internal temperature for planet b37 present a possible tension that merits further investigation.

Theoretical modelling of the system under the influence of extreme-ultraviolet- and X-ray-driven photoevaporation indicates that these planets will continue to lose mass over the next 100 million years8,29, even though they have already experienced significant atmospheric loss. For our measured masses, standard evolutionary models predict that all the planets will retain a small fraction of their initial atmospheres, although the inner two could become stripped, depending on the future spin evolution of the star29. Interestingly, observational searches for continuing atmospheric escape have so far yielded inconclusive results5,38,39,40, possibly because strong stellar winds act to suppress planetary outflows41,42,43.

Methods

Transit observations and analysis

We analysed a heterogeneous dataset of light curves from space- and ground-based telescopes (Supplementary Table 1) to measure transit times for the ultimate purpose of modelling TTVs. We used PyMC344, exoplanet (https://docs.exoplanet.codes/en/stable/)45 and starry46 to fit the light curve, incorporating tailored models for correlated noise and instrumental systematics appropriate for each dataset.

Our analysis of the K2 and Transiting Exoplanet Survey Satellite (TESS) light curves involved two distinct approaches with different noise models. For the joint analysis of all transits in both light curves (described below), we modelled stellar variability as a Gaussian process47. By contrast, for measuring individual transit times (see below), a third-order basis spline was sufficient to model the local correlated noise.

To account for systematics in the Spitzer data, we used pixel-level decorrelation (PLD)48, which uses a linear model with a design matrix formed by the PLD basis vectors (see below for more details). For the ground-based datasets, we included a linear model with a design matrix formed by airmass, pixel centroids, and the pixel response function peak and width covariates, when available.

The limb-darkening coefficients were calculated using stellar parameters from ref. 2 by interpolation of the parameters tabulated by refs. 49,50. These were fixed for individual transit fits but sampled with uninformative priors in the joint K2 and TESS analysis described below.

We used Broyden–Fletcher–Goldfarb–Shanno optimization51 as implemented in scipy.optimize for initial parameter estimates, followed by posterior sampling with the No-U-Turn Sampler52, an efficient gradient-based Hamiltonian Monte Carlo sampler implemented in PyMC3. The chains were well mixed (Gelman–Rubin statistic  less than about  1.01) with negligible sampling error.

We first performed a joint fit of K2 and TESS data assuming a linear ephemeris (see below). We then measured all individual transit times uniformly using Gaussian priors from the joint fit for Rp/R⋆, b (the transit impact parameter), and T14 (the total transit duration), and uniform priors for Tc (the transit centre time) centred on predicted times. We verified that Tc posteriors were Gaussian and isolated well from prior edges.

In all individual transit fits, we assumed Gaussian independent and identically distributed noise and included a jitter parameter σjit to account for underestimated photometric uncertainties. The log-likelihood was, thus,

$$\text{ln}{\mathcal{L}}=-\frac{1}{2}\text{ln}| \varSigma | -\frac{1}{2}{{\bf{r}}}^{{\rm{T}}}{\varSigma }^{-1}{\bf{r}}+{\rm{const.}},$$

where Σ is the diagonal covariance matrix with entries equal to the total variance (that is, the ith entry is \({\sigma }_{{\rm{tot,}}i}^{2}={\sigma }_{{\rm{obs,}}i}^{2}+{\sigma }_{{\rm{jit}}}^{2}\), where σobs,i is the observational uncertainty of the ith data point), and r is the residual vector (\({\bf{r}}=[{\widehat{y}}_{1}-{y}_{1},{\widehat{y}}_{2}-{y}_{2},\ldots ,{\widehat{y}}_{n}-{y}_{n}]\), where \(\widehat{y}\) is the model and y is the data consisting of n measurements). When a given transit event was observed by several telescopes (for example, at Las Cumbres Observatory (LCO))53, or several band-passes from the same instrument (for example, from MuSCAT3)54, we jointly fitted all light curves covering the same event.

We obtained ground-based follow-up transit observations from a variety of facilities spanning several observing seasons. Early in the project, observations were distributed diversely among a half-dozen telescopes, but later we focused almost exclusively on the LCO telescope network, which enabled both the acquisition of data and its analysis to be conducted more uniformly. The individual dates, facilities, band-passes and exposure times of these observations are listed in chronological order in Supplementary Table 1. The measured transit times are provided in Supplementary Table 2.

Joint analysis of the K2 and TESS light curves

V1298 Tau (EPIC 210818897) was observed between 7 February and 23 April 2015 during campaign 4 of the K2 mission9. We analysed the K2 light curve produced by the EVEREST pipeline (https://github.com/rodluger/everest)55,56, which is available at the Mikulski Archive for Space Telescopes (MAST) (https://archive.stsci.edu/hlsp/everest).

V1298 Tau (TIC 15756231) was observed at 2-min cadence in Sectors 43 and 44 (16 September to 6 November 2021) of the TESS mission57 as part of the Director’s Discretionary Time (DDT) programme 036 (PI T. David).

We conducted a joint fit to the K2 and TESS light curves assuming a linear ephemeris, using a Gaussian process to account for correlated noise arising from a combination of stellar variability and instrumental systematics (based on the tutorial available at https://gallery.exoplanet.codes/tutorials/lc-multi/). We used a simple-harmonic-oscillator covariance function with a power spectral density given by:

$$S(\omega )=\sqrt{\frac{2}{{\rm{\pi }}}}\frac{{S}_{0}{\omega }_{0}^{4}}{{({\omega }^{2}-{\omega }_{0}^{2})}^{2}+{\omega }_{0}^{2}{\omega }^{2}/{Q}^{2}},$$

where ω is the angular frequency, ω0 is the undamped angular frequency of the oscillator and S0 is a scale factor that sets the amplitude of the variability. This was re-parameterized by the undamped period of the oscillator ρ (defined as ρ = 2π/ω0), the standard deviation of the process σ (defined as \(\sigma =\sqrt{{S}_{0}{\omega }_{0}Q}\)) and the quality factor Q (fixed to 1/3). Like our model for individual transits, we included a photometric jitter term (σjit), the square of which was added to the diagonal of the covariance matrix. The likelihood was, thus, identical to that shown for individual transits above, but the covariance matrix contained non-zero off-diagonal elements determined by the covariance function. The results of this fit are shown in Extended Data Fig. 2 and the posteriors are summarized in Extended Data Table 1.

Individual K2 and TESS transits

To create a uniform transit-timing dataset, we analysed individual transits from the long-baseline K2 and TESS light curves in the same manner as our short-duration follow-up observations. We constructed individual datasets from windows of three times the transit duration centred on each transit event. When there were overlapping transits, we used the longest transit duration and centred the window on the approximate midpoint of the dimming event. Unlike follow-up datasets, which are often partial transits, stellar variability is typically nonlinear on the timescale of these datasets. To account for this, we included a third-order basis spline with five evenly spaced knots. The transits of V1298 Tau c on 10 and 26 October 2021 ut resulted in poor-quality fits, probably due to the presence of short-timescale red noise close to ingress or egress or a low signal-to-noise ratio; as the timing posteriors from these fits were highly non-Gaussian, we discarded them from subsequent analyses.

Spitzer

We used the ephemeris derived from the K2 observations2 to predict transits of V1298 Tau b within Spitzer visibility windows in 2019. Subsequently, we did the same for V1298 Tau c,d using the ephemerides from ref. 3. Another transit of V1298 Tau b was scheduled in early 2020 using an updated ephemeris based on ref. 2 and the first Spitzer observation of that planet. The Spitzer data and best-fitting transit models are shown in Extended Data Fig. 3.

The first epoch of Spitzer observations of V1298 Tau were acquired as part of the DDT programme 14227 (PI E. Mamajek) and executed on 1 June 2019 ut. The second epoch of Spitzer observations were acquired as part of the target of opportunity programme 14011 (PI E. Newton) and executed on 28 December 2019 ut. In both epochs, data were acquired with channel 2 of the infrared array camera (IRAC) onboard Spitzer (with effective wavelength λeff = 4.5 μm) in the subarray mode using 2-s exposures. A third epoch of Spitzer observations were acquired in IRAC channel 1 (λeff = 3.6 μm) as part of DDT 14276 (PI K. Todorov) and executed on 4 January 2020 ut.

We extracted photometry following ref. 58 and modelled the instrumental systematics using PLD, which combines normalized pixel light curves as basis vectors in a linear model:

$${M}_{{\rm{PLD}}}^{t}({\boldsymbol{\alpha }})=\frac{{\sum }_{i=1}^{9}{c}_{i}{P}_{i}^{t}}{{\sum }_{i=1}^{9}{P}_{i}^{t}},$$

where Pi is the ith pixel light curve, the superscript t denotes the value at a specific time step, and α = {c1, …, c9} are the coefficients of the PLD basis vectors. The first epoch, which captured a partial transit of V1298 Tau b over approximately 11.5 h, was fitted well by including a linear trend in addition to PLD. The second epoch, which contained transits of both planets c and d over an approximately 14-h baseline, exhibited significant nonlinear variability that required the inclusion of a basis spline. Similarly, the third epoch, containing a full transit of planet b over approximately 12.5 h, also warranted the inclusion of a basis spline; although IRAC1 systematics are typically larger than those of IRAC2, PLD performed well and we attribute this to stellar variability. We validated our approach of selecting the baseline model by inspecting the fit residuals for the longest and most complex observation (the second epoch). A quantitative comparison confirmed that a basis spline was strongly preferred over a simple linear trend by the Bayesian information criterion59.

Ground-based observations

Most of our follow-up transit observations were obtained from 2020 to 2024 using LCO. We primarily used the Sinistro53 and MuSCAT3 instruments on the 1-m and 2-m telescopes, respectively.

In addition to LCO, we used data from a variety of other facilities, including Apache Point Observatory (APO)/Astrophysical Research Consortium Telescope Imaging Camera (ARCTIC)60, Fred Lawrence Whipple Observatory/KeplerCam61, WIYN/half degree imager62, Three-hundred MilliMeter Telescope63, MuSCAT64, MuSCAT265 and Araki/ADLER. Data were obtained using a variety of filters and reduced using standard pipelines and methods66,67,68,69,70,71. See Supplementary Information for more details.

Recovering planet e

The outermost planet, V1298 Tau e, transited only once during the K2 mission. TESS recovered transits of all four planets, including a second transit of planet e10. It was not clear how many transits occurred between the K2 and TESS observations given the 6.5-year gap between the two campaigns. Thus, a discrete comb of periods was allowed, such that P = Δt/n, where Δt is the measured time between transit midpoints and the integer \(n=1,2,3,\ldots ,{n}_{\max }\). The upper bound on n, and thus, the lower bound on a period of 42.7 days, was provided by the absence of other transits by planet e within the K2 and TESS time series10.

By the summer of 2022, a preliminary version of our timing dataset had revealed large TTVs of planet b that we assumed were dominated by interactions with planet e. We ran a suite of TTV models at each of the possible Pe between 42.7 days and 120 days. Few trial periods yielded good fits to the timing dataset, and dynamical simulations revealed that only a fraction of those were stable over \({\mathcal{O}}(1{0}^{6})\) years. One of the stable solutions with Pe = 48.7 days corresponded to a near 2:1 commensurability for the b–e pair, a common configuration among the Kepler planets exhibiting large and detectable TTVs. With this prediction, we recovered a partial transit of planet e from the ground on 18 October 2022. LCO datasets used to recover planet e and confirm its orbital period are shown in Extended Data Fig. 4.

Datasets containing flares

Several observations were affected by stellar flares and were excluded from our TTV analyses to avoid potential timing measurement biases. These datasets were modelled using our standard approach, augmented with a parametric flare model72 (Extended Data Fig. 5). Significant flares were observed in ARCTIC data (12 October 2020; see also ref. 38), KeplerCam data (24 September 2023) and LCO data (18 December 2023), with amplitudes ranging from 6 parts per thousand (ppt) to 42 ppt and timescales of 14 min to 21 min. The parameters of these flares are detailed in the Supplementary Information, and they may prove valuable for future studies of the activity of V1298 Tau.

Mass constraints from analytic TTV modelling

To build intuition for the system dynamics, we first performed a preliminary analysis using analytic models of TTVs. Based on the foundational analytic frameworks for TTVs11,12,73, we determined that the system dynamics can be effectively decoupled into two pairs of planets: c–d and b–e.

To quantify the TTV behaviour, we fitted a multi-harmonic sinusoidal model to the transit time series (see Supplementary Information for the model equations). We explored the posterior distributions of the 16 model parameters using a Markov chain Monte Carlo sampler, like approaches used by other public TTV analysis codes74,75. The posteriors of these parameters are listed in Supplementary Table 3, and the model fits are shown in Extended Data Fig. 6.

The results for the c–d pair are consistent with the planets being in a near-resonant regime. The TTVs are described well by a single sinusoid with a period Pcd = 1,604 ± 12 days and an r.m.s. of the residuals of only 11 min. This sinusoidal signal is dominated by variations in the planetary mean longitudes (λ), characteristic of systems very close to resonance. The ratio of the TTV amplitudes is sensitive to the planetary mass ratio, indicating nearly equal masses (Md/Mc ≈ 1.2). From the full fit, we derived preliminary masses \({M}_{{\rm{c}}}\approx {2.7}_{-0.8}^{+1.7}\) M⊕ and \({M}_{{\rm{d}}}\approx {3.2}_{-1.0}^{+2.1}\) M⊕.

By contrast, the b–e pair is described well by a simpler, linear TTV model, as it is further from resonance. The TTVs arising from variations in mean longitude and eccentricity have the same frequency in this regime. In this case, a well-known degeneracy exists between the planet masses and their orbital eccentricities16,76, leading to broader initial constraints of \({M}_{{\rm{b}}}=3{1}_{-17}^{+14}\) M⊕ and \({M}_{{\rm{e}}}=2{4}_{-8}^{+4}\) M⊕. A full theoretical treatment and a discussion of strategies for breaking the mass–eccentricity degeneracy, such as measuring secondary eclipse times77, can be found in the Supplementary Information.

Mass constraints from N-body TTV modelling

Guided by our analytic models, our primary analysis relies on a full N-body dynamical model to derive the final planet parameters. We fitted the model to the observed transit times using a Bayesian framework. To be robust against outlier measurements, we adopted a log-likelihood function based on Student’s t-distribution78,79, with priors as listed in Extended Data Table 2. The posterior probability distribution was sampled using the No-U-Turn Sampler80,81. The model is implemented in JAX to enable automatic differentiation and is available as part of the jnkepler package27,82. The full mathematical details of the model implementation, the log-likelihood equation and the sampler set-up are provided in the Supplementary Information. The resulting mass and eccentricity posterior distributions are shown in Extended Data Fig. 7.

To verify the physical plausibility of our solution, we performed a detailed dynamical analysis of the posterior. We investigated both the long-term stability and the resonant state of the system using several complementary methods. First, to assess stability, we used a probabilistic classifier (SPOCK)83 on 1,000 samples from our posterior, which yielded a median stability probability of 95% over 109 orbits. We confirmed this with direct N-body integrations of 128 samples for 1 Myr, which showed that the system is deeply stable and regular (minimum separation over 12RH (mutual Hill radii), maximum semimajor axis drift of less than 0.01%, and MEGNO (Mean Exponential Growth factor of Nearby Orbits) = 2.000). As a final check, we integrated 32 posterior samples for 4 Myr, all of which were found to be stable. Second, to characterize the resonant state, our integrations show that all classical resonant angles are circulating, which we confirmed by projecting our solution onto the resonant representative plane12. The solution lies clearly outside the resonant island where libration would occur, confirming the non-resonant nature of the system.

Initial thermal state and planetary evolution

Young planets with hydrogen-dominated atmospheres contract over time due to mass loss and thermal evolution. Reference 32 showed that young planets with measured masses and radii can be used to constrain their initial entropies. Planets with a measured mass and radius have a degeneracy between their hydrogen envelope mass fraction and their thermal state. The hydrogen envelope mass of the planet can be reduced and compensated for by an increase in its entropy. However, this can only go so far; the envelope mass cannot be reduced arbitrarily to the point where it is too small to survive mass loss. Thus, one can place a bound on the initial entropy of the planet such that it survives until today. To perform this calculation, we computed a grid of MESA evolutionary models that include photoevaporation (a comparison with ref. 84 indicates that these planets will be undergoing photoevaporation rather than core-powered mass loss). This model grid comprised 36 core masses, 128 initial mass fractions and 96 initial entropies. We used an identical method to that in ref. 32. We then compared this model grid with the observed masses and radii of the V1298 Tau planets to derive posterior distributions of the core masses, initial envelope mass fractions and initial entropies (which we encode as the initial Kelvin–Helmholtz cooling timescale of the planets). Our results indicate that all the planets had initial envelope mass fractions and core masses that are consistent with typical sub-Neptunes at billion year ages. Furthermore, the initial cooling timescales are constrained to require boil-off for planets c and d, whereas an evolution without boil-off cannot be ruled out for the outer planets. Extended Data Fig. 8 shows the models that best reproduce the present-day masses and radii of planets c and d. Interestingly, they require an initial low entropy; that is, an initial Kelvin–Helmholtz contraction time that is longer than the age of the system. Furthermore, if one considers only models with a high initial entropy, one can match the current mass or radius, but not both.