Background & Summary

Craig and Gordon1 (1965) were the first to propose the application of stable isotope analysis of seawater (δ¹⁸O, δ²H, referred to as δD) as tracers for water masses and global hydrological cycles. These water isotopes are influenced by processes such as evaporation, precipitation, runoff, high-salinity water intrusion, and sea ice formation1,2,3. Consequently, distinct dual water isotope signatures have been identified across different oceanic regions globally4,5,6,7,8. Additionally, vertical profiles of water masses exhibit unique isotopic characteristics9,10,11, providing a theoretical foundation for quantifying water mass transport and ocean current dynamics.

To date, stable seawater isotopes have been employed to validate ocean circulation models and characterize processes governing spatial variability12. Furthermore, they have been used to infer control information on oxygen isotope ratios in calcareous plankton shells, enabling reconstructions of paleo-ocean salinity and circulation patterns13. The NASA Goddard Institute for Space Studies (GISS) Global Seawater Oxygen-18 Database has compiled and homogenized most pre-1998 isotope data14. Since 1998, the isotopic platform facility at LOCEAN (CISE-LOCEAN) has expanded global coverage by analyzing water isotope samples from the North Atlantic, equatorial Pacific, Atlantic, South Indian Ocean, and Southern Ocean15, regions previously underrepresented in the GISS database14. Although the LOCEAN dataset spans 1998–2021 and continues to grow, it lacks comprehensive coverage of the South China Sea (SCS), particularly the northern SCS (NSCS), where dynamic oceanographic processes dominate. This highlights the urgent need to establish a dedicated isotope dataset encompassing surface-to-bottom layers in the NSCS.

The combined use of hydrogen-oxygen isotopes and the SIAR (Stable Isotope Analysis in R) isotope mixing model has been successfully applied in diverse contexts, including nearshore estuaries and quantitative assessments of typhoon-induced upwelling16,17. Traditional approaches rely on extensive cruise-based temperature-salinity and velocity measurements to characterize NSCS currents18. However, these methods often fail to fully resolve contributions from distinct water masses, such as coastal waters. In contrast, water isotopes act as intrinsic fingerprints of water masses, encapsulating cumulative signatures of long-term hydrographic interactions17. Even in coastal regions with multiple freshwater sources and homogenized low salinity, isotopes provide a novel perspective for tracing water mass origins19,20. Wang et al.21 further investigated summer circulation in the NSCS using a 3D numerical model. While model outputs offer spatially continuous data, their accuracy is constrained by resolution limitations and nonlinear complexities. Isotope-based methods, when integrated with mixing models, thus serve as a complementary quantitative tool to enhance monitoring capabilities for ocean circulation.

The shelf and slope circulation in the NSCS is highly complex and variable, driven by seasonal monsoon reversals, water exchange with the Northwest Pacific through the Luzon Strait, and intricate topography22. Although prior studies have partially characterized shelf and slope currents18,21,23, critical gaps remain in understanding: (1) dynamic linkages and material exchange between the SCS basin-scale circulation and shelf currents, (2) cross-slope transport mechanisms in the NSCS, and (3) the influence of terrestrial runoff and coastal currents on regional circulation. This study seeks to advance understanding of these gaps by compiling and augmenting a comprehensive dual-isotope dataset covering the NSCS during summer, providing a foundational resource for investigating unresolved questions. Utilizing unified end-member selection criteria, an isotope correction method, and an isotope mixing model, we generate a quantitative dataset to resolve circulation-driven transport processes, including the impacts of freshwater plumes, coastal water contributions, and cross-shelf exchanges between the SCS basin and shelf regions.

Methods

Sample collection and storage

The EH (Eastern Hainan Island) cruise comprised three transects conducted in September 2015 within the eastern Hainan Island upwelling region. Seawater samples were collected using a rosette sampler equipped with Niskin bottles. To minimize post-sampling biological processes that could alter water isotope signatures, the collected water was filtered through 0.45 μm pore-size cellulose acetate membranes and transferred into pre-cleaned 100 mL high-density polyethylene (HDPE) bottles. To reduce bioavailability and prevent evaporation-induced isotopic fractionation, the bottle caps were tightly sealed and secured with Parafilm (PM-996; country of origin: USA) wrapped around the cap interface. Samples were then stored at −20 °C in a freezer and transported to a land-based laboratory for isotopic analysis. Full-depth profiles of temperature, salinity, and depth were concurrently measured using a calibrated SBE 911plus CTD unit (Sea-Bird Electronics, Inc., USA). Sampling details and references for cruises other than EH are summarized in Table 1 and Fig. 1a.

Table 1 List of cited cruises (see referenced publications for detailed information).
Full size table
Fig. 1
figure 1

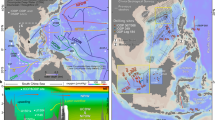
Study area and sampling information in the northern South China Sea. (a) Topographic distribution and sampling regions from different cruises. (b) Number of sampling layers per station. c Maximum sampling depth at each station. Abbreviations: EH (Eastern Hainan), LZ (Luzon Strait), NBBG (Northern Beibu Gulf), PRE (Pearl River Estuary), SBBG (Southern Beibu Gulf), WG (Western Guangdong Province).

Full size image

Isotopic measurements

For hydrogen isotope analysis, 200 μL of seawater was aliquoted into a 12 mL Labco Exetainer® vial containing a hydrophobic platinum catalyst rod. The vial was tightly sealed, and a mixed gas of hydrogen (2% by volume) and helium was injected to initiate equilibrium exchange between the water sample and hydrogen gas under platinum catalysis. After 40 minutes of equilibration, the isotopic composition of the hydrogen gas was analyzed using a Gasbench II coupled to an isotope ratio mass spectrometer (Gasbench II-IRMS; Thermo Scientific). Isotopic values were calibrated against reference materials provided by the United States Geological Survey (USGS): USGS47 (δDV-SMOW = −150.2‰), USGS45 (δDV-SMOW = −10.3‰), USGS48 (δDV-SMOW = −2.0‰), and USGS50 (δDV-SMOW =  + 32.8‰). Analytical precision was ± 0.5‰ (n = 8), with an accuracy of −2.0 ± 0.5‰ (n = 8, USGS48).

The δD value, expressed relative to the Vienna Standard Mean Ocean Water (VSMOW), was calculated as:

$${\rm{\delta }}{\rm{D}}=\frac{{R}_{{sample}}-{R}_{V-{SMOW}}}{{R}_{V-{SMOW}}}\times 1000$$
(1)

where RV-SMOW is the D/H ratio of VSMOW, and Rsample is the D/H ratio of the sample. The final δD values had an analytical precision of ±0.5‰.

For oxygen isotope analysis, 200 μL of seawater was transferred into a 12 mL Labco Exetainer® vial. A mixed gas of carbon dioxide (1% by volume) and helium was injected to initiate equilibrium exchange between the water sample and CO2. After 24 hours of equilibration, the isotopic composition of CO2 was analyzed using the Gasbench II-IRMS system, following protocols described in Lao et al.16,17. Calibration was performed using USGS reference materials: USGS47 (δ¹⁸OV-SMOW = −19.8‰), USGS45 (δ¹⁸OV-SMOW = −2.2‰), USGS48 (δ¹⁸OV-SMOW = −2.2‰), and USGS50 (δ¹⁸OV-SMOW = + 5.0‰) (IAEA). Analytical precision was ± 0.1‰ (n = 8), with an accuracy of −2.2 ± 0.1‰ (n = 8, USGS48).

The δ¹⁸O value, normalized to VSMOW, was calculated as:

$${\rm{\delta }}{}^{18}{\rm{O}}=\frac{{R}_{{sample}}-{R}_{V-{SMOW}}}{{R}_{V-{SMOW}}}\times 1000$$
(2)

where Rsample is the 18O/16O ratio of the sample and RV-SMOW is the 18O/16O ratio of VSMOW. The δ¹⁸O values had an analytical precision of ±0.1‰. Deuterium excess, defined as d-excess = δD−8 × δ¹⁸O, serves as an indicator of kinetic fractionation associated with phase changes and inversely correlates with δ¹⁸O during evaporation processes24.

Stable isotope mixing model

The proportional contributions of distinct water masses can be quantified using a Bayesian stable isotope mixing model, implemented via the Stable Isotope Analysis in R (SIAR) package (SIAR v4.2, R v4.1.1). The general framework of the model is defined as follows:

$${X}_{{ij}}=\frac{\mathop{\sum }\limits_{k=1\,}^{K}{p}_{k}{q}_{{jk}}\left({s}_{{jk}}+{c}_{{jk}}\right)}{\mathop{\sum }\limits_{k=1}^{K}{p}_{k}{q}_{{jk}}}+{{\varepsilon }}_{{ij}}$$
(3)
$${s}_{{jk}} \sim N({\mu }_{{jk}},{\omega }_{{jk}}^{2})$$
(4)
$${c}_{{jk}} \sim N({\lambda }_{{jk}},{\tau }_{{jk}}^{2})$$
(5)
$${{\varepsilon }}_{{ij}} \sim N(0,{\sigma }_{j}^{2})$$
(6)

Here, Xij denotes the j-th isotopic observation at the i-th mixed sample. \({s}_{{jk}}\) represents the j-th isotopic value of the k-th source, modeled as a normal distribution with mean \({\mu }_{{jk}}\) and variance \({\omega }_{{jk}}^{2}\). \({c}_{{jk}}\) is the fractionation factor for the j-th isotope in the k-th source, characterized by mean \({\lambda }_{{jk}}\) and variance \({\tau }_{{jk}}^{2}\). pk denotes the proportional contribution of source k, estimated by the SIAR model. \({q}_{{jk}}\) corresponds to the concentration of the j-th isotope in the k-th source. \({{\varepsilon }}_{{ij}}\) represents residual variance unexplained by the model, following a normal distribution with mean 0 and variance \({\sigma }_{j}^{2}\), where \({\sigma }_{j}^{2}\) is inferred during model calibration.

The Bayesian framework allows incorporation of prior information to refine the precision of contribution estimates25. Priors may be uninformative (vague) or informative, depending on existing knowledge of water mass mixing. The natural prior distribution for \({p}_{k}\) is the Dirichlet distribution, a multivariate generalization of the Beta distribution. The Dirichlet prior assumes independence among sources while constraining their summed contributions to unity. In SIAR, users can specify prior mean proportions (summing to 1) for each source and the standard deviation of the first proportion to derive parameters \({\rm{{\rm K}}}\) and \({\rm{\alpha }}\). However, the Dirichlet prior does not permit individual uncertainty specifications for each proportion. In this study, an uninformative prior assuming equal proportions was adopted.

Marginal distributions generated by the Dirichlet distribution with parameters \({\rm K}\) and \(\alpha \) are defined as:

$${\alpha }_{T} \sim \mathop{\sum }\limits_{k=1}^{K}{\alpha }_{k}$$
(7)

Distributional properties are further described by:

$${\bar{p}}_{k}=\frac{{\alpha }_{k}}{{\alpha }_{T}}$$
(8)
$${var}({p}_{k})={\alpha }_{k}({\alpha }_{T}-{\alpha }_{k})/{\alpha }_{T}^{2}({\alpha }_{T}+1)$$
(9)
$${cov}\left({p}_{k},{p}_{p}\right)=-{\alpha }_{k}{\alpha }_{p}/{\alpha }_{T}^{2}({\alpha }_{T}+1)$$
(10)

where \({p}_{k}\) and \({p}_{p}\) (with Dirichlet parameters \({\alpha }_{k}\) and \({\alpha }_{p}\)) denote the proportional contributions of the k-th and p-th sources, respectively. The default SIAR configuration sets all \({\rm{\alpha }}\) values to 1, corresponding to an uninformative prior with equal mean contributions (\(1/{\rm{{\rm K}}}\)) and variance \(\left({\rm{{\rm K}}}-1\right)/({{\rm{{\rm K}}}}^{2}\left({\rm{{\rm K}}}+1\right))\). This study employs the default uninformative Dirichlet prior, ensuring that results are predominantly data-driven. Model fitting proceeds via Markov Chain Monte Carlo (MCMC) simulations to generate posterior distributions of \({p}_{k}\) consistent with observations.

The SIAR framework has been widely validated for quantifying source contributions in stable isotope studies26,27. Due to their conservative behavior and minimal alteration by biogeochemical processes, water isotopes (δ¹⁸O and δD) are robust tracers of hydrological cycling1,6,17,24. Furthermore, distinct isotopic signatures among water masses enable successful applications in tracing proportional contributions and circulation features8,10,17,28.

Correction of water isotopes affected by kinetic fractionation

It is noteworthy that incorporating accurate fractionation factors into the SIAR model can eliminate the need for explicit corrections. Previous studies have estimated fractionation factors for water isotopes, primarily linked to temperature and atmospheric humidity24. However, a critical limitation arises when considering full-depth water masses as end-members or mixtures: isotopic fractionation predominantly occurs in surface layers (e.g., evaporation and condensation), making the estimation of integrated fractionation factors across the entire water column highly uncertain. Consequently, this approach was deemed unsuitable for the present study.

d-excess, a key parameter, reflects kinetic fractionation processes during oceanic evaporation24. Evaporation increases δ¹⁸O while reducing d-excess, leading to an inverse correlation between d-excess and δ¹⁸O. This relationship, observed in the LZ (Luzon Strait), EH, WG (Western Guangdong Province), and PRE (Pearl River Estuary) voyages (Fig. 2e), signifies significant kinetic fractionation in these regions4,15,24. To account for these effects in the SIAR model, we identified samples from these four voyages where d-excess values fell below the minimum end-member d-excess or δ¹⁸O values exceeded the maximum end-member δ¹⁸O (gray points with black borders in Fig. 3a–d). These samples were interpreted as having undergone additional kinetic fractionation during transport from source regions to the study area.

Fig. 2
figure 2

Water isotope characteristics in the northern South China Sea. (a) Spatial distribution of surface δD. (b) Spatial distribution of bottom δD. (c) Spatial distribution of surface δ¹⁸O. (d) Spatial distribution of bottom δ¹⁸O. Black-bordered circles in (a–d) represent the GISS dataset; black double-headed arrows indicate adjacent stations used for comparison between this study and the GISS dataset. (e–f) Two-dimensional linear relationships between water isotope parameters and salinity.

Full size image
Fig. 3
figure 3

Isotope corrections for the SIAR model. (a–d) Screening of scatter points for correction. (e–h) Deviation of scatter points relative to the δ¹⁸O–S linear regression. (i–l) Spatial distribution of corrected δD values in δD–S space. Gray points: non-end-member scatter points; gray points with black borders: pre-correction scatter points; green points with black borders: post-correction scatter points.

Full size image

The δ¹⁸O–salinity (δ¹⁸O–S) relationship serves as an empirical diagnostic tool for distinguishing water masses and quantifying contributions from terrestrial runoff or glacial meltwater4,29. Both δ¹⁸O and salinity increase with evaporation, resulting in a positive linear correlation when mixing high-salinity/high-δ¹⁸O and low-salinity/low-δ¹⁸O water masses (Fig. 2f). Samples deviating above this regression line likely experienced enhanced evaporation. We thus attributed positive Δδ¹⁸O (δ¹⁸O deviations from the δ¹⁸O–S regression line) to additional kinetic fractionation. Following Benetti et al.5, Δδ¹⁸O values were corrected using the Δd-excess–Δδ¹⁸O relationship derived from the slope of the d-excess–δ¹⁸O regression line. Corrected samples are shown as green points with black borders in Fig. 3.

The primary uncertainty in this correction method stems from insensitivity to samples with low anomalous fractionation, which are assumed to reflect end-member mixing. However, since selected end-members and mixing zones are geographically proximate, they likely experienced similar meteorological and evaporative conditions, minimizing systematic biases in relative contribution estimates. Furthermore, kinetic fractionation associated with evaporation-condensation processes predominantly affects surface layers, whereas this study integrates full-depth water mass contributions. Consequently, surface-driven fractionation errors have limited impact on the quantification of subsurface contributions.

End-member selection and quantification of water mass transport

NSCS exhibits unique circulation features, necessitating careful identification of appropriate end-members and corresponding stations based on prior research before quantifying circulation characteristics (Fig. 4 and Table 2). In the northeastern SCS, Kuroshio water (KW) intrudes into the SCS all the year round via the Luzon Strait, with weaker intensity in summer and stronger in winter22,30. A southwestward slope current persists between 200 m and 1000 m depths, even during summer under prevailing southwesterly winds31,32. Along the southern coast near mainland China, a westward coastal current dominates west of the Pearl River Estuary for most of the summer, termed the Western Guangdong coastal current (WGCC)22. This current flows into the Beibu Gulf via the Qiongzhou Strait, with a branch diverging southward along the eastern coast of Hainan Island before entering the gulf8. The Beibu Gulf features a dual-gyre structure, with a cyclonic circulation in the north and an anticyclonic circulation in the south33. During summer, the coastal current along eastern Hainan Island flows northeastward under the influence of the southwestern monsoon34. This current, referred to as the SCS Warm Current (SCSWC), subsequently moves eastward along the shelf and eventually toward the western Luzon Strait22, designated as the coastal current (CC) end-member. Additionally, diluted water (DW) end-members from coastal river discharge and the South China Sea Water (SCSW) end-member representing southern SCS exchange were identified in specific coastal cruises.

Fig. 4
figure 4

Selection of end-member stations. (a) Major circulation patterns in the northern South China Sea during summer and spatial distribution of selected stations. (b) Temperature-salinity (T-S) diagram; gray points represent non-end-member scatter points. Abbreviations: CC (coastal current), KW (Krushio water), SCSW (South China Sea water), DW (diluted water), WGCC (Western Guangdong coastal current).

Full size image
Table 2 Criteria and station selection features for end-member identification.
Full size table

Data Records

The cruise information and references associated with the dataset are summarized in Table 1 and Fig. 1a. Sampling spanned depths of 0–3700 m in the northern South China Sea (SCS), with the number of sampling layers per station ranging from 1 to 12 (Fig. 1b,c). Spatial distributions of surface and bottom water isotopes are illustrated in Fig. 2a–d. All data are archived in the Excel file “water_isotope_NSCS.xlsx”. The file comprises two sheets:

  • Basic Data: Station, Longitude, Latitude, Date, Bot. (bottom depth in meters), Depth (sampling depth in meters), δD (in ‰), δ¹⁸O (in ‰), T (temperature in °C), S (practical salinity in psu), d_excess (in ‰), Voyage, δD correction (δD values corrected for SIAR modeling), and δ¹⁸O correction (δ¹⁸O values corrected for SIAR modeling). Missing values are denoted as NA.

  • Dynamic Data: Includes variables such as Area, Source (end-member name), Mean_δ¹⁸O (mean δ¹⁸O of the end-member), SD_δ¹⁸O (standard deviation of δ¹⁸O), Mean_δD, SD_δD, Contribution (%), End-Member Criteria, and Station Selection Features.

The SIAR model code is stored in the file “NSCS_SIAR.R.” For each subregion (Area), a dedicated folder ccontains three files: source-raw.xlsx (detailed station information for end-members), ConsumerData.xlsx (mixed water mass data), and SourceData.xlsx (end-member isotope data), which are used to execute the SIAR model. Spatial distributions of water mass contributions are presented in Fig. 5.

Fig. 5
figure 5

Quantification of water mass transport derived from dual water isotopes. (a) Spatial distribution of water mass contributions. (b) Output results of the SIAR model.

Full size image

Technical Validation

To ensure internal consistency across measurement batches from six voyages, three replicate samples of aged open-ocean seawater were analyzed for each cruise. The results demonstrated that mean differences among triplicate samples were smaller than the analytical precision (±0.5‰ for δD and ±0.1‰ for δ¹⁸O) (Table 3), confirming appropriate sample preservation (no significant evaporative fractionation) and stable instrument calibration (no drift). However, potential offsets between datasets may arise from differences in internal standards, processing protocols, or instrument configurations. Thus, cross-validation with external datasets is critical for future data integration and expansion.

Table 3 Comparative measurements of δD and δ¹⁸O in aged seawater across six cruises.
Full size table

The NASA GISS Global Seawater Oxygen-18 Database, comprising over 26,000 δ¹⁸O values and limited δD values (relative to V-SMOW) since the 1950s14, includes only six stations in the SCS and adjacent western Pacific, all sampled in the 1990s (black-bordered points in Fig. 2a–d). Comparisons between the nearest stations in this study and the GISS dataset revealed minor discrepancies in bottom δ¹⁸O (mean difference: 0.01‰, within the δ¹⁸O range of [−2, 1]‰) and bottom δD (0.31‰ and 2.30‰, within the δD range of [−15, 20]‰). Surface δD differences were 2.18‰ and 1.06‰, while surface δ¹⁸O exhibited a larger mean discrepancy (0.92‰), likely due to Kuroshio influence and associated dynamic processes. Overall, isotopic values in this dataset showed a slight positive bias relative to GISS, suggesting systematic offsets.

Finally, water mass contributions in the NSCS, as quantified by SIAR, align with qualitative circulation features (Figs. 4, 5). For example, the SIAR-derived 75% contribution of the SCSW end-member in the southern EH area corroborates prior observations of strong northward currents along eastern Hainan Island under summer southwestern monsoons34. Similarly, Kuroshio intrusion and Pearl River discharge were identified as significant factors influencing volume transport in the northern PRE region35, with our quantified contributions also revealing 36% Kuroshio water (KW) and 35% diluted water (DW) in this area. Furthermore, the 35% DW contribution in PRE substantially exceeds the 17% DW in EH, attributable to the Pearl River (China’s second-largest river) whose summer-dominant discharge exerts extensive influence across the NSCS36. Notably, the DW end-member contribution reaches 46% in the NBBG, primarily due to multiple rivers along its coast and restricted water exchange capacity characteristic of this semi-enclosed bay17. These results validate the robustness of the SIAR model in resolving regional circulation dynamics.