Salvador Urban Network Transportation (SUNT): A Landmark Spatiotemporal Dataset for Public Transportation

Abstract

Efficient public transportation management is essential for the development of large urban centers, providing several benefits such as comprehensive coverage of population mobility, reduction of transport costs, better control of traffic congestion, and significant reduction of environmental impact limiting gas emissions and pollution. Realizing these benefits requires a deeply understanding the population and transit patterns and the adoption of approaches to model multiple relations and characteristics efficiently. This work addresses these challenges by providing a novel dataset that includes various public transportation components from three different systems: regular buses, subway, and BRT (Bus Rapid Transit). Our dataset comprises daily information from about 700,000 passengers in Salvador, one of Brazil’s largest cities, and local public transportation data with approximately 2,000 vehicles operating across nearly 400 lines, connecting almost 3,000 stops and stations. With data collected from March 2024 to March 2025 at a frequency lower than one minute, SUNT stands as one of the largest, most comprehensive, and openly available urban datasets in the literature.

Background & Summary

In this work, we focus our investigation on efficient urban mobility by modeling data from public transportation systems due to its importance to the population. Any decision regarding this system directly impacts urban mobility, especially in developing countries, where it is often the only means of transport available to low-income populations. When poorly planned, it delivers low-quality services with delayed and overloaded vehicles, concentrates traffic in specific regions while leaving others unattended, and aggravates pollution with higher gas emission rates.

Efficient urban mobility depends on a comprehensive set of strategies to optimize traffic management, yielding benefits such as improved safety, reduced travel time, lower costs, and enhanced environmental sustainability. These strategies have led researchers to explore various solutions, including vehicle-to-vehicle communication, route optimization, the integration of the Internet of Things for connected transportation systems, and more effective public transit scheduling^1,2,3,4,5.

According to Ceder⁶, the success of intelligent transportation systems (ITS) relies on collecting and analyzing accurate data, which has led several studies to focus on data-driven approaches. In this sense, Wang et al. and Gordon et al.^7,8 have used passenger fare data and vehicle location tracking to develop heuristics to better estimate boarding and alighting times and locations in London (England). Similarly, researchers collected passenger and vehicle data from Harbin (China), which was later modeled using unsupervised machine learning methods to understand public transit riders’ travel patterns better⁹. Researchers from Seoul (the Republic of Korea) also developed a methodology for estimating non-tagged alighting stop information gradually, by considering the characteristics of trip types and utilizing transportation card data¹⁰. In New York (USA), researchers analyzed data from the transit system, where riders swipe a fare card only when entering a station or boarding a bus. They used this information to estimate alighting stops based on the bus boarding locations¹¹. A similar problem was addressed in Southeast Queensland (Australia) by using a Deep Neural Network to predict unknown alighting locations after being trained in a dataset with a combination of transactional and public transit network attributes¹². Although these aforementioned citations are more related to our work, further research on the problem of inferring boarding-alighting locals in public transportation systems is detailed in a review published by Mohammed and Oke (2023)¹³.

As extensively discussed in the literature, understanding and improving public transportation directly impact urban mobility, particularly in developing countries, where it is often the primary means of transport for low-income populations. Poorly planned systems provide low-quality services, leading to delays, overcrowded vehicles, traffic congestion in specific areas while neglecting others, and increased pollution due to higher gas emissions. After an in-depth investigation of published manuscripts focused on public transportation, we noticed a limitation in the availability of a totally public dataset containing comprehensive quantitative, spatial, and temporal information about passengers, vehicles, lines, stops, and stations. Moreover, despite the increasing advancements in Machine Learning (ML) methodologies, particularly for intelligent transportation systems (ITS), there remains a significant lack of datasets with detailed information about public transportation with their respective passengers.

To address this limitation, we present the Salvador Urban Network Transportation (SUNT) dataset, the most comprehensive public transportation dataset currently available in the literature. Collected in Salvador, Brazil, between March 2024 and March 2025, SUNT covers an area of approximately 694 km² and serves nearly 3 million residents. The transportation used by the local population in Salvador comprises three systems: regular buses, subway, and BRT (Bus Rapid Transit). The regular bus system is the most extensive transportation in Salvador, serving most of the population. Currently, there are about 1,900 buses distributed on approximately 400 lines with around 3,000 stops and stations, supporting roughly 470,000 passengers daily. The subway system spans about 35 km across 2 lines with 20 stations. Approximately 210,000 passengers use this system daily. The BRT (Bus Rapid Transit) system was recently inaugurated, further enhancing urban mobility and serving about 30,000 passengers daily. Currently, about 40 buses are operating on 3 lines and 20 stations.

In addition to publicly available vehicle information, which is commonly shared by several cities worldwide, SUNT stands out for its innovative inclusion of passenger data, such as boarding and alighting details, and its diverse data formats. These include graph representations with over 2,000 nodes and 4,000 edges, as well as temporal data streams with a granularity of less than one minute.

In Table 1, we summarize important related works, which models different urban datasets. The missing information ("NA”) in this table reflects the fact that several datasets commonly used in research articles are partially described in the publications and are not freely shared in public repositories with the same level of detail as ours. For example, we have noticed that information about the number of nodes, edges, or specific temporal intervals is often unavailable. As a result, researchers face challenges in reproducing experiments or fully understanding the scope and limitations of the datasets referenced in these studies.

Table 1 Key Characteristics of SUNT in Comparison with Existing Datasets from the Literature.

On the other hand, we offer the Salvador Urban Network Transportation (SUNT) dataset, which stands out as an exception, offering 2,871 nodes, 4,526 edges, and a temporal granularity of less than one minute, with an in-depth dataset construction, which are pivotal for addressing key deficiencies identified in recent studies on learning benchmarks. SUNT offers a robust foundation for developing models that can learn complex spatiotemporal patterns and adapt to rapidly changing conditions in ITS scenarios. Additionally, being recently collected, it reflects an updated urban configuration, in contrast to the most recent previously available dataset, which dates back to 2019.

The significance of sharing the SUNT dataset lies in its dual impact: advancing scientific research and informing public policy. For researchers, SUNT provides a comprehensive and high-quality resource to develop and evaluate a wide range of data-driven methods, such as supervised and unsupervised learning, concept drift and anomaly detection, time series analysis, graph-based optimization, and high-performance computing techniques for large-scale transit data. For policymakers and transit agencies, SUNT enables the simulation of real-world transportation scenarios, supporting evidence-based decisions and reducing risks when planning or modifying public transportation systems. This combination of scientific utility and practical application underscores the dataset’s relevance and potential to contribute meaningfully to the fields of urban mobility and smart city development.

Methods

This section describes the steps taken to create the SUNT dataset. First, we present in detail the data collected from four distinct public transportation sources. We then explain the use of the Trip Chaining approach to integrate these data sources, resulting in a complete origin-destination matrix. Finally, we describe the process of modeling this matrix as a graph that connects stops, enriched with several attributes related to passenger boarding and alighting.

Raw Datasets

In this study, we utilized an Automated Data Collection System (ADCS) to gather data from multiple sources¹³. The first source was the Automatic Vehicle Location (AVL) system, which monitors all regular and BRT buses, providing details about their geospatial positions over time.

In summary, AVL records real-time vehicles’ geographical locations, which are important to estimate several relevant information, such as passengers boarding and alighting, public transportation network planning, and monitoring and controlling traffic operations. The daily AVL information shared in our repository¹⁴ contains two different set of features: AVL-lines and AVL-vehicles. AVL-lines comprise static information regarding the lines, whose features are shown in Table 2. These columns provides different information about the lines: route_short_name – identification; pt_sequence – stop sequence order; direction_id – direction, where 1 stands for one-way and 0 for return trip; longitude and latitude – geographical coordinates for the bus stop identified in column stop_id;route_long_name – stop names; service_code – the trip along the line.

Table 2 AVL-lines features: information regarding bus lines.

Table 3 presents AVL-vehicles features, which comprise information concerning vehicles’ routes and bus schedules. One of the most important columns is gps_datetime, which provides the vehicle’s arrival date and time at the stop identified by the stop_id column. If gps_datetime contains two values, the earlier timestamp corresponds to the bus arrival time at the stop, while the later one represents the departure time. The stop sequence of the bus line must be consistent with the values in gps_datetime; that is, for each stop, the arrival time must be earlier than the departure time, and the departure time must be earlier than the arrival time at the next stop. The remaining columns are similar to those described in Table 2.

Table 3 AVL-vehicle features: information concerning vehicles’ routes and bus schedules.

The second collecting source is the Automatic Fare Collection (AFC) system, which contains information from the ticketing systems, recording the time when users’ contactless cards are used for payments. In addition to the exact time of card usage, it also includes details on the vehicles and their respective lines. In our scenario, AFC is used to gather data from passengers using regular buses, subway, and BRT. For buses, data collection occurs at two points: when passengers validate their tickets either at the vehicle’s built-in turnstile or at a mobile turnstile. In the case of the subway, the AFC system records entries through turnstiles located at station entrances. For the BRT system, AFC combines both methods—collecting data through turnstiles inside vehicles as well as those installed at station entrances.

A subsample of AFC, shown in Table 4, illustrates the available attributes: cod_card is the number of passenger’s card, randomly generated to avoid recovering any user identification, afc_datetime represents the time when the passenger registers the payment, integration indicates the possibility of a connection between vehicles, route_short_name is the route identification, direction_id shows the bus direction (I – one way or V – return) considering its initial and final stops, value is the trip cost, and vehicle is the code used to identify the vehicle. This dataset contains approximately 35 million records per month.

Table 4 Illustrative example of the AFC dataset.

Additionally, we used static data based on the General Transit Feed Specification (GTFS) format, which defines a standard format for public transportation schedules associated with geographic information (http://gtfs.org/). Using this format, we provided geospatial details about stations and stops along with their sequential order, lines, and directions. In the SUNT dataset, the GTFS provides 5 files (GTFS Agency, GTFS Routes, GTFS Trips, GTFS Stops Times, and GTFS Stops) that describe the entire network and services of public transportation related to local companies. GTFS Agency, illustrated in Table 5, contains information about the bus companies, which are associated with GTFS Routes (Table 6) by the attribute agency_id. GTFS Routes contains information about bus lines and is associated with GTFS Trips (Table 7) by the attribute route_id. GTFS Trips shows all the trips and the paths followed by the bus and is directly associated with GTFS Stops Times (Table 8), which maps the chronological order of bus stops where each trip paused. Finally, GTFS Stops (Table 9) contains information about each bus stop and is associated with the GTFS Stops Times by the attribute stop_id.

Table 5 GTFS Agency: information about the bus companies.

Table 6 GTFS Routes: information about bus lines.

Table 7 GTFS Trips: information about the trips and the paths followed by the bus.

Table 8 GTFS Stops Times: the chronological order of bus stops where each trip paused.

Table 9 GTFS Stops: information about each bus stop.

Finally, we also provide a dataset containing Local Trip Information (LTI), which includes details about the expected and actual departure and arrival times for all vehicles on every line and in each direction. Due to the dynamic nature of data collected from the AVL system, missing data may occur, resulting in random loss of information about vehicle activities. This issue can be easily addressed by combining redundant vehicle information from GTFS and LTI. Table 10 summarizes the attributes of the trip mapping dataset. The most important attributes are start_trip and end_trip, which indicate the start and end times of each trip, respectively. The activity attribute categorizes the trip as either a regular service, a departure from the garage, or a return to the garage. This dataset complements the AVL dataset by providing trip-level information, which is not included in the AVL records. On average, it contains approximately 700,000 records per month.

Table 10 LTI: the start of each trip made by a vehicle on a specific route.

Trip Chaining

After organizing these four datasets (AVL, AFC, GTFS, and LTI), the first challenge is to find out the boarding locations for all users. As illustrated in Fig. 1(a), this information is computed by integrating AVL and AFC, and retrieving the exact latitude and longitude positions when the users’ cards performed the payments. Using these positions, we can estimate the closest stop or station that indicates the boarding local. Next, we merge multiple boarding locations to classify the users’ trips as initial, intermediate, and final. Such a classification is relevant to map all possible connections that compose a complete user’s trip. Finally, all boarding positions with their respective time instants are used to organize trip chains that describe passengers’ behavior, as summarized in Table 11. As shown, most attributes in this table result from the integration process, with bus type being a particularly important attribute in the dataset.

Fig. 1

Steps used to create our origin-destination dataset. Red boxes represent boarding data with no alighting correspondence.

Table 11 Description of Columns in the Dataset Boarding.

In the next phase, Fig. 1(b), we assess the validity of the boarding registration by checking two specific conditions. Firstly, a user’s boarding is discarded if the time difference between the AFC-recorded fare payment and the AVL-recorded bus arrival at the stop exceeds a certain threshold. This threshold has two possible values: (i) 20 minutes for bus stations; and (ii) 5 minutes for regular stops. This differentiation is necessary because buses typically remain longer at stations. Secondly, another discarding possibility happens when there is no direct connection between AVL and AFC records, which is considered in this figure as “out of trip”. According to the literature⁷, appropriate time intervals for integration depend on the specific dynamics of each city. For instance, in London, a 5-minute interval is considered suitable for integrating payment and boarding processes. In the case of Salvador, local studies conducted by the bus operating companies, taking into account factors such as delays, low-frequency routes, scheduled departures, and traffic conditions, led to the definition of time intervals considered most appropriate for modeling the dynamic interactions between passengers and buses.

In the subsequent phase, Fig. 1(c), we analyzed user types to determine the feasibility of estimating their alighting points. In Salvador, there is no device to validate the passengers’ alighting; therefore, the main challenge is to estimate it by analyzing the following boarding. Moreover, in Salvador, passengers aged 65 or older are entitled to free public transportation and are not required to use any form of electronic ticket or identification card. They can board simply by presenting a personal document. As a result, their boarding and alighting events are not recorded in the system. However, this group represents only a small portion of the total passenger volume. To account for their presence in the dataset, we apply a probability distribution to allocate these passengers along the bus line within the analyzed time interval. Another particular case that prevents us from identifying users’ alighting points occurs when there is only a single trip registration on a given day. In such cases, we can only determine the boarding point, with no information available about the alighting point. Therefore, we cannot consider such situations in our analyses. The alighting dataset, illustrated in Table 12, is one of the most important dataset produced by our research, whose examples of relevant attributes are: stop_time_ali – the estimated alighting time, stop_id_ali – the stop ID where alighting is inferred; walk_target – classification of walking behavior post-alighting, walk_dis – estimated walking distance in kilometers, walk_time – estimated walking time in minutes, wait_time – estimated waiting time at the stop in minutes, trip_dis – distance covered during the trip in kilometers, and trip_time – duration of the trip in minutes. A complete description of all features is available in our repositories.

Table 12 Dataset summary Alighting.

For all remaining cases, alighting points can be inferred by analyzing each user’s sequence of boarding points, i.e., by applying the Trip Chaining strategy, which is widely adopted in the ITS literature as discussed in the previous section^{6,7,8,10,11,13}. To better understand this inference, consider the three scenarios illustrated in Fig. 2. In Scenario I, we observe a passenger boarding at 8:00 AM (B1) at Stop (b) and then boarding again at 6:00 PM (B2) at Stop (f). Therefore, it can be inferred that the passenger boarded at Stop (b), disembarked at Stop (f) on the first trip (b → f), and then made the return journey at the end of the day (f → b).

Fig. 2

Scenarios illustrating three different boarding-alighting situations: (I) a single line, (II) lines with a connection, and (III) two lines connected by walking distance.

In the second scenario, we observe a user trip with a connection. In this situation, there are two boarding points for each trip. Initially, the user boarded at Stops (b), at 8:00 AM (B1), and (d), 8:20 AM (B2), being the first alighting registered at Stop (d). At the end of the day, the user boarded at Stops (j), at 6:00 PM (B3), and (d), at 6:10 PM (B4), respectively. Therefore, we infer the first user’s trip was b → j starting at 8:00 AM, and their return was j → b at 6:00 PM.

In our final scenario, we illustrate a situation when a user utilizes a connection between two different stops by walking a short distance between them. In this case, they register a first boarding at Stop (b), at 8:00 AM (B1), and the second one at Stop (x), 8:50 AM (B2). As one may notice, Stop (x) is in a different line. Hence, we look for its closest stop, respecting the maximum walking distance (Δ), Stop (f) in this case, to represent the first alighting. Considering they register another boarding at Stop (u), at 7:00 PM (B3), followed by boarding at Stop (f), at 7:30 PM (B4), we can map their full daily trip using the same rule previously considered. Therefore, we infer the first user’s trip was b → fΔx → u starting at 8:00 AM, and their return was u → xΔf → b at 7:00 PM.

As shown in Fig. 1(d), a walking distance is deemed acceptable if it is limited to 1.1 km. Concerning the average velocity, Fig. 1(e), and the trip time, Fig. 1(f), all registers with values greater than 80 km/h and 2 hours are unconsidered. These values were estimated by local specialists based on the passengers’ usage patterns and the transportation infrastructure in Salvador. Similar to the time interval, walking distance is also influenced by the specific infrastructure of each city. In London, for example, two different studies adopted thresholds of 1 km⁸ and 750 meters⁷. In the case of Salvador, the walking distance was defined by the operational planning team of the city’s bus consortium, based on the typical spacing between local stops and stations. It is important to note that both the time and distance thresholds can be adjusted by readers to suit their own scenarios, as we provide access to both raw and processed data.

In Fig. 1, all red boxes represent situations in which we cannot precisely use the passengers’ occurrences in our analyses. Nevertheless, even in minority cases, it is essential to consider their general behavior to mitigate imprecision in further estimations, such as the load of passengers on the buses. In this case, we use the data distribution for each line to allocate these occurrences across different buses, as recommended by the literature. After this correction, we have the processed Origin-Destination (OD) dataset, whose attributes are illustrated in Table 13. In this example, it is important to clarify that, at the first stop or station of each trip, the same timestamp is recorded for both the “start_trip” and “stop_time” attributes. This occurs because the bus is initiating its route, as indicated by the attribute “pt_sequence = 1”. At this initial point, the bus is empty, as expected at the beginning of all trips. For instance, in such cases, the number of boardings ("n_boardings”) reflects the total number of passengers entering the bus, while no alighting occurs ("n_alighting” = 0, “lag_loading” = 0, and “balance” = 0). Consequently, the loading after this first stop corresponds exactly to the number of boarded passengers.

Table 13 Summary of the OD dataset.

Graph Modeling

The organization of the OD dataset with passengers’ boarding and alighting allowed us to create the SUNT dataset, embedding a set of quantitative, temporal, and geospatial variables as a complex network. Formally, we have used information on latitude, longitude, and time to create a spatial-temporal graph G = {G₁, G₂, ..., G_T}. For all t = 1, ..., T, G_t = (V, E) stands for an attributed and directed graph at time t, where V = {v₁, v₂, ..., v_N} is the set of N vertices corresponding to the bus stops and stations, and E is the set of edges corresponding to feasible routes. A directed edge (v_i, v_j) ∈ E connects vertices v_i, v_j ∈ V if, and only if, there is a feasible route for the bus traffic from the corresponding station v_i to v_j in the network. G_t is a fixed graph structure since sets V and E do not change over time.

Figure 3(a) shows the map of Salvador with all vertices stored in our SUNT dataset, i.e., stops and stations used by regular and BRT buses, as well as subways. The geospatial information allows us to place them on the map, respecting their actual geographic position and the distances connecting them by the physical streets.

Fig. 3

(a) Salvador map with all stops and stations used by regular buses, BRT, and subway; (b) a sample of stops and stations (nodes) represented by blue dots and their respective lines (edges).

In our context, spatial data do not depend on time t, i.e., their information is time-invariant. Specifically, in every vertex v_i ∈ V, we store the following features: geographical position, number of boarding and alighting per vehicle, and passenger load. The features specifically concerning edges (v_i, v_j) ∈ E include the distance between stops and stations, the trip duration, the mean velocity, and the Renovation Factor (RF). RF is a well-known metric used in transportation research to assess the total demand in a line, i.e., it is computed on a set of edges that belong to the line¹⁵. Formally, this metric is the ratio of the total demand of a line to the load on its critical link. Higher renovation factors occur when there are many short trips along the line. Corridors with very high renovation factor rates are more profitable because they handle the same number of paying customers with fewer vehicles¹⁵. Besides the individual features, there is relevant information shared by both vertices and edges, such as the number of passengers per vehicle, lines and directions, vehicle characteristics, altitude, and trips.

The black bounding box in Fig. 3(a) represents an essential region of the city, which gathers different lines and connections. Figure 3(b) zooms in this region with a portion of the full graph, illustrating some bus stops as vertices and lines connecting them as edges. The red explaining box contains some features related to that bus stop (vertex) such as its latitude and longitude position, and the amount of boarding and alighting passengers. In the green explaining box, we illustrate some features related to a line (edge), such as the distance connecting two stops, the mean velocity and trip duration among the buses in that section, and the total amount of traveling passengers.

In Table 14, we illustrate how edge information is shared: src – origin stop/station; dst – the destination; distance – the distance between them; src_lat, dst_lat, src_lon, and dst_lon – their geospatial locations; average_speed – the average speed; trip_time – the total time trip; and loading – the passenger load in a given edge (street or avenue).

Table 14 Sample of edge features.

In Table 15, we share information about nodes, i.e., details related to stops and stations. Some relevant information containing average values considering vehicles are: loading – passenger loading that crossed a given node; n-boarding and n-alighting – amount of boarding and alighting; n-routes, n-trips, and n-vehicles contain the number of routes, trips, and vehicles; and average_speed is the average of speed for each vehicle during their last trip up to the destination node. A complete discussion of all datasets is documented at https://github.com/LabIA-UFBA/SUNT/blob/main/docs/datasets.md, and the corresponding source code is available at https://github.com/LabIA-UFBA/SUNT/blob/main/docs/dataloader_sample.ipynb.

Table 15 Examples of node features.

Positive Impacts and Future Works

This paper introduced SUNT, a novel dataset collected from public transportation in Salvador, Brazil. This dataset is notably relevant to the scientific community for supporting investigations in several domains, such as planning public transportation, designing computational approaches, and managing environmental impact. As previously mentioned, other researchers have published related datasets, ratifying the importance of this subject. However, our dataset stands out due to its massive information and complete availability. Unlike manuscripts that only share outcomes, we have fully shared collections of raw and graph-based details of vehicles, passengers, stations, time, and geographic properties.

In summary, SUNT paves new ways to provide positive social impacts, such as better planning the allocation of buses to lines, reasonably defining regular and express trips, thus reducing traffic jams and carbon emissions, and offering better trip experiences. By sharing SUNT, we expect to provide a robust dataset for the community, supporting the advancement of several investigation possibilities like time-based models, graph algorithms, spatial approaches, deep neural networks, routing simulations, and search heuristics. To illustrate such possibilities, we have listed future work that is worth investigating from our perspective: (i) graph-based learning approaches designed to pass messages using both temporal and spatial information; (ii) Multi-objective optimization approaches to find the shortest path based on edges weighted by distance and time considering traffic jam; (iii) Multimodal ML models that combine different features (e.g., temporal, spatial, numerical, and categorical data) with varying encoding approaches as message passing; (iv) Queue theory to address the problem of attending passengers from a stop A to B; (v) Concept Drift methods designed to identify when passengers’ pattern changes in real-world automatically; (vi) in multi-agent evolutionary algorithms, each agent handles a part of the search and, in each generation, spatial-temporal model could help to select the most suitable agent at each step of the evolutionary process; and (v) SUNT can be used to fine-tune time series foundation models, enabling similar transportation analyses in cities that lack equally complete and detailed datasets.

Ethical Declarations

Our datasets has no human ethical concern. The identification of users’ cards in the AFC data does not correspond to the actual card numbers, but rather an internal code that cannot be used to retrieve any personal information from external access. Although such recovery is highly unlikely, we implemented a hash-based solution (collision-free) to convert all internal identifications, adding a layer of privacy. It is important to note that no other attribute links individual users to their public transportation usage.

Data Records

The dataset is available at Mendeley Data¹⁴. The raw data were categorized into the following folds: AFC (Automatic Fare Collection), AVL (Automatic Vehicle Location), GTFS (General Transit Feed Specification), and LTI (Local Trip Information). The processed data were then organized into three distinct folds: Alighting, containing information about where passengers began their trips; Boarding, including all estimated stops where passengers ended their trips; and OD, which provides complete origin-destination information, enabling the data to be modeled as a graph. These folds contain data from March 2024 to March 2025. For updates and new data, we recommend accessing the GitHub repository: https://github.com/LabIA-UFBA/SUNT.

Technical Validation

This section aims to demonstrate the quality, consistency, and technical validity of SUNT by detailing the procedures implemented to ensure data integrity. It includes statistical and temporal visualizations that confirm the dataset contains accurate and practically useful information. It is important to emphasize that this section focuses on evaluating the dataset itself (its structure, reliability, and coherence) rather than performing extensive machine learning experiments or domain-specific analyses.

Statistical Validation

This section presents a set of descriptive statistics used to demonstrate whether our datasets contains accurate and useful information about public transportation in Salvador. Table 16 summarizes the statistics of the five most relevant attributes in the OD dataset: “n_boardings”, “lag_loading”, “n_alighting”, “balance”, and “loading”. A detailed examination of these attributes provides valuable insight into the overall dynamics of public transportation in Salvador. Moreover, these statistics provide a foundational understanding of data distribution, variability, and potential anomalies, which is essential for designing experiments, selecting models, and interpreting results using the SUNT dataset.

Table 16 Basic descriptive statistics.

In addition to the basic statistics, Fig. 4 presents box plots for all attributes, highlighting the challenges of modeling transport data. These challenges arise from sensitivity to rush hours, unexpected transit events, and various seasonal and daily patterns. An important detail in both Table 16 and Fig. 4 is the presence of outliers with values exceeding 250. For instance, a recorded boarding count (n_boardings) of 264 for a single vehicle far surpasses its actual capacity. This occurs in rare cases when a mobile turnstile registers multiple passengers at a location, even though they board different buses. Although this is part of the local public transportation dynamic, such events are rare, occurring in only 0.5% of cases. The presence of a mobile turnstile also impacts other variables, but with the same low probability.

Fig. 4

Box plots summarizing descriptive statistics focused on passengers’ behaviors.

Figure 5 illustrates the data distribution for these attributes. While the box plots reveal the presence of outliers, the overall distribution follows a skewed distribution, as expected in public transportation, with a majority of values concentrated near the lower stops and occasional extreme values indicating stops with significantly higher activity. The “n-boardings” and “n-alightings” histograms confirm that the previously discussed outliers are rare, low-frequency events.

Fig. 5

Histogram describing different attributes related to passengers’ behaviors.

The exponential distribution pattern suggests that while most bus stops experience relatively low passenger movement, a few stops handle significantly higher volumes. Together, these figures emphasize the high variability in passenger demand, the presence of peak usage at specific stops, and the challenges associated with modeling and optimizing transit operations.

The next statistics (Table 17) extracted from SUNT summarize key aspects of vehicle trips, including individual and cumulative distances between stops, total trip time, cumulative stop time, and cumulative trip duration. In addition to cumulative data, SUNT also provides individual trip details. We compiled the accumulated values to highlight the volume of processed data.

Table 17 Descriptive statistics of the variables related to vehicle trips.

Figure 6 presents box plots for the variables presented in Table 17, illustrating both general trends and the presence of outliers. In these cases, outlier values remain within the expected range. However, an analysis of “Total Trip Time” (Total Time) and “Cumulative Trip Duration” (Cum. Trip Duration) reveals negative values, which are inconsistent with time-based attributes. These anomalies arise due to real-world monitoring challenges, where delays in the internal clocks of devices collecting GTFS data can cause discrepancies. The apparent magnitude of these negative values, exceeding 4, 000, is a result of the large dataset. In practice, the actual time differences between stops amount to only a few seconds. To mitigate this issue, transportation companies aggregate data into one-hour intervals, and delayed clocks can be corrected through interpolation.

Fig. 6

Box plots summarizing descriptive statistics focused on trips’ behaviors.

Likewise, the histograms in Fig. 7 highlight that the overall trip behavior follows the expected pattern for public transportation. The outliers with negative time values are rare events that can be excluded from analyses without impacting modeling performance. However, we chose to retain these values in SUNT to preserve the dataset’s real-world nature and provide researchers with the flexibility to address them through alternative methods, such as estimating corrected values.

Fig. 7

Histogram describing different attributes related to trips’ behaviors.

The statistical patterns observed in the OD dataset are also reflected in the derived datasets, supporting further exploration and analysis. Building on the previous descriptive analysis, the SUNT dataset was examined as a time series to investigate temporal patterns, including cyclical and seasonal behaviors related to weekdays, weekends, and holidays. This analysis of temporal dynamics helps identify key characteristics, contributing to the validation of the dataset’s consistency and overall quality.

Temporal Validation

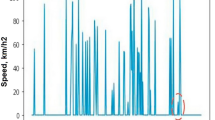
To check the temporal characteristics of the SUNT dataset, we selected several stops and stations with high passenger flow and multiple connection options between lines and buses. Figure 8 shows a time series (in blue) whose observations represent the loading of passengers at a given station, collected every 5 minutes from March 1st, 2024 to March 9th, 2024. As one may notice, the time series is characterized by a significant frequency fluctuation as noise that may affect its modeling and prediction. To address this issue, a simple moving average (SMA) with a window size of 12 observations can be applied to smooth the time series, as illustrated by the red line. The key advantage of selecting this window size is its ability to capture seasonal and cyclical patterns. As expected, analyzing SUNT as a time series allows for modeling daily variations (higher frequencies during rush hours) and differences between business days and weekends (lower frequencies on weekends).

Fig. 8

In blue, the time series containing loading information in a bus station, collected every 5 minutes between March 1st, 2024, and March 9th, 2024. In red, we show the time series transformed by SMA using a window size of 12 observations.

Similarly, to illustrate the seasonal relationships between stations and highlight the importance of the underlying graph structure, we selected the top five stations (nodes: 694, 2772, 1203, 592, and 561) with the highest passenger transit from a total of 2,871 possible stations represented in the SUNT graph. Figure 9 presents the smoothed time series for these stations, revealing how their patterns relate to one another while exhibiting distinct amplitude variations.

Fig. 9

Five time series with intense transit of passengers to illustrate the node regression task.

Continuing the focus on temporal relationships, Fig. 10 illustrates passenger volume over time across three transportation modes: BRT, subway, and regular bus. This analysis enables the investigation of how demand varies and interacts across different systems, supporting the development of forecasting models that incorporate multiple modes of transportation.

Fig. 10

Time series representing multiple transportation modes.

Spatial Validation

Leveraging the inherent spatial structure of SUNT represented as a graph, where nodes represent stop-time events and edges denote direct connections between them, we conducted two preliminary graph-based learning tasks, node classification and edge classification. These illustrative experiments highlight the dataset’s spatio-temporal potential and its applicability to real-world scenarios, particularly in the context of route optimization.

We selected eight features from the dataset, including passenger loading, mean velocity, distance between stops or stations, boarding and alighting counts, and the total number of lines, vehicles, and trips. To validate the spatial utility of SUNT, passenger loading was used as the target variable for node classification, while mean velocity served as the target for edge classification. These tasks are particularly relevant for route optimization, as they leverage the rich spatio-temporal information embedded in the graph structure to uncover patterns in passenger demand and traffic flow—key factors for improving transit planning, operational efficiency, and overall network performance.

For the node classification, passenger loading, a numerical variable, was discretized into four categories based on its quartiles: “maximum”, “high”, “medium”, and “low”. Similarly, for edge classification, mean velocity was binarized using the median value as a threshold. These class intervals were designed to illustrate local transportation demand. Alternative discretization schemes can be easily applied using our publicly available dataset. The spatial relationships between these attributes were then assessed using Graph Neural Networks (GNNs): Graph Convolutional Network (GCN)¹⁶, Chebyshev spectral graph convolutional operator (CHEB)¹⁷, SAmple and aggreGatE (SAGE)¹⁸, and Graph Attention Networks (GAT)¹⁹. GCN employs a graph convolution operation to learn representations of nodes in a graph. A key characteristic of GCNs is weight sharing, meaning the same weight matrix is applied to all nodes. This is achieved through symmetric normalization of the adjacency matrix and the inclusion of self-loops to ensure each node incorporates its own features during the aggregation process. CHEB implements an efficient generalization of Convolutional Neural Networks (CNNs) to arbitrary graph structures by expressing graph convolutional filters as polynomials of the graph Laplacian L of a graph G. As discussed in²⁰, using a polynomial of degree M ensures that the output at each node is influenced by information from its M-hop neighborhood, enabling localized and scalable filtering on graphs. SAGE is a GNN architecture that, instead of learning individual embeddings for each node, learns a set of aggregation functions that operate over a node’s local neighborhood to generate its embedding¹⁸. Each aggregator function combines information from neighbors at a specific distance, referred to as the number of hops or search depth, allowing the model to capture multi-scale structural and feature information. GAT is a type of GNN that incorporates attention mechanisms to learn node representations in a graph¹⁹. These mechanisms enable the model to assign different importance weights to each neighbor, allowing it to focus on the most relevant nodes during the aggregation process and thereby improving performance. GATs can also employ multiple attention heads, a concept closely related to the multi-head attention mechanism introduced in the transformer architecture by (Vaswani, Ashish, et al., 2017)²¹. Our validation of node and edge classification employed 10-fold cross-validation, a widely accepted method in machine learning to ensure robust and reliable evaluation. We used the same set of evaluation metrics for both tasks: Accuracy, F1-score, Matthews Correlation Coefficient (MCC), Precision, and Recall.

These comprehensive metrics are particularly important given the nature of transportation data, where certain categories (e.g., high passenger loads or low velocities) may be less frequent but critical for decision-making. The detailed evaluation framework thus ensures that the models’ strengths and limitations are fully understood, guiding future improvements and practical applications of the SUNT dataset in transit system analysis.

Table 18 summarizes all results obtained from our illustrative experiments. In Table 18(a), SAGE achieved the best performance across all metrics, except for precision, where CHEB performed slightly better. In Table 18(b), all models exhibited very similar behavior, with a slight advantage for GCN. The results demonstrate satisfactory performance, with values exceeding 60%, which is notable given the inherent complexity of predicting numerical values on edges. The balanced nature of the dataset ensures that the models are effectively learning meaningful patterns. Furthermore, these outcomes highlight opportunities for future research, encouraging the development of novel GNN architectures and preprocessing strategies to further enhance performance using our dataset as a benchmark.

Table 18 GNN results for node and edge classification.

Importantly, the results from both node and edge classification tasks underscore the value of representing urban mobility data as a graph. The SUNT dataset, by encoding spatio-temporal relationships in a graph structure, enables the application of graph-based learning methods that can capture complex patterns, such as variations in passenger flow and average velocity across different segments of the network, that are often lost in traditional flat or tabular representations. These preliminary experiments GNNs demonstrate the feasibility and potential of such models to extract meaningful insights from our dataset. This reinforces not only the relevance of the graph-based representation itself, but also the utility of the SUNT dataset as a foundation for future research on graph-based learning tasks.

Transportation Planning Validation

By analyzing passenger loads through an Origin-Destination (OD) dataset and applying these insights to timetable planning, we demonstrate how SUNT is currently used to support transportation planning decisions. In the first example, the OD dataset was utilized to determine the maximum passenger load across different time intervals. According to (Ceder, 2016)⁶, one of the fundamental objectives of transit service provision is to ensure sufficient capacity to accommodate the maximum number of passengers on board along the entire route within a given time period. Let us denote this time period (typically one hour) as j. Based on the peak-load factor concept, the required number of vehicles for period j is given by:

$${{\mathscr{M}}}_{j}=\frac{{\bar{P}}_{mj}}{{\gamma }_{j}c}$$

(1)

In this equation, ${\bar{P}}_{mj}$ is the average maximum number of passengers (max load) observed on-board in period j, c denotes the vehicle’s capacity (the total number of seats plus the maximum allowable standees), and γ_j is the load factor for period j, where 0 ≤ γ_j ≤ 1.0.

To illustrate the importance of calculating the max load ${{\mathscr{M}}}_{j}$, we have selected a specific line and analyzed the max-load stops in Fig. 11 during four different time intervals: (a) 7 a.m. (morning rush hour), (b) 4 p.m. (afternoon rush hour), (c) 10 a.m. (morning off-peak), and (d) 3 p.m. (afternoon off-peak). By analyzing these maps, one can observe how the locations of maximum load stops vary across different time intervals. This information has been used to improve bus planning and allocation, enhancing service delivery to better meet the needs of the population. Notably, the highlighted maximum-load stops align well with the actual local transportation dynamics.

Fig. 11

Max load calculated for a specific line during different relevant time intervals.

In our second example presented in Fig. 12, we illustrate how the information about max load can be used in practice to plan timetables, specifying which buses must be set as Express and Normal. Typically, when passenger data at stops/stations and along routes is unavailable, it becomes difficult to optimize bus services effectively. For example, during a rush hour interval (e.g., 8 AM-9 AM) with arrivals randomly defined, 9 buses (3 normal and 6 express) might be scheduled to serve passengers traveling from stop A to stop B, passing through intermediate stops. Without an estimate of maximum passenger load, all buses would need to return from stop B to stop A via the same route, stopping at all intermediate stations. Such a strategy has some problems: it wastes time and fuel, besides delaying the arriving time at A. Considering A is a neighborhood and B downtown, the amount of passengers from B to A is considerably lower during this rush time. Knowing the optimal number of buses required for the return trip and their appropriate schedules can significantly mitigate these issues.

Fig. 12

Planning timetables after calculating max load.

In Fig. 12, we illustrate three strategies for determining the bus type: (i) randomly selecting buses (Random information); (ii) dividing the hour into intervals based on the expected number of normal buses and designating the next bus within each interval as normal (Next information); and (iii) assigning normal buses based on the nearest neighbor approach, aiming to minimize the interval between them (Nearest information). The errors shown in this figure represent the differences, in minutes, between the estimated intervals – obtained using the random, next, and nearest neighbors strategies – and the optimal intervals. With this information, policymakers can effectively reduce passengers’ waiting times at stops and stations while optimizing the management of bus transit within the city.

Cross-Dataset Validation

Another important validation was performed by integrating SUNT with other urban data sources. By combining it with a publicly available dataset on public schools in Salvador, made available by the Municipal Department of Education at https://dados.salvador.ba.gov.br/search?tags=educacao (in Portuguese), it was possible to confirm the expected passenger load near schools during specific time periods. This dataset contains information on public schools, including their name, geographic coordinates (latitude and longitude), neighborhood, full address, and administrative details.

This example demonstrates the feasibility of integrating the SUNT dataset with external urban data sources, such as public school records, thereby expanding its range of applications beyond traffic analysis. As illustrated in Fig. 13, specialists analyze student passenger loads at bus stops or stations located near schools on specific days and times. In the visualization, the total number of passengers per stop or station is shown in red, while school locations are marked with blue dots. To enable this integration, each school is matched to its nearest stop or station based on geographic coordinates. Additionally, passengers in the SUNT dataset are identified as students through their transportation card classification.

Fig. 13

Integrating SUNT with data from public schools. The total number of passenger per stop/station is shown in red. Students are represented by blue dots.

This integrated analysis supports a variety of new research directions, such as evaluating school accessibility, understanding student mobility patterns, and informing policies for public transport planning in educational contexts.

Usage Notes

The dataset is licensed under Creative Commons (CC) BY 4.0. We encourage all interested researchers to download and use it to develop new AI-based methods and approaches aimed at enhancing urban mobility and public transportation management.