Background & Summary

Soil Moisture (SM), defined as the amount of water held in the soil, is a fundamental variable for characterizing land-atmosphere interactions, land surface processes, and the exchange of water and heat fluxes. It also serves as an essential input to land surface models that support a wide range of applications in hydrology, agriculture, ecology and meteorology1,2,3,4,5,6,7,8,9. Over the past several decades, satellite remote sensing has enabled global monitoring of SM through passive and active microwave instruments onboard Earth observation satellites. Compared to traditional point-scale ground-based measurements from field surveys, remotely sensed SM provides continuous, spatially distributed data with revisit intervals as short as 1–2 days. This not only improves representation of spatial heterogeneity in soils and land cover, and but also ensures more consistent data quality10,11,12,13,14,15. In particular, SM can be estimated from brightness temperature (TB) observations at passive microwave frequencies using retrieval algorithms7,16,17,18,19. The National Aeronautics and Space Administration’s (NASA) Soil Moisture Active Passive (SMAP) mission provides global SM retrievals from L-band passive microwave radiometer TB observations, representing the top 0–5 cm depth layer, at a native spatial resolution of ~36 km with a revisit time of 1–2 days20,21. However, the spatial resolution of microwave radiometer-based SM retrievals is limited to tens of kilometers due to antenna size constraints. Although the Jet Propulsion Laboratory (JPL) SMAP enhanced the 36 km SMAP radiometer SM product to 9 km21, this resolution remains insufficient for many fine-scale hydrological studies and applications.

To address this limitation, numerous research has focused on downscaling passive microwave SM retrievals22,23. Depending on the datasets and mathematical approaches used, downscaling methods generally fall into three categories:

  1. (1)

    Integration of multi-sensor observations, combining optical/thermal with microwave radiometer or radar data7,24,25,26,27,28,29,30,31.

  2. (2)

    Model-based approaches, which establish relationships between SM and other high-resolution land surface variables32,33,34,35,36,37,38,39,40,41.

  3. (3)

    Advanced mathematical or data assimilation techniques, including statistical methods and physics informed assimilation frameworks42,43,44,45,46,47,48.

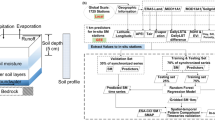
In this study, we developed and implemented a SM downscaling algorithm based on apparent thermal inertia (ATI) principle, which falls under the category (1). The algorithm downscales the SMAP enhanced 9-km radiometer product to 400 m resolution using high resolution land surface temperature (LST) and leaf area index (LAI) data derived from the Visible Infrared Imaging Radiometer Suite (VIIRS). The downscaled product covers the period 2015–2023 and was validated against in situ measurements from 31 SM monitoring networks provided by the International Soil Moisture Network (ISMN). For methodological details on the VIS/IR downscaling framework, readers are referred to the article26. Comparing to the original study, this article makes the following contributions:

  1. (1)

    We generated the first global remotely sensed SM product at 400 m resolution, derived from VIIRS-based downscaling, which improves the previously published 1 km downscaled SMAP SM product from the National Snow and Ice Data Center (NSIDC).

  2. (2)

    We introduced a new hybrid bias-correction approach that combines additive and ratio-based corrections, replacing the earlier additive-only method and thereby improving the robustness of the 400 m downscaled dataset.

  3. (3)

    We assessed the performance of the VIS/IR downscaling algorithm across multiple spatial scales, using global in situ SM data from the ISMN website, as well as discussed its implications for fine-scale hydrological applications.

Method

Downscaling algorithm

The 400 m downscaled SMAP SM data was generated using the visible/infrared (VIS/IR) algorithm26. This method is based on the thermal inertia relationship between SM and diurnal changes in LST, expressed as the SM-temperature difference (θ – ΔT). The implementation of the VIS/IR algorithm relies on several key assumptions: (1) There is an inverse relationship between SM and ΔT between the two VIIRS overpasses at 1:30 a.m. and 1:30 p.m., which can be approximated as the maximum diurnal temperature difference6,49,50. (2) The θ – ΔT relationship can be parameterized using long-term outputs from the Global Land Data Assimilation System (GLDAS) Noah model (1981–2020), including surface skin temperature and 0–10 cm SM content under dry-day conditions. A linear regression model was fit to establish this relationship. (3) Following the universal triangular relationship among Normalized Difference Vegetation Index (NDVI), LST and SM51,52, regression fitting was conducted separately for different NDVI classes. To represent the spatial heterogeneity of vegetation and microwave penetration, the 5 km Long-Term Data Record (LTDR) NDVI data were used. In this study, the θ – ΔT pairs were grouped into 10 NDVI classes with an interval of 0.1 across the valid NDVI range of 0–1, and regression models were fit for each class. (4) Variability of the θ – ΔT relationship within a GLDAS grid (25 km) can be neglected. Thus, regression coefficients derived from GLDAS data were applied uniformly to all 400 m pixels within the grid. It should be noted that θ – ΔT correlation weakens under extreme weather events (e.g., heat waves, droughts and heavy precipitation), introducing uncertainty into the model.

Figure 1 illustrates θ-ΔT scatter plots and regression fits for three SM networks: REMEDHUS (40.33°N, 5.04 °W), SoilSCAPE (34.94 °N, 97.65 °W), and TxSON (30.31 °N, 98.78 °W), derived from GLDAS Noah outputs between 1981 and 2020 at 6:00 a.m. Across all networks, θ – ΔT shows a consistent inverse relationship. Regression lines across NDVI classes are generally parallel, though in cases with sparse data, some class specific lines cross others. The averaged R2 values across NDVI classes for REMEDHUS, SoilSCAPE, and TxSON are 0.41, 0.533, and 0.513, respectively.

Fig. 1
figure 1

Data points and best fit regression lines of the θ-∆Ts model derived from GLDAS Noah outputs at SMAP descending overpass time (6:00 a.m.) for 1981–2020 at three networks: REMEDHUS, SoilSCAPE, and TxSON. Data points are classified into 10 NDVI classes with an interval of 0.1.

Full size image

The θ – ΔT regression model at the GLDAS grid scale (6:00 a.m. or 6:00 p.m.) is expressed as:

$${\theta }_{i,j}={a}_{0}+{a}_{1}{\triangle T}_{i,j}$$
(1)

where \({a}_{0}\) and \({a}_{1}\) are regression coefficients for a given NDVI class, \({\theta }_{i,j}\) is the simulated SM estimate, and \({\triangle T}_{i,j}\) is the diurnal temperature difference at pixel (i, j). Thus, each GLDAS grid contains 10 sets of regression coefficients corresponding to NDVI classes.

A discrepancy exists between SM simulated from VIIRS data (via the GLDAS-based θ – ΔT relationship) and SMAP L-band retrievals, due to differences in sensing depth, (0–10 cm for GLDAS vs. 0–5 cm for SMAP) and sensing modality (optical vs. passive microwave). However, prior studies have shown that surface layer SM correlates strongly with shallow soil depths (~10 cm)53,54, making the datasets comparable after bias correction. The corrected 400 m estimate is defined as:

$${\theta }_{i,j}^{{\prime} }=\alpha \cdot \left[{\theta }_{i,j}+\left(\Theta -\frac{1}{n}\sum _{n}\theta \right)\right]+(1-\alpha )\cdot [{\theta }_{i,j}\cdot \left(\frac{\Theta }{\frac{1}{n}\sum _{n}\theta }\right)]$$
(2)

where \({\theta }_{i,{j}}^{{\prime} }\) is the corrected 400 m SM, \({\theta }_{i,j}\) is the model-simulated SM from Equation (1), and \(\Theta \) is the 9 km SMAP value. The correction was applied within a 36-km SMAP footprint by adjusting \({\theta }_{i,j}\) using both the additive difference and multiplicative ratio between \(\Theta \) and the mean of all n 400 m pixels in the footprint. The weighting parameter \(\alpha \) balances additive and ratio-based corrections:

$$\alpha =\frac{{\sigma }_{\theta }}{{\sigma }_{\theta }+k}$$
(3)

where \({\sigma }_{\theta }\) is the local standard deviation within a 9 km grid, and k is a tuning constant (set to 0.02 following a previous study55. In areas of high variability, the correction relies more on the additive component, while in smoother regions it emphasizes the ratio-based adjustment. Compared with the original additive-only correction method26, the hybrid approach reduces blocky artifacts while preserving spatial patterns.

Validation metrics

To assess the accuracy of the original 9 km and the downscaled SMAP SM products, several statistical metrics were calculated: the coefficient of determination (R2), mean square error (RMSE), bias (\(b\)), unbiased RMSE (ubRMSE), mean absolute error (MAE), and spatial standard deviation (SSD). They are defined as:

$${R}^{2}=1-\frac{\sum {({\theta }_{i}-\hat{{\theta }_{i}})}^{2}}{\sum {({\theta }_{i}-\bar{\theta })}^{2}}$$
(4)
$${RMSE}=\sqrt{\frac{\mathop{\sum }\limits_{i=1}^{n}{(\hat{{\theta }_{i}}-{\theta }_{i})}^{2}}{n}}$$
(5)
$$b=\frac{\mathop{\sum }\limits_{i=1}^{n}(\hat{{\theta }_{i}}-{\theta }_{i})}{n}$$
(6)
$${ubRMSE}=\sqrt{{{RMSE}}^{2}-{b}^{2}}$$
(7)
$${MAE}=\frac{\mathop{\sum }\limits_{i=1}^{n}|{\theta }_{i}-\hat{{\theta }_{i}}|}{n}$$
(8)
$${SSD}=\sqrt{\frac{\mathop{\sum }\limits_{i=1}^{n}{(\hat{{\theta }_{i}}-\bar{\theta })}^{2}}{n}}$$
(9)

where \(\theta \) represents in situ SM measurement and \(\hat{\theta }\) is the SMAP SM estimate at resolutions of 400 m, 1 km or 9 km. The ubRMSE removes the effect of bias (\(b\)) from RMSE. MAE represents the mean absolute error, while SSD quantifies the spatial variability of SM across all stations within a given network. Each in situ measurement was compared with the closest SMAP grid cell at the corresponding resolution, ensuring the same number of point pairs across products of fair comparison.

Data

This study used multiple satellite and model datasets to implement the VIS/IR downscaling algorithm and to validate the downscaled and original SMAP SM products.

The SMAP satellite, launched by NASA in January 2015, operates in a near-polar, sun-synchronous orbit with local overpasses at 6:00 a.m. and 6:00 p.m. The system carries an L-band microwave radiometer operating at multiple polarizations20,21,56,57. In this study, we used the enhanced Level 2 half-orbit 9 km product (SPL2SMP_E), derived from radiometer TB observations using the Single Channel Algorithm (SCA)2, and spatially enhanced via the Backus-Gilbert optimal interpolation method21. The 9 km SM product was downloaded from the NSIDC repository (https://nsidc.org/data/spl2smp_e/versions/6)58. For comparison, the 1 km downscaled SM product generated with the VIS/IR algorithm was obtained from the NSIDC repository (https://nsidc.org/data/nsidc-0779/versions/1)59.

The GLDAS system provides land surface variables generated by integrating satellite and ground observations with land surface modeling and data assimilation techniques to ensure consistency and quality60,61. We used GLDAS V2.0 (1981–1999) and V2.1 (2000–2020) outputs from the Noah land surface model (LSM) Level 4 model, specifically surface skin temperature and 0–10 cm SM content (https://ldas.gsfc.nasa.gov/gldas)62. The Noah model was originally developed by the National Centers for Environmental Prediction (NCEP), as a land component for the Eta mesoscale model63,64.

The LTDR project provides global land surface climate records from 1981 to the present, using data of Advanced Very High Resolution Radiometer (AVHRR) onboard National Oceanic and Atmospheric Administration (NOAA) N07 ~ N19 satellites and Moderate Resolution Imaging Spectroradiometer (MODIS) onboard Aqua/Terra satellites. The LTDR products include daily surface reflectance, NDVI, LAI and Photosynthetically Active Radiation (FPAR) at 0.05° resolution65,66,67,68. We used AVHRR NDVI Version 5 data, downloaded from NASA’s LTDR website (https://ladsweb.modaps.eosdis.nasa.gov/), to represent vegetation dynamics in the θ – ΔT downscaling framework.

The VIIRS instrument, onboard Suomi National Polar-orbiting Partnership (NPP) and NOAA-20 satellites, provides global observations in 22 visible and infrared bands for variables including temperature, vegetation, snow/ice, and clouds. VIIRS offers improved spatial resolution and accuracy compared to AVHRR and MODIS69. In this study, we used two VIIRS products: (1) daily LST at 375 m, derived from I5 band (10.5–12.4 μm) using the VIIRS LST/emissivity algorithm with atmospheric correction, and (2) 8-day LAI at 500 m, retrieved with the MODIS LAI/FPAR operational algorithm70,71, from NASA’s website (https://www.earthdata.nasa.gov/data/instruments/viirs). They both were resampled via nearest-neighbor interpolation method to 400 m resolution. LAI values were normalized to 0-1 to match NDVI class coefficients in Equation(1).

The Global Precipitation Measurement (GPM) mission, launched in 2014 as a successor to Tropical Rainfall Measuring Mission (TRMM), provides precipitation and snow estimates globally72,73,74. The Integrated Multi-satellitE Retrievals for GPM (IMERG) Version 6 daily dataset, gridded at 0.1o resolution and covering 60oN - 60oS, was used to assess the effect of precipitation on SMAP retrievals from NASA’s website (https://gpm.nasa.gov/data)75.

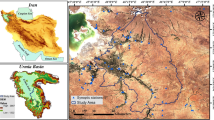
The ISMN is a global repository of long-term in situ SM measurements, hosting data from 80 networks and over 3000 stations since 195276,77,78,79,80. For this study, in situ of 0–5 cm SM measurements from 31 networks were obtained from the ISMN website (https://ismn.geo.tuwien.ac.at/). The networks span diverse continents, climates (humid to semi-arid) and land cover types (e.g., grassland, forest, agriculture, and shrubland). Their locations and details are presented in Fig. 2 and Supplementary Table 1.

Fig. 2
figure 2

Locations of 31 ISMN SM networks used to validate the 400 m, 1 km downscaled, and original 9 km SMAP SM datasets. The bottom three panels show land cover maps for SoilSCAPE, TxSON, and REMEDHUS, along with their watershed boundaries. The 9 km SMAP SM grids are shown in light blue.

Full size image

Data Records

The global 400 m downscaled SMAP soil moisture dataset is available through the University of Virginia’s data repository (https://doi.org/10.18130/V3/IVOU1T)81. The repository provides daily global SM data from April 1, 2015, to December 31, 2024. Files are named using the prefix “smap_sm_400m” followed by the corresponding year, and in Geographic Tagged Image File Format (GeoTIFF). Each file includes two layers corresponding to ascending and descending SMAP overpass SM observations and each layer is with raster dimensions of 36,540 rows × 86,760 columns. The SM raster layer is mapped in the Equal-Area Scalable Earth Grid 2.0 (EASE 2.0) projection, covering the global extent from 180° W to 180° E and 86° N to 86° S, with a grid spacing of 400.36 m.

Data Overview

Examples of the dataset are illustrated in Figs. 3 and 4. Figure 3 shows monthly mean 400 m downscaled SMAP SM on a global scale, while Fig. 4 presents weekly averages at three spatial resolutions (400 m, 1 km and 9 km) for three representative sub-basins: the Middle Colorado River basin, the Duero River basin and the San Joaquin River basin. Both inter-seasonal and inter-annual variability can be clearly captured. However, blocky artifacts are visible in the 400 m and 1 km SM maps, primarily due to (1) the coarse resolution of GLDAS inputs (25 km) used to construct the downscaling model, and (2) spatial heterogeneity in the θ – ΔT relationship.

Fig. 3
figure 3

Global maps of monthly-averaged 400 m downscaled SMAP SM for April and July in 2022, derived from the enhanced 9 km Level 2 SMAP product using the VIS/IR downscaling algorithm.

Full size image
Fig. 4
figure 4

Weekly-averaged SMAP SM at 400 m, 1 km, and 9 km resolutions in 2022 for three sub-watersheds: (a) Middle Colorado River basin, (b) Duero River basin, and (c) San Joaquin River basin, corresponding to the SoilSCAPE, TxSON, and REMEDHUS networks.

Full size image

Figure 5 illustrates the spatial patterns of SMAP SM data availability in percentage of valid daily observations, aggregated seasonally for the four climatological seasons: January-March (JFM), April-June (AMJ), July-September (JAS), and October-December (OND). Consistent spatial pattern can be observed across resolutions, with higher availability in arid and semi-arid regions (e.g., northern Africa, the Middle East, central Australia), where persistent clear-sky conditions lead to fewer retrieval gaps. In contrast, heavily vegetated and persistently cloudy regions, including the Amazon Basin, the Congo Basin, Southeast Asia, and parts of high-latitude boreal forests, exhibit lower availability due to frequent radio-frequency interference (RFI), dense vegetation canopy attenuation, and retrieval mask conditions. Seasonal contrasts are also evident: availability generally increases during the dry seasons and decreases during periods of enhanced cloudiness or vegetation growth. The strong agreement in spatial patterns across the 400 m, 1 km, and 9 km products demonstrates that the downscaling preserves the fundamental climatology of SMAP data availability while revealing finer-scale spatial heterogeneity at higher resolutions.

Fig. 5
figure 5

Seasonal data availability of the SMAP 400 m, 1 km, and 9 km products for 2015–2023.

Full size image

Technical Validation

Figures 6–7 and Tables 1–2 summarize validation results for the 400 m, 1 km, and 9 km SMAP SM products during the descending overpass (6:00 a.m.), evaluated against in situ SM observations. From Fig. 7 and Table 2, both ubRMSE (0.072 m3/m3) and MAE (0.066 m3/m3) for the 400 m product are lower than those for either the 1 km or 9 km SM data, demonstrating improved accuracy of the downscaled SM relative to the original SMAP retrievals. Scatter plots from Fig. 7a (TxSON) and Fig. 7c (SoilSCAPE) show that while 9 km point pairs are more concentrated, their regression fits are more biased compared with the 400 m and 1 km SM products. Consistently, the statistical metrics in Table 1 confirm that both downscaled products outperform the 9 km product. Only two networks (IMA_CAN1 and KIHS_SMC) exhibit higher ubRMSE at 400 m than at 9 km, while all others show improvements. Because the scale difference between 400 m and 1 km is smaller, the relative gains in ubRMSE and MAE are less pronounced than those between 400 m and 9 km.

Fig. 6
figure 6

Averaged validation metrics by network: (a) R2, (b) ubRMSE, and (c) MAE for the 400 m, 1 km, and 9 km SMAP SM datasets at descending overpass time (6:00 a.m.) from 31 ISMN SM networks (2015–2023).

Full size image
Fig. 7
figure 7

Validation scatter plots comparing SMAP SM data at 400 m, 1 km, and 9 km resolutions with in situ SM measurements at descending overpass time (6:00 a.m.) from 2015–2023 at three networks: (a) TxSON, (b) REMEDHUS, and (c) SoilSCAPE.

Full size image
Table 1 Validation metrics (R2, ubRMSE, and MAE) for 12 stations from three ISMN SM networks (TxSON, RENEDHUS, and SoilSCAPE), comparing the 400 m, 1 km, and 9 km SMAP SM products at descending overpass time (6:00 a.m.) in 2015–2023.
Full size table
Table 2 Overall validation metrics: (R2, ubRMSE, and MAE) for the 400 m, 1 km, and 9 km SMAP SM datasets at descending overpass time (6:00 a.m.) during 2015–2023, validated against in situ SM from 31 ISMN networks.
Full size table

A slight degradation in R2 is observed when moving from the original 9 km product (R2 = 0.426) to the downscaled versions (R2 = 0.409 at 1 km and R2 = 0.406 at 400 m). This reflects the classic bias-variance trade-off in downscaling. Increasing resolution introduces finer-scale variability, which raises variance and slightly lowers R². At the same time, the lower ubRMSE indicates a reduction in bias, meaning that although accuracy may fluctuate locally at the pixel level, the downscaled products provide a closer approximation to the true spatial distribution. This conclusion is further supported by SSD results in Fig. 8, which show that the downscaled values align more closely with the 1:1 diagonal compared to the 9 km data, particularly at TxSON (Fig. 7a) and SoilSCAPE (Fig. 7c). Across networks, only 5 sites (IMA_CAN1, NGARI, PBO_H2O, TAHMO, and TxSON) show a notable reduction in R2 at 400 m compared to 9 km, while most networks exhibit little or no degradation.

Fig. 8
figure 8

Averaged SSD values by network for in situ SM, and for the 400 m, 1 km, and 9 km SMAP SM datasets at descending overpass time (6:00 a.m.) during 2015–2023 across 31 ISMN networks.

Full size image

When comparing SSD values across datasets, the 400 m product (0.041 m3/m3) is the closest to the in situ benchmark (0.1 m3/m3), whereas the 1 km (0.039 m3/m3) and 9 km (0.033 m3/m3) products underestimate variability to a greater extent. This indicates that the 400 m downscaled SM better preserves spatial variability and captures finer-scale SM features, consistent with the scatter plots patterns shown in Fig. 7.

Figure 9 compares monthly averaged SMAP SM with accumulated GPM IMERG precipitation. All three SMAP products generally track in situ SM dynamics, though biases emerge during rainfall periods. For instance, the CR200_13 station in TxSON underestimates SM in early 2017 and late 2018, with reduced bias in both the 400 m and 1 km products. Such discrepancies likely reflect the impact of precipitation on SMAP retrieval quality, as rapid SM changes of SM following rainfall events are not always fully captured by the satellite estimates.

Fig. 9
figure 9

Time-series of monthly-averaged SMAP SM (400 m, 1 km, and 9 km) and in situ SM for descending overpass time (6:00 a.m.) from 2015–2023 at three networks: (a) TxSON, (b) REMEDHUS, and (c) SoilSCAPE. Blue bars represent the monthly accumulated GPM IMERG precipitation.

Full size image

Usage Notes

In a summary, a VIS/IR downscaling algorithm, based on the vegetation-modulated thermal inertia relationship between SM and diurnal changes in LST, was developed to generate a global daily downscaled SMAP SM product at 400 m resolution. The downscaled SM datasets at 400 m and 1 km (obtained from the NSIDC repository) resolutions, together with the original 9 km product, were validated against in situ SM measurements from 31 monitoring networks worldwide, provided by the ISMN. Validation results show that the 400 m product achieved lower ubRMSE (0.025–0.365 m3/m3) and MAE (0.024–0.344 m3/m3) compared with both the 1 km and 9 km SM products. In addition, the average SSD of the 400 m dataset (0.041 m3/m3) was closer to the in situ benchmark (0.1 m3/m3) than either 1 km or 9 km data. These findings confirm that the 400 m downscaled SMAP SM product not only provides finer spatial detail but also improves overall accuracy relative to the native 9 km retrievals.

It should be noted that the global downscaled SMAP SM product is available only between approximately 65o N and 45o S, and contains missing data in some regions, mainly due to the limited availability of input datasets required for the downscaling algorithm.

Several limitations should also be considered when using this product. First, VIIRS data are derived from visible and infrared observations, which are unavailable in regions with persistent cloud cover. Second, SMAP retrievals have reduced accuracy under dense vegetation condition and pixels with vegetation water content greater than 5 kg/m2 should be excluded. Third, the algorithm relies on datasets from multiple sources with different sensing depths, introducing potential uncertainties and biases. Finally, there is an inherent spatial mismatch: remote sensing and LSM data are available at kilometer-scale resolutions, while in situ observations are point measurements.

Despite these limitations, the global 400 m downscaled SMAP SM product represents a significant advancement for remote sensing SM applications. Fine-scale SM data can better characterize the spatial patterns of small watersheds, supporting a wide range of regional and local applications, including precision agriculture, land-use planning, hydrology and water resources management, forestry, land management, and monitoring and assessment of hydrological extremes.