Economic statistical model of the np chart for monitoring defectives

Abstract

When monitoring manufacturing processes, managing an attribute quality characteristic is easier and faster than a variable quality characteristic. Yet, the economic-statistical design of attribute control charts has attracted much less attention than variable control charts in the literature. This study develops an algorithm for optimizing the economic-statistical performance of the np chart for monitoring defectives, based on Duncan’s economic model. This algorithm has the merit of the economic model to minimize expected total cost, and the benefit of the statistical design to enhance the effectiveness of detecting increasing shifts in defectives. The effectiveness of the developed np chart is investigated under different operational scenarios. The results affirm a considerable superiority of the proposed np chart over the traditional np chart. Real-life data are used to demonstrate the applicability of the proposed np scheme, in comparison to the traditional np chart.

Introduction

Control charts are widely employed to establish and monitor statistical control of a process. It is an effective tool for assessing process parameters. Control charts design requires the selection of a sample size (n), a sampling interval (h), and the control limits (upper control limit (UCL) and lower control limit (LCL)). The process of selecting the control chart parameters is generally known as the control chart design¹. Various analysis techniques are required to model shifting processes^2,3,4,5. Different design models of control charts have been developed in the literature. They are usually grouped into three main classifications: statistical, economic, and economic-statistical designs. Conventionally, the control limits of the statistical charts are calculated to be equal to $\mu \pm 3\sigma$, where $\mu$ and $\sigma$ are the mean and standard deviation of the process. The sample size (n) is usually suggested to be equivalent to 4 or 5 and the sampling interval (h) is selected based on production rate and/or availability of inspection resources^6,7. In practice, these heuristically designed Shewhart charts are the most common since they are simple to understand and use with minimal operator training needed. Even though Shewhart charts assess the expenses implicitly by selecting n and h, the resultant charts are not guaranteed to be economically optimal.

The performance of statistically designed charts is typically determined in terms of the Average Run Length (ARL) or Average Time to Signal (ATS) where ATS = ARL × h^8,9. The out-of-control ARL can be defined as the average number of samples required to detect a process shift after it occurs^10,11,12. Similarly, the out-of-control ATS can be defined as the average time required to detect a process shift after it occurs^13,14,15. The establishment of a cost-related design of control charts is needed due to the lack of any measure that directly represents costs. Therefore, the economic design of control charts was introduced to evaluate the performance in terms of monetary value. The chart parameters, n, h, LCL and UCL, are usually searched to maximize the total expected profit or to minimize the total expected cost^16,17,18.

Both statistical and economic designs have their own strengths and weaknesses. Statistical designs of the control charts result in high detection power and low Type I error but then the related expenses are not investigated. On the other hand, the primary focus of the economic designs is on minimizing the cost associated with the poor quality. While economic design aims to achieve cost efficiency, it ignores the control of false alarm rate which in turn can deteriorate the detection effectiveness of the control chart^19,20,21,22. Thus, the initiation of a model that combines the advantages of both designs was really required. The economic-statistical design was initially introduced by Saniga²⁰. It successfully reduced the disadvantages of both economic and statistical designs and resulted in minimizing the expected cost, while improving the detection effectiveness of the control charts. The purpose of economic-statistical design of control charts is to minimize the expected total cost under statistical constraints²³. Economic-statistical designs are generally more expensive than economic designs because of the extra statistical constraints. However, such statistical constraints successfully reduce the process variability and enhance product quality. Economic-statistical design is used to avoid the disadvantages of economic and statistical designs, by utilizing an economic objective function which is usually a function of cost parameters and out-of-control ATS, in addition to constraints on the false alarm rate (${ATS}_{0}$) and/or inspection rate (r)^24,25,26,27.

Since the introduction of the economic design of control charts, several economic models have been proposed in the literature²⁸. In Duncan’s model, an economic design of $\overline{X }$ chart was established to determine its optimal parameters n, h, LCL, and UCL. The parameters were identified to minimize the expected total cost per operational cycle. Recently, many authors considered the economic-statistical design of control charts. Safe et al.²⁹ designed a multi objective genetic algorithm for economic-statistical design of $\overline{X }$ control chart. The findings of the study provide a listing of feasible optimal results and graphical interpretations that proves the flexibility and adaptability of the proposed approach. Naderi et al.³⁰ presented an economic-statistical design of $\overline{X }$ chart under Weibull model using correlated samples under non-uniform and uniform sampling. The objective of the study was to optimize the average cost while considering different combination of Weibull distribution parameters estimates. Similarly, Lee and Khoo³¹ investigated the economic-statistical design of double sampling (DS) S chart. The optimum DS S chart design parameters were found by minimizing the cost while keeping statistical constraints in consideration. The study shows that the DS S chart is better than Shewhart-type chart, with a minimal cost increase and higher statistical performance. Further, Katebi and Pourtaheri³² proposed an economic-statistical design of exponentially weighted moving average (EWMA) control chart to monitor the average number of defects. Evaluation of the economic performance in terms of the hourly expected cost and the statistical performance in terms of ARL was conducted using the cost function developed by Woodall³³. Using the design of experiment (DOE), a sensitivity analysis was undertaken to explore the effect of the factors on the result of the economic-statistical model. The results revealed that EWMA outperforms the typical Shewhart control chart. The DOE results showed that the most effective parameters are the size of the shift and assignable cause rate of occurrence. In addition, Saleh et al.³⁴ assessed the in-control performance of EWMA in terms of standard deviation of ARL. Lu and Reyonlds³⁵ created an Exponentially Weighted Moving Average (EWMA) control chart to monitor the mean of autocorrelated processes because process autocorrelation has a significant impact on control chart performance. Namin et al.³⁶ developed an economic-statistical model for the acceptance control chart (ACC) where there is uncertainty in the parameters of some processes. Tavakoli and Pourtaheri³⁷ proposed an economic-statistical design of the variable sample size (VSS) multivariate Bayesian chart. The developed VSS multivariate Bayesian chart was found to perform better than the T² multivariate Bayesian chart. Although there has been a lot of interest in the economic-statistical design of control charts in the literature, there have only been a few articles that deal with the economic-statistical design of control charts^36,38,39, mostly on the design of p control chart⁴⁰. In general, the economic-statistical design of the attribute control charts has been extremely oversighted in the literature compared with variable charts, although in practice they have wider applications. The attribute chart popularity comes from the ease of understanding and implementation, compared with variable charts⁴¹.

The motivation behind this study stems from the observation that while variable control charts received significant attention in the literature, attribute charts have been relatively overlooked in terms of their economic-statistical design despite their widespread applications and ease of implementation. The economic-statistical design of control charts aims to optimize the chart’s parameters to minimize the expected total cost, while simultaneously enhancing its statistical properties and detection effectiveness for detecting out-of-control scenarios. Traditionally, control charts have been designed using statistical considerations, such as setting control limits based on specific Type I error probability. However, these charts do not explicitly address the economic aspects of quality control. On the other hand, economic designs of control charts focus primarily on minimizing costs associated with poor quality but may neglect the control of false alarm rates, which can deteriorate the detection effectiveness.

To bridge this gap, this research proposes an algorithm for optimizing the economic-statistical design of the np chart for monitoring shifts in fraction nonconforming (p) based on Duncan’s model, which is a well-established model in the literature and due to its elegance in terms of considering all essential costs needed in manufacturing applications. In this design, two statistical constraints on the false alarm rate and the inspection rate are incorporated to overcome the weakness of the economic design. By optimizing the design of the np chart, the researchers aim to improve the overall efficiency of quality control processes in industries. The developed optimal np chart is compared with its traditional np counterpart, EWMA chart and synthetic chart in a real-world application within the water bottle manufacturing industry. In addition, a sensitivity analysis is performed to investigate the impact of the design specifications and process shift distributions on the performance of the proposed np chart under different operational scenarios.

The rest of the article is organized as follows: “Methodology” section explains the proposed methodology, including the operation and optimization of the chart. In “Comparative studies and sensitivity analyses” section, comparisons and sensitivity analyses are carried out. Finally, “Conclusions” section concludes the article by summarizing the findings, discussing the theoretical contributions, exploring practical implications, and providing suggestions for future research directions.

Methodology

The operation and optimization design of the proposed np control chart is explained in this section.

Operation of the np chart

The np chart is a type of attribute chart that is employed to monitor the number of defectives (d) in a sample. When using an np chart to monitor a process, the process is assumed to be in control if LCL ≤ d ≤ UCL, where LCL and UCL are the np chart’s lower and upper control limits, respectively. That is, if d < LCL and/or d > UCL, the control chart will declare an out-of-control condition. However, the focus of this research is to develop an np chart that detects the increasing shift in defectives since a decreasing shift of defectives, when d < LCL, is actually a desired goal and not of any risk. Consequently, the LCL is not considered as a decision variable in this research.

If the in-control fraction nonconforming p₀ of a process shifted to an out-of-control fraction nonconforming p, then the relationship is defined as follows:

$$p=\delta \times {p}_{0,}$$

(1)

where δ > 1 means that the process is out-of-control and δ = 1 indicates that the process is in control (i.e., p = p₀). The monitoring process using np chart can be described as follows:

• 1. A sample of n units is obtained at the end of each h, and d is counted for that sample.

• 2. On the np chart, the counted d is plotted for each sample.

• 3. If d > UCL, then an out-of-control signal will be produced. Otherwise, the process considers in-control, and return to step 1.

The following assumptions are taken into consideration in this research. First, the procedure begins with an in-control condition where the number of defectives follows a binomial distribution. Second, the random shift follows a uniform and Rayleigh distributions. Third, in-control fraction nonconforming (${p}_{0}$) is known. Fourth, upward shifts in p are only considered. Finally, it is assumed that the out-of-control condition is occurred due to a single assignable cause and the occurrence of the single assignable cause follows a homogeneous Poisson distribution with mean ε⁷.

As mentioned earlier, the economic-statistical model in this research is developed based on Duncan’s model, which considers two main design specifications: process specifications and cost specifications. These design specifications are shown in Table 1.

Table 1 Design specifications of the economic statistical model.

Optimization design of the np chart

The suggested optimization algorithm for the np chart is presented in this section. The design algorithm optimizes the decision variables, n, h, and UCL in order to minimize ETC. The economic-statistical design of the np control chart proposed in this study can be formulated as follows:

$$\begin{array}{*{20}c} {{\text{Objective}}\;{\text{function}}:} & {{\text{Minimize}}\;ETC} \\ \end{array} ,$$

$$\begin{array}{*{20}c} {{\text{Constraints}}:} & {ATS_{0} \ge \tau ,} \\ \end{array}$$

(2)

$$\mathrm{r }=\frac{n}{h},$$

(3)

$$\begin{array}{*{20}c} {{\text{Independent decision variables}}:} & n \\ \end{array} ,$$

$$\begin{array}{*{20}c} {{\text{Dependent decision variables}}:} & {h\;{\text{and}}\;UCL} \\ \end{array} .$$

In this optimization model, n is an independent variable, while h and UCL are dependent variables on values of r and τ, respectively. The parameter, r is the inspection rate, and it is equal to the sample size divided by the sampling interval. The constraint on r in Eq. (3) ensures that the resources are fully utilized to improve the detection effectiveness of the control chart. The measure ATS₀ in Eq. (2) is the in-control average time to signal. It is equal to h/α, where α is Type I error probability that the np chart will show an out-of-control signal even though the process is actually in-control as shown in Eq. (4). On the other hand, ATS is the out-of-control average time to signal and equivalent to h/(1 − β) where β is the Type II error probability that the np chart states that the process is in-control when it is actually out-of-control as illustrated in Eq. (5). The values of α and β can be determined as follows:

$$\alpha =\mathrm{Pr}\left\{d>UCL\right\}=1-\sum \limits_{i=0}^{UCL}{C}_{i}^{n}(1-{p}_{0}{)}^{n-i}{{p}_{0}}^{i},$$

(4)

$$\beta =\mathrm{Pr}\left\{d\le UCL\right\}=\sum \limits_{i=0}^{UCL}{C}_{i}^{n}(1-p{)}^{n-i}{p}^{i}.$$

(5)

In the optimization design, ATS₀ is considered as a constraint while ATS is incorporated into the objective function ETC which needs to be minimized. This guarantees that the optimal np chart will have a smaller ATS across the entire range of shifts, and eventually leads to better detection effectiveness. The objective function ETC is computed as follows:

$$ETC=\underset{1}{\overset{\delta max}{\int }}\delta \cdot L\left(\delta \right)\cdot {f}_{\delta }\left(\delta \right)d\delta ,$$

(6)

where ${f}_{\updelta }\left(\updelta \right)$ is the probability density function of the shift. The cost per unit time, $L\left(\delta \right)$ for a given p shift (in Eq. 6) is estimated based on Duncan’s²⁸ economic model as follows:

$$L\left(\delta \right)=\frac{b+cn}{h}+\frac{\left[\frac{h}{1-\beta }-\frac{h}{2}+\frac{\varepsilon {h}^{2}}{12}+en+D\right]M\varepsilon +\frac{\alpha T}{h}+\varepsilon W}{1+\varepsilon [\frac{h}{1-\beta }-\frac{h}{2}+\frac{\varepsilon {h}^{2}}{12}+en+D]}.$$

(7)

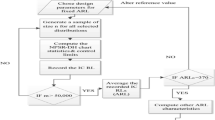
The optimization model identifies the optimal values of n, h and UCL that minimize ETC throughout a shift domain of ($1$≤ δ ≤ δ_max) while ensuring that ${ATS}_{0}$ is no less than a specified value of τ. Figure 1 explains the optimization process of the np chart. It can be explained as follows:

• 1. Start by specifying the design specifications and the cost parameters.

• 2. Initiate the variable ${ETC}_{min}$ as a very large number (${ETC}_{min}$ will be used to keep track of the ETC’s minimum value).

• 3. Begin by raising n by one at a time, beginning with n = 1.

• 4. Find h that satisfies constraint (3) for each n.

• 5. For every set of (n, h), search the value of UCL that meets constraint (2).

• 6. Find the ETC value that corresponds to the related n, h, and UCL.

• 7. Replace ETC_min by the calculated ETC if the calculated ETC is smaller and save the current n, h, and UCL values as a temporary optimal solution.

• 8. Step 4 is repeated for each n value trial until ETC cannot be decreased anymore. The optimal np decision variables will generate the lowest ETC while satisfying requirements (2) and (3).

Figure 1

Optimization algorithm flowchart.

It is worth mentioning that the traditional np chart in this study refers to an np chart designed based on the proposed economic-statistical model and utilizing the same optimization algorithm. However, that the traditional np chart only adjusts the UCL to maintain ATS₀ greater than τ, without optimizing n and h. Instead, these two parameters (n and h) are predetermined by the user. In contrast, the optimal np chart is designed to optimize all charting parameters (UCL, n, and h) through the above-mentioned optimization procedure.

The proposed economic-statistical optimization algorithm results in the best optimal combination of the charting parameters for the np chart. The design algorithm is coded using C programming language. In a couple of seconds, a personal computer can complete the optimization design of the np chart.

EWMA and synthetic control charts

The Exponentially Weighted Moving Average (EWMA) and synthetic control charts exhibit high sensitivity to small and moderate shifts in the fraction nonconforming (p) when compared to the np chart^7,9,42. The EWMA chart differs from the np chart as it takes into account the real-time accumulation of all samples, rather than solely relying on the latest sample^43,44. The plotting statistic E_t is updated for each tth sample as follows⁴⁵:

$${E}_{t}=\lambda \left({d}_{t}-{d}_{0}\right)+\left(1-\lambda \right){E}_{t-1},$$

(8)

where ${d}_{t}$ is the number of nonconforming items in the tth sample, d₀ (= n × p₀) is the in-control fraction nonconforming, and $\lambda$ ($0 < \lambda \le 1$) is the smoothing parameter. Typically, E₀ and λ are set as zero and 0.1, respectively⁷. If the value of E_t exceeds the control limit H of the EWMA control chart, the process is considered out of control.

On the other hand, the synthetic chart combines the functionalities of the conforming run length (CRL) and np charts^46,47. Consequently, it utilizes two charting parameters: the warning limit w (for the np sub-chart) and the lower control limit L (for the CRL sub-chart). The CRL represents the number of samples between two successive nonconforming samples, including the nonconforming sample at the end^9,48. If d_t ≤ w in a tth sample, the process is declared as in control. However, if d_t > w, the sample is deemed nonconforming, and the value of CRL needs to be determined and compared with L. If CRL ≥ L, the process is in-control. Otherwise (i.e., if CRL < L), the process is considered as out-of-control.

In this study, the n and h of both the EWMA and synthetic charts satisfy constraint (3). The H of the EWMA chart is adjusted to fulfil constraint (2) and produce the smallest ETC. The value of λ is set as 0.1 as considered by Montgomery⁷. Similarly, the design of a synthetic chart is to find the best combination of the w and L so that the chart gives the minimum ETC and meanwhile meets constraint (2).

Comparative studies and sensitivity analyses

This section compares the overall performance of the optimal np control chart with that of its competitors in terms of ETC, while the detection speed at each shift point is evaluated using the out-of-control ATS.

Comparative study using real application

This section demonstrates the application and design of the optimal np chart using a real-life data in water bottle manufacturing. Quality control is a process that ensures that the specifications of product or service are met. Majority of statisticians approved that the design of control charts should be implemented in two stages: Phase I, where the main goal is to collect sufficient data to evaluate the process stability, and Phase II, where monitoring and controlling the actual process is performed. In Phase I, the data are employed to design a Shewhart np chart for estimating the in-control process parameters. The manufacturing of water bottles starts from the blow moulding where the Polyethylene Terephthalate (PET) is heated and then placed in a long thin tube mould. It is then transferred to bottle shaped mould where a thin steel rod fills the tube with highly pressured air to shape the bottle. Subsequently, the mould must be cooled quite fast, so the newly shaped component is appropriately set. Once the bottle has cooled and set, it is ready to be removed from the mould. Finally, the bottle is filled, capped, and labelled. Figure 2 shows the different stages of bottle manufacturing.

Figure 2

Bottle manufacturing process (Plastic Technologies, 2021).

A water bottle can be classified as defective if it exhibits any of the following issues: foil tightness, uncentered labeling, plastic overheating, leakage, or low water filling level. To identify the defects with the highest frequency leading to defective products, we constructed a Pareto chart. Figure 3 illustrates that approximately 77% of defective units result from the first three defects: bottle leakage, foil tightness, and improper labeling. Therefore, a bottle is deemed defective if any of these three defects are present. The decision to focus on the three defects with the highest frequency was made by the quality control engineer (QC) at the water bottle manufacturing company. By targeting the most frequently occurring defects, the company can allocate resources and efforts more effectively, address the root causes of the most impactful issues, and achieve significant improvements in overall product quality. It is worth mentioning that if the QC engineer decided to consider all five defects, the estimated in-control fraction nonconforming (p₀) would change. However, the optimization algorithm proposed in this paper can still be applied straightforwardly to design the optimal np control chart, ensuring effective monitoring of the number of defective bottles.

Figure 3

Pareto chart for water bottle defects.

The aim is to detect a rise in the fraction nonconforming p of the water bottles production. 30 samples (m = 30) with a sample size n of 250 were collected in Phase I. This phase aims at ensuring that the process is statistically in-control and estimating ${p}_{0}$. A Shewhart np chart is designed as shown in Fig. 4, which shows that the 30 sample points are all plotted within the control limits (UCL = 7.220, CL = 2.5, and LCL = 0). Since the process is statistically in-control, the fraction nonconforming ${p}_{0}$ can be estimated as follows:

Figure 4

Shewhart np chart in Phase I.

$${p}_{0}=\frac{{\sum }_{i=1}^{m}{d}_{i}}{m\times n}=\frac{75}{30\times 250}= 0.01.$$

(8)

Most of the design and cost specifications were decided in consultation with the quality engineer. A list of the values of all specifications needed to design the np charts are shown below.

• p₀ = 0.01.

• τ = 300 days.

• r = 50 units per day.

• ${\delta }_{max}$ = 10.

• $\varepsilon$ = 0.05 occurrences per day.

• e = 0.0125 day.

• D = 1 day.

• b = 1 $.

• c = 0.01 $.

• W = 300 $.

• T = 100 $.

• M = 10,000 $.

The traditional, optimal np, EWMA and synthetic control charts are designed in Phase II. The design parameters obtained for these four charts, along with their respective performance in terms of ETC, are as follows:

Traditional np chart::

n = 50, h = 1, UCL = 3 and ETC = 103.88.

Optimal np chart::

n = 65, h = 1.3, UCL = 3 and ETC = 89.06.

EWMA chart::

n = 50, h = 1, H = 1.210, λ = 0.2 and ETC = 81.95.

Synthetic chart::

n = 50, h = 1, w = 2, L = 20 and ETC = 103.05.

A normalized ATS curves ($ATS/{ATS}_{Optimal}$) are established to compare the detection speed of the four charts over the given range of shifts, as presented in Fig. 5. Economically, the ETC of the optimal np chart is less than its traditional np opponent, which indicates that the optimal np chart is more economical than traditional np chart. The ratio ${ETC}_{Traditional}$/${ETC}_{Optimal}$ = 103.88/89.06 $=$ 1.17 reveals that the optimal np chart outpaces the traditional np chart by 17%, from an overall perspective. On the statistical side, the values of ${ATS}_{0}$ and out of control ATS are presented in Table 2.

Figure 5

Normalized ATS for optimal np, traditional np, EWMA and synthetic chart.

Table 2 ATS values of optimal np, traditional np, EWMA and synthetic charts.

From Fig. 5 and Table 2, the following highlights can be obtained:

• 1. When the process is in-control (i.e., δ = 1), all charts result in an ${ATS}_{0}$ that is greater than τ, which satisfies constraint (2) in the optimization model. This is an indication of meeting the false alarm requirement. It is also worth mentioning that constraint (3) on the inspection rate is fulfilled as n/h for both charts is equal to r (= 50 units per day).

• 2. The ATS values of traditional and optimal np charts indicate that the latter outperforms the former over shift range of (1 < δ ≤ 10). Through all shift points, the out-of-control ATS of the optimal np chart is always less than that of the traditional np chart. This emphasizes the superiority of the optimal np chart over the traditional np chart for detecting both small and large shifts and its ability to detect an out-of-control scenarios faster.

• 3. In addition, the value of ATS for optimal np chart is closer to the specified τ = 300. On the other hand, ATS of the traditional np chart is much larger than τ which indicates the lower effectiveness of the traditional np chart in identifying out-of-control conditions.

• 4. The optimal np chart’s dominance over the traditional np chart diminishes with increasing the shift. For example, when $\delta$ = 2, the optimal np chart detects an out-of-control signal faster than the traditional one by 81%, but when $\delta$ = 8, the former is quicker than the latter by only 20%.

• 5. The results suggest that the synthetic chart performs better than the optimal np chart in detecting small shifts (when δ < 3), whereas the EWMA chart outperforms the optimal np chart in detecting small to moderate shifts (when δ < 5.5). These findings align with the existing literature that indicates the superior performance of the synthetic and EWMA charts in detecting small to moderate shifts^7,9,42. This is justifiable as the EWMA chart takes into consideration not only the latest sample but also the real-time accumulation of all samples^7,49,50. Meanwhile, the synthetic chart, which combines the np chart with the conforming run length (CRL) chart, has been recognized as a more effective scheme for detecting small and moderate shifts compared to the np chart alone^51,52,53. Notably, the synthetic chart exhibits almost identical overall performance to the optimal np chart in terms of the ETC. However, it is worth mentioning that the EWMA chart outperforms both the synthetic and np charts in terms of ETC, demonstrating a smaller cost value.

As the developed optimal np chart represents an optimized version of the traditional np chart, an additional investigation using simulation is conducted to compare the detection speed of both charts. This assessment was carried out under various scenarios to examine their respective performance in detecting anomalies. Simulated data for the number of defective bottles (d_i) that follows binomial distribution in 20 samples were generated using Minitab to illustrate the detection speed of the traditional and optimal np charts under four scenarios with different shift sizes (δ = 2, 4, 6 and 8) within the shift range of 1 < δ ≤ 10. As shown in Fig. 6, the optimal np chart consistently provided an out-of-control signal (plotted in red) before the traditional chart in all scenarios. This demonstrates that the former has a better detection speed than the latter. Furthermore, it can be observed that the superiority of the traditional np chart approaches that of the optimal np chart as the shift δ increases. This finding is consistent with the results of the ATS values presented in Fig. 5 and Table 2.

Figure 6

Comparison of the detection speed of the two np charts under four different scenarios.

Sensitivity analysis using uniform distribution

In this section, a ${2}^{12-6}$ fractional factorial design is conducted where the design specifications (${p}_{0}$, r, τ, ${\delta }_{max}$, $\lambda$, e and D) and cost parameters (b, c, W, T and M) are used as input factors to investigate their effect on the response, that is the expected total cost (ETC). Each one of the 12 factors varies at 2-levels as shown in Table 3. The levels are selected according to Refs.^22,54. In this section, a uniform distribution is assumed for the p shift where the probability density function ${f}_{\updelta }\left(\updelta \right)$ is depicted in as follows:

Table 3 Factors levels.

$${f}_{\updelta }\left(\updelta \right)=\frac{1}{{\updelta }_{\mathit{max}}- 1}.$$

(9)

The results of the factorial design are shown in Table 4. As shown in Table 4, the performance of the traditional and the optimal np charts are compared in terms of ETC. The relative improvement is then calculated by ${ETC}_{Traditional}$/${ETC}_{Optimal}$ which is shown in the right-most column in Table 4 to illustrate the superiority of the optimal np chart against its opponent. It is obvious that the relative improvement is always larger than 1, which denotes that the optimal np chart always outperforms the traditional np chart in terms of ETC. Eventually, the grand average over the 64 runs represents the overall performance as calculated by $\overline{{ETC }_{Traditional}/{ETC}_{Optimal} }=1.45$. This percentage shows that from an overall viewpoint (considering different design specifications and cost parameters combinations), the optimal np chart effectiveness (in terms of ETC) exceeds its opponent, the traditional np chart by about 45%.

Table 4 ${2}^{12-6}$ experiment using uniform distribution as the shift distribution.

To identify the factors that affect the performance of the optimal np chart significantly, an Analysis of Variance (ANOVA) is conducted at 5% level of significance. However, the data on the ETC of the optimal np chart should be normally distributed in order to perform ANOVA. Thus, a normality test is performed on the data of the ETC values of the optimal np chart. However, the original ETC values are not normally distributed as shown in Fig. 7 as the p-value is smaller than 0.05, hence Johnson transformation is performed to ensure the normality of ETC values, and it is found that p-value of 0.129 is produced after the transformation which emphasizes that the transformed ETC values are normally distributed. ANOVA results for the main effects are summarized in Table 5. It shows the effects of the input factors on ETC of the optimal np chart and the corresponding p-value. Since the replication size is 1, the high order interactions (third order and higher) are combined to determine the sum of square errors. Table 5 shows that there are three significant input factors with p-value smaller than 0.05, namely ${p}_{0}$, $\varepsilon$ and M. The ETC of an optimal np chart is positively influenced by $\varepsilon$(p-value $=0.001$), implying that a higher $\varepsilon$ would result in a higher ETC and vice versa. On the other hand, ${p}_{0}$ (p-value $=0.004$) and M (p-value $=0.0001$) have a negative impact on the ETC, implying that a bigger ${p}_{0}$ or M lowers the ETC and vice versa.

Figure 7

Normality test and transformation of ETC for optimal np chart data.

Table 5 Effect of input factors using ANOVA. Significant factors are in bold.

Sensitivity analysis using Rayleigh distribution

In many SPC research, uniform distribution was assumed to represent the p shift^22,23,30. However, in reality, the p shift is not predictable and can follow any probability distribution. In this study, the random shift $\delta$ is assumed to follow a uniform distribution where the probability of the occurrence of any shift size over the range of interest is equal. However, it is worthwhile to use another probability distribution such as Rayleigh distribution to describe the p shift in order to reach a general conclusion about the performance of the proposed optimal np chart under different shift distributions. Rayleigh distribution gives less weight to large shifts, and consequently, it is more realistic to represent the process shift in practice. Rayleigh distribution is used to characterize the potential deviation from the target in geometric tolerance. The probability density function ${f}_{\delta }(\delta )$ and the cumulative distribution function $F(\delta )$ of the Rayleigh distribution are denoted as follows:

$${f}_{\delta }\left(\delta \right)=\frac{\pi \left(\delta -1\right)}{{2\left({\mu }_{\delta }-1\right)}^{2}}{\text{exp}}\left(\frac{\pi {\left(\delta -1\right)}^{2}}{{4\left({\mu }_{\delta }-1\right)}^{2}}\right),$$

(10)

$$F\left(\delta \right)=1-{\text{exp}}\left(\frac{-\pi {\left(\delta -1\right)}^{2}}{{4\left({\mu }_{\delta }-1\right)}^{2}}\right),$$

(11)

where $\delta$ is the increasing p shift (1 < δ ≤ ${\delta }_{max}$), ${\mu }_{\delta }$ is the mean of δ and ${\delta }_{max}$ is the maximum value of $\delta$. To facilitate the comparison of both distributions, ${\mu }_{\delta }$ of the Rayleigh distribution is calculated based on ${\delta }_{max}$ and ${p}_{0}$ of the uniform distribution such that the probability of p $>{p}_{max}$ is negligible (lower than 0.001) as follows:

$${\mu }_{\delta }={p}_{0}+\sqrt{\frac{{- \pi {p}_{0} ({\delta }_{max}- 1)}^{2}}{4\,{\text{ln}}\,0.001}}.$$

(12)

The 64 cases in Table 6 generated by the ${2}^{12-6}$ fractional factorial design shows the comparison of the traditional and optimal np charts while the shift follows a Rayleigh distribution. It is clear from Table 6 that the ETC of the traditional np chart exceeds the ETC of the optimal np chart for all 64 runs. This indicates the superiority of the optimal np chart against its opponent, as reflected by the relative improvement calculated in the right-most column of Table 6. Lastly, the grand average that represents the overall performance over 64 runs is calculated as $\overline{{ETC }_{Traditional}/{ETC}_{Optimal} }=1.30$, which indicates the overall superiority of the optimal np chart against its opponent through all 64 runs. The results of “Sensitivity analysis using uniform distribution” and “Sensitivity analysis using Rayleigh distribution” sections pinpoint that the optimal np chart always outperforms its counterpart, regardless of the distribution of the p shift.

Table 6 ${2}^{12-6}$ experiment using Rayleigh distribution as the shift distribution.

Conclusions

This research proposes an economic-statistical model for the optimal design of np control chart. The developed optimal np chart is compared with the traditional np, EWMA and synthetic control charts. In the proposed model, the decision variables, which are the sample size (n), sampling interval (h), and upper control limit (UCL), are optimized such that the expected total cost (ETC) is minimized while ensuring that the constraints on the inspection rate and the false alarm are satisfied. The effectiveness of the optimal np scheme is demonstrated by a real-life data in water bottle manufacturing. It is found that the optimal np chart economically exceeds its opponent by 17% and statistically always detect an out-of-control signal faster than the traditional np chart over the entire shift range. The proposed optimal np scheme is compared with its traditional version under different design specifications using different probability distributions of the shift. The sensitivity analysis is conducted to evaluate the impact of design specifications on the overall performance of the optimal np chart. It is found that ${p}_{0}$, $\varepsilon$ and M significantly affect ETC.

Theoretical contribution

The main theoretical contribution of our research lies in the development of an economic-statistical optimization algorithm for the np chart. This algorithm effectively identifies the optimal charting parameters for the np chart to minimize the expected total cost (ETC) while adhering to statistical constraints on inspection rate and false alarm rate, ensuring that practical considerations are incorporated. Additionally, our study addresses the gap in the literature by focusing on the economic-statistical design of attribute control charts, particularly the np chart. Attribute control charts have wide-ranging applications and are easier to manage in manufacturing processes. However, they have received less attention in terms of economic-statistical design compared to variable control charts. Therefore, our research fills this gap by providing a comprehensive framework for optimizing the np chart’s statistical performance and cost efficiency. The study also conducts a sensitivity analysis to provide insights into the impact of changes in the design parameters on the performance of the np chart. By identifying the significant factors that influence the expected total cost, the study offers valued guidance for practitioners in designing effective control charts tailored to their specific process characteristics. By achieving enhanced cost efficiency and detection effectiveness, this research considerably contributes to the theoretical understanding of control chart design and optimization, thus expanding the existing body of literature in the field of statistical process control.

Practical implications

The findings of this research hold significant practical implications for manufacturing organizations and service sectors. The developed optimal np chart presents a practical and cost-effective alternative to the traditional np chart, offering substantial benefits to quality control practitioners. By optimizing n, h, and UCL, practitioners can achieve significant cost savings while ensuring effective process monitoring. Moreover, this study emphasizes the importance of striking a balance between statistical properties and financial considerations in the design of control charts. By considering both aspects, industries can promptly respond to process shifts, take appropriate actions to maintain product quality, and minimize costs. The code developed in this study allows practitioners to input their desired design specifications, enabling the optimization of np chart parameters on a personal computer within seconds. This streamlines the implementation process, eliminating the need for extensive computational expertise and facilitating improved process control. The code can be obtained from authors upon request. Companies can leverage this tool to make data-driven decisions regarding process monitoring and quality control. By considering economic and statistical factors, practitioners can tailor the np chart design to suit their specific operational requirements, leading to cost reduction and overall enhanced product quality. Additionally, this research contributes to the investigating the performance of the optimal np chart under different scenarios. The insights gained provide practitioners with valuable guidelines to enhance their quality control design and achieve superior process control outcomes.

Future research

Future research might be conducted to study the performance of the optimal np chart when ${p}_{0}$ is estimated and not known or when d follows Poisson distribution. In addition, the proposed economic-statistical model might be used to optimize other attribute charts such as EWMA and cumulative sum (CUSUM) charts. To further enhance the np chart’s capabilities, an important area for future exploration is the development of an optimal economic-statistical design that incorporates variable sample size and sampling interval (VSSI), curtailment, and other related features. However, integrating these aspects into the optimization process of the np control chart can introduce computational burdens for practitioners. To mitigate this challenge, it becomes crucial to consider novel technologies that can address such computational complexities. Adaptive sampling systems with switching mechanisms and efficient dual sampling systems are two promising approaches that warrant investigation^55,56,57. These technologies have demonstrated the potential to alleviate computational burdens and enhance the practicality and effectiveness of the np chart optimization process. By incorporating these advancements, practitioners across various industries can benefit from improved decision-making and enhanced quality control.