Crop water productivity assessment and planting structure optimization in typical arid irrigation district using dynamic Bayesian network

Abstract

Enhancing crop water productivity is crucial for regional water resource management and agricultural sustainability, particularly in arid regions. However, evaluating the spatial heterogeneity and temporal dynamics of crop water productivity in face of data limitations poses a challenge. In this study, we propose a framework that integrates remote sensing data, time series generative adversarial network (TimeGAN), dynamic Bayesian network (DBN), and optimization model to assess crop water productivity and optimize crop planting structure under limited water resources allocation in the Qira oasis. The results demonstrate that the combination of TimeGAN and DBN better improves the accuracy of the model for the dynamic prediction, particularly for short-term predictions with 4 years as the optimal timescale (R² > 0.8). Based on the spatial distribution of crop suitability analysis, wheat and corn are most suitable for cultivation in the central and eastern parts of Qira oasis while cotton is unsuitable for planting in the western region. The walnuts and Chinese dates are mainly unsuitable in the southeastern part of the oasis. Maximizing crop water productivity while ensuring food security has led to increased acreage for cotton, Chinese dates and walnuts. Under the combined action of the five optimization objectives, the average increase of crop water productivity is 14.97%, and the average increase of ecological benefit is 3.61%, which is much higher than the growth rate of irrigation water consumption of cultivated land. It will produce a planting structure that relatively reduced irrigation water requirement of cultivated land and improved crop water productivity. This proposed framework can serve as an effective reference tool for decision-makers when determining future cropping plans.

Introduction

Water resources are one of the most important natural resources, also indispensable for the survival and development of human beings¹. Agriculture accounts for the largest share of water allocation, accounting for about 70% of annual freshwater use². FAO estimates that the irrigated area in developing countries will increase by 34% in 2030. The agricultural water use will increase by 14% under the irrigation management and practices. In the context of rapid population growth, economic development and environmental change, water and food scarcity become a global issue³. How to achieve sustainable development of water resources and agriculture is a topic of concern for countries⁴.

The water footprint, water scarcity and crop water productivity are currently used as main indicators to assess water resources and agricultural sustainability^5,6,7,8. Crop water productivity variation is closely related to climate, soil, socio-economic, human activities and other factors⁹. The crop water productivity is usually considered as ideal indicator to reflect the spatial variability affecting crop growth yield and water consumption. Therefore, assessing the impact of changes in cropping patterns on changes in water productivity is crucial for optimal utilization of water resources in agriculture.

At present, the research on the crop water productivity assessment and optimal allocation of agricultural water mainly includes three aspects. The first aspect is to optimize regional crop planting area using traditional mathematical optimization algorithms¹⁰. The second one is to establish a spatial distribution model to achieve spatial optimization of crops¹¹. The third one is to simulate optimization based on some kinds of agent systems or dynamic systems. However, most of the studies focus on static optimization. Few studies are considering to assess the spatial heterogeneity and temporal dynamics of crop water productivity to optimize agricultural planting structure using an effective dynamic approach. Dynamic Bayesian networks (DBN) as a temporal extension of Bayesian networks is mainly used for ideal approach to model the dynamic process¹². The thorny issue is that the data-driven DBNs place certain demands on the amount of data¹³. Yoon proposed a machine deep learning method (time series adversarial generative networks (TimeGAN)) for synthesizing time series¹⁴. TimeGAN has shown good performance in dynamic data augmentation. Therefore, how to combine TimeGAN and DBN to realize dynamic prediction of crop water productivity poses greater challenge.

The aim of this study establishes a dynamic optimization model framework integrating TImeGAN, Dynamic Bayesian networks (DBN) and multi-objective models to be applied in the Qira oasis of Xinjiang, Northwest China. The frameworks are to conduct (1) data augmentation of existing remote sensing data and statistical data by TimeGAN; (2) dynamic prediction of crop water demand and planting scale using DBN based on generated data; and (3) optimization of future crop planting structure using crop suitability assessment and multi-objective optimization model. This study can serve as an effective reference tool for decision-makers when determining future cropping plans.

Study area

Qira oasis in Hotan Prefecture of Xinjiang, Northwest China was selected as the research area ($80^{ \circ } \,03^{\prime}\,{\text{E}} - 82^{ \circ } \,13^{\prime}\,{\text{E}}$, $35^{ \circ } \,18^{\prime}\,{\text{N}} - 39^{ \circ } \,30^{\prime}\,{\text{N}}$) (Fig. 1), covering an area of 274.63 ${\text{km}}^{{2}}$. The Qira oasis belongs to a warm temperate arid desert climate. The annual average rainfall is only 33.5 mm, while the evaporation of water surface is 2505 mm. The Qira oasis relies primarily on the Qira River for water supply and agricultural irrigation. Originating from the central region of the northern slope of Kunlun Mountain, the Qira River is predominantly fed by a combination of meltwater from ice and snow as well as rainfall. The annual runoff volume between 1985 and 2018 amounted to 1.23 m³.

Figure 1

The location of the Qira Oasis in the Hotan region of Xinjiang.

Qira oasis is a thriving place for agriculture, 90% of which can be farmed. Agriculture accounts for 97.7% of water resources, of which 82.1% comes from the Qira River and the remaining 17.9% comes from groundwater¹⁵. The wheat, maize, cotton, Chinese dates and walnut are major crops. The Chinese dates and walnu account for 59.4% and 23.0% of the Qira area, respectively. In recent years, due to the sustainable development of agriculture and water resources, irrigation water and water supply for arable land are increasing. This exacerbates the contradiction between supply and demand. To ensure certain water and food security, it is very important for water resource managers to adjust agricultural planting structure based on crop water demand and planting scale.

Methods and data

The research framework of this paper is shown in Fig. 2: (1) the index system is determined from the four aspects of driving force, pressure, state and influence through the conceptual framework of DPSIR¹⁶. Due to the finiteness of time series data, the time series generation Adversarial network (TimeGAN) in machine learning method is used to learn the whole index system and get more time series data; (2) the generated data were evaluated from both qualitative and quantitative aspects. Qualitative evaluation is to initially determine the fit between the original data and the generated data by the violin diagram of each index, and then consider the degree of coincidence after dimensionality reduction by applying principal component analysis (PCA) and T-Distributed Neighbor Embedding (t-SNE). The quantitative assessment is the Kolmogorov–Smirnov test to analyze the difference between the two sample distributions; (3) the generated data is used to build a dynamic Bayesian network prediction model to realize the dynamic change of the crop water productivity. Meanwhile, the multi-objective optimization model is applied to optimize the planting structure of five characteristic crops.

Figure 2

Research framework in this study.

Dynamic prediction model based on TimeGAN and DBN

Construction of prediction index system

The model is conceptualized through the DPSIR (driver, pressure, state, impact, and response) framework¹⁷. By identifying the main system variables and the link relationship between them, and then determining variables based on expert knowledge and literature review, each variable should be guaranteed to be observable and measurable¹⁸. 12 indicators are finally determined. The driving force variables include drought index, irrigation water consumption, available land and crop prices. The pressure variables include actual evapotranspiration, crop water requirements and crop size. The state variables include crop relative productivity and crop water productivity. The impact variables include the economic productivity of crops, the proportion of people farming and the reliability of crops. The formulas of DPSIR can be seen in the Complementary Formulas 1.1 of supplementary materials.

Data augmentation processing of TimeGAN

The GAN, proposed by Ian J. Goodfellow, is one of the most popular approaches in the field of deep learning.TImeGAN (time-series generative adversarial network) is a variant of GAN, which is a time-series generative data generation model. The approach has shown good performance in time-series data enhancement tasks. The main idea is to combine the versatility of unsupervised GAN methods with the conditional probability principles provided for supervised autoregressive models to produce time-preserving dynamic time series. TImeGAN is mainly composed of four network components: embedded function, recovery function, sequence generator and sequence discriminator. The first two are self-coding components, while the last two are adversarial components. The specific flow chart is shown in Fig. 3.

Figure 3

Schematic diagram of TimeGAN's data processing¹⁹.

The variables in this study such as aridity index and actual evapotranspiration are affected by historical data and have certain autocorrelation, so the relationship between data autocorrelation and features should be considered in the process of data generation²⁰.The verification of synthetic data mainly includes univariate and overall data. The univariate is mainly obtained by drawing a violin graph, and then the Kolmogorov–Smirnov test (K-S test) is used to verify whether the data trend is consistent with the original distribution. The overall data is presented after dimensionality reduction using principal component analysis and t-Distributed Stochastic Neighbor Embedding (t-SNE).

Dynamic Bayesian network modeling

A Bayesian network, also known as a Bayesian belief network, is a graphical model that allows for the design of random relationships between a set of variables²¹. Applications of BN can be found in a variety of fields ranging from social to economic and biological disciplines. The formulas of Bayesian network can be found in the Complementary Formulas 1.2 of supplementary materials. Dynamic Bayesian network (DBN) is an extension of Bayesian network, which can model variables that affect with time. It extends the classical Bayesian network (BN) by adding time dimension, and is suitable for describing the dynamic fluctuations of complex systems²². A DBN is composed of multiple BNs among which each individual BN is called a time slice. Multiple time slices are linked by some variables to form a dynamic Bayesian network. Figure 4 shows a dynamic Bayesian network with three nodes and three time slices. In the process of DBN modeling, it mainly includes structure learning and parameter learning. Structural learning can be learned according to expert knowledge or from data according to EM algorithm, mountain climbing algorithm, etc. Parameter learning is the internal parameter of learning network structure, and it can also be learned through expert knowledge or maximum likelihood estimation and EM algorithm²².

Figure 4

A simple DBN of three nodes and three time slices.

Mean absolute error (MAE), standard deviation (SD) and fitting coefficient (R²) were used to evaluate the predictive effect of the final model:

$$MAE=\frac{1}{m}{\sum }_{i=1}^{m}\left|\stackrel{\Lambda }{{y}_{i}}-{y}_{i}\right|,$$

(1)

$$SD=\sqrt{\frac{{\sum }_{i=1}^{m}{\left(\stackrel{\Lambda }{{y}_{i}}-{y}_{i}\right)}^{2}}{m}} ,$$

(2)

$${R}^{2}=1-\frac{{\sum }_{i=1}^{m}{\left(\stackrel{\Lambda }{{y}_{i}}-{y}_{i}\right)}^{2}}{{\sum }_{i=1}^{m}{\left({{y}_{i}}-\overline{{y}_{i}}\right)}^{2}} ,$$

(3)

where $\mathop {y_{i} }\limits^{\Lambda }$ represents the predicted value, $y_{i}$ represents the true value, $\overline{y}_{i}$ represents the average value, $m$ represents the number of samples.

Crop suitability assessment

The evaluation of crop suitability refers to the suitability of crop growth for the corresponding planting land. The growth and development of different crops are closely related to climate, topography, soil and other natural environmental conditions. There are obvious differences in crop yield and quality under different natural environmental conditions. Crop suitability can quantify the effect of spatial variability on crop growth. It is the main basis for crop selection in the process optimizing regional planting layout²³. The suitability of a crop for a given location can be measured by a suitability index, which is the product of the affiliation value and the weight of the indicator with a value between 0 and 1.

The crop suitability evaluation in this study consisted of nine indicators related to topographic factors and soil characteristics. The topographic factor were mainly slope. The soil data were pH, soil bulk weight, soil organic matter, effective phosphorus, alkaline dissolved nitrogen, effective potassium, total nitrogen, clay, silt, and sandy soils. In the process determining the weights of the indicators, the main method of calculation is to utilize a combination of subjective and objective methods. A comprehensive analysis was conducted by the empirical data of crop cultivation in the study area and the historical data summarized in the literature and CRITIC method^24,25. The final weights of the indicators were calculated as:

$${w}_{ni}=\frac{{a}_{ni}{b}_{n}}{k} ,$$

(4)

where $w_{ni}$ denotes the weight of the first $n$ indicator for the first $i$ crop, $a_{ni}$ denotes the weight of the first $i$ crop obtained from the literature, and $b_{n}$ denotes the weight calculated from the raster data using the CRITIC method.

The suitability index was categorized into four grades from high to low using the natural breakpoint classification. The lower the grade, the higher the suitability. The suitability evaluation can compare the suitability of the same crop in different geographic locations and the suitability of different crops in the same geographic location. It can provide the necessary data basis for the optimization of planting layout.

Multi-objective planting structure optimization model

Objective function

The standard function is mainly considered from two perspectives, one is the manager and the other is the farmer. From the perspective of managers, the consumption of irrigation water, ecological benefits and productivity are taken into account. From the farmer's level, the main consideration is crop yield and economic benefits.

Irrigation water consumption refers to the amount of irrigation water including losses during transportation and the amount of irrigation water required for normal crop growth. The objectives are described as:

$$Min={\sum }_{i=1}^{5}{w}_{i}{A}_{i},$$

(5)

where$w_{i}$ is the irrigation quota of the crop $i$ ($m^{3}$), $A_{i}$ represents the planting area of the crop $i$($ha$).

Ecosystem benefits can be described as the benefits that humans derive directly or indirectly from ecosystem functions, which refer to the habitat, biological or systemic characteristics or processes of an ecosystem²⁴. The equivalent weight coefficient of individual crops is set as the equivalent weight coefficient of farmland, and the economic value of an equivalent ecological benefit weight factor is equal to 1/7 of the market value of the corresponding crop of 1 hectare. Therefore, the comprehensive ecological benefits of crops and crop yield are given as:

$$Max={\sum }_{i=1}^{5}{s}_{i}{A}_{i},$$

(6)

$$Max={\sum }_{i=1}^{5}{z}_{i}{A}_{i}$$

(7)

where $s_{i}$ represents the ecological service value of crop $i$ ($yuan$).$z_{i}$ denotes the average yield of a hectare of crop $i$ ($kg$).

Water productivity can be expressed as crop productivity per unit of water, which can measure the yield per unit of water The average water productivity and economic benefits are written as:

$$Max=\frac{{\sum }_{i=1}^{5}{z}_{i}{A}_{i}}{{\sum }_{i=1}^{5}{w}_{i}{A}_{i}},$$

(8)

$$Max={\sum }_{i=1}^{5}{P}_{i}{A}_{i}.$$

(9)

Constraints

According to the Qira County Statistical Yearbook, the resident population of Qira County was 160,000 in 2018. The minimum annual per capita demand for wheat is 250 kg and that for maize is 100 kg according to the setting of food security by Erenstein²⁶. The average growth rate of planting scale was taken as the largest variable proportion of planting scale according to the statistical yearbook of Qira County from 2008 to 2018. Similarly, the proportion of growth and reduction of each crop is also based on the corresponding variable proportion.

Crop water requirement constraint:

$${\sum }_{i=1}^{5}{w}_{i}{A}_{i}\le \stackrel{\Lambda }{CWR} .$$

(10)

Planting area constraints:

$$\sum\limits_{i = 1}^{5} {A_{i} } \le \mathop A\limits^{\Lambda } \alpha ,$$

(11)

$$T_{{}}^{i} \cdot (1 - \alpha_{\min }^{i} ) \le A_{i} \le T_{\max }^{i} \cdot (1 + \alpha_{\max }^{i} ).$$

(12)

Yield constraint:

$$Y_{\min } \le \sum\limits_{i = 1}^{5} {z_{i} } A_{i} ,$$

(13)

where $\alpha$ is the variable proportion of the planting scale,$T^{i}$ is the average of the planting scale of the crop $i$, $T_{\max }^{i}$ is the maximum of the crop $i$ planting scale, $\alpha_{\min }^{i}$ and $\alpha_{\max }^{i}$ is the proportion of the crop that can be reduced and increased respectively. $Y_{\min }$ is the total minimum production ($kg$).

Data collection

The water resources data in this paper are from the water resources Bulletin of Hotan Prefecture from 2008 to 2018. The planting area and output data are from the statistical yearbook of Hotan Prefecture from 2008 to 2018. Rainfall (1 km spatial resolution) was obtained from Goddard Earth Sciences Data and Information Services (https://disc.gsfc.nasa.gov). Potential evapotranspiration (1 km spatial resolution) was obtained from the CGIAR Spatial Information Consortium (https://cgiarcsi.community). Irrigation quotas are determined according to agricultural irrigation water quotas issued by Bureau of Quality and Technical Supervision of Xinjiang Uygur Autonomous Region (Table 1). The crop coefficient of crop water demand involved in the calculation process is derived from literature data (Table S1)^21,27. The land data involved in the crop suitability assessment were obtained from the Harmonized World Soil Database version 1.2) (HWSD) by the Food and Agriculture Organization of the United Nations (FAO) and the International Institute for Applied Systems (IIASA) in Vienna. The basic soil indicators extracted by using ArcGIS 10.8. The digital elevation model (DEM) data (1 km spatial resolution) were obtained from the geospatial data cloud.

Table 1 Basic data of irrigation area.

Results

Expansion results of time series data

Figures 5 and 6 show the distribution and comparison between the original dataset and the expanded dataset. Although there are some differences between the expanded dataset and the original dataset in 12 indicators, it is basically consistent. The median of the indicator is basically consistent, indicating that the average level of the data is consistent. The simultaneous decrease of the two quantiles of drought index and actual evapotranspiration indicates that the fluctuation degree of data is small. The simultaneous increase of irrigation water consumption and crop economic water productivity indicates that the fluctuation degree of data is large. The box plots of crop water demand and crop scale are skewed from the original data. The difference between the original dataset and the expanded dataset was analyzed to further test whether the expanded dataset was consistent with the original dataset using the Kolmogorov–Smirnov test (K-S test). According to the test results in Table 2, the P-values of all indicators are greater than 0.05, indicating that all the dataset pass the test. The distribution of the expanded dataset is consistent with that of the original dataset.

Figure 5

Distribution of original dataset and extended dataset. The green one is the original dataset, and the orange one is the expanded dataset. The black part in the middle of each figure is the boxplot of the dataset. The small white circle in the middle is the median.

Figure 6

Comparison between the original dataset and the extended dataset over five consecutive periods. The green one is the original dataset, and the orange one is the expanded dataset. The black part in the middle of each figure is the boxplot of the dataset. The small white circle in the middle is the median.

Table 2 K-S test results of indicators.

Due to the particularity of time series data, it is necessary to evaluate it from the aspect of data integrity. Figure S1 shows the presentation of the overall data after dimensionality reduction by principal component analysis and t-SNE, respectively. It can be seen that the original data points basically overlap with the expanded data points. t-SNE has a higher coincidence degree, because it can maintain the local structure of the dataset. Therefore, the synthetic dataset after dimensionality reduction has high similarity with the original dataset, presenting certain reliability and trustworthiness.

Prediction of crop water requirement and planting scale using DBN

According to the synthesized data, the correlation between the variables was tested by Pearson correlation coefficient (Fig. 7). The correlation coefficients between crop water demand and planting scale and other variables in the original data are basically above 0.6, while the overall correlation in the synthetic data is somewhat weakened with around 0.5. The correlation coefficient between evapotranspiration and drought index is approximately 1, indicating that there is a very strong linear relationship between the two.

Figure 7

Correlation coefficients of original data and synthetic data (CP crop price, IWU the consumption of irrigation water, PL plowland, CWR crop water requirement, CS crop scale, ET the maximum evapotranspiration of crop, AI aridity index, AGR the proportion of agricultural planting population, CY crop yield, EWP economic water productivity, CWP crop water productivity, RE reliability).

According to the synthesized dataset, a dynamic Bayesian network model is established by using R software, which is a free software environment for statistical computing and graphics with R version 4.4.0 (https://www.r-project.org/). The data is randomly divided into training set and test set. Through the training, it is found that the prediction accuracy of network structure established by discretized data is much higher than that by direct numerical data. Therefore, this paper finally uses quantile discretized data for structure learning. The structure learning algorithm is the max–min hill-climbing algorithm (MMHC). As the amount of data increases, the network structure becomes more and more complex, but the prediction accuracy rises first and then declines. After continuous debugging, the first 800 observations of the data set are selected to learn the structure, and the final network structure is as shown in Fig. 8. It can be seen that the drought index affects the actual evapotranspiration, which is consistent with the actual situation. The actual evapotranspiration further affects the crop price and the consumption of irrigation water. Crop yield affects reliability, crop water productivity, crop water demand and crop scale by affecting crop economic water productivity and the proportion of agricultural employees. Ultimately, there is a causal relationship between the amount of irrigation water and the available land.

Figure 8

Prediction model structure of dynamic Bayesian network. Each color represents a time slice, and each node is a variable. The time increases from left to right.

The maximum likelihood estimation (MLE) is used to learn the parameters in the training set. The final complete dynamic Bayesian network model is formed. Since the network structure is relatively complex and there are many influence relationship arcs, this paper only selects the relationship of the first time slice to show in Table 3. The influence intensity between nodes in the first time slice can be specifically understood from the formulas. The parameters in the last four time slices are not consistent with those in the first time slice, because they change due to the influence of nodes in some previous time slices.

Table 3 Relationships for the first time slice.

Based on the results of the dynamic Bayesian network model, the crop water requirement and planting scale were respectively predicted. Table S2 shows the prediction results on the extended dataset. It can be seen that the R² of the four time periods is relatively high with a good fitting effect. Table S3 displays the prediction results on the original dataset. The prediction effect on the planting scale is better than that on the crop demand water, but it is still worse than that on the expanded dataset. This may be due to certain information loss during the expansion of the dataset. The data of 2013 is selected as the parent node of the first time slice, and the crop water demand and planting scale in the next four years are predicted (Fig. S1). The optimization results can be obtained by expanded dataset into the optimization model.

Evaluation of planting suitability

Figure 9 shows the spatial distribution of topographic factor and soil properties. The sandy loam and loamy sandy soils are mainly distributed in Qira oasis. There are a few sandy clay loam soils in the north and east. The slope of the study area is very small and close to 0. The pH of the soil is mainly in the range of 4.3 to 8.0 with an average value of 6.21, showing a weak acidity. The spatial distribution of soil organic matter, quick-acting phosphorus, alkaline-dissolved nitrogen, quick-acting potassium and total nitrogen were more concentrated, with contents of 0.39–33.63%, 3.27–6.4 mg/kg, 10.82–104.06 mg/kg, 119.84–301.75 mg/kg and 1.44 g/100 g–2.28 g/100 g. However, the mean values were lower with 1.81%, 5.33 mg/kg, 65.12 mg/kg, 228.75 mg/kg and 1.76 g/100 g, respectively. The soils in the study area were anti-organic matter and quick-acting phosphorus. The alkaline dissolved nitrogen belonged to the medium level. The quick-acting potassium and total nitrogen were more abundant. Although the soil organic matter content was low, the data dispersion was still high. This may be related to the amount of fertilizers used by farmers in the area.

Figure 9

Spatial distribution of topographic factor and soil properties. (a) SLOPE: Slope. (b) PH. (c) BD: Bulk density. (d) ST: Soil texture. (e) SOM: Soil organic matter. (f) AP: Effective phosphorus. (g) AN: Alkaline Nitrogen. (h) AK: Quick-acting potassium. (i) TN: Total Nitrogen. The image is generated by Arcgis10.8 (https://desktop.arcgis.com/zh-cn/desktop/index.html).

After determining the evaluation system of crop indicators, it is necessary to determine the weight of indicators for each crop. Table S4 displays the weights for crop evaluation indicators using the CRITIC method Wheat is sensitive to soil texture and quick-acting potassium content, while maize has a high demand for three fertilizers: nitrogen, phosphorus and potassium. Cotton has a more pronounced need for alkaline dissolved nitrogen and effective phosphorus, while walnuts and Chinese dates are mainly sensitive to nitrogen fertilizers.

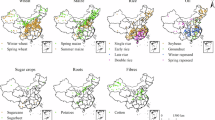
Based on the affiliation and index weights, the suitability indices of different crops were calculated on each grid cell. Figure 10 shows the spatial distribution of the suitability of five crops in Qira oasis. The suitability indices of wheat, maize, cotton, walnut and Chinese date are 0.36–0.66, 0.41–0.67, 0.33–0.65, 0.23–0.67, 0.18–0.69, respectively. According to the topographic factors and soil properties as evaluation indexes, the most suitable areas for wheat and maize are the central and eastern parts of Qira oasis. Cotton is not suitable for planting in the western region, while walnut and Chinese date are less suitable for planting due to their strong adaptability, mainly distributed in the southeastern part of the oasis.

Figure 10

Suitability analysis of different crops. (a) Spatial distribution of suitability for wheat in the study area, (b) Spatial distribution of suitability for maize in the study area, (c) Spatial distribution of suitability for cotton in the study area, (d) Spatial distribution of suitability for walnut in the study area, (e) Spatial distribution of suitability for dates in the study area. The image is generated by Arcgis10.8 (https://desktop.arcgis.com/zh-cn/desktop/index.html)).

Planting structure optimization

According to the prediction results and the corresponding multi-objective functions, NSGA-II algorithm is used to solve the problem, and the solution set of the optimal solution is obtained. The Pareto front line is obtained by optimization (Fig. S3). To select the most appropriate solution in a set, the entropy weight method and random forest are used to determine the weights of each objective function (Table 4). The entropy weight method determines the weight according to the variability of the index. The weight of irrigation water consumption is the largest, while the random forest ranks the contribution degree to crop scale based on the Gini index judgment. The final results are all relatively average around 0.2, indicating high importance.

Table 4 Weights of entropy weight method and random forest.

The solution set is weighted and sorted according to the weight, and the largest one is taken as the optimal solution to obtain the optimal planting structure. There is little difference between the optimization results of the two methods (Fig. 11). The planting proportion of cotton and walnut is significantly increasing, while the planting area of wheat and maize fluctuates in a small range. Compared with the original planting area, the overall planting area after optimization showed an increasing trend. In addition, the Chinese date and walnut are the characteristic crops in this area. The planting proportion of them can be increased to improve economic benefits under the condition ensuring food security.

Figure 11

Planting proportion of various crops. On the left are pie charts of the original crop planting ratio from 2014 to 2017, and on the right are stack charts of the original data and optimized structure, where real data refers to the original data, EWN refers to the optimization results using entropy weight method, and RF refers to the results after random forest optimization.

Figures S4 and S5 show the comparison between the five optimization objectives and the actual data during the four years of prediction. The most significant change is crop output value, which increases significantly due to the increase in the planting scale of cotton and walnut. When the entropy weight method and random forest were used to calculate weights, the value of ecological services after optimization increased by 3.53% and 10.66%, crop water productivity also increased from 0.8 to 1.03 and 1.00, and total crop output also increased by − 2.74% and 9.30%, respectively (Table 5). The consumption of irrigation water increased by 7.59% and 15.76%, respectively, which was related to the overall increase of planting area. From the changes of planting area of each crop, it can be seen that the fluctuation of wheat and maize is small. In general, the entropy weight method is closer to the real situation of Qira oasis than the random forest after optimization.

Table 5 Comparison of planting area and objective function before and after optimization in 2014.

Discussion

In face of spatial heterogeneity of crop water productivity and data limitation issues, this study proposes an integrated approach combining TimeGAN, dynamic Bayesian network, and multi-objective optimization to enhance planting planning under drought conditions. Qira oasis in the Hotan region of Xinjiang, China is used as a case study to demonstrate the applicability of this methodology. The key advantages of this approach are: (1) to enable the establishment of data relationships among multiple indicators and visualizes their temporal expansion; (2) to facilitate simultaneous prediction of multiple indicators for the next four years, surpassing traditional single-indicator predictions at specific time points; and (3) to further enhanced its applicability by incorporating spatial heterogeneity and temporal dynamics.

The results indicate that the dynamic prediction over a span of four years yielded optimal results with an R² value exceeding 0.8 for multi-indicator forecasting—demonstrating high precision. This method proves more suitable for short-term predictions consistent with Roos²⁸. Many studies employed the data-driven methods for constructing predictive models where training data quantity and quality significantly impact model performance according to Jones¹³. In dynamic Bayesian network model of this study, we utilized a dataset synthesized by TimeGAN. Qualitative and quantitative evaluations reveal minimal differences in prediction accuracy between original and generated datasets, displaying the certain reliability and trustworthiness. When the sufficient data is available, the integrated structural model can be established to improve the predictive accuracy encompassing multiple time periods and indicators.

According to the optimization model’s planting planning results, the entropy weight method is closer to the real situation of Qira oasis than the random forest after optimization. it is evident that the weights assigned to the objective functions differ significantly between the entropy weight method and random forest weight method. Within the weights calculated by the entropy weight method, irrigation water holds the highest importance. Conversely, in the random forest approach, the weights of objective functions are relatively evenly distributed around 0.2. When considering the optimized planting structure, their differences become negligible. This finding is basically consistent with Jayathilaka²³.

The indexes of crop productivity and ecological benefit were also assessed and optimized, as these indicators are closely intertwined with water and food sustainability. According to FAO estimates, irrigated farmland in developing countries is projected to increase by 34% in 2030^6,29. Due to enhancing irrigation management and practices, agricultural water usage will only rise by 14%. The optimization outcomes presented in this study demonstrate that from the base year (2013) to the initial year of dynamic optimization target (2014), there was a respective increase of 7.84% and 7.07% in irrigation water volume and crop planting area. Notably, the crop productivity experienced a substantial growth of 28.75%, while ecological service value witnessed a modest increment of 3.45%. These results support FAO's estimations and offer certain advantages concerning ecology and water productivity.

To sum up, the combination of dynamic Bayesian network and time series adversarial production network can achieve the effect of dynamic prediction. Moreover, the remote sensing data can be combined with common data to reduce spatial heterogeneity. Multi-objective optimization is more suitable for complex situation analysis than single objective optimization. In practical application, users can choose different time slices and objective functions according to the actual situation to learn modeling, and can also improve it in DBN¹². In addition, Zou³⁰ and Li³¹ respectively pointed out that soil characteristics and agricultural management practices are the main driving factors affecting irrigation water scheduling and regional water productivity. In practice, different planting methods such as planting proportion and density also have certain effects on crop growth and yield³². Therefore, future studies should pay more attention to the effects of different crop densities, soil characteristics and irrigation methods on crop optimization models.

Meanwhile, it is important to note that there might be some loss of information during the data generation process. The prediction outcomes can also be influenced by different parameter configurations and methods used for generating time series data^33,34. Therefore, future research should employ diverse data generation techniques to compare and select the most optimal approach to enhance prediction accuracy. In addition, only a few indicators are considered in this research for prediction purposes, incorporating additional relevant indicators may further improve accuracy—for instance investigating various irrigation methods—An important aspect within agricultural cultivation which will be addressed in future studies.

Conclusion

To enhance agricultural water use efficiency and mitigate water and food scarcity, this study establishes a research framework based on the Dynamic Bayesian Network (DBN) model for optimizing water resource allocation and crop planting structure. Using the Qira oasis of Northwest China as a case study, dynamic predictions are conducted using DBN with data augmentation by TimeGAN. DBN proves to be an effective method for parametric and structural learning within this framework, providing managers with a powerful tool to determine crop water demand and planting scale across different time periods. Despite the linear connection between different time slices and internals in DBN, it offers users a clear and concise topology with arc strength while improving prediction accuracy (R² > 0.8). The prediction period aligns well with general agricultural planning requirements, meeting daily agricultural planning needs.

Based on the prediction results, the method combined with TimeGAN and DBN has better accuracy in dynamic prediction model and is suitable for short-term prediction with four years. Maximizing crop water productivity while ensuring food security has led to increased acreage for cotton, Chinese dates and walnuts. Under the combined action of the five optimization objectives, the average increase of crop water productivity is 14.97%, and the average increase of ecological benefit is 3.61%, which is much higher than the growth rate of irrigation water consumption of cultivated land. It will produce a planting structure that relatively reduced irrigation water requirement of cultivated land and improved crop water productivity. However, to better address the relationship between water resources and food security, it is crucial to consider soil characteristics, agricultural management practices, and different irrigation methods when developing a research framework for water resource allocation and sustainable agricultural development in the future study.