Introduction

In modern studies, it is important to examine complex models that represent nonlinear processes and examine their behaviour. Mathematics plays a very significant role in explaining their nature in relation to time and other dependent aspects. Since the beginning of calculus development till now, its fundamentals and applications have gained a lot of attention. In light of the fact that it is the only tool capable of reliably and successfully predicting the behaviour of processes that are raised in nature as issues facing living things or as potential solutions. Many pioneers and young scholars have recently brought to give specific limitations when using classical calculus to model or construct complex phenomena. In particular, when looking at historical mechanisms, long-range propagations, hereditary traits, non-Morkian processes and others. Meanwhile, the idea of non-integer order calculus emerged from an association between two renowned mathematicians shortly after the classical one1,2,3,4,5. Due to the concept’s unfamiliarity with its essence and accompanying applications compared to classical notions, few scholars were drawn to it during the seventeenth and eighteenth centuries. However, as a result of the previously mentioned limitations of integer order calculus and the advancement of computational tools, the idea of fractional calculus (FC) has recently captured the interest of many physicists, engineers, and mathematicians in an effort to develop the necessary theory and corresponding computational tools to address real-life problems and improve human lifestyles. The foundation for the FC was supplied by numerous prominent scholars who acknowledged the scientific requirements for bringing this idea to life6,7,8,9,10.

Differential equations of classical integer order are unable to express the memory property. Since fractional order derivatives may be utilized for expressing memory and inherited features in a number of domains, it is necessary to introduce fractional order differential equations. Sun et al. describe a variety of practical uses of fractional calculus in science and engineering.11 The study of the exact and computational solutions of fractional differential equations has led to the development of significant approaches due to their importance in several domains. Divergence and convergence of the solutions are equally significant as the models. For a physical model to be fractionally simplified, it must have an appropriate definition. In the past few decades, several definitions of fractional derivatives were developed. Riemann-Liouville (R-L), Caputo, CF, ABC, Grunwald-Letnikov, and Riesz fractional derivatives are a few of the commonly used definitions found in the literature12,13. The R-L derivative of constant is not zero, and the R-L and Caputo fractional derivatives have a unique kernel. Recently, novel fractional derivatives with a nonsingular kernel have been introduced to address these limitations. Two fractional derivatives are presented here: one is a Caputo-Fabrizio derivative with an exponential kernel14,15,16,17,18, and the other is an Atangana-Baleanu derivative with a modified Mittag-Lefller function as the kernel19,20,21,22,23. In fact, these derivatives may also be thought of as a filter regulator in addition to being a differential operator. An additional advantage of these intriguing derivatives are the explanation of some materials macroscopic behaviour. In recent years, numerous scientists have paid close attention to these derivatives motivating behaviours.

Fractional differential equations (FDEs) are applied in many fields, including hydrodynamics, solid-state physics, optic fibres, quantum science, computational biology, physical sciences, and astrophysics. These FDEs have become quite attractive for modelling natural phenomena because of the substantial expansion of the use of fractional calculus in applied mathematics. Solving these equations has been shown by many scientists from other disciplines to be a useful and interesting area of research. In the fields of mathematical science and engineering, many researchers have recently found effective methods for handling various kinds of models, including Laplace-residual power series method24,25, Homotopy perturbation general transform method26,27, Adomian decomposition general transform method28, optimal auxiliary function method29, General residual power series method30,31, Laplace transform decomposition method32, Adams-Bashforth-Moulton method33, Yang transform decomposition method34,35 and many more36,37,38,39. This study examines a model that represents important events in quantum field theory. The study of photonics, water waves, quantum field theory, and other areas is significantly improved by the nonlinear Schrödinger (NLS) equation. The two best-known models that explain the self-interactions of a Dirac field are the massive Thirring model (MTM) and the Kundu-Eckhaus equation (KE). The Kundu-Eckhaus equation was introduced in the 1980s as a linearizable version of the NLS equation by Kundu40 and Eckhaus et al.41,42. In this case, we looked at the fractional massive Thirring model (FMTM) and the fractional Kundu-Eckhaus (FKE) equation. To better capture the fundamental behaviour of the complicated model, the fractional-order approach has been used to represent the memory consequences in the system43. The FKE equation

$$\begin{aligned} \begin{aligned} \iota D_\aleph ^\texttt {q}{{{\textbf {f}}}(\xi ,\aleph )}={{\textbf {f}}}_{\xi \xi }+2{{\textbf {f}}}(|{{\textbf {f}}}|^{2})_{\xi }+{{\textbf {f}}}|{{\textbf {f}}}|^{4}=0, \ \ \ \ \ 0<\texttt {q}\le 1, \end{aligned} \end{aligned}$$
(1)

with

$$\begin{aligned} {{\textbf {f}}}(\xi ,0)={{\textbf {a}}}e^{\imath \xi }. \end{aligned}$$
(2)

The FMTM equations are given by

$$\begin{aligned} \begin{aligned}{}&\iota (D_\aleph ^\texttt {q}{{{\textbf {f}}}(\xi ,\aleph )}+{{\textbf {f}}}_{\xi })+{{\textbf {g}}}+{{\textbf {f}}}|{{\textbf {g}}}|^{2}=0,\\&\iota (D_\aleph ^\texttt {q}{{{\textbf {g}}}(\xi ,\aleph )}+{{\textbf {g}}}_{\xi })+{{\textbf {f}}}+{{\textbf {g}}}|{{\textbf {f}}}|^{2}=0, \ \ \ \ \ 0<\texttt {q}\le 1,\\ \end{aligned} \end{aligned}$$
(3)

with

$$\begin{aligned} {{\textbf {f}}}(\xi ,0)={{\textbf {a}}}e^{\imath \xi }, \quad {{\textbf {g}}}(\xi ,0)={{\textbf {b}}}e^{\imath \xi }. \end{aligned}$$
(4)

where \(\texttt {q}\) is the arbitrary order, \(\iota\) is the imaginary number (i.e., \(\iota =\sqrt{-1}\)), and \({{\textbf {f}}}(\xi ,\aleph )\) and \({{\textbf {g}}}(\xi ,\aleph )\) are the complex smooth envelop functions of spatial \((\xi )\) and temporal \((\aleph )\) variables. The connection between a Miura transformation and the complex Burgers equations and Kundu-Eckhaus was demonstrated by the authors in44. The KE equation is a useful tool for studying the behaviour of many phenomena emerging in chemistry and for modelling the propagation of very short pulses in quantum and nonlinear optics. It may also be used to show the optical properties of fem-to-second lasers. Furthermore, a nonlinear complex system with two components is the massive Thirring model (MTM)45,46. The propagation of an optical pulse in nonlinear or periodic optical medium is depicted using this model. The relationship between the quantums in the quantum Thirring model and the e-Gordon model has received a lot of attention47,48. This relationship aids the problem under consideration in determining the model either in terms of perturbation theory or in terms of standard perturbation theory for quantum solitons.

The primary goal of this work is to solve the FKE equation and FMT model while examining the process by which the resulting solutions behave in relation to fractional order. Numerous authors have found and examined the numerical as well as analytical solutions to these equations since they are crucial in explaining a wide range of complicated phenomena. For an example, rogue-wave solutions for the KE equation were found by the authors in49, and auxiliary equation expansion and modified unified algebraic approaches are taken into consideration to determine the soliton solution for the KE problem. Additionally, a number of effective methods are used for examining these equations, including q-homotopy analysis transform technique50, extended trial function method51, modified simple equation scheme52 and numerous methods for KE and MTM equations with classical and non-integer order derivatives53,54,55,56,57,58.

This paper presents an approach for analysing the analytical solution of the fractional coupled Kundu-Eckhaus equations and the Massive Thirring equations. The technique is based on the formulation of the Natural transform with ADM. In comparison to the traditional Adomian technique, the proposed method simplifies the estimate of the series terms by eliminating the need to compute the fractional integrals or the fractional derivative in the recursive mechanism. NTDM avoid all round-off errors and do not require linearization, predefined assumptions, perturbation, or discretization. The recommended technique yield reliable outcomes that provide accurate solution to the required problems. In the numerical examples, our methods yielded infinite series as a result. It is observed that the computational series gets very close to the exact solution after a certain number of iterations, and the resulting series gives us the results very quickly. This paper provides a basic framework for researchers to analyse this approach and use them in a variety of applications to obtain precise and approximate results in a short amount of time. The problems are also examined from a fractional aspect using the findings of fractional problem analysis performed using the recommended methodology. This study is designed in a way that: Sect. Basic definitions provides a brief discussion of the necessary definitions of FC, the natural transform, and its fractional derivatives. In Sect. Formulation of the methodology, we provide a general analysis of the indicated methodology. We discuss the suggested technique’s convergence analysis in Sect. Convergence analysis. In Sect. Test problems, we offer two numerical applications to verify the validity of our suggested approach and also present it with certain graphical representations. The final portion discusses the conclusion.

Basic definitions

In this portion, we evoke some essential notions of FC.

Definition 2.1

The Riemann-Liouville integral is termed as below59:

$$\begin{aligned} \begin{aligned} I^{{{\texttt {q}}}}j(\varphi )=&\frac{1}{\Gamma ({{\texttt {q}}})}\int _{0}^{\varphi }(\varphi -\nu )^{{{\texttt {q}}}-1}j(\nu )d\nu , \ \ {{\texttt {q}}}>0, \ \ \varphi >0,\\ and \ \ I^{0}j(\varphi )=&j(\varphi ). \end{aligned} \end{aligned}$$
(5)

Definition 2.2

The Caputo derivative is described as follows59:

$$\begin{aligned} \begin{aligned} D_{\varphi }^{{{\texttt {q}}}}j(\varphi )=I^{{m}-{{\texttt {q}}}}D^{{m}}j(\varphi )=\frac{1}{{m}-{{\texttt {q}}}}\int _{\varphi }^{0}(\varphi -\nu )^{{m}-{{\texttt {q}}}-1}j^{{m}}(\nu )d\nu , \end{aligned} \end{aligned}$$
(6)

for \({m}-1<{{\texttt {q}}}\le {m},\ \ {m}\in N, \ \ \varphi >0,j\in C^{{m}}_{v}, v\ge -1\).

Definition 2.3

The CF derivative is described as follows59:

$$\begin{aligned} \begin{aligned} D_{\varphi }^{{{\texttt {q}}}}j(\varphi )=\frac{1}{1-{{\texttt {q}}}}\int ^{\varphi }_{0}\exp \left( \frac{-{{\texttt {q}}}(\varphi -\nu )}{1-{{\texttt {q}}}}\right) D(j(\nu ))d\nu , \end{aligned} \end{aligned}$$
(7)

having \(0<{{\texttt {q}}}<1\).

Definition 2.4

The ABC derivative is termed as below59:

$$\begin{aligned} \begin{aligned} D_{\varphi }^{{{\texttt {q}}}}j(\varphi )=\frac{U({{\texttt {q}}})}{1-{{\texttt {q}}}}\int ^{\varphi }_{0}E_{{{\texttt {q}}}}\left( \frac{-{{\texttt {q}}}(\varphi -\nu )}{1-{{\texttt {q}}}}\right) D(j(\nu ))d\nu , \end{aligned} \end{aligned}$$
(8)

with \(0<{{\texttt {q}}}<1\), and \(U(\texttt {q})\) illustrated the normalization function with \(U(0)=U(1)=1\) and the Mittag-Leffler function is \(E_{{{\texttt {q}}}}(z)=\sum _{m=0}^{\infty }\frac{z^{m}}{\Gamma ({{\texttt {q}}}^{m}+1)}\).

Definition 2.5

The NT of \({{\textbf {f}}}(\aleph )\) is described as follows:

$$\begin{aligned} \begin{aligned} \mathbb{N}\mathbb{T}({{\textbf {f}}}(\aleph ))={\mathcal {P}}({\varrho },{{\rho }})=\int _{-\infty }^{\infty }e^{-\varrho \aleph }{{\textbf {f}}}(\aleph )d\aleph , \ \ \varrho \in (-\infty ,\infty ). \end{aligned} \end{aligned}$$
(9)

For \(\aleph \in (0,\infty )\), NT of \({{\textbf {f}}}(\aleph )\) is stated as

$$\begin{aligned} \begin{aligned} \mathbb{N}\mathbb{T}({{\textbf {f}}}(\aleph )H(\aleph ))=\mathbb{N}\mathbb{T}^{+}{{\textbf {f}}}(\aleph )={\mathcal {P}}^{+}({\varrho },{{\rho }})=\int _{-\infty }^{\infty }e^{-\varrho \aleph }{{\textbf {f}}}(\aleph )d\aleph , \ \ \varrho \in (0,\infty ), \end{aligned} \end{aligned}$$
(10)

with \({\mathcal {G}}(\aleph )\) demonstrating the Heaviside function.

Definition 2.6

The inverse NT of \({\mathcal {P}}({\varrho },{{\rho }})\) is described as follows:

$$\begin{aligned} \begin{aligned} \mathbb{N}\mathbb{T}^{-1}[{\mathcal {P}}({\varrho },{{\rho }})]={{\textbf {f}}}(\aleph ),\ \ \forall \aleph \ge 0. \end{aligned} \end{aligned}$$
(11)

Lemma 2.1

If NT of \({{\textbf {f}}}_{1}(\aleph )\) is \({{\textbf {f}}}_{1}({\varrho },{{\rho }})\) and \({{\textbf {f}}}_{2}(\aleph )\) is \({{\textbf {f}}}_{2}({\varrho },{{\rho }})\), then

$$\begin{aligned} \begin{aligned} \mathbb{N}\mathbb{T}[c_{1}{{\textbf {f}}}_{1}(\aleph )+c_{2}{{\textbf {f}}}_{2}(\aleph )]=c_{1}\mathbb{N}\mathbb{T}[{{\textbf {f}}}_{1}(\aleph )]+c_{2}\mathbb{N}\mathbb{T}[{{\textbf {f}}}_{2}(\aleph )]=c_{1}{{\textbf {f}}}_{1}({\varrho },{{\rho }})+c_{2}{{\textbf {f}}}_{2}({\varrho },{{\rho }}), \end{aligned} \end{aligned}$$
(12)

where \(c_{1}\) and \(c_{2}\) are constants.

Lemma 2.2

If inverse NT of \({\mathcal {P}}_{1}({\varrho },{{\rho }})\) and \({\mathcal {P}}_{2}({\varrho },{{\rho }})\) are \({{\textbf {f}}}_{1}(\aleph )\) and \({{\textbf {f}}}_{2}(\aleph )\) then

$$\begin{aligned} \begin{aligned} \mathbb{N}\mathbb{T}^{-1}[c_{1}{\mathcal {P}}_{1}({\varrho },{{\rho }})+c_{2}{\mathcal {P}}_{2}({\varrho },{{\rho }})]=c_{1}\mathbb{N}\mathbb{T}^{-1}[{\mathcal {P}}_{1}({\varrho },{{\rho }})]+c_{2}\mathbb{N}\mathbb{T}^{-1}[{\mathcal {P}}_{2}({\varrho },{{\rho }})]=c_{1}{{\textbf {f}}}_{1}(\aleph )+c_{2}{{\textbf {f}}}_{2}(\aleph ), \end{aligned} \end{aligned}$$
(13)

where \(c_{1}\) and \(c_{2}\) are constants.

Definition 2.7

The NT of Caputo derivative is described as follows59:

$$\begin{aligned} \begin{aligned} \mathbb{N}\mathbb{T}[D_{\aleph }^{{{\texttt {q}}}}]=\left( \frac{\varrho }{{\rho }}\right) ^{{{\texttt {q}}}}\left( \mathbb{N}\mathbb{T}[{{\textbf {f}}}(\aleph )]-\left( \frac{1}{\varrho }\right) {{\textbf {f}}}(0)\right) . \end{aligned} \end{aligned}$$
(14)

Definition 2.8

The NT of CF derivative is described as follows59:

$$\begin{aligned} \begin{aligned} \mathbb{N}\mathbb{T}[D_{\aleph }^{{{\texttt {q}}}}]=\frac{1}{1-{{\texttt {q}}}+{{\texttt {q}}}(\frac{{\rho }}{\varrho })}\left( \mathbb{N}\mathbb{T}[{{\textbf {f}}}(\aleph )]-\left( \frac{1}{\varrho }\right) {{\textbf {f}}}(0)\right) . \end{aligned} \end{aligned}$$
(15)

Definition 2.9

The NT of ABC derivative is described as follows59:

$$\begin{aligned} \begin{aligned} \mathbb{N}\mathbb{T}[D_{\aleph }^{{{\texttt {q}}}}]=\frac{U[{{\texttt {q}}}]}{1-{{\texttt {q}}}+{{\texttt {q}}}(\frac{{\rho }}{\varrho })^{{{\texttt {q}}}}}\left( \mathbb{N}\mathbb{T}[{{\textbf {f}}}(\aleph )]-\left( \frac{1}{\varrho }\right) {{\textbf {f}}}(0)\right) . \end{aligned} \end{aligned}$$
(16)

Formulation of the methodology

In this portion, we construct the idea of NTDM which is utilized to derive the approximate results.

$$\begin{aligned} \begin{aligned} D_{\aleph }^{{{\texttt {q}}}}{{\textbf {f}}}(\xi ,\aleph )={\mathcal {J}}({{\textbf {f}}}(\xi ,\aleph ))+{\mathcal {K}}({{\textbf {f}}}(\xi ,\aleph ))+h(\xi ,\aleph ), \end{aligned} \end{aligned}$$
(17)

with

$$\begin{aligned} \begin{aligned} {{\textbf {f}}}(\xi ,0)=\phi (\xi ). \end{aligned} \end{aligned}$$
(18)

Case I \((NTDM_{CF} ):\)

Operating NT on Eq. (17) with CF derivative results in

$$\begin{aligned} \begin{aligned} \frac{1}{p({{\texttt {q}}},{{\rho }},{\varrho })}\left( \mathbb{N}\mathbb{T}[{{\textbf {f}}}(\xi ,\aleph )]-\frac{\phi (\xi )}{\varrho }\right) =\mathbb{N}\mathbb{T}[M(\xi ,\aleph )], \end{aligned} \end{aligned}$$
(19)

with

$$\begin{aligned} p({{\texttt {q}}},{{\rho }},{\varrho })=1-{{\texttt {q}}}+{{\texttt {q}}}\left( \frac{{\rho }}{\varrho }\right) , \end{aligned}$$
(20)

and

$$\begin{aligned} M(\xi ,\aleph )={\mathcal {J}}({{\textbf {f}}}(\xi ,\aleph ))+{\mathcal {K}}({{\textbf {f}}}(\xi ,\aleph ))+h(\xi ,\aleph ). \end{aligned}$$
(21)

Operating inverse NT on Eq. (19) results in

$$\begin{aligned} \begin{aligned} {{\textbf {f}}}(\xi ,\aleph )=\mathbb{N}\mathbb{T}^{-1}\left( \frac{\phi (\xi )}{\varrho }+p({{\texttt {q}}},{{\rho }},{\varrho })\mathbb{N}\mathbb{T}[M(\xi ,\aleph )]\right) . \end{aligned} \end{aligned}$$
(22)

The nonlinear term \({\mathcal {K}}({{\textbf {f}}}(\xi ,\aleph ))\) is represented as

$$\begin{aligned} \begin{aligned} {\mathcal {K}}({{\textbf {f}}}(\xi ,\aleph ))=\sum _{t=0}^{\infty }A_{t}. \end{aligned} \end{aligned}$$
(23)

Now, we will expand the function \({{\textbf {f}}}(\xi ,\aleph )\) in series form as

$$\begin{aligned} \begin{aligned} {{\textbf {f}}}(\xi ,\aleph )=\sum _{i=0}^{\infty }{{\textbf {f}}}_{i}(\xi ,\aleph ). \end{aligned} \end{aligned}$$
(24)

Use Eqs. (23)-(24) in (22) yields

$$\begin{aligned} \begin{aligned} \sum _{i=0}^{\infty }{{\textbf {f}}}_{i}(\xi ,\aleph )=&\mathbb{N}\mathbb{T}^{-1}\left( \frac{\phi (\xi )}{\varrho }+p({{\texttt {q}}},{{\rho }},{\varrho })\mathbb{N}\mathbb{T}[h(\xi ,\aleph )]\right) \\&+\mathbb{N}\mathbb{T}^{-1}\left( p({{\texttt {q}}},{{\rho }},{\varrho })\mathbb{N}\mathbb{T}\left[ \sum _{i=0}^{\infty }{\mathcal {J}}({{\textbf {f}}}_{i}(\xi ,\aleph ))+A_{i}\right] \right) . \end{aligned} \end{aligned}$$
(25)

Similarly,

$$\begin{aligned} \begin{aligned} {{\textbf {f}}}_{0}^{CF}(\xi ,\aleph )=&\mathbb{N}\mathbb{T}^{-1}\left( \frac{\phi (\xi )}{\varrho }+p({{\texttt {q}}},{{\rho }},{\varrho })\mathbb{N}\mathbb{T}[h(\xi ,\aleph )]\right) ,\\ {{\textbf {f}}}_{1}^{CF}(\xi ,\aleph )=&\mathbb{N}\mathbb{T}^{-1}\left( p({{\texttt {q}}},{{\rho }},{\varrho })\mathbb{N}\mathbb{T}\left[ {\mathcal {J}}({{\textbf {f}}}_{0}(\xi ,\aleph ))+A_{0}\right] \right) ,\\&\vdots \\ {{\textbf {f}}}_{l+1}^{CF}(\xi ,\aleph )=&\mathbb{N}\mathbb{T}^{-1}\left( p({{\texttt {q}}},{{\rho }},{\varrho })\mathbb{N}\mathbb{T}\left[ {\mathcal {J}}({{\textbf {f}}}_{l}(\xi ,\aleph ))+A_{l}\right] \right) , \ \ l=1,2,3,\cdots \\ \end{aligned} \end{aligned}$$
(26)

The solution of (17) in \(NTDM_{CF}\) manner is obtained by utilizing (26) in (24) as

$$\begin{aligned} \begin{aligned} {{\textbf {f}}}^{CF}(\xi ,\aleph )={{\textbf {f}}}_{0}^{CF}(\xi ,\aleph )+{{\textbf {f}}}_{1}^{CF}(\xi ,\aleph )+{{\textbf {f}}}_{2}^{CF}(\xi ,\aleph )+\cdots \end{aligned} \end{aligned}$$
(27)

Case II \((NTDM_{ABC} ):\)

Operating NT on Eq. (17) with CF derivative results in

$$\begin{aligned} \begin{aligned} \frac{1}{j({{\texttt {q}}},{{\rho }},{\varrho })}\left( \mathbb{N}\mathbb{T}[{{\textbf {f}}}(\xi ,\aleph )]-\frac{\phi (\xi )}{\varrho }\right) =\mathbb{N}\mathbb{T}[M(\xi ,\aleph )], \end{aligned} \end{aligned}$$
(28)

with

$$\begin{aligned} \begin{aligned} j({{\texttt {q}}},{{\rho }},{\varrho })=\frac{1-{{\texttt {q}}}+{{\texttt {q}}}(\frac{{\rho }}{\varrho })^{{{\texttt {q}}}}}{U({{\texttt {q}}})}. \end{aligned} \end{aligned}$$
(29)

Operating inverse NT on Eq. (28) results in

$$\begin{aligned} \begin{aligned} {{\textbf {f}}}(\xi ,\aleph )=\mathbb{N}\mathbb{T}^{-1}\left( \frac{\phi (\xi )}{\varrho }+j({{\texttt {q}}},{{\rho }},{\varrho })\mathbb{N}\mathbb{T}[M(\xi ,\aleph )]\right) . \end{aligned} \end{aligned}$$
(30)

The nonlinear term \({\mathcal {K}}({{\textbf {f}}}(\xi ,\aleph ))\) is represented as

$$\begin{aligned} \begin{aligned} {\mathcal {K}}({{\textbf {f}}}(\xi ,\aleph ))=\sum _{i=0}^{\infty }A_{i}. \end{aligned} \end{aligned}$$
(31)

The series form solution for the function \({{\textbf {f}}}(\xi ,\aleph )\) is illustrated as

$$\begin{aligned} \begin{aligned} {{\textbf {f}}}(\xi ,\aleph )=\sum _{i=0}^{\infty }{{\textbf {f}}}_{i}(\xi ,\aleph ). \end{aligned} \end{aligned}$$
(32)

Use Eqs. (31)-(32) in (30) yields

$$\begin{aligned} \begin{aligned} \sum _{i=0}^{\infty }{{\textbf {f}}}_{i}(\xi ,\aleph )=&\mathbb{N}\mathbb{T}^{-1}\left( \frac{\phi (\xi )}{\varrho }+j({{\texttt {q}}},{{\rho }},{\varrho })\mathbb{N}\mathbb{T}[h(\xi ,\aleph )]\right) \\&+\mathbb{N}\mathbb{T}^{-1}\left( j({{\texttt {q}}},{{\rho }},{\varrho })\mathbb{N}\mathbb{T}\left[ \sum _{i=0}^{\infty }{\mathcal {J}}({{\textbf {f}}}_{i}(\xi ,\aleph ))+A_{i}\right] \right) . \end{aligned} \end{aligned}$$
(33)

Similarly,

$$\begin{aligned} \begin{aligned} {{\textbf {f}}}_{0}^{ABC}(\xi ,\aleph )=&\mathbb{N}\mathbb{T}^{-1}\left( \frac{\phi (\xi )}{\varrho }+j({{\texttt {q}}},{{\rho }},{\varrho })\mathbb{N}\mathbb{T}[h(\xi ,\aleph )]\right) ,\\ {{\textbf {f}}}_{1}^{ABC}(\xi ,\aleph )=&\mathbb{N}\mathbb{T}^{-1}\left( j({{\texttt {q}}},{{\rho }},{\varrho })\mathbb{N}\mathbb{T}\left[ {\mathcal {J}}({{\textbf {f}}}_{0}(\xi ,\aleph ))+A_{0}\right] \right) ,\\&\vdots \\ {{\textbf {f}}}_{l+1}^{ABC}(\xi ,\aleph )=&\mathbb{N}\mathbb{T}^{-1}\left( j({{\texttt {q}}},{{\rho }},{\varrho })\mathbb{N}\mathbb{T}\left[ {\mathcal {J}}({{\textbf {f}}}_{l}(\xi ,\aleph ))+A_{l}\right] \right) , \ \ l=1,2,3,\cdots \\ \end{aligned} \end{aligned}$$
(34)

The solution of (17) in \(NTDM_{ABC}\) manner is obtained by utilizing (34) in (32) as

$$\begin{aligned} \begin{aligned} {{\textbf {f}}}^{ABC}(\xi ,\aleph )={{\textbf {f}}}_{0}^{ABC}(\xi ,\aleph )+{{\textbf {f}}}_{1}^{ABC}(\xi ,\aleph )+{{\textbf {f}}}_{2}^{ABC}(\xi ,\aleph )+\cdots \end{aligned} \end{aligned}$$
(35)

Convergence analysis

The convergence analysis for \(NTDM_{CF}\) and \(NTDM_{ABC}\) is illustrated below.

Theorem 4.1

The \(NTDM_{CF}\) result for (17) is unique at \(0<({\mathcal B }_{1}+ {\mathcal B} _{2})(1-{{\texttt {q}}}+{{\texttt {q}}} \aleph )<1.\)  

Proof

Assume \({\mathcal {G}}=(C[J],||.||)\) having norm \(||\phi (\aleph )||={max}_{\aleph \in J}|\phi (\aleph )|\) is Banach space,\(\forall\) continuous function on J. Let \(I:{\mathcal {G}}\rightarrow {\mathcal {G}}\) is a non-linear mapping, here

$$\begin{aligned} {{\textbf {f}}}^{C}_{l+1}={{\textbf {f}}}^{C}_{0}+\mathbb{N}\mathbb{T}^{-1}[p({{\texttt {q}}},{{\mu }},{\rho })\mathbb{N}\mathbb{T}[{\mathcal {J}}({{\textbf {f}}}_{l}(\xi ,\aleph ))+{\mathcal {K}}({{\textbf {f}}}_{l}(\xi ,\aleph ))]], \ \ l\ge 0. \end{aligned}$$

Let \(|{\mathcal {J}}({{\textbf {f}}})-{\mathcal {J}}({{\textbf {f}}}^{*})|<{\mathcal B }_{1}|{{\textbf {f}}}-{{\textbf {f}}}^{*}|\) and \(|{\mathcal {K}}({{\textbf {f}}})-{\mathcal {K}}({{\textbf {f}}}^{*})|<{\mathcal B }_{2}|{{\textbf {f}}}-{{\textbf {f}}}^{*}|\), where \({{\textbf {f}}}:={{\textbf {f}}}(\xi ,\aleph )\) and \({{\textbf {f}}}^{*}:={{\textbf {f}}}^{*}(\xi ,\aleph )\) are values of two separate functions and \({\mathcal B }_{1}\),\({\mathcal B }_{2}\) are Lipschitz constants.

$$\begin{aligned} \begin{aligned} ||I{{\textbf {f}}}-I{{\textbf {f}}}^{*}||&\le max_{t\in J}|\mathbb{N}\mathbb{T}^{-1}\Big [p({{\texttt {q}}},{{\mu }},{\rho })\mathbb{N}\mathbb{T}[{\mathcal {J}}({{\textbf {f}}})-{\mathcal {J}}({{\textbf {f}}}^{*})]\\&\quad +p({{\texttt {q}}},{{\mu }},{\rho })\mathbb{N}\mathbb{T}[{\mathcal {K}}({{\textbf {f}}})-{\mathcal {K}}({{\textbf {f}}}^{*})]|\Big ]\\&\le max_{\aleph \in J}\Big [{\mathcal B }_{1}\mathbb{N}\mathbb{T}^{-1}[p({{\texttt {q}}},{{\mu }},{\rho })\mathbb{N}\mathbb{T}[|{{\textbf {f}}}-{{\textbf {f}}}^{*}|]]\\&\quad +{\mathcal B }_{2}\mathbb{N}\mathbb{T}^{-1}[p({{\texttt {q}}},{{\mu }},{\rho })\mathbb{N}\mathbb{T}[|{{\textbf {f}}}-{{\textbf {f}}}^{*}|]]\Big ]\\&\le max_{t\in J}({\mathcal B }_{1}+{\mathcal B }_{2})\left[ \mathbb{N}\mathbb{T}^{-1}[p({{\texttt {q}}},{{\mu }},{\rho })\mathbb{N}\mathbb{T}|{{\textbf {f}}}-{{\textbf {f}}}^{*}|]\right] \\&\le ({\mathcal B }_{1}+{\mathcal B }_{2})\left[ \mathbb{N}\mathbb{T}^{-1}[p({{\texttt {q}}},{{\mu }},{\rho })\mathbb{N}\mathbb{T}||{{\textbf {f}}}-{{\textbf {f}}}^{*}||]\right] \\&=({\mathcal B }_{1}+{\mathcal B }_{2})(1-{{\texttt {q}}}+{{\texttt {q}}} \aleph )||{{\textbf {f}}}-{{\textbf {f}}}^{*}|| \end{aligned} \end{aligned}$$
(36)

I is contraction as \(0<({\mathcal B }_{1}+{\mathcal B }_{2})(1-{{\texttt {q}}}+{{\texttt {q}}} \aleph )<1\). Thus the result of (17) is unique in terms of Banach fixed point theorem. \(\square\)

Theorem 4.2

The \(NTDM_{ABC}\) result for (17) is unique when \(0<({\mathcal B }_{1}+{\mathcal B }_{2})\left( 1-\texttt {q}+\frac{\texttt {q}\aleph ^\texttt {q}}{\Gamma (\texttt {q}+1)}\right) <1.\)  

Proof

Due to the fact that this proof is the same as that of Theorem 1, it was skipped. \(\square\)

Theorem 4.3

The \(NTDM_{CF}\) result of (17) is convergent.

Proof

Let \({{\textbf {f}}}_{m}=\sum _{r=0}^{m}{{\textbf {f}}}_{r}(\varphi ,\aleph )\). To show that \({{\textbf {f}}}_{m}\) is a Cauchy sequence in \({\mathcal {G}}\). Assume,

$$\begin{aligned} \begin{aligned} ||{{\textbf {f}}}_{m}-{{\textbf {f}}}_{n}||&=max_{\aleph \in J}|\sum _{r=n+1}^{m}{{\textbf {f}}}_{r}|, \ \ n=1,2,3,\cdots \\&\le max_{\aleph \in J} \left| \mathbb{N}\mathbb{T}^{-1}\left[ p({{\texttt {q}}},{{\mu }},{\rho })\mathbb{N}\mathbb{T}\left[ \sum _{r=n+1}^{m}({\mathcal {J}}({{\textbf {f}}}_{r-1})+{\mathcal {K}}({{\textbf {f}}}_{r-1}))\right] \right] \right| \\&=max_{\aleph \in J} \left| \mathbb{N}\mathbb{T}^{-1}\left[ p({{\texttt {q}}},{{\mu }},{\rho })\mathbb{N}\mathbb{T}\left[ \sum _{r=n+1}^{m-1}({\mathcal {J}}({{\textbf {f}}}_{r})+{\mathcal {K}}({{\textbf {f}}}_{r}))\right] \right] \right| \\&\le max_{\aleph \in J}|\mathbb{N}\mathbb{T}^{-1}[p({{\texttt {q}}},{{\mu }},{\rho })\mathbb{N}\mathbb{T}[({\mathcal {J}}({{\textbf {f}}}_{m-1})-{\mathcal {J}}({{\textbf {f}}}_{n-1})+{\mathcal {K}}({{\textbf {f}}}_{m-1})-{\mathcal {K}}({{\textbf {f}}}_{n-1}))]]|\\&\le {\mathcal B }_{1}max_{\aleph \in J}|\mathbb{N}\mathbb{T}^{-1}[p({{\texttt {q}}},{{\mu }},{\rho })\mathbb{N}\mathbb{T}[({\mathcal {J}}({{\textbf {f}}}_{m-1})-{\mathcal {J}}({{\textbf {f}}}_{n-1}))]]|\\&\quad +{\mathcal B }_{2}max_{\aleph \in J}|\mathbb{N}\mathbb{T}^{-1}[p({{\texttt {q}}},{{\mu }},{\rho })\mathbb{N}\mathbb{T}[({\mathcal {K}}({{\textbf {f}}}_{m-1})-{\mathcal {K}}({{\textbf {f}}}_{n-1}))]]|\\&=({\mathcal B }_{1}+{\mathcal B }_{2})(1-{{\texttt {q}}}+{{\texttt {q}}} \aleph )||{{\textbf {f}}}_{m-1}-{{\textbf {f}}}_{n-1}|| \end{aligned} \end{aligned}$$
(37)

Let \(m=n+1\), then

$$\begin{aligned} \begin{aligned} ||{{\textbf {f}}}_{n+1}-{{\textbf {f}}}_{n}||\le {\mathcal B }||{{\textbf {f}}}_{n}-{{\textbf {f}}}_{n-1}||\le {\mathcal B }^{2}||{{\textbf {f}}}_{n-1}{{\textbf {f}}}_{n-2}||\le \cdots \le {\mathcal B }^{n}||{{\textbf {f}}}_{1}-{{\textbf {f}}}_{0}||, \end{aligned} \end{aligned}$$
(38)

where \({\mathcal B }=({\mathcal B }_{1}+{\mathcal B }_{2})(1-{{\texttt {q}}}+{{\texttt {q}}} \aleph )\). Similarly, we have

$$\begin{aligned} \begin{aligned} ||{{\textbf {f}}}_{m}-{{\textbf {f}}}_{n}||&\le ||{{\textbf {f}}}_{n+1}-{{\textbf {f}}}_{n}||+||{{\textbf {f}}}_{n+2}{{\textbf {f}}}_{n+1}||+\cdots +||{{\textbf {f}}}_{m}-{{\textbf {f}}}_{m-1}||,\\&({\mathcal B }^{n}+{\mathcal B }^{n+1}+\cdots +{\mathcal B }^{m-1})||{{\textbf {f}}}_{1}-{{\textbf {f}}}_{0}||\\&\le {\mathcal B }^{n}\left( \frac{1-{\mathcal B }^{m-n}}{1-{\mathcal B }}\right) ||{{\textbf {f}}}_{1}||, \end{aligned} \end{aligned}$$
(39)

As \(0<{\mathcal B }<1\), we get \(1-{\mathcal B }^{m-n}<1\). Therefore,

$$\begin{aligned} \begin{aligned} ||{{\textbf {f}}}_{m}-{{\textbf {f}}}_{n}||\le \frac{{\mathcal B }^{n}}{1-{\mathcal B }}max_{\aleph \in J}||{{\textbf {f}}}_{1}||. \end{aligned} \end{aligned}$$
(40)

Since \(||{{\textbf {f}}}_{1}||<\infty ,\ \ ||{{\textbf {f}}}_{m}-{{\textbf {f}}}_{n}||\rightarrow 0\) when \(n \rightarrow \infty\). Thus, the series \({{\textbf {f}}}_m\) is convergent due to fact that \({{\textbf {f}}}_m\) is a Cauchy sequence in \({\mathcal {G}}\).

Theorem 4.4

\(NTDM_{ABC}\) solution of (17) is convergent.

Proof

Due to the fact that this proof is the same as that of Theorem 3, it was skipped.

Test problems

In this potion, we implemented NTDM to obtain the analytical approximate solutions in the form of convergent series.

Problem 1

Assume the FKE equation given:

$$\begin{aligned} \begin{aligned} \iota D_\aleph ^\texttt {q}{{{\textbf {f}}}(\xi ,\aleph )}={{\textbf {f}}}_{\xi \xi }+2{{\textbf {f}}}(|{{\textbf {f}}}|^{2})_{\xi }+{{\textbf {f}}}|{{\textbf {f}}}|^{4}=0, \ \ \ \ \ 0<\texttt {q}\le 1, \end{aligned} \end{aligned}$$
(41)

with

$$\begin{aligned} {{\textbf {f}}}(\xi ,0)={{\textbf {a}}}e^{\imath \xi }. \end{aligned}$$
(42)

By simplification

$$\begin{aligned} D_\aleph ^\texttt {q}{{{\textbf {f}}}(\xi ,\aleph )}=\iota \Bigg ({{\textbf {f}}}_{\xi \xi }+2({{\textbf {f}}}{{\textbf {f}}}_{\xi }\bar{{{\textbf {f}}}}+{{\textbf {f}}}^{2}\bar{{{\textbf {f}}}}_{\xi })+{{\textbf {f}}}^{3}\bar{{{\textbf {f}}}}^{2}\Bigg ). \end{aligned}$$
(43)

Operating NT on Eq. (1) results in

$$\begin{aligned} \begin{aligned}{}&{\mathbb{N}\mathbb{T}}[D_{\aleph }^{\texttt {q}}{{\textbf {f}}}({\xi },{\aleph })]=\iota \Bigg ({\mathbb{N}\mathbb{T}}\Bigg \{{{\textbf {f}}}_{\xi \xi }\Bigg \}+2\Bigg ({\mathbb{N}\mathbb{T}}\Bigg \{{{\textbf {f}}}\bar{{{\textbf {f}}}}{{\textbf {f}}}_{\xi }\Bigg \}+{\mathbb{N}\mathbb{T}}\Bigg \{{{\textbf {f}}}^{2}\bar{{{\textbf {f}}}}_{\xi }\Bigg \}\Bigg )+{\mathbb{N}\mathbb{T}}\Bigg \{{{\textbf {f}}}^{3}\bar{{{\textbf {f}}}}^{2}\Bigg \}\Bigg ). \end{aligned} \end{aligned}$$
(44)

This implies

$$\begin{aligned} \begin{aligned}{}&\frac{1}{\varrho ^{\texttt {q}}}{\mathbb{N}\mathbb{T}}[{{\textbf {f}}}({\xi },{\aleph })]-{\varrho }^{2-\texttt {q}}{{{{\textbf {f}}}}({\xi },0)}=\iota {\mathbb{N}\mathbb{T}}\Bigg [{{\textbf {f}}}_{\xi \xi }+2({{\textbf {f}}}{{\textbf {f}}}_{\xi }\bar{{{\textbf {f}}}}+{{\textbf {f}}}^{2}\bar{{{\textbf {f}}}}_{\xi })+{{\textbf {f}}}^{3}\bar{{{\textbf {f}}}}^{2}\Bigg ]. \end{aligned} \end{aligned}$$
(45)

Operating inverse NT on Eq. (45) results in

$$\begin{aligned} \begin{aligned}{}&{{\textbf {f}}}({\xi },{\aleph })=\Bigg [{{\textbf {a}}}e^{\imath \xi }\Bigg ]-{\mathbb{N}\mathbb{T}}^{-1}\Bigg [\iota \frac{{{\texttt {q}}}(\varrho -\texttt {q}({\varrho }-{{\texttt {q}}}))}{{\varrho }^2}\mathbb{N}\mathbb{T}\Bigg \{{{\textbf {f}}}_{\xi \xi }+2({{\textbf {f}}}{{\textbf {f}}}_{\xi }\bar{{{\textbf {f}}}}+{{\textbf {f}}}^{2}\bar{{{\textbf {f}}}}_{\xi })+{{\textbf {f}}}^{3}\bar{{{\textbf {f}}}}^{2}\Bigg \}\Bigg ]. \end{aligned} \end{aligned}$$
(46)

Application of \(NTDM_{CF}\)

Now, we will expand the function \({{\textbf {f}}}(\xi ,\aleph )\) in series form as

$$\begin{aligned} {{\textbf {f}}}({\xi },{\aleph })=\sum _{{l}=0}^{\infty }{{\textbf {f}}}_{{l}}({\xi },{\aleph }). \end{aligned}$$
(47)

The nonlinear terms \({{\textbf {f}}}{{\textbf {f}}}_{\xi }\bar{{{\textbf {f}}}}=\sum _{{l}=0}^{\infty }\mathcal A_{{l}},{{\textbf {f}}}^{2}\bar{{{\textbf {f}}}}_{\xi }=\sum _{{l}=0}^{\infty }\mathcal B_{{l}},{{\textbf {f}}}^{3}\bar{{{\textbf {f}}}}^{2}=\sum _{{l}=0}^{\infty }\mathcal C_{{l}},\) in terms of Adomian polynomials are taken as follows:

$$\begin{aligned} \begin{aligned}{}&\sum _{{l}=0}^{\infty }{{\textbf {f}}}_{{l}+1}({\xi },{\aleph })=\Bigg [{{\textbf {a}}}e^{\imath \xi }\Bigg ]\\&\quad -{\mathbb{N}\mathbb{T}}^{-1}\Bigg [\iota \frac{{{\texttt {q}}}(\varrho -\texttt {q}({\varrho }-{{\texttt {q}}}))}{{\varrho }^2}\mathbb{N}\mathbb{T}\Bigg \{{{\textbf {f}}}_{\xi \xi }+2\Bigg (\sum _{{l}=0}^{\infty }{\mathcal {A}}_{{l}}+\sum _{{l}=0}^{\infty }{\mathcal {B}}_{{l}}\Bigg )+\sum _{{l}=0}^{\infty }{\mathcal {C}}_{{l}}\Bigg \}\Bigg ]. \end{aligned} \end{aligned}$$
(48)

Similarly,

$$\begin{aligned} {{\textbf {f}}}_{0}({\xi },{\aleph })= & {} {{\textbf {a}}}e^{\imath \xi },\nonumber \\ {{\textbf {f}}}_{1}({\xi },{\aleph })= & {} \imath e^{\imath \xi }({{\textbf {a}}}^{5}-{{\textbf {a}}})\left( \texttt {q}(\aleph -1)+1\right) , \end{aligned}$$
(49)
$$\begin{aligned} {{\textbf {f}}}_{2}({\xi },{\aleph })= & {} -e^{\imath \xi }{{\textbf {a}}}({{\textbf {a}}}^{4}-1)^{2}\Bigg ((1-\texttt {q})^{2}+2\texttt {q}(1-\texttt {q})\aleph +\frac{\texttt {q}^{2}\aleph ^2}{2}\Bigg ). \end{aligned}$$
(50)

Lastly, it can be continued to the following series:

$$\begin{aligned} \begin{aligned} {{\textbf {f}}}({\xi },{\aleph })&=\sum _{{l}=0}^{\infty }{{\textbf {f}}}_{{l}}({\xi },{\aleph })={{\textbf {f}}}_{0}({\xi },{\aleph })+{{\textbf {f}}}_{1}({\xi },{\aleph })+{{\textbf {f}}}_{2}({\xi },{\aleph })+\cdots ,\\ {{\textbf {f}}}({\xi },{\aleph })&={{\textbf {a}}}e^{\imath \xi }+\imath e^{\imath \xi }({{\textbf {a}}}^{5}-{{\textbf {a}}})\left( \texttt {q}(\aleph -1)+1\right) -e^{\imath \xi }{{\textbf {a}}}({{\textbf {a}}}^{4}-1)^{2}\Bigg ((1-\texttt {q})^{2}+2\texttt {q}(1-\texttt {q})\aleph +\frac{\texttt {q}^{2}\aleph ^2}{2}\Bigg )+\cdots . \end{aligned} \end{aligned}$$
(51)

Application of \(NDM_{ABC}\)

Now, we will expand the function \({{\textbf {f}}}(\xi ,\aleph )\) in series form as

$$\begin{aligned} {{\textbf {f}}}({\xi },{\aleph })=\sum _{{l}=0}^{\infty }{{\textbf {f}}}_{{l}}({\xi },{\aleph }). \end{aligned}$$
(52)

The nonlinear terms \({{\textbf {f}}}{{\textbf {f}}}_{\xi }\bar{{{\textbf {f}}}}=\sum _{{l}=0}^{\infty }\mathcal A_{{l}},{{\textbf {f}}}^{2}\bar{{{\textbf {f}}}}_{\xi }=\sum _{{l}=0}^{\infty }\mathcal B_{{l}},{{\textbf {f}}}^{3}\bar{{{\textbf {f}}}}^{2}=\sum _{{l}=0}^{\infty }\mathcal C_{{l}},\) in terms of Adomian polynomials are taken as follows:

$$\begin{aligned} \begin{aligned}{}&\sum _{{l}=0}^{\infty }{{\textbf {f}}}_{{l}+1}({\xi },{\aleph })=\Bigg [{{\textbf {a}}}e^{\imath \xi }\Bigg ]\\&\quad -{\mathbb{N}\mathbb{T}}^{-1}\Bigg [\iota \frac{\rho ^\texttt {q}(\varrho ^\texttt {q}+\texttt {q}(\rho ^\texttt {q}-{\varrho }^\texttt {q}))}{{\varrho }^{2\texttt {q}}}\mathbb{N}\mathbb{T}\Bigg \{{{\textbf {f}}}_{\xi \xi }+2\Bigg (\sum _{{l}=0}^{\infty }{\mathcal {A}}_{{l}}+\sum _{{l}=0}^{\infty }{\mathcal {B}}_{{l}}\Bigg )+\sum _{{l}=0}^{\infty }{\mathcal {C}}_{{l}}\Bigg \}\Bigg ].\\ \end{aligned} \end{aligned}$$
(53)

Similarly,

$$\begin{aligned} {{\textbf {f}}}_{0}({\xi },{\aleph })= & {} {{\textbf {a}}}e^{\imath \xi },\nonumber \\ {{\textbf {f}}}_{1}({\xi },{\aleph })= & {} \imath e^{\imath \xi }({{\textbf {a}}}^{5}-{{\textbf {a}}})\left( 1-\texttt {q}+\frac{\texttt {q}\aleph ^\texttt {q}}{\Gamma (\texttt {q}+1)}\right) , \end{aligned}$$
(54)
$$\begin{aligned} {{\textbf {f}}}_{2}({\xi },{\aleph })= & {} -e^{\imath \xi }{{\textbf {a}}}({{\textbf {a}}}^{4}-1)^{2}\left[ \frac{\texttt {q}^{2}\aleph ^{2\texttt {q}}}{\Gamma (2\texttt {q}+1)}+2\texttt {q}(1-\texttt {q})\frac{\aleph ^{\texttt {q}}}{\Gamma (\texttt {q}+1)}+(1-\texttt {q})^{2}\right] . \end{aligned}$$
(55)

Lastly, it can be continued to the following series:

$$\begin{aligned} \begin{aligned} {{\textbf {f}}}({\xi },{\aleph })&=\sum _{{l}=0}^{\infty }{{\textbf {f}}}_{{l}}({\xi },{\aleph })={{\textbf {f}}}_{0}({\xi },{\aleph })+{{\textbf {f}}}_{1}({\xi },{\aleph })+{{\textbf {f}}}_{2}({\xi },{\aleph })+\cdots ,\\ {{\textbf {f}}}({\xi },{\aleph })&={{\textbf {a}}}e^{\imath \xi }+\imath e^{\imath \xi }({{\textbf {a}}}^{5}-{{\textbf {a}}})\left( 1-\texttt {q}+\frac{\texttt {q}\aleph ^\texttt {q}}{\Gamma (\texttt {q}+1)}\right) -e^{\imath \xi }{{\textbf {a}}}({{\textbf {a}}}^{4}-1)^{2}\Bigg [\frac{\texttt {q}^{2}\aleph ^{2\texttt {q}}}{\Gamma (2\texttt {q}+1)}+2\texttt {q}(1-\texttt {q})\\&\frac{\aleph ^{\texttt {q}}}{\Gamma (\texttt {q}+1)}+(1-\texttt {q})^{2}\Bigg ]+\cdots . \end{aligned} \end{aligned}$$
(56)

On switching \(\texttt {q}=1\), we obtain the close form solution as

$$\begin{aligned} {{\textbf {f}}}({\xi },{\aleph })=\frac{e^{\iota \xi }}{(1+(\frac{1}{{{\textbf {a}}}^{4}}-1)e^{4\iota \xi })^{\frac{1}{4}}}. \end{aligned}$$
(57)
Table 1 Numerical analysis among the real part of the accurate and our method solutions.
Full size table
Table 2 The absolute error comparison among q-Homotopy analysis transform method (q-HATM) and our method.
Full size table
Figure 1
figure 1

Graphical depicts of the approximate solution for example 1 in 3D with respect to contour for \({{\textbf {a}}}=1,\) and \(\texttt {q}=1.\) (a) Real surface, (b) Real contour, (c) Imaginary surface and (d) Imaginary contour.

Full size image
Figure 2
figure 2

Graphical depicts of the approximate solution for example 1 in 2D at various \(\texttt {q}\) orders (a) Real part, (b) Imaginary part.

Full size image

Example 2

Assume the coupled fractional equations describing the MT model:

$$\begin{aligned} \begin{aligned}{}&\iota (D_\aleph ^\texttt {q}{{{\textbf {f}}}(\xi ,\aleph )}+{{\textbf {f}}}_{\xi })+{{\textbf {g}}}+{{\textbf {f}}}|{{\textbf {g}}}|^{2}=0,\\&\iota (D_\aleph ^\texttt {q}{{{\textbf {g}}}(\xi ,\aleph )}+{{\textbf {g}}}_{\xi })+{{\textbf {f}}}+{{\textbf {g}}}|{{\textbf {f}}}|^{2}=0, \ \ \ \ \ 0<\texttt {q}\le 1,\\ \end{aligned} \end{aligned}$$
(58)

with

$$\begin{aligned} {{\textbf {f}}}(\xi ,0)={{\textbf {a}}}e^{\imath \xi }, \quad {{\textbf {g}}}(\xi ,0)={{\textbf {b}}}e^{\imath \xi }. \end{aligned}$$
(59)

By simplification

$$\begin{aligned} \begin{aligned}{}&D_\aleph ^\texttt {q}{{{\textbf {f}}}(\xi ,\aleph )}=\iota [\iota {{\textbf {f}}}_{\xi }+{{\textbf {g}}}+{{\textbf {f}}}({{\textbf {g}}}\bar{{{\textbf {g}}}})],\\&D_\aleph ^\texttt {q}{{{\textbf {g}}}(\xi ,\aleph )}=\iota [\iota {{\textbf {g}}}_{\xi }+{{\textbf {f}}}+{{\textbf {g}}}({{\textbf {f}}}\bar{{{\textbf {f}}}})].\\ \end{aligned} \end{aligned}$$
(60)

Operating NT on Eq. (3) results in

$$\begin{aligned} \begin{aligned}{}&{\mathbb{N}\mathbb{T}}[D_{\aleph }^{\texttt {q}}{{\textbf {f}}}({\xi },{\aleph })]=\iota \Bigg (\iota {\mathbb{N}\mathbb{T}}\Bigg \{{{\textbf {f}}}_{\xi }\Bigg \}+{\mathbb{N}\mathbb{T}}\Bigg \{{{\textbf {g}}}\Bigg \}+{\mathbb{N}\mathbb{T}}\Bigg \{{{\textbf {f}}}({{\textbf {g}}}\bar{{{\textbf {g}}}})\Bigg \}\Bigg ),\\&{\mathbb{N}\mathbb{T}}[D_{\aleph }^{\texttt {q}}{{\textbf {g}}}({\xi },{\aleph })]=\iota \Bigg (\iota {\mathbb{N}\mathbb{T}}\Bigg \{{{\textbf {g}}}_{\xi }\Bigg \}+{\mathbb{N}\mathbb{T}}\Bigg \{{{\textbf {f}}}\Bigg \}+{\mathbb{N}\mathbb{T}}\Bigg \{{{\textbf {g}}}({{\textbf {f}}}\bar{{{\textbf {f}}}})\Bigg \}\Bigg ).\\ \end{aligned} \end{aligned}$$
(61)

This implies

$$\begin{aligned} \begin{aligned}{}&\frac{1}{\varrho ^{\texttt {q}}}{\mathbb{N}\mathbb{T}}[{{\textbf {f}}}({\xi },{\aleph })]-{\varrho }^{2-\texttt {q}}{{{{\textbf {f}}}}({\xi },0)}=\iota {\mathbb{N}\mathbb{T}}\Bigg [\iota {{\textbf {f}}}_{\xi }+{{\textbf {g}}}+{{\textbf {f}}}({{\textbf {g}}}\bar{{{\textbf {g}}}})\Bigg ],\\&\frac{1}{\varrho ^{\texttt {q}}}{\mathbb{N}\mathbb{T}}[{{\textbf {g}}}({\xi },{\aleph })]-{\varrho }^{2-\texttt {q}}{{{{\textbf {g}}}}({\xi },0)}=\iota {\mathbb{N}\mathbb{T}}\Bigg [\iota {{\textbf {g}}}_{\xi }+{{\textbf {f}}}+{{\textbf {g}}}({{\textbf {f}}}\bar{{{\textbf {f}}}})\Bigg ].\\ \end{aligned} \end{aligned}$$
(62)

Operating inverse NT on Eq. (62) results in

$$\begin{aligned} \begin{aligned}{}&{{\textbf {f}}}({\xi },{\aleph })=\Bigg [{{\textbf {a}}}e^{\imath \xi }\Bigg ]-\iota {\mathbb{N}\mathbb{T}}^{-1}\Bigg [\frac{{{\texttt {q}}}(\varrho -\texttt {q}({\varrho }-{{\texttt {q}}}))}{{\varrho }^2}\mathbb{N}\mathbb{T}\Bigg \{\iota {{\textbf {f}}}_{\xi }+{{\textbf {g}}}+{{\textbf {f}}}({{\textbf {g}}}\bar{{{\textbf {g}}}})\Bigg \}\Bigg ],\\&{{\textbf {g}}}({\xi },{\aleph })=\Bigg [{{\textbf {b}}}e^{\imath \xi }\Bigg ]-\iota {\mathbb{N}\mathbb{T}}^{-1}\Bigg [\frac{{{\texttt {q}}}(\varrho -\texttt {q}({\varrho }-{{\texttt {q}}}))}{{\varrho }^2}\mathbb{N}\mathbb{T}\Bigg \{\iota {{\textbf {g}}}_{\xi }+{{\textbf {f}}}+{{\textbf {g}}}({{\textbf {f}}}\bar{{{\textbf {f}}}})\Bigg \}\Bigg ].\\ \end{aligned} \end{aligned}$$
(63)

Application of \(NTDM_{CF}\)

Now, we will expand the function \({{\textbf {f}}}(\xi ,\aleph )\) and \({{\textbf {g}}}(\xi ,\aleph )\) in series form as

$$\begin{aligned} {{\textbf {f}}}({\xi },{\aleph })=\sum _{{l}=0}^{\infty }{{\textbf {f}}}_{{l}}({\xi },{\aleph }),\quad {{\textbf {g}}}({\xi },{\aleph })=\sum _{{l}=0}^{\infty }{{\textbf {g}}}_{{l}}({\xi },{\aleph }). \end{aligned}$$
(64)

The nonlinear terms \({{\textbf {f}}}({{\textbf {g}}}\bar{{{\textbf {g}}}})=\sum _{{l}=0}^{\infty }\mathcal A_{{l}},{{\textbf {g}}}({{\textbf {f}}}\bar{{{\textbf {f}}}})=\sum _{{l}=0}^{\infty }\mathcal B_{{l}},\) in terms of Adomian polynomials are taken as follows:

$$\begin{aligned} \begin{aligned}{}&\sum _{{l}=0}^{\infty }{{\textbf {f}}}_{{l}+1}({\xi },{\aleph })=\Bigg [{{\textbf {a}}}e^{\iota \xi }\Bigg ]-\iota {\mathbb{N}\mathbb{T}}^{-1}\Bigg [\frac{{{\texttt {q}}}(\varrho -\texttt {q}({\varrho }-{{\texttt {q}}}))}{{\varrho }^2}\mathbb{N}\mathbb{T}\Bigg \{\iota {{\textbf {f}}}_{\xi }+{{\textbf {g}}}+\sum _{{l}=0}^{\infty }{\mathcal {A}}_{{l}}\Bigg \}\Bigg ],\\&\sum _{{l}=0}^{\infty }{{\textbf {g}}}_{{l}+1}({\xi },{\aleph })=\Bigg [{{\textbf {b}}}e^{\iota \xi }\Bigg ]-\iota {\mathbb{N}\mathbb{T}}^{-1}\Bigg [\frac{{{\texttt {q}}}(\varrho -\texttt {q}({\varrho }-{{\texttt {q}}}))}{{\varrho }^2}\mathbb{N}\mathbb{T}\Bigg \{\iota {{\textbf {g}}}_{\xi }+{{\textbf {f}}}+\sum _{{l}=0}^{\infty }{\mathcal {B}}_{{l}}\Bigg \}\Bigg ].\\ \end{aligned} \end{aligned}$$
(65)

Similarly,

$$\begin{aligned}{} & {} {{\textbf {f}}}_{0}({\xi },{\aleph })={{\textbf {a}}}e^{\iota \xi },\nonumber \\{} & {} {{\textbf {g}}}_{0}({\xi },{\aleph })={{\textbf {b}}}e^{\iota \xi },\nonumber \\{} & {} {{\textbf {f}}}_{1}({\xi },{\aleph })=\iota e^{\iota \xi }({{\textbf {b}}}+({{\textbf {b}}}^{2}-1){{\textbf {a}}})\left( \texttt {q}(\aleph -1)+1\right) ,\nonumber \\{} & {} {{\textbf {g}}}_{1}({\xi },{\aleph })=\iota e^{\iota \xi }({{\textbf {a}}}+({{\textbf {a}}}^{2}-1){{\textbf {b}}})\left( \texttt {q}(\aleph -1)+1\right) , \end{aligned}$$
(66)
$$\begin{aligned}{} & {} {{\textbf {f}}}_{2}({\xi },{\aleph })=-e^{\iota \xi }({{\textbf {a}}}^{3}{{\textbf {b}}}^{2}-{{\textbf {a}}}^{2}{{\textbf {b}}}(-3+{{\textbf {b}}}^{2})+{{\textbf {b}}}(-2+{{\textbf {b}}}^{2})+{{\textbf {a}}}(2-4{{\textbf {b}}}^{2}+{{\textbf {b}}}^{4}))\Bigg ((1-\texttt {q})^{2}+2\texttt {q}(1-\texttt {q})\aleph +\frac{\texttt {q}^{2}\aleph ^2}{2}\Bigg ),\nonumber \\{} & {} {{\textbf {g}}}_{2}({\xi },{\aleph })=-e^{\iota \xi }(2{{\textbf {b}}}+{{\textbf {a}}}^{4}{{\textbf {b}}}+{{\textbf {a}}}^{2}{{\textbf {b}}}(-4+{{\textbf {b}}}^{2})-{{\textbf {a}}}^{3}(-1+{{\textbf {b}}}^{2})+{{\textbf {a}}}(-2+3{{\textbf {b}}}^{2}))\Bigg ((1-\texttt {q})^{2}+2\texttt {q}(1-\texttt {q})\aleph +\frac{\texttt {q}^{2}\aleph ^2}{2}\Bigg ). \end{aligned}$$
(67)

Lastly, it can be continued to the following series:

$$\begin{aligned} {{\textbf {f}}}({\xi },{\aleph })= & {} \sum _{{l}=0}^{\infty }{{\textbf {f}}}_{{l}}({\xi },{\aleph })={{\textbf {f}}}_{0}({\xi },{\aleph })+{{\textbf {f}}}_{1}({\xi },{\aleph })+{{\textbf {f}}}_{2}({\xi },{\aleph })+\cdots ,\nonumber \\ {{\textbf {f}}}({\xi },{\aleph })= & {} {{\textbf {a}}}e^{\iota \xi }+\iota e^{\iota \xi }({{\textbf {b}}}+({{\textbf {b}}}^{2}-1){{\textbf {a}}})\left( \texttt {q}(\aleph -1)+1\right) -e^{\iota \xi }({{\textbf {a}}}^{3}{{\textbf {b}}}^{2}-{{\textbf {a}}}^{2}{{\textbf {b}}}(-3+{{\textbf {b}}}^{2})+{{\textbf {b}}}(-2+{{\textbf {b}}}^{2})\nonumber \\{} & {} +{{\textbf {a}}}(2-4{{\textbf {b}}}^{2}+{{\textbf {b}}}^{4}))\Bigg ((1-\texttt {q})^{2}+2\texttt {q}(1-\texttt {q})\aleph +\frac{\texttt {q}^{2}\aleph ^2}{2}\Bigg )+\cdots . \end{aligned}$$
(68)
$$\begin{aligned} {{\textbf {g}}}({\xi },{\aleph })= & {} \sum _{{l}=0}^{\infty }{{\textbf {g}}}_{{l}}({\xi },{\aleph })={{\textbf {g}}}_{0}({\xi },{\aleph })+{{\textbf {g}}}_{1}({\xi },{\aleph })+{{\textbf {g}}}_{2}({\xi },{\aleph })+\cdots ,\nonumber \\ {{\textbf {g}}}({\xi },{\aleph })= & {} {{\textbf {b}}}e^{\iota \xi }+\iota e^{\iota \xi }({{\textbf {a}}}+({{\textbf {a}}}^{2}-1){{\textbf {b}}})\left( \texttt {q}(\aleph -1)+1\right) -e^{\iota \xi }(2{{\textbf {b}}}+{{\textbf {a}}}^{4}{{\textbf {b}}}+{{\textbf {a}}}^{2}{{\textbf {b}}}(-4+{{\textbf {b}}}^{2})-{{\textbf {a}}}^{3}(-1+{{\textbf {b}}}^{2})\nonumber \\{} & {} +{{\textbf {a}}}(-2+3{{\textbf {b}}}^{2}))\Bigg ((1-\texttt {q})^{2}+2\texttt {q}(1-\texttt {q})\aleph +\frac{\texttt {q}^{2}\aleph ^2}{2}\Bigg )+\cdots . \end{aligned}$$
(69)

Application of \(NDM_{ABC}\)

Now, we will expand the functions \({{\textbf {f}}}(\xi ,\aleph )\) and \({{\textbf {g}}}(\xi ,\aleph )\) in series form as

$$\begin{aligned} {{\textbf {f}}}({\xi },{\aleph })=\sum _{{l}=0}^{\infty }{{\textbf {f}}}_{{l}}({\xi },{\aleph }),\quad {{\textbf {g}}}({\xi },{\aleph })=\sum _{{l}=0}^{\infty }{{\textbf {g}}}_{{l}}({\xi },{\aleph }). \end{aligned}$$
(70)

The nonlinear terms \({{\textbf {f}}}({{\textbf {g}}}\bar{{{\textbf {g}}}})=\sum _{{l}=0}^{\infty }\mathcal A_{{l}},{{\textbf {g}}}({{\textbf {f}}}\bar{{{\textbf {f}}}})=\sum _{{l}=0}^{\infty }\mathcal B_{{l}},\) in terms of Adomian polynomials are taken as follows:

$$\begin{aligned} \begin{aligned}{}&\sum _{{l}=0}^{\infty }{{\textbf {f}}}_{{l}+1}({\xi },{\aleph })=\Bigg [{{\textbf {a}}}e^{\iota \xi }\Bigg ]-\iota {\mathbb{N}\mathbb{T}}^{-1}\Bigg [\frac{\rho ^\texttt {q}(\varrho ^\texttt {q}+\texttt {q}(\rho ^\texttt {q}-{\varrho }^\texttt {q}))}{{\varrho }^{2\texttt {q}}}\mathbb{N}\mathbb{T}\Bigg \{\iota {{\textbf {f}}}_{\xi }+{{\textbf {g}}}+\sum _{{l}=0}^{\infty }{\mathcal {A}}_{{l}}\Bigg \}\Bigg ],\\&\sum _{{l}=0}^{\infty }{{\textbf {g}}}_{{l}+1}({\xi },{\aleph })=\Bigg [{{\textbf {b}}}e^{\iota \xi }\Bigg ]-\iota {\mathbb{N}\mathbb{T}}^{-1}\Bigg [\frac{\rho ^\texttt {q}(\varrho ^\texttt {q}+\texttt {q}(\rho ^\texttt {q}-{\varrho }^\texttt {q}))}{{\varrho }^{2\texttt {q}}}\mathbb{N}\mathbb{T}\Bigg \{\iota {{\textbf {g}}}_{\xi }+{{\textbf {f}}}+\sum _{{l}=0}^{\infty }{\mathcal {B}}_{{l}}\Bigg \}\Bigg ].\\ \end{aligned} \end{aligned}$$
(71)

Similarly,

$$\begin{aligned}{} & {} {{\textbf {f}}}_{0}({\xi },{\aleph })={{\textbf {a}}}e^{\iota \xi },\nonumber \\{} & {} {{\textbf {g}}}_{0}({\xi },{\aleph })={{\textbf {b}}}e^{\iota \xi },\nonumber \\{} & {} {{\textbf {f}}}_{1}({\xi },{\aleph })=\iota e^{\iota \xi }({{\textbf {b}}}+({{\textbf {b}}}^{2}-1){{\textbf {a}}})\left( 1-\texttt {q}+\frac{\texttt {q}\aleph ^\texttt {q}}{\Gamma (\texttt {q}+1)}\right) ,\nonumber \\{} & {} {{\textbf {g}}}_{1}({\xi },{\aleph })=\iota e^{\iota \xi }({{\textbf {a}}}+({{\textbf {a}}}^{2}-1){{\textbf {b}}})\left( 1-\texttt {q}+\frac{\texttt {q}\aleph ^\texttt {q}}{\Gamma (\texttt {q}+1)}\right) , \end{aligned}$$
(72)
$$\begin{aligned}{} & {} {{\textbf {f}}}_{2}({\xi },{\aleph })=-e^{\iota \xi }({{\textbf {a}}}^{3}{{\textbf {b}}}^{2}-{{\textbf {a}}}^{2}{{\textbf {b}}}(-3+{{\textbf {b}}}^{2})+{{\textbf {b}}}(-2+{{\textbf {b}}}^{2})+{{\textbf {a}}}(2-4{{\textbf {b}}}^{2}+{{\textbf {b}}}^{4}))\Bigg [\frac{\texttt {q}^{2}\aleph ^{2\texttt {q}}}{\Gamma (2\texttt {q}+1)}+2\texttt {q}(1-\texttt {q})\nonumber \\{} & {} \quad \frac{\aleph ^{\texttt {q}}}{\Gamma (\texttt {q}+1)}+(1-\texttt {q})^{2}\Bigg ],\nonumber \\{} & {} {{\textbf {g}}}_{2}({\xi },{\aleph })=-e^{\iota \xi }(2{{\textbf {b}}}+{{\textbf {a}}}^{4}{{\textbf {b}}}+{{\textbf {a}}}^{2}{{\textbf {b}}}(-4+{{\textbf {b}}}^{2})-{{\textbf {a}}}^{3}(-1+{{\textbf {b}}}^{2})+{{\textbf {a}}}(-2+3{{\textbf {b}}}^{2}))\Bigg [\frac{\texttt {q}^{2}\aleph ^{2\texttt {q}}}{\Gamma (2\texttt {q}+1)}+2\texttt {q}(1-\texttt {q})\nonumber \\{} & {} \quad \frac{\aleph ^{\texttt {q}}}{\Gamma (\texttt {q}+1)}+(1-\texttt {q})^{2}\Bigg ]. \end{aligned}$$
(73)

Lastly, it can be continued to the following series:

$$\begin{aligned} {{\textbf {f}}}({\xi },{\aleph })= & {} \sum _{{l}=0}^{\infty }{{\textbf {f}}}_{{l}}({\xi },{\aleph })={{\textbf {f}}}_{0}({\xi },{\aleph })+{{\textbf {f}}}_{1}({\xi },{\aleph })+{{\textbf {f}}}_{2}({\xi },{\aleph })+\cdots ,\nonumber \\ {{\textbf {f}}}({\xi },{\aleph })= & {} {{\textbf {a}}}e^{\iota \xi }+\iota e^{\iota \xi }({{\textbf {b}}}+({{\textbf {b}}}^{2}-1){{\textbf {a}}})\left( 1-\texttt {q}+\frac{\texttt {q}\aleph ^\texttt {q}}{\Gamma (\texttt {q}+1)}\right) -e^{\iota \xi }({{\textbf {a}}}^{3}{{\textbf {b}}}^{2}-{{\textbf {a}}}^{2}{{\textbf {b}}}(-3+{{\textbf {b}}}^{2})+{{\textbf {b}}}(-2+{{\textbf {b}}}^{2})\nonumber \\{} & {} {{\textbf {a}}}(2-4{{\textbf {b}}}^{2}+{{\textbf {b}}}^{4}))\Bigg [\frac{\texttt {q}^{2}\aleph ^{2\texttt {q}}}{\Gamma (2\texttt {q}+1)}+2\texttt {q}(1-\texttt {q})\frac{\aleph ^{\texttt {q}}}{\Gamma (\texttt {q}+1)}+(1-\texttt {q})^{2}\Bigg ]+\cdots . \end{aligned}$$
(74)
$$\begin{aligned} {{\textbf {g}}}({\xi },{\aleph })= & {} \sum _{{l}=0}^{\infty }{{\textbf {g}}}_{{l}}({\xi },{\aleph })={{\textbf {g}}}_{0}({\xi },{\aleph })+{{\textbf {g}}}_{1}({\xi },{\aleph })+{{\textbf {g}}}_{2}({\xi },{\aleph })+\cdots ,\nonumber \\ {{\textbf {g}}}({\xi },{\aleph })= & {} {{\textbf {b}}}e^{\iota \xi }+\iota e^{\iota \xi }({{\textbf {a}}}+({{\textbf {a}}}^{2}-1){{\textbf {b}}})\left( 1-\texttt {q}+\frac{\texttt {q}\aleph ^\texttt {q}}{\Gamma (\texttt {q}+1)}\right) -e^{\iota \xi }(2{{\textbf {b}}}+{{\textbf {a}}}^{4}{{\textbf {b}}}+{{\textbf {a}}}^{2}{{\textbf {b}}}(-4+{{\textbf {b}}}^{2})-{{\textbf {a}}}^{3}(-1+{{\textbf {b}}}^{2})\nonumber \\{} & {} +{{\textbf {a}}}(-2+3{{\textbf {b}}}^{2}))\Bigg [\frac{\texttt {q}^{2}\aleph ^{2\texttt {q}}}{\Gamma (2\texttt {q}+1)}+2\texttt {q}(1-\texttt {q})\frac{\aleph ^{\texttt {q}}}{\Gamma (\texttt {q}+1)}+(1-\texttt {q})^{2}\Bigg ]+\cdots . \end{aligned}$$
(75)
Figure 3
figure 3

Graphical depicts of the approximate solution for \({{\textbf {f}}}({\xi },{\aleph })\) of example 2 in 3D with respect to contour for \({{\textbf {a}}}=1.3,{{\textbf {b}}}=1\) and \(\texttt {q}=1.\) (a) Real surface, (b) Real contour, (c) Imaginary surface and (d) Imaginary contour.

Full size image
Figure 4
figure 4

Graphical depicts of the approximate solution for \({{\textbf {g}}}({\xi },{\aleph })\) of example 2 in 3D with respect to contour for \({{\textbf {a}}}=1.3,{{\textbf {b}}}=1\) and \(\texttt {q}=1.\) (a) Real surface, (b) Real contour, (c) Imaginary surface and (d) Imaginary contour.

Full size image
Figure 5
figure 5

Graphical depicts of the approximate solution for \({{\textbf {f}}}({\xi },{\aleph })\) of example 2 in 2D at various \(\texttt {q}\) orders (a) Real part, (b) Imaginary part.

Full size image
Figure 6
figure 6

Graphical depicts of the approximate solution for \({{\textbf {g}}}({\xi },{\aleph })\) of example 2 in 2D at various \(\texttt {q}\) orders (a) Real part, (b) Imaginary part.

Full size image

Physical interpretation of results

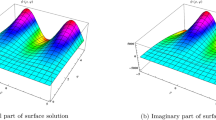
The approximate analytical solution for the FKE equation and FMT model is presented in this part of the article. Here, we use NTDM to solve complex nonlinear issues that arise in quantum field theory. The method’s applicability is demonstrated by the numerical findings, and its accuracy is evaluated by comparing it to exact and numerical solutions found in the literature. The outcomes of applying our strategy demonstrate good performance and simple results implementation. Tables 1 and 2 present the evaluation of the error. The comparison demonstrates that our results are more precise than those obtained using the literature’s techniques. We compare the absolute errors of our method with the existing q-HATM results, which are shown in Table 2. These tables demonstrate that the existing method provides a good approximation solution for the given problems. In reality, the outcomes displayed in these tables support the effectiveness of the suggested strategy. Tables indicate that the provided approach appears to be more accurate. We also show that the repetitions improve the NTDM findings, giving them access to the numerical solutions. We used MAPLE 15 to display the numerical analysis as graphs. The real part for the obtained results and the nature of the imaginary part in contour plots have been immersed in Fig. 1 at \(\texttt {q}=1\) for the FKE equation. Fig. 2 displays the 2-dimensional behaviour of the NTDM result for Eq. (41) of the real and imagionary part with various values of fractional order \(\texttt {q}\). When examining the nonlinear Schrödinger equation counterpart, these kinds of studies can impact researchers’ capacity to investigate physical phenomena of the single humped self-localized soliton type solution of the FKE equation. The FKE equation self-localized soliton system is more sensitive than the nonlinear Schrödinger equation; that is, its saturation efficiency is produced with a broadening contour that can be assessed using a mainlobe thickness. This is to be expected as the quintic nonlinear component in the FKE causes complex physical nonlinearity in the outputs. We use NTDM to help us find the solution to the coupled fractional nonlinear differential equations that describe the massive Thirring model. In particular, the model’s complexity is rather great, and it’s crucial to look at how its physical interpretation with matching parameters is captured. Plotting the nature of the imaginary part in contour plots and surfaces real part for the fractional-order MR model findings is carried out at \(\texttt {q}=1\) in Figs. 3 and 4. The 2-dimensional representation of exact and approximate solutions for the real and imagionary part of Eq. (58) at various fractional order \(\texttt {q}\) is depicted in Figs. 5 and 6. As we can see, the projected system is heavily dependent on the scheme’s and the fractional operator’s available parameters. More specifically, some interesting and realistic outcomes can be aided by the imaginary part’s nature in the form of counterplots.

Conclusion

In this work, we used FNDM to obtain the solution for the projected nonlinear complex system that serves as an example of the enormous Thirring model that arises in quantum field theory and the fractional Kundu-Eckhaus equation. In particular, the projected system’s more intriguing effects are understood by providing coupled and counter surfaces. The proposed solution approach allows us to locate the solution for nonlinear models related with complex functions without perturbation or dissertation. The novelty of the scheme under consideration is cleared away to study coupled systems. The obtained plots help us comprehend the effects of the projected model by demonstrating the large differences that occur with even a slight alteration in the system’s order. As the current study shows, the system under consideration is highly dependent on time and equivalent effects with fractional order. In addition, it can assist in solving many classes of coupled nonlinear and complicated differential equations. Our findings demonstrate the superior performance of this method in locating the analytical solution for the coupled fractional Massive Thirring and fractional Kundu-Eckhaus equations. Lastly, the algorithm under consideration provides results which are interesting, therefore it can be used to study and investigate a variety of complex phenomena. The non-local and non-singular kernel characteristics of the suggested derivatives are essential for describing the key components and dynamic behaviour of complex issues. Thus, academics can address a variety of dynamically complex issues by employing the CF and ABC derivatives. As a future research direction, readers might combine hybrid approaches with our suggested schemes to achieve better results. We expect that further fractional differential issues in science and engineering can be quickly and effectively solved using this approach in the future.