Quantitative classification evaluation model for tight sandstone reservoirs based on machine learning

Abstract

Tight sandstone reservoirs are a primary focus of research on the geological exploration of petroleum. However, many reservoir classification criteria are of limited applicability due to the inherent strong heterogeneity and complex micropore structure of tight sandstone reservoirs. This investigation focused on the Chang 8 tight reservoir situated in the Jiyuan region of the Ordos Basin. High-pressure mercury intrusion experiments, casting thin sections, and scanning electron microscopy experiments were conducted. Image recognition technology was used to extract the pore shape parameters of each sample. Based on the above, through grey relational analysis (GRA), analytic hierarchy process (AHP), entropy weight method (EWM) and comprehensive weight method, the relationship index Q1 between initial productivity and high pressure mercury injection parameters and the relationship index Q2 between initial productivity and pore shape parameters are obtained by fitting. Then a dual-coupled comprehensive quantitative classification prediction model for tight sandstone reservoirs was developed based on pore structure and shape parameters. A quantitative classification study was conducted on the target reservoir, analyzing the correlation between reservoir quality and pore structure and shape parameters, leading to the proposal of favourable exploration areas. The research results showed that when Q1 ≥ 0.5 and Q2 ≥ 0.5, the reservoir was classified as type I. When Q1 > 0.7 and Q2 > 0.57, it was classified as type I₁, indicating a high-yield reservoir. When 0.32 < Q1 < 0.47 and 0.44 < Q2 < 0.56, was classified as type II. When 0.1 < Q1 < 0.32 and 0.3 < Q2 < 0.44, it was classified as type III. Type I reservoirs exhibit a zigzag pattern in the northwest part of the study area. Thus, the northwest should be prioritized in actual exploration and development. Additionally, the initial productivity of tight sandstone reservoirs showed a positive correlation with the porosity, permeability, sorting coefficient, coefficient of variation, and median radius. Conversely, it demonstrated a negative correlation with the median pressure and displacement pressure. The perimeters of pores, their circularity, and the length of the major axis showed a positive correlation with the porosity, permeability, sorting coefficient, coefficient of variation, and median radius. On the other hand, they exhibited a negative correlation with the median pressure and displacement pressure. This study quantitatively constructed a new classification and evaluation system for tight sandstone reservoirs from the perspective of microscopic pore structure, achieving an overall model accuracy of 93.3%. This model effectively predicts and evaluates tight sandstone reservoirs. It provides new guidance for identifying favorable areas in the study region and other tight sandstone reservoirs.

Introduction

With the depletion of conventional oil and gas reservoirs, tight oil reservoirs have gradually become a hot topic and a focal point for exploration and development, both domestically and internationally^{1,2,3,4,5,6,7,8,9}. However, tight sandstone oil reservoirs exhibit complex reservoir characteristics, primarily manifested in their deep burial depths, wide distribution, and complex depositional processes. The reservoirs exhibit characteristics of low porosity, poor permeability, and high heterogeneity. The dominant pores are micro- and nano-scale, with narrow and dispersed throats, and are unfavorable for the migration and accumulation of oil and gas^{10,11,12,13,14,15}. These factors necessitate considering the interdependent influences of multiple factors when classifying and evaluating tight sandstone reservoirs, which affects the accuracy of reservoir evaluation and hinders the selection of high-quality reservoirs. Therefore, the rapid and effective classification and evaluation of tight sandstone reservoirs has long been a focal point of scholarly research.

The quality of the reservoir is a key factor that determines the oil and gas production capacity. The classification and evaluation of reservoirs are central to reservoir studies and play a significant role in oilfield development. With the continuous advancement of oilfield development technologies, reservoir classification and evaluation methods have become increasingly diverse, gradually evolving from qualitative to quantitative research and from macro-parameter to micro-parameter evaluation. At present, both domestic and international scholars classify reservoirs using two main methods. The first is the traditional classification and evaluation method, which directly uses indicators such as the lithology, physical properties, pore structure, sedimentary facies, and oil and production experiments for classification. For example, Wei et al. classified the tight sandstone reservoirs of the Sha Creek Formation in the central Sichuan Basin based on the transverse relaxation (T₂) distribution of nuclear magnetic resonance¹⁶. Xu et al. studied the characteristics and controlling factors of tight sandstone using thin-section casting, scanning electron microscopy, X-ray diffraction (XRD), and spontaneous imbibition experiments¹⁷. Wu et al. analyzed the logging response characteristics using core data and electric imaging logging data and identified the reservoir type with the highest industrial production in the study area¹⁸. Zhang et al. established classification criteria for the third member of the Quan Formation based on mercury injection curves, core physical properties, and sedimentary facies characteristics¹⁹. Talib et al. quantitatively characterized tight oil and gas reservoirs through rock physics experiments and seismic inversion profiles²⁰.

The second approach to reservoir classification involves initially choosing evaluation parameters that align with the geological conditions of the target area. Subsequently, machine learning techniques such as GRA the AHP, the EWM, and fuzzy analysis are employed to assign weight coefficients to each evaluation parameter. Finally, the reservoir is comprehensively scored. For example, Fang et al. proposed an automatic classification and verification method for reservoir types based on k-means clustering and Bayesian discriminant theory, using core logging and logging data from coring wells, combined with physical characteristics such as reservoir deposition and diagenesis²¹. Li et al. classified the Fuyu reservoir using GRA, Q clustering analysis, and discriminant analysis²². Wang et al.combined AHP and EWM, used the multi-factor superposition method, and established a new reservoir classification and evaluation method²³. Fan et al. quantified the weight of evaluation parameters’ contribution to production by combining the relationships between variables and directional good production using the GRA²⁴. Niu et al. proposed a new machine learning framework (GCA-CE-MGPK) for shale reservoirs, achieving efficient and accurate multi-scale evaluation of shale reservoirs²⁵. In summary, traditional classification and evaluation methods are costly, inefficient and require extensive experimental data. They are mainly suitable for specific regions, making them inadequate for large-scale reservoir evaluation and prediction. Although machine learning techniques can improve efficiency and reduce costs, their accuracy often depends on the optimization of various mathematical methods, leading to high subjectivity in some models and lower overall precision, failing to meet the practical needs of production. Moreover, previous studies have primarily focused on evaluating single factors, lacking the integration of macro and micro perspectives. Based on these, this study combined multiple machine learning methods to directly link actual oilfield production data with micro-scale pore shape and structure parameters, effectively integrating macro and micro parameters.

Given the significant influence of subjective factors on the classification criteria for the quantitative evaluation of conventional reservoirs, adopting a new method for reservoir evaluation is essential. This study focuses on the Chang 8 tight sandstone reservoir in the Jiyuan area of the Ordos Basin, extracting pore shape parameters from 52 rock samples. Combined with the experimental data of high pressure mercury injection and the actual initial production capacity of the oil field. Through GRA, AHP, EWM and comprehensive weight method, the relationship index Q1 between initial productivity and high pressure mercury injection parameters and the relationship index Q2 between initial productivity and pore shape parameters are obtained by fitting. Then a dual-coupled comprehensive quantitative classification prediction model for tight sandstone reservoirs was developed based on pore structure and shape parameters. A quantitative classification study was conducted on the target reservoir, analyzing the correlation between reservoir quality and pore structure and shape parameters, leading to the proposal of favourable exploration areas. This method effectively combined the subjectivity-influenced AHP with the objectivity-influenced EWM to calculate the comprehensive weight coefficient, mitigating the impact of subjective factors and enhancing the model's accuracy. Validation results indicate that the model has an overall accuracy of 93.3%. Therefore, it was an effective tool for predicting and classifying tight sandstone reservoirs. It is significant for further exploration in the study area and other similar reservoirs.

Geological setting

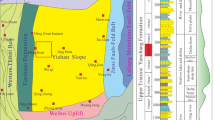
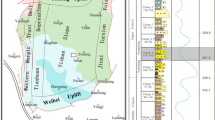
The Ordos Basin is a large, multi-cycle, cratonic basin that formed on the crystalline basement during the Paleoproterozoic–Mesoproterozoic. The Ordos Basin, the second-largest sedimentary basin in China, has experienced five significant stages of sedimentary evolution. These stages include the middle to late Proterozoic rift valley, the early Paleozoic shallow marine platform, the late Paleozoic nearshore plain, the Mesozoic inland lake basin, and Cenozoic peripheral subsidence. This basin is known for its substantial reserves of oil and gas. The Ordos Basin extends across five provinces and regions, namely, Shaanxi, Gansu, Shanxi, Ningxia, and Inner Mongolia. Geographically, it stretches from the Yin Mountains in the north to the Qinling Mountains in the south, and from the Liupan Mountains in the west to the Lvliang Mountains in the east. The basin’s total area is 25 × 10⁴ km², with favorable areas covering 9.9 × 10⁴ km². The estimated resource volume is 6.2 × 10¹² m³, indicating significant exploration and development potential. Based on the basin’s geological nature, tectonic evolution, and structural pattern, the Ordos Basin can be divided into six primary tectonic units: the northern Shaanxi slope, the Tianhuan Depression, the western thrust fault zone, the Yimeng Uplift, the Weihebei Uplift, and the western Shanxi fold belt. The Jiyuan area, located in the central-western part of the Ordos Basin, covers a total area of 1302 km² (Fig. 1a, c). This area spans the two primary tectonic units of the northern Shaanxi slope and the Tianhuan Depression, exhibiting a gently inclined monocline structure towards the west. Since the Mesozoic, the basin has developed thick fluvio-lacustrine deposits. In the Cenozoic, rift valleys were formed around the basin due to fault subsidence. The overall geological conditions are relatively complex, posing challenges for exploration. However, the area is rich in oil and gas resources, indicating favourable exploration prospects^26,27,28,29. The proven petroleum geological reserves in this area amount to 800 × 10⁶ t, with annual crude oil production of 700 × 10⁴ t, making it the oilfield with the largest reserves and production levels in the Ordos Basin from the Mesozoic. Existing exploration results indicate that the Chang 8 oil-bearing formation is one of the most favourable hydrocarbon accumulation zones in the Jiyuan area, with a proven favourable oil-bearing area of 1500 km².

Fig. 1

(a) Location of the study area(modified from Tong²⁹), (b) columnar diagram of the Chang 8 formation, (c) well location distribution map of the study area.

The Chang 8 reservoir is located in the lower part of the Upper Triassic Yan’an Formation. It is primarily composed of grey sandstone and dark black mudstone interbeds. These sedimentary microfacies are predominantly characterized by subaqueous distributary channels and underwater distributary bays, indicating a deposition pattern typical of a shallow-water deltaic environment (Fig. 1b). Based on the thin-section identification of the study area (Fig. 2), the lithology of the Chang 8 reservoir is predominantly composed of fine-grained feldspathic sandstone, feldspathic lithic sandstone, and a small amount of feldspar sandstone. The detrital components in the study area mainly consist of quartz, feldspar, and detritus. The ranges of contents are as follows: the quartz content is 20.1% to 58.6%, with an average of 31.21%; the feldspar content is 23.56% to 57.62%, with an average of 34.43%; and the detritus content is 6.25% to 29.45%, with an average of 21.38%.

Fig. 2

Triangular diagram and detrital composition diagram of the study area. (a) Triangular classification diagram of the sandstone in the Chang 8 reservoir, (b) histogram of the relative content of detrital components in the Chang 8 reservoir.

Materials and statistical methods

Materials and experiments

Materials

In this study, 52 drilling core samples were obtained from the Chang 8 reservoir in Jiyuan, Ordos Basin, with all samples exhibiting a fine sandstone lithology. The samples underwent oil washing, gas permeability measurements, and the weight method for porosity calculation, allowing the determination of the reservoir’s petrophysical parameters (Table 1). The samples' average porosity was 8.23%, between 2.41 and 13.6%. The average permeability was 0.18 × 10^–3 µm², ranging between 0.01 × 10^–3 µm² and 1.10 × 10^–3 µm². Subsequently, thin-section casting and scanning electron microscopy experiments were conducted, resulting in 300 photographs. Additionally, high-pressure mercury intrusion was performed on the 52 samples to obtain the micropore throat characteristic parameters.

Table 1 Petrophysical parameters of the experimental samples.

High pressure mercury intrusion and scanning electron microscopy

High pressure mercury intrusion experiment was used to evaluate the micropore throat characteristics of reservoirs quantitatively. This is achieved by observing the pressure changes during mercury injection into the pores, analyzing the characteristics of the capillary pressure curves, and studying the relationship between the intrusion volume of mercury and these characteristics^30,31. In this experiment, the Auto Pore IV 9530 fully automated mercury porosimeter was utilized, with a pore diameter measurement range of 3 nm to 1100 μm. Continuous mercury injection was employed, with volume accuracy of less than 0.1 μl for both injection and withdrawal. The experimental procedure followed the national standard GB/T29171-2012, and the maximum mercury injection pressure reached 95.39 MPa.

Scanning electron microscopy (SEM) allows for high-resolution morphological observation and analysis of samples, as well as structural and compositional characterization. It also enables direct observation of the development characteristics of the micro-pore throats in the reservoir^32,33,34. The experiment employed the Japanese Electron JSM-7500F field emission scanning electron microscope, which achieves a secondary-electron image resolution of 1 nm and magnification ranging from 20 to 300,000 times.

Pore parameter extraction technology

The ImageJ software, initially developed by Wayne Rasband at the National Institutes of Health in the United States, is a powerful open-source image processing system written in Java. It was initially applied in the fields of biomedical and agricultural sciences³⁵. Recently, an increasing number of scholars have used it to identify and extract reservoir pores and fracture features^36,37,38,39. In this study, the ImageJ software was used to process 210 scanning electron microscope images, extracting various pore parameters, including the perimeter, circularity, major axis length, aspect ratio, and solidity.

Statistical methodology

GRA

GRA is to address infinite space problems using finite sequences. It aims to evaluate the correlations between various factors within a system and determine the significance of each factor to the target function. This approach helps to avoid the subjective process of manually assigning weights to factor indicators⁴⁰. In recent years, GRA has been applied in production forecasting and development plan optimization for tight sandstone reservoirs^41,42,43,44. The specific steps are as follows.

• (1) Determine the initial sequence:

  $$X_{0} = \{ X_{0} {(1),}\quad X_{0} {(2)}\quad {,} \ldots ,\quad X_{0} {\text{(n)}}\} ,$$

  (1)
  $$X_{i} = \{ X_{i} {(1),}\quad X_{i} {(2)}\quad {,} \ldots ,\quad X_{i} {\text{(n)}}\} ,\quad (i = {1,2,} \ldots ,{\text{m),}}$$

  (2)

  where X₀ is the reference sequence, X_i is the comparative sequence, i is the number of comparative sequences, m is the number of independent variables, and n is the number of samples.

• (2) Normalize the data using the extreme value method:

  $$\overline{{X_{i} }} (k) = \frac{{X_{i} (k) - \min \left[ {X_{i} (k)} \right]}}{{\max \left[ {X_{i} (k)} \right] - \min \left[ {X_{i} (k)} \right]}}\quad ({\text{i}} = {1},{2},{3} \ldots ,{\text{m}};{\text{ k}} = {1},{2},{3}, \ldots ,{\text{n}})$$

  (3)

• (3) Calculate the gray correlation coefficient:

  $$\gamma (x_{0} (k),x_{i} (k)) = \frac{\Delta \min + \rho \Delta \max }{{\Delta_{ik} + \rho \Delta \max }}$$

  (4)
  $$\Delta \min = \min_{i} \min_{k} \left| {x_{0} (k) - x_{i} (k)} \right|$$

  (5)
  $$\Delta \max = \max_{i} \max_{k} \left| {x_{0} (k) - x_{i} (k)} \right|$$

  (6)
  $$\Delta_{ik} = |x_{0} (k) - x_{i} (k)|$$

  (7)

  Obtain the gray correlation coefficient matrix:

  $$\left[ {\begin{array}{*{20}c} {\gamma_{01} (1)} & {\gamma_{02} (1)} & \cdots & {\gamma_{0m} (1)} \\ {\gamma_{01} (2)} & {\gamma_{02} (2)} & \cdots & {\gamma_{0m} (2)} \\ \vdots & \vdots & \vdots & \vdots \\ {\gamma_{01} (n)} & {\gamma_{02} (n)} & \cdots & {\gamma_{0m} (n)} \\ \end{array} } \right]$$

  (8)

  where ρ is the resolution coefficient, which takes values between 0 and 1. A smaller resolution coefficient indicates greater differences between the correlation coefficients and stronger discriminatory power. Usually, ρ is set to 0.5.

• (4) Determine the correlation degree. Represent the correlation strength between the series using the average of the n correlation coefficients:

  $$\mathop \varepsilon \nolimits_{{\mathop o\nolimits_{i} }} = \frac{1}{n}\sum\limits_{k = 1}^{n} {\mathop \gamma \nolimits_{{\mathop o\nolimits_{i} }} (K)}$$

  (9)

  where $\mathop \varepsilon \nolimits_{{\mathop o\nolimits_{i} }}$ represents the correlation degree between the i-th comparative sequence and the reference sequence.

• (5) Determine the weights and rank the correlation degrees. Normalize the correlation degrees to obtain the weight W_i of each comparative sequence:

  $$W_{i} = \frac{{\varepsilon_{0i} }}{{\sum\limits_{i = 1}^{m} {\varepsilon_{0i} } }}$$

  (10)

AHP

AHP is a methodology that categorizes the factors within a complex problem into interconnected and prioritized levels. This approach facilitates the process of making decisions based on multiple criteria. It is primarily used to determine the weighting coefficients for comprehensive evaluations^45,46,47. The process is as follows.

• (1) Construction of a judgment matrix: a judgment matrix is constructed to compare the importance of different factors:

  $${\text{AW}} = \lambda_{{{\text{max}}}} {\text{W}}$$

  (11)

  where A is the matrix of pairwise comparisons, W is the weight vector, and λ_max is the maximum eigenvalue.

• (2) Calculation of weights: the weight vector W is determined using the sum-product method.

• (3) Consistency check:

  $$I_{c} = \frac{{\lambda_{\max } - n}}{n - 1}$$

  (12)
  $$\mathop I\nolimits_{R} = \frac{{\lambda^{\prime } \max - n}}{n - 1}$$

  (13)
  $$I_{cR} = \frac{{I_{c} }}{{I_{R} }}$$

  (14)

  where n is the number of elements, I_c is the consistency index, I_R is the random consistency index, I_cR is the consistency ratio, and $\lambda^{\prime } \max$ is the average of the maximum eigenvalues.

  If I_cR < 0.10, the consistency of the judgment matrix is considered acceptable.

EWM

EWM is an objective weighting approach that comprehensively examines the underlying patterns and informational value of unprocessed data. It can determine the uncertainty in variables through entropy values, where larger information content corresponds to smaller uncertainty and smaller entropy, and vice versa. The entropy weighting method is characterized by high accuracy and strong objectivity, and many scholars have applied it to oilfield production with good results ^48,49. The basic steps are as follows.

• (1) Normalize the data and calculate the information entropy:

  $$E_{i} = - \sum\limits_{j = 1}^{N} {\frac{{X_{ij} \log_{2} X_{ij} }}{{\log_{2} N}}}$$

  (15)

  where E_i is the information entropy of the ith indicator, X_ij is the value of the ith indicator on the jth sample, and N is the number of samples.

• (2) Calculate the weights:

  $$W_{i} = \frac{{1 - E_{i} }}{{\sum\limits_{j = 1}^{M} {(1 - E_{j} )} }}$$

  (16)

  where W_i is the weight of the ith indicator, E_i is the information entropy of the ith indicator, and M is the number of indicators.

Comprehensive weight coefficient

Weight coefficients can be used to classify and evaluate the reservoir quality effectively, and several methods are currently available to determine the weight coefficients. These include GRA, the expert evaluation method, Q clustering analysis and discriminant analysis, and factor analysis^50,51,52. In this research, a comprehensive weight analysis methodology that integrated AHP and EWM was employed. The key advantage of this approach lies in its amalgamation of the subjective AHP analysis and the objective numerical analysis of EWM. This combination helps to mitigate the influence of subjective factors to a certain extent, thereby enhancing the reliability of the data.

$$w_{{\text{ comprehensive}}} = \frac{{w_{{i{\text{AHP}}}} \times w_{{i{\text{EWM}}}} }}{{\sum\limits_{i = 1}^{m} {w_{{i{\text{AHP }} \times }} } w_{{i{\text{EWM}}}} }}$$

(17)

where W_iAHP is the weight coefficient obtained from the AHP method, and W_iEWM is the weight coefficient obtained from the EWM method.

Results and discussion

Evaluation parameter selection

Tight sandstone reservoirs are influenced by deposition, tectonics, and diagenesis.. These reservoirs demonstrate significant heterogeneity and an intricate distribution of micropore throats. The pore structure plays a crucial role in governing the storage and flow behaviour of the reservoir, where the different shape parameters of the pores govern the micropore structure of the rock formation^{53,54,55,56,57}. Considering the characteristics above, this study aimed to provide a quantitative characterization of the reservoir by assessing three key aspects: the pore structure, the physical properties, and the pore shape parameters. Twelve parameters were selected to establish the relationship between the initial production capacity index and the pore structure and shape parameters. The actual initial production capacity of the oilfield was used as the indicator.

Sensitivity parameter selection for pore structure characteristics

The selected 52 samples were subjected to high-pressure mercury intrusion experiments using an Auto Pore IV 9530 automatic mercury porosimeter. The sorting coefficient varied between 1.5 and 2.74, with an average of 2.10. The coefficient of variation ranged between 13.94 and 17.32, with a mean value of 15.54. With an average value of 13.86 MPa, the median pressure varied between 10.5 and 18.79 MPa. The average displacement pressure was 1.23 MPa, ranging between 0.09 and 2.57 MPa. The median radius had a mean value of 0.09 μm and varied from 0.05 to 0.15 μm. With a mean value of 84.52%, the maximum mercury saturation varied from 62.77 to 93.76%. With an average of 34.90%, the mercury withdrawal efficiency varied between 16.7 and 46.6%. Overall, the pore structure of the reservoir in the study area was poor, with uneven sorting and poor connectivity among the pore throats, indicating strong heterogeneity. Correlation analysis was conducted on the initial production and mercury intrusion parameters (Fig. 3), and it was found that the correlation between the production capacity and permeability and porosity was the strongest, with correlation coefficients (R²) of 0.91 and 0.75, respectively. This is mainly because porosity plays a crucial role in determining the size of the pore space within a reservoir, while permeability governs its flow capacity. In the context of tight sandstone reservoirs, the reservoir quality often depends on favourable pore permeability. The sorting coefficient and coefficient of variation provide insights into the uniformity of the distribution of the pore throat sizes. Higher values of these parameters indicate an improved pore structure and increased reservoir productivity. The median radius and median pressure indicate the pore permeability of the reservoir. A larger median radius and smaller median pressure indicate a larger pore space and stronger flow capacity, resulting in a larger oil production capacity. Therefore, the median radius positively correlates with production, while the median pressure is inversely correlated. The displacement pressure is inversely correlated with production (R² = 0.65). This is because displacement pressure refers to the capillary pressure corresponding to the largest connected pore, and a higher displacement pressure means a higher capillary pressure, making it more difficult for fluid to flow through. This indicates that tight oil has poor flow capacity in the reservoir and is more difficult to accumulate and extract. In conclusion, the initial production capacity is sensitive to the porosity, permeability, sorting coefficient, coefficient of variation, median pressure, median radius, and displacement pressure.

Fig. 3

Relationship between initial production and porosity, permeability, selectivity coefficient, coefficient of variation, median pressure, median radius, and displacement pressure.

Selection of pore-shape-sensitive parameters

A total of 210 high-resolution SEM images were captured for the 52 samples. The rock core pores were identified and extracted using ImageJ, obtaining pore shape parameters such as the perimeter, circularity, major axis length, aspect ratio, and solidity (Fig. 4, Table 2). The average values of the identified pore shape parameters for each sample were then calculated. It was found that the pore perimeters of the 52 samples varied between 40.3 and 486.2 μm, with a mean value of 250.5 μm. The circularity ranged between 0.11 and 0.96, with a mean value of 0.31. The major axis lengths of the circumscribed ellipses spanned from 42.52 to 221.19 μm, with an average of 111.67 μm. The aspect ratios ranged from 1.14 to 2.92, and the average value was 2.32. The solidity values ranged between 0.09 and 0.89, with an average of 0.67. In general, the pore shape parameters of the tight sandstone reservoirs exhibited a wide range of variation, with relatively large average perimeters, average major axis lengths of the circumscribed ellipses, aspect ratios, and solidity, and with small average circularity (Fig. 5). This indicates that the pore shapes in tight sandstone are diverse, predominantly irregular and elongated, with few circular pores. Pearson correlation analysis was conducted between the most sensitive parameters for the prioritized pore structure characteristics and the extracted pore shape parameters (Fig. 6). The absolute value of the correlation coefficient always lies between −1 and 1. In this context, a value closer to 1 indicates a stronger positive relationship between the two independent variables, a value closer to -1 indicates a stronger negative relationship between the independent variables, and a value closer to 0 indicates a weak relationship between the variables. A significant and strong correlation (R² > 0.5) observed between the different shape parameters of the pores and the mercury injection parameters. This suggests that the shape parameters of the pores play a crucial role in determining the pore structures of tight sandstone reservoirs. In general, the perimeter, circularity, and major axis length of the pores displayed a positive correlation with the porosity (Φ), permeability (K), sorting coefficient (S_p), coefficient of variation (D_r), and median radius (R50). Conversely, they exhibited a negative correlation with the median pressure (P₅₀) and displacement pressure (Pd). On the other hand, the aspect ratio and solidity of the pores were inversely proportional to the porosity, permeability, sorting coefficient, coefficient of variation, and median radius. However, they were positively correlated with the median pressure and displacement pressure. Among them, there was a strong positive correlation (R² = 0.914) between the perimeter and porosity and a relatively strong negative correlation (R² = –0.766) with the displacement pressure. A larger pore perimeter results in a greater contact area between the reservoir fluid and the solid, facilitating fluid infiltration and storage. Circularity was strongly positively correlated with permeability (R² = 0.927) and negatively correlated with the displacement pressure (R² = –0.604). This is because larger circularity indicates a closer approximation to circular pores, which typically exhibit a uniform distribution, resulting in improved connectivity and fluid flow. The major axis length was strongly positively correlated with the permeability and porosity because the major axis length of the circumscribed ellipses of pores affects the connectivity and fluid flow path within the pores. A larger major axis length indicates better connectivity between pores, resulting in a more direct fluid flow path and higher permeability. Moreover, a longer major axis length corresponds to a larger pore size and higher porosity. The aspect ratio exhibited a strong negative correlation with the permeability and selectivity coefficient (R² = –0.866, R² = –0.754, respectively) and a strong positive correlation with the displacement pressure (R² = 0.652). As the aspect ratio increases, the pores become narrower and more uneven, resulting in longer and narrower flow channels, making fluid flow more difficult. As a result, the displacement pressure increases, the selectivity coefficient decreases, and the permeability decreases. Solidity exhibited a strong negative correlation with permeability (R² = –0.862) and a positive correlation with the displacement pressure (R² = 0.574). As the solidity increases, the pore shape becomes more concave, and the roundness deteriorates, making fluid flow between the pores more difficult. In conclusion, it can be observed that the perimeter, circularity, major axis of the circumscribed ellipse, aspect ratio, and solidity of the pores are sensitive to various parameters of mercury intrusion.

Fig. 4

Visualization of pore extraction results for rock samples. (A) Pore identification (sample no. 1), (B) pore extraction (sample no. 1), (C) pore identification (sample no. 10), (D) pore extraction (sample no. 10), (E) pore identification (sample no. 25), (F) pore extraction (sample no. 25).

Table 2 Extracted pore shape parameters.

Fig. 5

Distribution of pore shape parameters. (a) Distribution range of pore perimeter and major axis, (b) distribution range of pore circularity, solidity, and aspect ratio.

Fig. 6

Correlations between pore structural parameters and pore shape parameters.

Reservoir classification evaluation

Quantitative classification prediction formula

Based on the results of the GRA, AHP, and EWM, a comprehensive quantitative classification prediction formula was constructed using the superposition principle. This formula was then used to classify and evaluate tight sandstone reservoirs.

$${\text{Q}} = \sum\limits_{i = 1}^{n} {a_{i} } \cdot b_{i,N}$$

(18)

where Q is the productivity index, a_i is the dimensionless weight coefficients of various parameters, b_i,N is the dimensionless normalized parameters, and n is the number of parameters.

Determination of weight coefficients

In this study, the initial production rate directly reflecting the reservoir quality was taken as the fundamental sequence. Seven sensitive parameters, namely, the porosity, permeability, sorting coefficient, coefficient of variation, median pressure, median radius, and displacement pressure, were considered as sub-sequences. The principles and steps of GRA were employed to determine the weights of various parameters, thereby assessing the sensitivity of each factor to the initial production rate (Table 3). Combining the correlation degree between the sensitive parameters determined by the gray correlation method and the initial productivity. Then, the parameters were compared in pairs, and values were assigned based on the 9-point scale method. The judgment matrix was obtained by pairwise comparisons of the seven sensitive parameters (Table 4). Subsequently, the weight coefficients were determined using the weighted product method within the AHP (Table 5). Formula (14) shows that the judgment matrix I_cR = 0.093 is less than 0.1, meeting the consistency requirements. Subsequently, the EWM analysis method was employed to conduct an objective analysis of each sensitive parameter, resulting in objective weight indices. The comprehensive weight coefficients were calculated using Eq. (17) (Table 5). The formula for the initial productivity and the mercury intrusion sensitivity parameter can be obtained as follows:

$${\text{Q1}} = 0.{\text{228R}}_{{{5}0,{\text{N}}}} + 0.{\text{217K}}_{{\text{N}}} + 0.{191}\Phi_{{\text{N}}} + 0.{\text{143S}}_{{\text{p,N}}} + 0.{\text{116D}}_{{\text{r,N}}} + 0.0{\text{77P}}_{{{5}0,{\text{N}}}} + 0.0{\text{28P}}_{{\text{d,N}}}$$

(19)

where Φ_N is the normalized porosity, K_N is the normalized permeability, S_P,N is the normalized sorting coefficient, Dr,_N is the normalized coefficient of variation, P_50,N is the normalized median pressure, R_50,N is the normalized median radius, and P_d,N is the normalized displacement pressure.

Table 3 Correlation and ranking of factors with initial yield.

Table 4 Judgment matrix.

Table 5 Comprehensive weight coefficients for production capacity.

Then, using the mercury intrusion parameter as the fundamental sequence, five sensitive parameters related to the pore shape, namely, the perimeter, circularity, major axis length, aspect ratio, and solidity, were considered sub-sequences. The correlation between the mercury intrusion parameters and the pore-shape-sensitive parameters was determined using GRA. The comprehensive weight coefficients for each mercury intrusion parameter were calculated using a combination of the AHP and the EWM (Table 6). Based on these weight coefficients, the correlation formulas between each mercury intrusion parameter and the pore shape parameters were obtained as follows:

$$\Phi_{{\text{N}}} = 0.{\text{323C}}_{{\text{N}}} + 0.{3}0{\text{6M}}_{{\text{N}}} + 0.{\text{164P}}_{{\text{N}}} + 0.{1}0{\text{7A}}_{{\text{N}}} + 0.0{\text{98S}}_{{\text{N}}}$$

(20)

$${\text{K}}_{{\text{N}}} = 0.{\text{649C}}_{{\text{N}}} + 0.{\text{145P}}_{{\text{N}}} + 0.{\text{111M}}_{{\text{N}}} + 0.{1}0{\text{1S}}_{{\text{N}}} + 0.0{\text{94A}}_{{\text{N}}}$$

(21)

$${\text{S}}_{{{\text{P}},{\text{N}}}} = 0.{\text{332M}}_{{\text{N}}} + 0.{\text{247A}}_{{\text{N}}} + 0.{\text{176C}}_{{\text{N}}} + 0.{\text{126S}}_{{\text{N}}} + 0.{12}0{\text{P}}_{{\text{N}}}$$

(22)

$${\text{D}}_{{\text{r}}} ,_{{\text{N}}} = 0.{\text{378A}}_{{\text{N}}} + 0.{3}0{\text{1S}}_{{\text{N}}} + 0.{\text{139M}}_{{\text{N}}} + 0.{\text{113C}}_{{\text{N}}} + 0.0{\text{71P}}_{{\text{N}}}$$

(23)

$${\text{P}}_{{{5}0,{\text{N}}}} = 0.{\text{441A}}_{{\text{N}}} + 0.{25}0{\text{S}}_{{\text{N}}} + 0.{\text{136M}}_{{\text{N}}} + 0.{\text{127P}}_{{\text{N}}} + 0.0{\text{43C}}_{{\text{N}}}$$

(24)

$${\text{R}}_{{{5}0,{\text{N}}}} = 0.{\text{311M}}_{{\text{N}}} + 0.{\text{182P}}_{{\text{N}}} + 0.{\text{179C}}_{{\text{N}}} + 0.{\text{177A}}_{{\text{N}}} + 0.{15}0{\text{S}}_{{\text{N}}}$$

(25)

$${\text{P}}_{{{\text{d}},{\text{N}}}} = 0.{\text{419A}}_{{\text{N}}} + 0.{\text{272S}}_{{\text{N}}} + 0.{\text{156M}}_{{\text{N}}} + 0.0{\text{97P}}_{{\text{N}}} + 0.0{\text{54C}}_{{\text{N}}}$$

(26)

Table 6 Comprehensive weight coefficients for mercury pressure parameters.

Combined with Formula (19), the relationship between the initial productivity and pore shape parameters can be obtained:

$${\text{Q2}} = 0.{\text{286C}}_{{\text{N}}} + 0.{\text{231M}}_{{\text{N}}} + 0.{2}0{\text{6A}}_{{\text{N}}} + 0.{\text{147S}}_{{\text{N}}} + 0.{\text{13P}}_{{\text{N}}}$$

(27)

where P_N is the normalized perimeter, C_N is the normalized circularity, M_N is the normalized major axis, A_N is the normalized aspect ratio, and S_N is the normalized solidity.

Classification scheme and feature evaluation

Based on the indices Q1, which relate initial productivity to high-pressure mercury intrusion sensitivity parameters, and Q2, which relate initial productivity to pore shape parameters, a classification and evaluation scheme for the Chang 8 tight sandstone reservoir have been determined. As depicted in Fig. 7, Q1 for type III reservoirs ranges from 0.1 to 0.31, and Q2 ranges between 0.3 and 0.44. For type II reservoirs, Q1 ranges from 0.32 to 0.47, and Q2 ranges from 0.44 to 0.56. For type I reservoirs, Q1 ≥ 0.5 and Q2 ≥ 0.5. Moreover, type I reservoirs can be further divided into type I₁, comprising high-yield reservoirs, and type I₂, comprising high-quality reservoirs, with Q1 > 0.7 and Q2 > 0.57 indicating type I₁ high-yield reservoirs. Type I reservoirs are considered optimal for the Chang 8 formation, with 15 out of 52 samples belonging to this type, accounting for 28.8%. The characteristics associated with this type of reservoir include favourable pore permeability, featuring an average porosity of 11.1% and permeability of 0.4 × 10^–3 µm². Additionally, these reservoirs possess a low displacement pressure of 0.62 MPa, a low median pressure of 11.79 MPa, and a relatively high median radius of 0.12 µm. The reservoir exhibits good pore throat selectivity, characterized by a large sorting coefficient (2.5) and variation coefficient (16.43). The average pore perimeter of the reservoir is relatively long (360.30 µm), with good circularity (0.50) and a small aspect ratio (1.92). This indicates that the pore shape is more regular and almost circular. Generally, type II displays moderate petrophysical characteristics, characterized by an average porosity of 8.43% and permeability of 0.1 × 10^–3 µm². Within this classification, 19 samples contribute to 36.54% of the dataset. Compared to type I, this reservoir type has a somewhat higher average displacement pressure and median pressure (1.11 MPa and 13.48 MPa, respectively). The median radius is lower (0.10 µm), and the average sorting coefficient and coefficient of variation are 2.41 and 16.18, respectively, indicating moderate sorting. The average pore perimeter of this reservoir type is smaller than that of type I (261.61 µm), with smaller circularity (0.26) and a larger aspect ratio (2.41). Compared to type I, the pores of type II reservoirs exhibit irregular and more elongated shapes. Type III exhibits poorer petrophysical properties, with an average permeability of 0.06 × 10^–3 μm² and porosity of 5.7%, significantly lower than those of type I and type II. There were 18 samples belonging to this type, accounting for 34.62%. This reservoir type has an average displacement pressure of 1.89 MPa and a median pressure of 16.1 MPa, greater than type II. The median radius is the smallest (0.07 µm). The average sorting coefficient and coefficient of variation are 1.81 and 14.7, respectively, indicating poor pore throat sorting. The average pore perimeter is the smallest (147.37 µm), with the poorest circularity (0.19) and the largest aspect ratio (2.56). This indicates that the pores of type III reservoirs are more elongated and slender, making them unfavorable for fluid flow and leading to poor reservoir permeability. In summary, it can be observed that as the reservoir quality deteriorates, the pore structure becomes increasingly worse, and the pore shapes become more complex and variable.

Fig. 7

Comprehensive quantitative classification prediction model for the research area of the Chang 8 reservoir.

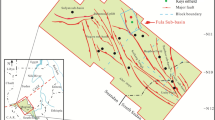
According to the distribution maps of the well locations and sedimentary microfacies (Figs. 1c, 8), it is observed that type I reservoir wells are mostly found in the northwest of the research region, within the subaqueous distributary channels, exhibiting a zigzag pattern. Most type II reservoir wells are located in the study area's centre, mainly within the middle portions of the subaqueous distributary channel's lateral sand bodies. On the other hand, the relatively poor type III reservoir wells are scattered around the type II reservoirs, with most of them located in the marginal areas adjacent to the interdistributary bay and the edge of the channel’s lateral sand bodies. Therefore, in practical exploration and development, the high-quality reservoirs (type I) in the study area's northwest part should be prioritised.

Fig. 8

Planar distribution map of comprehensive quantitative classification for the research area of the Chang 8 reservoir.

Additionally, the main reason for the high productivity of type I₁ reservoirs is the higher content of dissolved pores in type I reservoirs. According to Table 7 and Fig. 9, samples 3, 15, 16, and 20 from type I reservoirs exhibit significant development of feldspar dissolution pores, intergranular pores, and a small number of rock particles that dissolve pores. The average absolute contents of feldspar dissolution and intergranular pores are 1.2% and 5.15%, respectively. The average face rate is 0.8%, higher than the other samples. The greater the development of feldspar dissolution and intergranular pores, the larger the flow channels and storage space they provide, thus improving the reservoir’s porosity and permeability, resulting in high-productivity reservoirs. The pore shape parameters of samples 3, 15, 16, and 20 were compared with those of the other samples (Table 2). It was found that these four samples have longer pore perimeters and major axes, larger shape factor (roundness) coefficients, and relatively smaller aspect ratios and concavity. This indicates that high-productivity reservoirs (type I₁) have larger pore perimeters, an increased contact area between the pores and reservoir fluids, higher pore circularity, and more circular shapes favourable for fluid flow and storage. Furthermore, as shown in Fig. 8, the four high-productivity wells (JY-3, JY-15, JY-16, JY-20) are all located on the main channel of the subaqueous distributary channel. Therefore, from a macro perspective, thicker sand bodies may be another reason for their high productivity.

Table 7 Absolute porosity content of type I reservoir samples.

Fig. 9

Porosity structure of type I₁ reservoir. (A) Intergranular pores, developed dissolution pores (sample no. 3), (B) feldspar dissolution pores (sample no. 20), (C) rock fragment dissolution pores (sample no. 15), (D) intergranular pores, locally developed dissolution pores (sample no. 16).

Model validation

In order to verify the model, 15 coring wells in Jiyuan Chang 8 reservoir were selected. High-pressure mercury intrusion tests, scanning electron microscopy, and thin-section casting experiments were conducted on corresponding samples to extract the pore shape parameters. Next, the comprehensive indices Q1 and Q2, for reservoir categorization, were determined using the GRA, the AHP, and the EWM. Finally, the accuracy of the classification results was compared with that of the existing oil test parameters. As shown in Fig. 10, three wells were classified as type I reservoirs, with an average initial yield of 5.73 t/d. Six wells were classified as type II reservoirs, with an average initial yield lower than type I at 3.52 t/d. One well was misclassified, deviating from the expected value. Five wells were classified as type III reservoirs, with the lowest average initial yield of 1.32 t/d. The quantitative evaluation of the comprehensive parameters matched the actual production capacity results, demonstrating a high matching rate of 93.3%. Compared to conventional models by other scholars for tight sandstone reservoirs, this model establishes a direct connection between actual oilfield production data, microscale pore shape parameters, and pore structure parameters, leading to quantitative reservoir classification evaluation ^58,59,60. It demonstrates higher and more stable classification accuracy.

Fig. 10

Comparative analysis of the integrated quantitative classification prediction for the Chang 8 reservoir.

Conclusions

Tight sandstone reservoirs display significant heterogeneity and intricate microscopic pore structures, which impact the accuracy of reservoir assessment. This study employed scanning electron microscopy, thin section analysis, and high-pressure mercury intrusion data as samples. It utilized image recognition technology and machine learning methods to develop a novel classification and evaluation system for tight sandstone reservoirs based on microscopic pore structures. This method utilizes minimal experimental data, is cost-effective, demonstrates relatively high model accuracy, and is particularly suitable for tight sandstone reservoirs. The research conclusions are as follows:

• (1) By analyzing high pressure mercury parameters, scanning electron microscopy images, and thin sections of the study area in the Chang 8 reservoir, a comprehensive quantitative classification prediction model for tight sandstone reservoirs was established. The model was constructed using twelve sensitive parameters: porosity, permeability, sorting coefficient, coefficient of variation, median pressure, median radius, displacement pressure, pore perimeter, circularity, major axis length, aspect ratio, and solidity, all extracted using image recognition technology.

• (2) The case study based on the comprehensive quantitative classification prediction model showed that Q1 ≥ 0.5 and Q2 ≥ 0.5 corresponded to type I reservoirs, while Q1 > 0.7 and Q2 > 0.57 corresponded to type I₁ high-yield reservoirs. When 0.32 < Q1 < 0.47 and 0.44 < Q2 < 0.56, a type II reservoir was identified. When 0.1 < Q1 < 0.32 and 0.3 < Q2 < 0.44, a type III reservoir was identified. Additionally, the presence of high-content dissolution pores, intergranular pores, and larger pore perimeters, as well as higher pore circularity, were the main factors contributing to high-yield reservoirs (type I₁). The model was validated, achieving an overall accuracy of 93.3%, which indicates its effectiveness in predicting the classification and evaluation of tight reservoirs.

• (3) Reservoir quality is influenced by the pore structure characteristics and shape parameters. In tight sandstone reservoirs, the productivity is positively correlated with the porosity, permeability, sorting coefficient, coefficient of variation, and median radius, but negatively correlated with the median pressure and displacement pressure. The perimeter, circularity, and major axis length of the pores are positively correlated with the porosity, permeability, sorting coefficient, coefficient of variation, and median radius, but negatively correlated with the median pressure and displacement pressure.

• (4) Type I reservoir wells were primarily found in the northwest of the research region, within the subaqueous distributary channels, exhibiting a zigzag pattern. The majority of type II reservoir wells were located in the study area's center, mostly within the middle portions of the subaqueous distributary channel’s lateral sand bodies. In contrast, the relatively inferior type III reservoir wells were dispersed among the type II reservoirs, primarily situated in the marginal zones bordering the interdistributary bay and the periphery of the channel’s lateral sand bodies. Therefore, in terms of practical exploration and development, priority should be given to the superior reservoirs (type I) in the northwestern sector of the research region.

• (5) The evaluation results of the quantitative classification of tight sandstone reservoirs using machine learning are generally consistent with previous multiparameter conventional evaluation studies. However, this approach effectively integrates macroscopic and microscopic parameters, resulting in higher model accuracy, easier operation, and lower costs. It is particularly suitable for large-scale quality assessments of tight sandstone reservoirs, offering essential guidance for further exploration in the study area and other similar reservoirs.