Quantum annealing for nearest neighbour compliance problem

Abstract

Quantum Computing has emerged as a promising alternative, utilising quantum mechanics for faster computations. This paper explores the nearest neighbour compliance (NNC) Problem in Gate-based Quantum Computers, where quantum gates are constrained to operate on physically adjacent qubits. The NNC problem aims to optimise the insertion of SWAP-gates to ensure compliance with these constraints while minimising their count. This work introduces Quantum Annealing to tackle the NNC problem, proposing two Quadratic Unconstrained Optimisation Problem formulations. The formulations are tested on a contemporary Quantum Annealer, and their performance is compared with previous methods. It shows that the prospect of using Quantum Annealing is promising, however, the current state of the hardware makes that finding the embedding is the limiting factor.

Introduction

Contemporary devices such as smartphones and computers, as we know them today, would not be possible without the continuous advances in microchips, or more specifically, semiconductors. They play a pivotal role in modern society by facilitating communication across vast distances and enabling seamless access to information, transforming how we connect, acquire knowledge, and make decisions. Subsequently, advances in semiconductor technologies are a key source of increased productivity which in turn has been a primary driver for economic growth^1,2,3.

Over the last 50 years, the number of transistors on a microchip has grown exponentially, following the predictions by Moore⁴, known as Moore’s law. However, this growth has slowed down in recent years as the technology is soon to reach its fundamental physical limits^5,6,7.

In that context, Quantum Computing has emerged as an alternative paradigm to computing that harnesses the intricacies of quantum mechanics to perform certain computations more quickly and provide algorithms with an improved complexity scaling. Most prominently, there is Grover’s algorithm⁸ to more efficiently search large databases and Shor’s algorithm to factor large integers⁹.

Currently, there are two main realisations of Quantum Computers, the Quantum Annealer (QA) such as the Advantage Series by D-Wave Systems, and the Gate-based Quantum Computers (GQC) such as IBM’s Quantum System Two. While the QA is purpose-built to solve a specific class of binary optimisation problems, the GQC is universal and can theoretically perform any computation or algorithm that a classical computer could. Specifically, the GQC performs computations by executing a quantum circuit that applies a sequence of quantum gates to a set of quantum bits (qubits)¹⁰.

The potential advantages that GQC offers, in theory, are accompanied by limitations of physical implementations of such computers. In the context of this work, two such limitations are of direct relevance. Firstly, qubits can not store information indefinitely due to an inevitable exchange of energy with their environment¹¹. This process is referred to as quantum decoherence and is a direct consequence of the imperfect isolation of quantum computers from their surroundings. Consequently, any computation performed on a GQC has to be completed before the quantum system loses its coherence which ultimately implies that it is desirable to physically implement any quantum algorithm with as few gates as possible. Secondly, in many common physical implementations of GQCs, qubits are only coupled with their nearest neighbours, that is, a limited set of adjacent qubits¹². This limitation gives rise to Nearest Neighbour Constraints which indicate that quantum gates can solely be applied to physically adjacent qubits.

To ensure the compliance of each two-qubit gate in a circuit with the nearest neighbour constraint, one can insert so-called SWAP-gates that swap the information contained by two adjacent qubits to effectively interchange the qubits’ location in the coupling graph¹². Moreover, given the limited lifetime of the qubits due to decoherence, it is highly desirable to satisfy the constraints by inserting as few SWAP-gates into the circuit as possible. The resulting optimisation problem is the “Nearest Neighbour Compliance Problem” (NNC)¹³, which is also known under other names like qubit routing and circuit compilation¹⁴.

Nearest Neighbour Constraints have been considered in a wide variety of contexts, including specific circuit types and qubit architectures¹⁵. In the latter case, which is of interest in this work, the meaning of adjacency is defined by a coupling graph. Again, various cases of coupling graphs have been considered where qubits are placed on either a linear array (see Fig. 1), two-dimensional grid, three-dimensional grid, or manufacturer-specific architectures. Moreover, different research areas either focus on a global or local perspective on the reordering of the qubits¹⁶. While the global perspective aims to reduce the problem’s difficulty by producing an, on average, optimal initial ordering of qubits, the local reordering problem searches for a permutation of qubits before each gate in the circuit, so that the total number of swaps between all consecutive permutations is minimised. Therefore, local reordering allows for overall better solutions¹⁷ at the cost of an often exponentially growing number of variables in the model, often resulting in intractable running times for exact methods on large instances.

Fig. 1

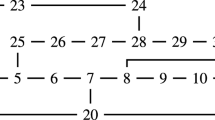
Linear coupling graph with n qubits. Figure from:¹⁵.

Given the combinatorial and discrete nature of the NNC problem arising in GQC, another form of quantum computing, quantum annealing, is a natural candidate to tackle this difficult optimisation problem¹⁸. Even in its current, early stages, QA can solve some first real-world problems and is seen as a soon-to-be-competitive machine heuristic to solve quadratic problems formulated as a Quadratic Unconstrained Binary Optimisation Problem (QUBO). Therefore, an efficient QUBO formulation that is solved on a QA has the potential to be an efficient general-instance heuristic optimisation method, which does not yet exist in the NNC literature¹⁵. To the best of the author’s knowledge, Quantum Annealing has not yet been applied to solve the NNC problem as is done in this work. However, Quantum Annealing has been applied to a variety of relevant problems in recent years, including the Nurse Scheduling Problem¹⁹, Traffic Flow Optimisation²⁰, Portfolio Optimisation²¹, Energy System Optimisation^22,23, and Job Scheduling²⁴.

This work proposes two novel reformulations of the NNC problem as Quadratic Unconstrained Binary Optimization (QUBO) instances, which are subsequently tackled using a contemporary Quantum Annealer developed by D-Wave Systems. This builds upon the method introduced by¹³, which provided an exact Integer Linear Programming (ILP) formulation for the local-reordering NNC problem on a linear array, thus avoiding the factorial scaling in qubit count suffered by previous approaches. The primary innovation lies in proposing a quantum-compatible formulation for a problem already addressed classically. Currently, this approach faces two main limitations: it is only applicable to linear architectures, precluding direct usage on most existing quantum processors, and it yields results inferior to both exact and heuristic classical solutions, either in quality or runtime. Nonetheless, the authors suggest that these limitations might be mitigated with the advent of more potent and scalable Quantum Annealer processors. The central contribution of this work is the transformation of an existing ILP model, proposed in reference¹³, into two QUBO formulations, where one achieves variable reduction for improved efficiency.

The remainder of this paper is organised as follows. "Literature" section reviews relevant literature on the reordering and NNC problem. "Quantum annealing" section introduces Quantum Annealing as an optimisation method and the QUBO problem formulation. "Modelling approach" section reviews the ILP formulation for the NNC problem on a linear graph proposed by¹³ and proposes two QUBO formulations of the same problem. "Experimental results" section presents and analyses the results obtained from applying both formulations to instances from the²⁵ dataset and compares those to the results obtained by¹³ and others. Finally, "Conclusions and further research" section concludes and points out ideas for further research. This paper is based on a thesis written by the first author.

Literature

The NNC problem on a linear array has been studied comprehensively. The methods with which the problem has been approached can be subdivided into two groups, exact methods and heuristics. The use of heuristics is motivated since the size of most exact models scales exponentially in the number of qubits^17,26.

NNC: exact methods

A naive approach, formalized by²⁶, enumerates all possible permutations of qubits for all gates and then selects the solution that requires the minimum number of inserted SWAP-gates. Having $\mathcal {N}$ qubits and $\mathcal {K}$ gates in a circtuim this entails generating all $(\mathcal {N}!)^\mathcal {K}$ solutions which is intractable even if the corresponding solution values can be computed efficiently.

Other approaches make use of graph theory by constructing Adjacent Transposition and Caley Graphs as in¹⁵ and²⁷ respectively. Both methods hinge on generating graphs where nodes correspond to qubit orders and subsequently identify a shortest path that corresponds to the solution of the NNC problem. While the shortest path can be found in polynomial time in terms of the size of the graph, the constructed graphs contain $O(\mathcal {N}!\mathcal {K})$ nodes. Therefore, these methods result again in the factorial-time scaling in terms of the number of qubits of the initial NNC problem.

In¹⁷, the authors propose a Pseudo-Boolean Optimisation (PBO) model to solve the NNC problem. The qubit permutations are encoded into binary variables $x_{ij}^{k}$, indicating if qubit i is located at location j before gate k. Moreover, the objective of counting the number of required SWAP-gates is then encoded by enumerating all permutations (and their corresponding costs) at each gate. Consequently, this method also fails to avoid the factorial scaling. However, their formulation paved the way for the following Integer Linear Programming (ILP) approach by¹³, which, for the first time, avoids the factorial scaling and produces a polynomial-size model. Ultimately, this ILP formulation will serve as the basis of the two polynomial-size QUBO formulations proposed in this work which will be presented in "Modelling approach" section).

NNC: heuristics

Numerous heuristics approaches have been proposed for the NNC problem. For relatively larger instances, these methods remain the only practical options. The proposed methods include: greedy searches where one qubit is moved toward another²⁸, a greedy heuristic similar to 2-opt²⁹, Sliding Window Search heuristics where only the next fixed number of gates are considered for the reordering^30,31, and a Fast Sliding Window Search where, additionally, only a restricted number of qubit orders are considered²⁸. Another Sliding Window approach uses the concept of the circuit tail³², in which only part of the tail is used to determine local optimal solutions, which are later on combined to obtain a complete strategy. Other attempts include the use of templates for circuits in the Multiple Control Toffoli (MTC) library³³. A divide and conquer technique, where the circuit is split into clusters that are considered separately, was developed in³⁴. Also³⁵ gives a decomposition approach. In³⁶, a solution method is proposed, based on a combination of MTC library templates and the heuristic method of³¹.

Quantum annealing

In order to solve the NNC problem, which arises within the context of Gate-based Quantum Computing, this work intends to exploit another form of Quantum Computing, namely Quantum Annealing, as the optimisation method of choice. A detailed explanation of QA, its advantages, limitations, and the quantum mechanics behind it is beyond the scope of this work. This section is limited to a brief description of Quantum Annealing as an optimisation method and a few examples of applications, while providing references for interested readers.

In contrast to Gate-based QC where universal computation is performed by a series of Quantum gates, Quantum Annealing is a hardware heuristic to specifically minimise an Ising Hamiltonian, or equivalently, solve Quadratic Unconstrained Optimisation (QUBO) Problems.

Definition 1

(QUBO Problem) Given a vector of n binary decision variables $x \in \{0,1\}^n$ and a $n \times n$ coefficient matrix Q, the QUBO is defined as:

$$\begin{aligned} min_{x}\hspace{3mm}x^{T}Qx. \end{aligned}$$

(1)

Note that $x_{i}^2=x_{i}$. Generally, the QUBO problem is NP-hard³⁷.

The QUBO problem’s (from now referred to as QUBO) objective function can equivalently be described by an Ising Hamiltonian (more commonly used in physics)¹⁸. This Hamiltonian effectively encodes the objective value, or energy, for any given solution. The challenge here is to reformulate the initial optimisation problem such that the minimum energy ground state of the Hamiltonian (that is, the QUBO’s optimal solution), corresponds to the optimal solution of the original optimisation problem.

Now the optimisation process, as performed by one of the most advanced Quantum Annealers, such as the D-Wave Advantage Systems, can be outlined as follows. Initially, the quantum system in the annealer starts from a simple, well-known Hamiltonian. Then, the initial Hamiltonian is slowly perturbed by applying magnetic fields until the problem Hamiltonian is obtained. If this process was successful, the system remained within the ground state throughout and the optimal solution to the optimisation problem is encoded in the final state of the system³⁸. There are claims of analytical and numerical evidence suggesting that Quantum Annealing can outperform classical methods such as Simulated (Thermal) Annealing for some problems^39,40, potentially offering a quadratic speedup^41,42. A more comprehensive analysis is given by⁴³.

The Quantum Processing Unit (QPU) of the D-Wave Advantage System has around 5600 qubits which are arranged in a Pegasus Graph structure¹⁸. This QPU graph and the qubits therein are not to be confused with the Gated-based Quantum Computer whose qubit ordering is optimised in the linear NNC problem. Note that the connectivity of the Advantage QPU is (at most) 15, indicating that each qubit is connected to and can interact with 15 others¹⁸. Therefore, to encode the QUBO on the QA, each logical variable in the QUBO is mapped to at least one or more qubits on the QPU. Specifically, multiple qubits are needed to present a single logical variable if that variable is connected to, or interacts with more than 15 others in the QUBO. A variable i is said to (quadratically) interact with another variable j if the corresponding off-diagonal entry in the Q matrix is non-zero. This process of mapping the QUBO onto the QA hardware is called embedding.

While the limited connectivity and number of qubits available pose a hard limit on QUBO instance sizes that can be solved on the QA, there are other factors that adversely impact the annealer’s performance as the instance size increases. First, Integrated Control Errors cause the representation of the QUBO on the hardware to be imprecise¹⁸. Secondly, the minimal energy gap between the ground-state and the first-excited state decreases as the problem size increases which in turn increases the probability to move away from the ground-state (optimal solution) during the anneal process⁴⁴.

Finally, the interested reader is referred to¹⁰ for the Quantum Mechanics involved, and to^18,45,46 for more information on Quantum Annealing as a heuristic optimisation method.

Modelling approach

This section discusses the polynomial-size ILP formulation of the linear NNC problem by¹³ and then proposes one QUBO formulation based on their ILP (referred to as ${\textsf{QUBO}_{1}}$ in the remainder of this paper). Subsequently, another improved QUBO formulation with fewer variables and constraints is proposed afterwards (referred to as ${\textsf{QUBO}_{2}}$).

NNP problem

The ILP formulation of the linear NNC proposed in¹⁵ and the companion paper¹³ serves as the basis of the QUBO formulations proposed in this work. Consequently, their model and some of their key definitions, including a formal definition of the NNC problem on a linear array, are summarised in this and the next section.

• $Q= {1,...,n}$ denotes the set of n qubits

• $L= {1,...,n}$ denotes the set of n locations on the linear array which the qubits can occupy

• A permutation $\tau ([n]) \in S_{n}$ is a bijective mapping of qubits to locations, $f: Q \mapsto L$. Here, [n] denotes the vector (1, .., n) and $S_{n}$ denotes the permutation group (of all permutations).

• A SWAP-gate applied to a qubit ordering $\tau$ interchanges the location of two adjacent qubits (by swapping the qubit’s states or information).

• Given two permutations $\tau _{1}, \tau _{2}$, qubits i, j are said to be inverted if $\tau _{1}(i) < \tau _{1}(j)$ and $\tau _{2}(i) > \tau _{2}(j)$.

The efficient encoding of the objective in the ILP formulation by¹³ builds on recognising that the minimally required number of SWAP-gates to transform one permutation into another is equal to the total number of inversions between the two permutations, or equivalently the Kendall-tau distance:

Definition 2

(Kendall-tau distance) Given two permutations $\tau _{1}, \tau _{2} \in S_{n}$, the Kendall-tau distance between the two permutations is

$$\begin{aligned} I(\tau _{1}, \tau _{2}) \equiv | \{(i,j) | 1 \le i,j \le n, \tau _{1}(i) < \tau _{1}(j), \tau _{2}(i) > \tau _{2}(j)\} |. \end{aligned}$$

(2)

The Nearest Neighbour Constraints of the NNC problem require that each quantum gate can only act on qubits that are neighbours, or adjacent, to each other in the corresponding topology graph. Since the meaning of adjacency is only well-defined for pairs of qubits, it only makes sense to consider two-qubit gates. Therefore, multiple-qubit gates are decomposed into two-qubit gates as described in¹³. Notably, such a decomposition is always possible¹⁰. Moreover, Nearest Neighbour Constraints do naturally not apply to gates acting on individual qubits, so these gates can be ignored in the context of the NNC problem. Additionally, the function of a gate is not relevant in this context either, but only the two qubits i, j that a gate acts on. Consequently, a two-qubit gate $g= g_{i,j}= \{q_{i}, q_{j}\}$ is completely defined for this purpose by specifying these two qubits $q_{i}, q_{j} \in Q$. Finally, this allows the definition of a quantum circuit in terms of only two-qubit gates and the subsequent formulation of Nearest Neighbour Compliance:

Definition 3

(Quantum circuit) Let Q be a set of n qubits and $G= (g^{1},...,g^{m})$ a sequence of m two-qubit gates. Then, the tuple $QC= (Q,G)$ is a quantum circuit.

Definition 4

(Nearest Neighbour Compliance) Given a quantum gate $g_{i,j}^{t} \in G$ and a corresponding qubit order $\tau ^{t}$ before that gate, the Nearest Neighbour Constraint requires qubits $q_{i}, q_{j}$ to be adjacent, namely $|\tau ^{t}(i) - \tau ^{t}(j)| = 1$, or equivalently $(\tau ^{t}(i) - \tau ^{t}(j))^2 = 1$. Finally, given a sequence of qubit orders, where each qubit order $\tau ^{t}$ corresponds to a quantum gate $g_{i,j}^{t}$ in the gate sequence G of the QC, the circuit QC is compliant with Nearest Neighbour Constraints if the above constraint holds for each pair of qubit order and gate $(\tau ^{t},g_{i,j}^{t})$.

Ultimately, the formal definition of the NNC problem is as follows: Given a quantum circuit $QC= (Q,G)$ with $|Q|= n$ qubits and $|G|= m$ gates, we have to find a sequence of qubit orders $\tau = (\tau ^{1},...,\tau ^{m})$, one for each gate $g \in G$, that minimises the sum of Kendall-tau distances between consecutive qubit orderings

$$\begin{aligned} \sum _{t=1}^{m-1} I(\tau ^{t},\tau ^{t+1}), \end{aligned}$$

such that the quantum circuit is compliant with Nearest Neighbour Constraints. Note that the NNC problem on a linear graph is conjectured to be NP-hard²⁶, while the NNC problem on a general graph is a known NP-hard problem⁴⁷.

Building a first QUBO

In this subsection we will introduce the variables and build ${\textsf{QUBO}_{1}}$ based on the objective functions and the constraints as introduced in¹³.

Variables

To work of¹³ introduces the following variables:

• $$\begin{aligned} x_{i}^{t} \in L= \{1,...,n\} \text { indicates the location of qubit } i \text { at gate } t. \end{aligned}$$

  (3)
• $$\begin{aligned} y_{ij}^{t}= {\left\{ \begin{array}{ll} 1 & \text {if qubit } i \text { is located before qubit } j \text { at gate } t \text {: } x_{i}^{t} < x_{j}^{t},\\ 0 & \text {otherwise.} \end{array}\right. } \end{aligned}$$

  (4)

Note that the $y_{ij}^{t}$ variables keep track of the relative ordering of qubits and that $|y_{ij}^{t} - y_{ij}^{t+1}|$ determines whether qubit i and j are inverted between permutation t and $t+1$. This key observation allows¹³ to count the total number of SWAP-gates while avoiding the explicit n! scaling of the model in the number of variables and constraints. Moreover, describing an ordering of qubits by these $y_{ij}^{t}$ variables, while efficiently being able to count the required SWAP-gates, will be the enabling observation for the significantly more efficient ${\textsf{QUBO}_{2}}$ introduced later in this section.

Objective function

Clearly, the objective is to minimise the sum of Kendall-tau distances between every two consecutive qubit orders, that is:

$$\begin{aligned} \min \sum _{\begin{array}{c} i,j \in Q \\ i < j \end{array}} \sum _{t \in [m-1]} |y_{ij}^{t} - y_{ij}^{t+1}|. \end{aligned}$$

(5)

This function is neither linear nor quadratic and thus had to be linearised by¹³ for their ILP. However, since the variables are binary and the QUBO allows quadratic interactions, we can equivalently write:

$$\begin{aligned} \min \sum _{\begin{array}{c} i,j \in Q \\ i < j \end{array}} \sum _{t \in [m-1]} (y_{ij}^{t} - y_{ij}^{t+1})^2. \end{aligned}$$

(6)

This expression will serve as the objective for both ${\textsf{QUBO}_{1}}$ and ${\textsf{QUBO}_{2}}$.

Ordering constraints

The following constraints relate the x-variables to the y-variables by enforcing the definition of the y-variables. Moreover, they also ensure that no two qubits can be located at the same location at the same time. For more details, see¹³.

$$\begin{aligned} x_{j}^{t} - x_{i}^{t} \le My_{ij}^{t} - 1&\qquad \forall i,j \in Q, i < j, t \in [m], \end{aligned}$$

(7)

$$\begin{aligned} x_{i}^{t} - x_{j}^{t} \le M(1-y_{ij}^{t}) - 1&\qquad \forall i,j \in Q, i < j, t \in [m], \end{aligned}$$

(8)

where $M= n+1$. Due to the QUBO being an unconstrained problem, all constraints have to be incorporated into the objective function. This can be done by adding additional terms to the objective that either penalise infeasible solutions or favor feasible solutions by increasing or decreasing the objective value respectively.

In ${\textsf{QUBO}_{1}}$, all penalty terms are constructed such that they are precisely zero if the corresponding constraint is satisfied and strictly positive if they are not satisfied. The following penalty term (added to the initial objective) achieves exactly that:

$$\begin{aligned} +\lambda ^{o}\cdot (x_{j}^{t} - x_{i}^{t} - My_{ij}^{t} + 1 + s_{ij}^{t})^2 \qquad \forall i,j \in Q, i < j, t \in [m], \end{aligned}$$

(9)

where $\lambda ^{o} > 0$ is a constant and $s_{ij}^{t}$ represents an integer-valued slack variable that can take on values in $[0,M-2]$. It can easily be verified that there only exists a value for $s_{ij}^{t} \in [0,M-2]$ that sets this term to zero if both Eq. (7) and Eq. (8) are satisfied. Finally, to encode the integer variable $s_{ij}^{t} \in [0,M-2]$ in binary variables (as the QUBO requires), we can do as Section 2.4 of³⁷ and write:

$$\begin{aligned} s \mapsto \sum _{k=0}^{K-1} 2^{k}a_{k} + (U+1-2^{K})a^{K}, \end{aligned}$$

(10)

using $K+1$ binary variables $a_{k}$, where U is the maximum value that s can take, such that $2^{K} \le U < 2^{K+1}$. The same holds for the encoding of the $x_{i}^{t}$-variable. Throughout the remainder of this paper, we will refrain from explicitly writing out this encoding when specifying (parts of) a QUBO for the sake of readability. Therefore, whenever an integer variable appears in a QUBO formulation, this encoding is implied.

Nearest neighbour constraints

To ensure that the Nearest Neighbour Constraint is satisfied at each gate¹³, also added the following constraints to their ILP:

$$\begin{aligned} -1 \le x_{i}^{t} - x_{j}^{t} \le 1 \qquad \forall g_{ij}^{t} \in G. \end{aligned}$$

(11)

The corresponding penalty terms in ${\textsf{QUBO}_{1}}$ are:

$$\begin{aligned} +\lambda ^{nn}\cdot \bigl ((x_{i}^{t} - x_{j}^{t})^2 - 1\bigl ) \qquad \forall g_{ij}^{t} \in G, \end{aligned}$$

(12)

where $\lambda ^{nn}>0$. Note that this expression favours $x_{i}^{t} = x_{j}^{t}$, which implies that qubits i and j are located in the same position in the ordering at gate t, corresponding to an infeasible solution. However, the penalty terms of Eq. (9) penalise this behaviour. Therefore, we can resolve this issue by requiring $\lambda ^{o} > \lambda ^{nn}$.

An improved QUBO formulation

The ${\textsf{QUBO}_{1}}$ formulation introduces a lot of additional binary variables to model the slack and x-variables required in Eq. (9). This is undesirable due to the limited number of 5600 qubits available in the D-Wave Quantum Annealer to embed the QUBO and its variables. ${\textsf{QUBO}_{2}}$ reformulates the NNC problem only in terms of the y-variables to eliminate both the x-variables and the need to introduce slack variables as in Eq. (9).

For this, observe that $x_{i}^{t}$, the location of qubit i in the ordering at gate t, can be obtained by counting how many other qubits are located before qubit i, specifically:

$$\begin{aligned} x_{i}^{t}= \sum _{k=1}^{n} y_{ki}^{t}. \end{aligned}$$

(13)

Since $y_{ij}^{t}$-variables are only defined for $i < j$, we need to write Eq. (13) more precisely as:

$$\begin{aligned} x_{i}^{t}= \sum _{k=1}^{i-1} y_{ki}^{t} + \sum _{k=i+1}^{n} (1 - y_{ik}^{t}). \end{aligned}$$

(14)

Nonetheless, for the sake of readability, the notation of Eq. (13) will be used in the remainder of this paper.

Finally, recognising this, we can write ${\textsf{QUBO}_{2}}$ only in terms of the y variables. The initial objective function in Eq. (6) is unaffected. However, we need to specify a partially new set of constraints. Firstly, we need to ensure that the ordering of qubits described by the y-variables is feasible, i.e., each qubit takes exactly one location. Secondly, we need to specify the Nearest Neighbour Constraints as before.

Observe that the requirement of each qubit to take exactly one location is equivalent to requiring that any two qubits can not be located in the same location. In terms of the y-variables this can be expressed by requiring that no two qubits have an equal number of other qubits appearing before them in the ordering, that is:

$$\begin{aligned} \sum _{k=1}^{n} y_{ki}^{t} \ne \sum _{k=1}^{n} y_{kj}^{t} \qquad \forall i,j \in Q, i \ne j, t \in [m]. \end{aligned}$$

(15)

To incorporate these constraints into the objective of ${\textsf{QUBO}_{2}}$ without introducing slack variables, we take a different approach than previously. Rather than penalising infeasible solutions, we favour feasible solutions. In other words, we add additional terms to the objective that are strictly negative if Eq. (15) is satisfied and strictly zero if not. Adding the following terms achieves this:

$$\begin{aligned} -\lambda ^{o}\cdot \biggl (\sum _{k=1}^{n} y_{ki}^{t} - \sum _{k=1}^{n} y_{kj}^{t}\biggr )^2 \qquad \forall i,j \in Q, i \ne j, t \in [m]. \end{aligned}$$

(16)

In ${\textsf{QUBO}_{2}}$, all added terms are zero for infeasible constraints, while taking on strictly negative values to favor feasible solutions.

Note that each individual term, corresponding to a specific constraint, is not always the same for all feasible solutions. However, it can be shown that the sum of all added terms (all constraints), needs to be identical for any feasible solution:

Proof Let $\tau$ be a feasible ordering of n qubits (permutation). Then, the location of the first qubit i and the last qubit j differs by $n-1$. Moreover, there are exactly two pairs of qubits whose location differs by $n-2$, three pairs differing by $n-3$, and so on. Formally, the following holds for any feasible solution:

$$\begin{aligned} |\{(i,j)|1 \le i \ne j \le n, |\tau ^{t}(i)-\tau ^{t}(j)|= k\}| = n-k \qquad \forall k \in [n-1], t \in [m]. \end{aligned}$$

(17)

Finally, as $\tau ^{t}(i) = \sum _{k=1}^{n} y_{ki}^{t}$,

$$\begin{aligned} \sum _{i,j \in [n], i \ne j} |\tau ^{t}(i) - \tau ^{t}(j)|^{2} = \sum _{i,j \in [n], i \ne j} \biggl (\sum _{k=1}^{n} y_{ki}^{t} - \sum _{k=1}^{n} y_{kj}^{t}\biggr )^{2} = \sum _{k=1}^{n-1} (n-k)^{2} \qquad \forall t \in [m]. \end{aligned}$$

(18)

This is necessary to ensure that the added terms do not affect the ranking of the feasible solutions. In other words, we can only guarantee that the optimal solution to the NNC problem will correspond to the optimal solution of the QUBO if the sum of added terms is identical for any feasible solution of the NNC problem.

Finally, the Nearest Neighbour Constraints are logically identical with Eq. (12) from ${\textsf{QUBO}_{1}}$, we substitute the x-variables by Eq. (13):

$$\begin{aligned} +\lambda ^{nn}\cdot \biggl (\biggl (\sum _{k=1}^{n} y_{ki}^{t} - \sum _{k=1}^{n} y_{kj}^{t}\biggr )^2 - 1\biggr ) \qquad \forall g_{ij}^{t} \in G, \end{aligned}$$

(19)

where $\lambda ^{o}> \lambda ^{nn} > 0$.

Experimental results

This section analyses and discusses the results obtained from applying the proposed QUBO formulation to circuits from the revLib library²⁵ and others, in order to address the remaining research questions. The results are compared to the exact method of¹³ in terms of the time needed to obtain them and to other heuristics in terms of solution quality. With consideration of the limitations of the D-Wave Advantage System mentioned before, it is also of interest for which instance sizes solutions can be obtained and at which point the solution quality starts to decrease significantly.

Experimental setting

We use various instances from different sources. Quantum Fourier Transform (QFT) instances were obtained from¹⁰, all other instances from the RevLib Library containing reversible circuits²⁵. Moreover, circuits with multi-qubit gates are decomposed into two-qubit gates as described in¹³. Notably, this process is not optimised over and can affect the required number of SWAP gates.

The Quantum Annealer D-Wave Advantage 5.3 by D-Wave is used to perform the Quantum Annealing, while a Dell XPS 13 2-in-1 7390 with an Intel i7-1065G7 with 4 cores at 1.30GHz and 16GB of RAM is used to do the pre-processing such as computing the embedding of the QUBO on the Annealer.

The parameters of the QUBOs were determined experimentally by extensive trial-and-error testing. The $\lambda$ parameters determine how the constraints’ contributions to the QUBO-objective are weighted relative to the initial objective. Choosing values too small for this parameter leads to sampling infeasible solutions, while setting values too high results in problem misrepresentation due to the limited range and fidelity with which the quantum annealer can represent the problem coefficients (see “Error Sources for Problem Representation” in¹⁸). It was found that setting $\lambda ^{o}=2$ and $\lambda ^{nn}=1$ for ${\textsf{QUBO}_{1}}$ performed relatively well. For ${\textsf{QUBO}_{2}}$, where feasible solutions could be obtained for a larger number of instances, it was found that $\lambda ^{o} \in [0.2,0.7]$ and $\lambda ^{nn}=\lambda ^{o}-0.01$ yielded the best results. Notably, as the number of gates m and the instance size increases, larger values in this range were found to perform better on average.

For the Quantum Annealer, there are two parameters that were manually tuned by trial-and-error. First, the annealing time, which determines the length of the annealing process, was chosen between 100 to 450 microseconds. Second, the number of samples parameter determines how many solutions are sampled by the Quantum Annealer. Chosen values were between 100 and 1250 samples. Obviously, in both cases, larger values correspond to longer compute times on the Quantum Annealer. In addition, the improvements in the best objective value among samples diminished as the number of obtained samples increased. Thus, exceeding 1250 samples showed close to no improvements in the obtained solutions. Note that we generally set the number of samples parameter lower for small instances, since this was sufficient to find the optimal solution. Moreover, since adiabatic theory indicates that the larger problems require longer annealing times to obtain good solutions⁴⁴, we use a higher value for larger instances. Moreover, setting larger values for the annealing time generally increased the likelihood to obtain better solutions, again with diminishing returns. Again, it was found that larger values within the given ranges produced relatively better results, especially for larger instances. Nevertheless, the lower-end values were sufficient for small instances to obtain the optimal solution. The specific parameter configurations that were used to obtain the presented results for each instance are given in Table 1.

Table 1 Parameter settings used for the various circuit instances.

Lastly, we use the heuristic tool minorminer⁴⁸ to find an embedding for the problem graph in the hardware graph. To find a feasible embedding, it might be necessary to represent a single logical variable by a chain of qubits on the hardware. If a sampled solution violates the chain, i.e. not all variables in the chain take on the same value, we resolve these conflicts by a majority-vote mechanism where the more often occurring value is chosen for the logical variable.

Results

The feasibility of all solutions was validated by checking that all penalty terms (corresponding to the constraints) indeed do evaluate to zero. ${\textsf{QUBO}_{1}}$ failed to obtain feasible solutions for all instances except of QFT_QFT3 and peres_8, where it did not obtain the optimal solution. A possible explanation of the poor performance is the inefficient encoding of the qubit permutations by the integer x-variables and the inefficient encoding of the constraints via slack variables that might significantly decrease the minimal energy gap. The hugely improved performance of ${\textsf{QUBO}_{2}}$, which encodes the problem only through the y-variables, provides anecdotal evidence for these hypotheses.

Consequently, only for ${\textsf{QUBO}_{2}}$ results are reported. The benchmark instances are grouped according to the number of qubits in the circuits, n, over multiple tables, starting with Table 2 for $n=3,4$, Tables 3 and 4 for $n=5$ and Table 5 for $n=6-10$. Moreover, tables are sorted by the number of two-qubit gates in the decomposed circuits, $|G|=m$. In each table, column OPT states the optimal minimum number of SWAP gates needed to make the circuit compliant (from¹³, assuming the decomposition procedure used there), column SWAPSQ presents the objective value obtained through a single run of ${\textsf{QUBO}_{2}}$ on the D-Wave Quantum Annealer, column QUBO Time shows the time to compute the QUBO expression, column EmbedT shows the time to (heuristically) find an embedding of the QUBO on the hardware graph of the annealer using “minorminer.find_embedding()” with default parameters⁴⁸, and column QPU Time shows the time to perform the actual annealing on the QPU following the definition of the QPU access time in¹⁸ (which varies depending on the NumReads and Annealing Time parameters). Note that all classical timings refer to elapsed time using a single core. The TimeQ column shows the overall time of the quantum algorithm (i.e. $TimeQ= QUBO\ Time + EmbedT + QPU\ Time$), column TimeE shows the running time of the exact method of¹³, and column SWAPSH shows the objective values obtained by other heuristic approaches. If SWAPSQ is reported to be $-2$, this indicates that no feasible solutions could be obtained, while $-3$ indicates that no embedding was found by 10 attempts (the default setting) of the heuristic tool minorminer⁴⁸, which usually implies that the instance is too large to fit on the Annealer (yet there is no proof due to heuristic nature of minorminer). Consequently, a dash “-” in the TimeQ or QPU Time columns is the result of the fact that no feasible embedding was found and thus the problem could not be run on the annealer. Subscripts in the SWAPSH column indicate the source of the results, where: c: Kole et al.⁴⁹, d: Shafaei et al.⁵⁰, e: AlFailakawi et al.⁵¹, f: Kole et al.³¹ and g: Wille et al.³², while a dash “-” indicates that neither of c-g reported a result for this instance. Asterisks in column SWAPSH indicate that the number of gates after decomposition differs, or that the objective value of the heuristic is lower than that of the exact method. This is believed to be the consequence of decomposing multi-qubit gates differently.

Table 2 Benchmark circuit instances with three or four qubits.

Table 3 Benchmark circuit instances with five qubits and less than 40 gates.

Table 4 Benchmark circuit instances with five qubits and more than 40 gates.

Table 5 Benchmark circuit instances with six or more qubits.

Discussion on computation time

The time to perform the Quantum Annealing and to obtain a given number of samples, QPU Time, depends on the aforementioned parameter values annealing time and number of samples, rather than on the instance size. The choice of these parameters is instance-size-dependent within the practical upper bounds discussed previously. The QPU Time peaks at around 0.9 seconds and does not further increase even for large instances. Also the QUBO time is in almost all cases lower than 1 second. This means that for the larger instances the Embedding time is by far the dominating factor.

As concluded, QPU Time and QUBO time are in the same order of magnitude as the run time of the exact method for small instances and significantly smaller for larger instances ($n=4$ and $m > 30$ or $n=5$ and $m > 20$). Thus, Quantum Annealing as a heuristic has the potential to significantly reduce the running time to obtain solutions for large instances if the embedding can be computed efficiently or if no embedding is required at all. The latter would be true, for example, if the hardware graph of the Quantum Annealer has a fully-connected subgraph of sufficient size. Alternatively, one could pre-compute the embedding of the largest fully-connected graph that can be embedded on the hardware in advance, and use this embedding when possible.

However, in practice, this would limit the maximum number of variables too significantly to be a viable solution and the computation of the embedding can not be avoided. As the results indicate, the time to (heuristically) find an embedding exceeds the run time of the exact method for almost all instances with five or more qubits. Therefore, the limited connectivity of the hardware graph and the computational task to find an embedding pose two major limitations to the proposed method.

Finally, the authors want to note that the reported compute times for the computations that were performed on classical computers highly depend on the hardware configuration of the system and therefore may not be directly comparable to other reported run times.

Discussion on solution quality

All instances with three qubits were solved to optimality in run times comparable to the exact method of¹³. The same holds for four-qubit instances with at most 23 gates. For instances with 29 to 42 gates, the deviation from optimality remains small with at most four additional SWAP-gates. Then, the deviation rises to around $50\%$ and peaks at $100\%$ of OPT for the largest four-qubit instance with 75 gates. Nonetheless, it can be argued that it is more insightful to compare the total number of gates in the circuit, $m+$SWAPSQ, to the total minimum $m+$OPT. In this case, the relative deviation rises first to $20\%$ and then peaks at $50\%$. Figure 2 illustrates this measure for the majority of instances.

Fig. 2

For circuit instances with 4,5, and 6 qubits respectively, the y-axis plots the difference between the solution’s objective value obtained by our method and the optimal objective value ($SWAPSQ-OPT$), as a percentage of the minimum number of gates to implement a given circuit instance ($m+OPT$), against the number of gates m in the non-compliant circuit instance on the x-axis.

Tables 3 and 4 show the results for the benchmark instances with 5 qubits. A similar trend as previously can be identified here. For smaller values of m, an optimal or near-optimal solution is obtained by the proposed method, while for larger values of m the obtained objective values start diverging. This divergence again starts at around 20 gates, but is significantly more pronounced for instances with 5 qubits. Nonetheless, up until 24 gates the obtained results are comparable to other heuristic solutions that were reported. However, for the largest five-qubit instance for which a feasible solution was obtained, 4gt12-v1_89 with 44 gates, the obtained number of SWAP-gates is more than five times the optimum and more than four times the best heuristic value. For instances with more gates, no feasible solutions could be obtained.

For benchmark instances with 6 or more qubits, this trend continues again more extremely, while also starting earlier at instances with as little as 15 gates. Moreover, for six-qubit instances with more than 71 gates and seven-qubit instances with more than 49 gates, it was not possible anymore to find an embedding due to the size of the resulting QUBOs.

To compare these trends graphically, panel (A) of Fig. 3 plots the absolute deviation from OPT (excess) against the number of gates m, for instances with 4, 5, and 6 qubits. Moreover, it is expected that these trends become more pronounced as the number of qubits n increases since the number of possible permutations at each gate scales with n!. Similarly, the number of variables in ${\textsf{QUBO}_{2}}$ is $n(n-1)/2\cdot m$ and therefore scales with $n^{2}$. Consequently, it is better to compare instances with the same number of QUBO variables rather than with the same number of gates if the number of qubits differs. Therefore, panel (B) plots the excess number of SWAP gates against the number of variables in ${\textsf{QUBO}_{2}}$. While the previously observed differences in the trends of 4, 5, and 6 qubits are now less pronounced, they still do show clearly. They indicate that even for instances, for which the size of the resulting QUBO is identical in terms of the number of variables, the instance corresponding to a circuit with more qubits is more difficult to solve.

In order to better understand why this is the case, consider the two instances decod24-v0_39, in Table 2 and QFT_QFT5, in Table 3. While the former is a circuit with $n=4$ qubits and $m=15$ gates, and the latter is a circuit with $n=5$ qubits and $m=10$ gates, the QUBOs of both instances have 90 y-variables. However, there are $n(n-1)/2$$y_{ij}^{t}$-variables for each gate t, which will be (almost) fully connected due cross-terms from the ordering constraints, while only one $y_{ij}^{t}$-variable at gate t will be connected to exactly one $y_{ij}^{t+1}$-variable at gate $t+1$ due to the objective function. Therefore, the number of interactions in the QUBO corresponding to a circuit with more qubits will be larger even if the number of QUBO variables is identical. Finally, panel (C) plots the number of excess SWAP gates against the number of interactions in ${\textsf{QUBO}_{2}}$ of the benchmark instances. It can indeed be observed that the four- and five-qubit instances follow a now almost identical exponential trend. For the six-qubit instances, the number of data points is most likely too low to observe the same trend graphically. Conclusively, these results indicate that the quality of the solution obtained with the proposed method inversely scales with the number of interactions in the ${\textsf{QUBO}_{2}}$ formulation and therefore scales more poorly as the number of qubits n increases (compared to the number of gates m). In general, the observed exponential decay of the obtained objective values with increasing instance sizes is believed to be the consequence of the previously discussed physical limitations of the D-Wave Advantage 5.3 Quantum Annealer.

Fig. 3

For circuit instances with 4,5, and 6 qubits respectively, the y-axis plots the difference between the solution’s objective value obtained by our method and the optimal objective value ($SWAPSQ-OPT$), against (A) the number of gates m in the non-compliant circuit instance, (B) the number of binary variables in ${\textsf{QUBO}_{2}}$, (C) the number of interactions (quadratic terms with non-zero coefficients) in ${\textsf{QUBO}_{2}}$ on the x-axis.

Conclusions and further research

In this paper we proposed a polynomial-size QUBO formulation of the NNC problem. Both QUBO formulations proposed in this work are based on the polynomial-size ILP model by¹³. It was recognised that the number of additionally introduced slack variables in ${\textsf{QUBO}_{1}}$ do scale polynomial in n and m. ${\textsf{QUBO}_{2}}$ reduces the number of variables relative to the ILP formulation by reformulating the NNC problem purely in terms of the relative ordering variables y, which can be seen as the main contribution of this work. Therefore, as the number of constraints scales polynomially too, both QUBO formulations of the NNC problem, proposed in 4, are of polynomial size in n and m.

For all benchmark instances where the number of variables in ${\textsf{QUBO}_{2}}$, namely $n(n-1)/2\cdot m$, did not exceed 450, feasible solutions were obtained. The quality of the obtained solutions was competitive with both heuristic and exact methods for smaller instances. However, as the problem size increased, the required time to compute an embedding of the problem on the Quantum Annealer limited any upside in terms of running time, even compared to the exact method by¹³. Moreover, the solution quality increasingly worsened for large instances, so that the proposed method did not remain competitive with other heuristic approaches.

Lastly, it was graphically demonstrated that the obtained objective values’ absolute deviation from optimality seems to increase exponentially with the problem size, specifically, with the number of interactions in the resulting ${\textsf{QUBO}_{2}}$ formulation of an instance.

Concluding, we can state that while the linear NNC problem can be effectively solved for smaller instances, the physical limitations of contemporary state-of-the-art Quantum Annealers are restricting the scalability to larger instances where neither an advantage in terms of solution quality or run time compared to existing methods could be observed.

Given the relatively strong performance on small instances and the discussed connectivity of the ${\textsf{QUBO}_{2}}$ formulation, the authors see the use of decomposition methods such as the method proposed by⁵² as an avenue of further research. Their method identifies strongly connected components, which should exist in the ${\textsf{QUBO}_{2}}$ formulation, and then splits the overall problem into sub-problems accordingly. This might significantly increase the solution quality while also reducing the overall run time due to an reduction in the time needed to find embeddings.

Moreover, further research to identify minor-embeddings more efficiently by exploiting the problem-specific structure seems of interest, given that this step is the major contributor to the overall runtime.