Distance based topological characterization, graph energy prediction, and NMR patterns of benzene ring embedded in P-type surface in 2D network

Abstract

Nanostructures are tiny objects at the molecular and microscopic scale, with carbon nanotubes being the most notable among them. The elements possess exceptional microelectronic properties and other unique characteristics. Researchers have recently focused on the mathematical features of these materials. Molecular descriptors are crucial in mathematical chemistry, particularly in QSAR and QSPR modeling. Topological indices hold a significant position among them. This study presents the precise formulation of the ten most crucial topological indices for a benzene ring positioned on a P-type surface within the highly symmetric 2D lattice $\hbox {BCZ}_{48}$. We have incorporated the computed indices to develop a predictive model for the graph energy of the 2D lattice and, in addition, provided the NMR patterns and the HOMO-LUMO gap.

Introduction

A mathematical model is an explanation of a structure, exhausting mathematical and linguistic ideas. The process of mounting a mathematical model is called mathematical modeling. These models are used in the sciences of nature, the various disciplines of engineering, and social sciences. One such example is the graph-theoretic model. A study of the graph is an essential branch of discrete mathematics. It is a mathematical structure used to model pairwise relationships among entities. The entities could be anything; in particular, we take the entities as atoms of the molecule, and pairwise relationships among entities are called bonds. Graph-theoretically, vertices are mapped as atoms, and edges are mapped to bonds. This leads to another new subfield of mathematical chemistry, which is called chemical graph theory. Molecular descriptors are crucial in mathematical chemistry, particularly in QSPR and QSAR modelling^1,2. Topological indices hold a significant position among them. Currently, there are numerous topological indices with applications across different branches of chemistry. A topological index (TI) is a numerical value calculated from the chemical structure using mathematical methods^{3,4,5,6,7,8,9}.

In 1947, Wiener first proposed the concept of the topological index while conducting an experiment on the boiling point of paraffin¹⁰. This index was based on the sum of the shortest distances between every pair of vertices. The shortest distance is the length of a shortest path. The shortest path problem in network science has many applications in engineering, science and technology. For example, shortest path in LEO satellite constellation networks¹¹. The real-life application on network science can be found in^12,13,14,15. Topological indices are associated with physicochemical properties such as stability, strain energy, boiling point, ESR spectroscopy, and NMR spectroscopy. For recent work on this topic, see^{17,18,19,20,21,22}.

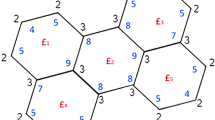
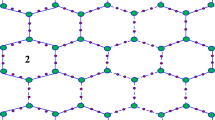
Carbon materials can be categorized based on their dimensions, electronic band structures, and hybridized states. The $\hbox {sp}^2$-hybridized carbon allotropes are further subdivided into three categories according to surface curvature. Fullerenes exhibit spherical shapes with positive Gaussian curvature, while carbon nanotubes (CNTs) have cylindrical structures with zero Gaussian curvature. Conversely, schwarzites are characterized as carbon allotropes with typical negative curvature^23,24,25,26. C-schwarzites are graphite-like networks characterized by negative Gaussian curvature, typically referred to as P and D surfaces. In contrast to the positive curvature in fullerenes, which is caused by 5-membered rings, the negative curvature in schwarzites arises from the presence of 7- or 8-membered rings. BN-schwarzites, as binary compounds, are hypothesized to feature architectures composed solely of 6- and 8-membered rings, as shown in Figure 1.

Fig. 1

(a) The unitcell $BCZ(1\times 1)$; (b) $BCZ(3\times 3)$.

In the study conducted in²⁷, polybenzene was characterized as a $6\cdot 8^2$ net embedded in the infinite periodic minimal D-surface. It consisted of a single type of carbon atom and was anticipated to possess significantly lower energy per atom compared to the reference structure $\hbox {C}_{60}$ in the field of nanoscience. It is alternatively referred to as a $6\cdot 8^2$ framework integrated within the periodic minimal P-surface. The development of a rational structure for three benzene-based units is examined in the study conducted by²⁸. The benzene ring is embedded in the D-surface with a value of $\hbox {BTA}_{48}$, in the P-type-surface with a value of $\hbox {BCZ}_{48}$, and in the P-type-surface with a value of $\hbox {BCA}_{96}$.

The construction of these structures was made with the help of some experiments on maps^29,30,31, applied on Platonic solids: the sequence of polygon-4 and leapfrog operations, $Le(P_4(M))$, the tetrahedron (T), cube (C) was used to construct the molecular structures $\textrm{BCA}_{96}$ and $\textrm{BTA}_{48}$. By extending the cage produced by the octahedron, the molecular structure of $\textrm{BCZ}_{48}$ is defined. In all these structures, B connotes the benzene path of tessellation. C or T denotes the Platonic on which the map operations acted, A stands for armchair, and Z comes from the zig-zag ending of a nanotube. The last number in the notation denotes the cardinality of carbon atoms in the structures. We denote the molecular graph of $\textrm{BCZ}_{48}$ as BCZ(m, n). Similarly, the molecular graphs of $\textrm{BTA}_{48}$ and $\textrm{BCA}_{96}$ are denoted as BTA(m, n) and BCA(m, n), respectively. In this study, we focus on the molecular graph BCZ(m, n), which contains 24mn vertices and $32mn-2m-2n$ edges. Furthermore, the graph is bipartite, as evident from the unit cell of $\textrm{BCZ}_{48}$ and its construction shown in Figure 1.

The M-polynomial of BCZ(m, n) was obtained in³², and thereby the authors found few degree-based topological indices. Zagreb polynomials and a few more TIs were discussed in³³. The degree-based TIs of line graphs of BCZ(m, n) were dealt with in³⁴. A theoretical investigation of $\textrm{BTA}_{48}$ based on density functional theory was done in³⁵. With this motivation, we compute the ten most important distance based topological indices, develop a predictive model for graph energy, and provide NMR patterns for BCZ(m, n).

Graph-theoretical concepts

Let G be a graph with vertex set V(G) and edge set E(G). For $e_1= u_1u_2 \in E(G)$, we define

$$\begin{aligned} N_{u_1}(e_1|G)= \{v \in V(G): d_G(u_1,v)< d_G(u_2,v)\}, \\ M_{u_1}(e_1|G)= \{e_2 \in E(G): d_G(u_1,e_2) < d_G(u_2,e_2)\}. \end{aligned}$$

Their cardinalities, $|N_{u_1}(e_1|G)|=n_{u_1}(e_1|G)$ and $|M_{u_1}(e_1|G)|=m_{u_1}(e_1|G)$. The terms $n_{u_2}(e_1|G)$ and $m_{u_2}(e_1|G)$ are similar. The strength-weighted concept was initiated in³⁶ and later used in^{37,38,39,40,41,42} as $G^* = (G, (v_{w}, v_s), e_s)$ where $v_w$ is vertex weight, $v_s$ is the vertex strength and $e_s$ is the edge strength. Table 1 summaries the TIs with strength-weighted parameters, while for simple graphs, refer to^43,44. It should be noted that $d_{G^*}(u_1, u_2)= d_G(u_1, u_2)$ for any $u_1,u_2 \in V(G^*)$ and $D_{G^*}(e_1, e_2)= D_G(e_1, e_2)$ for any $e_1,e_2 \in E(G^*)$. Similarly, the sets $N_{u_1}(e_1|{G^*})= N_{u_1}(e_1|G)$ and $M_{u_1}(e_1|{G^*})= M_{u_1}(e_1 |G)$ are defined with cardinality

$$\begin{aligned} \begin{array}{l l} n_{u_1}(e_1|G^*) & = \sum \limits _{v \in N_{u_1}(e_1 |G^*)}v_{w}(v), and\\ m_{u_1}(e_1|G^*) & = \sum \limits _{v \in N_{u_1}(e_1 |G^*)}v_s(v)+\sum \limits _{e_2 \in M_{u_1}(e_1 |G^*)}e_s(e_2). \end{array} \end{aligned}$$

The values of $n_{u_2}(e_1|G^*)$ and $m_{u_2}(e_1|G^*)$ are analogous. The degree of the vertex $u_1$ in $G^*$ is defined as $d_{G^*}(u_1) = \sum \limits _{v \in N_{G^*}(u_1)}e_s(u_1v)$. Denote $\{1,2,3,\ldots , n\}$ as $\mathbb {N}_n$, and therefore $1\le i \le n$ as $i\in \mathbb {N}_n$.

Table 1 TIs and their mathematical expressions.

The cut approach proved to be very useful for handling distance-based graph invariants, which are fundamental ideas in chemical graph theory. There are other methods to find the distance-based invariants, but they do not serve the purpose of finding all indices. Those techniques explained in^45,46 are restricted to serving a few. For a comprehensive understanding of the cut process, please consult the latest survey by⁴³. Partial cubes, isometric subgraph, Djoković-Winkler $\varTheta$ condition, and convex subgraph are important components of the cut method. The well-defined collection of hypercubes’ subgraphs is termed a partial cube⁴⁷. The canonical metric representation was discussed in⁴⁸ to prove all benzenoid systems are partial cubes. The condition, $d_G(s_1,s_2)+d_G(t_1,t_2)\ne d_G(s_1,t_2)+d_G(t_1,s_2)$ for two edges $e_1=s_1t_1$ and $e_2=s_2t_2$ is called Djoković-Winkler ($\varTheta$) relation. Recently, Prabhu et al. proved that the anti-kekulene system also falls under partial cubes²⁰. It satisfies the first two conditions of the equivalence relation and fails to follow the third in general. Hence, the $\varTheta$ partitions of the edge set of a partial cube G into classes $F_1, F_2,\ldots F_r$, called $\varTheta$-classes or convex cuts. However, its transitive closure $\varTheta ^{*}$ forms an equivalence relation and partitions the edge set into many convex components. A partition $\mathscr {E} = \{E_{1},E_{2}, \ldots E_{k}\}$ of E(G) is considered coarser than partition $\mathscr {F}$ if every set $E_{i}$ is composed of one or more $\varTheta ^{*}$-classes of G. The quotient graph $G/E_i$ is created from the disconnected graph $G-E_i$ by treating the connected components as vertices. Two components $C_j^i$ and $C_k^i$ are connected in $G/E_i$ if there exists an edge $xy\in E_i$ where x is in $C_j^i$ and y is in $C_k^i$.

Mathematical results

Theorem 1

Let G be a BCZ(m, n) lattice structure, where $m,n\ge 1$. Then,

• (i) $W(G)= -(4m(216m^4 - 1080m^3n - 720m^2n^2 + 20m^2 - 2880mn^3 + 120mn + 180n^2 + 30n - 101))/15$.

• (ii) $W_e(G)= (- 1536m^5 + 7680m^4n + 5120m^3n^2 - 2560m^3n - 120m^3 + 20480m^2n^3 - 12480m^2n^2$$+ 1060m^2n - 60m^2 - 2560mn^3 + 460mn^2 + 560mn + 681m + 80n^3 - 60n^2 - 35n)/15$.

• (iii) $W_{ve}(G)= -(4m(288m^4 - 1440m^3n - 960m^2n^2 + 240m^2n + 20m^2 - 3840mn^3 + 1170mn^2$$+ 90mn + 240n^3 + 150n^2 - 45n - 128))/15$.

• (iv) $Sz_v(G)= (8m(- 96m^3 + 1152m^2n^3 + 156m^2n - 8m^2 + 24mn + 69m - 36n^3 - 6n + 8))/3$.

• (v) $Sz_e(G)= (- 384m^5 + 9600m^4n - 8400m^4 + 81920m^3n^3 - 39680m^3n^2 + 16680m^3n + 520m^3$$- 12800m^2n^3 + 2640m^2n^2 - 5560m^2n + 5880m^2 - 120mn^3 + 200mn^2 + 100mn - 256m - 120n^3)/15$.

• (vi) $Sz_{ev}(G)= (8m(- 18m^4 + 450m^3n - 660m^3 + 7680m^2n^3 - 1860m^2n^2 + 1170m^2n + 5m^2 - 600mn^3$$- 180mn + 480m - 150n^3 + 15n^2 - 30n + 13))/15$.

• (vii) $Sz_t(G)= (- 672m^5 + 16800m^4n - 22800m^4 + 250880m^3n^3 - 69440m^3n^2 + 41640m^3n + 280m^3$$- 22400m^2n^3 + 2640m^2n^2 - 7480m^2n + 16320m^2 - 3960mn^3 + 440mn^2 - 620mn + 272m - 120n^3)/15$.

• (viii) $PI(G)= 32m^3 + 1024m^2n^2 - 232m^2n + 8m^2 - 136mn^2 + 8mn - 16m + 8n^2$.

• (ix) $S(G)= -(16m(288m^4 - 1440m^3n - 960m^2n^2 + 240m^2n + 20m^2 - 3840mn^3 + 450mn^2$$+ 135mn + 240n^3 + 195n^2 - 45n - 128))/15$.

• (x) $Gut(G)= (- 6144m^5 + 30720m^4n + 20480m^3n^2 - 10240m^3n + 81920m^2n^3 - 19200m^2n^2 - 1160m^2n$$- 60m^2 - 10240mn^3 - 2120mn^2 + 2480mn + 2484m + 320n^3 - 60n^2 - 140n)/15$.

Proof

Let $\{Z_{1i} : i \in \mathbb {N}_{m-1}\}$, $\{Z_{2i} : i \in \mathbb {N}_{n-m+1}\}$, $\{O_{1i} : i \in \mathbb {N}_m\}$, $\{O_{2i} : i \in \mathbb {N}_{n-m}\}$, $\{V_i : i\in \mathbb {N}_{2n-1}\}$ and $\{H_i : i \in \mathbb {N}_{2m-1}\}$ be the different cuts of BCZ(m, n). For reference, cuts of BCZ(4, 6) are depicted in Figures 2, 3, and 4. The quotient graphs $G/ Z_{1i}$, $G/ Z_{2i}$ are isomorphic to $K_{2,4i}$ and $K_{2,4m}$, depicted in Figures 5(a) and (b). The quotient graphs corresponding to obtuse, vertical and horizontal cuts $G/O_{1i}$, $G/O_{2i}$, $G/ V_{i}$ and $G/ H_{i}$ are path on two vertices and respectively depicted in Figures 6(a), (b), (c) and (d) along with their edge strengths. The vertex strength-weighted values of all these quotient graphs are given in Table 2.

Fig. 2

Zig-zag cuts.

Fig. 3

Vertical and horizontal cuts.

Fig. 4

Acute and obtuse cuts.

Fig. 5

(a) $G/Z_{1i}\cong K_{2,4i}$ (b) $G/Z_{2i}\cong K_{2,4m}$.

Fig. 6

(a) $G/O_{1i}: i \in \mathbb {N}_{m}$; (b) $G/O_{2i}: i \in \mathbb {N}_{n-m}$; (c) $G/V_i: i \in \mathbb {N}_{2n-1}$; (d) $G/H_i: i \in \mathbb {N}_{2m-1}$.

Table 2 Strength-weighted values of $G^*$.

$$\begin{aligned} W(G)&= 2\Big [2 \sum _{i \in \mathbb {N}_{m-1}} [4i (x_1+x_2)+2x_1x_2 +4i(4i-1)] + \sum _{i \in \mathbb {N}_{n-m+1}} [4m (x_3+x_4)+2x_3x_4 +4m(4m-1)] \Big ]&\\&\ \ \ + 2\Big [2\sum _{i \in \mathbb {N}_{m}} x_5x_6+ \sum _ {i \in \mathbb {N}_{n-m}} x_7x_8\Big ]+ \sum _{i \in \mathbb {N}_{2n-1}} x_{9}x_{10}+\sum _{i \in \mathbb {N}_{2m-1}} x_{11}x_{12}.\end{aligned}$$

$$\begin{aligned} W_e(G)&= 2\Big [2 \sum _{i \in \mathbb {N}_{m-1}} [4i (y_1+y_2)+2y_1y_2 +4i(4i-1)] + \sum _{i \in \mathbb {N}_{n-m+1}} [4m (y_3+y_4)+2y_3y_4 +4m(4m-1)] \Big ]&\\&\ \ \ + 2\Big [2\sum _{i \in \mathbb {N}_{m}} y_5y_6+ \sum _{i \in \mathbb {N}_{n-m}} y_7y_8\Big ]+ \sum _{i \in \mathbb {N}_{2n-1}} y_{9}y_{10}+\sum _{i \in \mathbb {N}_{2m-1}} y_{11}y_{12}.\end{aligned}$$

$$\begin{aligned}W_{ve}(G)&= \frac{1}{2}\Bigg [2\Big [2 \sum _{i \in \mathbb {N}_{m-1}} [4i (x_1+x_2+y_1+y_2)+2(x_1y_2+x_2y_1) +8i(4i-1)]&\\&\ \ \ + \sum _{i \in \mathbb {N}_{n-m+1}} [4m (x_3+x_4+y_3+y_4)&\\&\ \ \ +2(x_3y_4+x_4y_3) +8m(4m-1)] \Big ]&\\&\ \ \ +2\Big [2\sum _{i \in \mathbb {N}_{m}} (x_5y_6+x_6y_5)+\sum _{i \in \mathbb {N}_{n-m}} (x_7y_{8}+x_{8}y_7)\Big ]&\\&\ \ \ + \sum _{i \in \mathbb {N}_{2n-1}} (x_{9}y_{10}+x_{10}y_{9})+ \sum _{i \in \mathbb {N}_{2m-1}} (x_{11}y_{12}+x_{12}y_{11})\Bigg ].\end{aligned}$$

$$\begin{aligned}Sz_v(G)&= 2\Bigg [2 \sum _{i \in \mathbb {N}_{m-1}} 4i [(x_1+4i-1)(x_2+1)+(x_2+4i-1)(x_1+1)]&\\&\ \ \ + \sum _{i \in \mathbb {N}_{n-m+1}} 4m[(x_3+4m-1)(x_4+1)&\\&\ \ \ +(x_4+4m-1)(x_3+1)] \Bigg ]+ 2\Big [2 \sum _{i \in \mathbb {N}_{m}} (4i-2)x_5x_{6}+ \sum _{i \in \mathbb {N}_{n-m}} 4mx_{7}x_{8} \Big ]&\\&\ \ \ + \sum _{i \in \mathbb {N}_{2n-1}} 2mx_{9}x_{10}+ \sum _{i \in \mathbb {N}_{2m-1}} 2nx_{11}x_{12}.&\end{aligned}$$

$$\begin{aligned}Sz_e(G)&= 2\Bigg [2 \sum _{i \in \mathbb {N}_{m-1}} 4i [(y_1+4i-1)(y_2+1)+(y_2+4i-1)(y_1+1)]&\\&\ \ \ + \sum _{i \in \mathbb {N}_{n-m+1}} 4m[(y_3+4m-1)(y_4+1)&\\&\ \ \ +(y_4+4m-1)(y_3+1)] \Bigg ]+ 2\Big [2 \sum _{i \in \mathbb {N}_{m}} (4i-2)y_5y_{6}+ \sum _{i \in \mathbb {N}_{n-m}} 4my_{7}y_{8} \Big ]&\\&\ \ \ + \sum _{i \in \mathbb {N}_{2n-1}} 2my_{9}y_{10}+ \sum _{i \in \mathbb {N}_{2m-1}} 2ny_{11}y_{12}.\end{aligned}$$

$$\begin{aligned}Sz_{ev}(G)&= \frac{1}{2}\Bigg [2\Bigg [2 \sum _{i \in \mathbb {N}_{m-1}} 4i [(x_1+4i-1)(y_2+1)&\\&\ \ \ +(y_1+4i-1)(x_2+1)+(x_2+4i-1)(y_1+1)+(y_2+4i-1)(x_1+1)]&\\&\ \ \ + \sum _{i \in \mathbb {N}_{n-m+1}} 4m [(x_3+4m-1)(y_4+1)&\\&\ \ \ +(y_3+4m-1)(x_4+1)+(x_4+4m-1)(y_3+1)+(y_4+4m-1)(x_3+1)\Bigg ]&\\&\ \ \ + 2\Big [2 \sum _{i \in \mathbb {N}_{m}} (4i-2)(x_5y_6+x_{6}y_5)+ \sum _{i \in \mathbb {N}_{n-m}} 4m(x_7y_8+x_{8}y_7) \Big ]&\\&\ \ \ + \sum _{i \in \mathbb {N}_{2n-1}} 2m(x_9y_{10}+x_{10}y_9)&\\&\ \ \ + \sum _{i \in \mathbb {N}_{2m-1}} 2n(x_{11}y_{12}+x_{12}y_{11})\Bigg ].\end{aligned}$$

$$\begin{aligned}Sz_{t}(G)&= Sz_{v}(G)+Sz_{e}(G)+2Sz_{ve}(G).\end{aligned}$$

$$\begin{aligned}PI(G)&= 2\Bigg [2 \sum _{i \in \mathbb {N}_{m-1}} 4i (2(y_1+y_2)+8i) + \sum _{i \in \mathbb {N}_{n-m+1}} 4m(2(y_3+y_4)+8m) \Bigg ]\\&\ \ \ +2\Bigg [2 \sum _{i \in \mathbb {N}_{m}} (4i-2) (y_5+y_6) + \sum _{i \in \mathbb {N}_{n-m}} 4m(y_7+y_8) \Bigg ]\\&\ \ \ + \sum _{i \in \mathbb {N}_{2n-1}} 2m(y_9+y_{10})+\sum _{i \in \mathbb {N}_{2m-1}} 2n(y_{11}+y_{12}).\end{aligned}$$

$$\begin{aligned}S(G)&= 2\Bigg [2 \sum _{i \in \mathbb {N}_{m-1}} [4i (2(x_1+x_2+y_1+y_2)+8i)&\\&\ \ \ +2[x_1(2y_2+4i)+x_2(2y_1+4i)]+16i(4i-1)]&\\&\ \ \ + \sum _{i \in \mathbb {N}_{n-m+1}} [4m (2(x_3+x_4+y_3+y_4)+8m)&\\&\ \ \ +2[x_3(2y_4+4m)+x_4(2y_3+4m])+16m(4m-1)] \Bigg ]&\\&\ \ \ + 2\Big [2\sum _{i \in \mathbb {N}_{m}} [x_5(2y_6+4i-2)+x_6(2y_5+4i-2)]&\\&\ \ \ +\sum _{i \in \mathbb {N}_{n-m}} [x_7(2y_{8}+4m)+x_{8}(2y_7+4m)]\Big ]&\\&\ \ \ +\sum _{i \in \mathbb {N}_{2n-1}} x_9(2y_{10}+2m)+x_{10}(2y_9+2m)&\\&\ \ \ +\sum _{i \in \mathbb {N}_{2m-1}} x_{11}(2y_{12}+2n)+x_{12}(2y_{11}+2n).\end{aligned}$$

$$\begin{aligned}Gut(G)&=2\Bigg [2 \sum _{i \in \mathbb {N}_{m-1}} [8i (2(y_1+y_2)+8i)+2[(2y_1+4i)(2y_2+4i)]+16i(4i-1)]&\\&\ \ \ + \sum _{i \in \mathbb {N}_{n-m+1}} [8m(2(y_3+y_4)+8m)+2[(2y_3+4m)(2y_4+4m)]+16m(4m-1)] \Bigg ]&\\&\ \ \ + 2\Big [2\sum _{i \in \mathbb {N}_{m}} [(2y_6+4i-2)(2y_5+4i-2)] +\sum _{i \in \mathbb {N}_{n-m}} [(2y_{8}+4m)(2y_7+4m)]\Big ]&\\&\ \ \ +\sum _{i \in \mathbb {N}_{2n-1}} (2y_{10}+2m)(2y_9+2m)+\sum _{i \in \mathbb {N}_{2m-1}} (2y_{12}+2n)(2y_{11}+2n).\end{aligned}$$

The above expressions are simplified using Table 2 to derive the mathematical results. $\square$

The degree-based indices of BCZ(m, n) were discussed in^32,33 and are stated below. The numerical values of the distance based indices discussed in this paper are given in Table 3, while the degree based indices are provided in Table 4. Figures 7(a) and (b) depict the graphical representation of Tables 3 and 4, respectively.

Theorem 2

^32,33 Let G be a BCZ(m, n), $m,n\ge 1$. Then,

• (i) $M_{1}(G) = 176mn-20m-20n.$

• (ii) $M_{2}(G) = 240mn-38m-38n.$

• (iii) $HM(G) = 196mn-152m-152n.$

• (iv) $H(G) =\frac{1}{15}\left[ 176mn\right] .$

• (v) $GA(G)= \frac{1}{5}\left[ \left( 32\sqrt{6}+80\right) mn-10m-10n\right] .$

• (vi) $AZ(G) =\frac{1}{32} \left[ 9928mn-1163m-1163n\right] .$

• (vii) $ABC(G)=\frac{1}{3}\left[ (24\sqrt{2}+32)mn+\left( 6\sqrt{2}-12\right) m+\left( 6\sqrt{2}-12\right) n\right] .$

• (viii) $R(G)=\frac{1}{3}\left[ 8\sqrt{6}+16\right] mn.$

• (ix) $SDD(G) =\frac{1}{3}\left[ 200mn-12m-12n\right] .$

• (x) $ISI(G)=\frac{1}{5}\left[ 216mn-25m-25n\right] .$

Table 3 Numerical values of distance based TIs of 2D lattice.

Fig. 7

(a) Graphical comparison of 2D lattice BCZ(m, n) (a) Distance based TIs (b) Degree based TIs.

Table 4 Numerical values of degree based TIs of 2D lattice.

Applications to graph energy and $^{13}$C NMR signals

Graph energy was introduced as a mathematical abstraction of $\pi$-electron energy, based on the idea that the two are approximately proportional. This connection emerged from the study of molecular orbital theory in conjugated hydrocarbons, such as benzene^49,50. As a result, graph energy has become a useful tool for developing mathematical models⁵¹ to analyze molecular stability and reactivity.

The graph energy of a molecular graph G is mathematically defined as the sum of the absolute values of the eigenvalues of the adjacency matrix of G. Suppose $\lambda _1, \lambda _2, \dots , \lambda _p$ are the eigenvalues of G with order p. Then, the graph energy $E_\pi$ of G is defined as

$$\begin{aligned} E_{\pi }(G)= \sum _{i=1}^{p} |\lambda _{i}| \end{aligned}$$

The computational difficulties of calculating graph energy arise primarily from determining the eigenvalues from the characteristic polynomial, which becomes increasingly challenging for large and complex graphs. This challenge has spurred the development of algorithms and mathematical models. In this study, we formulate a mathematical model for predicting graph energy using distance-based topological indices, as discussed in the earlier section. We use the newGRAPH package⁵² to compute the graph energy for specific dimensions, as presented in Table 5. As we see from Table 3, the distance-based indices increase rapidly with the structure’s dimension. Therefore, we scale the indices based on their vertex and edge contributions during computation. Vertex-contributed indices, such as W, $W_{e}$, $W_{ve}$, S, and Gut, are divided by the number of vertices, while indices such as $Sz_{v}$, $Sz_{e}$, $Sz_{ev}$, $Sz_{t}$, and PI are divided by the number of edges. These scaled indices are then correlated with the graph energy values, revealing that PI has the highest correlation, as shown in Table 5, where $PI^* = PI/|E|$. The resulting equation is given below.

$$\begin{aligned} E_{\pi }(BCZ(m,n))= 1.116595(PI^*(BCZ(m,n)))+10.60676 \end{aligned}$$

where correlation coefficient $r=0.999993384$, F-value $F=453447.0452$, and standard error $SE=3.102795978.$

Table 5 Correlation between the graph energy and the scaled PI index of BCZ(m, n).

Applications of machine learning related to spectroscopy and BCZ stability can make use of the topological information stored in the adjacency and distance matrices of these structures. It is feasible that we will be able to design a strategy for the vertex partitioning of BCZ if we take the distance matrices of these structures and use them to create the distance degree sequence vectors (DDSV) for each vertex of BCZ. Such a strategy would allow us to partition the vertex connections of these structures. For the purpose of generating the vertex divisions, graph theory is the only instrument that is employed within the context of this approach; experimental reference values are not utilized in any way. In spite of the fact that the DDSV equivalence does not always exhibit isomorphism with the automorphic equivalence of vertices, Quintas and colleagues⁵³ demonstrated that DDSVs can be employed to study network vertices. The number of vertices in BCZ that are at distance j from any vertex $v_i$ is represented as $D_{ij}$. The set $\{D_{i0}, D_{i1}, D_{i2},... D_{ij},...\}$ represents the DDSV of every vertex in BCZ.

It is possible to produce the DDSV of each vertex in any dimension of BCZ, as described in the sources given in⁵². This can be accomplished by utilising the newGRAPH interface. Following that, Python code is utilized in order to study the DDSVs that have been assigned to each vertex. When a significant number of DDSVs are exchanged, sets of vertices will begin to converge. Constructing nuclear divisions is challenging due to the presence of multiple nuclei associated with vectors of varying DDSV lengths, which complicates the process. However, with the assistance of MATLAB code developed using analytical equations, the numerical findings for the topological descriptors of BCZ were successfully verified.

According to the data presented in Table 6, the four distinct dimensions each exhibit their own unique nuclear equivalence classes. All of their atomic identities, connectivities, and automorphic symmetries are highly distinct from one another. Given the considerable number of different carbon nuclear equivalence classes, nuclear magnetic resonance (NMR) spectroscopy of carbon-13 (C-13) should be an effective tool for comparing the various dimensions. For the purpose of forecasting the quantity of $^{13}$C nuclear magnetic resonance (NMR) signals, as well as the patterns of their intensity, the nuclear equivalence class structures, which are displayed in Table 6, can be utilized. Consequently, $^{13}$C NMR spectroscopy is an effective tool for investigating the structures of specific assemblies.

Table 6 $^{13}$C NMR signals and intensity patterns.

The HOMO-LUMO gaps, which are indicative of kinetic stability, tend to decrease in the BCZ as the values of m and n increase, as can be seen by examining Table 7. With each increase in m and n, the gap gets closer and closer to being equal to zero. In light of the fact that this is the situation, the vast majority of chains exhibit HOMO-LUMO gaps of BCZ that are almost small. Because this shows that they have triplet spin ground states, it is feasible that BCZ could be advantageous to topological spintronics. This is because of the fact that they have triplet spin ground states. Table 7 contains the energy measurements, which take into consideration the total energy of the $\pi$-electron as well as the delocalisation energies for each bond. On the basis of the theoretical estimation of the potential energy, these observations have been accomplished.

Let p be the number of vertices in BCZ. The energy of the highest occupied molecular orbital (HOMO) is $\hbox {E}_{HOMO}$=$\lambda _{p/2}$ and the energy of the lowest unoccupied molecular orbital (LUMO) is $\hbox {E}_{LUMO}$=$\lambda _{p/2+1}$. Therefore, HOMO-LUMO gap is $\delta _{HL}= \lambda _{p/2}-\lambda _{p/2+1}$. The total $\pi$-electron energy is $E_{\pi }=2\sum _{i=1}^{p/2}\lambda _i$ and the delocalization energy is $E_{Deloc}= E_{\pi }-p$⁵⁴. In the above formulas, the energies are stated in conventional $\beta$-units in Table 7.

Table 7 Spectral and energetic properties of BCZ(m, n).

To develop hybrid quantum chemistry techniques better suited for handling large systems, quantum chemical parameterizations can leverage the topological characteristics and matrices that have been computed. For instance, graph theory, in conjunction with Pariser-Parr-Pople processes, effectively manages $\pi$-electrons. By applying the CASSCF/CI methods⁵⁵ to a collection of smaller molecular building blocks, it is possible to determine parameters related to hybrid techniques. Consequently, topological indices that account for distance, such as those using resistance as an indicator, can provide significant advantages and insights into deriving more precise parameters from quantum chemical approaches.

Conclusion

In recent years, molecular topology has emerged as an effective method for drug design and discovery. It involves identifying molecules with similar structural characteristics that exhibit comparable pharmacological activities. In this study, we employed the strength-weighted graph approach to derive distance based topological indices for the 2D lattice of BCZ benzene structures. We developed a linear regression model to predict the graph energy of these structures based on the computed topological indices, achieving high correlation. Additionally, we provided $^{13}$C NMR signals and intensity patterns by incorporating distance matrices and presented the HOMO-LUMO gaps for these structures.