Detecting significant expression patterns in single-cell and spatial transcriptomics with a flexible computational approach

Abstract

Gene expression data holds the potential to shed light on multiple biological processes at once. However, data analysis methods for single cell sequencing mostly focus on finding cell clusters or the principal progression line of the data. Data analysis for spatial transcriptomics mostly addresses clustering and finding spatially variable genes. Existing data analysis methods are effective in finding the main data features, but they might miss less pronounced, albeit significant, processes, possibly involving a subset of the samples. In this work we present SPIRAL: Significant Process InfeRence ALgorithm. SPIRAL is based on Gaussian statistics to detect all statistically significant biological processes in single cell, bulk and spatial transcriptomics data. The algorithm outputs a list of structures, each defined by a set of genes working simultaneously in a specific population of cells. SPIRAL is unique in its flexibility: the structures are constructed by selecting subsets of genes and cells based on statistically significant and consistent differential expression. Every gene and every cell may be part of one structure, more or none. SPIRAL also provides several visual representations of structures and pathway enrichment information. We validated the statistical soundness of SPIRAL on synthetic datasets and applied it to single cell, spatial and bulk RNA-sequencing datasets. SPIRAL is available at https://spiral.technion.ac.il/.

Biological processes are often characterized by consistent and concerted changes in the levels of expression of some set of genes. The current common pipeline to discover gene expression dynamics in single cell RNA-seq (scRNA-seq) data is to first cluster the cells into cell types or states, then to perform differential expression analysis between clusters^1,2. Another approach is trajectory inference: a method that reconstructs the primary biological process in the data by ordering the cells based on similarities of their expression profiles^3,4. Trajectory inference is mostly employed to recognize developmental processes³. Once the pseudo-time of each cell has been established, it is possible to use regression to identify genes whose expression changes along the trajectory^1,5.

However, both clustering and trajectory inference are usually done after dimensionality reduction, which is either performed with principal component analysis (PCA), diffusion maps or simply by filtering for highly variable genes^1,2,6,7,8. While this step ensures that the principal cell partitioning or trajectory in the data would be captured, it lowers the chance of discovering less dominant biological processes. For example, processes that only involve a small fraction of the genes. Small but distinctive populations of cells may also be missed². Even if the clustering or trajectory inference are done on the original space (i.e. using all genes), gene expression levels are only compared between predetermined clusters or along a predetermined trajectory, making it impossible to find biological processes that do not agree with these principal, most significant, orderings. Finally, since both clustering and trajectory inference are ultimately determined by gene expression levels, the significance of differential expression of genes between clusters or along a trajectory cannot be evaluated without correcting for this selection bias^1,9.

Another analysis approach is to detect co-expression modules by clustering the genes. Since the clustering is done based on the gene expression values across all cells, genes which are only coexpressed in a subpopulation of cells (for example, in certain states or cell types) might not be grouped together, and structures will go undetected. Also, while gene-clustering ensures that every gene would be assigned to a cluster, it does not provide any confidence score as to the level of fitness of every gene to its cluster. As a result, we might get large and non-accurate clusters of genes¹⁰. The option of fuzzy clustering of genes would provide membership grades, however, they would still rely on the expression pattern in all cells (rather than the expression levels in an unknown relevant subset of cells). Another caveat to both cell-clustering and gene-clustering (hard and fuzzy), is that the user must specify the clustering level in advance.

Recently, spatial transcriptomics technologies emerged, enabling the measurement of gene expression in spots laid out on a slice of tissue, maintaining both transcriptomic and spatial information^11,12,13,14. Data analysis approaches for spatial data are also under active development^11,15. Some analysis methods use the spatial coordinates to find spatially variable (sometimes called: spatially coherent) genes. These are genes whose expression profile fits a spatial pattern. These methods include SpatialDE¹⁶, trendsceek¹⁷, SPARK¹⁸, SPARK-X¹⁹, the BinSpect method (which is implemented in the Giotto platform)²⁰, GPcounts²¹ and singleCellHaystack² (the latter can also be applied to scRNA-seq data using its tSNE coordinates). However, all of these methods focus on identifying individual genes, and only some of them eventually cluster these genes into gene sets. singleCellHaystack does so with kmeans, SpatialDE clusters the genes based on a spatial clustering model and Giotto clusters them with hierarchical clustering. While this clustering based approach produces spatially coherent modules, it limits the flexibility of these modules. First, only the genes that were found to be spatially variable are considered. Second, the known caveats of gene-clustering (described above) apply here, namely that the clusters do not have significance scores and that the chance of finding partly-cooperating genes is low. And third, a gene cannot be a member of more than one module. Finally, in all three methods the user must define both the number of modules, and either a p-value threshold or a number of top genes to participate in the clustering process. Given the diversity of gene expression datasets (sizes, sequencing technologies and spatial patterns), these parameters cannot be easily determined by the user.

In this work we present SPIRAL: Significant Process InfeRence ALgorithm. To our knowledge, this is the first analysis method that uses trends of gene expression, possibly on sample subsets, as its sole detection criterion. SPIRAL detects structures: sets of genes with a similar expression pattern in a subset of cells, samples or spots. Each of these structures reveals information that pertains to a biological process in the data. Namely- the cells or spots represent stages or states of the process and the set of genes has expression dynamics that is consistent between the stages. SPIRAL provides a list of genes, and a partitioning of the cells or spots into layers based on the expression values of these structure defining genes. The output list of structures provides an overview of the data, with statistical significance components. The flexibility of structures within SPIRAL allows each gene and cell or spot to participate in zero, one, or multiple structures. Finally, SPIRAL’s web interface enables users to easily navigate through diverse structure visualizations and thoroughly explore the gene expression patterns that have been identified within the data.

We compared SPIRAL’s performance to state-of-the-art methods using various datasets, including a simulated dataset, single-cell datasets acquired through 10X and inDrops technologies, as well as spatial transcriptomics datasets obtained by the ST method (“Spatial Transcriptomics” as presented in¹²) and Visium. Additionally, we employed SPIRAL to analyze bulk RNA-seq samples (see Supplementary Table 1 for the list of datasets). We found that SPIRAL not only performed best on synthetic data, but also found significant and biologically important processes in real datasets. For example, SPIRAL identified both a translational process involving 99 genes and an immune process involving 142 genes in a lymphoblastoid cell line. In a dataset of Zebrafish differentiation, SPIRAL detected four different structures, each pertains to a different step of development. In spatial datasets, SPIRAL identified many region-specific structures, although it does not use the spatial coordinates as input. An illustrative instance is the identification of a distinct and clearly delineated area within the mouse brain, characterized by the overexpression of 321 genes. Employing the gene ontology (GO) enrichment analysis, which SPIRAL conducts for all identified structures, led us to infer that the active biological processes in this region are neuron ensheathment and myelination. Likewise, another more refined region was identified as a blood vessel using the same approach. Users cannot pinpoint the blood vessel based on the clustering offered by Visium, since the blood vessel region was not clustered separately. SPIRAL also detected structures enlightening different development stages and various stages of an immune process in bulk datasets, as well as batch effects. Finally, when comparing the active biological processes detected by the different methods, we found that in all single cell and spatial datasets, there was a subset of these enriched processes that was exclusively identified by SPIRAL.

Results

Algorithm overview

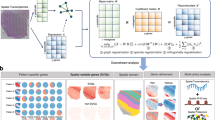
SPIRAL first performs fine agglomerative clustering of the cells or spots based on their full gene expression profile. Each cluster is represented by its average expression profile and referred to as “repcell”. The default number of repcells is $\sim 100$. This step reduces both technical noise and computational load. SPIRAL then computes the difference in expression values for every pair of repcells, for all genes. Then, in an iterative manner, it finds a gene set and a repcell-pair set in which the genes have significantly large expression-difference values (Fig. 1). The gene set and the set of repcells constitute a consistent structure, representing a consistent change in the biology of the cells or spots.

SPIRAL structures are evaluated using a statistical significance criterion based on the gene expression level differences (p-value), and a biological significance score ($\widetilde{\sigma }$- see Methods, “Evaluating the structure of repcells consisting of the sub-matrix columns”). These are used to filter out non-significant structures. Also, the list of structures is narrowed down to structures that are unique in terms of their Jaccard index of gene sets and repcell-pair sets, and the user may fine-tune the resulting list of structures by further adjusting the maximal allowed Jaccard index (JaccThr) of gene sets (Methods, “Post-filtering of structures”). SPIRAL can also be applied to bulk RNA-seq. SPIRAL outputs several different visual representations of each structure, including information about the enriched GO terms of the structure defining gene set.

SPIRAL thus takes single cell, spatial transcriptomics or bulk data as input and provides significant and consistent expression patterns$\backslash$structures as output.

Figure 1

The SPIRAL algorithm pipeline. Structures marked with an X are filtered out; structures marked with a V are included in the reported structures. See text and Methods for details on the algorithm steps and the filtering criteria.

SPIRAL best predicts gene clusters in synthetic data

We demonstrate SPIRAL’s performance on a synthetic single cell dataset. We then compare SPIRAL to other methods that output multiple sets of genes: nsNMF, Slingshot combined with tradeseq, Hotspot, Seurat and singleCellHaystack. Full details on the execution of these benchmark methods can be found in Methods.

We used Splatter²² to synthesize scRNA-seq data with a branching lineage of 7000 cells and 10000 genes (Methods, Fig. 2a). “True gene clusters” were determined as the sets of genes with ascending or descending expression along each of the three paths- overall six gene clusters (Methods). We repeated this process 10 times, each time computing the fuzzy rand index (FRI)²³ between the clustering of genes suggested by SPIRAL and each of the benchmark methods and the “true gene clusters”. As shown in Fig. 2b, SPIRAL’s FRIs were better than the other methods.

Also, for each “true gene cluster”, we evaluated how well each method predicted this cluster by computing the Jaccard index between the “true gene cluster” and each of the method clusters, and picking the highest score. The Jaccard index is defined as $\frac{size(G_1\cap G_2)}{size(G_1\cup G_2)}$ for gene clusters $G_1$ and $G_2$. We then aggregated these scores for each method- the best Jaccard indices for all “true gene clusters” in all repetitions (Fig. 2c). Overall, SPIRAL’s prediction rates were better than those of the other methods.

For a more qualitative assessment, we depict in Fig. 2d the structures detected by SPIRAL for the first dataset (out of the 10 repetitions). Choosing JaccThr=0.05, SPIRAL outputs 6 structures for this dataset. The UMAP layouts of these structures are displayed (gene sets are not shown). For Structure E, which involves 361 genes, we also present a panel of visualization layouts. The network layout (E.1) is a graphical representation of the repcell-pairs participating in the structure. Every repcell is represented by a node, and an edge exists between two repcells if the repcell-pair is part of the structure, that is, if SPIRAL detected a significant change in expression (of the structure genes) between the two repcells (Detailed information about the network construction process can be found in Methods, “Producing the network layout and partitioning the repcells to layers”). The network layout provides information regarding the level of connectivity and skewness of the structure. Here all repcells (nodes) in layer 1 (low expression layer) and in layer 3 (high expression layer) have similar sizes (which means their degrees are similar), so the structure is well-connected and not skewed. The UMAP layout of repcells (E.2) allows us to place the process on a timeline, based on our preliminary information of the dataset. Here, we can conclude that the structure genes increase their expression along the lineage of Path1 and then reduce their expression along Path2 and Path3. The UMAP layout of the original data (E.3) ensures that the repcells faithfully represent the original data. SPIRAL’s partition to layers, depicted by the columns of E.1 and the colors in E.2 and E.3, tells us about how this structure was spotted by the algorithm. However, more detailed insights regarding change over time can be captured by looking at the above UMAP layout (E), in which the colors correspond to average expression level of the structure genes. The clustering made in the first step to create 100 repcells in this dataset appears in Supplementary Fig. 1.

Figure 2

SPIRAL output and a comparison between methods for synthetic data. (a) a UMAP layout of the synthetic data. (b) Level of concordance (FRI) between the “true gene clustering” and the methods’ gene modules over 10 repetitions. (c) Best Jaccard index for each of the 6 “true gene clusters” over 10 repetitions, aggregated for each method (see text). This can be interpreted as the degree to which the methods were able to predict the true clusters. P-values annotated in (b,c) were produced by a two-sided Wilcoxon rank-sum test comparing SPIRAL values to all other values. (d) UMAP layouts for SPIRAL structures. Colors indicate the average expression level of the structure genes (see Methods, “SPIRAL visualizations and gene enrichment”). For example, Structure A indicates that there are 482 genes with high expression values along Path 1 and Path 3, and a declining expression pattern along Path 2. For Structure E, three additional visual representations are shown: (E.1) a network layout. Every node is a repcell, repcells are divided into three layers of expression. Every edge links two repcells which significantly differ in the expression values of the structure genes. (E.2) UMAP layout of repcells. Repcells are colored based on their layer of expression. (E.3) UMAP layout of cells. Cells are colored based on the layer of expression of the repcell they were assigned to.

SPIRAL uniquely identifies active biological processes in single-cell RNA-seq

We applied SPIRAL to a set of lymphoblastoid cells of the GM12891 cell line, sequenced using 10X technology²⁴. Figure 3a depicts two SPIRAL structures for this dataset. SPIRAL’s assignment of cells to layers (network and left UMAP layout, for each of the structures) remarkably fit the average expression levels of the structure genes (right UMAP layout). Also, the GO enrichment analysis of the gene sets reveals that Structure A captured a translational process, while Structure B identified an immune process.

Figure 3

SPIRAL analysis of a single-cell RNAseq dataset of lymphoblastoid cells²⁴. (a) Two SPIRAL structures. The structures are presented in a network layout (top), in which nodes represent repcells, edges represent repcell-pairs, size of nodes corresponds to their degree; UMAP layouts (middle), in which “average expression level” refers to the average expression level of structure genes; and a GO term enrichment figure (bottom). (b) Heatmap of p-values of specific GO terms discovered by the different methods. (c) Sizes of the gene modules reported by the different methods.

We also applied SPIRAL to a single-cell dataset of Zebrafish differentiation (Fig. 4a), taken in 7 time points post fertilization (library preparation by inDrops)²⁵. Four SPIRAL structures for this dataset are depicted in Fig. 4b, revealing an upregulation in RNA splicing on hours $4-8$ post fertilization, followed by an upregulation in ribosomal process on hours $6-~18$, in chordate embryonic development and in eryhthrocyte differentiation on hours $14-24$ and in active cytoskeleton organization at the very late stages.

Figure 4

SPIRAL analysis of a single cell dataset of Zebrafish differentiation²⁵. (a) PCA layout of raw data. Markers correspond to hours post fertilization. (b) PCA layouts of four SPIRAL structures. “average expression level” refers to the average expression level of structure genes. (c) Heatmap of p-values of specific GO terms discovered by the different methods. (d) Sizes of the gene modules reported by the different methods.

We sought to compare the most meaningful biological processes revealed by SPIRAL in these two datasets to those of Seurat, singleCellHaystack, Slingshot combined with tradeseq, Hotspot and nsNMF (Methods). For that purpose we used the goatools package²⁶ to curate a list of the most specific GO terms (tinfo $>9$) discovered by each method. As seen in Figs. 3b and 4c, SPIRAL identified several processes for the lymphoblastoid cells that were not detected by other methods, such as ’interleukin-21-mediated signaling pathway’ and ’interleukin-9-mediated signaling pathway’. Both interleukin-21 and interleukin-9 are cytokines that are known to have a role in lymphoid development and differentiation²⁷. In the Zebrafish embryo dataset, SPIRAL uniquely identified ’DNA replication proofreading’, ’single-stranded 3’-5’ DNA helicase activity’ and ’otic placode development’. While other methods also identified meaningful processes, it seems that no single method could predict the entirety of active biological processes in any of the datasets. We also note that we could not run Hotspot on the relatively large Zebrafish dataset using a standard server (Methods).

As to the sizes of the reported gene modules, SPIRAL’s modules in these two single cell datasets are similar in size to those of SingleCellHaystack and Seurat. They are larger than the gene modules of Slingshot+tradeSeq, Hotspot (for the lymphoblastoid dataset) and nsNMF (Figs. 3c and 4d).

SPIRAL identifies spatially defined active processes in spatial transcriptomics datasets

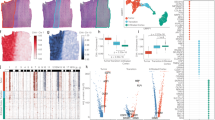
We applied SPIRAL to two Visium datasets and one ST dataset (Figs. 5, 6 and 7). SPIRAL does not use the spatial coordinates as input, and yet- many of the detected biological processes in all analysed samples are region-specific. In a sagittal-posterior section of a mouse brain²⁸, SPIRAL detected several significant structures, spatially mapping active biological processes to specific regions in the slide. For example: ensheathment of neurons and myelination, dendritic spine morphogenesis, and cell motility and angiogenesis (Fig. 5a). We note that although some angiogenesis related genes were found to be up-regulated in some clusters in Visium’s analysis of this dataset²⁹, none of them fit the blood vessel pattern clearly seen in Structure F. An interesting observation is that some genes appear in more than one structure. For example, Structure B shares 104 genes with Structure C, 34 genes with Structure D and 10 genes with Structure E (Fig. 5c). Further analyzing the difference between structures B and D, we note that the genes participating in Structure D play a role in a regional distinction in the brain. The genes participating in Structure B, however, play a role in distinguishing cells belonging to different types.

When comparing the specific GO terms (see former section) between SPIRAL and Seurat, Hotspot, SpatialDE, SingleCellHaystack and nsNMF (Fig. 5b, Methods), we found that SPIRAL, as well as Seurat and Hotspot, predict unique GO terms. For instance, SPIRAL uniquely discovered ’postsynaptic endocytic zone cytoplasmic component’ and ’piccolo -bassoon transport vesicle’, which may indicate high rates of neurotransmission at certain brain regions³⁰.

Figure 5

SPIRAL analysis of a spatial transcriptomics dataset (Visium) of a mouse brain²⁸. (a) Visium’s H &E slide, and spatial layouts of six SPIRAL structures. average expression level refers to the average expression level of structure genes (Methods). (b) Heatmap of p-values of specific GO terms discovered by the different methods. (c) Overlap between gene sets of structures presented in (a).

In a smaller ST dataset of a coronal section of an 18 month old mouse brain with Alzheimer disease (AD)³¹, SPIRAL divided the tissue spots to roughly three structures, identifying the sample periphery as engaged with synaptic transmission related processes (Structure A) and the right central part of the sample as engaged with neurotransmission related terms (Structure C, Fig. 6a). Importantly, the left central region of the tissue (Structure B) was found to have high expression levels of genes relating to positive regulation of aspartate secretion- a term that was uniquely identified by SPIRAL (Fig. 6b). It is known that aspartate levels are decreased in the brain of AD patients³², so this finding may indicate that the left central region is less affected by the disease compared to the other regions.

Figure 6

SPIRAL analysis of a spatial transcriptomics dataset (ST) of a coronal section of an 18 month old mouse brain with Alzheimer disease³¹.(a) Spatial layouts of three SPIRAL structures. “high expression” and “low expression” refer to the expression levels of structure genes (Methods). (b) Heatmap of p-values of specific GO terms discovered by the different methods.

Finally, in a section of a normal human prostate preserved in FFPE (formalin-fixed paraffin-embedded)³³, SPIRAL identified and spatially mapped significant biological processes, including muscle contraction, angiogenesis and programmed cell death (Fig. 7b). Specifically, the muscle region of the prostate sample is well defined in Structure A (with a set of 64 genes) and small blood vessels can be easily located in Structure E (with 159 genes)(Fig. 7a). Structure D shows that a region in the low periphery of the tissue highly expresses 64 genes that are related to oxidative stress, positive regulation of transcription and positive regulation of cell death, which may indicate that this part of the tissue was more susceptible to the effects of formalin fixation³⁴.

Figure 7

SPIRAL analysis of a spatial transcriptomics dataset (Visium) of a normal human prostate (FFPE)³³.(a) Visium’s H &E slide, and spatial layouts of five SPIRAL structures. average expression level refers to the average expression level of structure genes (Methods). (b) Heatmap of p-values of specific GO terms discovered by the different methods.

SPIRAL detects temporal changes in active biological processes in bulk RNA-seq datasets

We applied SPIRAL to two bulk RNA-seq datasets. The first consists of 31 bulk samples of human embryonic stem cells undergoing undirected differentiation. The samples were collected at 16 time points on days 0 and $7-21$ of differentiation (Methods). SPIRAL results indicate that genes involved in translation activity are highly expressed at the beginning of differentiation, moderately expressed at the middle and less expressed at the end of differentiation process (Supplementary Fig. 2, Structure A). Expression of genes involved in anatomical structure development starts low (days 0-10), increases in the middle of the process (11-17) and then decreases again towards the end of the process (Supplementary Fig. 2, Structure B). Finally, genes responsible for regulating cell differentiation, cell migration, and T-cell activation displayed an initial low expression, followed by a consistent increase throughout the differentiation process, reaching their peak expression levels towards the end (Supplementary Fig. 2, Structure C). SPIRAL also detected batch effects between replicates, manifested as one replicate in each color (Supplementary Fig. 2, Structure D).

The second dataset covers 50 samples of mouse B cells treated with anti-IgM mAb to mimic B cell receptor stimulation, with expression measured every 15 minutes during six hours post stimulation^35,36. SPIRAL identified increased regulation of B cell activation at $0-30$ minutes post stimulation (Supplementary Fig. 3, Structure C), increased regulation of cell morphogenesis and cell differentiation at $15-90$ minutes post stimulation (Supplementary Fig. 3, Structure B), increased lymphocyte and leukocyte differentiation at $45-225$ minutes (Supplementary Fig. 3, Structure D), and increased translational activity at $165-360$ minutes (Supplementary Fig. 3, Structure A). SPIRAL also detected batch effects (Supplementary Fig. 3, structures E and F).

SPIRAL website

SPIRAL’s website at https://spiral.technion.ac.il/ incorporates examples of SPIRAL output for several datasets (some were included in this paper). These gene trends and biological active processes, identified by SPIRAL, are accessible and freely available to the biological community.

Additionally, SPIRAL’s website provides an option to download the packaged SPIRAL software, and offers a results panel. Users can use the packaged software to analyze their own data and subsequently explore their findings in SPIRAL’s results panel. The panel enables easy navigation between different visualizations and structures, illustrating significant gene expression trends in the data.

Discussion

The computational biology community has developed a wide variety of analysis techniques and algorithms for scRNA-seq and spatial transcriptomics data^37,38. However, most of these methods are aimed at finding the main data partition or time-line. In this paper we presented SPIRAL: a highly flexible method that seeks to capture all significant patterns in the data and allows for the determination of statistically significant structures, distinguished from noise. Every gene and sample can be members of one, none or more than one SPIRAL structures.

Biological aspects

As noted, due to SPIRAL’s flexibility, genes and samples may appear in any number of structures. This, in turn, creates possible overlaps between structures. This feature is unique to SPIRAL and is not supported by other approaches. SPIRAL structures typically highlight a biological (or experimental) process or phenomenon. The overlap of genes, cells, or sample regions (in spatial data) allows us to infer the relationship between structures and get a more comprehensive view of the data. On the other hand, this overlap leads to challenges when selecting which structures to report (Methods).

A demonstration of SPIRAL’s scope is seen in the mouse brain dataset, where SPIRAL structures point to transcription programs that distinguish between cell types and function (for example, Fig. 5a, Structure B) as well as to transcription programs that distinguish regions of the brain (for example, structures D and E). Moreover, SPIRAL uncovers processes that are not identified by other methods. Examples include interleukin-21 and interleukin-9 mediated signaling pathways in the lymphoblastoid cells (Fig. 3b), otic placode development in Zebrafish differentiation (Fig. 4c), as well as positive regulation of synaptic vesicle transport and adherens junctions organization in the mouse brain (Fig. 5b). These are all valuable biological insights that were not captured by alternative methods.

Computational aspects

SPIRAL was inspired by the work of Amir Ben-Dor, Benny Chor, Richard Karp & Zohar Yakhini³⁹, who developed a greedy algorithm that searches for order-preserving submatrices (OPSMs) in gene expression matrices. OPSMs are defined as submatrices in which it is possible to find a permutation of the samples (columns), such that the expression values of every gene (row) in the sub-matrix monotonically increase with respect to that permutation^39,40. OPSM’s main drawback is its insistence on a perfectly increasing set of expression values for all involved genes, a clean structure that may be too strict for biological data. Two research groups^41,42 presented “relaxed” versions of the problem, both by using ideas from sequential pattern mining, and specifically- using a depth-first traversal of a prefix tree to find frequent subsequences. However, these approaches lack statistical considerations in defining the required properties of the structures of interest. In the spirit of OPSM and its relaxed versions, SPIRAL structures arrange the involved samples in a monotonically increasing order of their expression values. But unlike these methods, each step of the ordering (layer) may include more than one sample, the number of layers is usually much lower and there is a minimum threshold for the expression value differences between two adjacent layers. Also, unlike the relaxed versions, each structure has a statistical significance score, based on an adequately defined no-signal null model.

A central step of the SPIRAL protocol is the identification of dense submatrices in a large binary matrix, where we define “dense” as having at least a minimum fraction of 1’s (denoted by $\mu$) in every column and in every row of the submatrix. We note that methods that aim to find “all 1’s” sub-matrices in binary matrices are irrelevant due to the noisy character of biological data, and specifically scRNA-seq data. Therefore, we focus on finding dense sub-matrices.

In the past two decades, several studies have proposed heuristic algorithms to solve similar problems. Both Koyuturk et al.⁴³ and Uitert et al.⁴⁴ focused on finding submatrices with a significantly large fraction of 1’s. We note that this definition of the problem is global, that is, it requires density in the entire sub-matrix and not in individual columns or rows. Their proposed heuristic algorithms begin with a random set of columns or rows, and then iteratively improve the choice of row and column sets, until no further improvement in the significance score is possible. In both cases, the significance scores are computed based on Chernoff bounds and the null assumption is that the binary matrix was generated by a Bernoulli distribution on each of the matrix elements, with success probability $p=\frac{K}{M\cdot N}$ (where the input matrix has M rows by N columns with overall K entries of 1). The independence assumption does not apply to our model. Our definition of a dense sub-matrix is also slightly different (Methods, Definition 1). Nonetheless, our algorithm also uses an iterative approach, in the spirit of Koyuturk et al.⁴³ and Uitert et al.⁴⁴.

The problem of finding dense sub-matrices in a binary matrix can also be formulated as the quasi-biclique problem. Both Mishra et al.⁴⁵ and Li et al.⁴⁶ address this computational task. We discuss our work in this perspective in Supplementary Section 1.

Our work extends the above literature by:

• We propose a different probabilistic modelling approach for dense submatrices, that is more adequate to matrices wherein each row is not assumed to represent a distribution with a diagonal covariance matrix. That is: elements within rows can be statistically dependent. This more general approach is necessary for modelling progression in single cell and spatial data. Our approach specifically applies to rows with any multivariate Gaussian distribution.

• We use our approach to find significant trends in matrices representing scRNA-seq and spatial transcriptomics data. To do so, we model such data as coming from Gaussian distributions and then translate trends to structures in a binary matrix derived from this representation.

• We assign a significance score to the trends discovered as above and further investigate the related biology.

• We develop a simple and efficient algorithmic approach to all components of the above discovery process.

Future extensions

SPIRAL uses a parameter of 100 for the number of repcells. This is the default number but does not represent an optimum. The number of repcells affects three aspects of the analysis: computational power needed, resolution and noise. Even if more computational power is available, high resolution can lead to more noise in the data. The user can seek a balance between these three aspects by working with parameters that deviate from the default. A future extension of SPIRAL may offer a more specific guidelines regarding the optimal number of repcells.

We also wish to add additional structure visualizations, for example: a UMAP layout whose coordinates are computed based on the set of genes that defines each structure (rather than all the dataset genes). Another possibly useful adaptation would be to develop an option to merge the SPIRAL results (and specifically, the membership of samples to layers) into commonly used gene expression data objects, such as the Seurat object⁸ (R) and the Anndata object used by Scanpy⁴⁷ (Python).

To summarize, we developed SPIRAL: an analysis pipeline that identifies statistically significant patterns in single cell RNAseq data, as well as in spatial transcriptomics data and bulk gene expression data. We benchmarked SPIRAL on synthetic single cell data, and found active biological pathways only detected by SPIRAL in two real single cell datasets and three spatial datasets. SPIRAL’s website at https://spiral.technion.ac.il/ offers examples of output for various datasets, as well as the downloadable packaged software for users to run on their data.

Methods

The SPIRAL protocol

We start by observing an expression matrix A with M rows (genes) and N columns (cells for scRNA-seq or spots for spatial transcriptomics). We assume that there is a set of genes acting in concordance with one another to execute some biological process on a set of cells. Some of these genes may be driving the process and some associated with it in other ways. The coordinated expression pattern can be inferred from the data, providing an indication of the biological process.

We aim to find this process by finding a collection of pairs of columns (cells$\backslash$spots) in which the expression of the relevant genes changes significantly and concordantly.

Pre-processing the data

To eliminate the effect of outliers and technical artifacts, we filter out cells$\backslash$spots (scRNA-seq$\backslash$spatial transcriptomics respectively) with abnormally high or low number of expressed genes (which may be doublets and empty cells)¹. Then, for the species homo sapiens, mus musculus, rattus norvegicus, drosophila melanogaster, danio rerio or saccharomyces cerevisiae, we identify mitochondrial genes by querying a local copy of the Ensembl database⁴⁸ (version 110), and remove cells$\backslash$spots with a large percent of mitochondrial RNA, as this could suggest cell stress^49,50. As a final pre-processing step, we normalize each cell$\backslash$spot to the median number of counts per cell$\backslash$spot.

Computing representing cells

In order to avoid dropouts and inaccuracies which stem from technical issues, we cluster the cells$\backslash$spots into small low variance clusters. Then, for each cluster, we consider its member cells$\backslash$spots to be biological replicates and compute their average expression profile. This average expression profile is the “representing cell” of that cluster. This idea is inspired by Iacono et al.⁵¹’s iCells. Specifically, the clustering is executed here by employing hierarchical agglomerative clustering with the ’ward’ linkage. The default number of clusters is set to a 100; However, users can change this value in the running process according to need and available computing power. After clustering, for datasets with 2000 cells$\backslash$spots or more, clusters with less than 10 cells$\backslash$spots are discarded. For datasets with less than 2000 cells$\backslash$spots, clusters are discarded is they have less than half the expected number of cells$\backslash$spots. For example, for a dataset with a 1000 cells, the expected number of cells per cluster is $1000/100=10$, so clusters with less than 5 cells are discarded. For convenience, we refer to the representing cells as “repcells”.

The expression profiles of all repcells are then stored in a new expression matrix $A_c$ with size M by $N_c$, whose rows are genes and columns are the repcells.

This step improves accuracy by averaging biological replicates, eliminates dropouts, and reduces the number of samples while preserving all genes. The reduction in data size shortens the execution time of the SPIRAL algorithm without removing significant information from the data (as demonstrated on a synthetic dataset, see Fig. 2).

Registering changes in expression values

We first standardize each gene separately. In this step, the (g, j)th entry in the normalized matrix $\hat{A_c}$ is computed as $\hat{A_c}(g,j)=\frac{A_c(g,j)-m_g}{\sigma _g}$, where $m_g$ is the gene average expression and $\sigma _g$ is its standard deviation over all $N_c$ repcells. Explicitly: $m_g=\frac{\sum _{j\in \{1,...,N_c\}} {A_c(g,j)}}{N_c}$, $\sigma _g=\sqrt{\frac{\sum _{j\in \{1,...,N_c\}} {(A(g,j)-m_g)^2}}{N_c-1}}$.

We compute the difference in expression values between every two repcells, for all genes, by multiplying $\hat{A_c}$ on the right by a pairwise subtraction matrix B:

$$\begin{aligned} S=\hat{A_c}\cdot B \end{aligned}$$

(1)

B is constructed so that all repcell pairs (in both directions) will be evaluated. It has $N_c$ rows and $N_c\cdot (N_c-1)$ columns. For example, for 4 repcells ($N_c=4$), B would be:

$$\begin{aligned} B= \left[ {\begin{array}{cccccccccccc} 1 & 1 & 1 & -1 & 0 & 0 & -1 & 0 & 0 & -1 & 0 & 0\\ -1 & 0 & 0 & 1 & 1 & 1 & 0 & -1 & 0 & 0 & -1 & 0\\ 0 & -1 & 0 & 0 & -1 & 0 & 1 & 1 & 1 & 0 & 0 & -1\\ 0 & 0 & -1 & 0 & 0 & -1 & 0 & 0 & -1 & 1 & 1 & 1\\ \end{array} } \right] \end{aligned}$$

The resulting matrix S represents the repcells’ differences. It has rows that correspond to genes, and columns that correspond to ordered repcell-pairs. An entry S(g, (i, j)) is the difference in expression levels of gene g between a repcell i and a repcell j, i.e:

$$\begin{aligned} S(g,(i,j))=\hat{A_c}(g,j)-\hat{A_c}(g,i) \end{aligned}$$

(2)

Seeking dense sub-matrices

We now wish to find a set of genes (rows in S) and a set of repcell-pairs (columns in S) that would constitute a sub-matrix that is populated by almost exclusively high values (a formal definition is given later in this section). For this purpose we first binarize the matrix S such that

$$\begin{aligned} S_{bin}(g,(i,j))= {\left\{ \begin{array}{ll} 1, & \text {if}\ S(g,(i,j))\ge \alpha \\ 0, & \text {otherwise} \end{array}\right. } \end{aligned}$$

(3)

where $\alpha$ is a parameter determining the minimal number of standard deviations (of a gene) to be considered a significant change in expression (since we can also write: $S_{bin}(g,(i,j))=1 \iff {A_c}(g,j)-{A_c}(g,i)\ge \alpha \sigma _g$). The results in this paper were obtained with $\alpha \in \{0.5, 0.75, 1, 1.25, 1.5\}$. Users have the option to use this default set of values for $\alpha$, or to adjust it to fit the data better.

We now wish to find a dense sub-matrix in the binary matrix $S_{bin}$. For that purpose, we introduce the following definition:

Definition 1

a $\mu$-dense sub-matrix is a collection of rows $\Gamma$ and columns $\Pi$ of a binary matrix such that every row in $\Gamma$ has at least $\mu |\Pi |$ non-zero values within the columns $\Pi$ and every column in $\Pi$ has at least $\mu |\Gamma |$ non-zero values within the rows $\Gamma$.

Formally: $S_{bin}(\Gamma ,\Pi )$ is $\mu$-dense if:

$$\begin{aligned} \begin{aligned} \sum S_{bin}(g,\Pi ) \ge \mu |\Pi | \;\;\; \forall g \in \Gamma \;\;\;\;\;\;\;\;\;\;\; \\ \sum S_{bin}(\Gamma ,(i,j)) \ge \mu |\Gamma | \;\;\; \forall (i,j) \in \Pi \end{aligned} \end{aligned}$$

(4)

where $|\Gamma |$ is the number of rows in $\Gamma$, $|\Pi |$ is the number of columns in $\Pi$, and $\mu$ is a density parameter in the range $( \, 0,1] \,$, which, in practice, is typically close to 1.

The iterative dense sub-matrix algorithm Inspired by both Koyuturk et al.⁴³ and Uitert et al.⁴⁴, we aim to find $\mu$-dense sub-matrices by using an iterative algorithm (see Algorithm 1). The algorithm initiates each of its T iterations with a random path of repcells with length L, and then repeatedly improves its choice of genes (rows) and repcell-pairs (columns), until convergence to a single structure (when the structure remains unchanged after executing the while loop). The results in this paper were obtained with $\mu \in \{0.9, 0.95\}$, $L=3$ and $T=10000$. Users have the option to change the set of values for $\mu$.

Algorithm 1

The iterative dense sub-matrix algorithm

Evaluating the statistical significance of a given sub-matrix

We now wish to calculate a score representing the statistical significance of a $\mu$-dense sub-matrix of the matrix S, which consists of the set of columns (repcell-pairs) $\Pi$ and the set of rows (genes) $\Gamma$. We clarify that although the sub-matrix was found using a binarized version of S, the significance evaluation is done on the original S which contains continuous values.

This sub-matrix in S was originally produced by

$$\begin{aligned} S(\Gamma ,\Pi )=\hat{A_c}(\Gamma ,:) \cdot B(:,\Pi ) \end{aligned}$$

(5)

Computing the statistical significance of a single gene and a set of repcell-pairs. For the null model, we assume that a standardized expression value of a gene g in a repcell i is distributed as $\mathscr {N}(0,1)$. Moreover, we assume independence and thus the set of standardized expression values $\varvec{X_g}$ of a gene g in all $N_c$ repcells is distributed as

$$\begin{aligned} \varvec{X_g}\sim \mathscr {N}_{N_c}(0,I) \end{aligned}$$

(6)

and any row g of $\hat{A_c}$ is, under the null model, a single instance drawn from that distribution.

For a set of repcell-pairs $\Pi$ and a single gene g, we now define $\varvec{Y_g^{\Pi }}$ to be an affine transformation of $\varvec{X_g}$ (both $\varvec{Y_g^{\Pi }}$ and $\varvec{X_g}$ are row vectors):

$$\begin{aligned} \varvec{Y_g^{\Pi }}=\varvec{X_g} \cdot B(:,\Pi ) \end{aligned}$$

(7)

In the null case, the set of values $S(g,\Pi )$ is a single draw of $\varvec{Y_g^{\Pi }}$.

At this point we wish to clarify that although the standardized expression values of a gene g (denoted by the vector $\varvec{X_g}$) are assumed, under the null model, to be collectively independent, such assumption regarding their pairwise differences (represented by $\varvec{Y_g^{\Pi }}$) is not valid. Also, if $B(:,\Pi )$ is not full rank, $\varvec{Y_g^{\Pi }}$’s distribution is singular.

We now define:

$$\begin{aligned} \overline{\varvec{Y_g^{\Pi }}}=\varvec{Y_g^{\Pi }} \cdot u^{|\Pi |} \end{aligned}$$

(8)

where $u^{|\Pi |}$ is a column vector with all elements equal to $\frac{1}{|\Pi |}$, i.e. an averaging vector.

We can conclude from Eqs. (6), (7) and (8) that $\overline{\varvec{Y_g^{\Pi }}}$ is a real valued normal variable with mean 0 and variance $\widetilde{\sigma }^2 = {u^{|\Pi |}}^T \cdot B(:,\Pi )^T\cdot B(:,\Pi ) \cdot u^{|\Pi |}$. That is,

$$\begin{aligned} \overline{\varvec{Y_g^{\Pi }}}\sim \mathscr {N}(0,\widetilde{\sigma }^2={u^{|\Pi |}}^T \cdot B(:,\Pi )^T\cdot B(:,\Pi ) \cdot u^{|\Pi |}) \end{aligned}$$

(9)

(see Fig. 8).

Therefore, the significance of the observed average change in expression values of gene g over the set of repcell-pairs $\Pi$ can be computed as

$$\begin{aligned} pVal(g,\Pi ) = 1-\Phi \Big (\frac{S(g,\Pi )\cdot u^{|\Pi |}}{\sqrt{{u^{|\Pi |}}^T \cdot B(:,\Pi )^T\cdot B(:,\Pi ) \cdot u^{|\Pi |}}} \Big ) \end{aligned}$$

(10)

where $\Phi$ is the cumulative distribution function of the standard normal distribution, the numerator is the observed average of values in $S(g,\Pi )$ (the average of the observed expression differences of g throughout $\Pi$), and the denominator is $\overline{\varvec{Y_g^{\Pi }}}$’s standard deviation, as developed above.

We note that this test is one-sided, since we observe the value of the average change in expression of a gene g over the repcell-pairs $\Pi$ (this value is: $S(g,\Pi )\cdot u^{|\Pi |}$), and then compute its p-value $pVal(g,\Pi )$ as the probability of observing a value this large (or larger).

Figure 8

A flow chart of the null assumption of our model.

Computing the significance of a set of genes and a set of repcell-pairs. For the null model we also assume that the genes are collectively independent. We can then compute the significance of a given sub-matrix with columns (repcell-pairs) $\Pi$ and rows (genes) $\Gamma$ by multiplying the significance scores of the individual genes:

$$\begin{aligned} pVal_{init}(\Gamma ,\Pi ) = \prod _{g \in \Gamma } {pVal(g,\Pi )} \end{aligned}$$

(11)

Correcting for multiple testing. We correct the initial p-value for multiple testing as follows

$$\begin{aligned} pVal(\Gamma ,\Pi ) = \left( {\begin{array}{c}M\\ |\Gamma |\end{array}}\right) {\left( {\begin{array}{c}N_c\cdot (N_c-1)\\ |\Pi |\end{array}}\right) }\cdot pVal_{init}(\Gamma ,\Pi ) \end{aligned}$$

(12)

where M is the total number of genes and $N_c$ is the total number of repcells. Note that $N_c\cdot (N_c-1)$ is then the total number of repcell-pairs.

Evaluating the structure of repcells consisting of the sub-matrix columns

The significance score indicates how statistically rare a discovered sub-matrix would be under the null hypothesis. However, we argue that due to the properties of real-life data, there is a need for a second measure to assess biological significance. For that purpose, we examine the structure consisted of the set of repcell-pairs.

We may think of a set of repcell-pairs $\Pi =\{(i,j),(t,s),...\}$ as a network in which the nodes are repcells, and an arrow is drawn from repcell i to repcell j only if the repcell-pair (i, j) is in $\Pi$.

Using three toy examples, we will now demonstrate that different sub-matrices may have similar significance scores (and also, similar number of repcell-pairs), but very different contributions to the understanding of biological processes in the data. We will then offer a second measure that addresses biological significance.

Consider the structures in Fig. 9: All three have 33 repcell-pairs (arrows), and their numbers of participating genes are 100, 30 and 50 for structures (a),(b),(c) respectively. We assume $\alpha =1$, $\mu =1$, and that the difference in expression values along each of the arrows in structures (a) and (b) is exactly 1 for each of the genes (i.e. $S(g,(i,j))=1 \;\; \forall g\in \Gamma , (i,j)\in \Pi$), and for structure (c) this is also true for all arrows but the ones connecting the first and the last layers (i.e. $S(g,(i,j))=1 \;\; \text {if} \;\; \big [(i\in \{0,1,2\} \; \& \; j\in \{3,4,5,6\}) \;||\; (i\in \{3,4,5,6\} \; \& \; j\in \{7,8,9\})\big ]$, otherwise $S(g,(i,j))=2$). In this case their initial significance scores (computed as in Eq. (11)) are 1e-79.0, 1e-68.5 and 1e-64.4 respectively. Despite the similarity in significance scores, it is clear that while structures (b) and (c) might suggest evidence to a biological process in the data, structure (a) might as well be a result of a technical issue involving one outlier.

As mentioned before (see Eq. (9)), the average of differences along all repcell-pairs in the structure is distributed in the null case as a normal variable. Consider the standard deviation of this variable, denoted by $\widetilde{\sigma }$. When it is lower, the structure is more complex and might offer more biological insights. For structures (a), (b) and (c), $\widetilde{\sigma }$ is 1.02, 0.58 and 0.52 respectively, allowing us to easily determine which of the structures is more informative.

Figure 9

Toy examples of structures.

Filtering sub-matrices

After evaluating the statistical significance of the resulting sub-matrices, we filter out non-significant ones (p-value above 1e-15). Note that in random data, we get no structures with p-value below this threshold. Then, we perform a disjointification-like process to avoid having very similar sub-matrices in the algorithm output list. The process begins by sorting the sub-matrices in an ascending order of their structures’ $\widetilde{\sigma }$s (see former section). Then, we go through the list of sub-matrices and remove every sub-matrix that is similar to any of the former sub-matrices in the list, where two sub-matrices are considered similar if the Jaccard index of their gene lists is above 0.75 or if the Jaccard index of their repcell-pair lists is above 0.5. At this point, different datasets may result in very different numbers of structures. To assure that the resulted number of structures is within a certain range, we cut the structure list (still, sorted by structures’ $\widetilde{\sigma }$’s) at $\min (\max (3, n_{\widetilde{\sigma }\le 0.8}), 50)$, where $n_{\widetilde{\sigma }\le 0.8}$ is the number of structures with $\widetilde{\sigma }\le 0.8$.

Post-filtering of structures: At SPIRAL’s results panel, a user may narrow down the list of structures by adjusting the Jaccard index threshold (JaccThr) of the gene lists.

SPIRAL visualizations and gene enrichment

Producing the network layout and partitioning the repcells to layers

For structures that can be drawn as a bipartite graph (such as the toy examples in Figs. 9a and 9b), we can label the repcells on the left (layer 1 in the network) as “low expression” and the repcells on the right (layer 2) as “high expression”. However, for other structures, there are several options of partitioning into network layers. We chose to draw the network from right to left, so that the arrows are short as possible (see Algorithm 2). After the partition is established, we assume that in general the expression levels of the structure genes are increasing from left to right: the repcells on layer i would likely have lower expression values of the structure genes than the repcells on layer $i+1$. In the simple network visualization, the repcells are colored based on their assigned layer. However, to test the former assumption, SPIRAL also produces a network visualization in which the repcells are colored based on their average expression level of the structure genes (see layout E.1 in Fig. 2d and network layouts in Fig. 3a). The sizes of nodes in the network layout correspond to their degree: the number of edges connecting them to other repcells. This is a visual indication of the level of connectivity of each repcell in the structure.

Algorithm 2

The network drawing process

Visualizing significant sub-matrices on a PCA$\backslash$UMAP layout of repcells

SPIRAL visualizes structures over a PCA $\backslash$UMAP layout by coloring the repcells based on their assigned layers (see Methods, “Evaluating the structure of repcells consisting of the sub-matrix columns”; layout E.2 in Fig. 2d). As with the network layout, SPIRAL also produces a more informative visualization by coloring the repcells based on their average expression level of the structure genes.

Visualizing significant sub-matrices on a PCA$\backslash$UMAP$\backslash$spatial layout of cells$\backslash$spots

SPIRAL visualizes structures on a PCA$\backslash$UMAP layout of the original cells$\backslash$spots, and on the spatial coordinates of the spots, by assigning each cell$\backslash$spot with a layer based on its repcell (see Methods, “Evaluating the structure of repcells consisting of the sub-matrix columns”; PCA$\backslash$UMAP layouts: layout E.3 in Fig. 2d and middle-left pane of each of structures in Fig. 3a; spatial layouts: Fig. 6a). SPIRAL also offers a similar visualization, in which the assigned layers are ignored, and instead- the cells$\backslash$spots are colored based on their average expression level of the structure genes (PCA$\backslash$UMAP layouts: layouts A-F in Fig. 2d, middle-right pane of each of structures in Fig. 3a, and Fig. 4b; spatial layouts: Figs. 5a and 7a).

Evaluating the set of genes $\Gamma$

In order to assess whether the structure genes are enriched for known biological processes or functions, SPIRAL performs a GO enrichment query through GOrilla^52,53, using the “two unranked lists of genes” mode.

The structure gene list is used as the target list, while all the genes in the data set are used as the background list. All three GO ontologies are queried: process, function and component. Then, GO terms with p-values of less than 0.01 are saved to the results file.

Producing synthetic data

We used Splatter²² to synthesize scRNA-seq data with a branching lineage of 7000 cells and 10000 genes. The lineage was constructed such that each cell belongs to one of three paths (with probabilities 0.2, 0.2, 0.6 to belong to Path1, Path2, Path3 respectively). Path2 and Path3 begin where Path1 ends. Also- the location of each cell along its path (i.e. step) is also known (overall 1000, 1000, 3000 steps in Path1, Path2, Path3 respectively). We defined the differential expression factor “de.facLoc” to be 0.01, which is considered small (which translates to small differences between cells in different paths)⁵⁴. We then used the lineage rowdata file to construct a list of “true gene modules” by selecting the genes with differential expression factor (DEFac) above 1.1 or below 0.9 (separately), for each path, creating overall six true gene modules for the three paths.

Implementation of other methods

SPIRAL outputs structures, each contains a set of genes working in concordance with one another. Thus, we sought to compare SPIRAL to other methods that output multiple sets of genes.

Seurat^55,56 is a commonly used pipeline which performs clustering of the cells (for single cell data) or spots (for spatial data), and outputs differentially expressed genes for each cluster with the “FindAllMarkers” function.

Slingshot⁵⁷ is a well-established package for pseudo-time inference³, which may be accompanied by the tradeSeq⁵⁸ pipeline to find sets of genes with similar expression patterns with the “clusterExpressionPatterns” function. As there is no default value for the “npoints” parameter required for this function, we ran it with “npoints” equals 20 and 200. We then filtered out sets with less than 20 genes.

Hotspot⁵⁹ is a graph-based procedure to identify informative genes and gene modules in single cell and spatial datasets. In Hotspot, the user has to define a model and the “n_neighbors” parameter. We ran Hotspot with the ’danb’ model and “n_neighbors” equals 30 and 300 for all datasets but the Zebrafish differentiation dataset. Several attempts to run Hotspot on the this dataset ended in error (probably due to the relatively large number of cells: 10, 500). We also tried to run Hotspot with the ’bernoulli’ model but unfortunately we encountered errors.

Nonsmooth nonnegative matrix factorization (nsNMF) is a procedure that can be used to find gene modules in single cell and spatial datasets, as done in Moncada et al.⁶⁰, Carmona-Saez et al.⁶¹. We applied this procedure by using the R NMF package⁶².

SingleCellHaystack² is a clustering-independent method for finding differentially expressed genes in single-cell and spatial data, which takes as input the expression matrix as well as dimensionality reduction coordinates for single cell data, or spatial coordinates for spatial data. After detecting differentially expressed genes, it clusters them to k modules, where k is a user defined parameter. We ran SingleCellHaystack with k equals 3, 5 and 6 for the synthetic dataset, and with k equals 3 and 5 for the real datasets.

SpatialDE¹⁶ is a method to identify spatially variable genes in spatial datasets. These genes may later be clustered to C clusters, where C is a user-defined parameter. We ran SpatialDE with C equals 3 and 5 for all spatial datasets.

We ran these methods on a standard Linux machine (64GB RAM, 10 cores).

Generating bulk RNA-seq data

The following pipeline was used to generate the bulk RNA-seq dataset of human embryonic stem cells (hESCs) differentiation.

Spontaneous differentiation of hESCs

Suspension cultures of TE03 cells were routinely maintained in hESC-medium with 100 ng/ml bFGF. To induce spontaneous differentiation, cells were transferred to differentiation medium consisting of DMEM/F-12 supplemented with 10% FBS (BI, Cat$\#$ 04-002-1A), 10% KnockOut Serum Replacement (KSR), 1 mM L-glutamine, 1% non-essential amino acids, and 0.1 mM $\beta$-mercaptoethanol, media changed every 1-2 days. After one week media was replaced with FBS media, consisting of DMEM supplemented with 20% FBS 1 mM L-glutamine, 1% non-essential amino acids, and 0.1 mM $\beta$-mercaptoethanol, media changed every 2-4 days for 2 weeks. Samples collected on the indicated days, RNA extracted by TRI-reagent according to protocol.

Library preparation and sequencing

2 ng RNA of each sample was taken for library preparation using the CEL-Seq2 protocol⁶³. Briefly, The CEL-Seq primer selects for polyA RNA via an anchored polyT stretch, and adds a sample specific barcode, a UMI, the Illumina adaptor and a T7 promoter sequence to the resulting dsDNA (2 different CEL-Seq primers added to each sample as technical replicates). At this point, multiple samples can be pooled together, and an In-Vitro Transcription (IVT) reaction is performed to linearly amplify the RNA. The second Illumina adaptor is introduced at a second Reverse Transcription step (RT) as an overhang to a random hexamer primer. A short PCR reaction selects for the 3’ most fragments and add the full Illumina adaptors needed for sequencing. Sample and molecule origin are identified by read 1, and gene of origin is identified by read 2. Library was sequenced on Nextseq550, 25 bases for read 1 and 60 bases for read 2.

Bioinformatic analysis

Demultiplexing was performed using Je-Demultiplex⁶⁴ in Galaxy platform. R2 reads were split into their original samples using the CEL-Seq barcode from R1. Reads from two technical replicates were joint for further processing. The reads were cleaned using Cutadapt⁶⁵ for removal of adaptors, polyA, low-quality sequences (Phred$< 20$) and short reads ($<30$bp after trimming). Reads were mapped to the GRCh38 genome (Ensembl) using STAR package⁶⁶ to create Bam files. We used SAMtools⁶⁷ to convert BAM to SAM file and index the files. Then the reads were annotated and counted using HTseq-count package⁶⁸.