Ensemble genetic and CNN model-based image classification by enhancing hyperparameter tuning

Abstract

Model optimization is a problem of great concern and challenge for developing an image classification model. In image classification, selecting the appropriate hyperparameters can substantially boost the model’s ability to learn intricate patterns and features from complex image data. Hyperparameter optimization helps to prevent overfitting by finding the right balance between complexity and generalization of a model. The ensemble genetic algorithm and convolutional neural network (EGACNN) are proposed to enhance image classification by fine-tuning hyperparameters. The convolutional neural network (CNN) model is combined with a genetic algorithm GA) using stacking based on the Modified National Institute of Standards and Technology (MNIST) dataset to enhance efficiency and prediction rate on image classification. The GA optimizes the number of layers, kernel size, learning rates, dropout rates, and batch sizes of the CNN model to improve the accuracy and performance of the model. The objective of this research is to improve the CNN-based image classification system by utilizing the advantages of ensemble learning and GA. The highest accuracy is obtained using the proposed EGACNN model which is 99.91% and the ensemble CNN and spiking neural network (CSNN) model shows an accuracy of 99.68%. The ensemble approaches like EGACNN and CSNN tends to be more effective as compared to CNN, RNN, AlexNet, ResNet, and VGG models. The hyperparameter optimization of deep learning classification models reduces human efforts and produces better prediction results. Performance comparison with existing approaches also shows the superior performance of the proposed model.

Introduction

The optimization of hyperparameters is a difficult task with broad ramifications across industries including driverless cars and medical applications. The deep learning model’s performance is highly dependent on a number of hyperparameters including learning rates, batch sizes, network topologies, and regularization parameters. These all have a significant impact on the model’s effectiveness. The collective representation of hyperparameter tuning is a difficult and time-consuming procedure due to the intricate structure, interdependencies, and the large search space of these parameters¹. Finding the ideal configuration frequently requires navigating this complex landscape which takes a lot of time and computer power to complete through iterative trial and error. Furthermore, the optimal hyper-parameter sets might vary greatly between datasets and classification issues. It is essential to address this challenge successfully by maximizing the efficacy and accuracy of image classification models, enabling them to realize their full potential in real-world applications. However, there is no one-size-fits-all solution to this problem².

The main goal of this research is to investigate cutting-edge methods and techniques for image classification by hyperparameter optimization. Improving the model’s performance is important but it is reducing the human efforts and computer labor needed to complete the task³. Handwritten numbers have numerous applications including handwriting recognition, postal zip code extraction, and processing bank checks. However, recognizing these numbers is challenging due to their unique stroke types, sizes, and orientations⁴. Various methods have been attempted including artificial neural network (ANN), support vector machine (SVM), rule-based reasoning, and multi-column deep neural networks. User-independent online handwritten digit recognition faces challenges in categorizing strokes. The objective is to use a deep learning model to identify handwritten digit patterns and train a model that can categorize numbers based on their patterns⁵. Recent studies show that deep hierarchical neural networks improve supervised pattern categorization through unsupervised pre-training. These networks focusing on deep convolutional neural networks (DCNNs) have shown potential in various data sets. However, educating them on central processing units (CPUs) can be time-consuming and expensive⁶. Fast parallel neural net code for graphics cards has solved this issue allowing for faster image classification than CPU-based methods⁷.

The network’s capacity optimizes to identify intricate patterns and features in images through the iterative adjustments to weights and biases of the back-propagation training method⁸. Through this procedure, CNN can accurately complete tasks like segmentation, object identification, and image categorization⁹. CNN is the key component of deep learning that enables complex image mapping and classification. It improved the computer vision systems using their ability to automatically learn hierarchical representations. CNN-based LeNet-5 architecture excels in image classification, and computer vision-related tasks¹⁰.

The problems of hyperparameter tuning in Image classification are the main topic especially as they relate to CNNs. The work suggests a novel method to optimize hyperparameters and raise the accuracy of image classification by merging ensemble genetic algorithms (EGAs) with CNN models. The goal of this research is to address problems with model complexity, genetic algorithm (GA) optimization, processing power needs, and dataset generalization. Preparing the dataset, training individual CNN models, optimizing genetic algorithms, adjusting hyperparameters, and evaluating the models are all part of the proposed technique. The difficulties and suggested method are described emphasizing the expected advances in image recognition and computer vision technologies. With an emphasis on thorough experiments using industry-standard datasets like MNIST. This research seeks to offer insightful information for practical applications in a range of sectors.

• This study explores the impact of hyperparameter tuning on ensemble model performance using an evolutionary algorithm for improved precision, generalization, and resilience in image classification applications.

• The GA-based hyperparameter optimization for deep learning model using the stacking ensemble technique called ensemble genetic algorithm and CNN (EGACNN) has been proposed for image categorization and to enhance model performance.

• The deep learning models such as CNN, recurrent neural network (RNN), AlexNet, residual neural network (ResNet), VGG, convolutional recurrent neural network (CRNN), and ensemble of CNN and spiking neural network (CSNN) have been used and combined with GA to enhance dataset comprehension and decision-making in image classification. Ensemble learning enhances image classification system flexibility by combining CNN architectures, especially when dataset differences cause individual models to struggle.

• Experiments results of these models highlight the superiority of the proposed ensemble model for image classification by evaluating through accuracy, precision, recall, and F1 score.

Although optimizing hyperparameters is essential for improving the performance of image classification models current approaches frequently encounter considerable difficulties. Recent research takes more time to execute simple tasks and is computationally expensive. These traditional grid search and random search strategies necessitate a thorough investigation of the hyperparameter space without ensuring optimal outcomes¹¹. Furthermore, these techniques result in inefficiencies particularly with complicated models like deep neural networks because they fail to adaptively focus on the most promising areas of the hyperparameter space¹². Although more successful Bayesian optimization can suffer in high-dimensional hyperparameter spaces and may lose its effectiveness in noisy or costly objective function evaluations. Furthermore, a fundamental component of real-world applications with constrained resources is the capacity to balance the trade-offs between accuracy and computing cost something that many optimization techniques fail to do well. These drawbacks emphasize the need for more sophisticated and flexible optimization methods including those incorporating genetic algorithms to quickly and accurately adjust hyperparameters for better model performance in image classification applications¹³.

The structure of the preceding paper is as follows: Section 2 presents the literature analysis of the current systems and their limitations. Section 3 presents the methodology which describes the methods and techniques adopted to carry out experiments and the structure of the methodology. Section 4 presents the performance of deep learning models in comparative analysis. Section 5 describes the conclusion of the research.

Related work

One of the most important tasks in computer vision is classifying images into predefined classes based on their visual information. CNN has become the industry standard for image classification. CNN can learn complex feature relationships from raw data¹⁴. The deep learning models consist of many layers carrying out operations such as convolving, pooling, etc. Different levels of abstraction are used by these layers to extract and integrate data. CNN are trained on large datasets which enable them to learn the relationships between input features and output classes by analyzing images and the labels that correspond to them¹⁵. CNN uses the learned representations during inference to analyze previously unseen images and predict their classes.¹⁶.

A CNN model for small dataset regularization techniques and model average ensemble enhance generalization and classification accuracy in cloud categorization research¹⁷. Evaluation using the SWIMCAT dataset demonstrates perfect classification accuracy highlighting the model’s tenacity¹⁸. An MCUa dynamic deep CNN model classifies breast histology images using multilevel context-aware models and uncertainty quantification achieving high accuracy by addressing categorization challenges due to visual heterogeneity and lack of contextual information in large digital data¹⁹. Researchers examine the performance effects of hyperparameters and model optimization techniques on four DNN models. The findings indicate that different models and performance factors are affected by hyperparameters²⁰. Moreover, the research advises practitioners to take into account a variety of performance indicators and to be aware of the cumulative nature of optimization and hyperparameter tuning²¹.

CNN image classification using data augmentation and batch normalization enhances precision and effectiveness by normalizing input and creating fresh training samples from existing data²². The EnsNet ensemble learning method combines FCSNs with a basic CNN segmenting feature maps into subsets and training FCSNs to forecast class labels²³. A majority vote from both CNNs determines the model’s output aiming to improve object identification performance²⁴. The CE-ResNet model was developed by combining a ResNet with a capsule neural network (CapsNet) technique. CNNs are utilized as classifiers for fruit recognition and pricing in supermarkets²⁵.

To improve image classification methods, this work combines the capabilities of CNNs and Genetic Algorithms. Inspired by the evolutionary processes found in nature GAs are remarkably adept at exploring intricate solution spaces to find nearly optimal configurations²⁶. These algorithms explore a wide range of options through iterative refinement focusing on solutions that perform better. Meanwhile, CNNs are industry mainstays in image classification because of their intrinsic capacity to extract complex patterns and hierarchical features from unprocessed pixel data. However, the CNN performance is highly dependent on the fine-tuning of hyperparameters like learning rates, network topologies, and regularization strategies. Adjusting these hyperparameters by hand is time-consuming and frequently does not fully capture the range of possible combinations.²⁷.

This work aims to overcome the difficulties associated with hyperparameter optimization, model generalization, and robustness in image classification tasks by integrating GAs into CNN training. A new era of efficiency in this field is anticipated as a result of the mutually beneficial combination of CNNs and GAs which promises to improve the flexibility and robustness of image classification models in addition to streamlining the optimization process²⁸. Researchers consider many different hyperparameters and architectural choices that significantly affect the CNN model’s performance while fine-tuning it with GAs. These parameters include things like the number of layers, learning rates, batch and filter sizes, and how the convolutional and pooling processes are set up. Each set of parameters indicates a potential CNN architecture generating a diverse set of options for the GA²⁹.

The process begins with an assessment of each specific CNN design using a validation dataset. Each architecture’s fitness is evaluated using performance metrics like classification accuracy or loss function values. This initial evaluation serves as the foundation for further optimization phases and provides a benchmark to compare different configurations. Through iterative evolution, GAs improve the population of CNN structures across multiple generations. With every cycle genetic processes including crossover and mutation result in the production of new individuals. Crossover produces offspring with a variety of features by combining traits from two-parent architectures³⁰. Mutation introduces small random modifications to particular structures which promotes exploration of new solution areas. Individuals with greater fitness levels have a higher probability of producing progeny due to mechanisms of selection. Natural selection is a process that results in advantageous traits being passed down to the following generation. Configurations that perform better in terms of classification accuracy and loss minimization are gradually adopted by the population³¹.

GAs have the potential to be optimized but they face a number of obstacles that limit their effectiveness. The great dimensionality of images, each pixel representing features a significant obstacle since it creates a vast search field for solutions. Furthermore, the optimization landscape is complicated by the non-linear and non-convex relationship between image characteristics and class labels, which frequently causes GAs to struggle to converge to global optima³². In picture classification jobs, where it can be difficult to discover an ideal trade-off, the GAs become problematic. Moreover, to guarantee both efficacy and computational efficiency, CNN designs or hyperparameters must be represented and encoded in a way that is appropriate for GAs. To overcome these obstacles, novel algorithmic designs and hybrid strategies are required, which combine GAs with other optimization methods or make use of parallel computing frameworks to increase GAs’ efficiency in CNN architecture optimization for image classification applications³³.

The genetic algorithm improves the CNN model’s hyperparameters using a population-based optimization technique. This technique compares new algorithms to different parameters to enhance classification performance on the MNIST dataset³⁴. EAs optimize artificial neural network design and parameters automating hyperparameter tweaking and simulating natural evolution. This research utilizes a two-level genetic algorithm and neuro evolution to find CNN and neural network’s topologies balancing the search time and fitness integrity³⁵. The method speeds up fitness evaluation and allows adaptable CNN structures to outperform previous techniques and reduce training time³⁶. Wound treatment optimization (WTO) a distributed method inspired by biological processes was used to train a LeNet CNN model learning parameters³⁷. This method improved training time and accuracy on the MNIST dataset. This technique can be applied in various fields including robotics, multi-agent systems, etc.³⁸.

The MR-DCAE model detects reconstruction problems and employs a deep convolutional autoencoder to identify radio transmissions that are not allowed. To maintain manifold invariance the model incorporates a similarity estimator and is optimized via entropy-stochastic gradient descent. MR-DCAE demonstrates cutting-edge performance when tested on the AUBI2020 dataset successfully identifying unauthorized signals in intricate settings³⁹. Ms-RaT model which uses multi-scale analysis to improve feature learning from radio signals employs dual channel representation. Extensive simulations and ablation investigations validate that the model provides greater accuracy with equivalent or lower computing complexity than existing deep learning methods⁴⁰.

The lightweight MobileViT neural network which uses clustered constellation pictures from I/Q sequences for real-time modulation classification was recently introduced in Automatic Modulation Classification (AMC) work. On the RadioML 2016.10a dataset, this model which was created for edge computing platforms performs better than previous approaches and has shown to be resilient in a variety of scenarios. When it comes to using deep learning for real-time AMC on devices with limited resources MobileViT is a trailblazing method⁴¹. For real-time AMC in drone communication systems MobileRaTis a lightweight transformer model with pruning based on information entropy has been presented. It achieves higher accuracy and efficiency on public datasets. This method shows flexibility to different communication scenarios by combining pruning for the first time with a transformer model for temporal signal processing⁴². In order to recognize partial discharge patterns in power transformers a hybrid CNN-LSTM model that makes use of dual-channel pictures from PRPD and PRPS has been presented. This method outperforms both conventional and sophisticated deep learning techniques as it is the first to leverage dual-channel spectrum inputs⁴³.

There are clear benefits and drawbacks to using both genetic algorithms and CNNs for image classification especially when using the MNIST dataset. Because CNNs can automatically extract and learn features from the images they perform exceptionally well and accurately on the MNIST dataset making them highly useful for this purpose. They are preferred for image classification because they take advantage of their robust findings and translation invariance which allow them to extract hierarchical features. CNNs can be limited in contexts with limited resources though as they need higher processing power and a lot of data to train well. On the other hand evolutionary algorithms can be used to choose feature subsets or tune hyperparameters which may enhance CNN performance however they are less frequent for direct image classification applications. Although they provide a population-based flexible method of problem solving their iterative nature can make them computationally expensive and less effective for direct classification problems. Due to their direct approach and high accuracy, CNNs typically perform better than genetic algorithms for image classification tasks in practical applications genetic algorithms on the other hand might be more appropriate for problems linked to optimizing CNN configurations. Table 1 provides a critical summary of discussed research works.

Table 1 Advantages and disadvantages of existing research works.

Methodology

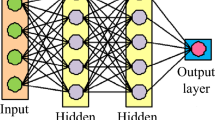
The efficiency of image classification has been increased in this research based on hyperparameter optimization using a GA. The MNIST dataset is a well-known benchmark dataset for image classification tasks and serves as the main source of data. The MNIST dataset is used in experiments with deep learning approaches because it contains a sizable collection of hand-drawn digits from 0 to 9 in grayscale images. The dataset is collected from the well-known dataset repository Kaggle. The normalization and one hot encoding technique are used on the MNIST dataset images to improve model resilience. Then image augmentation is applied to scale the images to a uniform dimension by standardizing pixel values and increasing the dataset images. To make sure the data is appropriate for training for deep learning learning models, data preparation is an essential first step. The MNIST dataset is used to train deep learning models such as CNN, RNN, AlexNet, ResNet, VGG, CSNN, and proposed EGACNN. Figure 1 shows the methodological architecture of the proposed model. To get the best classification results and accuracy, the training process involves fine-tuning model parameters and optimizing hyperparameters. Each model’s performance is evaluated using measures including F1-score, recall, accuracy, and precision.

Fig. 1

CNN and genetic algorithm-based methodological architecture.

The validation approach is also used such as cross-validation to ensure the model’s generalizability. The ensemble method is used to improve the performance of categorization and bagging, boosting, and stacking affect the accuracy of the model. The predictions of deep learning base models will be combined with genetic algorithms to construct ensemble models that will produce more effective results. This research employs a strict experimental design that includes cross-validation and the right statistical testing to confirm the findings. This research determines the best models and ensemble procedures for MNIST digit classification as well as highlights the model’s weaknesses and plus points.

Dataset

The MNIST dataset, a commonly used dataset in computer vision, consists of 60,000 handwritten numbers divided into training and test sets with 50,000 and 10,000 samples respectively as shown in Table 2 and Fig. 2.

Table 2 Training and testing images in the MNIST datasets.

Fig.2

Samples from the MNIST dataset.

Image normalization

Since data normalization has a major impact on the convergence and performance of deep learning models in the proposed image classification framework. The processes and techniques utilized to preprocess and normalize the entered image data are referred to as image normalization. The goal of data normalization is to guarantee that differences in the strength and distribution of the input features do not obstruct the model’s training procedure. More pixel standardization and attention to problems like lighting or contrast variance can result in more stable and convergent models. Gaining an understanding of the subtitle of data normalization is critical to the success of the image classification system because it guarantees that the features in the input images can be efficiently learned and represented by deep learning models.

Genetic algorithm

The GA algorithm belongs to the heuristic class that follows the concepts of genetics and natural selection. GA is used to determine the ideal collection of hyperparameters for a deep learning model such as a CNN when it comes to hyperparameter optimization. Hyperparameters are configurations that control a model’s performance and behavior they are not determined by the data. Finding the ideal set of these parameters to optimize model performance is the difficult part of hyperparameter optimization.

Population and individuals

The population in GA for hyperparameter tuning is a group of possible solutions where each member represents a particular set of hyperparameters. A person is organized as a vector with each gene representing a certain hyperparameter. A person could be represented as [0.001, 32, 64, 3x3, 0.5] where 0.001 stands for learning rate, 32 for batch size, 64 for number of filters, 3x3 for filter size, and 0.5 for dropout rate. Collectively these members of the population investigate various combinations of hyperparameters guiding the optimization procedure in the direction of the optimal model configuration.

Crossover

The process of creating offspring by fusing the genetic material (hyperparameters) of two-parent people is known as crossover. By doing this the natural reproduction process is mimicked and the children are able to inherit traits (hyperparameters) from both parents. The crossover procedure adds variety without compromising the integrity of the previously discovered solutions. If parent 1 has hyperparameters $[0.001, 32, 64, 3\text {x}3, 0.5]$ and parent 2 has $[0.01, 64, 128, 5\text {x}5, 0.2]$, a crossover might produce offspring like $[0.001, 32, 128, 5\text {x}5, 0.2]$ and $[0.01, 64, 64, 3\text {x}3, 0.5]$. Let $\theta _{p1}$ and $\theta _{p2}$ be the parent vectors, and $\theta _{o1}$ and $\theta _{o2}$ be the offspring vectors. The crossover operation can be expressed as:

$$\begin{aligned} \theta _{o1}= & [ \theta _{p1}[1:k], \theta _{p2}[k+1:n] ] \end{aligned}$$

(1)

$$\begin{aligned} \theta _{o2}= & [ \theta _{p2}[1:k], \theta _{p1}[k+1:n] ] \end{aligned}$$

(2)

where k is a randomly chosen crossover point.

Mutation

A mutation modifies a person’s CNN model hyperparameters at random. By keeping the population’s genetic variety intact, this procedure keeps the algorithm from settling too rapidly on a local optimum. Usually, there is little chance involved in applying mutation.For instance in the individual $[0.001, 32, 64, 3\text {x}3, 0.5]$ a mutation might alter the learning rate to $0.0001$ resulting in a new individual $[0.0001, 32, 64, 3\text {x}3, 0.5]$. Mutation introduces small random changes to the offspring’s hyperparameters to maintain diversity. The mutation operation can be expressed as:

$$\begin{aligned} \theta _i^{\text {mut}} = \theta _i + \delta \end{aligned}$$

(3)

where $\delta$ is a small random perturbation applied to the hyperparameter $\theta _i$, often sampled from a normal distribution.

Environmental selection

After the offspring generation, environmental selection is used to decide which individuals participate to make the next generation. This can be based on elitism where the best-performing individuals are always carried over. The next generation is formed by selecting the top M individuals from the union of parents and offspring:

$$\begin{aligned} \text {Next Generation} = \text {Top } M \text { individuals from } \{ \text {Parents} \cup \text {Offspring} \} \end{aligned}$$

(4)

where M is the population size.

Fitness function

Every member of the population is assessed according to their quality by the fitness function. When it comes to hyperparameter optimization the fitness function is usually determined by the model’s performance which includes validation loss, accuracy, and F1-score after training with the hyperparameters that the individual represents. Better model performance is indicated by a higher fitness score.

The fitness function evaluates the performance of a CNN model with a specific set of hyperparameters. Let $\theta = [\theta _1, \theta _2, \ldots , \theta _n]$ represent the vector of hyperparameters for the CNN where $\theta _i$ is a specific hyperparameter (e.g., learning rate, batch size). The fitness function $F(\theta )$ is typically based on the model’s performance on a validation set:

$$\begin{aligned} F(\theta ) = \text {Accuracy}(\theta ) \quad \text {or} \quad F(\theta ) = -\text {Loss}(\theta ) \end{aligned}$$

(5)

Selection

The process of selecting members of the current population to produce future generations’ offspring is known as selection. larger fitness scorers have a larger chance of being chosen since they are superior candidates.

Best solution

The set of hyperparameters with the highest fitness score, or the best-performing individual, is chosen as the ideal hyperparameter configuration for the model once the GA ends. The final model is then trained using this solution. Figure 3 shows the flow of this whole process.

Fig. 3

Optimization of CNN hyperparameter with GA.

Deep learning models

The use of deep learning models has drastically changed the fields of computer vision and image classification. This research investigates the crucial significance of deep learning that combines the power of CNNs with the efficiency of GA for image classification. The deep learning models are employed in detail by providing clarity on the architecture, training protocols, and hyperparameter tuning strategies that underpin the innovative approach.

ResNet model

The input images are reshaped using the ResNet Model which scales the pixel values to an appropriate range. In the ResNet model design, residual blocks are included allowing the network to learn residual mappings rather than the intended mappings directly. There are numerous residual blocks in a typical ResNet design and each block has several convolutional layers with skip connections that omit one or more levels. The ResNet model includes setting the number of residual blocks, the number of filters in each convolutional layer, and other hyperparameters. The model is then assembled using an appropriate loss function and an optimizer such as Adam. The training data is employed to train the ResNet model based on the given label that is used to learn the model for optimization of the parameters during training. To update the model’s weights forward and backward propagation is used throughout the training phase. The test data is utilized to evaluate the trained ResNet model. The evaluation is performed using measures to evaluate the model’s performance on unknown data is a common practice in assessment. The fundamental units of the network are called residual blocks and are introduced by the ResNet concept. The equation below defines a residual block:

$$\begin{aligned} y = F(x, W_i) + x \end{aligned}$$

(6)

where $x$ is the input to the residual block, typically the feature map output from a previous layer or block. $W_i$ denotes the weights of the layers within the residual block, which could include convolutional layers, batch normalization, and activation functions. $F(x, W_i)$ represents the transformation applied to the input $x$ by these layers.

Instead of merely outputting $F(x, W_i)$, a residual block adds the original input $x$ to the transformed input $F(x, W_i)$, creating a residual or skip connection. The result $y$ is the sum of the original input $x$ and the transformation $F(x, W_i)$.

The main idea behind using residual blocks is to address the vanishing gradient problem, which can hinder the training of very deep neural networks. By incorporating the input $x$ into the output, residual blocks facilitate the flow of gradients during backpropagation, enabling the training of deeper networks that perform better on complex tasks.

The ResNet model used in this study contains several layers. The first layer is a conv2d layer with (None, 26, 26, 64) output shape and has 640 parameters. It is followed by another convolutional layer conv2d-I with (None, 24, 24, 64) output shape and 36,928 trainable parameters. Next is the max-pooling2d layer with an output shape of (None, 12, 12, 64), followed by a dropout layer with a (None, 12, 12, 64) output shape and a flatten layer with an output shape of (None, 9216). These three layers have zero trainable parameters. They are followed by a dense layer with (None,128) output shape and have 11,79,776 trainable parameters. In the end, dropout-I and dense-I layers are placed with output shapes of (None,128) and (none, 10), respectively, and have 0 and 1290 trainable parameters.

Convolutional neural network

The following layers make up the CNN model that is used to classify images on the MNIST dataset. The conv2D layer has a ReLU activation function and 32 3x3 filter elements. It accepts a single channel of 28x28 input images. The selection of the largest value within each pool the max-pooling 2D layer with a pool size of 2x2 reduces the spatial dimensions of the 64 3x3-pixel Conv2D filters with a ReLU activation function. Using a pool size of 2x2, the MaxPooling2D layer is a layer of flattening that converts 2D feature maps into 1D vectors 64-unit dense layer with a ReLU activation function Class probabilities are produced via a dense layer with a softmax activation function.

The sparse categorical cross entropy loss function and the Adam optimizer are used to create the model. The model is trained with a batch size of 32 throughout 1 epoch. The test dataset is used to evaluate the model. The model summary also offers a thorough explanation of the model’s architecture. A CNN model’s equation can be shown as a series of operations. The convolutional layer involves the following operation

$$\begin{aligned} Z_1 = \phi _1(F_1 * X + b_1) \end{aligned}$$

(7)

where $F_1$ represents the convolutional filter applied to the input $X$, and $b_1$ is the bias term added to the result. The function $\phi _1$ denotes the activation function that is applied element-wise to the convolution result. The output of this layer, $Z_1$, is a feature map that captures important features from the input data.

$$\begin{aligned} Z_2 = \phi _2(F_2 * Z_1 + b_2) \end{aligned}$$

(8)

where $Z_1$ is the input to the second convolutional layer, $F_2$ is the filter applied to $Z_1$, and $b_2$ is the bias term. The activation function $\phi _2$ is applied to the result, producing the output feature map $Z_2$.

The pooling layers involve:

$$\begin{aligned} P_1&= P_m(Z_1)^2 \end{aligned}$$

(9)

$$\begin{aligned} P_2&= P_m(Z_2) \end{aligned}$$

(10)

where $P_m$ represents the pooling function applied to the feature map $Z_1$. This operation produces $P_1$, which is the down-sampled version of $Z_1$. Similarly, $P_m$ is applied to the feature map $Z_2$, resulting in the pooled feature map $P_2$.

Fully connected layers can be represented as:

$$\begin{aligned} Y = \sigma (D_l(P_k) + c) \end{aligned}$$

(11)

where $P_k$ is the input, $D_l$ is the weight matrix, and $c$ is the bias term. The activation function $\sigma$ is applied to the result of the linear transformation $D_l(P_k) + c$, producing the final output $Y$ which can be used for tasks such as classification.

The CNN model designed for this study contains seven layers. The first layer is a conv2d layer with (None, 26, 26, 32) output shape and 320 trainable parameters followed by a max-pooling2d layer with (None, 13,13, 32) output shape. After that, another conv2d layer is placed with an output shape of (None, 11, 11, 64) and has 18,496 trainable parameters. It is followed by a max-pooling2d-I layer with a (None, 5, 5, 64) output shape. A flatten layer is placed after that followed by a dense layer with 64 neurons and has 102,464 trainable parameters. In the end, a dense-I layer is placed for the number of classes, i.e., 10.

Recurrent neural network

RNNs are particularly well-suited for tasks involving sequential data due to their ability to analyze information sequentially. The RNN model is used to analyze the image pixels sequentially considering each row or column of pixels as a time step even if the MNIST dataset comprises static images. RNNs excel at capturing local dependencies within sequential data, making them adept at processing images where such dependencies exist. Their ability to handle variable-length sequences allows RNNs to accommodate images of different sizes effectively. RNNs can help work with datasets that have fluctuating image dimensions, even if the MNIST collection only contains fixed-size images. After training on sequence-related tasks such as text or time series analysis, RNN models can be refined or utilized as a starting point for addressing image classification challenges. Pre-trained RNN models can capture high-level features or contextual data that prove beneficial for image classification tasks. This computational effectiveness is particularly advantageous when operating under constraints of time or computing resources, thus rendering RNNs a valuable asset in such scenarios. Layer-wise model summary of RNN is given in Table 3. An expression for the central equation of a basic RNN model is as follows

$$\begin{aligned} H_t = \sigma (W_{hx} \cdot X_t + W_{hh} \cdot H_{t-1} + b_h) \end{aligned}$$

(12)

where $X_t$ represents the input at $t$, and $H_{t-1}$ is the hidden state. The weight matrix $W_{hx}$ is for the input $X_t$, while $W_{hh}$ is for the previous hidden state $H_{t-1}$. The bias term $b_h$ is added to the result of the linear combination. The function $\sigma$ denotes the activation function applied to the linear transformation, introducing non-linearity into the hidden state calculation.

$$\begin{aligned} Y_t&= \text {softmax}(W_{yh} \cdot H_t + b_y) \end{aligned}$$

(13)

In Equation 13, $W_{yh}$ is the weight matrix for state $H_t$. The bias term $b_y$ is added to the result of the linear transformation. The softmax function is then applied to the result, which converts the raw scores into probabilities, suitable for classification tasks. The softmax makes $Y_t$ a probability distribution over possible classes.

Table 3 RNN model layer summary.

AlexNet model

With the MNIST dataset for image classification, AlexNet can recognize handwritten digits with a high degree of accuracy. For tasks like digit identification, AlexNet’s design which includes several convolutional and pooling layers enables it to learn complicated information from images. Additionally, the MNIST dataset is a wonderful place to start learning about image classification and deep learning techniques because it is comparably small and straightforward to other image datasets. The convolutional layers and max-pooling layers of the AlexNet model work similarly to the CNN model. Convolutional layers of AlexNet are represented as:

$$\begin{aligned} Z_1&= \phi _1(F_1 * X + b_1) \end{aligned}$$

(14)

$$\begin{aligned} Z_2&= \phi _2(F_2 * Z_1 + b_2) \end{aligned}$$

(15)

where $X$ represents the input to the first convolutional layer, where $F_1$ is the convolutional filter applied to $X$, and $b_1$ is the bias term. The function $\phi _1$ denotes the activation function. The output $Z_1$ is a feature map that highlights important features from the input. The second convolutional layer operates on $Z_1$ using a different filter $F_2$ and bias $b_2$, with $\phi _2$ applied to the result, producing $Z_2$ as the output feature map.

Max-pooling layers are represented as:

$$\begin{aligned} P_1&= P_m(Z_1) \end{aligned}$$

(16)

$$\begin{aligned} P_2&= P_m(Z_2) \end{aligned}$$

(17)

where $P_m$ represents the pooling operation, applied to the features $Z_1$ and $Z_2$. Pooling reduces the spatial dimensions of the feature maps $Z_1$ and $Z_2$, resulting in $P_1$ and $P_2$, respectively. This reduction helps in decreasing the computational complexity and mitigating overfitting by preserving the most important features while discarding less significant details.

The AlexNet is made of 11 layers to identify characters in this study. The first layer is a conv2d with a (None, 26, 26, 32) output shape and has 320 trainable parameters. It is followed by a batch normalization layer having a (None, 26, 26, 32) output shape and 128 parameters. Next comes the max-pooling2d layer which has a (None, 13, 13, 32) output shape. Another conv2d layer is placed after this with an output shape of (None, 11, 11, 64) and has 18,496 trainable parameters. The batch-normalization-1 layer is placed after that with an output shape of None, 11, 11, 64) and 256 trainable parameters. The max-pooling2d-1 layer has an output shape of (None, 5, 5, 64), followed by the conv2d-2 layer with (None, 3, 3, 128) output shape and 73,856 trainable parameters. After that, the flatten and dense layers are placed with the dense layer having 256 neurons. The dropout layer has an output shape of (None, 256), followed by the final dense layer with 10 neurons to predict the final class.

VGG model

The CNN architecture known as VGG is renowned for its intricate and detailed design. It is widely recognized for its remarkable depth and is available in two primary variations: VGG16, which comprises 16 weight layers, and VGG19, which consists of 19 weight layers. These designs are increasingly prevalent due to their ability to extract intricate information from images, making them well-suited for various computer vision applications, including image categorization. Employing deeper CNN architectures like VGG in more complex datasets, such as those found in large-scale image recognition tasks or datasets containing numerous objects, intricate backgrounds, and fine features, could provide insights into their full capabilities. T

For more complicated datasets with a large variety of objects and scenarios, the additional layers of VGG can help it learn hierarchical features and abstract representations of input images. When compared to a shallower architecture like AlexNet the extra depth of VGG may not significantly improve accuracy for MNIST which largely includes identifying handwritten digits. When compared to a shallower architecture like AlexNet, the additional depth of VGG may not significantly enhance accuracy for datasets like MNIST, which primarily involves identifying handwritten digits. In conclusion, while VGG stands as a robust CNN architecture capable of learning complex features, its full potential may not be realized when applied to straightforward datasets like MNIST. Assessing the performance of neural networks on more challenging and intricate image classification tasks often yields greater insights into their functionality and advantages. Convolutional layers of VGG can be represented as

$$\begin{aligned} Z_{1,1}= & \phi _1(F_{1,1} * X + b_{1,1}) \end{aligned}$$

(18)

$$\begin{aligned} Z_{1,2}= & \phi _2(F_{1,2} * Z_{1,1} + b_{1,2}) \end{aligned}$$

(19)

where $X$ represents the input image. In the first convolutional layer, $F_{1,1}$ is the filter applied to $X$, and $b_{1,1}$ is the associated bias term. The activation function $\phi _1$ introduces non-linearity to the convolutional output, producing $Z_{1,1}$. The second convolutional layer takes $Z_{1,1}$ as input, applies the filter $F_{1,2}$ with bias $b_{1,2}$, and applies the activation function $\phi _2$ to yield $Z_{1,2}$.

The max-pooling layer operates as follows

$$\begin{aligned} P_1= & \text {max-pool}(Z_{1,2}) \end{aligned}$$

(20)

$$\begin{aligned} P_2= & \text {max-pool}(Z_{2,2}) \end{aligned}$$

(21)

where $\text {max-pool}$ denotes the max-pooling operation applied to $Z_{1,2}$ and $Z_{2,2}$. This operation reduces the spatial dimensions of the feature maps while retaining the most significant features.

In the end, the fully connected layer can be represented as

$$\begin{aligned} Y = \sigma (D_l(P_k) + c) \end{aligned}$$

(22)

where $P_k$ represents the output from the pooling layers, which is flattened and passed through the fully connected layer. $D_l$ is the weight matrix for this layer, and $c$ is the bias term. The activation function $\sigma$ (e.g., softmax for classification) is applied to produce the final output $Y$, which represents the predicted class probabilities for the input image.

This study adopts a 14-layer VGG model comprising convolutional, max-pooling, flatten, and dense layers. The first and second layers are conv2d layers each with an output shape of (None, 28, 28, 64), followed by a max-pooling2d layer with a (None, 14, 14, 64) output shape. After that, conv2d-III and conv2d-IV layers are placed each with an output shape of (None, 14, 14, 128). Another max-pooling layer is placed after these layers which has an output shape of (None, 7, 7, 128). After the second max-pooling layer, three conv2d layers are placed and each layer has the same output shape of (None, 7, 7, 256). Afterward, a max-pooling2d layer is placed with a (None, 3, 3, 256) output shape is placed. It is followed by a flatten layer. In the end, three dense layers are placed with 4096, 4096, and 10 neurons.

CSNN model

A CSNN model is used to handle visual categorization tasks. The input images are utilized to extract features using the CNN and the retrieved features are processed using the SNN in a spiking manner. To increase accuracy numerous models are combined through stacking. This architecture has the advantage of being even more accurate than CSNN or stacking alone when used with the MNIST dataset for image classification. While stacking can be effective for combining the capabilities of many models the SNN can be useful for jobs that require temporal processing such as recognizing sequences of digits in a handwritten number. SNNs are also renowned for their energy economy and capacity for data processing in a way that is more biologically believable. To fully benefit from the energy efficiency advantages of SNNs, the design might be more difficult to implement and needs specialized hardware. However, it might be a useful exercise to comprehend how several neural network types can be integrated to carry out challenging tasks like image categorization. Let’s combine these layers to produce the layered model equation:

$$\begin{aligned} Y = \text {SNN}(Z_{\text {CNN,last}}) \end{aligned}$$

(23)

Equation 23 represents the integration of Convolutional Neural Network (CNN) features with Spiking Neural Network (SNN) processing. In this equation, $Z_{\text {CNN, last}}$ denotes the output feature map from the final convolutional layer of a CNN. This feature map encapsulates the high-level abstracted features extracted by the convolutional layers. The function $\text {SNN}(\cdot )$ signifies the processing by the spiking neural network, which takes $Z_{\text {CNN, last}}$ as its input. The SNN is designed to handle temporal aspects of data and can provide a more biologically plausible model of neural processing. The output $Y$ represents the final classification or prediction result of the CSNN model, derived after the SNN has processed the features from the CNN. This integration allows the CSNN to leverage the spatial feature extraction capabilities of CNNs while benefiting from the temporal dynamics and spiking behavior of SNNs.

For the CSNN model, conv2d-4 has an output shape of (None, 26, 26, 32) with 320 parameters, followed by max-pooling2d-4 and flatten-4 layers with an output shape of (None, 13, 13, 32) and (None, 5408). Afterward, two dense layers are added with (None, 64) and (None,10) shape, followed by a conv2d-5 layer with (None, 26, 26, 32) output shape. Another max-pooling layer is added with a (None, 13, 13, 32) shape which is followed by a (None, 5408)-shaped flatten layer. In the end, four dense layers are added with (none, 128), (None, 10), (None, 64), and (None, 10).

CNN-LSTM

The MNIST dataset is classified using the CNN-LSTM model, which combines sequential and convolutional learning techniques. The MNIST dataset is first preprocessed independently for CNN and LSTM inputs. It consists of grayscale photographs of handwritten digits. In order to extract high-level representations, the CNN component processes the spatial properties of the images via a succession of convolutional and max-pooling layers, followed by flattening and dense layers. By restructuring the images into sequences, the LSTM component is able to capture temporal dependencies and handle the sequential character of the input. To get the classification results, the outputs from both models are concatenated and input into a final dense layer with a softmax activation function. After compilation, the merged model is validated on the test set and trained on the training set. Accuracy and loss measures are used to evaluate the model’s performance and epoch-specific accuracy trends are displayed to gauge the model’s capacity for generalization and learning. The summary of the model’s layer is given in Table 4.

Table 4 CNN-LSTM model layer summary.

DCAE

Handwritten digits are classified using the deep convolutional autoencoder (Mr-DCAE) on the MNIST dataset. First, the photos in the dataset are reshaped and normalized. The Mr-DCAE architecture is composed of an encoder that uses convolutional and max-pooling layers to compress the input images into lower-dimensional representations, and a decoder that uses convolutional and upsampling layers to reconstruct the images. To the encoded information, a classification layer is additionally included, which enables the model to predict digit classes. Accuracy is the main evaluation parameter, and the model is trained using sparse categorical cross-entropy loss and the Adam optimizer. By monitoring training and validation accuracy throughout epochs and producing a classification report based on test predictions, performance is evaluated. Table 5 provides a summary of layers.

Table 5 DCAE model layer summary.

EGACNN

CNN and GA are combined to solve image categorization tasks, as shown in Fig. 4. The evolutionary algorithm is used to optimize the CNN hyperparameters while the CNN itself is utilized to extract features from the input images. This architecture has the advantage of being able to automatically optimize the CNN hyperparameters without requiring user adjustment when used with the MNIST dataset for image classification. When compared to manually adjusting the hyperparameters this can result in greater accuracy and quicker convergence.

Fig. 4

Ensemble genetic and CNN model-based image classification approach.

While more complex architectures like the one mentioned may be challenging to construct and require greater processing power compared to simpler designs like AlexNet or VGG, it can still be a beneficial exercise to understand how various optimization methods can improve the efficiency of deep learning systems. The ensemble model contains different layers comprising various output shapes and parameters which are given in Table 6.

Table 6 The layer-wise summary of the proposed EGACNN model.

Evaluation parameters

The proposed model is evaluated using accuracy, precision, recall, and F1 score all have complementing qualities it is imperative to employ them all in conjunction. Determining the percentage of correctly classified instances in the total accuracy offers a wide indication of overall correctness nevertheless in scenarios where there is an imbalance in classes accuracy may be deceptive. Precision measures the percentage of real positive predictions among all predicted positives highlighting the model’s critical ability to prevent false positives which can be expensive. Recall illustrates the model’s capacity to find all pertinent occurrences by calculating the percentage of true positives out of all actual positives. This is crucial when there is a substantial problem with missing positives. As the harmonic mean of recall and precision, the F1 score strikes a balance between the two metrics and offers a single, all-encompassing performance score that is particularly helpful in situations when datasets are unbalanced. When combined these metrics provide a comprehensive and detailed assessment of the model’s performance in several different areas.

Precision is a crucial metric used in evaluating the performance of classification models, particularly in scenarios where the balance between the number of true positive and false positive predictions is important. The precision of a model is defined by the formula:

$$\begin{aligned} \text {Precision} = \frac{TP}{TP + FP} \end{aligned}$$

(24)

In Equation 24, $TP$ (True Positives) show instances correctly classified as positive while $FP$ (False Positives) show incorrectly classified as positive. Precision measures the ratio of correctly predicted positive samples. A high precision value shows the model’s capability to give low false positives, which is desirable in applications where false positive errors are costly or critical. Conversely, low precision suggests that the model has a high rate of false positives, indicating that many of the positive predictions made by the model are incorrect. Recall also known as sensitivity or true positive rate, is a performance metric used to assess the effectiveness of a classification model, especially in detecting positive instances. The recall of a model is defined by the formula:

$$\begin{aligned} \text {Recall} = \frac{TP}{TP + FN} \end{aligned}$$

(25)

Recall measures the proportion of actual positive instances that were correctly classified by the model, providing insight into the model’s ability to identify positive cases. A high recall value indicates that the model is effective at detecting most of the positive instances, which is particularly important in scenarios where missing a positive case has significant consequences, such as in medical diagnostics or fraud detection. Conversely, low recall signifies that the model is missing many of the positive instances, leading to a higher number of false negatives.

The F1-Score is a metric used to evaluate the performance of classification models, particularly in situations where both precision and recall are important. It provides a single measure that balances the trade-off between precision and recall, offering a comprehensive assessment of a model’s accuracy. The F1-Score is defined by the formula:

$$\begin{aligned} \text {F1-Score} = \frac{2 \cdot \text {Precision} \cdot \text {Recall}}{\text {Precision} + \text {Recall}} \end{aligned}$$

(26)

The F1-Score is the harmonic mean of precision and recall, which ensures that both metrics contribute equally to the final score. A high F1-Score indicates that the model achieves a good balance between precision and recall, which is desirable in the case of imbalanced class distribution. Conversely, a low F1-Score suggests that there is a significant imbalance between precision and recall, highlighting the need for further model refinement.

Results and discussion

The proposed ensemble model combines GA and CNN where GA is used to enhance the model’s performance by hyperparameter tuning. We provide the research findings and demonstrate how the proposed method works for image classification tasks. We systematically provide the empirical results achieved through rigorous experimentation and explore the ramifications of conclusions to improving image categorization system performance. The promising results have been obtained from the confluence of these two different paradigms. The representational strength of CNNs and the computational efficiency of genetic algorithms. In the end, we hope to add to the continuing conversation in the field of computer vision and image categorization by thoroughly examining these results and elucidating the benefits, drawbacks, and revelations derived from our methodology.

Results for CNN model

Figure 5 shows the training and validation accuracy and loss of the CNN model. It can be seen that the model improves its accuracy with each epoch and reaches a 99% accuracy.

Fig. 5

CNN model’s training and validation graph.

Table 7 shows the performance results of the CNN model. The CNN model performs much better when the epoch is raised for image classification using the MNIST dataset. The maximum accuracy of this model is 0.9921 and the maximum epoch is 30. The accuracy for the 5 epoch is 0.9891 it rose by 0.9914 for epoch 10, 0.9916 for epoch 15, 0.9916 for epoch 20, and 0.9917 for epoch 25.

Table 7 Summary of CNN model’s performance.

Results of RNN model

The performance of the RNN model concerning training and validation accuracy and training and validation loss is presented in Fig. 6. The model’s performance is improved with each passing epoch and it obtains a stable accuracy once it reaches epoch 17.

Fig. 6

RNN model’s training and validation graph.

In terms of image classification, the RNN model performs better when the epoch is raised these improvements are substantial, as shown in Table 8. The maximum accuracy in this research is 0.9638 for the maximum epoch at 30. The accuracy of the model for the first 5 epochs is 0.9575 it increases to 0.9445 for epoch 10 it gets to 0.9661 for epoch 15 it reaches 0.9663 for epoch 20 and it reaches 0.9611 for epoch 25.

Table 8 Summary of RNN model’s performance.

Results using AlexNet model

The AlexNet model performs much better when the epoch is raised when it is used with the MNIST dataset for image classification, shown in Table 9. This model shows maximum accuracy is 0.9919 and the maximum epoch is 30. The accuracy of the 5 epoch is 0.9897 it increased by 0.9907 for epoch 10 it increased by 0.9922 for epoch 15; by the 20 epoch accuracy is 0.9991 and it increased by 0.9933 for epoch 25.

Table 9 Summary of AlexNet model’s performance.

Results using ResNet model

Table 10 presented the recall, f1-score, accuracy, and precision of the model. When a ResNet model is used with the MNIST dataset for Image classification improves its performance considerably with an increase in epoch. The maximum accuracy in this research is 0.9929 and the maximum epoch is 30. The accuracy of the 5 epoch model is 0.9909 it increases to 0.9915 for epoch 10 it increases to 0.9922 for epoch 15 it is 0.9922 for epoch 20 and it is 0.9926 for epoch 25.

Table 10 Summary of ResNet model’s performance.

Results using VGG model

Table 11 displays the accuracy, precision, recall and f1-score. Enhancing the epoch of a VGG model with the MNIST dataset is used to improve the performance of image classification dramatically. The maximum epoch and accuracy in this research are 30 and 0.9915 respectively. The accuracy for the 5-epoch model is 0.9904 for epochs 10 through 25 the accuracy rises to 0.9968, 0.9912, and 0.9922 for epochs 20 and 25 respectively.

Table 11 VGG model’s performance summary.

Results using RSNN model

The model’s accuracy, precision, recall, and F1 score are shown in Table 12. Increasing the epoch greatly improves the performance of the proposed Model RSNN with the MNIST dataset in image classification. The highest accuracy achieved by the model is 0.9719 and its maximum epoch is 30. The accuracy of the 5-epoch model is 0.9742, which increases to 0.9744 for epoch 10, 0.9749 for epoch 15, 0.9748 for epoch 20, and 0.9760 for epoch 25.

Table 12 RSNN model’s performance summary.

Results using CRNN model

Table 13 shows the performance of the CRNN model used in this study. The suggested CRNN model performs much better when the epoch is raised when it comes to Image classification using the MNIST dataset. The maximum epoch and accuracy of this model are 30 and 0.9911 respectively. The five-epoch model’s accuracy is 0.9868 which increases to 0.9876 for epoch 10 it increases to 0.9890 for epoch 15 it is 0.9898 for epoch 20 and it is 0.9904 for epoch 25.

Table 13 CRNN model’s performance summary.

Results using CSNN model

When the epoch is raised the suggested CSNN model performs significantly better for image classification using the MNIST dataset, as shown in Table 14. The maximum accuracy in this research is 0.9931 and the maximum epoch is 30. The accuracy of the 5-epoch model is 0.9893 it grows to 0.9917 for epoch 10, 0.9910 for epoch 15, 0.9910 for epoch 20, and 0.9931 for epoch 25 with its increased accuracy.

Table 14 CSNN model’s performance summary.

Results using CNN-LSTM model

The CNN-LSTM model on the MNIST dataset for image classification when the epoch is increased. In this research, the maximum epoch is 20 and the maximum accuracy is 0.9922. The five-epoch model’s accuracy is 0.9900; with its enhanced accuracy, it grows to 0.9919 for epoch 10, 0.9886 for epoch 15, 0.9909 for epoch 25, and 0.9899 for epoch 30. The graphical representation in Fig. 7 of the model with accuracy, precision, recall, and F1 score is shown in Table 15.

Fig. 7

CNN-LSTM model graph.

Table 15 CNN-LSTM model performance summary.

Results using DCAE model

The DCAE model on the MNIST dataset image classification increases with the epoch. In this research, the maximum epoch is 20 with a maximum accuracy is 0.9914. The accuracy of the five-epoch model is 0.9891, for epochs 10 through 30, it increases to 0.9902, 0.9901, 0.9897, and 0.9899 with its enhanced precision. The graphical representation in Fig. 8 of the model with accuracy, precision, recall, and F1 score is shown in Table 16.

Fig. 8

DCAE model graph.

Table 16 DCAE model performance summary.

Results using proposed EGACNN model

Figure 9 shows the training accuracy and training loss of the proposed EGACNN model when used with different generations of the GA algorithm. It can be observed that with each generation of GA, the training accuracy is increased while the training loss is reduced.

Fig. 9

Training accuracy and training loss graphs for the proposed EGACNN model.

Table 17 shows the performance of the proposed approach concerning accuracy, precision, etc. When the epoch is increased there is a noticeable improvement in the suggested (EGACNN) model performance for image classification using the MNIST dataset. The maximum accuracy in this research is 0.9901, and the maximum epoch is 30. The accuracy for the 5-epoch model is 0.9991, for epoch 10 it is 0.9905, for epoch 15 it is 0.9912, for epoch 20 it is 0.9901, and for epoch 25 it is 0.9894.

Table 17 EGACNN model’s performance summary.

Analysis

The EGACNN model surpasses individual models like CNN, RNN, AlexNet, ResNet, and VGG. The CNN’s capacity to learn and generalize from the data is greatly enhanced by the GA iterative and adaptive optimization of critical hyperparameters like learning rates, batch sizes, and regularization techniques. Compared to alternative models that do not make use of such thorough optimization this leads to improved accuracy and faster model convergence. While the CNN and CSNN ensemble has strong performance as well it is not as hyperparameter-refined as EGACNN. This demonstrates the advantages of merging and optimizing several algorithms and performs better in image classification tasks as a result of integrating CNN’s strengths in feature extraction with GA’s optimization techniques.

Performance of all deep learning models

A performance comparison of all deep learning models with the proposed EGACNN model would provide insight into the better results of the proposed approach. Table 18 provides the comparative results of all models concerning their best performance in terms of accuracy and the associated epoch at which they get the best accuracy. It can be seen that the proposed model obtains the best results with an accuracy score of 0.9991 which is the highest among all the employed models thereby indicating its potential to produce better results with fewer epochs.

Table 18 Comparative analysis of deep learning models with the proposed EGACNN.

Ablation study

For further corroboration, 10-fold cross-validation is also done using 10-fold and 5-fold cross-validation to see how the proposed approach performs on smaller data folds. The proposed is to check how the model will behave in the case of using small dataset samples. In addition, different numbers of epochs are also used for cross-validation, thereby providing the performance analysis of the proposed model from multiple aspects.

Table 19 Performance using 5 folds.

Table 19 shows the results using 5-folds where the dataset is divided into 5 folds, each containing 10% of the original dataset. Results suggest that the performance of the model is best using five folds as discussed previously. Compared to the results reported earlier, scores for performance metrics vary slightly when using five-fold cross-validation. However, the differences in evaluation metrics are higher in the case of using ten-fold cross-validation, as shown in Table 20. It is so because, in the case of using ten folds, the sample size for training is smaller which affects the performance of the model. The best accuracy is obtained using 20 epochs which obtains a 0.9909 accuracy score which is reduced compared to the previous best accuracy score of 0.9991. Despite that, the performance is good and generalizable thereby showing the robustness of the proposed approach.

Table 20 Performance using 10 folds.

Performance with existing approaches

The performance of the proposed approach is considered against existing approaches that perform image classification. For a fair comparison, we have selected the studies that utilized the MNIST dataset for experiments. Performance comparison is provided in Table 21. We considered several recent state-of-the-art models for comparison. For example,⁵⁵ utilized an AlexNet model and achieved an accuracy score of 0.923. Similarly, the study⁵⁶ used an AlexNet model on the MNIST dataset and showed an accuracy score of 0.9874. The authors designed a custom CNN model in⁵⁷ and obtained a 0.98 accuracy score. Performance analysis indicates that the proposed ensemble model shows the best results compared to existing approaches by obtaining an accuracy score of 0.9991.

Table 21 Comparative analysis of the proposed EGBACNN model with existing models.

Future work

In this research, to tackle the problem of hyperparameter tuning in image classification the ensemble GA and CNN EGACNN has been proposed. Through the integration of CNN and GA for optimization the EGACNN model achieves impressive accuracy as demonstrated by its maximum reported score of 99.91% on the MNIST dataset. This ensemble method works better than individual models like CNN, RNN, AlexNet, ResNet, and VGG proving that combining several approaches can improve Image classification performance. The findings point to a great deal of promise for using ensemble methods to increase the effectiveness and prediction accuracy of image classification tasks. This has important ramifications for future studies and applications in a variety of domains, such as autonomous cars, agriculture, security, and surveillance. Currently, the ensemble model has higher training time which is not suitable for real-time response-requiring applications, however, in the future we intend to work on reducing its computational complexity.

Conclusion

Image classification is used in many fields and sectors including autonomous vehicles, agriculture, security and surveillance, and medical imaging. Image classification is finding ever-wider applications as new use cases and technological advancements occur. Accurate image classification is essential for a variety of tasks in each of these fields from threat identification in security and surveillance to disease diagnosis in medical imaging. Hyperparameter tuning is essential to improving image classification models’ performance. The accuracy convergence speed and generalization abilities of the model can all be greatly enhanced by carefully modifying hyperparameters like learning rates, batch sizes, and regularization strategies. The process of optimization guarantees that the model is precisely adjusted to the unique features and intricacies of the data it is supposed to categorize.

This study proposes an ensemble model EGACNN, leveraging the genetic algorithm and CNN to tackle the problem of hyperparameter tweaking in image classification. This methodology uses stacking techniques based on the MNIST dataset to combine the power of CNN with the optimization skills of a genetic algorithm. The objective of this approach is to improve image classification task efficiency and prediction rates. The EGACNN model yielded remarkably accurate results with a 99.91% accuracy. The results indicate that the ensemble method EGACNN is more effective than individual models like CNN, RNN, AlexNet, ResNet, and VGG. This suggests that integrating multiple techniques can lead to enhanced image classification performance. Using the genetic algorithm for hyperparameter optimization tends to reduce the effort of model optimization and produce better results with less training.