Introduction

Climate changes due to anthropogenic activities are causing significant alterations in the hydrogeological cycle1,2,3. The Mediterranean is a hotspot for current global warming4,5,6, exhibiting variations in river discharge and precipitation across various areas7,8,9,10,11. Future projections for hydrogeological regimes indicate a general decrease in annual precipitation with an increased risk of drought12,13,14,15,16,17,18, but also an intensification of extreme and fast events8,19,20,21. The effects of climate evolution in the Mediterranean will be enhanced by the characteristics of medium and small catchments22. The management of small catchments is challenging on account of their hydrogeological features, which often provide insufficient time for effective emergency intervention. These drawbacks also depend on the current lack of suitable meteorological forecasts at this scale23.

Italy is no exception to this reality, and it is one of the Mediterranean countries in Europe with the highest annual expenditure for damages caused by hydrogeological events24,25,26,27. Italian territorial entities responsible for river risk management currently lack efficient predictive models allowing for timely interventions in small catchments, which are those characterizing a significant part of the peninsula. Strict requirements in terms of knowledge of the territory and of hydrogeological parameters are necessary to build an efficient river flow modelling system based on a physical approach. The definition of several parameters, the often-missing information, and the difficulty in simulating the real natural system may produce strong model uncertainties, which play a predominant role in error quantification28,29,30. For these reasons, very few tools have so far been able to provide rapid alerts for flood risk mitigation, in particular for these types of catchments. Machine learning models have proven to be a valuable tool for runoff modelling31,32,33,34,35,36,37, thanks to the use of neural networks that enable to handle the noise and chaotic nature of time series in prediction problems38. In this respect, some recent works have focused on the development of models in small catchments39,40,41, which currently represent a challenge in the research and application of flood risk mitigation. Several authors have applied different deep learning techniques to predict river flows, with promising results42,43,44,45,46. Long short-term memory (LSTM) is one of the most popular, efficient and deeply used learning techniques47, widely applied in flood prediction studies48,49,50.

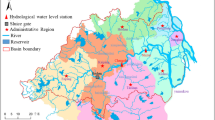
The study area, located in central Italy (Fig. 1), is particularly vulnerable to climate changes, owing to the presence of the cyclonic area of the Gulf of Genoa51 and of the steep reliefs orthogonal to the direction of prevailing winds52,53,54. The area is characterized by the presence of the Apuan Alps, a mountain range with large slopes and a complex karstic system53,55 (Fig. 1). The region features a complex river network, a coastal lake (Lake Massaciuccoli), and wetland areas. The plain area is subject to regulations designed to maintain the water table below ground level. The area experiences high annual precipitations (even more than 3000 mm56,57,58), among the highest in the Mediterranean, and sometimes very intense. Furthermore, owing to the presence of the Apuan Alps, hydrogeological events such as floods, debris flows, and landslides often occur52,57,59,60,61.

The intricate karstic systems in this area make it difficult to provide efficient tools for predicting river dynamics30,55,62. The steep slopes of the mountains induce rapid runoff times, but their estimation is complicated by the poorly understood karstic systems. The plains are characterized by a significant human presence, with over 300,000 inhabitants, and more than3 million individuals during the summer, presenting a high population density. In this context, for the future effects of climate change, enhanced by the environmental characteristics of the territory and the substantial presence of human activities, we have developed a group of models based on deep learning approaches that can predict river discharge in a regulated lake and in small watercourses. The set of constructed models diverges from the input data matrix employed for training. We chose to create this ensemble primarily for two purposes: (i) to understand the pros and cons associated with incorporating diverse input data types; and (ii) to have models that react variably (or not) from identical initial conditions, thereby yielding a broader spectrum of scenarios and varying levels of prediction certainty.

Different territorial entities have collaborated to the design and implementation of a computer system providing real-time predictions of watercourses up to 6 h in advance for 8 monitoring points (see stars in Fig. 1). Table 1 shows the main hydraulic characteristics of the water system investigated. Prediction models are limited by the inability to understand how the conditions may evolve in the future. As for the hydraulic models, the primary predictive limitation is rainfall, which is the main time-related input variable. Therefore, machine learning models tend to underestimate flows during the forecasting time, due to data uncertainties and potential biases63. In this work, we experimented an error analysis of the results of predictive models through a combination with additional machine learning models that allow an increase in the lead time for alarms regarding the hydraulic systems studied.

Fig. 1
figure 1

Study area (a) Input and output gauges; (b) Spatial location of the study area; (c) Morphology of the study area where green indicates an elevation lower than 10 m and red an elevation higher than 1200 m. OpenStreetMap provides basemap.

Full size image
Table 1 Main characteristics of hydrometric time series used as output of the models.
Full size table

Results and discussion

Figure 2 summarizes the Root Mean Square Errors (RMSE) for the 25 steps of forecasting, for each model and for each output station. The deep learning models developed in this work have small errors for the entire test dataset, and they focus on events higher than the 95th percentile. We will refer to observations exceeding the 95th percentile as extreme events64 by recording errors of only a few centimetres compared to those found in other works32,35,63,64,65,66. The results of this work are in agreement with those of other works which used sub-daily river flow data in catchments with a comparable size41,67. However, a direct comparison with other works is not always simple owing to the different measures simulated (hydrometric height or flow rate) and to the different hydraulic condition and behaviour of the rivers. For the Avenza and Carrara (Carriore River), and for the Ponte Tavole and Seravezza (Versilia River) stations the OOM model is the worst, with a clear increase of the performances following the introduction of other gauges. As already said, for the Mutigliano and Ponte Guido stations, the difference between the OOM and the other models is not relevant. However, the NM and the ORM are the best models with the lowest RMSE. For Massaciuccoli and Viareggio (Massaciuccoli Lake system), the OOM model performs similarly to the other ones, highlighting an unclear importance of the introduction of rain and hydrometric gauges as input data. These results indicate the differences in behaviour between the four hydraulic systems studied in this work. For the Carrione and Versilia Rivers, which are characterized by the highest hydraulic ranges, the introduction of more gauges as input to the model increase the possibility of creating accurate models. With the decrease in variability of the system’s simulated hydraulic regimes, the importance of the other input gauges decreases. Such behaviour may be observed in the Freddana and Contesora torrents as well as in the Massaciuccoli Lake system, where the difference between the minimum and the maximum regimes is lower than 50 cm(Table 1).

It is worth noting that for step t = 0 of each station, and in some cases also for some steps below, the OOM has performances analogous to those of other models. This is an important point because, in the last years, several works (e.g36,46,68,69). have yielded positive results with regard to deep learning and machine learning models for the prediction of river flows. Complex data input matrices have been used but the role of the time series output on the models has not been understood. The complexity of the neural networks and the high number of parameters estimated during the training phase make it difficult to well understand the input influence on the deep learning models. However, this study underlines the importance of investigating in further detail the real effect of the inputs on the results in these types of models. If the aim of this study had been the construction of models for the analysis of t = 0 (making a simple reconstruction of the river flow time series with the river flow data up to step t-1), the use of a network of stations would have resulted useless.

Figures 3 and 4 show some selected applications for each station. These selections derive from an analysis of the 10 highest events in the test dataset (see Supplementary Material for all events). In Fig. 3, we report a case for each station when the models have great performances while, in Fig. 4, we report the cases in which the models have lower performances. No model performs better than the others. The models sometimes produce similar results (see in particular Fig. 3), so that there is a small variability in the predictions; other times there are differences between the predictions (see in particular Fig. 4). This suggests that the combination of models can provide a more exhaustive forecast during the decision-making processes. The hydrological cases of Fig. 4 are affected by a fast variation of the river levels characterized by an increase in river flow in a few tens of minutes. This makes it difficult for the models to provide an efficient prediction, especially with the increase in forecasting time, which induces an underestimation of the real river flow observed. However, for the cases shown in Figs. 3 and 4, the models generally have excellent performances until 2–4 h of forecasting, although in some cases even up to 6 h (see also the Supplementary Material).

The analysis of the Mean Errors (ME; Fig. 5) shows that with the increase of forecasting time, the models present negative errors. In other words, with the increase of the forecasting time, the models always underestimate the flow, and this induces a possible systematic missing alarm, in particular for extreme events (higher than the 95th percentile), as observed during the analysis of Fig. 4. The main factor that can cause an underestimation of the predictions in the highest forecasting times can be the lack of information on the evolution of weather conditions over time. The models can provide a prediction if they know the progressive amount of precipitation falling into the basin and, once the rainfall has started, the models do not know what will be the total amount of precipitation in the future. For this reason, we observe a progressive decrease in the underestimation of the river flows, so that the forecasting time is reduced. In the small hydrographic catchments, we think that the weather predictions cannot solve this limit completely on account of the current small resolution of the weather prediction, with grids greater than 30 km. However, we think that an analysis of the uncertainties can be more efficient to mitigate the likelihood of missing the alarms. The probability of taking wrong decisions is partly linked to the knowledge of the phenomenon, which may result in potentially dubious predictions.

For this reason, the choice of introducing the use of Gradient Boosting Regression (GBR) in this work is key. An example of application of the GBR models to estimate the confidence intervals of the errors on the predictions appears in Fig. 6. The GBR models allow to quantify the uncertainties of the LSTM models on the basis of the last observed hydrometric measures of the output station. The effects of the introduction of the GBR models are crucial. Figures 7 and 8 show the capacity of the models to forecast the alarms for cases higher than the 95th percentile (extreme events). The metrics observable in the figure are True Positive Rate (TPR; Fig. 7) and False Positive Rate (FPR; Fig. 8), which are defined as follows:

$$\:TPR=\frac{TP}{P}$$
$$\:FPR=\frac{FP}{N}$$

where \(\:P\) in the number of real cases higher than the 95th percentile in the test dataset; \(\:N\) is the number of real cases lower than the 95th percentile in the test dataset; \(\:TP\) is the number of simulated data that correctly indicates cases higher than the 95th percentile; and \(\:FP\) is the number of simulated data which wrongly indicates cases higher than the 95th percentile (false alarms). The application of the GBR models must increase the \(\:TPR,\) maintaining the \(\:FPR\) acceptable (Fig. 8). Otherwise, the possibility of predicting real alarms may be hindered by the creation of additional false alarms. The estimation of the uncertainties of the LSTM models can increase the capacity of the models to forecast an alarm (Fig. 7). By analysing the errors of the LSTM models (Figs. 3 and 4), the GBR models provide confidence intervals of only a few centimetres. For example, for the Avenza station, we applied the GBR models by adding an average value of the upper limits of the 50% confidence interval of about 0.01 cm and of the 90% confidence interval of about 0.04 cm. The values for Ponte Guido are about 0.02 cm and 0.04 cm, respectively. These values are very small, but thanks to the nature of the rivers investigated, these very low uncertainties can make the difference between a correct and a missing alarm. Such effects are greater for the smaller hydraulic systems investigated in this work (for example, Mutigliano, Ponte Guido, and Massaciuccoli; Fig. 7). Probably, these hydraulic systems are also affected by the uncertain measurements that are not estimated by the territorial authorities responsible for monitoring the weather network. It is plausible to think that for small channels, lakes, and rivers, the simple error and the instrumental uncertainties used to acquire the data can induce more effects on the results than the hydraulic systems, which are characterized by greater flow rate, and variation from the lower and higher levels. It is thus important to introduce a study of the uncertainties of the deep learning models, so as to provide more efficient forecasting systems like the GBR models proposed in this work. The data-driven characteristics of the deep learning models require an efficient sample and archive of the data, as demonstrated by several authors who found the highest errors in presence of wrong or anomalous data70,71.

Fig. 2
figure 2

Root Mean Square Errors (RMSE) of the deep learning models for forecasting time from 0 h to 6 h with a step of 15 min: the lines with ● marker indicate the Standard Model (SM); the lines with ▲ marker indicate the Normalized Model (NM); the lines with ▼marker indicate the Only Rainfall Model (ORM); the lines with ■ marker indicate the Only Output Model (OOM). The contours indicate a confidential interval of 90%. The blue lines indicate the RMSE using the entire test dataset, while the orange lines indicate the RMSE by analysing the hydrometric height higher than the 95th percentile.

Full size image
Fig. 3
figure 3

Selected examples when the models allow good predictions of extreme events. Each row corresponds to a specific station, respectivelyAvenza, Carrara, Mutigliano, Ponte Guido, Seravezza, Versilia, Massaciuccoli and Viareggio. Each column corresponds to a specific model, respectively: Only Output Model (OOM), Standard Model (SM), Normalized Model (NM), and Only Rainfall Model (ORM). The grey line indicates the observed data, the black line indicates the prediction at 0 h; the violet line indicates the prediction at 2 h; the orange line indicates the prediction at 4 h; and the yellow line indicates the prediction at 6 h.

Full size image
Fig. 4
figure 4

Selected examples where models do not allow very good predictions of extreme events. Each rowcorresponds to a specific station, respectively Avenza, Carrara, Mutigliano, Ponte Guido, Seravezza, Versilia, Massaciuccoli and Viareggio. Each column corresponds to a specific model, respectively Only Output Model (OOM), Standard Model (SM), Normalized Model (NM), and Only Rainfall Model (ORM). The grey line indicates the observed data, the black line indicates the prediction at 0 h; the violet line indicates the prediction at 2 h; the orange line indicates the prediction at 4 h; and the yellow line indicates the prediction at 6 h.

Full size image
Fig. 5
figure 5

Mean Errors (ME) of the deep learning models for forecasting time from 0 h to 6 h with a step of 15 min: the lines with ● marker indicate the Standard Model (SM); the lines with ▲ marker indicate the Normalized Model (NM); the lines with ▼marker indicate the Only Rainfall Model (ORM); the lines with ■ marker indicate the Only Output Model (OOM). The contours indicate a confidential interval of 90%. The blue lines indicate the ME using the entire test dataset, while the orange lines indicate the ME analysing the hydrometric height higher than the 95th percentile.

Full size image
Fig. 6
figure 6

An example of the applied regression using the Gradient Boosting Regressor (GBR) for the estimation of uncertain predictions. The GBR model is used to estimate the confidential intervals of 50% and 90% based on the observed hydrometric height.

Full size image
Fig. 7
figure 7

Sensitivity analysis of the models for events higher than the 95th percentile: True Positive Rate (TPR). The lines with ● marker indicate the Standard Model (SM); the lines with ▲ marker indicate the Normalized Model (NM); the lines with ▼marker indicate the Only Rainfall Model (ORM); the lines with ■ marker indicate the Only Output Model (OOM).

Full size image
Fig. 8
figure 8

Sensitivity analysis of the models for events higher than the 95th percentile: False Positive Rate (FPR). The lines with ● marker indicate the Standard Model (SM); the lines with ▲ marker indicate the Normalized Model (NM); the lines with ▼marker indicate the Only Rainfall Model (ORM); the lines with ■ marker indicate the Only Output Model (OOM).

Full size image

The dataset used to train the machine learning models contains, in general, a part of missing values, anomalous data, and redundancy with one or more attributes, which must be eliminated to build a trained generic model71,72. However, the automatization of the procedure aimed at solving these issues is very complicated because it depends on several factors such as anomalous or missing data resulting from instrumental anomalies, and their persistence in the time series. Furthermore, several techniques used to solve these types of problems require computational resources and time71, which in the field of early warning is pressing. In a real application of these models, we cannot exclude the anomalous or missing data provided by a single or a group of stations. For this reason, we need to understand the robustness of these methodologies and the number of anomalous or erroneous data. Figure 9 shows the results obtained when simulating a variable number of not working stations (5-10-20-30%) and comparing the RMSE to the models, without missing data for events higher than the 95th percentile (extreme events). For each percentage, we select a group of stations and we change their input data with a value of 0, simulating missing values from these stations. The selection of the not-working station was applied using a pseudo-random method and the library Random of Python Language. This procedure was replicated using the 10 duplications of the same model and repeating it for five times, by simulating a total of 50 cases for each step of prediction and for each model. The results were encouraging because the variation of also a large number of stations induced a small variation in the results, demonstrating a good capacity of the models to manage the missing values, as demonstrated by63 for a bigger catchment but using an analogous architecture of the neural networks.

Fig. 9
figure 9

Susceptibility analysis of the models to the missing values for events higher than the 95th percentile. Blue, green, orange, red bands and markers indicate the results obtained simulating 5%, 10%, 20 and 30%, respectively of the input station as missing values. The lines with ● marker indicate the Standard Model (SM); the lines with ▲ marker indicate the Normalized Model (NM); the lines with ▼marker indicate the Only Rainfall Model (ORM); the lines with ■ marker indicate the Only Output Model (OOM).

Full size image

After the models have been trained, machine learning techniques do not require any specific parameters, and this simplifies the procedure considerably for the application of these methods by users with poor skills in programming languages or in mathematics or statistics. The machine learning algorithm can be implemented in web and desktop software, which allow the application of the models. In this way, the user requirements are minimal and completely objective, making it possible to obtain the same predictions from different individuals. These possibilities are very important for civil protection and for mitigation of the hydraulic risk, when users need to receive rapid replies for important decisions. The deep learning models are perfect for these aims because the prediction of an event requires very few seconds when using a server machine without great computing capacity. For example, in this work we tested a server machine with 8 Gb of RAM and 6 CPU with a computational capacity of 2.2 GHz, which allowed us to obtain the response of a model (25 t step) in about 20–30 s. Using physical models, this capacity to reply promptly is very rare and in several cases the application of the models needs to determine the specific parameters. This requires further time, slowing down the predictions and then the decisions of the territorial authorities. If these concepts are valid for large river basins, they become even more important in small basins, where response timeliness is in constant struggle with the short flow times characterizing these basins.

Conclusions

The availability of efficient instruments for risk mitigation is crucial also in relation to current global warming and to change in the rainfall regimes, as demonstrated by several authors from different countries. In the field of hydraulic risk mitigation, we need to solve several challenges to the different geological and environmental characteristics of the catchments. A fundamental characteristic is the size of the catchment that can induce great difficulty in providing instruments able to predict the river flows also amplified by specific geological and climatic conditions. In this work, the study area possesses all these properties since it is characterized by small catchments, by a complex karst system, and by high steep mountains. Our work presents an instrument that is able to mitigate hydraulic risk in the study area. We can summarize the main results in the following points:

  1. 1.

    The errors of the models consist in only a few centimetres for the different forecasting times.

  2. 2.

    By using the previous river flow data up to step t-1, a regression only of the output time series can be sufficient for reconstruction of the hydrometric time series (forecasting time of 0 h), but also for some forecasting steps.

  3. 3.

    The models tend to underestimate the river flow with an increase of the forecasting time resulting in a systematic possibility of missing the alarms.

  4. 4.

    A blend of various models enables a spectrum of scenarios, enhancing the reliability and certainty of forecasts during critical decision-making.

  5. 5.

    The uncertainty of the models (also due to the sensor measures that are often not estimated) has an important influence on the results for small rivers.

  6. 6.

    The introduction of a statistical method able to estimate uncertainty (in GBR models) allows to increase the capacity of the models to provide alarms on the basis of objective methodologies.

  7. 7.

    The models are sturdy to the presence of the missing values that can affect the results during the real application of these systems.

  8. 8.

    The objective and rapid employment of these systems makes it possible to provide informatic applications that the territorial authorities can use for risk mitigation.

In conclusion, deep learning models can be used to provide instruments for hydraulic mitigation. This will become increasingly important with the development of the Internet of Things (IoT) in the field of weather sensors, which will provide additional data in terms of length of time sensors and of spatial density. Furthermore, the deep learning methodology can be applied to different catchments, with very few modifications. In the future, for a more efficient application of these models in small catchments, researchers will need to further investigate the issue of uncertainty management, try to introduce weather prediction providing different models (using or not artificial intelligence), and try to create different strategies for common and extreme events, which can improve forecasting time.

Methods

In this section, we describe the methodology used in this work. Figure 10 shows the main workflow we employed and that will be described in more detail in the next sections. Step 1 is the analysis and selection of the rainfall and river flow rate time series; Step 2 is the definition of four different input matrices to the deep learning models; Step 3 is the training of the deep learning models based on Long-Short Term Memory; Step 4 is the training of Gradient Boosting Models for estimation of the confidence intervals of the predictions derived from Step 3.

Fig. 10
figure 10

Workflow of the methodology applied. Step 1: management of the hydrological time series (rainfall and river flow rates). Step 2: definition of four input matrices (Only Output Model; Standard Model; Normalized Model and Only Rainfall Model). Step 3: training of the Long-Short Term Memory Models. Step 4: Application of Gradient Boosting Models for quantification of the confidence intervals of the predictions derived from Step 3.

Full size image

Data and pre-processing

The dataset used in this work is provided by the Servizio Idrologico Regionale (SIR) of the Tuscany Region, the public authority that manages the weather and climatic monitoring system. We selected the best hydrometric and rainfall gauges for this area by identifying 8 hydrometers as output of the DL models (from north to south): Carrara and Avenza (Carrione River): Seravezza 1 and Ponte Tavole (Versilia River); Viareggio 1 and Torre del Lago (Massaciuccoli Lake system); Ponte Guido (Contesora Torrent); and Mutigliano (Freddana Torrent). Figure 1 shows the output gauges (yellow stars), the hydrometric gauges (red points), and the rainfall gauges (blue points) selected and used in this work. The time series used has had a sample frequency of 15 min and a temporal range since 2002. The data, which are sourced from the SIR, lack validation, and undergo no automatic nor manual quality control. Nevertheless, the inherent data-driven nature of machine learning models prompts efforts to address and mitigate issues related to data quality70,71. Consequently, we conducted both manual and graphical checks on the time series utilized. Additionally, the territorial authority employs semi-automatic procedures to validate daily data. Leveraging this process, we excluded sampled data from days in which these procedures had not validated the measurements.

We developed an individual deep learning model for every output hydrometer in order to forecast its 15-minute measurements (\(\:Ht\)). The mathematical representation of the model, applicable to all the sub-basins examined, can be articulated as follows:

$$\:\widehat{H}=f\left({X}_{t}\right)=f\:({H}_{t-1},\:{H}_{t-2},\:\dots\:,{H}_{t-n},\:{\:R}_{t-1},\:{R}_{t-2},{\dots\:,\:R}_{t-n}$$

where \(\:\widehat{H}\) stands for the predicted hydrometric height at time t; \(\:{H}_{t-1},\:{H}_{t-2},\:\dots\:,{H}_{t-n}\:\)are the antecedent hydrometric heights (up to t–1, t–2,…, t–n time steps); \(\:{\:R}_{t-1},\:{R}_{t-2},{\dots\:,\:R}_{t-n}\) are the antecedent rainfall (t–1, t–2, …, t–n time steps). To mitigate the noise inherent in numerous steps and closely spaced measurements, we supplied timestamps for each hour of the preceding period and, subsequently, one timestamp every 4 steps (e.g., t-0, t-1, t-2, t-3, t-4, t-8, t-12, t-16,…, t-96) up to the 24th hour.

We composed four different input matrices for each station:

  • Only Output Model (OOM): this model exploits only the output station by performing a regression, using this time series alone;

  • Standard Model (SM): this model is developed using the best rainfall and hydrometric historical series useful for each output station;

  • Normalized Model (NM): this model is based on SM. Furthermore, the input data are normalized in a 0–1 range using the maximum and minimum values recorded for each time series;

  • Only Rainfall Model (ORM): this model only uses inlet rain gauges.

In theory, each input matrix has advantages (but also disadvantages) that allow a more flexible system for the real application. OOM is the simplest model which makes it scientifically possible to distinguish the next models from a simple regression of the output time series. This is very important because several works have demonstrated the efficiency of complex models without a baseline. Therefore, we can understand the real effect of introducing several data and different datasets. On the other hand, in the application of this system, we need to bear in mind that some gauges cannot work correctly during a flood event. For a nearby area with a similar monitoring system, Luppichini et al. (2022) found that DL models can perform quite well with even a high percentage of missing data (also higher than 25%). In theory, OOM is the model that we can simulate and that in any case always provides us with a prediction model. At the outset, SM is the reference model which, in ideal conditions, should be the best one. The studied hydraulic systems sometimes present a very small range of values if compared to the possible rainfall measurements. In this case, normalization of the values in fixed ranges (for example 0–1) can be useful to train the models and this is represented by NM. The hydrometric data are occasionally influenced by several factors which can produce faulty measurements. For example, in rivers characterized by pebble beds, it is easy to observe that the mainstream of the river is not below the sensor or, in the case of bridges with pillars, the measure can be distorted as a result of the accumulation of wood and of similar materials. In these cases, ORM allows the user to have a model based only on rainfall data. The real strength of this work is the creation of a system based on diverse approaches which can, in principle, perform differently and provide valid tools for prediction under various conditions of use. A summary of the input matrices used in this work is reported in Table 2. For the station of Seravezza1, the SM model coincides with ORM on account of the absence of other significant hydrometers in the catchment of this station.

Table 2 Characteristics of the input matrices for each station.
Full size table

LSTM regression models

To develop the deep learning models in this study, we primarily utilized the open-source framework Tensorflow73 and the libraries Numpy, Pandas, Scikit-Learn, and Keras74 in the Python language v3.9. The architecture of the developed models is based on an encoder-decoder LSTM (LSTM-ED), consisting of two pairs of LSTM nodes. This architecture permits the use of an LSTM able to read the input sequence, one step at a time, and to obtain a fixed-size vector representation in a data structure that occupies a large amount of memory. We then introduced another LSTM to extract the output sequence from that vector75. The encoder is composed of two sequential layers (LSTM) of 32 and 16 units, respectively, followed by a repeat vector node. The repeat vector layer repeats the incoming inputs for a specific number of times. The decoder is composed of two LSTM layers of 16 and 32 units respectively, followed by a time-distributed dense node as output of our model.

To evaluate the discrepancy between the predicted and the measured values, we used a loss function for each observation, which allowed us to calculate the cost function. We needed to minimize the cost function by identifying the optimized values for each weight. Through multiple iterations, the optimization algorithm computes the weights that minimize the cost function. In our implementation, we used the Adam optimizer76, which is an adaptive learning speed method that computes individual learning rates for several parameters76. To halt the training, we employed the specific API of Keras and, specifically, the early stopping method by which the training procedure can be stopped when the monitored metric (namely the value of the cost function) ceases to improve.

We divided the dataset into three parts with a partition of 60% − 20% − 20% for training, validation, and test dataset respectively. This division of the dataset has been tested in previous studies35,66,77,78 and ensures sufficient data for both training and evaluating the model.

The cost function used was the mean square error (MSE) calculated on the validation dataset. This partitioning of the entire dataset helped to minimize the overfitting effect on the training set.

We built a model for each hydrometric station, for each input matrix, and for 25 forecasting steps (from 0 to 6 h every 15 min), totalling 775 models. We repeated the entire procedure ten times, managing to analyse statistically the uncertainty linked to the training procedure based on a study of 7,750 models.

GBR models

The model errors can be analysed using other algorithms that allow to apply prediction uncertainty more efficiently than a simple error metric based on the entire dataset (such as Mean Squared Error or Mean Absolute Error). The combination with a second algorithm able to analyse the residuals obtained from the LSTM-ED model is an innovative approach that can improve the ability to predict a flood event. In this work, we used a Gradient Boosting Regressor (GBR), which is a machine learning algorithm belonging to a group of boosting algorithms that build a predictive model, combing different versions of weaker models79. The main idea of Gradient Boosting is to iteratively train models sequentially, where each new model attempts to correct residual errors made by previous models. In other words, each new model focuses on cases that previous models have failed to predict correctly. GBR uses the last observed hydrometric data with the aim of estimating the confidence intervals (50% and 90%) of absolute errors relative to the predictions extracted by the test dataset. The algorithm GBR works with the Scikit-learn library developed in Python language.