Introduction

Ensuring quality assurance has emerged as a significant challenge for both the manufacturing and service sectors. The sustainability of businesses relies heavily on reputation. In fiercely competitive markets, building a strong reputation depends on consistently delivering high-quality services or products. Within every organization, quality planning, quality assurance and quality improvement are ongoing processes. The role of statistical quality control (SQC) in the science of quality enhancement or assurance is substantial. The revolution of using SQC tools in the science of quality improvement is entitled to quality gurus Shewhart, Deming and Juran. Customer expectations centred on ‘delivering more with less’ while the service provider’s aim to ‘provide high quality at a reasonable cost’. Achieving this trade-off between the producer’s objectives and the consumer’s expectations requires industries to continuously monitor for common causes and unusual variations.

Control charts, as a tool of SQC play a vital role in understanding assignable causes of variation and also help in correcting the system and assuring quality. They typically consist of three lines: the lower control limit, upper control limit and central line. There are broadly two types of control charts: variable control charts and attribute control charts. Variable control charts are useful for analysing quantitative quality indicators while Attribute control charts apply to binomial classification problems such as ‘confirming to the pre-specified quality’ or ‘non-confirming’. Several types of attribute control charts available in the literature are the np chart for the number of non-conforming products or services, p chart for fraction non-conformities, c chart, q chart and u chart. The p chart plots the percent of defectives, and control limits are constructed based on binomial distribution.

Control charts are employed in healthcare to monitor key indicators such as waiting time analysis in each department of hospital, laboratory turnaround times, time to discharge after physician note, time to medication administration after a note from a clinician, infection rates and readmission rates etc. They can also be used to evaluate healthcare facilities adherence to national, international and customized bench marks.Turnaround time (TAT) in hospital settings is dependent on the context. For example, in emergency department patient arrival to patient disposal: either assigning bed or discharging patient. Where as in outpatient department (OPD) it is time from arrival at OP registration to patient departure after completing required investigations and treatment orders. In laboratory settings it can be defined in many ways: Receipt to report TAT, sample collection to report TAT, lab receipt to lab report TAT, investigations order to result TAT. Specific national and international standards for the variable TAT are not available, but the governing bodies like Medical Council of India, National Accreditation Board for Hospitals and Healthcare providers (NABH), clinical practice guidelines and Local Hospital Policies may not directly set guidelines for TAT, but these governing bodies emphasize the importance of patient safety in relation to TAT standards. Each healthcare facility has to establish its own TAT goals based on the guidelines given by different national and international organizations. The factors to consider in deciding TAT goals are complexity, urgency and compliance to broader regulatory requirements related to safety and quality in patient care.

Applications of attribute control charts for different distributions under binomial distribution conditions have been explored by various researchers. Emphasis on different types of attribute control charts, efficiency and economic point of view are discussed by Woodall1. Process mean attribute inspection is designed with ‘npx’ chart and also application of ‘npS2’ control chart in understanding process variability is explained by Ho & Quinino2. An attribute control chart for Weibull lifetimes is proposed by Aslam & Jun3. A control chart for time truncated life tests using Pareto distribution of second kind is proposed by Aslam et al.4. Shafqat et al.5 examined the application of npattribute control charts, while Rao6 developed exponentiated half logistic distribution based on attribute control charts for different shifts in parameters. Rosaiah et al.7 discussed an attribute ‘np’ control charts for the lifetimes following exponentiated Frechet distribution under time truncated life tests. A time truncated attribute control chart for Weibull Pareto distribution is designed and performance is compared with inverse Gaussian in terms of ARL by Elrazik8. Time truncated attribute control chart for generalized Rayleigh distribution was discussed by Tripathi et al.9. Application of a new statistical sine function control charts to survival rates is introduced by Kamal et al10. and a new trigonometric modification to Weibull distribution application in quality control was discussed by Alomair et al.11. Some other recent advances in control charts literature to refer are12,13 developed time truncated attribute control charts for the generalized Rayleigh distribution.

Though the application of these variable and attribute control charts originated in manufacturing industries, to understand the raising trend of application in the healthcare industry one can refer to14,15,16. Control charts serve as an important tool and offers systematic approach to monitor quality of services provided at healthcare facilities, adherence to patient safety standards and outcome analysis in patient care. In part two and three of Faltin et al.15 book, the flexibility of control charts in healthcare outcome analysis is explained. They discuss the application of various control charts such as Shewhart chart, cumulative sum (CUSUM) chart, exponentially weighted moving average (EWMA) chart and multivariate EWMA (MEWMA) in health care. Finally, the need for distributional assumptions while using control charts is explained with false alarms in surgery duration.

The main assumption in designing a control chart is quality indicator data follows the normal distribution. However, it is not always possible to have normal data in all situations. In such cases, different existing distributions and newly derived distributions can be utilized to handle skewed data. Both the Lomax distribution and Rayleigh distribution are suitable for dealing with skewed data. In a paper by Saritha et al.17, a T-X family of distribution is proposed, and the new Lomax Rayleigh distribution is introduced. This distribution is used to construct attribute control charts, providing an alternative approach for handling non-normally distributed data. After reviewing the above literature it is understood that no such work is available for the newly proposed NLRD and hence preceded. The rest of the paper is organized as follows: Sect. 2 explains the construction of control limits for the proposed distribution NLRD. Section 3 presents an evaluation of the proposed plan parameters and average run length for simulated data. Comparative study results are presented Sect. 4. Illustration of the proposed chart is explained in Sect. 5. The proposed plan application to real data scenarios in understanding nonconformities is given in Sect. 6. Section 7 illustrates the proposed control charts performance with shift in process. In Sect. 8 concluding remarks about the performance of the proposed plan are given.

Design of the proposed time truncated attribute control chart for NLRD

Let \(T\) be a quality indicator following NLRD with parameters \(\theta ,\lambda\) and \(\sigma\) then the CDF and PDF of the variable T are given as follows:

$$G\left( {t;\;\theta ,\;\lambda ,\;\sigma } \right) = 1 - \left[ {1 + \frac{{t^{2} }}{{2\lambda \sigma^{2} }}} \right]^{ - \theta } {\text{ , t}}> 0,\;\theta ,\lambda ,\sigma> 0$$
(1)
$$g\left( {t;\theta ,\lambda ,\sigma } \right) = \frac{\theta t}{{\lambda \sigma^{2} }}\left[ {1 + \frac{{t^{2} }}{{2\lambda \sigma^{2} }}} \right]^{{ - \left( {\theta + 1} \right)}}$$
(2)

\(t> 0,\theta> 0,\lambda> 0,\sigma> 0\). Where \(\lambda\) and \(\sigma\) are the scale parameters and \(\theta\) is the shape parameter. The \(q^{th}\) quantile of NLRD is

$$t_{q} = \sigma .\left[ {2\lambda \left[ {\left[ {1 - q} \right]^{{\frac{ - 1}{\theta }}} - 1} \right]} \right]^{\frac{1}{2}}$$
(3)
$$\eta_{q} = \left[ {2\lambda \left[ {\left[ {1 - q} \right]^{{\frac{ - 1}{\theta }}} - 1} \right]} \right]^{\frac{1}{2}} ,\quad t_{q} = \sigma \eta_{q} \Rightarrow \sigma = {{t_{q} } \mathord{\left/ {\vphantom {{t_{q} } {\eta_{q} }}} \right. \kern-0pt} {\eta_{q} }}$$
(4)

For specified values, \(\lambda = \lambda_{0} ,\theta = \theta_{0}\), \(t_{q}\) is a function of the scale parameter \(\sigma = \sigma_{0}\). Let \(p\) be the probability of failure of the variable following NLRD with terminating time \(t_{0}\) and truncating time \(t_{q}\), then \(p = F(t_{0} )\). Experiment termination time is \(t_{0} = at_{{q_{0} }}\).

$$p = 1 - \left[ {1 + \frac{{t_{0}^{2} }}{{2\lambda \sigma^{2} }}} \right]^{ - \theta } \,$$
(5)

Let p be the probability of failure of the variable following NLRD with terminating time \(t_{0}\) and truncating time \(t_{q}\), then \(p = F(t_{0} )\). Experiment termination time is \(t_{0} = at_{{q_{0} }}\).

$$p = 1 - \left[ {1 + \frac{{t_{0}^{2} }}{{2\lambda \sigma^{2} }}} \right]^{ - \theta } \,$$
(6)

By substituting \(t_{q} = \sigma \eta_{q} \Rightarrow \sigma = {{t_{q} } \mathord{\left/ {\vphantom {{t_{q} } {\eta_{q} }}} \right. \kern-0pt} {\eta_{q} }}\), \(t_{0} = at_{{q_{0} }}\) and \(\sigma_{0}\) values in Eq. (6)

$$p = 1 - \left[ {1 + \frac{1}{{2\lambda \left( {{{t_{q} } \mathord{\left/ {\vphantom {{t_{q} } {t_{{q_{0} }} }}} \right. \kern-0pt} {t_{{q_{0} }} }}} \right)^{2} }}\left( {a\eta_{q} } \right)^{2} } \right]^{ - \theta }$$
(7)

The formulae for probability of failure differ for the situations process in control and process out of control. When the process is in control the quantile ratio, \({{t_{q} } \mathord{\left/ {\vphantom {{t_{q} } {t_{{q_{0} }} = 1}}} \right. \kern-0pt} {t_{{q_{0} }} = 1}}\), that is the actual and the observed lifetimes are the same.

According to Shafqat et al.5, the value of \(p_{0}\) for the process in control mentioned in the Eq. (7) can be rewritten as

$$p_{0} = 1 - \left[ {1 + \frac{1}{2\lambda }\left( {a\eta_{q} } \right)^{2} } \right]^{ - \theta } ;\;{\text{where}}\;\eta_{q} = \left[ {2\lambda \left[ {\left[ {1 - q} \right]^{{\frac{ - 1}{\theta }}} - 1} \right]} \right]^{\frac{1}{2}}$$
(8a)

For the process out of control, we consider the shift in the process denoted with the letter \(s\)\(\left[ {s = {{t_{q} } \mathord{\left/ {\vphantom {{t_{q} } {t_{{q_{0} }} }}} \right. \kern-0pt} {t_{{q_{0} }} }}{ = 0}{\text{.1,0}}{.2,0}{\text{.3,}}....{,0}{\text{.95,1,1}}{.05,1}{\text{.10,1}}{.15,1}{\text{.2,1}}{.3,}..{,4}} \right]\), then the probability of failure in Eq. (7) is

$$p_{1} = 1 - \left[ {1 + \frac{1}{2\lambda }\left( {\frac{{a\eta_{q} }}{s}} \right)^{2} } \right]^{ - \theta }$$
(8b)

The steps in the proposed time truncated attribute control chart

The steps in the proposed time truncated attribute \(np\) control chart with median life are as follows:

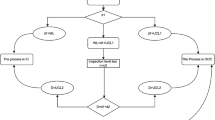
  • Step 1: Consider \(n\) sampling units of a quality indicator or characteristic under study from a manufacturing process or service industry or a health indicator. Let \(D\) be the number of non-conforming units out of \(n\) counted till the termination time \(t_{0} = at_{q}\), where \(t_{q}\) specified value of the median, \(l\) is the distance from central line to LCL and UCL.

  • Step 2: Decision Process: There are two control limits available in decision making: one upper control limit \(UCL\) and one lower limit \(LCL\). Reject the lot of quality indicators under inspection if \(D < LCL\) or \(D> UCL\) and declare the process as in control if otherwise.

Distribution of the number of failures is Binomial distribution with parameter \(n\) and \(p_{0}\) is the probability of failure of the item before the time \(t_{0}\) and \(p_{0}\) is defined in Eq. (8a).

Controls limits of \(np\) chart are defined in the following equations:

$$UCL = np_{0} + l\sqrt {np_{0} (1 - p_{0} )}$$
(9a)
$$LCL = \max \left[ {0,np_{0} - l\sqrt {np_{0} (1 - p_{0} )} } \right]$$
(9b)

Here \(l\) is the constant to be determined and is the coefficient of control charts. In general, in many original situations the probability of failure may not be known. The control limits defined in the above equations may be written as follows:

$$UCL = \overline{D} + l\sqrt {\overline{D} (1 - \overline{D} /n)}$$
(10a)
$$LCL = \max \left[ {0,\overline{D} - l\sqrt {\overline{D} (1 - \overline{D} /n)} } \right]$$
(10b)

where \(\overline{D}\) is the average number of failures in the sample under inspection and the probability of the process in control is denoted as \(P_{InC}^{0}\) and is defined as

$$p_{inc}^{0} = P\left( {LCL \le D \le UCL/p_{0} } \right)$$

In terms of binomial probability theorem the above equation is

$$p_{inc}^{0} = \sum\limits_{d = LCL}^{UCL} {\left( \begin{gathered} n \hfill \\ d \hfill \\ \end{gathered} \right)} p_{0}^{d} \left( {1 - p_{0} } \right)^{n - d}$$
(11a)

In evaluating the above equation, lower control limit is assumed to be 0. If there is a shift in the process median to \(t_{q}^{1} = st_{{q_{0} }}\), \(s\) is a constant. Then the probability of failure of the shifted process, by assuming the process is out of control is as per Eq. (8b).

$$p_{1} = 1 - \left[ {1 + \frac{1}{2\lambda }\left( {\frac{{a\eta_{q} }}{s}} \right)^{2} } \right]^{ - \theta }$$

The probability of process in-control with shifted average is

$$p_{Inc}^{1} = P(LCL \le D \le UCL/p_{1} )$$

The above equation can also be written as follows:

$$p_{Inc}^{1} /p_{1} = \sum\limits_{d = LCL + 1}^{UCL} {\left( \begin{gathered} n \hfill \\ d \hfill \\ \end{gathered} \right)} p_{1}^{d} \left( {1 - p_{1} } \right)^{n - d}$$
(11b)

Average Run Length: The Performance measure of the designed control chart average run length (ARL) is the usual measure used to comment on the process quality and these measures for process with median or mean life time- \(ARL_{0}\) and shifted median or mean life times-\(ARL_{1}\) are

$$ARL_{0} = \frac{1}{{1 - p_{Inc}^{0} }}$$
(12)

and

$$ARL_{1} = \frac{1}{{1 - p_{Inc}^{1} }}$$
(13)

The control limit coefficient \(l\) is estimated on the basis of distance from central limit to LCL and UCL. For different values of pre-defined termination ratio constant \(a\) and different sample sizes, \(ARL_{1}\) values are calculated as per the formula given in Eq. (13).

Simulation results

Data given in Tables 1, 2, 3 are generated from NLRD with sample size \(n = 15\) for different combinations of the parameters \(\theta = 0.5,1.0,2.0\) and \(\lambda = 0.5,1.0,2.0\). Tables 4, 5, 6 are generated with \(n = 20\),\(\theta = 0.5,1.0,2.0\) and \(\lambda = 0.5,1.0,1.5,2.0\) for different in control ARL values \(ARL_{0}\) = 200, 250, 300, 370 and 500.

Table 1 ARL values for the parametric values \(\theta = 0.5\), \(\lambda = 0.5\) and n = 15 under truncated life test.
Full size table
Table 2 ARL values for the parametric values \(\theta = 1.0\), \(\lambda = 1.0\) and n = 15 under truncated life test.
Full size table
Table 3 ARL values for the parametric values \(\theta = 2.0\), \(\lambda = 2.0\) and n = 15 under truncated life test.
Full size table
Table 4 ARL values for the parametric values \(\theta = 0.5\), \(\lambda = 0.5\) and n = 20 under truncated life test.
Full size table
Table 5 ARL values for the parametric values \(\theta = 1.0\), \(\lambda = 1.0\) and n = 20 under truncated life test.
Full size table
Table 6 ARL values for the parametric values \(\theta = 2.0\), \(\lambda = 2.0\) and n = 20 under truncated life test.
Full size table

Steps used to generate values of \(ARL_{1}\) for different parametric combinations are as follows.

  • Step 1. For given n values specify the in control ARL values say \(ARL_{0}\) .

  • Step 2. Calculate the control chart constants ‘l’ and ‘a’ for specified values of ‘n’.

  • Step 3. Calculate the values of \(ARL_{1}\) for different shift constants and control chart parameters.

Results from Tables 1, 2, 3, 4, 5, 6 illustrate the application of the proposed attribute control charts for simulated data.

\(ARL_{1}\) values for different shift constants, for sample sizes \(n = 15,20\) are tabulated in Tables 1, 2, 3, 4, 5, 6. The distance between central line and the lines UCL, LCL denoted as l, termination ratio constant a, values are calculated first. Then \(ARL_{1}\) values are determined based on the formula given in Eq. (13) at termination ratio a and pre-defined n.

It is observed that in all the tables, as the termination ratio increases from 0.1 to 1.0 \(ARL_{1}\) values increases and from then onwards a decreasing trend is observed. The process is observed as in control for parametric values \(\theta = 1.0,\lambda = 1.0\) for sample sizes \(n = 15\,\,and\,\,20\). As the shift parameter increases from s = 1 to 4 there is a rapid decrease in values of \(ARL_{1}\). It is also observed that there is a drastic decrease in \(ARL_{1}\) for larger values of the shift constant ‘s’. We observed significant changes in Average Run Length (ARL) values as we varied both λ and sample size (n). When λ increases, we noted a substantial decrease in ARL values across almost all shift constants. For example, at a specific shift constant, as λ increased, shift constant \(s = 1.05\), at \(\lambda = 0.5,1.0,2.0,ARL_{0} = 500\) ARL values are \(ARL = 484.09,468.77,436.19\) respectively. This pattern was consistent across nearly all shift constants we examined. Regarding sample size, we observed that increases in ‘n’ led to decreases in ARL values, it is observed that there is a little decrease in ARL values initially, but for larger \(ARL_{0}\) there is a drastic decrease in ARL values for the same shift constant and parametric combinations. To illustrate at \(n = 15,\theta = 1,\lambda = 1,S = 1.05,ARL_{0} = 500\), \(ARL = 468.77\). With the same parametric combinations, at \(n = 20\), \(ARL = 446.11\). This pattern of decreasing ARL values with increasing n was consistent across all shift constant values and different parametric combinations we studied. These findings highlight the significant impact that both λ and sample size have on the performance of our control charts, as reflected in the ARL values.

Comparative study

Efficiency of the proposed control chart is compared with the Log-logistic distribution discussed by Rao & Paul18, Weibull distribution given by Adeoti & Rao19and NTS-Weibull distribution presented by Kamal et al.10, for sample size \(n = 20\) with \(ARL_{0} = 370\). Table 7 depicts ARL values of the distributions under comparison. The distribution with lesser out-of-control ARL value is considered as the best one among the comparing distributions. Table 7 and Fig. 1 explain that for each shift, ARL values of the proposed control chart are less than all other distributions under comparison. From this table and graph it is observed that proposed time truncated attribute control charts based on NLRD is more accurate in identifying process shifts when compared to other distributions under comparison.

Table 7 Comparison of ARL values of NLRD with existing distributions at \(n = 20\) and \(ARL_{0} = 370\).
Full size table
Fig. 1
figure 1

Comparison of ARL1 between distributions at \(n = 20\) and ARL0 = 370.

Full size image

Illustration of the proposed chart

In this section, how to use the proposed chart in real life is explained. Assuming a healthcare facility aims to improve its services by adopting control charts to monitor and improve different patient care outcome indicators. If they know that these data follow NLRD with parameters \(\theta = 1.0\), \(\lambda = 1.0\) and the mean target delay in any service is not more than 400 h. For certain surgeries and services, the timeframe from admission to completion may extend up to 10 to 15 days, contingent upon various factors such as priority, permissions, equipment availability, inspection times, and the availability of specific investigation reports. With 15 days equating to 360 h, a maximum delay of 400 h is considered acceptable in such cases. The waiting period of 10 to 15 days in a hospital significantly impacts not only the individuals but also their families in numerous ways. It causes physical, psychological and economic inconvenience. Additionally, prolonged hospital stays can exacerbate health issues, potentially leading to mortality or an increased risk of hospital-associated infections. So, healthcare facilities should strive to minimize service delays as much as possible by conducting continuous quality inspections and implementing process improvements.

A sub sample of size \(n = 20\) will be taken each time regarding that particular outcome indicator and put under truncated life test. The target in control ARL of the proposed control chart is \(ARL_{0} = 300\). Then from Table 5, \(l = 2.937\), \(a = 0.9456\) and from Eq. (8a) the probability obtained is \(p_{0} = 0.4705\). The values of UCL and LCL obtained from Eq. (9a) and (9b) are given by \(UCL = 15.9659\) and \(LCL = 2.8541\). Hence, the control chart procedure to be adopted by the healthcare facility is as follows:

  • Step 1: Reserve a sample of size 20 from each subgroup and subject them to life test for 378 h, plot the number of failures \(D\) per each sample.

  • Step 2: Decision: Declare the process as in control if \(2.8541 \le D \le 15.9659\). Declare the process as out of control if \(D> 15.9659\) or \(D < 2.8541\)

Real data application

Turnaround times influence patient outcomes like morbidity, mortality and length of stay ultimately impacting the burden of treatment cost. In India, many healthcare facilities have their own internal policies and protocols regarding TAT for urgent laboratory reports. These policies are often based on the urgency of clinical situation, the type of test being conducted, and the resources available within the institution. Some works to mention about the need for investigation and improvement of laboratory turnaround times by using different statistical quality control methods are mentioned the importance of monitoring and improving laboratory TAT on an ongoing basis20,21,22,23. In a study conducted in Northern Ireland of UK, department of Clinical Biochemistry, Southern HSC Trust and Belfast HCS Trust by Mckillop & Auld24mentioned that a consensus of less than one hour TAT for urgent investigations in ED and less than 4 h in inpatients (IP). Similarly the maximum thresholds for urgent investigations, above which patient safety is compromised, were identified, such as no longer than 2 h for urgent investigations from ED and no more than 24 h for General Practice (GP) and outpatient departments (OPD). This study also mentioned importance of prioritizing specific GP and OPD tests also which helps clinicians to decide about treatment orders. Lippi et al.25 investigated and proved that the longer turnaround time (TAT) of laboratory tests and time to testing (TTT) influences the ED length of stay (LOS).

In this paper, the data we considered for real data application of NLRD attribute control charts under repetitive sampling is information on the number of patients waiting for their imaging and laboratory investigations at Health and Social Care (HSC) trust hospitals in Northern Ireland. Data are presented by HSC trust and it belongs to five regions of Northern Ireland. Data is retrieved from data world website, data status is shared with everyone and data URL is https://www.data.gov.uk/dataset/59590bee-dfd1-4d03-b515-fa890bc64f2e/diagnostic-waiting-times. In this data, in five regions of Northern Ireland, number of patients waiting and the length of waiting time in the routine and urgent investigations are published. From this data we considered only the percentage of people waiting for their urgent investigations even after two days after ordering from 2010 to 2019. This doesn’t mention any information about the source where from these urgent investigations are ordered like ED, GP, or OPD. But according to Mckillop & Auld24, more than 24 h waiting time for any laboratory turnaround times in the case of urgent investigations from ED or GP or OPD is not accepted and leading to compromise in patient safety. With this motivation we tried to apply attribute control charts as a tool to warn the respective regions of Northern Ireland regarding out of control situations of urgent laboratory investigations turnaround times.

In this study, the proposed attribute control chart is applied to calculate the upper control and lower control limits for the proportion of people not received their urgent laboratory investigations even after two days from the order. This data belongs to Southeast region of Northern Ireland from 2014–19. There are 43 observations representing the proportion of people failed to receive their urgent physiological investigations within two days. Control chart limits, control chart coefficients and \(ARL_{1}\) values are estimated based on the equations derived above for the same.

Southeast: 1.2, 0.8, 4.9, 1.5, 3.1, 0.9, 2.4, 2, 1.4, 1.1, 1.1, 0.3, 2.9, 0.4, 0.7, 2.1, 1.6, 0.8, 0.4, 0.9, 0.4, 0.8, 0.4, 0.5, 0.3, 0.6, 0.5, 0.6, 0.3, 1.2, 0.4, 0.4, 1.2, 0.7, 0.5, 1.1, 0.5, 1.6, 0.7, 1.3, 0.9, 0.5, 0.7.

Figure 2 display the empirical and theoretical probability density functions, Q-Q plots, empirical and theoretical CDFs and P-P plots for Southeast data. From Table 8 and Fig. 2 it is evident that Southeast data is well fitted to the NLRD.

Fig. 2
figure 2

Empirical and theoretical probability density functions, Q-Q plots, empirical and theoretical CDFs and P-P plot for Southeast data.

Full size image
Table 8 Real data fitting results.
Full size table

At a target ARL0 = 370, \(n = 43\), \(l = 3.095\) and \(a = 1.203\) .The probability value obtained from Eq. 8(a) is \(p_{0} = 0.80365\). Therefore, from Table 9, at \(l = 3.095\) and the control limits for the number of failures \(D\) are calculated by using the Eqs. (9a) and (9b). The mean percentage of people failed to get their urgent investigations within two days is \(\overline{D} = 1.05909\), the values of UCL, LCL and central line (CL) are \(LCL = 0\), \(UCL = 4.2648\) and \(CL = 1.0837\). In Fig. 3, it becomes evident that the rate of failures in promptly receiving urgent investigations within a two-day timeframe escalates notably by the 33rd sample year and month. Given the established correlation between delays exceeding 24 h and compromised patient safety, it’s imperative for management to intervene. They can issue warnings to the pertinent laboratory departments and offer recommendations for refining the process. Such proactive measures are instrumental in strengthening patient safety and elevating the quality of patient outcomes.

Table 9 Optimal values of the parameters of NLRD for Southeast data \(\hat{\theta } = 1.529\), \(\hat{\lambda } = 2.0144\) and n = 43.
Full size table
Fig. 3
figure 3

Control chart for the proposed Southeast data.

Full size image

Proposed control chart monitoring using simulation

To investigate the performance of the developed control chart, the following simulation technique was used to generate data from NLRD and produce the control chart:

  • Step 1: Determine the subgroup sample size of n.

  • Step 2: Create an NLRD random variable T of size n with parameters \(\theta = 2,\lambda = 2\) and \(\sigma\) = 1.

  • Step 3: Identify the chart data point and the values of D for each subgroup.

  • Step 4: Repeat steps 1—3 until the desired number of sample groups (m = 15) is attained.

  • Step 5: Using Eqs. (10a) and (10b) , set the proposed chart control boundaries.

  • Step 6: Match all chart data points D to their subgroup numbers.

To create the new control chart, construct the first 15 samples of subgroup size 15 from NLRD using the in-control parameters \(\theta_{0} = 2,\lambda_{0} = 2\) and \(\sigma\) = 1. The second set of 15 samples of subgroup size 15 comes from NLRD with parameters \(\theta_{0} = 2,\lambda_{0} = 2\) and \(\sigma\) = 1.5 (i.e., scale parameter is shifted 0.5, i.e., s = 0.2). Table 3 demonstrates that when ARL is set to 300 and the parameters are in-control, the control chart constants are l = 2.937, a = 0.9531, and n = 15. The life test will end at \(t_{0} = at_{{q_{0} }} = 0.931 \times 1.28719 = 1.2268\). Table 10 displays the chart data points D and sample values. The average failure rate \(\overline{D}\) = 5.0, and the proposed chart control limits obtained from Eqs. (10a) and (10b) are UCL = 9.8451 and LCL = 0.00. Figure 4 depicts the suggested control chart based on simulated data. It illustrates that the process is out of control after the 18th sample, i.e., after the 3rd sample, when the process switched. When the scale parameter is adjusted to 0.5, Table 3 reveals that the estimated ARL1 is 14.62. As a result, the generated control chart detects process shifts with great resourcefulness.

Table 10 The simulated data and chart statistic for proposed chart.
Full size table
Fig. 4
figure 4

Control chart for simulated data.

Full size image

Summary and conclusions

A new attribute control chart, ‘np’ control chart for quality variables following the new Lomax Rayleigh distribution is proposed and designed. The constants of the control chart for different sample sizes are illustrated with simulated data. Results of the simulated study shows that in all the tables as the termination ratio increases from 0.1 to 1.0, \(ARL_{1}\) value increases and from then onwards a rapid decreasing trend is observed with the increase in shift parameter from s = 1 to 4. It is also observed that there is a drastic decrease in \(ARL_{1}\) for larger values of the shift constant ‘s’. The developed control chart is innovatively applied in designing upper and lower control limits for the variable proportion of people not received their urgent lab investigations with in defined time frame in a healthcare facility. This application of SQC technique in monitoring quality and patient safety is confirmed and valid. Similarly, the proposed control chart can be used in industries for monitoring heavily right skewed quality indicators.