Introduction

Since the invention of Sanger sequencing in 19771, remarkable advances have been made in genome sequencing technologies. Currently, next-generation sequencing (NGS) is widely used due to its low cost and high throughput2,3,4. However, the present throughput and cost of NGS are still insufficient to meet the continuously expanding demands. To make genome sequencing technology more widely accessible, it is necessary to further increase the throughput and decrease the cost.

DNBSEQ is a representative NGS technology that uses rolling cycle amplification to generate DNBs. These DNBs are loaded onto a patterned array and massively imaged with a customized fluorescence microscopic system5,6. The throughput of DNBSEQ is affected by both the density of DNBs on the array and the time cost for each step in the designed workflow. Currently, the pitch of DNB binding sites on regular arrays varies from 600 to 900 nm. In this context, ‘pitch’ refers to the center-to-center distance between two adjacent DNB binding sites on the array. Small pitch refers to high DNB density. To increase throughput and reduce the per-base cost, an effective approach is to reduce the pitch of the DNB binding sites on the array. In the following sections, we will refer to the targeted array with a 360 nm pitch as the UHD array. As illustrated in Fig. 1, with the same array size, four times as many reads can be generated per run when the pitch is reduced from 720 to 360 nm. However, this cannot be accomplished solely through semiconductor and flowcell engineering. Due to the optical diffraction barrier, a typical wide-field (WF) fluorescence microscopic system is insufficient for resolving DNBs with a pitch beyond its resolution limit. Figure 2 demonstrates that under the same microscopic system, with an objective numerical aperture (NA) of 0.8, adjacent DNBs can be resolved at 720 nm pitch but not at 360 nm pitch due to the presence of blurred boundaries. This inevitably leads to poor base-calling performance of the UHD array. To address this problem, it is necessary to obtain super-resolution (SR) DNB images for UHD arrays.

Fig. 1
figure 1

Illustration of DNB binding sites increasing as the pitch decreases from 720 to 360 nm.

Full size image
Fig. 2
figure 2

Raw DNB images of 720 nm (a) and 360 nm (b) pitch arrays captured by the same microscopic system equipped with an NA 0.8 objective.

Full size image

Although there are a variety of SR fluorescence microscopic techniques available, including stimulated emission depletion microscopy (STED)7, structured illumination microscopy (SIM)8, stochastic optical reconstruction microscopy (STORM)9, and photoactivated localization microscopy (PALM)10, all of these techniques trade off imaging frame numbers for increased resolution, potentially resulting in a considerable decrease in sequencing throughput. Furthermore, some of these methods are incompatible with the biochemical workflow of DNBSEQ. Therefore, an innovative imaging or postprocessing method that can effectively resolve adjacent DNBs closer than the resolution limit while minimizing the associated time cost is needed. Recently, deep learning has demonstrated impressive performance in the single-image SR task, which refers to reconstructing a high-resolution (HR) image from its low-resolution (LR) counterpart11. Deep learning does not require modifications to the original fluorescence microscopic system and provides a relatively fast processing speed, making it potentially ideal for improving the resolution of DNB images.

The majority of deep learning research on single-image SR has focused on photorealistic images. Consequently, researchers have developed numerous advanced SR networks11,12,13,14,15,16,17,18,19,20,21,22,23, which could theoretically be applied to fluorescence microscopy images24. Due to the superior performance and widespread use of convolutional neural networks (CNNs), we discuss several representative CNN-based image SR networks in this study.

The super-resolution convolutional neural network (SRCNN)11 was the first neural network to tackle the single-image SR challenge. SRCNN used only three convolutional layers yet outperformed traditional SR algorithms, demonstrating the promising potential of deep learning. Since the introduction of the residual network in 201625, residual structures have been widely adopted in single-image SR tasks, driving the development of deeper and more advanced networks. The enhanced deep super-resolution network (EDSR)13, residual dense network (RDN)17, and residual channel attention network (RCAN)18 are three representative networks that utilized residual structures and achieved state-of-the-art (SOTA) performance in image reconstruction quality. EDSR leveraged residual structures to build a deep network and innovatively removed batch normalization layers, resulting in a notable improvement in SR accuracy over earlier networks. RDN was the first network to integrate dense connections with residual structures for image SR. This allowed for full utilization of hierarchical features from the original LR image, further enhancing SR accuracy. RCAN was the first to introduce the attention mechanism in image SR, enabling learnable channel weights. Additionally, RCAN employed a residual-in-residual structure to build an extremely deep network. These improvements enabled RCAN to further enhance SR accuracy.

As image SR networks evolved, many studies aimed to design more complex network structures to enhance SR accuracy13,17,18,20. However, this led to increased training and reconstruction times, as well as higher GPU memory consumption, making these networks unsuitable for practical applications. Recently, researchers have shown growing interest in developing efficient networks that optimize efficiency while maintaining satisfactory SR accuracy. Among the proposed efficient networks, the information multi-distillation network (IMDN)19, residual feature distillation network (RFDN)21, and residual local feature network (RLFN)23 are three representative networks that achieved SOTA performance in network efficiency. IMDN used the information multi-distillation block to reduce the number of parameters. By incorporating the contrast-aware attention mechanism, IMDN achieved fast and accurate image SR reconstruction. Building on IMDN, RFDN incorporated feature distillation connections to further reduce the number of parameters and introduced shallow residual block to improve accuracy. RFDN provided faster reconstruction speed than IMDN while maintaining comparable SR accuracy. RLFN further investigated RFDN’s speed bottleneck. By replacing the information distillation structure with several straightforward convolutional layers, RLFN further accelerated the reconstruction speed without sacrificing accuracy.

Although there are numerous SR networks available, their primary focus remains on producing visually appealing results and achieving a high peak signal-to-noise ratio. In contrast, DNB images are captured for base extraction, and the overall objective of DNB image SR is to improve the base-calling performance. Additionally, many of these networks exhibit deficiencies in reconstruction speed, directly reducing sequencing throughput. To satisfy the stringent requirements of the DNB image SR task and even broader NGS technology evolution, we propose an efficient network for DNB image SR, named DNBSRN.

Materials and methods

DNBSEQ workflow

We conducted DNBSEQ sequencing experiments on UHD arrays, generating four DNB image datasets (dataset 1, dataset 2, dataset 3, dataset 4) from single-end 50 bp (SE50) sequencing and four DNB image datasets (dataset 5, dataset 6, dataset 7, dataset 8) from paired-end 100 bp (PE100) sequencing. SE50 read length is sufficient for RNA-seq profiling or counting experiments, such as noninvasive prenatal testing (NIFTY), and PE100 read length is typical for whole-genome sequencing (WGS), which requires deep coverage.

Library preparation and sequencing

Standard reference E. coli DNA was used to construct a single-strand circular DNA library following the single-strand circularization protocol of DNBSEQ26. The insert fragment of the single-strand circular DNA was approximately 170 bp. To make DNBs, single-strand circular DNAs were hybridized with primers. Next, dNTPs and DNA polymerase were introduced into the reaction mixture to initiate rolling circle amplification for 30 min, which was then terminated by the DNB stopping buffer. Finally, a DNB concentration greater than 10 ng/µL was quantified using a Qubit ssDNA Assay Kit and a Qubit Fluorometer.

For loading DNBs, we added 1/3 volume of DNB loading buffer to the DNB product from the previous step. Then, the mixture was placed into the loader device and automatically loaded onto the UHD array. Here we waited 30 min to ensure that DNBs settled adequately on the chip. Finally, post-loading reagents were added to further stabilize the DNBs.

For sequencing by synthesis, DNBs were hybridized with primers complementary to the adapter region. During each cycle, a mixture of four individually labeled dNTPs was added and incorporated with the elongating complementary templates under the catalysis of DNA polymerase. Following the synthesis process, unbound dNTPs were removed by washing buffer, and the DNBs were protected from laser-induced damage by imaging buffer. Upon laser excitation, the DNBs emitted fluorescence, and a fluorescence microscopic system captured WF DNB images of the four base channels. Afterwards, the fluorochrome and termination groups were removed, and the next cycle began. This synthesis-imaging-cleavage cycle continues until the designed read length has been reached.

Base-calling

Zebracall (base-calling software provided by the DNBSEQ manufacturer MGI Inc.) was used to call bases from the DNB images. The general workflow is shown in Fig. 3. First, the background was removed for each image. Next, four channel images of the same cycle were aligned with a grid pattern template, and the raw intensities were extracted from each DNB site. The raw intensities were subjected to normalization, crosstalk correction, and phasing correction to remove spatial and temporal signal crosstalk. The crosstalk among channels is caused by imperfect wavelength filtering. Phasing correction is required because incorporations are out of phase among the hundreds of DNA copies within a single DNB, thereby degrading the purity of the DNB signal in the wavelength domain. After all correction steps, the bases with the highest probability were called based on the final intensities across the four channels. The possible error rate of each base was subsequently determined using a previously established probability model, and the corresponding quality score was calculated by

$$\begin{array}{c}Q=-10{\mathit{log}}_{10}P ,\end{array}$$
(1)

where \(P\) denotes the possible error rate and \(Q\) is the quality score. After base-calling for all cycles was completed, a binary file containing the raw reads and quality score of each base was converted to FASTQ format with the Phred+33 quality score.

Fig. 3
figure 3

The general workflow of the base-calling process, which converts cyclic raw DNB images collected from four wavelength channels into sequential reads. During each cycle, images from the four channels are registered based on a grid pattern template, and the base identity of each DNB spot is determined based on its relative intensities in the four channels. In this way, reads are called sequentially. Green, yellow, orange, and blue sites indicate fluorescence corresponding to A, T, G, and C bases, respectively, while black sites indicate no fluorescence.

Full size image

To assess the quality of the reads extracted from DNB images, global quality metrics such as the Q30, mapping rate (MR), and effective spot rate (ESR) were further calculated. Q30 represents the proportion of bases with an estimated error rate no more than 0.001 in all reads and serves as a measure of the overall quality of the reads. MR is the proportion of reads successfully mapped to the reference genome and serves as a measure of the accuracy of the reads. BWA27 was employed to calculate MR. ESR represents the proportion of effective reads to total reads following filtering and reflects the productivity of the array. Bases with a quality score less than 20 were considered bad bases. In SE50 sequencing, reads with a bad base proportion exceeding 20% were filtered out. In PE100 sequencing, when the percentage of bad bases exceeded 30% in the first read or 35% in the second read, the read was filtered out.

Training dataset preparation

To conduct deep learning for DNB image SR, it is necessary to generate a training dataset that contains pairs of LR-HR DNB images. Although generating LR images using a regular WF microscopic system and HR images using an SR microscopic system is feasible, co-register image pairs is not simple. On the other hand, various microscopic systems may not share the same optical specifications, which prevents the model from transferring in a convenient way. Therefore, we generated the training dataset by simulating pairs of LR-HR DNB images.

We performed a simulation of DNB images comprising multiple cycles. Each cycle consisted of four pairs of LR and HR images corresponding to the A, T, G, and C base channels. The simulation involved three stages: DNB preparation, placement, and imaging. First, sequence templates were sampled from the human reference genome and assigned different copy numbers to simulate DNBs. DNBs were randomly placed at each binding site within the simulated array for imaging purposes. The binding sites had a diameter of 130 nm and a pitch of 360 nm. Before imaging, the point spread function (PSF) of the microscopic system was modeled by a Gaussian function that is determined by two key parameters: the emission wavelength of the fluorochrome and the NA of the collection objective. The center emission wavelengths of the fluorochromes for the A, T, G, and C bases were 560 nm, 611 nm, 685 nm, and 728 nm, respectively. The objective’s NAs for generating LR and HR images were 0.8 and 1.39, respectively. The NA for the LR images was set to 0.8 following the imaging system’s specification. The NA for the HR images was set to 1.39 to clearly separate adjacent DNBs. During the imaging simulation of each cycle, numerous seed points were selected at 1 nm intervals within each DNB. For each base channel, the fluorescence intensity of every seed point was calculated based on a series of parameters, such as DNA sequence, copy number, and fluorochrome distribution, and the corresponding PSF was used to sequentially generate images of all seed points, which were subsequently superimposed to obtain the final LR and HR nanoscale images. The nanoscale images were digitized and transformed into grayscale with a pixel size of 130 nm. Gaussian noise was introduced as a global background to both the LR and HR images. Figure 4 illustrates the process of imaging simulation for a single DNB, and Fig. 5 shows a sample of simulated LR and HR image pairs.

Fig. 4
figure 4

The process of imaging simulation for a single DNB. (a) Numerous seed points are selected for imaging. (b) The seed points are imaged independently and then superimposed to generate a nanoscale image. (c) Digitized and converted into a grayscale image.

Full size image
Fig. 5
figure 5

The simulated LR (a) and HR (b) image pairs.

Full size image

DNBSRN structure

Inspired by the framework of RFDN, we propose the efficient network DNBSRN, which consists of one global residual connection, one coarse feature extraction (CFE) layer, three shallow residual blocks (SRBs), and three intermediate information collection (IIC) layers. Given a preprocessed LR image \({I}_{LR}\) as input, the SR image \({I}_{SR}\) can be generated by

$$\begin{array}{c}{I}_{SR}={H}_{DNBSRN}\left({I}_{LR}\right) ,\end{array}$$
(2)

where \({H}_{DNBSRN}\left(\cdot \right)\) is DNBSRN. It is optimized by the smooth L1 loss28. Given a training set that has \(N\) LR-HR image pairs with a pixel size of \(w\times h\), the loss function of DNBSRN can be expressed by

$$\begin{array}{c}{L}_{DNBSRN}\left(\theta \right)=\frac{1}{N}\sum_{n=1}^{N}\left(\frac{1}{w\times h}\sum_{i=1}^{w\times h}{loss}_{i}^{n}\right) ,\end{array}$$
(3)

where \(\theta\) represents the learnable parameters of DNBSRN. \({loss}_{i}^{n}\) denotes the loss value of the \(i\)-th pixel in the \(n\)-th image. It can be expressed as

$$\begin{array}{c}{loss}_{i}=\left\{\begin{array}{c}\frac{0.5{\left({\widehat{Y}}_{i}-{Y}_{i}\right)}^{2}}{\beta },if \left|{\widehat{Y}}_{i}-{Y}_{i}\right|<\beta \\ \left|{\widehat{Y}}_{i}-{Y}_{i}\right|-0.5\times \beta , otherwise\end{array} ,\right.\end{array}$$
(4)

where \({\widehat{Y}}_{i}\) and \({Y}_{i}\) denote the \(i\)-th pixel values of the predicted HR and ground truth HR, respectively. \(\beta\) is set to 1 in this study.

The detailed structure of DNBSRN is shown in Fig. 6. Initially, we use the CFE, which contains a convolutional layer, to extract coarse features from the input \({I}_{LR}\).

$$\begin{array}{c}{F}_{0}={H}_{CFE}\left({I}_{LR}\right) ,\end{array}$$
(5)

where \({H}_{CFE}(\cdot )\) represents the convolutional operation for coarse feature extraction and \({F}_{0}\) is the extracted coarse feature. Then, three SRBs are employed for deeper feature extraction. This process can be described as

$${F}_{k}={H}_{{SRB}_{k}}\left({F}_{k-1}\right),k=\text{1,2},3 ,$$
(6)

where \({H}_{{SRB}_{k}}\) denotes the \(k\)-th SRB and \({F}_{k}\) denotes the \(k\)-th feature extracted by the \(k\)-th SRB. Following each SRB, an IIC branch containing a convolutional layer is introduced to collect the intermediate information extracted by the preceding layers. This process can be described as

$${P}_{k}={H}_{{IIC}_{k}}\left({F}_{k}\right),k=\text{1,2},3 ,$$
(7)

where \({H}_{{IIC}_{k}}\) denotes the \(k\)-th IIC after the \(k\)-th SRB and \({P}_{k}\) denotes the \(k\)-th information collected by the \(k\)-th IIC. Finally, we add the collected information to the input \({I}_{LR}\) to obtain the SR image \({I}_{SR}\).

Fig. 6
figure 6

DNBSRN structure. “Conv-7” denotes the convolutional layer with a kernel size of 7 × 7. The number displayed on the right side of each layer indicates the number of output channels.

Full size image
$$\begin{array}{c}{I}_{SR}={I}_{LR}+\sum_{k=1}^{3}{P}_{k} \end{array}.$$
(8)

The highlights of the proposed DNBSRN can be summarized as follows:

  1. (1)

    Given that LR and HR DNB images have the same pixel size and similar features at corresponding positions, we establish a direct global residual connection between the input LR and output HR. This allows the main body of DNBSRN to focus on learning the disparity between LR and HR, leading to a considerable decrease in the complexity of DNB image SR.

  2. (2)

    The body of DNBSRN uses three SRBs to progressively extract deeper features. SRB consists of a convolutional layer, a ReLU activation layer, and a local residual connection. It can take advantage of residual learning while maintaining efficiency.

  3. (3)

    An IIC branch is constructed following each SRB to collect the intermediate information, which is subsequently used to hierarchically modify the pixel value of the LR to produce the HR. IIC is composed solely of a single convolutional layer and fully utilizes the extracted features.

  4. (4)

    Since a single DNB in LR images typically occupies no more than 7 × 7 pixels, we use 7 × 7 kernel size for all convolutional layers. This approach enables the extracted feature maps to effectively perceive the information from each DNB.

Image preprocessing

For preprocessing the training dataset, the LR and HR images were normalized and subsequently fed into the network for training. This can be expressed as

$$\begin{array}{c}{Input}_{1}=\frac{{I}_{1}}{percentile\left({I}_{1}, 99\right)\times random\left(0.9, 1.1\right)} ,\end{array}$$
(9)

where \({I}_{1}\) denotes the original image of the training dataset. \(percentile\left({I}_{1}, 99\right)\) calculates the \({99}^{th}\) percentile intensity value of image \({I}_{1}\). \(random\left(0.9, 1.1\right)\) provides a random number between 0.9 and 1.1, which is used to augment the training data. \({Input}_{1}\) represents the normalized image that is fed into the network.

In the training dataset, images of all cycles exhibit exceptional quality with strong DNB signals and high contrast. However, in real experiments, only the images captured during the first few cycles would exhibit equal quality as the training dataset, and the image quality progressively deteriorates due to incomplete biochemical reactions and DNB degradation, as shown in Fig. 7. The image quality degradation is evident for cycles between 10 and 50 rounds. This results in an increased disparity in the data distribution compared to that of the training dataset, thereby diminishing the quality of the reconstructed SR images. To address this problem, we introduce a histogram matching (HM) approach for preprocessing real images. HM enables us to increase the image quality of subsequent cycles without altering the pixel-to-pixel size relationship. The approach adheres to the same fundamental principle as the conventional HM algorithm29, which seeks to map pixel values from the gray histograms of the input and reference images and then adjusts the pixel value of the input image accordingly.

Fig. 7
figure 7

The image quality degradation over cycles in the real experiment.

Full size image

For preprocessing the real images, images from the first cycle are used as a reference. The images from subsequent cycles are adjusted to match the histogram of the reference. Subsequently, the images are normalized and fed into the network for SR reconstruction. This can be expressed as

$$\begin{array}{c}{Input}_{2}=\frac{HM\left({I}_{2}\right)}{percentile\left(HM\left({I}_{2}\right), 99\right)} ,\end{array}$$
(10)

where \({I}_{2}\) denotes the original image of the real images. \(HM\left(\cdot \right)\) denotes the HM operation, and the HM result is then normalized with its \({99}^{th}\) percentile intensity. \({Input}_{2}\) denotes the preprocessed image as input to the network.

Modification to other networks for comparison

We selected six representative image SR networks (EDSR, RDN, RCAN, IMDN, RFDN, and RLFN) for comparison with the proposed DNBSRN. These networks were proposed for improving the resolution of photorealistic RGB images, which consist of three input and output channels, along with an upscale module at the tail. Considering that DNB images are grayscale with only one channel and do not require upscaling for SR, these networks were adapted to satisfy the specific demands of the DNB image SR task. The number of input and output channels was reduced from three to one, and the upscale module was removed. It is worth emphasizing that the core structure of these networks remained unchanged.

Network training and real image reconstruction

Seven networks, including DNBSRN, EDSR, RDN, RCAN, IMDN, RFDN, and RLFN, were trained and evaluated. Additionally, five modified structures of DNBSRN were trained to conduct ablation experiments. A total of 50 cycles of simulated images were used to train the networks. The initial 40 cycles were allocated for training, and the remaining 10 cycles were allocated for validation. During each epoch, a total of 3200 sub-images with a size of 512 × 512 pixels (128 × 128 pixels for EDSR, RDN, and RCAN) were randomly cropped from training images (with a size of 2200 × 2200 pixels), as well as 800 sub-images from validation images. These sub-images were then shuffled, subjected to preprocessing, and fed into the network with a batch size of 8. The networks were trained for 70 epochs, and the final selected model was the one with the lowest loss in the validation set. The smooth L1 was employed as the loss function. The learning rate was set to 0.0001 throughout the training process. The networks were optimized using the Adam optimizer30 with β1 set to 0.9, β2 set to 0.999, and eps set to 10–8. All networks were trained using identical configurations and the same random seed, except for the differences in sub-images. The real images of the eight experimental datasets were also subjected to identical preprocessing steps before being fed into different networks for reconstruction. The training and reconstruction were performed on a computer workstation equipped with an Intel(R) Xeon(R) Gold 5115 CPU @ 2.40 GHz 2.40 GHz (2 processors) and an NVIDIA Tesla A100 GPU (80 GB). The networks were implemented using Python v.3.11.3 and PyTorch v.2.0.0.

Results

DNBSRN was used to perform SR reconstruction on the eight experimental DNB image datasets from UHD arrays. Comprehensive analyses were conducted as follows.

Comparison of WF and DNBSRN-reconstructed SR images

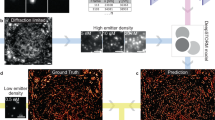
Initially, we demonstrated the improvement in resolving power achieved via DNBSRN by placing WF and DNBSRN-reconstructed SR images from channel A side by side. As shown in Fig. 8a, the raw WF image exhibits noticeable blurriness, making it difficult to differentiate adjacent DNBs. Following the reconstruction, the previously clustered DNBs are separated and individually identified in the SR image. To clearly visualize the improvement in resolving power, we present the intensity line scan profiles along the arrow-marked lines in the WF and SR images, as shown in Fig. 8b. The WF image shows a broad waveform, indicating that multiple DNBs are clustered and difficult to separate. In contrast, the SR image reveals four distinct waveforms, effectively separating the previously clustered DNBs.

Fig. 8
figure 8

Comparison of WF and DNBSRN-reconstructed SR images. (a) Resolving power illustration of WF and SR images. (b) Intensity profiles along the arrow-marked lines in the WF (orange) and SR (green) images.

Full size image

To quantitatively assess the resolution improvement, we use decorrelation analysis31, which does not require a reference image. This analysis provides a cut-off frequency, \({k}_{max}\), representing the highest resolvable spatial frequency in the image. A higher \({k}_{max}\) indicates better image resolution. Figure 9 displays the highest resolvable frequencies along 2π directions for WF and SR images across the four base channels. The theoretical optical transfer function (OTF) cut-off frequency, \({k}_{OTF}\), is also shown for various base channels. The results show that for all channels and radial directions, \({k}_{SR}\)>\({k}_{OTF}\)>\({k}_{WF}\), indicating that DNBSRN reconstruction effectively enhances image resolution across all base channels. In terms of cyclic sequencing, we calculated the variation in the highest resolvable frequencies of WF and SR images across the four base channels over 30 cycles, as shown in Fig. 10. The theoretical OTF is also shown for reference. The plot demonstrates that the resolution enhancement provided by DNBSRN is steady across the cycles. These results confirm that DNBSRN successfully improves the resolution of DNB images.

Fig. 9
figure 9

The highest resolvable spatial frequency of WF (\({k}_{WF}\)) and SR (\({k}_{SR}\)) images of four channels along different directions. \({k}_{OTF}\) denotes the theoretical OTF cut-off frequency. Color bar shows the magnitude of \(\text{log}(\text{power spectrum})\).

Full size image
Fig. 10
figure 10

Variation of highest resolvable frequency of WF (\({k}_{WF}\)) and SR (\({k}_{SR}\)) images over 30 cycles for the four base channels. \({k}_{OTF}\) denotes the theoretical OTF cut-off frequency.

Full size image

Since the ultimate goal of DNB image SR is to achieve good base-calling performance, we subsequently quantified the impact of resolution enhancement from the base-calling perspective. For all eight datasets, we used Zebracall to extract raw reads from WF and DNBSRN-reconstructed SR images and calculated the respective Q30, and MR of the total reads, and ESR. As shown in Fig. 11, the WF images of all eight datasets exhibit relatively poor base-calling performances due to the optical resolution limit. Following DNBSRN reconstruction, the four SE50 datasets show Q30 improvements ranging from 12.89 to 13.41%, MR improvements ranging from 12.75 to 17.15%, and ESR improvements ranging from 13.81 to 17.72%. The four PE100 datasets show Q30 improvements ranging from 9.63 to 10.07%, MR improvements ranging from 10.19 to 10.61%, and ESR improvements ranging from 11.1 to 11.52%. To assess the differences in base-calling metrics between WF and SR images, a paired t-test was conducted. The test revealed significant improvements in all key metrics, including Q30, MR, and ESR, each with a p-value of less than 0.001. These results indicate that DNBSRN significantly improved base-calling performance across all datasets, regardless of the read length and imaging conditions.

Fig. 11
figure 11

Base-calling performances of WF and DNBSRN-reconstructed SR images for the four SE50 datasets (a) and the four PE100 datasets (b).

Full size image

Enhancements through HM preprocessing

To further improve the performance of DNBSRN, we introduce HM, a novel support method for DNB image preprocessing. A group of images from channel A of dataset 1 were selected as examples. As shown in Fig. 12, the WF image of cycle 1 exhibits a similar quality as the LR training images (Fig. 5). As cyclic sequencing continues, the image quality progressively deteriorates, and the data distribution of the WF image of cycle 50 deviates from that of cycle 1, which is undesirable for DNBSRN reconstruction. Matching the histogram of cycle 50 images with that of cycle 1 images results in a substantial increase in image quality, and the gray histogram becomes more uniform. We then reconstructed the WF image of cycle 50 both with and without HM preprocessing. Image reconstruction without HM preprocessing exhibits artifacts marked by color circles, whereas image reconstruction with HM preprocessing shows a reduction in these artifacts. Moreover, base-calling performance is used to quantitatively demonstrate the benefits of the HM. After applying HM, the three base-calling metrics of all eight datasets show various degrees of improvement. Specifically, for the four SE50 datasets, HM preprocessing resulted in an average increase in Q30 of 1.72%, MR of 1.46%, and ESR of 1.28%. For the four PE100 datasets, HM preprocessing resulted in an average increase in Q30 of 0.65%, MR of 0.1%, and ESR of 0.14% (Table 1). These findings suggest that HM enhances image reconstruction as well as base-calling performance.

Fig. 12
figure 12

Visualization of the benefits of HM preprocessing. As cyclic sequencing progresses, the histogram of the WF image from cycle 50 deviates from that of cycle 1, resulting in artifacts generated after SR reconstruction, as highlighted in color circles. These artifacts are reduced following HM preprocessing.

Full size image
Table 1 Comparison of base-calling performances with and without HM preprocessing.
Full size table

Comparison of DNBSRN and other networks

We further compare DNBSRN with six representative image SR networks in terms of DNB image reconstruction quality and network efficiency. These networks include EDSR, RDN, and RCAN, which achieved SOTA performance in photorealistic image reconstruction quality, as well as IMDN, RFDN, and RLFN, which achieved SOTA performance in network efficiency.

We still employed base-calling performance to quantify the quality of DNB image reconstructions across different networks. Table 2 displays the Q30 and MR of the total reads, as well as the ESR of the eight datasets reconstructed by various networks using the same preprocessing approach. Among the four SE50 datasets, only in dataset 3, DNBSRN’s Q30 is marginally lower than RCAN by 0.03% and RDN by 0.05%, and ESR is marginally lower than RCAN by 0.06%. On dataset 1, dataset 2, and dataset 4, DNBSRN outperforms the other networks in terms of all three metrics. Among the four PE100 datasets, DNBSRN also exhibits the best base-calling performances for Q30, MR, and ESR. More importantly, as read length increases, the improved performances of DNBSRN compared to other networks become more pronounced. Combining the overall performances on different datasets, DNBSRN yields the best DNB image reconstruction quality, surpassing the three SOTA networks, EDSR, RDN, and RCAN.

Table 2 Comparison of base-calling performances between DNBSRN and other networks.
Full size table

In addition, the network efficiency is evaluated through the reconstruction time (Rec. Time), the number of parameters (#Params), the number of floating-point operations (FLOPs), the number of elements of all outputs of convolutional layers (#Acts), the maximum GPU memory consumption (GPU Mem.), and the number of convolutional layers (#Conv)32,33. These metrics affect network deployment on DNBSEQ sequencers in different aspects, among which the reconstruction time is the most important due to the stringent requirement of DNBSEQ online processing (on the order of tens of ms). The evaluations were performed on an NVIDIA Tesla A100 GPU, with an input image size of 500 × 500 pixels. As shown in Table 3, EDSR, RDN, and RCAN exhibit poor performance in all efficiency-related metrics due to their complicated structures. IMDN, RFDN, and RLFN exhibit notable efficiency due to their efficient structural design. In comparison, DNBSRN achieves the best efficiency across all the metrics, surpassing the three SOTA networks, IMDN, RFDN, and RLFN, and provides the greatest deployment convenience and lowest resource consumption. In terms of reconstruction time, DNBSRN takes only 7.61 ms to reconstruct an image with 500 × 500 pixels, which greatly minimizes the effect of reconstruction time on DNBSEQ online processing and throughput.

Table 3 Comparison of efficiency between DNBSRN and other networks.
Full size table

Figure 13 shows a scatter plot comparing the average Q30 values across four PE100 datasets and reconstruction times of different models. It is clear that DNBSRN not only achieves the fastest reconstruction speed but also delivers the highest reconstruction quality compared to other networks.

Fig. 13
figure 13

Comparison of DNBSRN and other networks. The x-axis representing reconstruction time and the y-axis representing the average Q30 values across the four PE100 datasets. Red solid circle indicates the best.

Full size image

Ablation experiments of DNBSRN

As detailed in the Materials and methods section, the superior performance of DNBSRN with only seven convolutional layers is primarily attributed to the use of SRB, IIC, and 7 × 7 convolutional kernels. Ablation experiments were conducted to further illustrate the benefits of these structures. In the ablation experiments, SRB and IIC were individually removed from DNBSRN. Figure 14a,b show the network structures after the removal of SRB and IIC, respectively. To assess the effect of 7 × 7 convolutional kernels, we replaced them with 3 × 3, 5 × 5, and 9 × 9 kernels, respectively. We then compared the base-calling performances and network efficiency of these modified structures to the original DNBSRN. As shown in Table 4, the removal of SRB or IIC led to a decrease in the average values of Q30, MR, and ESR, indicating that both SRB and IIC contribute to the enhanced performance of DNBSRN. Replacing the 7 × 7 kernels with 3 × 3 or 5 × 5 kernels also resulted in diminished base-calling performance. Conversely, replacing the 7 × 7 kernels with 9 × 9 kernels yielded comparable base-calling performance but decreased network efficiency. This demonstrates that employing 7 × 7 convolutional kernels indeed boosts the performance of DNBSRN.

Fig. 14
figure 14

The network structure after removal of SRB (a) or IIC (b).

Full size image
Table 4 Comparison of base-calling performance and efficiency of different structures in ablation experiments.
Full size table

Performance of the UHD array following DNBSRN processing

For end users, sequencing results are mostly delivered as effective reads after raw data filtering. In this section, the total reads extracted from the eight datasets reconstructed by DNBSRN were filtered following the filter rules briefed in the Materials and methods section.

Figure 15 shows that across all eight datasets, the ESR exceeded 78%, the Q30 of effective reads exceeded 86%, and the MR of effective reads exceeded 96%, indicating a generally satisfactory performance. In addition, the typical performance of the regular 720 nm pitch array, which has been widely used in commercial sequencers, serves as a benchmark for comparison. Both dataset 1 and dataset 4, as well as the four PE100 datasets, exhibit metrics that are either superior or comparable to the 720 nm array. Although the MR and ESR of dataset 2 and dataset 3 are slightly lower than the 720 nm array, they are still within an acceptable range. These results suggest that the base-calling performance of the 360 nm pitch UHD array following DNBSRN processing is as decent as that of the 720 nm pitch array.

Fig. 15
figure 15

Base-calling performances of the four SE50 datasets (a) and the four PE100 datasets (b) after total reads filtering. The dashed lines in different colors indicate the typical performance of the regular 720 nm pitch array.

Full size image

Although Q30, MR, and ESR are widely recognized as key metrics for evaluating sequencing quality, they do not capture certain critical details, such as base-calling errors that occur across sequencing cycles. These errors can lead to indels and affect single nucleotide polymorphism (SNP) detection in downstream bioinformatics analyses. Base-calling errors can be categorized into two primary types: mismatch and gap. Mismatch occurs when an incorrect base is called, whereas gap represents a missed base in the read. To provide a more comprehensive evaluation of the UHD array’s performance following DNBSRN processing, we quantified the percentages of mismatches and gaps during a PE100 run, both before and after DNBSRN reconstruction (Fig. 16). The results show that mismatches are the most common error type for our data. In the WF case, the fluctuation of mismatches is severe, primarily due to its relatively low resolution, which challenges the detection limits of the base-calling algorithm. Conversely, the variation is less pronounced after reconstruction, showing a monotonically increasing trend. DNBSRN reconstruction successfully reduces mismatch rates across all cycles, with a more pronounced reduction observed in the latter half of the run (cycles 101 to 200), where sequencing accuracy typically declines quickly. Importantly, for most cycles, the mismatch rate in SR images stays below 1%, except for the last few cycles, which is acceptable for most sequencing applications.

Fig. 16
figure 16

Variations in mismatches and gaps for WF and SR images throughout a single PE100 run. The left y-axis represents the percentage of mismatches, while the right y-axis represents the percentage of gaps. Note: All figures were created using Microsoft PowerPoint 2016 (MSO version 16.0.18025.20030, 64-bit), available at https://www.microsoft.com/powerpoint.

Full size image

These results demonstrate the effectiveness of DNBSRN in enhancing the performance of base-calling, confirming the practicality of the UHD array following DNBSRN processing. It is worth noting that the microscopic systems used for imaging 360 and 720 nm pitch arrays have the same optical resolution, suggesting that DNBSRN successfully overcomes the resolution limit of microscopic systems.

Discussion

Further analysis of the DNB image SR task

The DNB image SR task’s objective is twofold. The first objective is to achieve superior image reconstruction quality and consequently improved base-calling performance. The second objective is to accelerate image reconstruction and minimize the effect of reconstruction time on DNBSEQ online processing and throughput. Theoretically, it is challenging for an image SR network to achieve satisfactory results in terms of both quality and speed. Typically, we must sacrifice one aspect to improve the other. However, the morphological features of DNB images are simple, consisting of a large number of fluorescent dots with similar characteristics, which greatly simplifies the DNB image SR task. An efficient network can achieve excellent image reconstruction quality to fulfill these requirements, whereas a deeper network can become oversaturated with image reconstruction quality, which not only consumes additional reconstruction time but also provides no improvement. Based on the aforementioned considerations and the smart structure design, we propose a highly efficient network DNBSRN, which flawlessly satisfies the DNB image SR task. DNBSRN achieves both exceptional image reconstruction quality and rapid image reconstruction speed.

Incorporating image SR reconstruction into the DNBSEQ workflow

In the DNBSEQ workflow for the regular density array, base-calling is directly employed to analyze the images captured by the microscopic system. However, in the case of the UHD array, it is essential to conduct image SR reconstruction prior to base-calling to improve the base-calling performance. To maintain DNBSEQ online processing and maximize the enhancement of throughput, the image SR reconstruction speed must exceed the imaging speed of the microscopic system. The image SR method we developed can be divided into two stages: preprocessing and DNBSRN reconstruction. Preprocessing is currently implemented in Python and can be implemented in C/C++ and accelerated using CUDA programming, enabling it to achieve exceptional computational efficiency. By combining the rapid reconstruction capability of DNBSRN with the accelerated preprocessing technique, the image SR reconstruction speed can be considerably faster. Due to the variation in imaging speed among different fluorescence microscopic systems, it is challenging to present a specific requirement for image SR speed. Nevertheless, by stacking computing resources to parallel process images, it is feasible to attain faster image SR and flexibly meet specific demands.

Additional experiments

Considering that sequencing workflows for different libraries and read lengths are similar and generate comparable DNB images, this study focused on eight datasets from SE50 and PE100 sequencing experiments of the E. coli library on UHD arrays. The developed DNBSRN is potentially suitable for other libraries and read lengths. In the future, additional experiments involving human library may further broaden the applications of DNBSRN.

Conclusions

The inadequate resolution of the fluorescence microscopic system of DNBSEQ impedes the application of UHD arrays. In this study, we developed DNBSRN, an SR network specifically designed for DNB images, to solve this problem. Among the evaluations of the eight datasets, DNBSRN greatly improves the resolution of DNB images, consequently increasing base-calling performance of the UHD array to a comparable level with that of the regular density array. In terms of reconstruction speed, DNBSRN takes only 7.61 ms for an input image with 500 × 500 pixels, thereby minimizing its influence on throughput. Furthermore, DNBSRN outperforms other SR networks in terms of both image reconstruction quality and speed. The integration of DNBSRN into the DNBSEQ workflow will allow for the application of the UHD array in commercial equipment, hence enabling a considerable improvement in throughput and reduction in cost.