Longitudinal dynamic behavior study of a vibrating rod connected through an elastic nonlinear single degree freedom coupler

Abstract

This research explores the efficacy of integrating nonlinear single-degree-of-freedom systems in the vibration control of rod coupling systems. By interlinking two rods with a nonlinear single-degree-of-freedom system as the intermediary, the study employs the Lagrange method (LM) to forecast nonlinear vibrational behaviors. The findings, substantiated by numerical analyses, affirm the precision of LM in gauging the amplitude responses when such a nonlinear system is utilized. The nonlinear dynamics, characterized by intricate vibrational patterns, peak jumping phenomena, and the migration of resonance zones, are induced by the nonlinear single-degree-of-freedom system. By fine-tuning the system’s parameters, significant alterations in the vibrational states of the rod coupling system are achievable. This suggests that the application of a nonlinear single-degree-of-freedom system is a viable strategy for modulating vibrations in rod systems. Furthermore, optimal parameterization of this system is proven to effectively dampen vibrations, showcasing its potential as a sophisticated mechanism for vibration suppression in coupled rod configurations.

Introduction

Vibrational forces, caused by power machinery and working conditions, are prevalent across diverse engineering disciplines, invariably inducing structural vibrations. These vibrations often pose a risk to the integrity and stability of engineering structures. Thus, understanding and controlling these vibrational characteristics is fundamental. For analytical simplicity, many engineering structures can be conceptualized as assemblies of elemental units such as rods, beams, and plates. This modular approach allows for a more manageable examination of the structures’ vibrational properties.

In the machining engineering domain, the durability of boring bar systems is pivotal, and it hinges on controlling structural vibrations. Engineers have thus scrutinized the vibration characteristics of the rod system, the basic unit of the boring bar. Tang et al.¹ explored rods with complex boundary conditions, while Pritz² looked into the dynamic strain of viscoelastic rods with added end masses. Gürgöze³ meticulously studied the specific frequencies of rod systems with a tip mass and mid-span spring-mass arrangements. Candan and Elishakoff⁴ calculated the axial stiffness of rods based on their primary vibrational shapes, and Erol⁵ addressed the characteristic equations for internally supported rod systems with an end mass. Mei⁶ conducted a thorough analysis of four rod theories, enhancing the application of vibration theory in rod systems. Goldberg et al.⁷ investigated the movement at the contact points of rod systems under longitudinal vibrational forces, while Aydogdu⁸ considered axial vibrations in nanorods within a nonlocal continuum model. Xu et al.^9,10 applied an improved Fourier series method to study the longitudinal vibrations of nonlocal nanorods with various boundary conditions and supports. The field also delves into nonlinear vibrations; Cao and Tucker¹¹ employed Cosserat theory for the nonlinear dynamics of elastic rods. Andrianov et al.¹² researched the nonlinear vibrations of a rod with a microstructure. Considering rods with variable cross-sections and fractional derivative elements, Malara et al.¹³ explored nonlinear stochastic vibrations, and Shakhlavi et al.¹⁴ analyzed internal resonances in nanorod systems. These studies offered an extensive investigation into both the forced and natural vibrational characteristics of single-rod structures.

In the analysis of complex rod systems, academic inquiry has focused on the longitudinal vibrations of coupled rod configurations. Tomski et al.¹⁵ examined the vibrations within a compound two-rod system, while Kukla et al.¹⁶ explored how translation springs affect the vibrational behavior of two interconnected rods. Gürgöze¹⁷ introduced alternative frequency equations to assess the vibrations of rods linked by a dual spring-mass system. The work of Mermertas and Gürgöze¹⁸ extended this to the longitudinal vibrations of a double-rod system joined by two spring-mass systems. Li et al.¹⁹ derived exact solutions for the vibrational characteristics of rod systems coupled by translational springs. In scenarios involving multiple coupling spring-mass systems, Inceoğlu and Gürgöze²⁰ analyzed the longitudinal vibrations, and Erol and Gürgöze²¹ studied the vibration characteristics of double-rod systems connected by an array of springs and dampers. Lin et al.²² investigated th²³e free vibration characteristics of two rods coupled by multiple spring-mass systems. Zhao et al studied the nonlinear vibration responses of a double-rod system connected by a nonlinear element. Collectively, these studies offered a systematic examination of the longitudinal vibration characteristics of two-rod systems coupled by single, dual, and multiple spring-mass systems, within the context of linear dynamics.

Amidst the evolution of nonlinear vibration control theory, researchers have been experimenting with nonlinear elements to devise mechanisms for mitigating the vibrations of elastic structures. A particular focus has been on using cubic stiffness to craft nonlinear single-degree-of-freedom systems. These systems, devoid of linear stiffness components, are termed nonlinear energy sinks (NESs)^22,23,25. Felix et al.²⁷ deeply studied the energy pumping, synchronization and beat phenomenon in a nonideal structure coupled to an essentially nonlinear oscillator. Georgiades and Vakakis²⁸ pioneered the integration of NES into a linear beam to assess its vibration control capabilities. Subsequently, Ahmadabadi and Khadem²⁹ explored the nonlinear vibration control of a cantilever beam using NES. Kani et al.³⁰ designed an NES considering various support conditions and utilized it to dampen vibrations in a linear beam. They also investigated³¹ the vibration control of a nonlinear beam via NES. Felix et al.³² introduced a nonlinear energy sink into the nonlinear electromechanical pendulum arm, promoting its engineering application. Chen et al.³³ examined the suppression of vibrations in a beam system by incorporating parallel NESs, paying special attention to the system’s higher branch responses. The effectiveness of NES in an axially moving beam system was also studied by Moslemi et al.³⁴, focusing on both vibration control and system stability. Zhang et al.³⁵ introduced boundary inerter-enhanced NESs to quell vibrations in elastic beams, and in a separate study³⁶, they controlled vibrations in geometrically nonlinear beams using boundary inertial NESs. Further extending the application, He et al.³⁷ combined acoustic black hole effects with NES in a cantilevered beam to mitigate both low and high-frequency vibrations. Zhao et al.^{38,38,39,40,42} utilized adjustable nonlinear vibration absorbers, nonlinear energy sinks, and coupling nonlinear energy sinks for the vibration control of beams, plates, and vibroacoustic coupling systems and further^43,44 connected elastic structures with nonlinear single-degree-of-freedom systems to study its dynamic behavior. Furthermore, Zhan et al⁴⁶ used a nonlinear connecting intercalary plate and connecting nonlinear oscillators to hybrid suppress the vibration of a simplified floating raft system. Ding and Shao⁴⁵ first proposed the concept of NES cells and they⁴⁷ employed NES cells to effectively control the vibration of a plate platform. Tusset et al.^48,49 introduced nonlinear energy sinks to the high-speed elevator system and a portal frame, finding that nonlinear energy sinks can be employed to harvest the vibration energy of various engineering structures, promoting the engineering application of nonlinear energy sinks. The prevailing literature has largely centered on the vibration control of elastic beams, plates, and their coupling systems, through the use of nonlinear single-degree-of-freedom systems, often in the form of NESs. However, the application of these systems as coupling elements in rod systems remains under-explored, with limited attention given to their potential in controlling vibrations in such configurations.

To promote the nonlinear single-degree-of-freedom systems in the engineering application of rod systems, having an understanding of the influence of nonlinear single-degree-of-freedom systems on the longitudinal dynamic behavior of the rod system is necessary. Against this background, this research evaluates the use of nonlinear single-degree-of-freedom systems in managing vibrations within rod coupling assemblies. A nonlinear single-degree-of-freedom system is introduced as the coupling mechanism linking two rods. Utilizing LM, the study predicts the nonlinear vibrational responses when two rods are conjoined by such a system. Through numerical analysis, the precision and robustness of LM in deducing the vibratory behavior of the coupled rods are examined. The study meticulously analyzes how the nonlinear single-degree-of-freedom system influences the magnitude-frequency and single-frequency responses of the rod coupling system. Ultimately, the study arrives at several key conclusions regarding the system’s performance.

Theoretical formulations

Model description

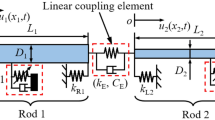
This study presents a model for the longitudinal vibrations of a rod system composed of two rods linked by a nonlinear single-degree-of-freedom system, as depicted in Fig. 1. The system comprises two sub-rods and a nonlinear coupling element. Vibrational forces, exhibiting harmonic properties, act upon sub-rod 1. Longitudinal support springs, representing general boundary conditions, are positioned at the ends of each sub-rod. Table 1 enumerates the specific parameters for the sub-rods, the vibrational forces, and the support springs. Additionally, u_i(x_i,t) denotes the displacement of the ith sub-rod.

Fig. 1

Longitudinal vibration model of two rods coupled through a nonlinear single-degree-freedom system.

Table 1 The symbol definitions.

$$\begin{gathered} {F_{\text{N}}}={k_{\text{L}}}\left[ {{u_{\text{N}}} - {u_1}\left( {{L_1},t} \right)} \right]+{k_{\text{L}}}\left[ {{u_{\text{N}}} - {u_2}\left( {0,t} \right)} \right] \hfill \\ \begin{array}{*{20}{c}} {}&{+{k_{\text{N}}}{{\left[ {{u_{\text{N}}} - {u_1}\left( {{L_1},t} \right)} \right]}^3}+{k_{\text{N}}}{{\left[ {{u_{\text{N}}} - {u_2}\left( {0,t} \right)} \right]}^3}} \end{array} \hfill \\ \begin{array}{*{20}{c}} {}&{+{C_{\text{N}}}\left( {\frac{{{\text{d}}{u_{\text{N}}}}}{{{\text{d}}t}} - {{\left. {\frac{{\partial {u_1}}}{{\partial t}}} \right|}_{{x_1}={L_1}}}} \right)+{C_{\text{N}}}\left( {\frac{{{\text{d}}{u_{\text{N}}}}}{{{\text{d}}t}} - {{\left. {\frac{{\partial {u_2}}}{{\partial t}}} \right|}_{{x_2}=0}}} \right)} \end{array} \hfill \\ \end{gathered}$$

(1)

where k_L is the linear stiffness of the nonlinear single-degree-freedom system; k_N is the cubic stiffness of the nonlinear single-degree-freedom system; C_N is the viscous damping of the nonlinear single-degree-freedom system; u_N is the vibration displacement of the nonlinear single-degree-freedom system; and m_N is defined as the motion mass of the nonlinear single-degree-freedom system.

LM is applied to analyze the vibrational responses of the coupled rod system. To do this, it is essential to formulate Lagrangian, which encapsulates the system’s kinetic energy, potential energy, and the work done by external forces. Building on these principles, the research progresses to derive the expressions for the energy terms specific to the coupled rod system.

According to the above derivation, the kinetic energy (T_N), potential energy (V_N), and work done by the viscous damping force (W_N) can be derived as follows:

$${T_{\text{N}}}=\frac{1}{2}{m_{\text{N}}}{\left( {\frac{{{\text{d}}{u_{\text{N}}}}}{{{\text{d}}t}}} \right)^2}$$

(2-a)

$$\begin{gathered} {V_{\text{N}}}=\frac{1}{2}{k_{\text{L}}}{\left[ {{u_{\text{N}}} - {u_1}\left( {{L_1},t} \right)} \right]^2}+\frac{1}{2}{k_{\text{L}}}{\left[ {{u_{\text{N}}} - {u_2}\left( {0,t} \right)} \right]^2} \hfill \\ \begin{array}{*{20}{c}} {}&{+\frac{1}{4}{k_{\text{N}}}{{\left[ {{u_{\text{N}}} - {u_1}\left( {{L_1},t} \right)} \right]}^4}+\frac{1}{4}{k_{\text{N}}}{{\left[ {{u_{\text{N}}} - {u_2}\left( {0,t} \right)} \right]}^4}} \end{array} \hfill \\ \end{gathered}$$

(2-b)

and

$${W_{\text{N}}}= - \left\{ {{C_{\text{N}}}\left( {\frac{{{\text{d}}{u_{\text{N}}}}}{{{\text{d}}t}} - {{\left. {\frac{{\partial {u_1}}}{{\partial t}}} \right|}_{{x_1}={L_1}}}} \right)\left[ {{u_{\text{N}}} - {u_1}\left( {{L_1},t} \right)} \right]+{C_{\text{N}}}\left( {\frac{{{\text{d}}{u_{\text{N}}}}}{{{\text{d}}t}} - {{\left. {\frac{{\partial {u_2}}}{{\partial t}}} \right|}_{{x_2}=0}}} \right)\left[ {{u_{\text{N}}} - {u_2}\left( {0,t} \right)} \right]} \right\}$$

(2-c)

Based on the vibration theory, the kinetic energy (T_Ri) and potential energy (V_Ri) of sub-rods can be determined as follows:

$${T_{{\text{R}}i}}=\int_{0}^{{{L_i}}} {\frac{{\pi {D_i}^{2}{\rho _i}}}{4}{{\left( {\frac{{\partial {u_i}}}{{\partial t}}} \right)}^2}{\text{d}}{x_i}}$$

(3-a)

and

$${V_{{\text{R}}i}}=\int_{0}^{{{L_i}}} {\frac{{\pi {D_i}^{2}{E_i}}}{4}{{\left( {\frac{{\partial {u_i}}}{{\partial {x_i}}}} \right)}^2}{\text{d}}{x_i}}$$

(3-b)

The work done by the vibration excitation (W_E) is derived as follows:

$${W_{\text{E}}}=\int_{0}^{{{L_1}}} {{\text{Dirac}}({x_1} - {x_{{\text{E1}}}}){F_0}\sin \left( {\omega t} \right){u_1}{\text{d}}{x_1}}$$

(4)

The potential energy of the longitudinal boundary springs (V_Bi) is expressed as follows:

$${V_{{\text{B}}i}}=\frac{1}{2}{k_{{\text{L}}i}}{u_i}{\left( {0,t} \right)^2}+\frac{1}{2}{k_{{\text{R}}i}}{u_i}\left( {{L_i},t} \right)$$

(5)

Based on the above forms of energy terms, the total kinetic energy (T_System), total potential energy (V_System), and total work done by the external force (W_System) can be determined as follows:

$${T_{{\text{System}}}}=\sum\limits_{{i=1}}^{2} {{T_{{\text{R}}i}}} +{T_{\text{N}}}$$

(6-a)

$${V_{{\text{System}}}}=\sum\limits_{{i=1}}^{2} {\left( {{V_{{\text{R}}i}}+{V_{{\text{B}}i}}} \right)} +{V_{\text{N}}}$$

(6-b)

and

$${W_{{\text{System}}}}={W_{\text{N}}}+{W_{\text{E}}}$$

(6-c)

Therefore, Lagrange term of two rods coupled through a nonlinear single-degree-freedom system can be developed as follows:

$${L_{{\text{System}}}}={T_{{\text{System}}}} - {V_{{\text{System}}}}+{W_{{\text{System}}}}$$

(7)

When using LM to forecast the vibrational responses of two rods linked by a nonlinear single-degree-of-freedom system, the Lagrange term represents the total energy of the system is of great importance.

Solution procedure

Following the mode superposition method, the vibrational displacements of the two sub-rods are expressed in an expanded form as follows:

$$u_{1} \left( {x_{1} ,t} \right) = \sum\limits_{{m = 1}}^{M} {\varphi _{{1~m}} \left( {x_{1} } \right)q_{{1~m}} \left( t \right)}$$

(8-a)

and

$${u_2}\left( {{x_2},t} \right)=\sum\limits_{{z=1}}^{{\text{Z}}} {{\varphi _{2z}}\left( {{x_2}} \right){q_{2z}}\left( t \right)}$$

(8-b)

where φ_1j(x₁) and φ_2j(x₂) are the modal functions of sub-rods; q_1j(t) and q_2z(t) are the unknown coefficients; and M and Z are the number of truncations.

To simply establish Lagrange function, the vibrational displacements of the sub-rods are reformed into specific terms, which are outlined as follows:

$${u_1}\left( {{x_1},t} \right)={{\boldsymbol{\varphi }}_1}{{\mathbf{q}}_1}$$

(9-a)

and

$${u_2}\left( {{x_2},t} \right)={{\boldsymbol{\varphi }}_2}{{\mathbf{q}}_2}$$

(9-b)

where the form terms shown in Eq. (9) are listed as,

$${\boldsymbol{\upvarphi }}_{1} = \left[ {\begin{array}{*{20}c} {\varphi _{{11}} } & \ldots & {\varphi _{{1m}} } & \ldots & {\varphi _{{{\text{1 M}}}} } \\ \end{array} } \right]$$

(10-a)

$${\boldsymbol{\upvarphi }}_{2} = \left[ {\begin{array}{*{20}c} {\varphi _{{21}} } & \ldots & {\varphi _{{2z}} } & \ldots & {\varphi _{{{\text{2Z}}}} } \\ \end{array} } \right]$$

(10-b)

$${\mathbf{q}}_{1} = \left[ {q_{{11}} \; \ldots \;q_{{1m}} \; \ldots \;q_{{{\text{1M}}}} } \right]^{{\text{T}}}$$

(10-c)

and

$${{\mathbf{q}}_2}={\left[ {\begin{array}{*{20}{c}} {{q_{21}}}&{\ldots}&{{q_{2z}}}&{\ldots}&{{q_{{\text{2Z}}}}} \end{array}} \right]^{\text{T}}}$$

(10-d)

To ensure the uniformity of the solution procedure, q₃ is defined as follow:

$${{\mathbf{q}}_3}={\left[ {{u_{\text{N}}}} \right]^{\text{T}}}$$

(11)

By substituting Eqs. (10) and (11) into Eq. (7) and proceeding with the subsequent step:

$$\frac{\partial }{{\partial t}}\left( {\frac{{\partial {L_{{\text{System}}}}}}{{\partial {{{\mathbf{\dot {q}}}}_i}}}} \right) - \frac{{\partial {L_{{\text{System}}}}}}{{\partial {{\mathbf{q}}_i}}}=0$$

(12)

The Lagrange function, representing the energy dynamics of two rods coupled through a nonlinear single-degree-freedom system, can be obtained as follows:

$$\begin{gathered} \left( {\int_{0}^{{{L_1}}} {\frac{{\pi {D_1}^{2}{\rho _1}}}{4}{{\boldsymbol{\varphi }}_1}^{{\text{T}}}{{\boldsymbol{\varphi }}_1}{\text{d}}{x_1}} } \right)\frac{{{{\text{d}}^2}{{\mathbf{q}}_1}}}{{{\text{d}}{t^2}}}+\left( {\int_{0}^{{{L_1}}} {\frac{{\pi {D_1}^{2}{E_1}}}{4}\frac{{{\text{d}}{{\boldsymbol{\varphi }}_1}^{{\text{T}}}}}{{{\text{d}}{x_1}}}\frac{{{\text{d}}{{\boldsymbol{\varphi }}_1}}}{{{\text{d}}{x_1}}}{\text{d}}{x_1}} } \right){{\mathbf{q}}_1}+\left[ {{k_{{\text{L1}}}}{{\boldsymbol{\varphi }}_1}{{\left( 0 \right)}^{\text{T}}}{{\boldsymbol{\varphi }}_1}\left( 0 \right)} \right]{{\mathbf{q}}_1} \hfill \\ +\left[ {{k_{{\text{R1}}}}{{\boldsymbol{\varphi }}_1}{{\left( {{L_1}} \right)}^{\text{T}}}{{\boldsymbol{\varphi }}_1}\left( {{L_1}} \right)} \right]{{\mathbf{q}}_1}+{F_0}\sin \left( {\omega t} \right){{\boldsymbol{\varphi }}_1}{\left( {{x_{{\text{E1}}}}} \right)^{\text{T}}}+{k_{\text{L}}}\left[ {{{\boldsymbol{\varphi }}_1}\left( {{L_1}} \right){{\mathbf{q}}_1} - {u_{\text{N}}}} \right]{{\boldsymbol{\varphi }}_1}{\left( {{L_1}} \right)^{\text{T}}} \hfill \\ +{k_{\text{N}}}{\left[ {{{\boldsymbol{\varphi }}_1}\left( {{L_1}} \right){{\mathbf{q}}_1} - {u_{\text{N}}}} \right]^3}{{\boldsymbol{\varphi }}_1}{\left( {{L_1}} \right)^{\text{T}}}+{C_{\text{N}}}\left[ {{{\boldsymbol{\varphi }}_1}\left( {{L_1}} \right)\frac{{{\text{d}}{{\mathbf{q}}_1}}}{{{\text{d}}t}} - \frac{{{\text{d}}{u_{\text{N}}}}}{{{\text{d}}t}}} \right]{{\boldsymbol{\varphi }}_1}{\left( {{L_1}} \right)^{\text{T}}}=0 \hfill \\ \end{gathered}$$

(13-a)

$$\begin{gathered} \left( {\int_{0}^{{{L_2}}} {\frac{{\pi {D_2}^{2}{\rho _2}}}{4}{{\boldsymbol{\varphi }}_2}^{{\text{T}}}{{\boldsymbol{\varphi }}_2}{\text{d}}{x_2}} } \right)\frac{{{{\text{d}}^2}{{\mathbf{q}}_2}}}{{{\text{d}}{t^2}}}+\left( {\int_{0}^{{{L_2}}} {\frac{{\pi {D_2}^{2}{E_2}}}{4}\frac{{{\text{d}}{{\boldsymbol{\varphi }}_2}^{{\text{T}}}}}{{{\text{d}}{x_2}}}\frac{{{\text{d}}{{\boldsymbol{\varphi }}_2}}}{{{\text{d}}{x_2}}}{\text{d}}{x_2}} } \right){{\mathbf{q}}_2}+\left[ {{k_{{\text{L2}}}}{{\boldsymbol{\varphi }}_2}{{\left( 0 \right)}^{\text{T}}}{{\boldsymbol{\varphi }}_2}\left( 0 \right)} \right]{{\mathbf{q}}_2} \hfill \\ +\left[ {{k_{{\text{R2}}}}{{\boldsymbol{\varphi }}_2}{{\left( {{L_2}} \right)}^{\text{T}}}{{\boldsymbol{\varphi }}_2}\left( {{L_2}} \right)} \right]{{\mathbf{q}}_2}+{k_{\text{L}}}\left[ {{{\boldsymbol{\varphi }}_2}\left( 0 \right){{\mathbf{q}}_2} - {u_{\text{N}}}} \right]{{\boldsymbol{\varphi }}_2}{\left( 0 \right)^{\text{T}}}+{k_{\text{N}}}{\left[ {{{\boldsymbol{\varphi }}_2}\left( 0 \right){{\mathbf{q}}_2} - {u_{\text{N}}}} \right]^3}{{\boldsymbol{\varphi }}_2}{\left( 0 \right)^{\text{T}}} \hfill \\ +{C_{\text{N}}}\left[ {{{\boldsymbol{\varphi }}_2}\left( 0 \right)\frac{{{\text{d}}{{\mathbf{q}}_2}}}{{{\text{d}}t}} - \frac{{{\text{d}}{u_{\text{N}}}}}{{{\text{d}}t}}} \right]{{\boldsymbol{\varphi }}_2}{\left( 0 \right)^{\text{T}}}=0 \hfill \\ \end{gathered}$$

(13-b)

and

$$\begin{gathered} {m_{\text{N}}}\frac{{{{\text{d}}^2}{u_{\text{N}}}}}{{{\text{d}}{t^2}}}+{k_{\text{L}}}\left[ {{u_{\text{N}}} - {{\boldsymbol{\varphi }}_1}\left( {{L_1}} \right){{\mathbf{q}}_1}} \right]+{k_{\text{L}}}\left[ {{u_{\text{N}}} - {{\boldsymbol{\varphi }}_2}\left( 0 \right){{\mathbf{q}}_2}} \right]+{k_{\text{N}}}{\left[ {{u_{\text{N}}} - {{\boldsymbol{\varphi }}_1}\left( {{L_1}} \right){{\mathbf{q}}_1}} \right]^3} \hfill \\ +{k_{\text{N}}}{\left[ {{u_{\text{N}}} - {{\boldsymbol{\varphi }}_2}\left( 0 \right){{\mathbf{q}}_2}} \right]^3}+{C_{\text{N}}}\left[ {\frac{{{\text{d}}{u_{\text{N}}}}}{{{\text{d}}t}} - {{\boldsymbol{\varphi }}_1}\left( {{L_1}} \right)\frac{{{\text{d}}{{\mathbf{q}}_1}}}{{{\text{d}}t}}} \right]+{C_{\text{N}}}\left[ {\frac{{{\text{d}}{u_{\text{N}}}}}{{{\text{d}}t}} - {{\boldsymbol{\varphi }}_2}\left( 0 \right)\frac{{{\text{d}}{{\mathbf{q}}_2}}}{{{\text{d}}t}}} \right]=0 \hfill \\ \end{gathered}$$

(13-c)

Vibration responses of two rods coupled through a nonlinear single-degree-freedom system can be obtained by numerically solving Eq. (13). Importantly, the Runge-Kutta method is employed to numerical solve Eq. (13).

Numerical analysis and discussion

This study focuses on deciphering the nonlinear vibrational properties of a system where two rods are connected by a nonlinear single-degree-of-freedom system. The computational methods detailed in Section “Theoretical formulations” are utilized to simulate the system’s nonlinear vibrational responses. The parameters set for the rod system include Young’s modulus E_i = 6.89 × 10¹⁰ Pa, ρ_i = 2.8 × 10³ kg/m³, D₁ = 0.06 m, D₂ = 0.04 m, k_Li = k_Ri = 5 × 10⁴ N/m, x_E1 = 0, and F₀ = 100 N. The observation points are selected at x₁ = L₁ for the first rod and x₂ = 0 for the second rod. The time domain for calculating the nonlinear vibration is set from 0 to 2000 times the excitation period (T_E), with the assumption that the responses within the interval [1801 T_E, 2000 T_E] will yield stable results. Besides, Fig. 2 gives the flowchart of this section, where the numerical results of this work are analyzed through the corresponding flowchart.

Fig. 2

The flowchart of Section “Numerical analysis and discussion”.

Verify the calculation results gained by the LM

This section is dedicated to verifying the accuracy of the results calculated using LM. The parameters for the nonlinear single-degree-of-freedom system are specified: m_N = 0.25 kg, k_L = 10⁴ N/m, k_N = 10⁸ N/m³, and C_N = 10 Ns/m. Prior to affirming the accuracy of these results, it is crucial to confirm their stability. Figure 3 illustrates the magnitude responses of the two-rod system coupled with a nonlinear single-degree-of-freedom system under various truncation levels. It is observed that the system’s magnitude responses stabilize when LM truncation reaches a single term. Therefore, a truncation value of one is adopted for all further calculations in this study.

Fig. 3

Magnitude responses of two rods coupled through a nonlinear single-degree-freedom system with different truncations.

Subsequently, to evaluate the accuracy of LM, this study compares the magnitude responses of two rods connected by a nonlinear single-degree-of-freedom system as calculated by LM against those obtained using the harmonic balance method (HBM) and Galerkin truncation method (GTM). For the GTM, the GTM employs the Galerkin condition to discrete the vibration-governing equations of the two rods connected by a nonlinear single-degree-of-freedom system. The detailed process of GTM is the same as those employed in Reference⁴³. It should be noted that the modeling processes of the GTM and LM are quite different. For the HBM, the aimed equations of the HBM are the same as those employed in LM. However, the HBM employs the harmonics to assume the unknown time terms. Considering the nonlinear forms studied in this work is cubic stiffness, the fundamental and third harmonics are employed to simulate the unknown time terms. Then, employing the above harmonics in the aimed equations, one can get a series of functions related to the coefficients of harmonics. Magnitude responses of two rods connected by a nonlinear single-degree-of-freedom system can be obtained by solving the above functions. It should be noted that the HBM calculates the magnitude responses of two rods connected by a nonlinear single-degree-of-freedom system from the frequency domain while the LM calculates those from the time domain. Considering the difference of the above three methods, Fig. 4 displays the magnitude responses derived from LM, HBM, and GTM. The close agreement among the responses from these methods as seen in Fig. 4 suggests that the computational outcomes from LM are reliable.

Fig. 4

Magnitude responses of two rods coupled through a nonlinear single-degree-freedom system gained by LM, HBM, and GTM.

Figure 5 gives the errors of magnitude responses of two rods coupled through a nonlinear single-degree-freedom system gained by LM, HBM, and GTM. From Fig. 5, it can be found that the errors stay at a reasonable level, which indicates that the computational outcomes from LM are reliable.

Fig. 5

Errors of magnitude responses of two rods coupled through a nonlinear single-degree-freedom system gained by LM, HBM, and GTM.

Magnitude-frequency vibration impacted by the nonlinear single-degree-freedom system

This section systematically investigates how a nonlinear single-degree-of-freedom system affects the magnitude-frequency responses of a coupled rod system, aiming to assess its potential for vibration control applications.

Figure 6 illustrates the influence of k_N on the magnitude-frequency responses of a two-rod coupling system, where k_L is 10⁴ N/m, C_E is 10 Ns/m, and m_N is 0.2 kg. The results indicate that variations in k_N significantly affect the system’s responses. Specifically, increasing k_N enhances vibration suppression in sub-rod 1, which is directly subject to vibrational excitation, by broadening the range of effective vibration suppression. However, this increase also intensifies the vibrations in sub-rod 2, indicating a transfer of vibratory energy from sub-rod 1 to sub-rod 2. This effect underscores the importance of selecting an optimal k_N value, as excessively increasing k_N can adversely affect vibration suppression in sub-rod 1. Additionally, the presence of the nonlinear single-degree-of-freedom system induces nonlinear vibratory behaviors in the coupling system, as seen when k_N is raised to 10⁹ N/m³ and 2 × 10⁹ N/m³. This includes complex vibrations and peak jumping, with resonance regions shifting to higher frequencies, particularly for the 1st resonance region. To further understand the nature of these complex vibrations, Fig. 7 presents phase and time diagrams for different k_N values. Figure 7a shows that at k_N = 10⁹ N/m³, Poincaré points form a closed curve, and the system demonstrates stable quasi-periodic behavior. In contrast, Fig. 7b reveals that at k_N = 2 × 10⁹ N/m³, Poincaré points are disordered, indicating chaotic behavior within a bounded range. This analysis demonstrates that by adjusting the nonlinear single-degree-of-freedom system’s parameters, particularly k_N, one can alter the working condition of the two-rod coupling system, thus influencing its vibrational characteristics.

Fig. 6

Magnitude-frequency responses of the two-rod coupling system influenced by k_N.

Fig. 7

Phase and time diagrams of compl ex vibration shown in Fig. 4.

Figure 8 presents the magnitude-frequency responses of a two-rod coupling system as influenced by C_N, with k_L = 10⁴ N/m, k_N = 10⁹ N/m³, and m_N = 0.2 kg. It is observed that changes in C_N significantly affect the system’s responses. At lower C_N values, nonlinear vibration phenomena, such as peak jumping and complex vibratory patterns, are evident. As C_N increases, these nonlinear effects diminish, and the overall vibration intensity for both sub-rods 1 and 2 decreases. Contrasting with the effects of k_N, as discussed in relation to Fig. 6, an increase in C_N dampens nonlinear vibrations—a reversal of the trend induced by increasing k_N. This underscores the pivotal role of C_N in mitigating nonlinear vibrations and reducing overall vibration levels in the two-rod coupling system. Thus, adjusting C_N upwards is beneficial for vibration control within this system. Additionally, the characteristics of complex vibrations in Fig. 6 are consistent with those observed in Fig. 6.

Fig. 8

Magnitude-frequency responses of the two-rod coupling system influenced by C_N.

Figure 9 depicts the magnitude-frequency responses of a two-rod coupling system impacted by m_N, with k_L = 10⁴ N/m, k_N = 10⁹ N/m³, and C_N = 15 Ns/m. An analysis of Fig. 9 reveals that the mass of the nonlinear single-degree-of-freedom system primarily affects the presence of nonlinear vibration phenomena in the response spectrum. When m_N is low, the response of the system is typical. However, as m_N is increased to 0.3 kg and 0.4 kg, nonlinear behaviors begin to manifest in the magnitude-frequency responses. The vibration levels of the sub-rods show slight variations with the increase in m_N. This observation suggests that m_N is a critical factor in either promoting or suppressing nonlinear vibrational phenomena, given a fixed set of other parameters in the nonlinear single-degree-of-freedom system. To further understand the complex vibrations indicated in Figs. 9 and 10 offers phase and time diagrams for these conditions. Specifically, Fig. 10a corresponds to m_N at 0.3 kg, and Fig. 10b to m_N at 0.4 kg. In both scenarios, Poincaré points in the phase diagrams form closed loops, and the phase and time diagrams indicate stability, leading to the conclusion that the complex vibration states at these masses are quasi-periodic.

Fig. 9

Magnitude-frequency responses of two rods coupling system influenced by m_N.

Fig. 10

Phase and time diagrams of complex vibration shown in Fig. 7.

Single-frequency vibration influenced by the nonlinear single-degree-freedom system

In engineering applications, the vibrational forces acting on a two-rod coupling system typically remain within a limited range. Therefore, examining how the nonlinear single-degree-of-freedom system affects the system’s response to a constant-frequency vibration is of considerable importance. In this context, the study sets the vibration excitation frequency at 27.0 Hz to investigate these effects.

Figure 11 illustrates the impact of k_N on the magnitude responses of a two-rod coupling system at a single excitation frequency of 27 Hz, with k_L = 10⁴ N/m, C_N = 15 Ns/m, and m_N = 0.3 kg. Observations from Fig. 11 reveal that variations in k_N markedly affect the system’s magnitude responses at this frequency. Initially, as k_N increases within the range of 10⁸ N/m³ to 10^8.7 N/m³, the vibration magnitude remains low, indicating effective vibration suppression. However, within the parameter range of [10^8.7 N/m³, 10¹¹ N/m³], an increase in k_N correlates with improved vibration suppression for the coupled system. Moreover, the progression of k_N values leads to nonmonotonic changes in the system’s working condition, with three distinct regions exhibiting complex vibrations. Within these regions of complex vibration, the magnitude of the single-frequency response is elevated compared to areas of normal vibration adjacent to them. Therefore, selecting an appropriate range for k_N is crucial for optimizing vibration control of the two-rod system when subjected to single-frequency excitation.

Fig. 11

Single-frequency responses of the two-rod coupling system influenced by k_N.

Figure 12 provides phase and time diagrams to analyze the complex vibratory states depicted in Fig. 11, at a single excitation frequency of 27 Hz. Figure 12a corresponds to k_N of 10^9.1 N/m³, Fig. 10b to 10^10.2 N/m³, and Fig. 10c to 10^10.7 N/m³. In Fig. 12a,c, Poincaré points form closed curves in the phase diagrams, indicating a quasi-periodic state due to the stable nature of the phase and time diagrams. Conversely, Fig. 12b shows disordered Poincaré points with fluctuating phase and time diagrams, signifying chaotic behavior at k_N = 10^10.2 N/m³. This suggests that varying k_N influences the working condition of the two-rod system’s single-frequency responses.

Fig. 12

Phase and time diagrams of complex vibration shown in Fig. 9.

Figure 13 displays the magnitude responses of a two-rod coupling system at a fixed excitation frequency of 27 Hz, affected by C_N, with k_L = 10⁴ N/m, k_N = 10⁹ N/m³, and m_N = 0.3 kg. The data indicates that changes in C_N have a significant impact on the magnitude responses at this frequency. Complex vibrational phenomena are observed when C_N ranges from 1 Ns/m to 24 Ns/m. Beyond a C_N value of 24 Ns/m, the system’s response normalizes, suggesting that higher C_N values help eliminate complex vibrations. Additionally, the amplitude of single-frequency vibrations consistently decreases as C_N increases, implying that a higher C_N is beneficial for reducing vibrations in the two-rod coupling system under single-frequency excitation.

Fig. 13

Single-frequency responses of the two-rod coupling system influenced by C_N.

To analyze the complex vibrational state shown in Figs. 13 and 14 provides the corresponding phase and time diagrams. These diagrams demonstrate stability, and Poincaré points form a complete curve. Therefore, it can be concluded that the complex vibration observed in Fig. 13 is in a quasi-periodic state.

Fig. 14

Phase and time diagrams of complex vibration shown in Fig. 13.

Figure 15 showcases how m_N influences the magnitude responses of a two-rod coupling system at an excitation frequency of 27 Hz, with k_L = 10⁴ N/m, k_N = 10⁹ N/m³, and C_N = 15 N/m. The data indicates that m_N significantly affects the system’s responses. Specifically, complex vibrational behaviors emerge when m_N is between 0.26 kg and 0.36 kg. Outside this range—below 0.26 kg or above 0.36 kg—the system’s single-frequency responses remain typical. The vibration magnitude fluctuates nonmonotonically with changes in m_N, suggesting that adjusting m_N is not a straightforward method for controlling vibrations at this frequency. To determine the nature of the complex vibrations indicated in Figs. 15 and 16 provides phase and time diagrams. These diagrams, upon analysis similar to that for Fig. 12, reveal that the complex vibrations are quasi-periodic in nature.

Fig. 15

Single-frequency responses of the two-rod coupling system influenced by m_N.

Fig. 16

Phase and time diagrams of complex vibration shown in Fig. 15.

Conclusion

This study develops a vibration analysis model for a two-rod coupling system interconnected by a nonlinear single-degree-of-freedom system. LM is utilized to determine the system’s vibrational responses. The accuracy and stability of LM calculations for this system are verified. Further, the influence of the nonlinear single-degree-of-freedom system on the system’s magnitude-frequency and single-frequency responses is extensively analyzed. The key findings from the numerical analysis are summarized as follows:

• (1) Vibration responses of the model consisting of two rods and a nonlinear single-degree-freedom system can be precisely solved by using LM.

• (2) The nonlinear single-degree-of-freedom system induces nonlinear vibrational phenomena such as complex vibrations, peak jumping, and shifts in resonance regions. Adjustments to the system’s parameters significantly affect the vibration states of the coupled rods, with changes in k_N and C_N proving to be effective in vibration control.

• (3) The single-frequency vibrational states of the coupled rods can be substantially altered by modifying the parameters of the nonlinear single-degree-of-freedom system. Selecting an appropriate range for these parameters is essential for suppressing vibrations under single-frequency excitation.

• (4) Overall, incorporating a nonlinear single-degree-of-freedom system is a viable method for controlling vibrations in a two-rod coupling system, with optimal parameterization crucial for effective vibration suppression.