Introduction

With the rapid expansion of the electric vehicle and mobile device markets, lithium-ion batteries have been widely used as efficient energy storage systems1,2,3. However, the performance of lithium-ion batteries gradually deteriorates over time during use, posing significant challenges to their safety and reliability. In battery management systems (BMS)4, accurately and quickly assessing the State of Health (SOH)5,6 and predicting the Remaining Useful Life (RUL)7 of batteries have become critical technical challenges.

SOH represents the health level of a battery relative to its initial state. This indicator is influenced by various factors, including the number of charge-discharge cycles, charging and discharging conditions, and environmental temperature8,9,10. Accurate SOH estimation not only helps users arrange battery use and maintenance rationally, extending the battery’s lifespan, but also allows for timely replacement or maintenance before significant performance degradation, ensuring user safety.

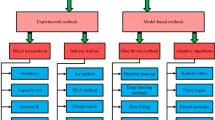
Currently, common SOH estimation methods mainly include model-based approaches and data-driven approaches11. Although model-based methods theoretically have certain advantages12,13,14, they are often limited in practical applications by the accuracy of the model and the availability of parameters. In contrast, data-driven methods have gradually become a research focus due to their efficiency in handling large-scale data and strong generalization capabilities15,16,17. Nevertheless, they also face challenges, such as the need for extensive labeled datasets and the potential for reduced prediction accuracy when applied to complex, multi-dimensional time-series data.

Qu et al.18 successfully integrate particle swarm optimization and an Attention mechanism based on the long short-term memory (LSTM) network for RUL prediction and SOH estimation of lithium-ion batteries. Venugopal et al.19 design a unique SOH estimation method that uses the independent recurrent neural network in a more realistic way by adopting the dynamic load curve conditions of electric vehicles to accurately predict the battery SOH.To improve the prediction accuracy, Li et al.20 design a variable length time memory neural network. The input gate and forget gate are coupled through a fixed connection, the element level product of new input and historical cell state is carried out, and a peephole connection from a “constant error carousel” is added to the output gate to enhance prediction accuracy. Wang et al.21 propose an ensemble model based on the stacked LSTM for predicting lithium-ion batteries’ capacity cycle life.

However, even with the success of data-driven methods, challenges remain. Accurately processing multi-dimensional time-series data, as well as balancing prediction accuracy and computational efficiency, is still a key issue. Existing methods often struggle to fully capture the complex and non-linear battery degradation patterns across different operational conditions, making SOH and RUL prediction less accurate in some cases.

To accurately estimate the SOH of lithium-ion batteries and predict RUL, this paper proposes a novel battery SOH and RUL prediction method based on Convolutional Neural Networks (CNN)22,23, Bidirectional Long Short-Term Memory networks (BiLSTM)24, and the Attention mechanism25. This method first mines battery data features deeply using CNN, then uses BiLSTM and the Attention mechanism to analyze the time series of battery parameters and enhance the weighting of key data.The results of experiments demonstrate the great prediction accuracy, stability, and robustness of this method.

The main contributions of this study are delineated across the following three dimensions:

  1. (a)

    To deeply analyze the complex information during the charge and discharge processes of lithium-ion batteries and extract key features, this research employs CNN to mine the deep features of the input data, thereby enhancing the stability of the prediction model.

  2. (b)

    Given the time-series nature of battery data, a BiLSTM network is integrated to accurately capture the dynamic evolution of the health state of lithium-ion batteries. BiLSTM possesses memory capabilities that effectively retain critical historical input information for analyzing long-term data correlations.

  3. (c)

    By incorporating an Attention mechanism, the training model learns to selectively focus on input data, assigning higher weights to input vectors that are highly correlated with the output, thus improving the computational efficiency of the prediction model.

The remainder of this paper is organized as follows: Section "Research contents" introduces the structure of lithium batteries, as well as the health status and remaining useful life metrics. Section "Model Architecture and Algorithms" presents the algorithms used in this study and the basic structure of the hybrid model. Section "Experiment Dataset" analyzes the lithium-ion battery dataset. Section "Experiment Results and Conclusion" presents the experimental results. Finally, Section "Conclusions" provides a summary of the conclusions drawn from this research.

Research contents

The core structure of a lithium-ion battery contains four basic components: positive electrode, negative electrode, electrolyte, and isolation membrane, and its configuration is shown in Fig. 126. Compared to the complex system structure of fuel cells, lithium-ion batteries exhibit a simpler design concept27.

Fig. 1
figure 1

Cross-sectional view of lithium-ion battery structure.

Full size image

The charging and discharging mechanism of lithium-ion batteries involves a cycle of embedding and de-embedding of lithium ions ( \(\textrm{Li}+\) ) in the positive and negative materials, which is accompanied by the storage and release of energy. Specifically, in the charging phase, lithium ions are liberated from the positive electrode material, travel through the electrolyte medium, capture electrons when they reach the negative electrode, and then embed themselves in the negative electrode material to form a complex with a higher energy state, as visualized in Fig. 2.

Fig. 2
figure 2

Electrochemical process in a lithium-ion battery.

Full size image

RUL refers to the number of charge-discharge cycles a battery is expected to withstand under a given charge-discharge pattern, starting from its current performance level until it fails to meet established requirements or reaches a predetermined failure threshold. In short, RUL predicts the remaining charge-discharge cycle life of a battery from the present moment to its failure, when it can no longer perform its intended function.

Typically, when the battery’s SOH drops to \(80 \%\), it is considered to be nearing failure. RUL prediction is the assessment of the remaining time until the battery reaches its failure state. The SOH calculated based on the capacity method is defined as follows:

$$\begin{aligned} \textrm{SOH}(t)=\frac{B C_{t}}{B C_{o}} \times 100 \% \end{aligned}$$
(1)

where \(B C_{t}\) is the current measured capacity of the lithium-ion battery, and \(B C_{0}\) is the initial capacity.

Based on this, we need to construct a model using existing historical data that can closely monitor any changes in the SOH of lithium-ion batteries and accurately predict their RUL.

Model architecture and algorithms

Convolutional neural network

The basic building blocks of a CNN28, including an input hierarchy as well as multiple successive convolutional and pooling layers, are designed in a framework specified in Fig. 3.

Fig. 3
figure 3

One-dimensional convolution process.

Full size image

The convolution layer performs convolution operations29 on the input data and the convolution kernel to extract potential features of the data. The specific operation of the convolutional layer is as follows:

$$\begin{aligned} Z_{j}=f\left( \sum A_{i} ^{*} W_{i}+b_{i}\right) \end{aligned}$$
(2)

where f is the activation function, W is the weight matrix, b is the bias matrix, * is the convolution operation.

The function of the pooling30,31 layer is to perform pooling on the output obtained from the convolutional layer. The formula is as follows:

$$\begin{aligned} d_{i}=\max \left( C_{1}, C_{2}, \cdots C_{m}\right) \end{aligned}$$
(3)

where \(d_{i}\) is the feature extracted by the convolutional layer, and m is the pooling width.

Bidirectional long short-term memory neural network

Incorporating three gates on the foundation of traditional RNNs, namely the forget gate and the input gate, LSTM32 demonstrates its structure as illustrated in Figure 4.

Fig. 4
figure 4

Structure diagram of LSTM unit.

Full size image

The input gate is responsible for filtering and determining which new information from the current time step should be incorporated into the unit state. This filtering operation is carried out based on the following mathematical formula:

$$\begin{aligned} i_{t}=\sigma \left( W_{i} \times \left[ h_{t-1}, X_{t}\right] +b_{i}\right) \end{aligned}$$
(4)
$$\begin{aligned} f_{t}=\sigma \left( W_{f} \times \left[ h_{t-1}, X_{t}\right] +b_{f}\right) \end{aligned}$$
(5)
$$\begin{aligned} o_{t}=\sigma \left( W_{o} \times \left[ h_{t-1}, X_{t}\right] +b_{o}\right) \end{aligned}$$
(6)
$$\begin{aligned} \tilde{C}_{t}=\tanh \left( W_{c} \times \left[ h_{t-1}, X_{t}\right] +b_{c}\right) \end{aligned}$$
(7)
$$\begin{aligned} C_{t}=f_{t} \times C_{t-1}+i_{t} \times \tilde{C}_{t} \end{aligned}$$
(8)
$$\begin{aligned} h_{t}=o_{t} \times \tanh \left( C_{t}\right) \end{aligned}$$
(9)

where W and b are the parameters of the LSTM cell, \(C_{t}\) is the current cell state, \(\tilde{C}_{t}\) is the new cell \(C_{t}\) state candidate value, \(f_{t}, i_{t}\) and \(o_{t}\) are the forget gate, input gate and output gate, respectively, expressed by the sigmoid function, its calculation is shown in Equations (4), (5) and (6). The activity of these gating mechanisms depends on the current input \(X_{t}\) and the previous output \(h_{t-1}\). A gate value of zero signifies blocked information transmission. Specifically, the forget gate \(f_{t}\) is responsible for deciding whether to inherit data from the prior state \(h_{t-1}\), updating the state \(h_{t-1}\) to the state \(C_{t}\) through Equation (8). Meanwhile, Equation (7) generates the potential state value \(C_{t}\), and Equation (9) calculates the current output \(h_{t}\) of the individual LSTM unit. Subsequently, \(C_{t}\) and \(h_{t}\) are sequentially transmitted to the following unit, repeating this cycle through the time series.

The BiLSTM structure is shown in Fig. 5, which consists of two LSTM networks in forward and backward directions, and can make bi-directional predictions using the backward and forward changes of the time series respectively33, making the prediction more global and holistic, and effectively improving the prediction accuracy of the battery SOH and RUL.

Fig. 5
figure 5

BiLSTM model structure.

Full size image
Fig. 6
figure 6

Schematic diagram of Attention mechanism.

Full size image

Attention mechanism

The Attention Mechanism34 is a key algorithmic model that mimics the human cognitive process by flexibly assigning different weights to multiple hidden states in a neural network. This allows the model to focus on the most relevant input features that contribute to the final prediction. The attention mechanism helps enhance the model’s ability to capture complex temporal relationships by selectively emphasizing certain parts of the input sequence over others. This intelligent screening process is illustrated in Fig. 6.

(1) At time t, the hidden state of the BiLSTM layer is obtain \(\left[ H_{t, 1}, H_{t, 2} \cdots H_{t, i}, \cdots H_{t, T}\right] ^{T}\).

(2) Calculate \(\alpha _{t}, i\), which is the Attention weight of the hidden layer state \(H_{i}\) to the current output at time t. This paper chooses the dot multiplication form to calculate the Attention weight, as shown in Equations (10) and (11).

(3) In our AT-CNN-BiLSTM model, the attention mechanism enhances the prediction accuracy by focusing on the most informative time steps of the battery degradation data. By assigning higher weights to crucial hidden states, the model is better equipped to capture both short-term fluctuations and long-term trends in the data, which is critical for accurate SOH and RUL predictions.

$$\begin{aligned} e_{t, i} =S_{t-1}^{T} \times H_{t, i} \end{aligned}$$
(10)
$$\begin{aligned} \alpha _{t, i} =\frac{\exp \left( e_{t, i}\right) }{\sum _{K=1}^{T} \exp \left( e_{t, k}\right) } \end{aligned}$$
(11)

CNN-BiLSTM-attention model

The integrated architecture of the CNN-BiLSTM-Attention neural network contains six key layers, and the specific details of its sophisticated design are clearly demonstrated in Fig. 7.

  1. (1)

    Input layer: In this research project, we record and deeply analyze the charging and discharging behaviors of Li-ion batteries over a specified time period. The measurements include current strength, voltage level, temperature fluctuation, and total battery capacity, which constitute the input data set for the model. For time series analysis, we set the size of the sliding window to T, ensuring that at any specified time point T, the data series received by the model can be explicitly expressed as:

    $$\begin{aligned} Z=\left[ A, A_{t 2}, \cdots , A_{t-T}, \cdots , A_{t}\right] ^{T} \end{aligned}$$
    (12)
    $$\begin{aligned} Z_{t}=\left[ B C_{t}, chI_{t}, chV_{t}, chT_{t}, disI_{t}, disV_{t}, disT_{t}\right] ^{T} \end{aligned}$$
    (13)

    where \(c h T_{t}\) is the average value of the charging temperature of the lithium-ion battery at the t-th cycle, \(chV_{t}\) is the average value of the charging voltage of the lithium-ion battery at the t-th cycle, chI \(I_{t}\) is the average value of the charging current of the lithium-ion battery at the t-th cycle, \(B C_{t}\) is the SOH data of the lithium-ion battery at the t-th cycle, dis \(_{t}\) is the average value of the discharging current of the lithium-ion battery at the t-th cycle, \(dis_{t}\) is the average value of the discharging voltage of the lithium-ion battery at the t-th cycle, and \(dis_{t}\) is the average value of the discharging temperature of the lithium-ion battery at the t-th cycle.

  2. (2)

    CNN convolutes the battery charge and discharge data in the convolution layer to extract features and output the depth feature sequence X .

  3. (3)

    BiLSTM uses forward and backward LSTM networks to calculate the deep feature sequence X . At cycle t, the sequence X is used to calculate the output state of the i-th input vector of the forward layer as \(\textbf{H}_{t, i}\), and the output state of the i-th input vector of the backward layer as \(\bar{H}_{t, i}\). The output of the BiLSTM layer at cycle t is \(\left[ H_{t, 1}, H_{t, 2}, \cdots H_{t, i} \cdots H_{t, T}\right] ^{T}, H_{t, i}\) contains the output of the forward layer \(\textbf{H}_{t, i}\) and the output of the backward layer \(\bar{H}_{t, i}\).

  4. (4)

    To enhance the flexibility and broad applicability of the CNN-BiLSTM-Attention model in dealing with unseen data, we added a Dropout layer35 to the network structure. The addition of Dropout can effectively solve the model overfitting problem.

  5. (5)

    The Attention mechanism receives its inputs from the hidden states \(H_{t}\) produced by the BiLSTM layer r , with the computation of the Attention weights \(\alpha _{t}\), i delineated by Equations (10) and (11). At each time step, the output from the Attention layer \(S_{t}\) is detailed in Equation (14).

    $$\begin{aligned} S_{t}=\alpha _{t, i} H_{t, i} \end{aligned}$$
    (14)

    In our study, the feature vectors highly correlated with the prediction results are highlighted by introducing an attention mechanism for differential weight allocation in the hidden layer of the CNN-BiLSTM model, comprehensively aggregating all relevant information in the time series. This approach not only significantly improves the accuracy of assessing the SOH of lithium-ion batteries but also ensures high confidence in the RUL prediction results.

Fig. 7
figure 7

CNN-BiLSTM-Attention.

Full size image

The dense layer outputs the estimated SOH value of a lithium-ion battery. Sigmoid is chosen as the activation function to output the predicted SOH value at time t, denoted as \(\textrm{SOH}_{t}\). The output layer calculation can be described as follows:

$$\begin{aligned} \textrm{SOH}_{t}={\text {sigmoid}}\left( w \mathrm {~S}_{t}+b\right) \end{aligned}$$
(15)

Experiment dataset

Lithium-ion battery dataset

In this work, the lithium-ion battery degradation monitoring dataset from the NASA Ames Prediction Center of Excellence are used to verify the validity and a ccuracy of our approach. In this paper, three lithium battery cells data, B0005 (B5), B0006 (B6) and B0007 (B7) are selected from the NASA dataset and their specific experimental dataset information is shown in Table 1. The capacity curves are shown in Figure 8.

Table 1 Information of experimental dataset.
Full size table
Fig. 8
figure 8

Curve of SOH decay for lithium-ion battery. According to the decommissioning standards for lithium-ion batteries, the SOH value of B7 batteries did not reach the failure threshold during the whole operation process.

Full size image

The charging and discharging process of NASA lithium-ion battery B5 is shown in Fig. 9.

Fig. 9
figure 9

The charge and discharge process of lithium-ion battery. (a) Charging temperature curve; (b) Charging voltage curve; (c) Charging current curve; (d) Discharging current curve; (e) Discharging temperature curve; (f) Discharging voltage curve.

Full size image

Compared with other methods, the complete charge-discharge cycle that combines constant-current charging and constant-voltage charging shows higher stability, which is conducive to the in-depth investigation of battery aging characteristics.

During the charging process, the B5 lithium-ion battery is charged with a constant current first, and then charged with a constant voltage, as shown in Fig. 9. Constant current charging process: the battery temperature first drops from about \(26^{\circ } \textrm{C}\), for a short time, then rises to \(29^{\circ } \textrm{C}\), and above; the voltage and current of the battery rise from 0 V to 4.2 V , from 0 A to 1.4 A , and then keep at 4.2 V .1 .4 A until the end of charging, as the number of cycles increases, the time for constant current charging of the battery is shortened. Constant voltage charging process: the battery temperature gradually drops to about \(24^{\circ } \textrm{C}\),; the battery voltage remains at 4.2 V until the end of the charge; the battery current remains at 1.4 A for a period of time, and then gradually drops to about 0 A .

The B5 lithium ion battery performs constant current discharge during the discharge process. Constant current discharge process: the battery current increases rapidly from 0 A to 2 A , then maintains for a period of time, and then drops to 0 A until the end of the discharge process; the battery temperature gradually increases from \(24^{\circ } \textrm{C}\) to above \(37^{\circ } \textrm{C}\), and then the battery temperature gradually decreases. Until the end of the discharge process; the battery voltage gradually drops from 4.2 V to about 2.6 V , and then gradually rises to the end of the discharge process. As the number of cycles increases, the constant current discharge time is shorter.

Evaluation criteria

In order to more intuitively characterize the performance of the proposed model and other models, the evaluation of RUL absolute error \(\left( \textrm{RUL}_{\textrm{ae}}\right)\), root mean square error (RMSE), mean absolute percentage error (MAPE) and r-square \(\left( R^{2}\right)\) are calculated as shown in Eqs. (16) to (19):

$$\begin{aligned} \text{ RUL } _{\textrm{ae}}=|\textrm{BLP}-\textrm{EOL}| \end{aligned}$$
(16)
$$\begin{aligned} \text{ RMSE } =\sqrt{\frac{1}{n} \sum _{i=1}^{n}\left( Q_{i}-\hat{Q}_{i}\right) ^{2}} \end{aligned}$$
(17)
$$\begin{aligned} \text{ MAPE } =\sum _{i=1}^{n}\left| \frac{\left( Q_{i}-\hat{Q}_{i}\right) }{Q_{i}}\right| \times \frac{100}{n} \end{aligned}$$
(18)
$$\begin{aligned} \textrm{R}^{2}=1-\frac{\sum _{i}^{i}\left( \hat{Q}_{i}-Q_{i}\right) ^{2}}{\sum _{i}\left( \bar{Q}_{i}-Q_{i}\right) ^{2}} \end{aligned}$$
(19)

In this context, \(Q_{i}\), \(\bar{Q}_{i}\) and \(\bar{Q}_{i}\) denote the actual, predicted, and average SOH values for lithium-ion batteries, respectively. The battery lifespan prediction (BLP) for lithium-ion batteries is defined as the number of charge and discharge cycles until the batteries reach a predefined failure threshold.

Experiment results and conclusion

CNN-BiLSTM-attention model forecasting procedure

The training process for the SOH estimation and RUL prediction model for lithium-ion batteries is shown in Fig. 10. Firstly, the charge and discharge data of the lithium-ion battery extracted and normalized, and the output is mapped to [0, 1]. The calculation of minimum and maximum normalization is shown in Equation (20).

Fig. 10
figure 10

Training workflow for the CNN-BiLSTM-Attention model.

Full size image
$$\begin{aligned} X^{*}=\frac{X-X_{\min }}{X_{\max }-X_{\min }} \end{aligned}$$
(20)

Secondly, initialize the weight and deviation of CNN-BiLSTM-Attention prediction model. The initialization of weights and weights will make the gradient of model algorithm more normal and easier to reach the global optimal solution.

Thirdly, through the forward and backward propagation of the model. Pass the input data forward until the output produces error, calculate the hidden layer partial derivative and loss of the model, update the weight and deviation of the model with the partial derivative calculated by back-propagation, and train the model until the end of the epoch.

Finally, the trained CNN-BiLSTM-Attention model predicts the test set data, outputs the SOH prediction curve of lithium-ion battery, and calculates the RUL of lithium-ion battery according to the fault threshold.

Model-based prediction experiment

We used pycharm software to compile battery SOH estimation and RUL prediction model. Intel(R) Core(TM) i5-6200U CPU @ 2.30 GHz is selected as the core processor. The version number of the keras framework is 2.3 .1 and the version number of tensorflow is 2.2.0.

To optimize our CNN-BiLSTM-Attention model, we adopted Adam as the optimizer with an initial learning rate set at 0.01 . The configuration of the model’s hyperparameters, such as the number of layers in the convolutional function’s filter Fn and the count of BiLSTM units Bu , was established after a thorough review of the literature36,37. Based on this review, Fn and Bu were variably set within the ranges of \(\{32,64,128\}\). This approach allowed us to experimentally determine the optimal hyperparameters, with the findings presented in Table 2.

Table 2 Hyperparameter Setup with B5 Dataset.
Full size table

When configured with \(\textrm{Fn}=64\) and \(\textrm{Bu}=64\), the model presents the best prediction performance, in which the value of MAPE is 0.5106 , the value of RMSE is 0.0060 , the value of \(R^{2}\) is 0.9959 , and the value of \(R^{2} L_{a e}\) is 0 . When the number of filters in the convolution layer and the number of BiLSTM units increase, the amount of network calculation increases, the network calculation time increases, and the network prediction ability decreases slightly.

In this paper, the charge and discharge data of B5, B6 and B7 lithium-ion batteries from NASA are selected as the experimental data. We compare different prediction models with prediction experiments of CNN-BiLSTM-Attention model. Table 3 presents the configurations of various predictive models. Detailed information on the SOH estimation and RUL prediction for lithium-ion batteries B5, B6, and B7 can be found in Table 4 and is illustrated in Figs. 11 and 12.

Table 3 B5 dataset-based hyperparameter configuration.
Full size table
Table 4 The predictive results of various models for the lithium-ion battery.
Full size table
Fig. 11
figure 11

The SOH estimation and RUL prediction results. (a) B5-SOH estimation; (b) B5-RUL prediction; (c) B6-SOH estimation; (d) B6-RUL prediction; (e) B7-SOH estimation; (f) B7-RUL prediction.

Full size image
Fig. 12
figure 12

Prediction metrics for the RUL of the lithium-ion battery. (a) The RULae results; (b) The RMSE results; (c) The MAPE results; (d) The Time results.

Full size image

In this section, we use the traditional method and the prediction accuracy of CNN-BiLSTM-Attention. This experiment selects CNN, a commonly used machine learning algorithm in regression problems, and LSTM, BiLSTM, and related hybrid neural networks commonly used in processing time series data in the field of deep learning as the baseline model. For CNN, LSTM, BiLSTM and related hybrid neural networks, the hyperparameters Fn and Bu are determined by grid search on \(\{32,64\), \(128\}\) and \(\{32,64,128\}\) respectively. Experiments have shown that when \(F n=64\) and \(\textrm{Bu}=64\) are Optimal parameter settings.

According to the experimental data presented in Table 4 and illustrated in Figs. 11 and 12, the discrepancy between the predicted and actual failure thresholds of the LSTM model ranges from one to two. The MAPE oscillates between 0.4667 and 1.0187, while the \(\textrm{R}^{2}\) values fluctuate from 0.9901 to 0.9947 . LSTM model has the ability of time series analysis, but its one-way analysis of input series has a relatively single ability of time series analysis.

BiLSTM model is improved on the basis of LSTM model. It uses two-way strategy to process data. Based on the analysis of three groups of experimental data, compared with LSTM model, the predicted index MAPE value of BiLSTM model is reduced by \(16.16 \%, 13.36 \%\) and \(10.69 \%\) respectively, and the value of RULae is 1 . BiLSTM can more accurately estimate the SOH change trend and RUL value than LSTM, and the prediction accuracy is higher, but the training prediction time of BiLSTM model is higher than that of LSTM model.

The CNN-LSTM and CNN-BiLSTM models incorporate a CNN while retaining the LSTM and BiLSTM structures, aiming to enhance the model’s effectiveness in capturing data features. Although these combined models do bring some improvement in RUL prediction accuracy and SOH curve matching in real prediction tasks, the enhancement is not at the desired level.

In order to improve the model’s ability to analyze effective information, the Attention mechanism is introduced in model training to increase the weight of important information. Compared with the CNN-LSTM-Attention model, the MAPE value of the CNN-BiLSTM-Attention model decreased by \(13.47 \%, 6.82 \%\), and \(13.52 \%\), respectively, the lowest \(\textrm{R}^{2}\) value is 0.9921 , and the RUL error value stabilized to 1 or 0 . This article analyzes the RUL of lithium-ion batteries from multi-dimensional data. LSTM has relatively simple timing analysis capabilities, and the addition of the Attention mechanism reduces the prediction accuracy.

Experimental tests with different models showed that although the CNN-BiLSTM-Attention model did not yield the best results in every experiment, it demonstrated higher prediction stability and accuracy when considering the integrated RUL error values and predictive index analysis. Notably, the CNN-BiLSTM-Attention model excels at capturing nuanced transitions in battery behavior during the regeneration phase, contributing to increased prediction accuracy. Despite the model’s complexity leading to longer training times, this trade-off is justified, as it exhibits superior stability and precision in predicting both early and late-stage capacity degradation as well as capacity regeneration.

Conclusions

This study introduces a sophisticated approach to estimate the SOH and predict the RUL of lithium-ion batteries, employing a model based on CNN, BiLSTM, and Attention mechanisms. This method aims to enhance the accuracy and reliability of existing RUL prediction techniques for lithium-ion batteries. The approach utilizes CNNs to delve into the intricate features of dataset, capitalizing on the unique properties of lithium-ion battery charge and discharge data. It incorporates a BiLSTM’s bidirectional approach to analyze temporal features of the input sequences, while the Attention mechanism prioritizes critical information during network training. Validation conducted on three NASA lithium-ion battery datasets reveals that the CNN-BiLSTM-Attention model achieves precise failure threshold predictions with minimal error. Furthermore, the predicted SOH curves align closely with the actual SOH curves, demonstrating a stable \(\textrm{R}^{2}\) value ranging between \(98.65 \%\) and \(99.65 \%\). This model significantly outperforms traditional prediction methodologies in terms of both accuracy and stability.

After that, we plan to mine more health factors related to the battery state of health to forecast the SOH trends. Considering the long training and prediction time of the CNN-BiLSTM-Attention model, we will try to use BiGRU instead of BiLSTM. Structurally, BiGRU has only two gates (update and reset), while BiLSTM has three gates (forget, input, and output). BiGRU directly transfers the hidden state to the next unit, while BiLSTM uses memory cells to encapsulate the hidden state. BiGRU has fewer parameters, so it is easier to converge.