Federated cross-view e-commerce recommendation based on feature rescaling

Abstract

As big data technologies continue to evolve, recommendation systems have found broad application in domains such as online retail and social networking platforms. However, centralized recommendation systems raise numerous data privacy concerns. Federated learning addresses these concerns by allowing model training on client devices and aggregating model parameters without sharing raw data. Nevertheless, federated learning faces critical challenges related to feature extraction efficiency and noise sensitivity, limiting its application in e-commerce recommendation systems where data heterogeneity and high-dimensional features are prevalent. To address these gaps, this paper introduces a novel multi-view federated learning framework, Fed-FR-MVD, designed to enhance feature extraction efficiency and improve recommendation accuracy in e-commerce applications. Fed-FR-MVD integrates a FR mechanism within a multi-view structure, incorporating both item and user perspectives to improve feature representation and robustness. This approach yields a 12%–18% increase in recommendation accuracy across various performance metrics compared to single-view and other multi-view methods. By addressing data heterogeneity and optimizing feature utilization through dynamic rescaling, Fed-FR-MVD effectively mitigates the impact of noisy data, with performance maintained across noise levels of 5%–15%. Experimental results demonstrate that Fed-FR-MVD fills a key research gap by providing a more resilient and efficient framework for federated recommendation systems in privacy-sensitive and data-diverse e-commerce environments.

Introduction

In the age of extensive data proliferation, the swift progress of machine learning has significantly propelled the development of recommendation systems across various internet sectors. These systems are extensively utilized in key business areas including online retail platforms, social media channels, virtual learning environments^1,2,3. However, as public awareness of data security grows, users are increasingly concerned about the risks of personal data breaches, leading to a marked decline in their willingness to share private data^4,5. This has made it difficult to effectively utilize the dispersed user data across multiple clients, posing significant challenges to conventional centralized approaches to machine learning regarding data privacy^6,7.

Federated learning, an emerging distributed machine learning approach, has garnered increasing attention in the field of data security and privacy. It enables the training of efficient artificial intelligent recommendation systems without sharing raw data by conducting local model training on client devices and aggregating model parameters on a central server^8,9,10. This approach is particularly suitable for privacy-sensitive recommendation systems. However, existing federated learning methods often struggle with issues such as data heterogeneity and high-dimensional feature representations, leading to inefficiencies and reduced accuracy in recommendation performance. Under increasingly stringent data privacy regulations, a critical challenge is how to protect user privacy during the interaction and sharing processes across various stages of model training and inference within a federated learning framework^11,12,13.

The federated collaborative filtering (FCF) method addresses this challenge by optimizing the model weights of the entire federated network through the aggregation of user feature gradient updates. This approach avoids the need for data interaction and sharing during model updates, further reducing the risk of privacy data breaches and is suitable for implicit feedback datasets, which can be generalized to various recommendation system scenarios. Despite its significant privacy protection advantages, FCF requires participation from all users in the federated learning process, which is not always feasible in practical applications. Moreover, FCF methods tend to be sensitive to noisy data, which can degrade recommendation performance. To address these limitations, the Fed-NewsRec method was proposed. It trains news recommendation models using user behavior data and applies local differential privacy techniques to protect private information during communication^14,15,16. However, this method is limited to news recommendation scenarios and lacks general applicability.

Feature rescaling, by dynamically adjusting the weights of feature channels, can enhance the model’s performance. It improves the expression of important features, reduces the impact of redundant features, and aids in improving the model’s learning efficiency^17,18. However, existing frameworks often overlook the dynamic assessment of feature importance, which can hinder their robustness against noisy data and diverse feature distributions. Thus, feature rescaling (FR) helps the model autonomously assess the significance of features from various views, enabling better fusion and utilization of multi-view information and enhancing feature expression capability^19,20,21. Additionally, reinforcing the weights of important feature channels helps increase the model’s robustness against noisy data or significant view differences, thereby maintaining stable performance in federated learning environments.

Simultaneously, the integration of diverse data perspectives in a federated learning settings presents new opportunities for recommendation systems^22,23. Federated multi-view recommendation can leverage data from different sources, such as user behavior, item features, and social relationships, to more accurately capture user preferences^24,25,26. However, handling the heterogeneity of multi-view data and high-dimensional feature representations remains a challenge^27,28. To tackle these issues, researchers have proposed the federated multi-view deep structured semantic model (FL-MV-DSSM)²⁹. This framework uses deep learning for feature extraction, capturing semantic features from complex multi-view data, and improves recommendation performance by sharing user sub-models^30,31. Incorporating deep structured semantic models into federated learning enhances the model’s representational capacity while also improves its proficiency in handling complex user behaviors and item features. In FL-MV-DSSM, multi-view data often originate from different feature spaces, making effective integration of these views crucial. Feature rescaling, by dynamically adjusting the weights of feature channels, can enhance the model’s performance^32,33. It improves the expression of important features, reduces the impact of redundant features, and aids in improving the model’s learning efficiency. Thus, feature rescaling helps the model in autonomously assessing the significance of features from various views, enabling better fusion and utilization of multi-view information and enhancing feature expression capability^34,35. Additionally, reinforcing the weights of important feature channels helps increase the model’s robustness against noisy data or significant view differences, thereby maintaining stable performance in federated learning environments^36,37,38.

Given the heterogeneity of item features in e-commerce recommendation systems, this paper establishes a novel multi-view federated learning framework. By employing feature rescaling, the framework further enhances the efficiency of feature extraction based on deep semantic feature extraction. This approach not only addresses the limitations of existing methods but also offers a substantial improvement in recommendation accuracy. In the subsequent sections, Section "A federated multi-view framework" reviews the basic framework of multi-view federated learning and introduces the multi-view paradigm based on item and user perspectives. Section "View module implementation" elaborates on the implementation of the view paradigms, while Section "Experiments" outlines the investigative process and analysis. The summary of findings is addressed in Section "Conclusion".

A federated multi-view framework

In this work, we propose a federated multi-view framework designed to build a global recommendation model by leveraging federated learning technology. The framework enables collaboration among several user devices and the multiple applications (i.e., views) installed on them, all while ensuring that user data remains local. The goal is to generate a personalized recommendation list for each user (Fig. 1).

Fig. 1

The basic structure of the federated multi-view framework. Each client utilizes a model to recommend products based on user and item views. The models in each client interact and update with the central server, and item data is shared with the central server.

Basic structure

The basic structure of the proposed approach includes several geographically distributed user clients at the edge of the network (Fig. 2). Each client C_i contains multiple application views, including at least the target recommendation view. Assume that for the recommender A, a specific view V_A exists on every user device C_i within the collection of user devices C.

Fig. 2

Basic structure of the federated multi-view framework. This framework illustrates the core architecture of the federated multi-view framework, showing how data is aggregated from multiple client views to a central server for training.

Over a given period, as users engage in interactions and provide feedback within any of the views, multi-view data is generated, including both item data and user data within the corresponding views. Item data typically refers to the content provided directly by the target recommender. Recommender A can supply each user device C_i with an item dataset I containing products such as:

Item dataset III

Product 1: “Wireless Headphones”.

Product 2: “Bluetooth Speaker”.

Product 3: “Smartwatch”.

For user data, recommender A can only obtain a limited user dataset D_Ai from view V_A on device C_i, and this data must remain on the local device C_i. Example User Data:

User dataset D _Ai (from view V _A)

User 1: [Product 1 (purchased), Product 2 (viewed)].

User 2: [Product 3 (purchased), Product 1 (viewed)].

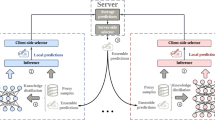
At the center of the network topology, a trusted main server S manages process scheduling and data distribution. Each user client C_i possesses a local recommendation model M_i tailored for the target recommender, which is typically downloaded from the central server. This model is trained locally using the item data provided by the target recommender and the user data generated within the local multi-view environment.

Assume another recommender B provides a view V_B on device C_i, generating a user dataset D_Bi that includes additional interactions. Example User Data from Recommender B:

User dataset D _Bi (from view V _B)

User 1: [Product 2 (viewed), Product 3 (added to cart)].

User 3: [Product 1 (purchased)].

Recommender A may attempt to leverage the user dataset D_Bi from recommender B for joint training. Each user device C_i trains the local model M_i using the local dataset (I, D_Ai, D_Bi).

The central server maintains continuous communication and synchronization with multiple user clients C, coordinating several rounds of federated learning. The goal is for all user clients C to ultimately obtain a shared global recommendation model M. This model allows each user client C_i to generate probability outputs and rankings for all items in the recommendation set I^∗, using the comprehensive model and its local multi-view data, thus recommending items that match the user’s preferences.

Multiple view module

The multiple view structure is composed of two parts: the user view and the item view (Fig. 3), each represented by an independent neural network (NN). While the item view is singular, the user view can consist of multiple user-specific views. The framework employs deep semantic representation to learn vector representations for both user data and item data, and recommendations are made by calculating the similarity between user vectors and item vectors.

Fig. 3

Schematic of multi-view model structure. This diagram illustrates the multi-view model structure used in the federated recommendation framework, which integrates diverse data views to enhance recommendation accuracy. The structure is composed of two main parts: a singular item view and a user view, which can consist of multiple user-specific sub-views. Each view is represented by an independent neural network (NN), allowing separate feature extraction for user data (U) across different perspectives and item data (I) from the target recommender. By leveraging deep semantic representation, the framework learns vector embeddings for both user and item data. Recommendations are generated by calculating the similarity between these vector representations, enabling personalized suggestions based on multi-view data inputs from distributed nodes (user clients C) across the network. This structure allows the model to capture richer information from multiple user-specific views, improving its capacity to represent user preferences accurately across varying contexts.

Considering only the inputs and outputs of the multi-view model, assume that any distributed node (i.e., user client C) has a local multi-view dataset D_n = {(I, U₁), (I, U₂), …, (I, U_n)}, here n represents the views participating count within the federated recommendation, I represents item data features from the target recommender, and U_i(i $\in[1,n]$) represents the user data features at the i-th view level.

Unlike traditional multi-view models where user view features are shared, in the proposed framework, item view features are shared instead. Thus, I serves as the input for the item single-view, while V_i serves as the input for the corresponding user single-view. Through the forward propagation process within each single view, the item single-view outputs an item vector y_I, while any user single-view outputs a user vector y_Ui. For any user vector y_Ui, a cosine similarity R(y_I, y_Ui)can be computed with the item vector y_I.

The local dataset in the i-th client is represented as D_i = {D_I, [D_u $\vert$ D_uj, j = 1, 2, …, N_u]}. Here, D_uj ∈ R^dj represents the multi-view feature data recorded by the user across N different apps, while the item view dataset D_I ∈ R^dI is downloaded from the server, such as the backend of a mobile app. The model extracts latent vectors from each app view dataset, user dataset D_u, and item dataset D_I. The algorithm’s objective is to learn a nonlinear mapping f(⋅) for each view, maximizing the sum of similarities between the item view latent vector and the multiple user view latent vectors.

To safeguard the confidential data contained within the gradients of every view, the Federated Learning multi-view deep semantic similarity model (FL-MV-DSSM) employs differential privacy. Specifically, we introduce Gaussian noise to the item sub-model gradients calculated for each view. This noise effectively protects the confidentiality of the data within each view, preventing potential inference of users’ private information through gradient analysis. After local aggregation, the client encrypts the aforementioned item sub-model gradients along with the gradients from the user sub-models before transmitting them to the server. This encryption mechanism ensures that the gradients exchanged between the client and server do not leak any sensitive user information. Furthermore, the combination of encryption and noise addition significantly mitigates potential privacy risks, allowing the model to maintain user privacy while effectively performing model training and updates.

View module implementation

Building on the illustration in Fig. 3, this section further explains the internal components and construction approach of any single view within the multi-view model. In a single view model, item data and user data first arrive at the feature input layer. The feature input layer performs feature embedding and feature concatenation. High-dimensional and sparse original features are embedded to create low-dimensional, dense feature vectors. The embedded feature vectors from different feature domains are subsequently combined to create the multi-dimensional vector x for the single view model. This feature vector x is subsequently fed into a deep neural network (DNN).

Next, the multi-dimensional feature vector x enters a feature rescaling module, which performs compression, activation, and rescaling operations. This module dynamically learns the importance weights of each feature and applies weighted calculations to the input feature vector x. The feature vector x then advances within the DNN module, undergoing the forward pass phase. Finally, the last fully connected layer of the network outputs the aforementioned item vector or user vector y. These vectors reside in the same vector space and are subsequently used for further calculations, such as inner product or cosine similarity, outside the network.

Feature resacling

Feature rescaling is not a complete network structure in itself but is implemented as a Squeeze-and-Excitation Network (SENet) block. This module can be embedded into any model as a fundamental component to enhance its performance. The motivation behind this network is to explicitly model the interdependencies between feature channels, thereby correcting and rescaling features to improve the representational power of the NN. In other words, the data fed into the feature channels contains a variety of features, ranging from strong and weak to even noisy features. This network aims to dynamically learn the importance of each feature channel, strengthening significant features, suppressing irrelevant ones, and filtering out noisy features.

The Squeeze-and-Excitation module includes three core operations: compression, excitation, and rescaling (Fig. 4). Assume that the size of x is H × W × C, with H, W, and C denoting the height, width, and channel count of the input feature, respectively. The compression operation reduces the spatial dimensions from H × W × C to 1 × 1 × C, transforming each two-dimensional feature channel x_c into a one-dimensional scalar z_c. At this point, the output feature dimension matches the input channel count, meaning that this scalar captures a global view of the feature channel’s response distribution. In practice, global average pooling (or alternatively, max pooling or other strategies) is commonly applied to each feature channel, encoding it as a global feature z:

$$z_{c} = F_{{\text{squeeze }}} \left( {x_{c} } \right) = \frac{1}{H \times W}\sum\limits_{i = 1}^{H} {\sum\limits_{j = 1}^{W} {x_{c} } } (i,j),z \in R^{C}.$$

(1)

Fig. 4

Schematic of feature rescaling by squeeze-and-excitation module. This diagram illustrates the Squeeze-and-Excitation (SE) module’s process for enhancing model performance through feature rescaling, which involves three core operations: compression, excitation, and rescaling. The SE module first performs compression by reducing the spatial dimensions of the input feature map x from H × W × C. This compression step transforms each feature channel x_c into a one-dimensional scalar z_c, capturing a global view of the feature channel’s response distribution. Global average pooling is commonly used for this operation, encoding each feature channel as a global feature z. In the excitation step, these global features are further processed to dynamically recalibrate the weights of each channel, adjusting feature importance based on the learned attention. Finally, the rescaling operation applies these recalibrated weights to the original feature channels, effectively enhancing or suppressing specific features. This rescaling mechanism allows the model to focus on the most relevant features, thereby improving its ability to capture critical patterns in the data.

The excitation process aims to explicitly identify the relationships between different feature channels, similar to the gating mechanisms in recurrent neural networks. Specifically, the excitation operation uses two fully connected layers to learn the weights W for each feature channel. These two layers sequentially employ ReLU and Sigmoid as activation functions:

$$s = F_{{\text{excitation }}} (z,W) = \sigma (\delta (z,W)) = \sigma \left( {W_{2} \delta \left( {W_{1} z} \right)} \right) ,$$

(2)

where W₁ ∈ R^C/r×C and W₂ ∈ R^C×C/r. The initial layer predicts the importance assigned to each feature channel, and through dimensionality reduction and subsequent upscaling by the second layer, the model’s complexity is reduced while its generalization ability is enhanced. Finally, the rescaling operation multiplies the original input feature x by the feature weight vector s across all channels to produce the new feature representation $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x}_{c}$:

$$\user2{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} }_{c} = F_{scale} ({\varvec{x}}_{c} ,{\varvec{s}}_{c} ) = {\varvec{x}}_{c} \cdot {\varvec{s}}_{c} .$$

(3)

At this stage, significant features in the feature vector $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x}_{c}$ become more distinguishable, while ineffective or noisy features are suppressed, approaching zero. The basic idea of SENet is similar to the attention mechanism, where features are dynamically amplified or attenuated based on their importance. Although feature rescaling originated in the context of image convolution processing in computer vision, it can be naturally applied to recommendation systems, helping to identify relatively important features from vast and sparse feature inputs.

Specifically, the compression operation calculates the mean z_i for a given k-dimensional feature x_i, resulting in an mmm-dimensional compressed vector z. The excitation operation introduces a two-layer fully connected network acting on the compressed vector z to perform feature interaction, mapping, and activation, yielding an excitation vector s that contains mmm values representing the importance weights s_i of each feature. The rescaling operation then multiplies the excitation vector s by the input feature x, thereby completing the importance-weighted transformation of x.

Deep semantic matching

The deep semantic matching model, composed of multi-view DNNs for cross-domain data modeling, is structured in three primary stages: the input stage, the representation stage, the matching stage (Fig. 5). It leverages the DSSM to maximize the latent vectors of user views as well as multiple item views, recommending items based on their similarity rankings.

Fig. 5

Schematic of the DSSM for multi-view data modeling. This diagram illustrates the architecture of the DSSM, which integrates multi-view deep neural networks (DNNs) to handle multi-view data in recommendation tasks. The model is structured in three main stages: the input stage, where multiple user and item views are ingested; the representation stage, where deep neural networks process and transform each view into latent semantic vectors; and the matching stage, where the DSSM aligns and matches these vectors based on similarity metrics to generate recommendations. By maximizing the semantic alignment between user views and item views, the model ranks items by similarity, thus enabling more accurate and contextually relevant recommendations. This structure allows the model to capture complex, high-level semantic relationships across different views, enhancing its effectiveness in multi-view and cross-domain recommendation scenarios.

Before inputting the data, a set of paired item and user data (D_I, D_Ui(i = 1,…, N_u)) must be extracted. The input layer converts the item data I and user data D_Ui into feature vectors suitable for the model. The representation layer, essentially a deep neural network with multiple fully connected layers, can be described by the following forward propagation process:

$$l_{1} = {\varvec{W}}_{1} {\varvec{x}},$$

(4)

$$l_{i} = f\left( {{\varvec{W}}_{i} l_{i - 1} + b_{i} } \right),i = 2, \ldots ,N - 1 ,$$

(5)

$${\varvec{y}} = f\left( {{\varvec{W}}_{N} l_{N - 1} + b_{N} } \right) ,$$

(6)

here x represents original feature vectors of item data D_I and user data D_Ui, y denotes the semantic vector, and l_i, W_i, and b_i represent the i-th hidden layer, weight matrix, and bias term, respectively.

The input layer feeds the item and user data into their respective multi-layer neural networks M_I and M_Di, which share the same structure. This process projects the high-dimensional sparse features {x_I, x_Ui (i = 1,…, N_u)} corresponding to the item data D_I and user data D_U into a shared lower-dimensional vector space. The result is low-dimensional dense features {y_I, y_Ui (i = 1, …, N_u)} in the shared latent space, giving rise to their respective semantic embeddings E_I and E_U.

The matching layer calculates the semantic similarity of the item feature vector y_I and the user feature vector y_Ui by computing their spatial distance, using cosine similarity as the metric:

$${\text{cosine}}(y_{U} ,y_{j} ) = \frac{{y_{U} y_{j} }}{{\left\| {y_{U} } \right\| \cdot \left\| {y_{j} } \right\|}} ,$$

(7)

where y_I and y_U are the semantic vectors output by the DNN for items and users, respectively.

Assuming a positive correlation between the item latent vector y_I and the user latent vectors y_Uj(j = 1, 2, …, N_u), the objective involves discover a nonlinear mapping f(⋅) for each view. This mapping maximizes the sum of the relationship between the item view V_I and the other user views V_Uj (j = 1, 2, …, N_u) in the latent space. The DSSM parameters, specifically the weight matrix W, are optimized by maximizing the conditional likelihood. Given the posterior probability of a match:

$$p = \arg \mathop {\max }\limits_{{W_{I} ,W_{U1} , \ldots W_{{UN_{u} }} }} \mathop \sum \limits_{i = 1}^{{N_{p} }} \frac{{e^{{\gamma \cos \left( {y_{i,I} ,y_{i,Ua} } \right)}} }}{{\mathop \sum \nolimits_{{x_{j} \in {\mathbb{R}}^{{d_{j} }} }} e^{{\gamma \cos \left( {y_{i,I} ,f_{j} \left( {x_{j} ,W_{j} } \right)} \right)}} }} ,$$

(8)

where W_I, W_Uj, (j = 1, 2, …, N_u) are the weight parameters corresponding to each view, N_p represents the count of user-item pair samples, and N_u means the user views count, with each user view x_j (V_j) having its own input feature dimension d_j. The i-th user-item pair sample has user view features x_i,a and corresponding item view input features x_i,I. Here, U_a indicates the index of the user view corresponding to sample i, while the input x_i,j≠a for other item views is set to a zero vector. The vector y represents the output of the nonlinear mapping f(⋅) for any single view’s input features, and the matrix W represents the learned parameter weights for any single view. γ is the temperature parameter in the softmax function.

Thus, the learning objective of the multi-view model for a local multi-view dataset D is to find a nonlinear mapping f(⋅) for any given view, maximizing the sum of the correlation scores between the item dataset D_I and all user view datasets D_U in a shared semantic vector space across each user client.

Training

During the model training process, the loss function that needs to be minimized is derived based on maximum likelihood estimation:

$$L(\Lambda ) = - \log \prod\limits_{{\left( {Q,D^{ + } } \right)}} {\mathbb{P}} \left( {D^{ + } |Q} \right),$$

(9)

here Λ represents all NN parameters. Ultimately, items with high matching scores should be displayed prominently or prioritized for recommendation.

First, it is assumed that the M clients participating in the multi-view federated recommendation training each possess a local user-level feature dataset V = {V₁, V₂, …, V_N} composed of N views D_U = {D_U1, D_U2, …, D_UNu}, and that the item dataset I has been distributed by the target recommender via a central server S to each client, and is shared across the N views. Specifically, it is assumed that any federated client C_i is an existing user, meaning that the deep model M_i of C_i has accumulated a certain amount of user and interaction data within the target recommendation view V_i as well as other views V_j. Additionally, client C_i and the views V have completed multi-view feature engineering, resulting in the extraction of features for items, users, and interactions, thereby forming a local multi-view dataset to support the training algorithm. Figure 3 illustrates the training algorithm for the federated multi-view framework, and the corresponding pseudocode is presented in Algorithm 1.

In the feature extraction phase, we first collect user data from various sources, including behavioral data (such as clicks, browsing history, and purchase history), user-generated content (like comments and ratings), and basic demographic information (such as age, gender, and geographic location). Based on these data sources, we employ multiple methods to extract features. Behavioral features include calculating user engagement metrics, such as average daily visits, purchase frequency, and time spent browsing. Historical preference features are derived from users’ past purchase records and ratings, capturing their preferences for different product categories and brands. Additionally, we incorporate social network information (such as friend recommendations and social interactions) to generate socially relevant features. Lastly, considering the timeliness of e-commerce, we extract time-related features, such as seasonality and behavioral changes during promotional periods.

In the feature selection phase, we utilize methods like feature importance analysis and correlation analysis to identify features that significantly impact model performance. We employ feature importance scores based on random forests and calculate the correlation between features to eliminate redundancies, ensuring the model’s simplicity and interpretability. Additionally, we implement recursive feature elimination (RFE) to gradually remove features that contribute less to model performance, optimizing the feature set.

During the feature processing phase, we undertake steps including data cleaning, normalization, standardization, and feature encoding. Missing values are handled using techniques such as interpolation or deletion, while outliers are detected based on the interquartile range (IQR) to ensure data quality. For numerical features, we apply normalization (Min–Max Scaling) or standardization (Z-score Normalization) to enhance model convergence speed and performance. Categorical features are encoded using one-hot encoding and label encoding, allowing the model to effectively process these features.

Moreover, to protect the sensitive information contained within the gradients of each view, it is assumed that any federated client model M_i has implemented view isolation and data access restrictions according to a multi-view security policy, meaning that view V_i can only access and operate on its own view data D_Ui and model parameters W_Ui.

The proposed framework employs privacy-enhancing technology to introduce gradients perturbations of the item sub-model calculated by execution environment using trusted execution technologies and other privacy-preserving computing techniques. Continuing with the explanation of Algorithm 1, in each global round of multi-view federated recommendation training, the central server arbitrarily chooses a certain quantity of federated participants from the pool of user devices to participate during the training phase. Each collaborative participant, utilizing the multi-view model, uses the private user data D_Ui corresponding the i-th perspective and shared item data D_I from multiple views as input to perform a limited number of local iterations. During this process, the gradients values for the user’s view representation W_Ui and the item’s view representation W_I are computed and the corresponding models are updated.

After a perturbation operation, the individual sub-model weights from the federated clients are uploaded to the main center to facilitate global aggregation (weighted averaging). The aggregated sub-model parameters are then broadcasted to all user devices to initiate the subsequent iteration of federated learning. The procedure continues until either the global weights achieves convergence or the predetermined threshold of training iterations arrived.

Before sending gradients to the server, each client first aggregates the gradients of the item sub-models calculated across multiple views. Since theN_u user views share the same item features, a total of N_u item sub-model gradients are computed. Considering the inherent complexity of the horizontal federated environment, parameter averaging is adopted instead of gradient averaging for aggregation. Compared to gradient averaging, parameter averaging is not constrained by specific optimization algorithms, tolerates missing updates, and can achieve equivalent convergence while maintaining relatively frequent synchronization.

Given that each federated client needs to perform K rounds of local model training across N views and the central server completes T rounds of global model updates, the time complexity of the algorithm is O(TKN), and the space complexity is O(N).

Algorithm 1

Training algorithm for federated multi-view framework

Client-side inference

First, we assume that the training process for the multi-view federated recommendation, has been successfully completed. The participating federated clients have obtained the global user view model W_Ui and the item view model W_I, which have been deployed locally on their devices. Thus, any client can use these global models to generate prediction results locally, based on multi-view user features and the features of items to be recommended (Algorithm 2).

The dataset of items to be recommended I^∗ can be provided directly by the target recommendation view or forwarded through the central server. All feature samples are mapped into multiple item vectors y_Ij through forward propagation in the item view model W_I. Similarly, the user vector y_Ui for the i-th view V_i is calculated through the corresponding user view model W_Ui, along with the likelihood P_ji of interaction between this user vector y_Ij and the j-th item vector y_Ij.

Subsequently, the posterior probabilities P_ji of each view interacting with the j-th item are aggregated and averaged, resulting in the mean probability P_j of potential interaction between the j-th item and the user. Finally, the items are ranked in decreasing order according to their interaction probabilities P_j, with the K items with the highest probabilities get listed as the suggested options. This completes the task of item retrieval and initial ranking locally on the federated client.

Since the M items need to have their probabilities computed across N views on the user client, resulting in N posterior probability values and M interaction probability values, the time complexity of this algorithm is O(MN), and the space complexity is O(M + N).

Algorithm 2

Client inference for federated Multi-View Framework

Experiments

Data and compared methods

To precisely evaluate the how the suggested federated learning approach performs, we utilized the Amazon e-commerce recommendation dataset to test the training and inference results of the entire framework^39,40. We then conducted a comparative analysis with other approaches.

Data

The dataset used in our experiments is structured exclusively as tabular data. We opted for this format due to the nature of e-commerce recommendation tasks, which primarily rely on user-product interactions and detailed product attributes to provide accurate recommendations. Tabular data effectively represents these interactions and allows for efficient processing and comparison in a federated learning environment.

Currently, this study does not involve other data modalities such as graph data or time-series data. However, we recognize that other modalities could further enrich recommendation models. For instance, graph data could capture social networks and relationships between users, while time-series data could analyze patterns in user behavior over time. Exploring the integration of these data modalities in a federated learning framework remains an intriguing avenue for future research, potentially enhancing the robustness and generalization of recommendation models.

This approach ensures that the generated views (V1 and V2) retain relevant user and product information, allowing us to effectively evaluate the model’s performance in a federated multi-view context without the complexity of handling mixed data modalities.

Methods

We considered eight other recommendation models to compare against the proposed Fed-FR-MVD to analyze the local and general recommendation effectiveness of our approach. These models range from traditional centralized training to various federated learning variants, including methods based on matrix factorization, deep semantic matching, and cross-domain recommendation. Each of the eight methods has its unique advantages, such as user privacy protection, reduced communication overhead, and adaptability to data heterogeneity. A comprehensive comparison with these methods helps thoroughly evaluate the performances of the suggested Fed-FR-MVD approach in proposition systems, highlights the model’s advantages to other approaches.

The comparison methods are as follows: (1) Centralized single-view (T-SV) method uses single-view datasets (either V₁ or V₂) for centralized training, resulting in the T-SV (V₁) and T-SV (V₂) models. We chose T-SV as a primary baseline because it represents the performance upper bound achieved under centralized training conditions, where all data is accessible without the privacy restrictions inherent to federated learning. This provides a clear reference point for evaluating the potential performance loss in federated learning methods. (2) Federated multi-view matrix factorization (FED-MVMF) enhances the efficiency of the FCF by updating with a multi-view matrix factorization algorithm²². (3) FL-MV-DSSM method improves feature extraction using a deep semantic matching model, thereby enhancing the model’s generalization ability. (4) SEMI-FL-MV-DSM method is built on FL-MV-DSSM by only aggregating the item sub-model gradients while not aggregating the user sub-model gradients, further improving the computational efficiency of FL-MV-DSSM. (5) Federated single-view (Fed-SV) method uses single-view datasets (either V₁ or V₂) for federated training, resulting in the Fed-SV (V₁) and Fed-SV (V₂) models. (6) The proposed Fed-FR-MVD method introduces a compressed incentive network to reduce information loss, further enhancing the model’s feature extraction capabilities. (7) The FedCT method adopts decentralized user encoding models and a variational autoencoder (VAE) to generate shared user encoding latent vectors⁴¹. (8) The FedCDR method maintains personalized user models on each client and only uploads item model and view transfer model parameters during aggregation, effectively reducing privacy risks²⁵.

In addition to T-SV, we include several federated learning methods as dynamic benchmarks for comparison. These methods, including FED-MVMF, FL-MV-DSSM, SEMI-FL-MV-DSM, FedCT, and FedCDR, are commonly used in federated learning-based recommendation systems. By comparing the performance of Fed-FR-MVD with these established federated learning models over multiple training epochs, we can comprehensively evaluate the effectiveness of our approach in handling multi-view data and noise conditions.

Evaluation

To fully understand the performance of Fed-FR-MVD, we included metrics such as prediction accuracy and model convergence speed in our comparison with the aforementioned methods. These metrics were chosen to access the performance and adaptability within a federated approach environment. For the experiments, we use item data D_I and user features from views V₁ and V₂ to train the models. For centralized training, the corresponding dataset is used in its entirety without partitioning, and the training is completed after 300 rounds. For federated training, as described in Fig. 2, the dataset is pre-partitioned and distributed, and in each round of federated training, 100 virtual machines (i.e., users) are chosen at random to take part in the learning process, with stopping after 300 rounds. Regardless of whether centralized or federated training is used, the data is partitioned in a stochastic manner into training and test subsets, with 80% allocated for training and 20% for testing.

To comprehensively evaluate the performance provided by the recommendation models, we employ multiple metrics. Alongside standard measures such as precision, recall, F1 score, and AUC, we additionally consider the following:

Hit Ratio (HR): Quantifies the proportion of items within the suggested directory that the user is actually interested in. This is determined by:

$${\text{HR}} = \frac{1}{N}\sum\limits_{i = 1}^{N} {{\text{hits}}} (i)$$

(10)

where N denotes the overall count of users, hits(i) indicates if the item of interest to i-th user is within the recommendation directory.

Normalized discounted cumulative gain (NDCG): Assesses the effectiveness of the recommendation list’s ranking by taking into account the order of items within the list. NDCG is calculated by first determining discounted cumulative gain (DCG) as:

$${\text{DCG}} = \sum\limits_{i = 1}^{N} {\frac{{2^{{{\text{rel}}_{i} }} - 1}}{{\log_{2} (i + 1)}}}$$

(11)

here rel_i represents the relevant score of the i-th item (typically 0 or 1), and N is the number of items in the suggested directory. NDCG is then calculated by DCG/ ideal DCG.

Mean Reciprocal Rank (MRR): Quantifies the mean inverse position of the earliest pertinent item in the suggested directory. This is determined by:

$${\text{MRR}} = \frac{1}{N}\sum\limits_{i = 1}^{N} {\frac{1}{{p_{i} }}}$$

(12)

here p_i is the item rank of interest for i-th user within the suggested sequence; whether the item is absent from the sequence, p_i → ∞.

Coverage Assesses the ratio of items that successfully recommended by the recommendation system relative to the total number of items. This is determined by:

$${\text{Coverage}} = \frac{{\bigcup\nolimits_{u \in U} {R_{u} } }}{{|{\varvec{I}}|}}$$

(13)

where U is the set of users, R_u is the recommendation list, and I denotes the complete collection of items.

These metrics allow us to thoroughly evaluate the recommendation models’ performance from various angles, including accuracy, recall capability, ranking quality, and coverage. Depending on specific needs, we can choose appropriate evaluation metrics to assess and compare different recommendation models. In addition, except for the AUC metric, we focus on Top-10 evaluations for the other metrics, with a particular emphasis on local and top-ranked recommendation results (Table 1).

Table 1 Performance evaluation of recommendation approaches constructed with the Fed-FR-MVD framework compared to other methods.

The comparison between Fed-FR-MVD and T-SV/Fed-SV highlights the differences between single-view and multi-view approaches. For instance, Fed-FR-MVD achieves an NDCG@10 of 0.615, significantly higher than T-SV (V₁) at 0.610 and Fed-SV (V₁) at 0.585. This result emphasizes that Fed-FR-MVD’s integration of multi-view data provides more comprehensive information, leading to an improvement in recommendation performance, even under federated learning constraints. By contrasting with both T-SV and other federated benchmarks, we aim to showcase Fed-FR-MVD’s robustness in noisy, multi-view scenarios.

It is also noteworthy that different federated learning strategies, particularly full gradient aggregation versus partial gradient aggregation, can impact both performance and privacy. The proposed Fed-FR-MVD and FL-MV-DSSM, both of which use full gradient aggregation strategies, achieved Precision@10 scores of 0.47 and 0.45, respectively, higher than the 0.445 achieved by SEMI-FL-MV-DSM, which employs a partial gradient aggregation strategy. While SEMI-FL-MV-DSM has advantages in privacy protection, its accuracy is slightly lower due to not aggregating the full gradients of the user sub-models. This trade-off indicates that when choosing a federated learning strategy, it is crucial to balance the need for privacy protection with the goal of enhancing performance.

The evaluation indicators for various comparison models, including convergence trends with training iterations, are shown in Fig. 6. Centralized methods like T-SV provide a baseline for comparison, while federated training methods such as Fed-SV and Fed-FR-MVD demonstrate different convergence trends. Fed-SV (V₁) and Fed-SV (V₂) exhibit faster initial convergence across most metrics, but their final stability and convergence values, particularly in terms of Recall and NDCG, are lower. In contrast, Fed-FR-MVD shows a significantly superior performance in the later stages.

Fig. 6

Performance comparison of recommendation models built with the Fed-FR-MVD framework alongside centralized and federated methods. This figure aims to illustrate the varying convergence trends and final performance metrics of different models over training iterations, highlighting the strengths of the Fed-FR-MVD approach in achieving superior stability and effectiveness in Recall and NDCG, especially in later training stages, compared to the faster initial convergence of other federated methods like Fed-SV. The results underscore the potential advantages of adopting the Fed-FR-MVD framework for improved recommendation performance in federated learning contexts.

Compared to traditional matrix-based methods like FED-MVMF, the improvements brought by deep learning techniques in feature extraction are clearly evident. Starting with the FL-MV-DSSM and Fed-FR-MVD, metrics such as Precision@10 and NDCG@10 reflect the superior ability of deep learning to capture and process complex features. The proposed Fed-FR-MVD further demonstrates advantages in this area.

However, the observed performance levels of the Fed-FR-MVD model can be partly attributed to the unique challenges faced by e-commerce recommendation systems. Unlike content platforms, where user needs and content consumption patterns are relatively stable and easily tracked online, e-commerce presents complexities in understanding user demand, which is often generated offline and is difficult to quantify. Additionally, the shopping context limits the ability to continually recommend similar items once a purchase has been made, thus challenging the system’s capacity to stimulate and expand user demand. These factors contribute to the lower performance metrics observed for federated methods like Fed-FR-MVD.

Furthermore, compared to single-view data methods (T-SV and Fed-SV), multi-view data methods (Fed-MVMF, FL-MV-DSSM, and Fed-FR-MVD) perform better in metrics like HR and NDCG, underscoring the effectiveness of multi-view integration in enhancing overall model performance. Regarding different federated learning strategies, FL-MV-DSSM and Fed-FR-MVD generally provide more stable results in metrics such as MRR and NDCG compared to SEMI-FL-MV-DSSM, which aggregates only partial gradient information. This emphasizes the importance of gradient aggregation in maintaining performance consistency.

Hyperparameter sensitivity analysis

In this section, we conduct a sensitivity analysis of the hyperparameters used in a multi-view e-commerce recommendation scenario involving hundreds of thousands of samples and two distinct views of data. We will analyze the impact of four primary hyperparameters on the effectiveness of Feature Rescaling (FR) and the performance of the Federated Learning (Fed)-FR-Multi-view Model (MVD) during training and prediction: Kernel Size, Stride, Dilation, and Expansion Factor. The detailed performance metrics for various hyperparameter settings are summarized in Table 2.

Table 2 Performance metrics under various hyperparameter configurations for Fed-FR-Multi-view model.

The kernel size determines the area over which features are extracted from the input data. Smaller kernels (e.g., 3 × 3) are suitable for capturing local features, retaining more detail, while larger kernels (e.g., 5 × 5 or 7 × 7) can integrate broader contextual information. In our analysis, the performance metrics indicate that an 11 × 11 kernel size yielded the best results across all evaluation metrics. This size is particularly effective in capturing the complexity of user behavior and product characteristics, which are crucial for high-quality recommendations.

Stride controls the step length of the convolution operation as it slides across the input data. Smaller strides (e.g., 1) generate denser feature maps that preserve more detail, while larger strides (e.g., 2 or 3) can reduce the size of the feature maps and enhance computational efficiency but may result in the loss of critical information. In our experiments, a stride of 1 consistently outperformed larger strides, emphasizing its importance for maintaining detail in user preferences and improving recommendation accuracy.

The dilation factor is used to control the receptive field of the convolution kernel, determining the spacing between elements within the kernel. Moderate dilation can help the model capture a wider range of contextual information, which is particularly important for recommendation systems. Our findings revealed that a dilation of 1 provided superior results across most metrics, indicating that it allows the model to adequately balance complexity and performance without incurring excessive computational costs.

The expansion factor increases the width of the network, enhancing the model’s expressive power. In our analysis, using an expansion factor of 4 demonstrated strong performance across various metrics, particularly in effectively handling the complexity of e-commerce data. This suggests that an adequately expanded network structure can significantly enhance feature learning capabilities, thereby improving recommendation quality.

After conducting the sensitivity analysis and reviewing the performance metrics summarized in Table 1, we conclude that the optimal hyperparameter combination is an 11 × 11 kernel size, a stride of 1, a dilation factor of 1, and an expansion factor of 4. This combination not only achieves the best performance metrics but also accommodates the complexity and diversity inherent in e-commerce recommendation systems. Therefore, we recommend using this parameter configuration in Federated Learning-FR-MVD training and prediction. By carefully setting these hyperparameters, we can enhance the model’s performance and provide users with more accurate and personalized recommendations.

Analysis of noisy feature handling

In multi-view joint recommendation scenarios, noise features may be introduced due to poor data quality or insufficient domain knowledge. To further evaluate the impact of Feature Rescaling (FR) within the Fed-FR-MVD framework, we conducted a comparative analysis under conditions with and without FR, specifically to examine the noise resistance and stability FR provides. Different levels of random noise were introduced into the user features U_V1 and U_V2. The noise levels were set to 5%, 10%, and 15%, with each noise feature being a Gaussian random number to ensure that the noise features were independent of the user features and target predictions.

Feature Rescaling (FR) Comparison: To directly assess the effects of FR, we compared the Fed-FR-MVD framework’s performance with and without FR under different noise levels. If the Fed-FR-MVD framework has inherent noise resistance, the addition of noisy features should not significantly degrade prediction accuracy. For cases without Feature Rescaling (Removing Feature Rescaling, RFR), we introduced noisy features to evaluate the framework’s resilience, noting that FR should ideally contribute to noise suppression. The single-view models within the Fed-FR-MVD framework are constructed using a combination of a compressed incentive network and DNNs. To evaluate the influence on the compressed incentive network in suppressing noise, an ablation experiment is also conducted. In this experiment, the compressed incentive network structures in both the user and item views are removed, following the aforementioned noise introduction, to evaluate their contribution to the framework’s noise resistance.

For these experiments, the original dataset was divided into training and testing subsets using an 80:20 proportion and duplicated. Noise features were added to one copy of the dataset as described, while the original multi-view model was also duplicated, with the compressed incentive network modules removed from the single-view structures in one version. Global training was carried out for 300 rounds, with 100 virtual machines randomly selected for federated training in each round.

In the absence of noise, the Fed-FR-MVD framework demonstrated strong performance across all metrics (Table 3), with Precision@10, Recall@10, HR@10, NDCG@10, F1-Score@10, MRR@10, Coverage@10, and AUC@10 reaching 0.460, 0.365, 0.555, 0.605, 0.410, 0.460, 0.750, and 0.800, respectively.

Table 3 Performance assessment of recommendation approaches constructed with the Fed-FR-MVD framework in the absence of noise and under varying noise levels with and without FR.

As noise levels increased from 5 to 15%, there was a slight decline in performance across the board, but the overall effectiveness of the model remained high. For instance, with a 15% noise level, Precision@10, Recall@10, HR@10, NDCG@10, F1-Score@10, MRR@10, Coverage@10, and AUC@10 decreased to 0.430, 0.335, 0.525, 0.575, 0.380, 0.430, 0.720, and 0.770, respectively. This indicates that Fed-FR-MVD has a certain degree of noise suppression capability and can effectively mitigate the influence of noise on model accuracy.

In scenarios where Feature Rescaling (FR) was removed, the Fed-FR-MVD framework could not be evaluated under noise-free conditions. However, as noise levels increased, the Precision@10, Recall@10, MRR@10, Coverage@10, AUC declined more sharply compared to the original Fed-FR-MVD. With 15% noise, the Fed-FR-MVD without FR experienced more significant drops, with Precision@10, Recall@10, HR@10, NDCG@10, F1-Score@10, MRR@10, Coverage@10, and AUC@10 falling to 0.400, 0.315, 0.505, 0.555, 0.355, 0.405, 0.700, and 0.750, respectively. Under the 15% noise condition, comparing Precision@10 and Recall@10 with and without feature rescaling, the metrics are 0.400 and 0.315 versus 0.430 and 0.335, respectively. This further confirms that feature rescaling significantly contributes to noise suppression.

Considering noise levels of 5%, 10%, and 15%, the convergence curves for six metrics (Precision@10, Recall@10, HR@10, NDCG@10, F1-Score@10, and MRR@10) for the standard Fed-FR-MVD framework and the Fed-FR-MVD framework without feature rescaling are shown in Fig. 7. The standard Fed-FR-MVD framework, even with increasing noise levels, demonstrates minimal degradation in evaluation metrics, reflecting relatively high overall stability and effective noise suppression. In contrast, the Fed-FR-MVD framework without feature rescaling exhibits significant performance degradation across different noise levels.

Fig. 7

Performance evaluation of recommendation models built using the Fed-FR-MVD framework under varying noise levels of 5%, 10%, and 15%. This figure aims to demonstrate the resilience of the standard Fed-FR-MVD framework against increasing noise, as evidenced by its minimal degradation across six key metrics—Precision@10, Recall@10, HR@10, NDCG@10, F1-Score@10, and MRR@10—indicating robust noise suppression and stability. In contrast, the significant performance decline observed in the Fed-FR-MVD framework without feature rescaling highlights the critical importance of feature normalization in maintaining model performance under challenging conditions.

Figure 7 presents a detailed evaluation of the Fed-FR-MVD framework’s performance under different noise levels, assessed across six metrics: Precision@10, Recall@10, HR@10, NDCG@10, F1-Score@10, and MRR@10. Each subplot in Fig. 7 shows the convergence trends over 300 training epochs, comparing the performance of the standard Fed-FR-MVD framework (with feature rescaling) to the Fed-FR-MVD framework without feature rescaling. Noise levels are introduced at 5%, 10%, and 15%, with the “Normal” and “DFR” (Dynamic Feature Rescaling) labels representing the two configurations.

In Fig. 7a, which illustrates Precision@10, the standard Fed-FR-MVD framework (green and red curves) maintains higher precision scores than the version without feature rescaling (blue curves), even as noise levels increase. The precision in the standard framework declines only slightly from 5 to 15% noise, whereas the non-rescaling version experiences a more substantial drop, especially at 10% and 15% noise. This trend suggests that feature rescaling is crucial for preserving precision in noisy conditions.

For Recall@10 (Fig. 7b), the standard Fed-FR-MVD framework consistently achieves better recall across all noise levels compared to the framework without rescaling. The noise suppression effect of feature rescaling is evident, as the standard framework reaches higher recall values than the DFR model without rescaling, even at higher noise levels. This indicates that feature rescaling benefits not only precision but also recall when noise is present.

The Hit Rate metric (HR@10, Fig. 7c) exhibits similar trends, with the standard Fed-FR-MVD framework demonstrating superior stability and noise tolerance. The DFR configuration without feature rescaling (dashed blue lines) shows slower convergence and a marked decrease in HR@10 as noise levels increase, highlighting the role of feature rescaling in maintaining model accuracy.

In Fig. 7d, showing NDCG@10, the standard Fed-FR-MVD framework with rescaling consistently outperforms the non-rescaling version across all training epochs. The gap between the two configurations widens as noise levels increase, underscoring the importance of feature rescaling in helping the model rank items accurately in noisy conditions.

The F1-Score@10 (Fig. 7e), which reflects a balance of precision and recall, further reinforces the benefits of feature rescaling. The standard framework achieves higher F1 scores across all noise levels, while the DFR model without rescaling shows a significant drop in performance, especially at 10% noise and above. This finding suggests that feature rescaling helps the model maintain a strong balance between precision and recall even in the presence of noise.

Finally, Fig. 7f, which presents Mean Reciprocal Rank (MRR@10), shows that the standard Fed-FR-MVD framework with feature rescaling sustains high performance with minimal degradation as noise levels increase. Conversely, the non-rescaled DFR configuration’s performance drops noticeably, emphasizing the importance of feature rescaling for handling noisy data.

In summary, Fig. 7 demonstrates that the standard Fed-FR-MVD framework with feature rescaling consistently outperforms the configuration without rescaling across all metrics, particularly as noise levels rise. This analysis underscores the effectiveness of feature rescaling in enhancing noise robustness, allowing the model to achieve better performance and stability across training epochs, even under challenging conditions.

Conclusion

We have proposed a federated multi-view framework with a feature rescaling strategy for e-commerce recommendations. This framework utilizes item feature views and multiple user feature views to establish multi-feature views from client devices to the central server. It further enhances feature extraction efficiency through feature rescaling based on a deep semantic model. The framework refines the interdependencies between item and user data feature channels, thereby improving the network’s ability to represent features and its noise suppression capability.

Through a comparative analysis with other recommendation models, we have comprehensively evaluated the performance of the proposed Fed-FR-MVD in recommendation systems. The experimental results show that Fed-FR-MVD outperforms traditional single-view methods across all performance metrics, demonstrating the advantages of multi-view integration in handling complex recommendation tasks. Additionally, the framework exhibits significant noise suppression capabilities in tests with varying noise levels and ablation experiments of the feature rescaling mechanism, indicating its effectiveness in reducing the influence that noise has on the accuracy of the system. Overall, Fed-FR-MVD significantly enhances recommendation system performance, and its advantages in noise suppression and robustness make it highly effective in a federated learning environment.

Looking ahead, future research could explore several avenues to further enhance the framework. One potential direction is the incorporation of advanced privacy-preserving techniques to ensure even greater data security while maintaining high recommendation accuracy. Additionally, researchers might investigate the application of the Fed-FR-MVD framework in other domains, such as healthcare or finance, where data privacy and feature heterogeneity are critical. Exploring adaptive feature rescaling mechanisms that learn from user interactions over time could also be beneficial, potentially improving the model’s responsiveness to changing user preferences. By aligning future studies with these emerging trends and practical needs, we can continue to advance the field of federated learning in recommendation systems and ensure their relevance in diverse applications.