Role of topological indices in predictive modeling and ranking of drugs treating eye disorders

Abstract

Topological indices (TIs) of chemical graphs of drugs hold the potential to compute important properties and biological activities leading to more thoughtful drug design. Here, we considered certain drugs treating eye-related disorders, including cataract, glaucoma, diabetic retinopathy, and macular degeneration. By combining modeling and decision-makings approaches, this study presents a cost-effective way to comprehend the behavior of molecules. First, the topological indices of chemical graphs of molecules are determined, which provides valuable insights into their behavior. These models are first trained using known data and are also validated by the dataset of known properties. Models for quantitative structure property relations (QSPR) are computed using the quadratic regression method. TIs having correlation value greater than 0.7 with properties like molar weight, index of refraction, molar volume, polarizability, and molar refraction are taken in this work. Weights are assigned to different properties of drugs depending upon the correlation of the properties with topological indices. Furthermore, we used the multiple-choice decision-making techniques TOPSIS and SAW, to rank the drugs treating eye disorders to create well-informed selections. We can precisely forecast the behavior of chemicals by utilizing machine learning to analyze large amounts of data. This method may contribute to the discovery of new relevant drugs with desirable properties and helpful in comprehending the effects of chemicals on their efficacy.

Introduction

The term eye disease refers to a wide range of disorders that can impact the condition and functionality of the eyes, from minor to severe and perhaps building¹. Cataracts is a frequent eye illness that causes impaired vision problems. Surgically removing the clouded lens and replacing it with an artificial one is the usual course of treatment². Glaucoma is another common eye illness. It is a set of disorders that harm the optic nerve and are frequently brought on by elevated intraocular pressure. Blurred vision, eye discomfort, tunnel vision, and progressive loss of peripheral vision are some signs of glaucoma³. To lower intraocular pressure and stop more optic nerve damage, glaucoma patients may be treated with laser treatment, oral or eye drops, or surgery⁴. An eye disorder that is frequent in the elderly is macular degeneration, which is characterized by the destruction of the macular and loss of central vision. Macular degeneration symptoms include dark or blank spots in vision, difficulty in reading, and a distorted or uncertain center⁵. To delay the course of the illness and maintain residual vision, treatment options for macular degeneration include photodynamic therapy, anti-VEGF injections, or laser surgery. One typical consequence of diabetes that damages the blood vessels in the retina is diabetic retinopathy. The American Optometric Association (2021) lists blurred vision, floaters and black patches in the eyesight, and vision loss as possible symptoms⁶. Pink eye, sometimes referred to as conjunctivitis, is an inflammation of the conjunctiva, the thin, transparent membrane that covers the inner surface of the eyelids and the white portion of the eye⁷. Conjunctivitis symptoms include crusting of the eyelids, redness, itching, watering, and discharge⁸. The therapy for conjunctivitis varies based on its etiology; antibiotic eye drops are usually used for bacterial conjunctivitis, whereas antihistamine eye drops and cold compresses are used for allergic conjunctivitis⁹.

Euler first introduced graph theory in 1736, and it is a field of discrete mathematics. It has been investigated in several fields, including physics, biology, computer science, and chemistry¹⁰. Chemical graph theory blends mathematical modeling with graph theory. It focuses on topological indices that are strongly connected with the features of molecules or chemical compounds. In quantitative structure–property/structure–activity relationship (QSPR/QSAR) modeling, topological indices are commonly employed to predict a molecule’s physicochemical and bioactivity attributes¹¹. The topological index is an accurate description of a molecule’s or chemical compounds’ topological structure¹². The first known topological index was the Wiener index in 1947, which was used to determine the physical characteristics of petroleum¹³.

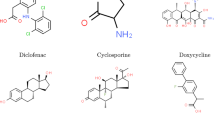
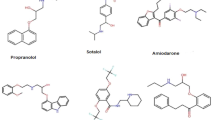
The molecular graph comprises unsaturated hydrocarbon skeletons from molecules and molecular compounds. The vertices of the molecular graph represent non-hydrogen atoms, and their set is specified by $V\left( G \right)$. The edges of a molecular graph represent covalent links between the respective atoms, and their set is specified by $E\left( G \right)$¹⁴.

Among the primitive indices created by Trinajstic and Gutman¹⁵ are the first and second Zagreb indices, which are described as

$$\begin{aligned} M_{1} \left( G \right) & = \mathop \sum \limits_{uv \in E} \left[ {d_{u} + d_{v} } \right], \\ M_{2} \left( G \right) & = \mathop \sum \limits_{uv \in E} \left[ {d_{u} d_{v} } \right]. \\ \end{aligned}$$

Estrada and colleagues¹⁶ introduced an additional topological metric known as the atom-bond connectivity index, which may be represented by the subsequent relationship.

$$ABC\left( G \right) = \mathop \sum \limits_{uv \in E} \sqrt {\frac{{d_{u} + d_{v} - 2}}{{d_{u} d_{v} }}} .$$

The definition of the Hyper Zagreb index $HM\left( G \right)$¹⁷ is as follows:

$$HM\left( G \right) = \mathop \sum \limits_{uv \in E\left( G \right)} \left( {d_{u} + d_{v} } \right)^{2} .$$

Ranjini et al. redefined the Zagreb indices¹⁸. The updated second Zagreb indices for a graph G are shown as.

$$ReZG_{2} \left( G \right) = \mathop \sum \limits_{uv \in E\left( G \right)} \frac{d\left( u \right)d\left( v \right)}{{d\left( u \right) + d\left( v \right)}}.$$

The definition of Max–min rodeg index $mMsde\left( G \right)$¹⁹ is

$$mMsde\left( G \right) = \mathop \sum \limits_{uv \in E} \sqrt {\frac{{{\text{max}}\{ d_{u} , d_{v} \} }}{{min\{ d_{u} ,d_{v} \} }}} .$$

Using edge partitioning, these indices are calculated for the medications listed in Fig. 1. We calculate the topological indices by counting the edges whose end vertices are of the same degree type $\left( {d_{u} ,d_{v} } \right).$

Fig. 1

Molecular structure of (a) Acetazolamide, (b) Acetylcysteine, (c) Aciclovir, (d) Tropicamide, (e) Xylometazoline, (f) Apraclonidine, (g) Brinzolamide, (h) Bromfenac, (i) Carteolol, (j) Cyclopentolate, (k) Lodoxamide, (l) Ganciclovir.

Material and methods

Chemists and pharmacists employ drug-related data to create new drugs, such as melting point, boiling point, molar refractivity, flash point, and complexity, using specific methods including QSPR, QSAR, and QSTR^{20,21,22,23,24}. QSPR analysis offers a methodical approach to comprehending the features of drugs that enhance their ability to target particular aspects of the illness. Both the targeted qualities and the drug’s features are taken into consideration when choosing which medications to use for quantitative structure–property relationship (QSPR) analysis using topological indices. A major factor in choosing a certain medicine is the availability of a data collection of chemicals or pharmaceuticals that includes both property values and structural information, which is needed to calculate topological indices. The medicinal molecule must have atomic connectivity and a well-defined chemical structure. This paper discusses the QSPR analysis of medications using topological indices for the treatment of eye disease. Using quadratic regression, we demonstrate the strong correlation between the physical qualities of reputable medications and features derived from relevant topological indices. In this study, the physiochemical characteristics of several pharmacological compounds are investigated, including molecular weight, complexity, density, melting point, and boiling point. Table 1 shows the values obtained from the mathematical expressions of the above-discussed topological indices.

Table 1 The values of the topological indices for the molecular structure of the drugs.

Regression modeling and quantitative structure analysis

The regression model (RM) for pharmaceuticals is assessed using the following equation:

$$P = A + B\left( {TI} \right)$$

‘’$P$’’ denotes the attribute of the provided medication. The TI is an independent variable, with $A$ representing a constant and $B$ representing the regression coefficient. We’re using a program called SPSS to do our calculations. With it, we’re looking at 12 different measurements related to medicines for eye diseases. We’re using a type of math called linear QSPR to understand how these measurements are connected. It’s like figuring out a big puzzle. We’re trying to find which medicines might work best for treating eye diseases by looking at their molecular structures. This study looks at twelve specific measurements to see how they relate to things like how big a molecule is, how it reacts to heat, and other properties.

Property values are computed using ChemSpider. Table 2shows the physicochemical properties of the potential drugs to be used in the treatment of eye disease. The most appropriate model to assess and use for the investigation is the linear regression model. For further information, we recommend that readers peruse the following articles^25,26,27,28. Previous research on the anti-cancer, blood cancer, and QSPR examinations of different topological indices for different chemical structures^29,30 served as inspiration for us to work on the current study challenge. This work aims to investigate the potential of TIs for imitating QSPR properties and the therapeutic management of eye disease treatment regimens.

$$P = A + B\left( {TI} \right) + C\left( {TI} \right)^{2}$$

Table 2 The physicochemical characteristics of potential drug candidates.

The quadratic equation linking the predictor variable TI to the response variable P offers more flexibility. We’re employing SPSS to apply quadratic regression to topological indices and properties identified by ChemSpider. This method allows us to explore how these indices relate to the properties of chemical compounds. By analyzing the results, we aim to determine which combinations demonstrate the strongest correlation. This approach enables us to uncover potential patterns or relationships between the topological indices and the chemical properties. Ultimately, it helps us better understand how these indices can be utilized to predict or explain various chemical characteristics. Tables 3, 4, 5, 6 and 7 show the statistical parameters for the quadratic QSPR model for topological indices. Table 8 shows the correlation coefficient obtained by the quadratic regression of different properties with topological indices computed from SPSS software. The graphs of the quadratic curve fitting are given in Fig. 2. Figure 3 shows the Comparison of the ranks of Multi-Criteria Decision Making Methods (SAW and TOPSIS).

Table 3 Statistical parameters for the quadratic QSPR model of topological index $mMsde$ (G).

Table 4 Statistical parameters for the quadratic QSPR model of topological index $HM(G)$.

Table 5 Statistical parameters for the quadratic QSPR model of topological index $ReZ{G}_{2}(G)$.

Table 6 Statistical parameters for the quadratic QSPR model of topological index ${M}_{1}\left(G\right)$.

Table 7 Statistical parameters for the quadratic QSPR model of topological index ${M}_{2}(G)$.

Table 8 Correlation coefficient of different properties with topological indices.

Fig. 2

Graphs of quadratic regression equations for the best physicochemical properties estimated by degree-based topological indices.

Fig. 3

Comparison of the ranks of Multi-criteria decision making methods (SAW and TOPSIS).

The topological indices we selected ($mMsde$ (G), $HM\left(G\right), ReZ{G}_{2}\left(G\right), {M}_{1}\left(G\right)$ and ${M}_{2}\left(G\right) )$ were chosen because they provided the best correlations when we applied the Quadratic Regression model using SPSS. This model was applied to examine the relationship between these topological indices and the physicochemical properties of the potential drugs used for treating eye diseases.

In summary, these topological indices were not chosen randomly but based on their strong correlation with drug properties, as confirmed through the SPSS analysis. This approach allowed us to rank the drugs more effectively and make well-informed decisions about their potential use in treating eye diseases.

The Quadratic Regression model between various physicochemical properties of the potential drugs and Topological indices against Eye disease computed from SPSS software are discussed below:

Regression models for ${\varvec{m}}{\varvec{M}}{\varvec{s}}{\varvec{d}}{\varvec{e}}$ (G)

$$\begin{aligned} & {\text{Index}}\;{\text{of}}\;{\text{Refraction}} = 0.{465} + 0.{123}\left( {mMsde} \right) - 0.00{3}\left( {mMsde} \right)^{2} \\ & {\text{Molar}}\;{\text{weight}} = {4}0.{783} + {8}.{771}\left( {mMsde} \right) + 0.0{45}\left( {mMsde} \right)^{2} \\ & {\text{Polarizability}} = {7}.{496} + 0.{2}0{7}\left( {mMsde} \right) + 0.0{26}\left( {mMsde} \right)^{2} \\ & {\text{Molar}}\;{\text{Volume}} = {266}.{837} - {21}.{227}\left( {mMsde} \right) + 0.{746}\left( {mMsde} \right)^{2} \\ & {\text{Molar}}\;{\text{Refraction}} = {19}.{184} + 0.{489} + 0.0{66}\left( {mMsde} \right)^{2} \\ \end{aligned}$$

Regression models for ${\varvec{H}}{\varvec{M}}({\varvec{G}})$

$$\begin{aligned} & {\text{Index}}\;{\text{of}}\;{\text{Refraction}} = 0.972 + 0.004(HM) + - 5.934E - 6(HM)^{2} \\ & {\text{Molar}}\;{\text{weight}} = 121.090 + 0.176(HM) + 0.000(HM)^{2} \\ & {\text{Polarizability}} = 14.864 - 0.019(HM) + 0.000(HM)^{{2}} \\ & {\text{Molar}}\;{\text{Volume}} = 224.928 - 0.916(HM) + 0.002(HM)^{2} \\ & {\text{Molar}}\;{\text{Refraction}} = 37.708 - 0.050(HM) + 0.000(HM)^{2} \\ \end{aligned}$$

Regression models for ${\varvec{R}}{\varvec{e}}{\varvec{Z}}{{\varvec{G}}}_{2}({\varvec{G}})$

$$\begin{aligned} & {\text{Index}}\;{\text{of}}\;{\text{Refraction}} = 0.770 + 0.120(ReZG_{2} ) - 0.004(ReZG_{2} )^{2} \\ & {\text{Molar}}\;{\text{weight}} = 118.816 + 4.235(ReZG_{2} ) + 0.155(ReZG_{2} )^{2} \\ & {\text{Polarizability}} = 22.563 - 1.462(ReZG_{2} ) + 0.079(ReZG_{2} )^{2} \\ & {\text{Molar}}\;{\text{Volume}} = 322.410 - 333.016(ReZG_{2} ) + 1.250(ReZG_{2} )^{2} \\ & {\text{Molar}}\;{\text{Refraction}} = 57.014 - 33.704(ReZG_{2} ) + 0.200(ReZG_{2} )^{2} \\ \end{aligned}$$

Regression Models for ${{\varvec{M}}}_{1}({\varvec{G}})$

$$\begin{aligned} & {\text{Index}}\;{\text{of}}\;{\text{Refraction}} = 0.700 + 0.029(M_{1} ) + 0.000(M_{1} )^{2} \\ & {\text{Molar}}\;{\text{weight}} = 125.265 + 0.549(M_{1} ) + 0.012(M_{1} )^{2} \\ & {\text{Polarizability}} = 21.209 - 0.307(M_{1} ) + 0.004(M_{1} )^{2} \\ & {\text{Molar}}\;{\text{Volume}} = 3325.41 - 7.650(M_{1} ) + 0.0676(M_{1} )^{2} \\ & {\text{Molar}}\;{\text{Refraction}} = 53.674 - 0.780(M_{1} ) + 0.010(M_{1} )^{2} \\ \end{aligned}$$

Regression models for ${{\varvec{M}}}_{2}({\varvec{G}})$

$$\begin{aligned} & {\text{Index}}\;{\text{of}}\;{\text{Refraction}} = 0.898 + 0.021(M_{2} ) + 0.000(M_{2} )^{2} \\ & {\text{Molar}}\;{\text{weight}} = 146.710 + 0.118(M_{2} ) + 0.011(M_{2} )^{2} \\ & {\text{Polarizability}} = 20.863 - 0.249(M_{2} ) + 0.003(M_{2} )^{2} \\ & {\text{Molar}}\;{\text{Volume}} = 283.903 - 5.695(M_{2} ) + 0.045(M_{2} )^{2} \\ & {\text{Molar}}\;{\text{Refraction}} = 52.821 - 0.635(M_{2} ) + 0.007(M_{2} )^{2} \\ \end{aligned}$$

Multi-criteria decision analysis of drugs

Multi Criteria Decision Making is the process of structuring and solving decision and planning issues that involve numerous criteria. When there is no one best solution for an issue, decision makers often rely on their desire to discriminate between options³¹. Solving a problem might be recognized differently. Choosing the “best” choice from a group of alternatives can refer to the decision maker’s favored alternative. Another definition of “solving” involves selecting a limited number of feasible alternatives or categorizing them based on preferences. The extreme interpretation is used to identify all “efficient” or "non-dominated" alternatives.

This section applies degree-based topological indices to the medicinal compounds used in the treatment of eye disease. The above-described topological indices are subjected to QSPR analysis, and the results demonstrate a strong correlation between these topological indices and the chemical and physical characteristics of several popular medications used to treat eye disease. This research looks at a few significant pharmaceuticals that are used to treat eye disease and its symptoms, including Acetazolamide, Acetyl cysteine, Aciclovir, Antazoline, Xylometazoline, Apraclonidine, Brinzolamide, Bromfenac, Cartelol, Cyclopentolate, Lodoxamide, and Ganciclovir. These medications can be used to treat a variety of illnesses, from systemic problems like viral infections to addressing ocular disorders including glaucoma, conjunctivitis, and cataracts. Because they have unique methods of action and potential negative consequences, it is imperative that you take them under appropriate medical care and prescription.

Figure 1 displays the molecular structures of several medications. These structures may be thought of as graphs, with the bonds connecting the atoms serving as the graph’s edges and the atoms acting as its vertices.

This research aims to provide a behavioral analysis of the chemical structures of therapeutic compounds for eye diseases utilizing many topological indices, including the atom-bond connectivity index, the Hyper Zagreb index $HM\left( G \right)$, and the first and second Zagreb indices. In this research attempt, we will also provide a weighted assessment of many topological indices. Chemical invariants are intended to give scientists and analysts a more cost-effective and efficient way to ascertain the physical and chemical characteristics of eye disease drugs. This weighted evaluation will be conducted using two distinct decision-making methodologies. The first method will be called Approach for Order Preference by Similarity to Ideal Solution (TOPSIS). The optimal solution and the option that is farthest from the worst will both be subject to this weighted examination. It also attempts to evaluate the precision of molecular compound specifications by mathematical means. The 1980s saw the introduction of this multi-criteria decision-making technique (MCDM).

We used the entropy method to determine the weights for each topological index. This method is popular in decision-making because it helps assign weights based on how much the data varies. In simple terms, the entropy method looks at how much each criterion (or topological index) differs among the different drugs we studied. By using this objective, data-driven approach, we make sure that the weights accurately represent how important each index is for predicting the properties of the drugs. This way, we avoid relying on personal opinions.

i. Weight allocation: Weights indicate the proportion of a drug structure that has to be considered. A drug structure that has a wide range of chemical and physical characteristics is advantageous. In such cases, we give them a lot more weight than the others, and as a result, so do the others (see Fig. 1). The weight is distributed using the following formula:

$$\mathop \sum \limits_{i = 1}^{j} w_{j}^{*} = 1$$

ii. The impact of a medicine is its ability to have either good or negative effects. For our medication structure, for instance, which physiochemical property is the ideal worst and which is the ideal best. One should consider the data values for a given factor to be standard units.

iii. Ideal best and ideal worst: To ascertain the ideal best and ideal worst, we must first address the features of the drug structure in question. Next, we must associate the aforementioned traits with the physical properties of each drug. A drug structure’s molecular weight, density, complexity, melting point, and boiling point are its five common characteristics. An essential component of pharmaceuticals, whether they be tablets or powders, is their solid density. We may use it to ascertain whether substances will float or sink in a liquid. The material will flow if its density is lower than that of the liquid it is submerged in³². Therefore, for our pharmacological structure, low density is ideal. In chemical and biological chemistry as well as medicinal science, the melting point is a key physical property that characterizes the transition. Lower-melting materials are more likely to be observed than higher melting point ones. Molecular weight is another essential feature employed in the pharmaceutical industry. When the polymer’s molecular weight decreased, its degree of crystallinity increased³³. We utilize low molecular weight medications because drug structures have a molecular weight less than 1000 g/mol. One of a medicine’s most crucial properties is its boiling point³⁴. It functions as both a transport and a container for storage. If our drug has a higher boiling point, we will have extra storage space. The complexity of medication therapy is acknowledged as a risk factor for disengagement and administration issues, which increase medical expenses³⁵.

In Table 12, the weights assigned to the properties (Index of Refraction, Molar Weight, Polarizability, Molar Volume, and Molar Refraction) were determined using the entropy method, which is a widely accepted data-driven technique. The logic behind the weight allocation is based on how much each property varies across the different drugs. Properties with greater variation provide more valuable information in distinguishing between the drugs, and thus receive higher weights. For instance, Index of Refraction and Polarizability are likely to receive higher weights because they play a crucial role in predicting drug performance. A higher refractive index and greater polarizability can enhance a drug’s interaction with light and other molecules, making these properties essential for certain treatments, such as those involving light-based therapies. On the other hand, properties like Molar Weight and Molar Volume might receive lower weights if their variation among the drugs is smaller. Although these properties are important for absorption, distribution, and formulation, if their values are similar across the drugs, they provide less distinction and are thus considered less significant for this particular analysis. Molar Refraction, which is linked to both refractive index and polarizability, is weighted according to how much it varies and contributes to drug behavior. By using the entropy method, we ensured that the weight distribution was objective and aligned with the importance of each property in distinguishing between the drugs, without relying on subjective judgment.

Ranking the drugs using TOPSIS

Let’s say that every property is assessed separately. Compromises can be evaluated by comparing their degree of similarity to ideal alternative³⁶. Table 9 provides n properties (atom-bond connectivity index, the Hyper Zagreb index $HM\left( G \right)$, and the first and second Zagreb indices) along with m possibilities (drug structure). To determine the optimal choice and achieve a balance between the qualities, we try to assign the right weights to the attributes³⁷.

Table 9 Attributes (topological indices) and alternatives (drugs).

Step 1: Create an assessment matrix with n criteria and m options. The intersection of each criterion and alternative should be shown as $r_{ij}$, and we have a matrix like $\left( {r_{ij} } \right)$ m$\times n$ in Table 9.

Step 2: The $\left( {r_{ij} } \right)m \times n$ matrix is then standardized to create the matrix. $N = \left( {n_{ij} } \right)m \times n$, by using the normalized matrix (Table 10);

$$n_{ij} = r_{ij} /\sqrt {\mathop \sum \limits_{k = 1}^{m} r_{kj}^{2} } , \forall i = 1,2,3, \ldots ,m \& j = 1,2,3, \ldots ,n$$

Table 10 Decision matrix.

Step 3: Compute the weighted normalized decision matrix $Y_{ij}$(Table 11). The weight is distributed (Table 12) using the following formula,

$$\mathop \sum \limits_{i = 1}^{j} w_{j}^{*} = 1$$

Table 11 Weighted Normalized Decision Matrix.

Table 12 Weight allocation to topological indices.

The weighted normalized value is $y_{ij} = w_{j}^{*} .n_{ij} \forall j = 1,2,3, \ldots ,n ,$ where $\mathop \sum \limits_{i = 1}^{j} w_{j}^{*} = 1$.

Step 4: Ascertain the ideal negative and positive solutions (Table 13). Finding the difference between an alternative and the ideal one, which is described as

$$\begin{aligned} & P^{ + } = \left\{ {y_{i}^{ + } , \ldots ,y_{j}^{ + } } \right\} = \left( {\max \left( {or {\text{min}}} \right) Y_{ij} \backslash j \in J} \right) \\ & P^{ - } = \left\{ {y_{i}^{ - } , \ldots ,y_{j}^{ - } } \right\} = \left( {\max \left( {or min} \right) Y_{ij} \backslash j \in J} \right) \\ \end{aligned}$$

Table 13 Calculation of the positive ideal solution and negative ideal solution.

Step 5: Use Table n-dimensional Euclidean distance to get the separation measure (Table 14). The ideal answer is distinguished from each alternative by

$$\begin{aligned} L_{i}^{ + } & = \sqrt {\mathop \sum \limits_{j = 1}^{n} \left( {Y_{ij} - P_{j}^{ + } } \right)} \\ L_{i}^{ - } & = \sqrt {\mathop \sum \limits_{j = 1}^{n} \left( {Y_{ij} - P_{j}^{ - } } \right)} \\ \end{aligned}$$

Table 14 Rank of the drugs via TOPSIS.

Step 6: Determine how near the ideal answer you are (Table 14). The definition of $B_{i}$ relative proximity to B is $O_{i}{\prime} = \frac{{L_{i}^{ - } }}{{L_{i}^{ + } + L_{i}^{ - } }}$, where $0 < O_{i}{\prime} < 1$,$i = 1,2,3, \ldots ,n.$

It is clear that $O_{i}{\prime} = 1 if P_{i} = P^{ + }$ and $O_{i}{\prime} = 0 if P_{i} = P^{ - }$.

Step 7: Rank the references in decreasing order according to $O_{i}{\prime}$ (Table14).

In our study, the criteria for defining ideal best and ideal worst choices are based on specific properties that influence drug effectiveness. The ideal best choices include a higher Index of Refraction, Polarizability, and Molar Refraction. A higher index of refraction indicates that the drug can bend light effectively, which is crucial for therapies involving light interaction. Similarly, higher polarizability signifies better interaction with other molecules, enhancing the biological activity of the drug, while higher molar refraction suggests stronger engagement with biological targets. Conversely, the ideal worst choices focus on lower values of Molar Weight and Molar Volume. A lower molar weight promotes better absorption and distribution within the body, thereby increasing the drug’s effectiveness, while lower molar volume implies a more compact molecular structure that can facilitate easier formulation and administration. This classification helps determine whether properties are beneficial or non-beneficial in terms of drug performance. Beneficial properties are characterized by higher values that contribute positively to effectiveness, thus receiving higher weights in our decision-making process. In contrast, non-beneficial properties are those where lower values are preferred, indicating their potential hindrance to drug performance, leading to their assignment of lower weights. By applying these criteria systematically, we ensure that our evaluations reflect the desired characteristics of effective drugs, thereby enhancing the decision-making process in selecting the most promising drug candidates for treating eye diseases.

Ranking the drugs using SAW

The simple additive weighting approach (SAW), often referred to as the weighted linear combination or scoring method, is a multi-criteria decision-making (MCDM) or multi-criteria decision analysis method³⁸. The weighted average is used to compose this approach. The SAW approach is used to obtain the weighted sum of the performance ratings for each choice among all criteria³⁹. Difference alternatives (drug structure) and qualities (augmented Zagreb index, forgotten topological index, and Randic index) exist. The phases in the compromise ranking algorithm of the SAW approach are as follows:

Step 1: Create the m alternatives and n attributes in (Table 15) into a decision matrix $\left( {j_{ij} } \right)m \times n$ and ascertain which attribute’s best and worst values are.

Table 15 Attributes (topological indices) and Alternatives (drugs).

Step 2: Compute the weights using the weighted criteria that were previously specified. Additionally, create a normalized decision matrix (Table 16) by using the given formulas;

$$\begin{aligned} n_{ij} & = \frac{{j_{ij} }}{{{\text{max}}\left( {j_{ij} } \right)}} \\ n_{ij} & = \frac{{{\text{min}}\left( {j_{ij} } \right)}}{{\left( {j_{ij} } \right)}} \\ \end{aligned}$$

where $i = 1,2,3, \ldots ,m \& j = 1,2,3, \ldots ,n$. Also construct a weight normalized decision matrix (Table 17).

Table 16 Normalized decision matrix.

Table 17 Weighted normalized decision matrix.

Step 3: Evaluate each alternative using the following formula (Table 18):

$$G_{i} = \mathop \sum \limits_{j = 1}^{n} w_{j}{\prime} n_{ij}$$

where $w_{j}{\prime}$ is the weighted criterion of the attributes and $n_{ij}$ is the alternative’s score in relation to the attribute.

Table 18 Ranks of drugs using SAW method.

The practical applications of our research are significant in the field of drug design, particularly for treating eye diseases. By using topological indices and decision-making models like TOPSIS and SAW, we can predict important drug properties more accurately and efficiently. This can help pharmaceutical companies in the early stages of drug development to rank potential drug candidates and focus on the ones that are most likely to succeed in treating eye disorders. Additionally, this method can save time and resources by reducing the need for extensive experimental testing. Instead of testing each drug extensively in the lab, researchers can use our model to predict how different drugs may behave, allowing for better drug selection and development. This approach can also be applied to other areas, such as environmental chemistry and material science.

Conclusion

This study presents a novel method to enhance quantitative structure–property relationship (QSPR) modeling in drug design by integrating multi-criteria decision-making with topological index analysis. This article evaluates the generic formulas of additive degree-based topological descriptors for specific drugs related to address eye disorders. Correlation of the topological indices with important physiochemical properties is computed. We used quadratic curve fitting method to the data of properties of drugs and indices. Correlation coefficient $r$ gives estimate of the best fitting of data along the quadratic curve. Value of $r$ closer to 1 gives best correlation and estimation of property from the topological index. Quantitative structural property relations are built using these correlation values which are helpful in predicting the properties of drugs. Our findings indicate that quadratic model of Max–min rodeg index gives best estimate of molar weight, while first Zagreb index outperformed other TIs in providing best estimates of index of refraction, molar volume, molar refractivity and polarizability of drugs. Then, MCDM approaches are employed to rank the drugs based on different criteria involving the correlation values of indices with properties. For validation, we used TOPSIS and SAW methods. Ranking obtained by two techniques agree to a good deal. The entropy approach is used for allocating weights to the specified criteria. The rankings of drug structures on the basis of favorable properties are depicted in Tables 14 and 18 by TOPSIS and SAW, respectively. Comparison of drug ranks is depicted in Fig. 3 according to both methods and it is observed that the rankings are in great agreement with each other. On the other hand, using SAW, we found a modest variation in drug behavior, as Tropicamide and Xylometazoline were rated oppositely.

Further research directions can be adopted by investigating distance based indices and cubic regression models and comparative analysis may enhance the predictive modeling strategy. However, there are certain limitations which may affect the outcomes, involving short dataset, availability.